Сравнить значения η и r и сделать вывод о возможности линейной связи между признаками Х и Y.

4.     Построить однофакторную линейную регрессионную модель связи признаков Х и Y, используя инструмент Регрессия надстройки Пакет анализа, и рассчитать доверительные интервалы коэффициентов уравнения линейной регрессии.

Построить теоретическую кривую регрессии.

Дать экономическую интерпретацию коэффициента регрессии.

Рассчитать коэффициент эластичности и дать его экономическую интерпретацию.

5.     Найти наиболее адекватное уравнение регрессии с помощью средств инструмента Мастер диаграмм.

II. Рабочий файл с результативными таблицами и графиками.

III. Выводы по результатам выполнения лабораторной работы.

Задача 1. Установление наличия стохастической связи между факторным признаком Х и результативным признаком Y:

а) графическим методом.

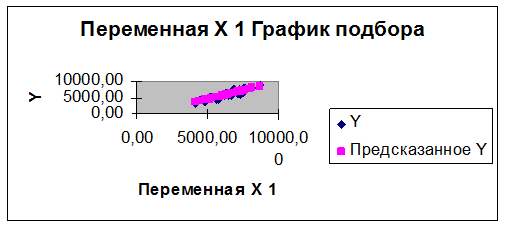
Вывод: На основе анализа диаграммы рассеяния из Лабораторной  работы №1, полученной после удаления аномальных значений, можно сделать вывод, что имеет место стохастическая связь. Предположительный вид связи: линейная прямая.

б) методом сопоставления параллельных рядов.

Вывод:  Табл.2.1, полученная путем ранжирования предприятий по возрастанию значения факторного признака Х, показывает, что с увеличением значений факторного признака увеличиваются (уменьшаются) значения результативного признака, за исключением некоторых отклонений, что позволяет сделать вывод о наличии  между факторным и результативным признаками стохастической связи. Предположительно связь имеет линейный прямой вид.

Задача 2. Установление наличия корреляционной связи между признаками Х и Y методом аналитической группировки.

Вывод:  Результаты выполнения аналитической группировки предприятий по факторному признаку Среднегодовая стоимость основных производственных фондов даны в табл. 2.2 Рабочего файла, которая показывает, что с увеличением

среднегодовой стоимости основных производственных фондов среднегодовой выпуск продукции также возрастает, следовательно, между исследуемыми признаками существует прямая корреляционная зависимость. Теснота этой связи может быть измерена как эмпирическим корреляционном отношением, так и на основе коэффициента корреляции признаков.

 Задача 3.Оценка тесноты связи признаков Х и Y:

а) на основе эмпирического корреляционного отношения

Для анализа тесноты связи между факторным и результативным признаками, рассчитывается показатель η - эмпирическое корреляционное отношение, задаваемое формулой

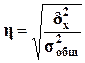
Для вычисления η необходимо знать общую диспе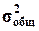рсию  и межгрупповую дисперсию 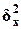 результативного признака Y - Выпуск продукции.

Результаты выполненных расчетов представляются табл. 2.4 Рабочего файла.

Вывод:  Величина η=0,959989 является близкой к единице, что свидетельствует об очень тесной связи между признаками, близкой к функциональной зависимости.

б) на основе линейного коэффициента корреляции признаков

В предположении, что связь между факторным и результативным признаком имеется, для определения тесноты связи на основе линейного коэффициента корреляции r был использован инструмент Корреляция надстройки Пакет анализа.

         Результатом работы инструмента Корреляции является табл. 2.5 Рабочего файла.

Вывод: Значение коэффициента корреляции r= 0,91318826 лежит в интервале от0.9 до 0.99, что в соответствии со шкалой Чэддока, говорит о весьма тесной связи между среднегодовой стоимостью основных производственных фондов и выпуском продукции.

Так как значение коэффициента корреляции r положительное, то связь между признаками прямая.

Посредством показателя η измеряется теснота связи любой формы, а с помощью коэффициента корреляции r – только прямолинейная, следовательно, значения η и r совпадают только при наличии прямолинейной связи. В теории статистики установлено, что если 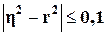, то гипотезу о прямолинейной связи можно считать подтвержденной.

Вывод: В работе гипотезу о прямолинейной связи  между изучаемыми признаками можно считать подтвержденной, поскольку 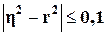,т.е. 0,087666001<0,1.

Задача 4. Построение однофакторной линейной регрессионной модели связи изучаемых признаков с помощью инструмента Регрессия надстройки Пакет анализа.

Построение регрессионной модели заключается в определении аналитического выражения связи между факторным признаком X и результативным признаком Y.

Инструмент Регрессия производит расчет параметров а₀ и а₁ уравнения однофакторной линейной регрессии 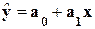 и проверка его адекватности исследуемым фактическим данным.

В результате работы инструмента Регрессия были получены результативные таблицы 2.6 – 2.9 Рабочего файла.

Вывод: Однофакторная линейная регрессионная модель связи факторного и результативного признаков имеет вид у=-1004,62048+1,089355181х. Коэффициент а1>0, следовательно, связь между рассматриваемыми признаками, как и ожидалось прямая.

Доверительные интервал коэффициентов уравнения регрессии представим в нижеследующей таблице

С увеличением надежности границы доверительных интервалов расширяются.

Экономическая интерпретация коэффициента регрессии а₁: Из нашего уравнения регрессии следует, что при увеличении среднегодовой стоимости основных производственных фондов на 1 тыс. руб. выпуск продукции увеличивается на 1,089 тыс. руб.

Коэффициент эластичности =6430/5999,93*1.089=1.16

Экономическая интерпретация коэффициента эластичности Э:  С повышением стоимости основных производственных фондов на 1% следует ожидать увеличение выпуска продукции на 1,16.

Задача 5. Нахождение наиболее адекватного уравнения регрессии с помощью средств инструмента Мастер диаграмм. Построение для этого уравнения теоретической линии регрессии.

Возможности инструмента Мастер диаграмм позволяют быстро производить построение и анализ адекватности регрессионных моделей, базирующихся на использовании различных видов зависимости между признаками X и Y.

Построение моделей осуществляется непосредственно на диаграмме рассеяния.

На диаграмме рассеяния отображается линия и уравнение регрессии, а также коэффициент детерминации R2.

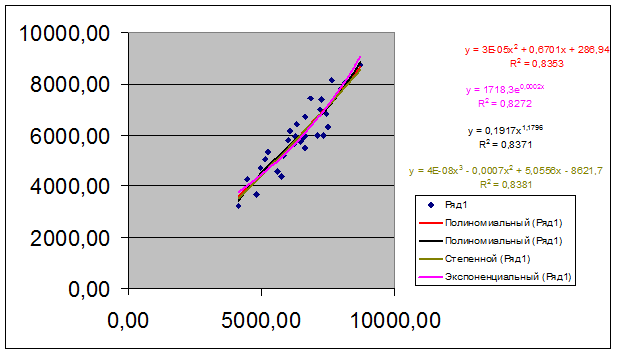
В лабораторной работе уравнения регрессии и их графики были построены для 5-ти видов зависимости между признаками и даны на диаграмме 2 Рабочего файла.

         Уравнения регрессии и соответствующие им коэффициент детерминации R2 даны в следующей таблице:

Регрессионные модели связи[1]

Выбор наиболее адекватного уравнения регрессии определяется максимальным значением коэффициента детерминации R2: чем ближе значение R2 к единице, тем более точно регрессионная модель соответствует фактическим данным

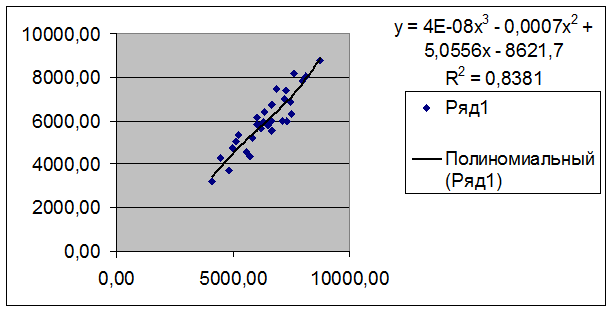
Вывод: Максимальное значение коэффициента детерминации R2 =0,8381

Вид искомого уравнения регрессии – У=4Е-0,8х³-0.0007х²+5.0556х-8621,7

Это уравнение регрессии и его график приведены на отдельной диаграмме рассеяния  диаграмма 3 Рабочего файла.

Вместе с тем, так как значения коэффициентов R2 кубического и линейного уравнения расходятся очень незначительно (на величину0.8381-0.8339=0.0042), а для показателей тесноты связи имеет место неравенство 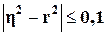, то в качестве адекватного уравнения регрессии может быть принято линейное уравнение -1004,62048+1,089355181х, совпадающее (не совпадающее) с найденным с помощью инструмента Регрессия надстройки Пакет анализа.

[1] Коэффициенты уравнений необходимо задавать не в компьютерном формате, а в общепринятой десятичной форме чисел.