ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
О Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы № 2
Автоматизированный
корреляционно-регрессионный анализ взаимосвязи статистических данных в среде MS
Excel
Вариант № _12___
Выполнил: студентка ФНО, 4поток
Поздеева Екатерина Викторовна
Проверил: Пампушина С. Н.
Архангельск
2008г.
1.
Постановка задачи статистического исследования
Корреляционно-регрессионный анализ взаимосвязи
признаков является составной частью проводимого статистического исследования
деятельности 30-ти предприятий и частично использует результаты ЛР-1.
В ЛР-2 изучается взаимосвязь между факторным признаком
Среднегодовая стоимость основных производственных фондов (признак Х) и результативным признаком Выпуск продукции (признак Y),
значениями которых являются исходные данные ЛР-1 после исключения из них
аномальных наблюдений.
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
5
|
620,00
|
490,00
|
|
23
|
669,00
|
651,00
|
|
27
|
725,00
|
560,00
|
|
1
|
746,00
|
721,00
|
|
8
|
774,00
|
770,00
|
|
32
|
788,00
|
812,00
|
|
22
|
844,00
|
693,00
|
|
19
|
865,00
|
665,00
|
|
2
|
879,00
|
791,00
|
|
3
|
907,00
|
882,00
|
|
13
|
914,00
|
938,00
|
|
26
|
935,00
|
861,00
|
|
9
|
949,00
|
903,00
|
|
4
|
956,00
|
980,00
|
|
28
|
977,00
|
875,00
|
|
17
|
984,00
|
896,00
|
|
6
|
1005,00
|
840,00
|
|
14
|
1005,00
|
1022,00
|
|
25
|
1005,00
|
910,00
|
|
7
|
1033,00
|
1134,00
|
|
30
|
1075,00
|
910,00
|
|
18
|
1089,00
|
1064,00
|
|
10
|
1096,00
|
1127,00
|
|
20
|
1103,00
|
910,00
|
|
24
|
1124,00
|
1043,00
|
|
29
|
1131,00
|
959,00
|
|
15
|
1152,00
|
1239,00
|
|
11
|
1201,00
|
1190,00
|
|
21
|
1229,00
|
1225,00
|
|
16
|
1320,00
|
1330,00
|
В процессе статистического
исследования необходимо решить ряд задач.
1. Установить наличие статистической
связи между факторным признаком Х
и результативным признаком Y
графическим методом.
2. Установить наличие корреляционной
связи между признаками Х и Y методом аналитической группировки.
3. Оценить тесноту связи признаков Х и
Y на основе эмпирического
корреляционного отношения η.
4. Построить однофакторную
линейную регрессионную модель связи признаков Х и Y, используя
инструмент Регрессия надстройки Пакет анализа, и оценить тесноту связи признаков Х и Y на основе линейного
коэффициента корреляции r.
5. Определить адекватность и
практическую пригодность построенной линейной регрессионной модели, оценив:
а) значимость и
доверительные интервалы коэффициентов а0,
а1;
б) индекс детерминации R2 и его значимость;
в) точность регрессионной
модели.
6. Дать экономическую
интерпретацию:
а) коэффициента регрессии а1;
б) коэффициента эластичности
КЭ;
в) остаточных величин εi.
7. Найти наиболее адекватное
нелинейное уравнение регрессии с помощью средств инструмента Мастер диаграмм.
Построить для этого уравнения теоретическую кривую регрессии.
2. Выводы по результатам
выполнения лабораторной работы[1]
Задача 1. Установление наличия статистической
связи между факторным признаком Х
и результативным признаком Y графическим методом.
Статистическая
связь является разновидностью стохастической (случайной) связи, при которой с
изменением факторного признака X закономерным образом изменяется
какой–либо из обобщающих статистических показателей распределения
результативного признака Y.
Вывод:
Точечный график
связи признаков (диаграмма
рассеяния, полученная в ЛР-1 после удаления аномальных наблюдений) позволяет
сделать вывод, что имеет место статистическая связь. Предположительный
вид связи – линейная прямая.
Задача 2. Установление наличия корреляционной
связи между признаками Х и Y методом аналитической группировки.
Корреляционная
связь – важнейший частный случай стохастической статистической связи, когда под
воздействием вариации факторного признака Х
закономерно
изменяются средние значения 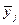 результативного
признака Y (усредняются значения
результативного
признака Y (усредняются значения 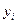 в каждой j-ой
группе, полученные под воздействием на Y фактора
в каждой j-ой
группе, полученные под воздействием на Y фактора 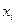 ). Для выявления наличия корреляционной связи используется
метод аналитической группировки.
). Для выявления наличия корреляционной связи используется
метод аналитической группировки.
Вывод:
Аналитическая группировка предприятий по факторному
признаку Среднегодовая стоимость основных
производственных фондов, построенная в табл. 2.2 Рабочего файла EXCEL,
показывает, что с увеличением значения факторного признака Х-стоимости ОПФ закономерно увеличивается среднее значение результативного признака Y-выпуска продукции. Следовательно, между признаками Х- стоимость ОПФ и Y-выпуск продукции существует корреляционная
связь.
Задача 3.Оценка тесноты связи признаков Х и
Y на основе эмпирического
корреляционного отношения.
Для анализа
тесноты связи между факторным и результативным признаками рассчитывается
показатель η – эмпирическое корреляционное отношение, задаваемое
формулой
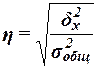 ,
,
где 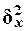 и
и 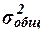 - соответственно
межгрупповая и общая дисперсии результативного признака Y - Выпуск продукции (индекс х дисперсии
- соответственно
межгрупповая и общая дисперсии результативного признака Y - Выпуск продукции (индекс х дисперсии 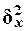 означает, что
оценивается мера влияния признака Х
на Y).
означает, что
оценивается мера влияния признака Х
на Y).
Для качественной оценки тесноты связи на основе
показателя эмпирического корреляционного отношения служит шкала Чэддока:
|
Значение η
|
0,1 – 0,3
|
0,3 – 0,5
|
0,5 – 0,7
|
0,7 – 0,9
|
0,9 – 0,99
|
|
Сила связи
|
Слабая
|
Умеренная
|
Заметная
|
Тесная
|
Весьма тесная
|
Результаты выполненных расчетов представлены в табл. 2.4 Рабочего
файла.
Вывод:
Значение коэффициента η =0,9,
что в соответствии с оценочной шкалой Чэддока говорит о весьма тесной степени
связи изучаемых признаков.
Задача 4. Построение однофакторной линейной регрессионной модели связи
изучаемых признаков с помощью инструмента Регрессия надстройки Пакет
анализа и оценка тесноты связи на
основе линейного коэффициента корреляции r.
4.1. Построение
регрессионной модели заключается в нахождении аналитического выражения связи
между факторным признаком X и результативным признаком Y.
Инструмент Регрессия на основе исходных данных (xi , yi), производит расчет параметров а0 и а1 уравнения однофакторной линейной регрессии 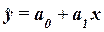 , а также вычисление ряда показателей, необходимых для
проверки адекватности построенного уравнения исходным (фактическим) данным.
, а также вычисление ряда показателей, необходимых для
проверки адекватности построенного уравнения исходным (фактическим) данным.
Примечание. В результате работы инструмента Регрессия получены четыре
результативные таблицы (начиная с заданной ячейки А75). Эти таблицы выводятся
в Рабочий файл без нумерации, поэтому необходимо присвоить им номера табл.2.5 –
табл.2.8 в соответствии с их порядком.
Вывод:
Рассчитанные в табл.2.7
(ячейки В91 и В92) коэффициенты а0
и а1 позволяют
построить линейную регрессионную модель связи изучаемых признаков в виде
уравнения 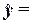 -143,64+1,09 х.
-143,64+1,09 х.
4.2. В случае линейности функции связи для оценки тесноты
связи признаков X и Y, устанавливаемой по
построенной модели, используется линейный коэффициент корреляции r.
Значение коэффициента
корреляции r приводится в табл.2.5 в ячейке В78 (термин "Множественный
R").
Вывод:
Значение коэффициента
корреляции r =0,91,
что в соответствии с оценочной шкалой Чэддока говорит о тесной степени связи
изучаемых признаков.
Задача 5. Анализ адекватности и практической пригодности построенной линейной
регрессионной модели.
Анализ
адекватности регрессионной модели преследует цель оценить, насколько
построенная теоретическая модель взаимосвязи признаков отражает фактическую
зависимость между этими признаками, и тем самым оценить практическую
пригодность синтезированной модели связи.
Оценка
соответствия построенной регрессионной модели исходным (фактическим) значениям
признаков X и Y
выполняется в 4 этапа:
1)
оценка
статистической значимости коэффициентов уравнения а0, а1
и определение их доверительных интервалов для заданного уровня надежности;
2)
определение
практической пригодности построенной модели на основе оценок линейного
коэффициента корреляции r и индекса детерминации R2;
3)
проверка
значимости уравнения регрессии в целом по F-критерию Фишера;
4) оценка
погрешности регрессионной модели.
5.1.
Оценка
статистической значимости коэффициентов уравнения а0, а1
и определение их доверительных интервалов
Так как коэффициенты уравнения а0 , а1 рассчитывались, исходя из значений признаков
только для 30-ти пар (xi , yi), то полученные значения коэффициентов являются лишь приближенными
оценками фактических параметров связи а0 , а1. Поэтому необходимо:
1.
проверить
значения коэффициентов на неслучайность (т.е. узнать, насколько они типичны для
всей генеральной совокупности предприятий отрасли);
2.
определить (с
заданной доверительной вероятностью 0,95
и 0,683) пределы, в которых могут
находиться значения а0, а1 для генеральной совокупности предприятий.
Для анализа коэффициентов а0, а1 линейного уравнения регрессии используется табл.2.7, в которой:
– значения коэффициентов а0, а1 приведены в ячейках В91 и В92 соответственно;
– рассчитанный уровень значимости
коэффициентов уравнения приведен в ячейках Е91
и Е92;
– доверительные интервалы коэффициентов с
уровнем надежности Р=0,95 и Р=0,683 указаны в диапазоне ячеек F91:I92.
5.1.1. Определение значимости
коэффициентов уравнения
Уровень
значимости – это величина a=1–Р, где Р – заданный уровень надежности
(доверительная вероятность).
Режим
работы инструмента Регрессия
использует по умолчанию уровень надежности Р=0,95. Для этого уровня надежности уровень значимости равен
a=1-0,95 = 0,05.
Этот уровень значимости считается заданным.
В
инструменте Регрессия надстройки Пакет анализа для каждого из
коэффициентов а0 и
а1 вычисляется уровень его значимости aр, который указан в результативной таблице (табл.2.7
термин "Р-значение"). Если для коэффициентов а0, а1 рассчитанный уровень значимости aр, меньше заданного уровня значимости a=0,05, то этот коэффициент
признается неслучайным (т.е.
типичным для генеральной совокупности), в противном случае – случайным.
Примечание. В случае, если признается случайным свободный член а0,
то уравнение регрессии целесообразно построить заново без свободного члена а0.
В этом случае в диалоговом окне Регрессия необходимо
задать те же самые параметры за исключением лишь того, что следует
активизировать флажок Константа-ноль (это означает, что модель будет
строиться при условии а0=0). В лабораторной работе такой шаг не
предусмотрен.
Если
незначимым (случайным) является коэффициент регрессии а1, то взаимосвязь между признаками X и
Y в принципе
не может аппроксимироваться линейной моделью.
Вывод:
Для свободного члена а0 уравнения регрессии рассчитанный уровень значимости есть aр =0,12 Так как он больше
заданного уровня значимости a=0,05, то коэффициент а0 признается случайным.
Для коэффициента
регрессии а1 рассчитанный
уровень значимости есть aр = 1,98 Так как он больше заданного
уровня значимости a=0,05, то коэффициент а1 признается случайным.
5.1.2.
Зависимость доверительных интервалов коэффициентов уравнения от заданного
уровня надежности
Доверительные интервалы коэффициентов а0, а1
построенного уравнения регрессии при уровнях надежности Р=0,95 и Р=0,683 представлены в табл.2.7, на
основе которой формируется табл.2.9.
Таблица 2.9 - Границы доверительных интервалов
коэффициентов уравнения
|
Коэффициенты
|
Границы доверительных
интервалов
|
|
Для уровня надежности Р=0,95
|
Для уровня надежности Р=0,683
|
|
нижняя
|
верхняя
|
нижняя
|
верхняя
|
|
а0
|
328,86
|
41,58
|
-25,77
|
-51,52
|
|
а1
|
0,90
|
1,28
|
0,99
|
1,18
|
Вывод:
В генеральной
совокупности предприятий значение коэффициента
а0 следует
ожидать с надежностью Р=0,95 в
пределах 328,86 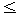 а0
а0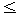 41,58, значение коэффициента а1 в пределах 0,90
41,58, значение коэффициента а1 в пределах 0,90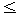 а1
а1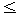 1,28. Уменьшение
уровня надежности ведет к сужению доверительных интервалов коэффициентов
уравнения.
1,28. Уменьшение
уровня надежности ведет к сужению доверительных интервалов коэффициентов
уравнения.
Определение
практической пригодности построенной регрессионной модели.
Практическую
пригодность построенной модели 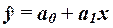 можно охарактеризовать по величине линейного коэффициента корреляции r:
можно охарактеризовать по величине линейного коэффициента корреляции r:
· близость 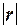 к единице
свидетельствует о хорошей аппроксимации исходных (фактических) данных с помощью
построенной линейной функции связи
к единице
свидетельствует о хорошей аппроксимации исходных (фактических) данных с помощью
построенной линейной функции связи 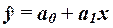 ;
;
· близость 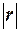 к нулю означает, что
связь между фактическими данными Х и Y нельзя аппроксимировать как
построенной, так и любой другой линейной моделью,
и, следовательно, для моделирования связи следует использовать какую-либо
подходящую нелинейную модель.
к нулю означает, что
связь между фактическими данными Х и Y нельзя аппроксимировать как
построенной, так и любой другой линейной моделью,
и, следовательно, для моделирования связи следует использовать какую-либо
подходящую нелинейную модель.
Пригодность построенной регрессионной модели для
практического использования можно оценить и по величине индекса
детерминации R2,
показывающего, какая часть общей вариации признака Y объясняется в
построенной модели вариацией фактора
X.
В основе такой оценки лежит
равенство R
= r (имеющее место
для линейных моделей связи), а также шкала Чэддока, устанавливающая качественную характеристику тесноты
связи в зависимости от величины r.
Согласно шкале Чэддока высокая степень тесноты связи
признаков достигается лишь при 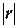 >0,7, т.е. при
>0,7, т.е. при  >0,7.
Для индекса детерминации R2
это означает выполнение
неравенства R2 >0,5.
>0,7.
Для индекса детерминации R2
это означает выполнение
неравенства R2 >0,5.
При недостаточно тесной
связи признаков X, Y (слабой, умеренной,
заметной) имеет место неравенство 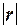
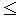 0,7, а следовательно, и неравенство
0,7, а следовательно, и неравенство 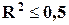 .
.
С учетом вышесказанного,
практическая пригодность построенной модели связи 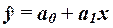 оценивается по
величине R2 следующим образом:
оценивается по
величине R2 следующим образом:
·
неравенство R2 >0,5 позволяет
считать, что построенная модель пригодна для практического применения, т.к. в
ней достигается высокая степень тесноты связи признаков X и Y, при
которой более 50% вариации признака Y объясняется влиянием фактора Х;
·
неравенство 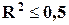 означает, что
построенная модель связи практического значения не имеет ввиду недостаточной
тесноты связи между признаками X и Y, при которой менее 50% вариации признака Y объясняется влиянием фактора Х,
и, следовательно, фактор Х влияет на вариацию Y в значительно меньшей степени, чем другие (неучтенные в модели)
факторы.
означает, что
построенная модель связи практического значения не имеет ввиду недостаточной
тесноты связи между признаками X и Y, при которой менее 50% вариации признака Y объясняется влиянием фактора Х,
и, следовательно, фактор Х влияет на вариацию Y в значительно меньшей степени, чем другие (неучтенные в модели)
факторы.
Значение
индекса детерминации R2 приводится в табл.2.5 в ячейке В79
(термин "R - квадрат").
Вывод:
Значение линейного
коэффициента корреляции r и значение индекса детерминации R2 согласно табл. 2.5 равны: r =0,91, R2 = 0,83.
Поскольку 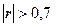 и
и 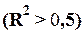 , то построенная линейная регрессионная модель связи пригодна для практического использования.
, то построенная линейная регрессионная модель связи пригодна для практического использования.
Общая оценка адекватности регрессионной модели по F-критерию Фишера
Адекватность построенной регрессионной
модели фактическим данным (xi, yi) устанавливается по критерию Р.Фишера, оценивающему
статистическую значимость (неслучайность) индекса детерминации R2.
Рассчитанная для уравнения регрессии
оценка значимости R2
приведена в табл.2.6 в ячейке F86 (термин "Значимость F"). Если
она меньше заданного уровня значимости a =0,05, то величина R2 признается
неслучайной и, следовательно, построенное уравнение регрессии 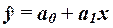 может быть использовано как модель связи между
признаками Х и Y для генеральной
совокупности предприятий отрасли.
может быть использовано как модель связи между
признаками Х и Y для генеральной
совокупности предприятий отрасли.
Вывод:
Рассчитанный уровень значимости αр индекса детерминации R2 есть aр=1,98
Так как он больше заданного
уровня значимости a=0,05, то значение R2 признается случайным
и модель связи между признаками Х и Y
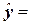 -143,64 + 1,09х неприменима для генеральной совокупности предприятий отрасли в
целом.
-143,64 + 1,09х неприменима для генеральной совокупности предприятий отрасли в
целом.
Оценка
погрешности регрессионной модели
Погрешность
регрессионной модели можно оценить по величине стандартной ошибки 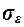 построенного
линейного уравнения регрессии
построенного
линейного уравнения регрессии 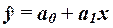 . Величина ошибки
. Величина ошибки 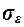 оценивается как среднее
квадратическое отклонение по совокупности отклонений
оценивается как среднее
квадратическое отклонение по совокупности отклонений  исходных (фактических)
значений yi признака Y от его теоретических значений
исходных (фактических)
значений yi признака Y от его теоретических значений 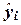 , рассчитанных по построенной модели.
, рассчитанных по построенной модели.
Погрешность регрессионной
модели выражается в процентах и рассчитывается как величина  .100.
.100.
В адекватных
моделях погрешность не должна превышать 12%-15%.
Значение 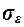 приводится в
выходной таблице "Регрессионная статистика"
(табл.2.5) в
ячейке В81 (термин "Стандартная
ошибка"), значение
приводится в
выходной таблице "Регрессионная статистика"
(табл.2.5) в
ячейке В81 (термин "Стандартная
ошибка"), значение 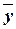 – в ячейке E47.
– в ячейке E47.
Вывод:
Погрешность линейной
регрессионной модели составляет  .100=83,73/2814,17*100= 2,98 %, что подтверждает адекватность
построенной модели
.100=83,73/2814,17*100= 2,98 %, что подтверждает адекватность
построенной модели 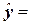 -143,64 + 1,09х
-143,64 + 1,09х
Задача 6. Дать экономическую
интерпретацию:
1) коэффициента регрессии а1;
3) остаточных величин 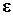 i.
i.
2) коэффициента эластичности КЭ;
6.1. Экономическая интерпретация коэффициента регрессии а1
В случае линейного уравнения регрессии 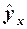 =a0+a1x
величина коэффициента регрессии a1 показывает, на
сколько в среднем (в абсолютном выражении) изменяется значение
результативного признака Y при
изменении фактора Х на единицу его
измерения. Знак при a1 показывает направление этого
изменения.
=a0+a1x
величина коэффициента регрессии a1 показывает, на
сколько в среднем (в абсолютном выражении) изменяется значение
результативного признака Y при
изменении фактора Х на единицу его
измерения. Знак при a1 показывает направление этого
изменения.
Вывод:
Коэффициент
регрессии а1 =
-143,64 показывает, что при увеличении факторного признака Среднегодовая стоимость основных производственных фондов на 1 млн. руб. значение результативного признака Выпуск продукции увеличивается (уменьшается) в среднем на1,09млн. руб.
6.2. Экономическая интерпретация коэффициента
эластичности.
С целью расширения возможностей
экономического анализа явления используется коэффициент эластичности 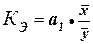 , который
измеряется в процентах и показывает, на
сколько процентов изменяется в среднем результативный признак при
изменении факторного признака на 1%.
, который
измеряется в процентах и показывает, на
сколько процентов изменяется в среднем результативный признак при
изменении факторного признака на 1%.
Средние значения 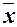 и
и 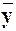 приведены в таблице
описательных статистик (ЛР-1, Лист 1, табл.3, ячейки B50
и D50).
приведены в таблице
описательных статистик (ЛР-1, Лист 1, табл.3, ячейки B50
и D50).
Расчет коэффициента эластичности:
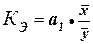 =1,09
* 980,5/ 906,5= 117,9%
=1,09
* 980,5/ 906,5= 117,9%
Вывод:
Значение коэффициента
эластичности Кэ= 1,18 показывает, что при увеличении факторного признака Среднегодовая стоимость основных
производственных фондов на 1%
значение результативного признака Выпуск
продукции увеличивается в
среднем на 18%.
6.3. Экономическая интерпретация остаточных величин
εi
Каждый их остатков 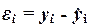 характеризует
отклонение фактического значения
yi от теоретического значения
характеризует
отклонение фактического значения
yi от теоретического значения 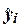 , рассчитанного по построенной регрессионной модели и
определяющего, какого среднего значения
, рассчитанного по построенной регрессионной модели и
определяющего, какого среднего значения 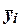 следует ожидать,
когда фактор Х принимает значение xi.
следует ожидать,
когда фактор Х принимает значение xi.
Анализируя остатки, можно
сделать ряд практических выводов, касающихся выпуска продукции на
рассматриваемых предприятиях отрасли.
Значения остатков 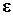 i (таблица остатков из
диапазона А98:С128) имеют как положительные, так и отрицательные
отклонения от ожидаемого в среднем объема выпуска продукции
i (таблица остатков из
диапазона А98:С128) имеют как положительные, так и отрицательные
отклонения от ожидаемого в среднем объема выпуска продукции 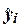 (которые в
итоге уравновешиваются, т.е.
(которые в
итоге уравновешиваются, т.е.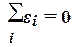 ).
).
Экономический
интерес представляют наибольшие расхождения между
фактическим объемом выпускаемой продукции yi и ожидаемым усредненным
объемом 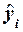 .
.
Вывод:
Согласно таблице остатков максимальное превышение
ожидаемого среднего объема выпускаемой
продукции 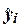 имеют три
предприятия - с номерами 19,20,29,а максимальные отрицательные отклонения - три
предприятия с номерами 7,15,32.Именно эти шесть предприятий подлежат
дальнейшему экономическому анализу для выяснения причин наибольших отклонений
объема выпускаемой ими продукции от ожидаемого среднего объема и выявления
резервов роста производства.
имеют три
предприятия - с номерами 19,20,29,а максимальные отрицательные отклонения - три
предприятия с номерами 7,15,32.Именно эти шесть предприятий подлежат
дальнейшему экономическому анализу для выяснения причин наибольших отклонений
объема выпускаемой ими продукции от ожидаемого среднего объема и выявления
резервов роста производства.
Задача 7. Нахождение наиболее
адекватного нелинейного уравнения регрессии с помощью средств
инструмента Мастер диаграмм. Построение
для этого уравнения теоретической кривой регрессии.
Уравнения регрессии и их графики построены для 3-х
видов нелинейной зависимости между признаками и представлены на диаграммах Рабочего
файла EXCEL.
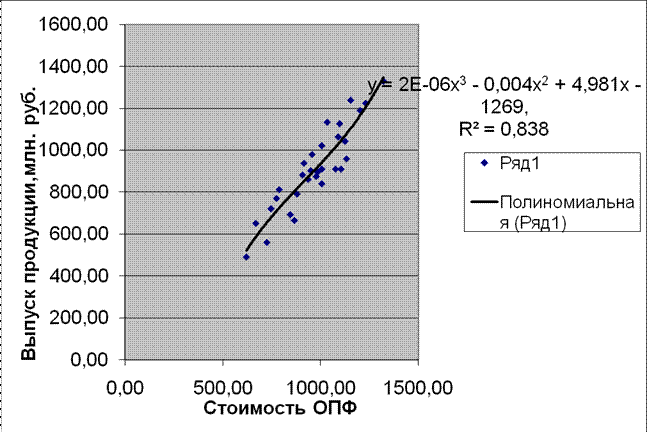
Уравнения регрессии и соответствующие им индексы
детерминации R2 приведены в табл.2.10 (при заполнении данной
таблицы коэффициенты уравнений необходимо указывать не в компьютерном формате,
а в общепринятой десятичной форме чисел).
Таблица 2.10 - Регрессионные
модели связи
|
Вид уравнения
|
Уравнение регрессии
|
Индекс
детерминации R2
|
|
Полином
2-го порядка
|
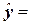 0х2 + 0,673х + 49,36 0х2 + 0,673х + 49,36
|
0,835
|
|
Полином
3-го порядка
|
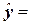 2Е-0,6 х3 – 0,004 х2 + 4,981х - 1269 2Е-0,6 х3 – 0,004 х2 + 4,981х - 1269
|
0,898
|
|
Степенная
функция
|
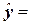 0,293 х 1,168 0,293 х 1,168
|
0,837
|
Выбор наиболее адекватного уравнения регрессии
определяется максимальным значением индекса детерминации R2: чем ближе значение R2
к
единице, тем более точно регрессионная модель соответствует фактическим данным.
Вывод:
Максимальное значение индекса детерминации R2 =0,898 Следовательно, наиболее адекватное
исходным данным нелинейное уравнение регрессии имеет вид 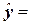 2Е-0,6
х3 – 0,004 х2 +
4,981х - 1269
2Е-0,6
х3 – 0,004 х2 +
4,981х - 1269
Это уравнение регрессии и его график приведены на рис.2.2 Полином
3-го порядка..
ПРИЛОЖЕНИЕ
Результативные таблицы и графики
|
Таблица 2.1 - Исходные данные
|
|
|
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
|
|
5
|
620,00
|
490,00
|
|
|
|
23
|
669,00
|
651,00
|
|
|
|
27
|
725,00
|
560,00
|
|
|
|
1
|
746,00
|
721,00
|
|
|
|
8
|
774,00
|
770,00
|
|
|
|
32
|
788,00
|
812,00
|
|
|
|
22
|
844,00
|
693,00
|
|
|
|
19
|
865,00
|
665,00
|
|
|
|
2
|
879,00
|
791,00
|
|
|
|
3
|
907,00
|
882,00
|
|
|
|
13
|
914,00
|
938,00
|
|
|
|
26
|
935,00
|
861,00
|
|
|
|
9
|
949,00
|
903,00
|
|
|
|
4
|
956,00
|
980,00
|
|
|
|
28
|
977,00
|
875,00
|
|
|
|
17
|
984,00
|
896,00
|
|
|
|
6
|
1005,00
|
840,00
|
|
|
|
14
|
1005,00
|
1022,00
|
|
|
|
25
|
1005,00
|
910,00
|
|
|
|
7
|
1033,00
|
1134,00
|
|
|
|
30
|
1075,00
|
910,00
|
|
|
|
18
|
1089,00
|
1064,00
|
|
|
|
10
|
1096,00
|
1127,00
|
|
|
|
20
|
1103,00
|
910,00
|
|
|
|
24
|
1124,00
|
1043,00
|
|
|
|
29
|
1131,00
|
959,00
|
|
|
|
15
|
1152,00
|
1239,00
|
|
|
|
11
|
1201,00
|
1190,00
|
|
|
|
21
|
1229,00
|
1225,00
|
|
|
|
16
|
1320,00
|
1330,00
|
|
|
|
Таблица 2.2 - Зависимость выпуска продукции от среднегодовой
стоимости основных фондов
|
|
|
Номер группы
|
Группы предприятий по
среднегодовой стоимости основных фондов, млн. руб.
|
Число предприятий, ед.
|
Выпуск продукции, млн. руб.
|
|
|
Всего
|
В среднем на одно предприятие
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
1
|
620-774
|
4
|
2422,00
|
605,50
|
|
|
2
|
774-907
|
5
|
2702,00
|
540,40
|
|
|
3
|
907-1033
|
11
|
2863,00
|
260,27
|
|
|
4
|
1033-1152
|
7
|
2996,00
|
428,00
|
|
|
5
|
1152-1320
|
3
|
2940,00
|
980,00
|
|
|
ИТОГО
|
|
30
|
13923,00
|
2814,17
|
|
|
таблица 2.3 - Расчет внутригрупповых дисперсий
|
|
|
Номер группы
|
Группы предприятий по
среднегодовой стоимости основных фондов, млн. руб.
|
Число предприятий, ед.
|
Внутригрупповая дисперсия
выпуска продукции
|
|
|
|
|
|
|
1
|
620-774
|
4
|
7705,25
|
|
|
|
2
|
774-907
|
5
|
3265,36
|
|
|
|
3
|
907-1033
|
11
|
6646,181818
|
|
|
|
4
|
1033-1152
|
7
|
12572
|
|
|
|
5
|
1152-1320
|
3
|
3538,888889
|
|
|
|
ИТОГО
|
|
30
|
218876,4667
|
|
|
|
Таблица 2.4 - Дисперсии и эмпирические показатели тесноты
взаимосвязи
|
|
|
Общая дисперсия выпуска
продукции
|
Средняя из внутригрупповых
дисперсий выпуска продукции
|
Межгрупповая дисперсия выпуска
продукции
|
Эмпирический коэффициент
детерминации
|
Эмпирическое корреляционное
отношение
|
|
|
|
39434,16556
|
7295,882222
|
32138,28333
|
0,814985759
|
0,902765617
|
|
|
Регрессионный анализ
|
|
|
|
|
|
|
|
|
ВЫВОД
ИТОГОВ
|
|
|
|
табл.
2.5.
|
|
|
|
|
Регрессионная статистика
|
|
|
|
Множественный
R
|
0,91318826
|
|
|
|
R-квадрат
|
0,833912798
|
|
|
|
Нормированный
R-квадрат
|
0,827981112
|
|
|
|
Стандартная
ошибка
|
83,76951935
|
|
|
|
Наблюдения
|
30
|
|
|
|
табл. 2.6.
|
|
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
|
|
Регрессия
|
1
|
986539,6603
|
986539,6603
|
140,5861384
|
1,97601E-12
|
|
|
|
Остаток
|
28
|
196485,3064
|
7017,332372
|
|
|
|
|
|
Итого
|
29
|
1183024,967
|
|
|
|
|
|
|
табл.2.7.
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
|
|
|
Y-пересечение
|
-143,64
|
90,42176509
|
-1,58856877
|
0,123387341
|
-328,8617791
|
|
|
|
Переменная
X 1
|
1,08936
|
0,09187519
|
11,85690257
|
1,97601E-12
|
0,901157387
|
|
|
|
Верхние 95%
|
Нижние 68,3%
|
Верхние 68,3%
|
|
|
|
41,57939475
|
-235,766891
|
-51,51549371
|
|
|
|
1,277552975
|
0,995748668
|
1,182961694
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД
ОСТАТКА
|
|
|
табл.
2.8.
|
|
|
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
20
|
1057,917572
|
-147,9175724
|
|
19
|
798,6510393
|
-133,6510393
|
|
29
|
1088,419517
|
-129,4195175
|
|
30
|
1027,415627
|
-117,4156273
|
|
6
|
951,1607647
|
-111,1607647
|
|
27
|
646,141314
|
-86,141314
|
|
22
|
775,7745805
|
-82,77458053
|
|
28
|
920,6588196
|
-45,6588196
|
|
5
|
531,75902
|
-41,75902
|
|
25
|
951,1607647
|
-41,16076467
|
|
24
|
1080,794031
|
-37,7940312
|
|
17
|
928,2843059
|
-32,28430587
|
|
2
|
813,9020119
|
-22,90201187
|
|
26
|
874,905902
|
-13,905902
|
|
9
|
890,1568745
|
12,84312547
|
|
18
|
1042,6666
|
21,33340013
|
|
11
|
1164,67438
|
25,32561987
|
|
21
|
1195,176325
|
29,8236748
|
|
16
|
1294,307647
|
35,69235333
|
|
3
|
844,4039569
|
37,59604307
|
|
1
|
669,0177728
|
51,9822272
|
|
23
|
585,1374239
|
65,86257613
|
|
8
|
699,5197179
|
70,48028213
|
|
14
|
951,1607647
|
70,83923533
|
|
10
|
1050,292086
|
76,70791387
|
|
4
|
897,7823608
|
82,2176392
|
|
13
|
852,0294432
|
85,9705568
|
|
32
|
714,7706904
|
97,2293096
|
|
15
|
1111,295976
|
127,7040237
|
|
7
|
981,6627097
|
152,3372903
|
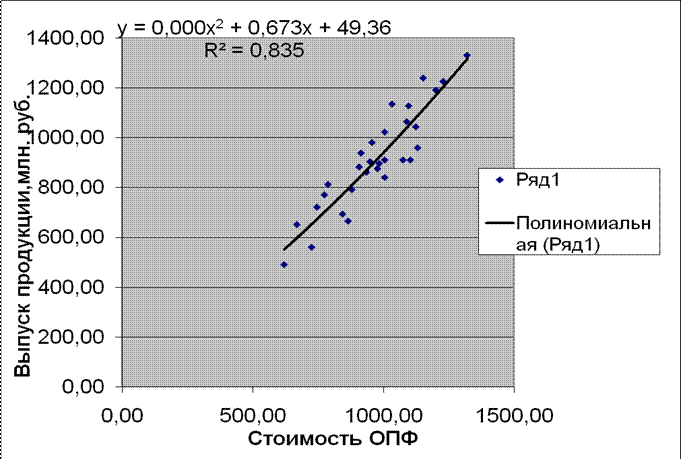
Рис. 2.1. Полином 2-го порядкка
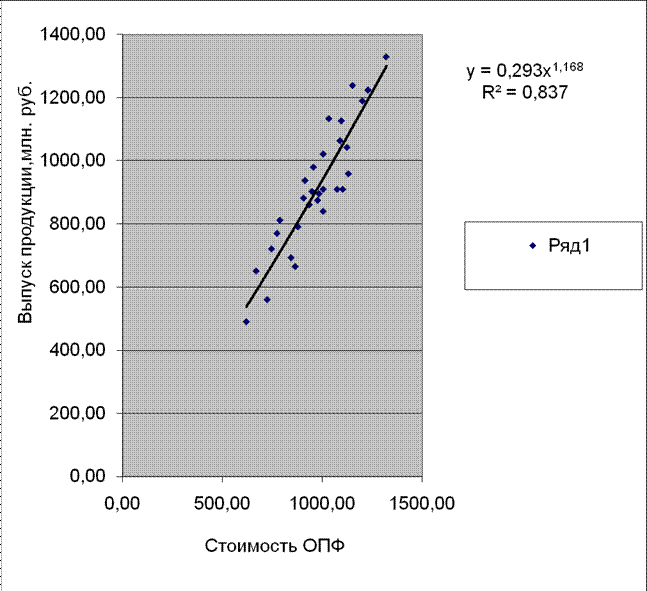
Рис.2.3. Степенная функция
[1] Все статистические показатели необходимо представить в таблицах с
точностью до 4-х знаков после запятой. Таблицы и пробелы в формулировках
выводов заполнять вручную. В выводах при выборе альтернативного
варианта ответа ненужный вариант вычеркивается.