ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
О
Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №2
Автоматизированный корреляционно-регрессионный анализ взаимосвязи
статистических данных в среде MS Excel
Вариант №7
Выполнил: .
Проверила: Голикова Анна Викторовна
ФИО
Москва,
2008 г.
I. Постановка
задачи
Корреляционно-регрессионный анализ взаимосвязи
признаков является составной частью проводимого статистического исследования и
частично использует результаты Лабораторной работы № 1.
В Лабораторной работе № 2 изучается взаимосвязь между
факторным признаком Среднегодовая стоимость
основных производственных фондов (признак Х)
и результативным признаком Выпуск продукции
(признак Y), значениями которых являются исходные данные
Лабораторной работы № 1 после исключения из них аномальных значений.
Таблица 1.
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
1
|
686.00
|
1139.00
|
|
5
|
605.00
|
875.00
|
|
23
|
636.50
|
1059.00
|
|
27
|
672.50
|
955.00
|
|
8
|
704.00
|
1195.00
|
|
32
|
713.00
|
1243.00
|
|
22
|
749.00
|
1107.00
|
|
19
|
762.50
|
1075.00
|
|
2
|
771.50
|
1219.00
|
|
3
|
789.50
|
1323.00
|
|
13
|
794.00
|
1387.00
|
|
26
|
807.50
|
1299.00
|
|
9
|
816.50
|
1347.00
|
|
4
|
821.00
|
1435.00
|
|
28
|
834.50
|
1315.00
|
|
17
|
839.00
|
1339.00
|
|
6
|
852.50
|
1275.00
|
|
14
|
852.50
|
1483.00
|
|
25
|
852.50
|
1355.00
|
|
7
|
870.50
|
1611.00
|
|
31
|
897.50
|
1355.00
|
|
18
|
906.50
|
1531.00
|
|
10
|
911.00
|
1603.00
|
|
20
|
915.50
|
1355.00
|
|
24
|
929.00
|
1507.00
|
|
29
|
933.50
|
1411.00
|
|
15
|
947.00
|
1731.00
|
|
12
|
978.50
|
1675.00
|
|
21
|
996.50
|
1715.00
|
|
16
|
1055.00
|
1835.00
|
В процессе статистического исследования
необходимо решить ряд задач.
1. Установить наличие статистической
связи между факторным признаком Х
и результативным признаком Y:
а) графическим методом;
б) методом сопоставления параллельных рядов.
2. Установить наличие корреляционной
связи между признаками Х и Y методом аналитической группировки.
3. Оценить тесноту связи признаков Х и
Y на основе:
а) эмпирического корреляционного отношения η;
б) линейного коэффициента корреляции r.
4. Построить однофакторную
линейную регрессионную модель связи признаков Х и Y, используя
инструмент Регрессия надстройки Пакет анализа.
5. Оценить адекватность и
практическую пригодность построенной линейной регрессионной модели, указав:
а) значимость и
доверительные интервалы коэффициентов а0, а1;
б) индекс детерминации R2 и его
значимость;
в) точность регрессионной
модели.
6. Дать экономическую
интерпретацию:
а) коэффициента регрессии а1;
б) коэффициента эластичности КЭ;
в) остаточных величин 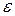 i.
i.
7. Найти наиболее адекватное нелинейное
уравнение регрессии с помощью средств инструмента Мастер диаграмм.
Построить для этого уравнения теоретическую кривую регрессии.
II. Выводы по результатам
выполнения лабораторной работы.
Задача 1. Установление наличия статистической связи
между факторным признаком Х и
результативным признаком Y графическим методом и
методом сопоставления параллельных рядов.
Статистическая связь
является разновидностью стохастической (случайной) связи, при которой с
изменением факторного признака закономерным образом изменяется какой –либо из
обобщающих статистических показателей распределения результативного признака.
Вывод:
Точечный
график связи признаков (диаграмма рассеяния, полученная в Лабораторной работы №1 после удаления аномальных
значений), а также табл.1, представляющая два параллельных ряда значений
признаков X и Y с ранжированными значениями
xi показывают, что с увеличением значений
факторного признака увеличиваются (уменьшаются) значения результативного
признака, за исключением некоторых отклонений от общей тенденции предприятия:
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
11
|
470.00
|
1515.00
|
|
30
|
1055.00
|
715.00
|
Это позволяет сделать вывод, что имеет место
статистическая связь. Предположительный вид связи – линейная прямая.
Задача 2. Установление наличия корреляционной связи между
признаками Х и Y методом аналитической группировки.
Корреляционная связь –
важнейший частный случай статистической связи, когда под воздействием вариации
факторного признака Х закономерно
изменяются средние значения 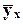 результативного
признака. Для выявления наличия корреляционной связи используется метод
аналитической группировки.
результативного
признака. Для выявления наличия корреляционной связи используется метод
аналитической группировки.
Вывод:
Результаты выполнения
аналитической группировки предприятий по факторному признаку Среднегодовая стоимость основных
производственных фондов даны в табл. 2.2, которая показывает, что с
увеличением факторного признака Х закономерно изменяются средние
значения 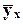
|
|
|
|
|
Таблица 2.2
|
|
Зависимость
выпуска продукции от среднегодовой стоимости основных фондов
|
|
Номер
группы
|
Группы
предприятий по стоимости основеных фондов
|
Число
предприятий
|
Выпуск
продукции
|
|
Всего
|
В
среднем
на одно
предприятие
|
|
1
|
605-695
|
4
|
4028.00
|
1007.00
|
|
2
|
695-785
|
5
|
5839.00
|
1167.80
|
|
3
|
785-875
|
11
|
15169.00
|
1379.00
|
|
4
|
875-965
|
7
|
10493.00
|
1499.00
|
|
5
|
965-1055
|
3
|
5225.00
|
1741.67
|
|
Итого
|
|
30
|
40754.00
|
1358.466667
|
Задача 3.Оценка тесноты связи признаков Х и Y:
а) на основе эмпирического корреляционного отношения.
Для анализа
тесноты связи между факторным и результативным признаками рассчитывается
показатель η - эмпирическое
корреляционное отношение, задаваемое формулой
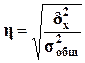 ,
,
где  и
и 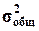 - соответственно
межгрупповая и общая дисперсии результативного признака Y - Выпуск продукции.
- соответственно
межгрупповая и общая дисперсии результативного признака Y - Выпуск продукции.
Результаты
выполненных расчетов представляются табл. 2.4.
Вывод:
Значение коэффициента η=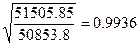 , что в соответствии с
оценочной шкалой Чэддока говорит о прямолинейной
степени связи изучаемых признаков.
, что в соответствии с
оценочной шкалой Чэддока говорит о прямолинейной
степени связи изучаемых признаков.
б) на основе линейного
коэффициента корреляции признаков.
В предположении, что связь
между факторным и результативным признаками прямолинейная, для оценки тесноты
связи на основе линейного коэффициента корреляции r был использован инструмент Корреляция
надстройки Пакет анализа, в
результате применения которого построена табл.2.5.
Вывод:
Значение
коэффициента корреляции r= 0.9132, что в соответствии со шкалой Чэддока говорит
о прямолинейной степени связи изучаемых
признаков.
Так
как значение коэффициента корреляции r положительное,
то связь между признаками прямолинейная.
Посредством
показателя η
измеряется теснота связи любой формы,
а с помощью коэффициента корреляции r – только прямолинейная, следовательно, значения η и r совпадают только при наличии прямолинейной связи. В
теории статистики установлено, что если 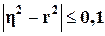 , то гипотезу о прямолинейности связи можно считать
подтвержденной.
, то гипотезу о прямолинейности связи можно считать
подтвержденной.
Вывод:
При
η= 0,9936 и r= 0,9132 величина 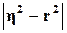 = 0,1533, следовательно, связь между признаками X и Y
предположительно прямолинейная.
= 0,1533, следовательно, связь между признаками X и Y
предположительно прямолинейная.
Задача 4. Построение однофакторной линейной регрессионной
модели связи
изучаемых признаков с помощью инструмента Регрессия надстройки Пакет
анализа.
Построение регрессионной
модели заключается в определении аналитического выражения связи между факторным
признаком X и результативным признаком Y.
Инструмент Регрессия производит расчет параметров а0 и а1 уравнения однофакторной линейной регрессии 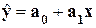 , а также вычисление ряда показателей для проверки
адекватности построенного уравнения фактическим данным.
, а также вычисление ряда показателей для проверки
адекватности построенного уравнения фактическим данным.
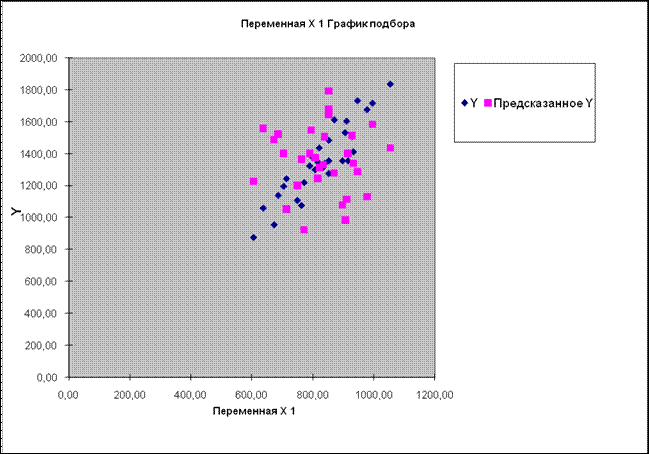
В результате работы
инструмента Регрессия были получены
четыре результативные таблицы 2.6 – 2.9 Рабочего файла.
Таблица 2.6
|
Регрессионная
статистика
|
|
Множественный
R
|
0.91318826
|
|
R-квадрат
|
0.833912798
|
|
Нормированный
R-квадрат
|
0.827981112
|
|
Стандартная
ошибка
|
95.73659354
|
|
Наблюдения
|
30
|
Таблица 2.7
|
Дисперсионный
анализ
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
1288541.60
|
1288541.60
|
140.59
|
1.98
|
|
Остаток
|
28
|
256633.87
|
9165.50
|
|
|
|
Итого
|
29
|
1545175.47
|
|
|
|
Таблица 2.8
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 68.3%
|
Верхние 68.3%
|
|
Y-пересечение
|
-248.94
|
136.69
|
-1.82
|
0.08
|
-528.93
|
31.06
|
-388.20
|
-109.67
|
|
Переменная
X 1
|
1.94
|
0.16
|
11.86
|
1.98
|
1.60
|
2.27
|
1.77
|
2.10
|
Таблица 2.9
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
1
|
1079.59174
|
59.40825966
|
|
2
|
922.7245943
|
-47.72459429
|
|
3
|
983.7284844
|
75.27151558
|
|
4
|
1053.447216
|
-98.447216
|
|
5
|
1114.451106
|
80.54889387
|
|
6
|
1131.880789
|
111.119211
|
|
7
|
1201.599521
|
-94.59952061
|
|
8
|
1227.744045
|
-152.744045
|
|
9
|
1245.173728
|
-26.17372785
|
|
10
|
1280.033094
|
42.96690636
|
|
11
|
1288.747935
|
98.25206491
|
|
12
|
1314.892459
|
-15.89245943
|
|
13
|
1332.322142
|
14.67785768
|
|
14
|
1341.036984
|
93.96301623
|
|
15
|
1367.181508
|
-52.18150811
|
|
16
|
1375.89635
|
-36.89634956
|
|
17
|
1402.040874
|
-127.0408739
|
|
18
|
1402.040874
|
80.9591261
|
|
19
|
1402.040874
|
-47.0408739
|
|
20
|
1436.90024
|
174.0997603
|
|
21
|
1489.189288
|
-134.1892884
|
|
22
|
1506.618971
|
24.38102872
|
|
23
|
1515.333813
|
87.66618728
|
|
24
|
1524.048654
|
-169.0486542
|
|
25
|
1550.193179
|
-43.19317851
|
|
26
|
1558.90802
|
-147.90802
|
|
27
|
1585.052544
|
145.9474557
|
|
28
|
1646.056434
|
28.94356556
|
|
29
|
1680.9158
|
34.08419977
|
|
30
|
1794.208739
|
40.79126095
|
Вывод:
Рассчитанные в табл.2.8
|
|
Коэффициенты
|
|
Y-пересечение
|
-248.94
|
|
Переменная
X 1
|
1.94
|
коэффициенты а0 и а1 позволяют
построить линейную регрессионную модель связи изучаемых признаков в виде
уравнения 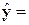 7-06x3 - 0,016x2 + 14,68x - 3535
7-06x3 - 0,016x2 + 14,68x - 3535
Задача 5. Оценка адекватности и практической пригодности построенной линейной
регрессионной модели.
Анализ адекватности регрессионной модели
преследует цель оценить, насколько построенная теоретическая модель взаимосвязи
признаков отражает фактическую зависимость между этими признаками, и тем самым
оценить практическую пригодность синтезированной модели связи.
Оценка
соответствия регрессионной модели наблюдаемым фактическим значениям признаков X и Y выполняется в 4 этапа:
1) оценка статистической значимости коэффициентов
уравнения а0,
а1 и определение их
доверительных интервалов для заданного уровня надежности;
2) определение практической пригодности построенной
модели на основе оценок коэффициента корреляции
r и индекса детерминации R2;
3) проверка адекватности уравнения регрессии в целом по F-критерию Фишера;
4) оценка
погрешности регрессионной модели.
1. Оценка
статистической значимости коэффициентов уравнения а0, а1 и определение их доверительных
интервалов.
Так как коэффициенты уравнения а0, а1
рассчитывались, исходя из
значений признаков только 30-ти пар (xi,yi),
то полученные значения коэффициентов являются лишь приближенными оценками
фактических параметров связи а0, а1. Поэтому необходимо: 1) вычислить средние
ошибки 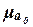 ,
, 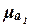 найденных
коэффициентов а0, а1, 2) проверить значения
коэффициентов на неслучайность (т.е.узнать, насколько они типичны для всей
генеральной совокупности предприятий отрасли), 3) (с заданной доверительной
вероятностью) пределы, в которых могут находиться значения а0, а1 для генеральной совокупности предприятий.
найденных
коэффициентов а0, а1, 2) проверить значения
коэффициентов на неслучайность (т.е.узнать, насколько они типичны для всей
генеральной совокупности предприятий отрасли), 3) (с заданной доверительной
вероятностью) пределы, в которых могут находиться значения а0, а1 для генеральной совокупности предприятий.
Для анализа коэффициентов используется таблица 2.8 в
которой:
·
значения коэффициентов а0, а1;
·
рассчитанный уровень значимости коэффициентов уравнения (термин"Р-значения");
·
доверительные
интервалы коэффициентов с уровнем надежности Р=0,95 и Р=0,683.
1.1. Определение значимости
коэффициентов уравнения.
Уровень
значимости – это величина α=1-Р, где Р заданный уровень надежности
(доверительная вероятность).
Если Р-значение коэффициента
в результативной таблице меньше заданного уровня значимости α=1-0,95=0,05, то этот коэффициент признается неслучайным (типичным для генеральной
совокупности).
Вывод:
Для свободного члена уравнения а0 уровень значимости есть 0.08 Так как этот
уровень больше заданного уровня значимости α=0,05, то коэффициент а0= -248.94 признается случайным.
Для коэффициента регрессии а1 уровень значимости есть 1.98 Так как этот
уровень больше заданного уровня значимости α=0,05, то коэффициент а1= 1.94 признается случайным.
1.2.
Оценка доверительных интервалов коэффициентов уравнения регрессии.
Доверительные интервалы коэффициентов уравнения
регрессии а0, а1 при уровнях надежности Р=0,95 и Р=0,683 приведены в следующей таблице:
|
Коэффициенты
|
Границы доверительных
интервалов, млн. руб.
|
|
с надежностью Р=0,95
|
с надежностью Р=0,683
|
|
нижняя
|
верхняя
|
нижняя
|
верхняя
|
|
а0
|
-528.93
|
31.06
|
-388.20
|
-109.67
|
|
а1
|
1.60
|
2.27
|
1.77
|
2.10
|
Вывод:
Увеличение уровня надежности ведет к расширению доверительных интервалов коэффициентов уравнения, в которых могут
находиться коэффициенты а0, а1 уравнения связи
признаков для генеральной совокупности предприятий.
2. Определение практической пригодности
построенной регрессионной модели.
В случае линейности функции связи для
оценки тесноты связи признаков X и Y, устанавливаемой по модели,
используется линейный коэффициент корреляции r. По величине r можно охарактеризовать
практическую пригодность модели:
·
близость 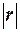 к единице
свидетельствует о хорошей аппроксимации фактических данных полученной линейной
функции связи
к единице
свидетельствует о хорошей аппроксимации фактических данных полученной линейной
функции связи 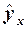 = a0
+ a1x;
= a0
+ a1x;
·
близость 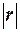 к нулю, означает, что
уравнение регрессии не может быть линейным и для моделирования связи следует
использовать нелинейные зависимости.
к нулю, означает, что
уравнение регрессии не может быть линейным и для моделирования связи следует
использовать нелинейные зависимости.
Пригодность построенной регрессионной модели для
практического использования можно оценить и по величине индекса
детерминации R2,
показывающего, какая часть общей вариации значений признака Y объясняется в модели вариацией фактора X:
·
неравенству R2 > 0,5 отвечают
значения 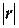 >0,7, что означает высокую степень тесноты связи признаков
X и Y, устанавливаемую по уравнению регрессии. При этом в модели более 50%
вариации значений признака Y объясняется влиянием фактора Х, что позволяет считать применение синтезированного уравнения
регрессии
>0,7, что означает высокую степень тесноты связи признаков
X и Y, устанавливаемую по уравнению регрессии. При этом в модели более 50%
вариации значений признака Y объясняется влиянием фактора Х, что позволяет считать применение синтезированного уравнения
регрессии 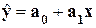 правомерным;
правомерным;
·
при 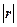
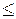 0,7 величина R2
всегда будет меньше 50%. Это означает, что согласно модели вариация
фактора Х влияет на вариацию Y в значительно меньшей степени, чем
другие (неучтенные в модели) факторы. При таких условиях построенная
математическая модель связи практического значения не имеет.
0,7 величина R2
всегда будет меньше 50%. Это означает, что согласно модели вариация
фактора Х влияет на вариацию Y в значительно меньшей степени, чем
другие (неучтенные в модели) факторы. При таких условиях построенная
математическая модель связи практического значения не имеет.
Вывод:
Согласно
таблице "Регрессионная статистика" r=0.9131, R2=0.8339.
Поскольку 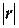 >0,7 и R2>0,5, то
построенная линейная регрессионная модель связи
пригодна для практического
использования.
>0,7 и R2>0,5, то
построенная линейная регрессионная модель связи
пригодна для практического
использования.
3. Общая оценка адекватности регрессионной модели по F-критерию Фишера.
Адекватность построенной регрессионной
модели фактическим данным (xi,yi)
устанавливается по критерию Р.Фишера, оценивающему статистическую значимость
(неслучайность) индекса детерминации R2.
Рассчитанная для уравнения оценка
значимости R2
= 1,98. Если она меньше заданного
уровня значимости α=0,05,
то величина R2 признается
неслучайной и, следовательно, уравнение регрессии не может быть использовано
как модель связи между признаками Х и Y для генеральной совокупности предприятий отрасли.
Вывод:
Уровень значимости индекса детерминации R2 =1,98. Так как этот уровень больше заданного уровня значимости
α=0,05, то значение R2
признается случайным и построенная модель связи между признаками Х
и Y применима для генеральной совокупности
предприятий отрасли в целом.
4. Оценка погрешности регрессионной модели.
Погрешность регрессионной
модели можно оценить по средней квадратической ошибке 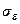 построенного
уравнения регрессии, представляющей собой среднее квадратическое отклонение
эмпирических значений yi признака Y от его теоретических значений
построенного
уравнения регрессии, представляющей собой среднее квадратическое отклонение
эмпирических значений yi признака Y от его теоретических значений 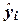 .
.
В адекватных моделях ошибка 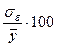 не должна превышать
12%-15%.
не должна превышать
12%-15%.
Вывод:
Погрешность линейной
регрессионной модели составляет 227,17 %,
что не подтверждает адекватность модели.
Задача 6. Дать экономическую интерпретацию:
1) коэффициента регрессии а1;
2) коэффициента эластичности
КЭ;
3) остаточных величин 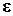 i.
i.
1. Экономическая
интерпретация коэффициента
регрессии а1.
В случае линейного уравнения регрессии 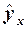 =a0+a1x
величина коэффициента регрессии a1
показывает, на сколько в среднем (в абсолютном выражении) изменяется
значения результативного признака Y
при изменении фактора Х на единицу
его измерения. Знак при a1
показывает направление этого изменения.
=a0+a1x
величина коэффициента регрессии a1
показывает, на сколько в среднем (в абсолютном выражении) изменяется
значения результативного признака Y
при изменении фактора Х на единицу
его измерения. Знак при a1
показывает направление этого изменения.
Вывод:
Коэффициент
регрессии а1=1,98
показывает, что на сколько в
среднем (в абсолютном выражении) изменяется значения результативного
признака Y при изменении фактора Х на единицу его измерения
2. Экономическая
интерпретация коэффициента эластичности.
С целью расширения возможностей
экономического анализа используется коэффициент эластичности 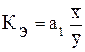 , который показывает, на
сколько процентов изменяется в среднем результативный признак при
изменении факторного признака на 1%.
, который показывает, на
сколько процентов изменяется в среднем результативный признак при
изменении факторного признака на 1%.
Среднее
значение признаков X и Y даны в таблице описательных
статистик
Вывод:
Коэффициент эластичности КЭ =1,98*830/1358= 1,2097% показывает, что на сколько процентов изменяется в среднем результативный признак при
изменении факторного признака на 1%.
3. Экономическая
интерпретация остаточных величин
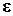 i.
i.
Каждый их остатков 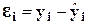 характеризует
отклонение фактического значения
yi от значения
характеризует
отклонение фактического значения
yi от значения 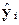 , рассчитанного по регрессионной модели и определяющего,
какое среднее значение
, рассчитанного по регрессионной модели и определяющего,
какое среднее значение 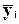 следует ожидать для
факторного признака xi.
следует ожидать для
факторного признака xi.
Анализируя остатки, можно
сделать ряд практических выводов, касающихся выпуска продукции на
рассматриваемых предприятиях отрасли.
Значения остатков 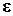 i имеют как положительные,
так и отрицательные отклонения от ожидаемого в среднем объема выпуска продукции
i имеют как положительные,
так и отрицательные отклонения от ожидаемого в среднем объема выпуска продукции
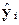 (которые в итоге
уравновешиваются, т.е.
(которые в итоге
уравновешиваются, т.е.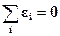 ).
).
Экономический
интерес представляют наибольшие отклонения от среднего объема 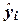 как в положительную,
так и в отрицательную сторону.
как в положительную,
так и в отрицательную сторону.
Вывод:
Согласно
таблице остатков, в построенной линейной регрессионной модели наибольшее
превышение среднего объема выпускаемой
продукции 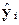 имеют три предприятия
- с номерами
имеют три предприятия
- с номерами
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
6
|
1131,880789
|
111,119211
|
|
27
|
1585,052544
|
145,9474557
|
|
20
|
1436,90024
|
174,0997603
|
а наибольшие
отрицательные отклонения от среднего объема выпуска - три предприятия с
номерами
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
24
|
1524,048654
|
-169,0486542
|
|
8
|
1227,744045
|
-152,744045
|
|
26
|
1558,90802
|
-147,90802
|
Именно эти
шесть предприятий подлежат дальнейшему экономическому анализу для выяснения
причин наибольших отклонений объема выпускаемого продукта от ожидаемого
среднего объема и выявления резервов роста производства.
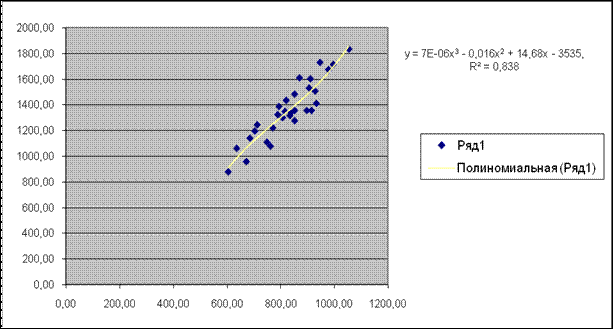
Задача 7. Нахождение наиболее адекватного нелинейного
уравнения регрессии с помощью средств инструмента Мастер диаграмм. Построение для этого уравнения теоретической
кривой регрессии.
Уравнения регрессии и их графики построены для 4-х
видов нелинейной зависимости между признаками и представлены на диаграмме 2.1.
Уравнения регрессии и соответствующие им индексы
детерминации R2 приведены в следующей таблице:
Регрессионные модели связи
|
Вид уравнения
|
Уравнение регрессии
|
Индекс
детерминации R2
|
|
Полином
2-го порядка
|
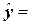 0.0006x2 + 0.9502x + 149.7 0.0006x2 + 0.9502x + 149.7
|
0.8353
|
|
Полином
3-го порядка
|
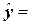 7.06x3 - 0.0162x2 + 14.681x - 3535.4 7.06x3 - 0.0162x2 + 14.681x - 3535.4
|
0.8381
|
|
Степенное
|
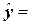 0.4628x1.1873 0.4628x1.1873
|
0.8368
|
|
Экспоненциальное
|
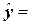 396.59e0.0015x 396.59e0.0015x
|
0.8326
|
Выбор наиболее адекватного уравнения регрессии
определяется максимальным значением индекса детерминации R2: чем ближе значение R2 к единице, тем более точно
регрессионная модель соответствует фактическим данным.
Вывод:
Максимальное значение индекса детерминации R2 =0,8381, следовательно, наиболее адекватное
нелинейное уравнения регрессии – ŷ = 7.06x3
- 0.0162x2 + 14.681x - 3535.4.
ПРИЛОЖЕНИЕ 2
|
|
|
Таблица 2.1
|
|
Исходные данные
|
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
1
|
686,00
|
1139,00
|
|
5
|
605,00
|
875,00
|
|
23
|
636,50
|
1059,00
|
|
27
|
672,50
|
955,00
|
|
8
|
704,00
|
1195,00
|
|
32
|
713,00
|
1243,00
|
|
22
|
749,00
|
1107,00
|
|
19
|
762,50
|
1075,00
|
|
2
|
771,50
|
1219,00
|
|
3
|
789,50
|
1323,00
|
|
13
|
794,00
|
1387,00
|
|
26
|
807,50
|
1299,00
|
|
9
|
816,50
|
1347,00
|
|
4
|
821,00
|
1435,00
|
|
28
|
834,50
|
1315,00
|
|
17
|
839,00
|
1339,00
|
|
6
|
852,50
|
1275,00
|
|
14
|
852,50
|
1483,00
|
|
25
|
852,50
|
1355,00
|
|
7
|
870,50
|
1611,00
|
|
31
|
897,50
|
1355,00
|
|
18
|
906,50
|
1531,00
|
|
10
|
911,00
|
1603,00
|
|
20
|
915,50
|
1355,00
|
|
24
|
929,00
|
1507,00
|
|
29
|
933,50
|
1411,00
|
|
15
|
947,00
|
1731,00
|
|
12
|
978,50
|
1675,00
|
|
21
|
996,50
|
1715,00
|
|
16
|
1055,00
|
1835,00
|
|
|
|
|
|
Таблица 2.2
|
|
Зависимость выпуска
продукции от среднегодовой стоимости основных фондов
|
|
Номер группы
|
Группы предприятий по стоимости
основеных фондов
|
Число предприятий
|
Выпуск продукции
|
|
Всего
|
В среднем
на одно
предприятие
|
|
1
|
605-695
|
4
|
4028,00
|
1007,00
|
|
2
|
695-785
|
5
|
5839,00
|
1167,80
|
|
3
|
785-875
|
11
|
15169,00
|
1379,00
|
|
4
|
875-965
|
7
|
10493,00
|
1499,00
|
|
5
|
965-1055
|
3
|
5225,00
|
1741,67
|
|
Итого
|
|
30
|
40754,00
|
1358,466667
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.3
|
|
|
Показатели
внутригрупповой вариации
|
|
|
Номер группы
|
Группы предприятий по стоимости
основеных фондов
|
Число предприятий
|
Внутригрупповая дисперсия
|
|
|
1
|
605-695
|
4
|
1002,38
|
|
|
2
|
695-785
|
5
|
720,90
|
|
|
3
|
785-875
|
11
|
633,27
|
|
|
4
|
875-965
|
7
|
254,57
|
|
|
5
|
965-1055
|
3
|
1066,50
|
|
|
Итого
|
|
30
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.4
|
|
|
Показатели дисперсии
и эмпирического корреляционного отношения
|
|
|
Общая дисперсия
|
Средняя из внутригрупповых дисперсия
|
Межгрупповая дисперсия
|
Эмпирическое корреляционное
отношение
|
|
|
51505,84889
|
652,05
|
50853,79889
|
0,993649975
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.5
|
|
|
|
Линейный коэффициент
корреляции признаков
|
|
|
|
|
Столбец 1
|
Столбец 2
|
|
|
|
Столбец 1
|
1
|
|
|
|
|
Столбец 2
|
0,91318826
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выходные
таблицы
|
|
|
|
|
|
|
|
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная статистика
|
|
|
|
|
Множественный
R
|
0,91318826
|
|
|
|
|
R-квадрат
|
0,833912798
|
|
|
|
|
Нормированный
R-квадрат
|
0,827981112
|
|
|
|
|
Стандартная
ошибка
|
95,73659354
|
|
|
|
|
Наблюдения
|
30
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
1288541,597
|
1288541,597
|
140,5861384
|
1,97601E-12
|
|
Остаток
|
28
|
256633,8696
|
9165,495343
|
|
|
|
Итого
|
29
|
1545175,467
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-
статистика
|
P-
Значение
|
Нижние
95%
|
Верхние
95%
|
Нижние
68.3%
|
Верхние
68.3%
|
|
Y-пересечение
|
-248,9374226
|
136,6891137
|
-1,821194211
|
0,079279289
|
-528,9326937
|
31,05784857
|
-388,2023588
|
-109,6724864
|
|
Переменная
X 1
|
1,936631433
|
0,163333672
|
11,85690257
|
1,97601E-12
|
1,602057197
|
2,271205668
|
1,770219838
|
2,103043028
|
|
ВЫВОД
ОСТАТКА
|
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
24
|
1524,048654
|
-169,0486542
|
|
8
|
1227,744045
|
-152,744045
|
|
26
|
1558,90802
|
-147,90802
|
|
21
|
1489,189288
|
-134,1892884
|
|
17
|
1402,040874
|
-127,0408739
|
|
4
|
1053,447216
|
-98,447216
|
|
7
|
1201,599521
|
-94,59952061
|
|
15
|
1367,181508
|
-52,18150811
|
|
2
|
922,7245943
|
-47,72459429
|
|
19
|
1402,040874
|
-47,0408739
|
|
25
|
1550,193179
|
-43,19317851
|
|
16
|
1375,89635
|
-36,89634956
|
|
9
|
1245,173728
|
-26,17372785
|
|
12
|
1314,892459
|
-15,89245943
|
|
13
|
1332,322142
|
14,67785768
|
|
22
|
1506,618971
|
24,38102872
|
|
28
|
1646,056434
|
28,94356556
|
|
29
|
1680,9158
|
34,08419977
|
|
30
|
1794,208739
|
40,79126095
|
|
10
|
1280,033094
|
42,96690636
|
|
1
|
1079,59174
|
59,40825966
|
|
3
|
983,7284844
|
75,27151558
|
|
5
|
1114,451106
|
80,54889387
|
|
18
|
1402,040874
|
80,9591261
|
|
23
|
1515,333813
|
87,66618728
|
|
14
|
1341,036984
|
93,96301623
|
|
11
|
1288,747935
|
98,25206491
|
|
6
|
1131,880789
|
111,119211
|
|
27
|
1585,052544
|
145,9474557
|
|
20
|
1436,90024
|
174,0997603
|