Федеральное агентство по образованию

Всероссийский заочный финансово-экономический институт

Филиал в г. Архангельске

Кафедра экономико-математических методов и моделей

КОНТРОЛЬНАЯ РАБОТА

по дисциплине

«ФИНАНСОВАЯ МАТЕМАТИКА»

Вариант 1

Студентки: 4 курса, ФК

г. Архангельск

2008

Задание 1

Приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года (всего 16 кварталов, первая строка соответствует первому кварталу первого года)

Квартал

Кредиты

1

28

2

36

3

43

4

28

5

31

6

40

7

49

8

30

9

34

10

44

11

52

12

33

13

39

14

48

15

58

16

36

Требуется:

1.     построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания ; ; .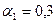

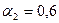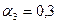2.     Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации.

3.     Оценить адекватность построенной модели на основе исследования:

- случайности остаточной компоненты по критерию пиков;

- независимости уровней ряда остатков по d – критерию (критические значения d1 = 1,10 и d2 = 1,37) по первому коэффициенту автокорреляции при критическом значении r1 = 0,32;

- нормальности распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.

4.     Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.

5.     Отразить на графике фактические, расчетные и прогнозные данные.

Задание 2

Даны цены (открытия, максимальная, минимальная и закрытия) за 10 дней.

Дни

Цены

макс. (Hn)

мин. (Ln)

закр. (Ct)

1

998

970

982

2

970

922

922

3

950

884

902

4

880

823

846

5

920

842

856

6

889

840

881

7

930

865

870

8

890

847

852

9

866

800

802

10

815

680

699

Интервал сглаживания принять равным пяти дням. Рассчитать:

- экспоненциальную скользящую среднюю;

- момент;

- скорость изменения цен;

- индекс относительной силы;

- %R, %K, %D.

Расчеты проводить для всех дней, для которых эти расчеты можно выполнить на основании имеющихся данных.

Решение

Дни (t)

Цена закрытия (Pt)

Повышение цен

Понижение цен

1

982

-

-

2

922

60

3

902

20

4

846

56

5

856

10

6

881

25

7

870

11

8

852

18

9

802

50

10

699

103

а).  экспоненциальная скользящая средняя;

ЕМА t = ЕМА t-1 + k(P t - ЕМА t-1 )

Pt – цена закрытия t-го дня;

t – сегодняшний день;

t-1 – предшествующий (вчерашний) день;

k – параметр сглаживания;

n – порядок скользящей средней (МА);

n=5

k = 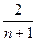= =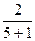=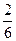0,333

ЕМА 5 - ?

ЕМА 5 =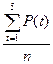==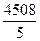 901,6

ЕМА 6 = ЕМА 5 + 0,333(P 6 - ЕМА 5) =901,6 + 0,333*(881 - 901,6) = 894,740

ЕМА 7 = ЕМА 6 + 0,333(P 7 - ЕМА 6)= 894,740 + 0,333*(870 - 894,740) = 886,502

ЕМА 8 = ЕМА 7 + 0,333(P 8 - ЕМА 7) = 886,502+ 0,333*(852 - 886,502) = 875,013

ЕМА 9 = ЕМА 8 + 0,333(P 7 - ЕМА 8) = 875,013+ 0,333*(802 - 875,013) = 850,699

ЕМА 10 = ЕМА 9 + 0,333(P 8 - ЕМА 9)= 850,699+ 0,333*(699 - 850,699) = 800,183

б). момент

МОМ t = Р t -P х

Pt – цена сегодняшнего дня;

Pх – цена х дней назад, включая текущий.

n=5

МОМ5 = Р5 - P1 = 856 – 982 = -126 < 0, значит тренд нисходящий, означает сигнал к продаже.

МОМ6 = Р6 - P2 = 881 – 922 = -41 < 0, значит тренд нисходящий, означает сигнал к продаже.

МОМ7 = Р7 - P3 = 870 - 902 = -32 < 0, значит тренд нисходящий, означает сигнал к продаже.

МОМ8 = Р8 - P4 = 852 – 846 = 6  > 0, значит тренд восходящий, означает сигнал к покупке.

МОМ9 = Р9 - P5 = 802 - 856 = -54 < 0, значит тренд нисходящий, означает сигнал к продаже.

МОМ10 = Р10 - P6 = 699 – 881 = -182 < 0, значит тренд нисходящий, означает сигнал к продаже.

в). скорость изменения цен

ROC t =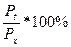

Pt – цена сегодняшнего дня;

Pх – цена х дней назад, включая текущий.

ROC 5 =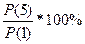= =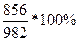 87,169%, так как ROC 5 <100%, то тренд

нисходящий

ROC 6 ===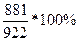 95,553%, так как ROC 6 <100%, то тренд

нисходящий

ROC 7 =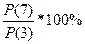=  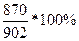= 96,452%, так как ROC 7 <100%, то тренд

нисходящий

ROC 8 ==  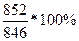= 100,709%, так как ROC 8 >100%, то тренд

восходящий

ROC 9 =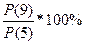=  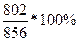= 93,692%, так как ROC 10 <100%, то тренд

нисходящий

ROC 10 =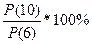=  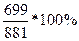= 79,342%, так как ROC 10 <100%, то тренд нисходящий.

г). индекс относительной силы

RSI t =100 -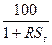

RS t =,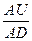

где, AU – сумма приростов конечных цен за n дней, включая текущий;

        AD – сумма убылей за n дней, включая текущий.

RS 5 =,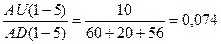

RSI 5 =100 - 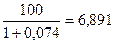, т.к. RSI 5 < 20%, значит цены находятся в «зоне перепроданности», т.е. цены упали слишком низко, надо ждать их роста и готовиться к покупке;

RS 6 =,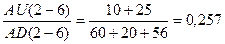

RSI 6 =100 -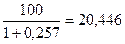

RS 7 =,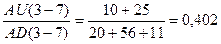

RSI 7 =100 -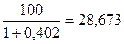

RS 8 =,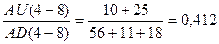

RSI 8 =100 -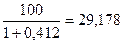

RS 9 =,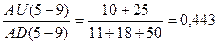

RSI 9 =100 -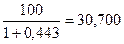

RS 10 =,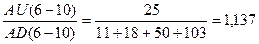

RSI 10 =100 -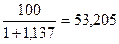

д). %R;  %K и %D

%К=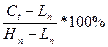

%К – значение индекса текущего дня;

Сt – цена закрытия текущего дня;

Hn – max цена за «n» предшествующих дней, включая текущий;

Ln – min цена за «n» предшествующих дней, включая текущий.

%К5=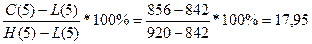%, т.к. %К5 < 20%,то цены находятся в «зоне перепроданности»;

%К6=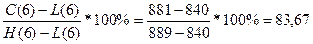%, т.к. %К6 > 80%, то цены находятся в «зоне перепроданности»;

%К7=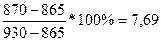%, т.к. %К7 < 20%,то цены находятся в «зоне перепроданности»;

%К8=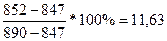% , т.к. %К8 < 20%,то цены находятся в «зоне перепроданности»;

%К9=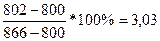%, т.к. %К9 < 20%,то цены находятся в «зоне перепроданности»;

%К10=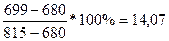%, т.к. %К10 < 20%,то цены находятся в «зоне перепроданности».

%R – значение индекса текущего дня

%Rn=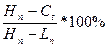

%R5=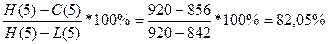, т.к. %R5 > 80%, то цены находятся в «зоне перекупленности»;

%R6=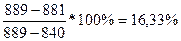, т.к. %R6 < 20%, то цены находятся в «зоне перепроданности»;

%R7=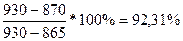, т.к. %R7 > 80%, то цены находятся в «зоне перекупленности»;

%R8=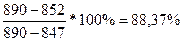, т.к. %R8 > 80%, то цены находятся в «зоне перекупленности»;

%R9=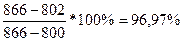, т.к. %R9 > 80%, то цены находятся в «зоне перекупленности»;

%R10=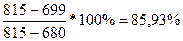, т.к. %R10 > 80%, то цены находятся в «зоне перекупленности».

%Dt =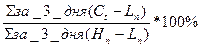

%D7 = = =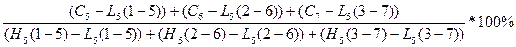

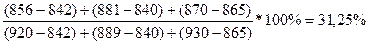
%D8=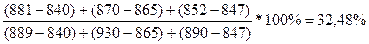

%D9=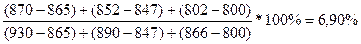, т.к. %D9 < 20%, то цены находятся в «зоне перепроданности»;

%D10=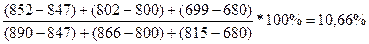, т.к. %D10 < 20%, то цены находятся в «зоне перепроданности».

Задание 3

Выполнить различные коммерческие расчеты, используя данные, приведенные в таблице. В условии задачи значения параметров приведены в виде переменных. Например, S означает некую сумму средств в рублях, Тлет – время в годах, i – ставку в процентах и т.д. По именам переменных таблицы необходимо выбрать соответствующие численные значения параметров и выполнить расчеты.

Сумма

Дата начальная

Дата конечная

Время в днях

Время в годах

Ставка

Число начислений

S

Tн

Тк

Тдн

Тлет

i

m

500000

21.01.02

11.03.02

180

4

10

2

3.1. Банк выдал ссуду, размером S руб. Дата выдачи ссуды – Тн, возврата – Тк. День выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой процентной ставке i % годовых.

Найти:

3.1.1) точные проценты с точным числом дней ссуды;

3.1.2) обыкновенные проценты с точным числом дней ссуды;

3.1.3) обыкновенные проценты с приближенным числом дней ссуды.

Решение

3.1.1) Р = 500000руб.

21.01.02. – 11.03.02.

к = 365 дн.

i = 0,1

I = ?

I = P * n * i            n = t/k

21.01 – 31.01. (11 дн.)

1.02 – 28.02. (28 дн.)

1.03. – 11.06 (11 дн.)

11+28+11 = 50 дн.

t = 50-1 = 49 дн.

n = 49/365

I = 500000 * 49/365 * 0,10 = 6712,32 руб. – точные проценты с точным числом дней ссуды.

3.1.2) Р = 500000руб.

21.01.02. – 11.03.02.

к = 360 дн.

i = 0,1

I = ?

I = P * n * i            n = t/k

11+28+11 = 50 дн.

t = 50-1 = 49 дн.

n = 49/360

I = 500000 * 49/360 * 0,10 = 6805,56 руб. - обыкновенные проценты с точным числом дней ссуды.

3.1.3) Р = 500000руб.

21.01.02. – 11.03.02.

к = 360 дн.

i = 0,1

I = ?

I = P * n * i            n = t/k

10+30+11 = 51 дн.

t = 51-1 = 50 дн.

n = 50/360

I = 500000 * 50/360 * 0,10 = 6944,44 руб. - обыкновенные проценты с приближенным числом дней ссуды.

3.2. Через Тдн дней после подписания договора должник уплатит S руб. Кредит выдан под i % годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?

Решение

S = 500000 руб.

i = 0,1

t = 180 дн.

к = 360 дн.

Р - ? ; D - ?

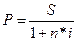;       n = t/k;       D = P – S

n = 180/360

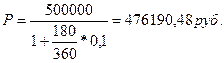 - первоначальная сумма кредита

D = 500000 – 476190,48 = 23809,52 руб. – размер дисконта.

3.3. Через Тдн дней предприятие должно получить по векселю S руб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке i % годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт.

Решение

S = 500000 руб.

d = 0,1

t = 180 дн.

к = 360 дн.

Р - ? ; D - ?

P = S*(1 – n*d);       n = t/k;       D = S - P

Р = 500000*(1 – 180/360*0,1) = 475000 руб. – полученная предприятием сумма;

D = 500000 – 475000 = 25000 руб. – размер дисконта.

3.4. В кредитном договоре на сумму S руб. и сроком на Тлет лет, зафиксирована ставка сложных процентов, равная i % годовых. Определить наращенную сумму.

Решение

P = 500000 руб.

n = 4

i = 0,1

S - ?

S = P*(1 + i)n

S = 500000*(1 + 0,1)4 = 732050 руб. – наращенная сумма.

3.5. Ссуда, размером S руб. предоставлена на Тлет. Проценты сложные, ставка - i % годовых. Проценты  начисляются m раз в году. Вычислить наращенную сумму.

Решение

P = 500000 руб.

n = 4

m = 2

j = 0,1

S - ?

S = P*(1 + j/m)m*n

S = 500000*(1 + 0,1/2)2*4 = 738727,72 руб. – наращенная сумма.

3.6. Вычислить эффективную ставку процента, если банк начисляет проценты m раз в году, исходя из номинальной ставки i % годовых.

Решение

m = 2

j = 0,1

iэ - ?

iэ = (1 + j/m)m - 1

iэ = (1 + 0,1/2)2 – 1 = 0,1025 = 10,25% - эффективная ставка процента.

3.7. Определить, какой должна быть номинальная ставка при начислении процентов m раз в году, чтобы обеспечить эффективную ставку i % годовых.

Решение

iэ = 0,1

m = 2

j - ?

j = m*(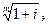 - 1)

j = 2*(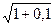 - 1) = 0,976 = 9,76% - номинальная ставка процентов.

3.8. Через Тлет предприятию будет выплачена сумма S руб. Определить ее современную стоимость при условии, что применяется сложная процентная ставка i % годовых.

Решение

S = 500000 руб.

n = 4

i = 0,1

Р - ?

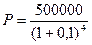= 341506,73 руб. – современная стоимость.

3.9. Через Тлет по векселю должна быть выплачена сумма S руб. Банк учел вексель по сложной учетной ставке i % годовых. Определить дисконт.

Решение

S = 500000 руб.

n = 4

dсл = 0,1

D - ?

D = S – P;       P = S*(1 - dсл)n

Р = 500000*(1-0,1)4 = 328050 руб.

D = 500000 – 328050 = 171950 руб. – размер дисконта.

3.10. В течение Тлет лет на расчетный счет в конце каждого года поступает по S руб., на которые m раз в году начисляются проценты по сложной годовой ставке i %. Определить сумму на расчетном счете к концу указанного срока.

Решение

n = 4

m = 2

R = 500000 руб.

j = 0,1

S - ?

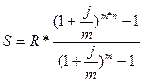
= 2329050 руб. – сумма на расчетном счету к концу 4-го года.