Контрольная работа №2
Задание №1
Комитетом по физической культуре и спорту были
проведены исследования спортсменов, занимающихся стрельбой. Было отобрано 200
стрелков из 4000 для определения среднего количества патронов, необходимых
одному спортсмену для одной тренировки. Результаты обследования представлены в
таблице:
|
Число
Патронов
(шт.)
|
Менее
200
|
200-300
|
300-400
|
400-500
|
500-600
|
600-700
|
Более
700
|
Итого
|
|
Число
спортсменов
|
4
|
20
|
57
|
65
|
31
|
15
|
8
|
200
|
|
Х
|
150
|
250
|
350
|
450
|
550
|
650
|
750
|
|
Найти: а) границы, в которых с вероятность 0,95
заключено среднее число патронов, необходимых для тренировки одного спортсмена;
б) вероятность того, что доля спортсменов, расходующих
более 500 патронов за тренировку, отличается от доли таких спортсменов в
выборке не более чем на 5% (по абсолютной величине);
в) объем бесповторной выборки, при котором те же
границы для среднего числа патронов можно гарантировать с вероятностью 0,9876.
Решение:
В крайних интервалах примем ширину интервалов равной
100, как и у внутренних интервалов. Обозначим признак «число спортсменов» через
Х. За значения признака примем середины интервалов, значения признака приведены
в третьей строке. Объем вариационного ряда равен n=200, и полный объем данных N=4000.
Вычислим выборочную среднюю и исправленную выборочную
дисперсию для распределения величины Х.
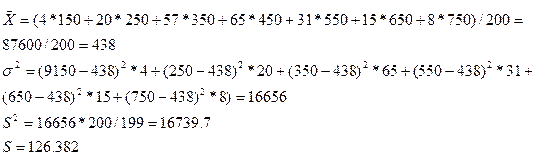
1)
Найдем границы, в
которых с вероятностью 0,95 заключено среднее число патронов.
Так как выборка бесповторная, то среднее
квадратическое отклонение генеральной средней вычисляется по формуле:
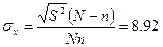
Получим 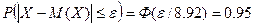 . Отсюда
. Отсюда 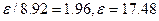
И получим неравенство для среднего числа патронов
420,52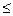 M(X)
M(X) 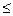 455.48
455.48
2) Выборочная доля спортсменов, у которых число
патронов более 500 по таблице равна (31+15+8)/200=0.27. Найдем вероятность того,
что доля таких спортсменов отличается не более чем на 5% (0,05).
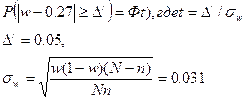
Тогда t=1,61
По таблице функции Лапласа находим , что при t=1,61 P=0,8923.
Таким образом, вероятность равна 989,23%.
2)
Найдем число
рабочих, которых следует выбрать, чтобы вероятность выполнения условия: 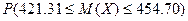 станет равной 0,9876.
станет равной 0,9876.
При бесповторной выборке для определения необходимого
объема выборки, при которой с вероятностью Р=0,9876 можно утверждать, что
средняя отличается от математического ожидания по абсолютной величине меньше
чем на 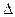 =17,48 используется формула:
=17,48 используется формула: 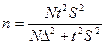
По таблице функции Лапласа находим, что при Р =0,9876 t=2,5 и, следовательно вычисляем необходимый объем
выборки по приведенной формуле: n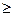 341.
341.
Задание №2
По данным задачи 1, используя критерий 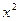 - Пирсона, при уровне значимости
- Пирсона, при уровне значимости 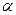 =0,05 проверить гипотезу о том, что случайная величина Х –число
патронов – распределена нормальному закону. Построить на одном чертеже
гистограмму эмпирического распределения и соответствующую нормальную кривую.
=0,05 проверить гипотезу о том, что случайная величина Х –число
патронов – распределена нормальному закону. Построить на одном чертеже
гистограмму эмпирического распределения и соответствующую нормальную кривую.
Решение:
Критерий Пирсона есть критерий проверки гипотезы о
предлагаемом законе неизвестного распределения. В последующей таблице
приводятся эмпирические частоты, рассчитываются теоретические вероятности,
исходя из предположения о нормальности распределения с параметрами,
рассчитанными в задаче 1. 
В третьем столбце приводятся теоретические частоты,
для чего вероятность попадания в данный интервал для величин, имеющих
нормальное распределение, умножаются на количество данных. В последних столбцах
рассчитаны вспомогательные величины.
Для расчета
вероятностей используем таблицы функции Лапласа.
Например,
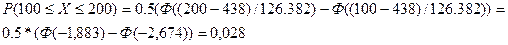
|
Интервал
|
|
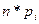
|
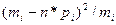
|
|
100-200
|
4
|
5,63
|
0,67
|
|
200-300
|
20
|
21,98
|
0,20
|
|
300-400
|
57
|
48,35
|
1,31
|
|
400-500
|
65
|
60,06
|
0,37
|
|
500-600
|
31
|
42,16
|
4,01
|
|
600-700
|
15
|
16,70
|
0,19
|
|
700-800
|
8
|
3,73
|
2,28
|
|
|
|
|
9,04
|
|
|
|
Теория
|
9,49
|
Вычисляем величину
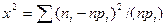
В рассматриваемом случае статистика
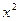 =9,81.
=9,81.
Так как число интервалов равно 7, то число степеней
свободы в данном случае равно 7-2-1=4. Соответствующее критическое значение статистики
на уровне значимости 0,05 равно 9,49. Так как 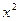 <9,49, то гипотеза о нормальности данного распределения не
отвергается. Таким образом, случайная величина – число спортсменов может быть
распределена по нормальному закону.
<9,49, то гипотеза о нормальности данного распределения не
отвергается. Таким образом, случайная величина – число спортсменов может быть
распределена по нормальному закону.
Для наглядности построим гистограмму эмпирического
распределения и соответствующую нормальную кривую.
Так как длинна интервала равна 100, эмпирические
частоты умножаем на 100, график нормальной кривой строим по точкам.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
70
|
|
|
|
|
|
|
|
|
|
|
|
|
60
|
|
|
|
|
|
|
|
|
|
|
|
|
50
|
|
|
|
|
|
|
|
|
|
─
Гистограмма
|
|
|
40
|
|
|
|
|
|
|
|
|
|
Норм.распр.
|
|
|
30
|
|
|
|
|
|
|
|
|
|
|
|
|
20
|
|
|
|
|
|
|
|
|
|
|
|
|
10
|
|
|
|
|
|
|
|
|
|
|
|
|
0
|
100
|
200
|
300
|
400
|
500
|
600
|
700
|
800
|
|
|
|
Задание №3
В таблице приведено распределение 200 драгоценных
изделий по количеству примесей в них Х(%) и стоимости Y(тыс.руб.):
|
Y
X
|
3-9
|
9-15
|
15-21
|
21-27
|
27-33
|
Более
33
|
Итого
|
|
20-30
|
|
|
|
2
|
5
|
2
|
9
|
|
30-40
|
|
|
4
|
8
|
4
|
3
|
19
|
|
40-50
|
|
|
4
|
10
|
20
|
10
|
44
|
|
50-60
|
|
5
|
36
|
23
|
6
|
|
70
|
|
60-70
|
|
12
|
11
|
11
|
|
|
34
|
|
70-80
|
6
|
10
|
|
|
|
|
16
|
|
80-90
|
8
|
|
|
|
|
|
8
|
|
Итого
|
14
|
27
|
55
|
54
|
35
|
15
|
200
|
Необходимо:
1)
вычислить
групповые средние и построить эмпирические линии регрессии;
2)
предполагая, что
между переменными X и Y существует
линейная корреляционная зависимость: а) найти уравнения прямых регрессии и
построить их графики на одном чертеже с эмпирическими
линиями регрессии; б) вычислить коэффициент корреляции на уровне значимости
а=0,05, оценить его значимость и сделать вывод о тесноте и направлении
связи между переменными X и Y; в) используя
соответствующее уравнение регрессии, определить количество примесей в
драгоценном изделии, если его стоимость составляет 25 тыс. руб.
Решение:
Составим таблицу для расчета вспомогательных величин,
через которое выражается средние и дисперсии случайных величин Х и Y.
Вычислим групповые средние.
В 8 и 9 колонках приведены следующие величины:
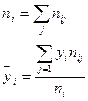
В 10 и 11 строках приведены следующие величины:

Для средних величин получаем значения по формулам:
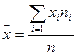 =54,05
=54,05
 =21,42
=21,42
Выборочная дисперсия переменной Х вычисляется по
формуле:
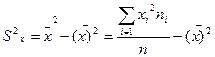 =184,6. Выборочная дисперсия переменнойY вычисляется
по формуле:
=184,6. Выборочная дисперсия переменнойY вычисляется
по формуле:
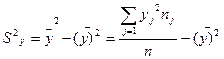 =62,46. В ячейке (11 строка, 9 колонка) вычислено значение
=62,46. В ячейке (11 строка, 9 колонка) вычислено значение 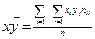 =1077,90.
=1077,90.
Выборочный корреляционный момент вычисляется по
формуле:
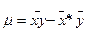 =-79,85.
=-79,85.
Приведем всю построенную таблицу:
|
Y
|
3-9
|
9-15
|
15-21
|
21-27
|
27-33
|
33-39
|
Сумма
|
Групповая средняя
|
|
|
X
|
|
|
6
|
12
|
18
|
24
|
30
|
36
|
|
|
|
|
25
|
|
|
|
2
|
5
|
2
|
9
|
30
|
|
|
35
|
|
|
4
|
8
|
4
|
3
|
19
|
25,89
|
|
|
45
|
|
|
4
|
10
|
20
|
10
|
44
|
28,91
|
|
|
55
|
|
5
|
36
|
23
|
6
|
|
70
|
20,57
|
|
|
65
|
|
12
|
11
|
11
|
|
|
34
|
17,82
|
|
|
75
|
6
|
10
|
|
|
|
|
16
|
9,75
|
|
|
85
|
8
|
|
|
|
|
|
8
|
6
|
|
|
Сумма
|
14
|
27
|
55
|
54
|
35
|
15
|
200
|
|
|
|
средняя
|
80,71
|
66,85
|
54,82
|
51,11
|
42,71
|
40,33
|
|
1077,9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
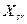
|
54,05
|

|
184,6
|
µ=
|
-79,85
|
|
|
|
|
|

|
21,42
|
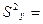
|
62,46
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Yx=ByxX+D1
|
|
Xy=BxyY+D2
|
|
|
|
|
|
|
|
|
Byx
|
D1
|
Bxy
|
D2
|
Xsr
|
Ysr
|
r
|
t
|
|
|
|
-0,43
|
44,8
|
-1,28
|
81,43
|
54,05
|
21,42
|
-0,74
|
15,65
|
|
|
Уравнения регрессий имеют вид: