Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Всероссийский заочный финансово-экономический институт

(филиал в г. Барнауле)

Факультет	Региональная кафедра
«Учетно-статистический»	Математики и Информатики

Контрольная работа по эконометрике

Студентка
Специальность	Бухгалтерский учет, анализ и аудит
№ личного дела Группа
Образование	Первое высшее
Дисциплина	Эконометрика
Научный руководитель

Допускается к защите                                             «__» _______ 200_г._____________  (подпись)

Работа защищена                 ___________             «__» _______ 200_г._____________  (подпись)

          (оценка)

Барнаул 2007

Задача №1.

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (X, млн. руб.).

Х	33	17	23	17	36	25	39	20	13	12
У	43	27	32	29	45	35	47	32	22	24

Требуется:

1.     Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2.     Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков Sε^2; построить график остатков.

3.     Проверить выполнение предпосылок МНК.

4.     Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α = 0,05.).

5.     Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α = 0,05.), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

6.     Осуществить прогнозирование среднего значения показателя Y при уровне значимости α = 0,1, если прогнозное значение фактора X составит 80% от его максимального значения.

7.     Построить графически: фактические и модельные значения Y, точки прогноза.

8.     Составить уравнение нелинейной регрессии:

·        Гиперболической;

·        Степенной;

·        Показательной.

    Привести графики построенных уравнений регрессии.

9.     Для указанных моделей найти коэффициенты детерминации и средние

относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

Решение:

1). Уравнение линейной регрессии имеет вид: ŷ = a + b ´ x;

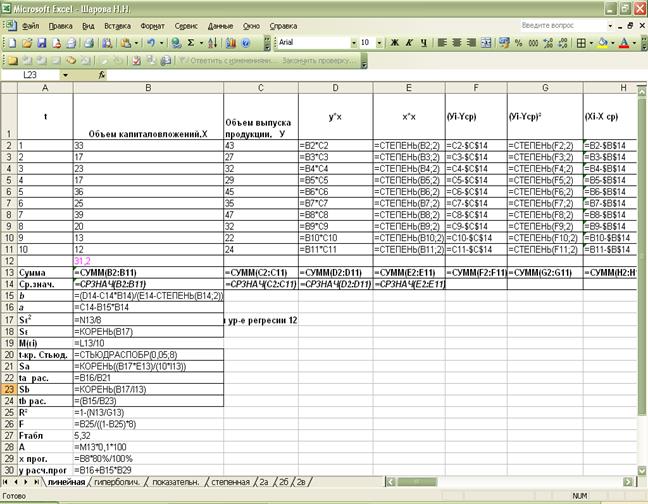
Значения параметров а и b линейной модели, определим используя данные таблицы 1 по формулам:

b =  (y∙x)_ср.- у_ср∙х_ср.: х²_ср.- х_ср.²

а = у_ср.- b∙х_ср.

 

t	Объем капиталовложений,Х	Объем выпуска продукции,   У	у*х	х*х	(Уi-Yср)	(Уi-Yср)²	(Хi-X ср)	(Хi-X ср)²	(Уi-Yср)*(Xi-X ср)
1	33	43	1419	1089	9,4	88,36	9,5	90,25	89,3
2	17	27	459	289	-6,6	43,56	-6,5	42,25	42,9
3	23	32	736	529	-1,6	2,56	-0,5	0,25	0,8
4	17	29	493	289	-4,6	21,16	-6,5	42,25	29,9
5	36	45	1620	1296	11,4	129,96	12,5	156,25	142,5
6	25	35	875	625	1,4	1,96	1,5	2,25	2,1
7	39	47	1833	1521	13,4	179,56	15,5	240,25	207,7
8	20	32	640	400	-1,6	2,56	-3,5	12,25	5,6
9	13	22	286	169	-11,6	134,56	-10,5	110,25	121,8
10	12	24	288	144	-9,6	92,16	-11,5	132,25	110,4
	31,2
Сумма	235	336	8649	6351	0,00	696,4	0	828,5	753,00
Ср.знач.	23,5	33,6	864,9	635,1

Рассчитаем параметры а и b, используя следующие данные, рассчитанные при помощи MS Excel:

b	0,91
a	12,24

Уравнение линейной регрессии имеет вид: ŷ = 12,24+0,91∙х.

С увеличением объема капиталовложений на 1млн.руб. объем выпускаемой продукции увеличиться в среднем на 910 тыс.руб. Это свидетельствует о эффективной работе предприятия.

Теперь находим Yрасч. путем подставления х в уравнение регрессии:

t	Объем капиталовложений,Х	Объем выпуска продукции,   У	Ŷ
1	33	43	42,234
2	17	27	27,692
3	23	32	33,146
4	17	29	27,692
5	36	45	44,961
6	25	35	34,963
7	39	47	47,688
8	20	32	30,419
9	13	22	24,057
10	12	24	23,148
	31,2		40,60
Сумма	235	336	336
Ср.знач.	23,5	33,6

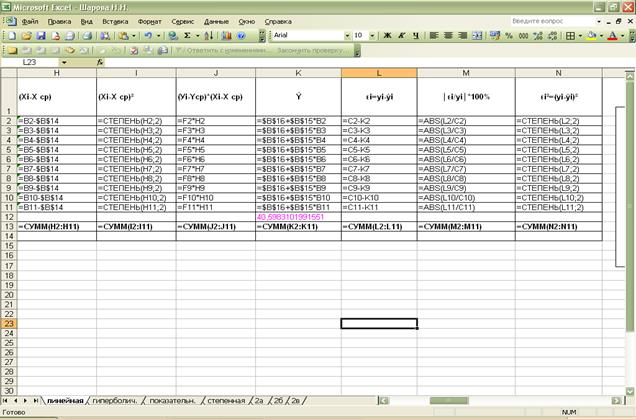
2). Вычисляем остатки по формуле: εi = Yi – Yрасч.

Находим остаточную сумму квадратов и оценим дисперсию остатков:

t	Объем капиталовложений,Х	Объем выпуска продукции,   У	Ŷ	εi=yi-ŷi	│εi/yi│*100%	εi²=(yi-ŷi)²
1	33	43	42,234	0,76572	0,01780747	0,5863289
2	17	27	27,692	-0,69234	0,02564206	0,4793285
3	23	32	33,146	-1,14556	0,03579888	1,3123175
4	17	29	27,692	1,30766	0,04509188	1,7099863
5	36	45	44,961	0,03911	0,00086904	0,0015293
6	25	35	34,963	0,03669	0,00104837	0,0013464
7	39	47	47,688	-0,68751	0,01462782	0,4726666
8	20	32	30,419	1,58105	0,04940782	2,4997194
9	13	22	24,057	-2,05685	0,09349317	4,2306308
10	12	24	23,148	0,85202	0,03550091	0,725941
	31,2		40,60
Сумма	235	336	336	1,07E-14	31,93%	12,019795
Ср.знач.	23,5	33,6

Sε2	1,502
Sε	1,226

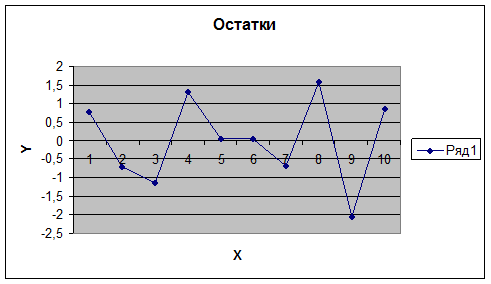
3). Проверка выполнения предпосылок МНК:

1-е условие:

M(εi) = 1,07E-14/10 = 1,07E-15 – что приблизительно равно нулю. Это означает, что первое условие выполняется. Оценка является несмещенной.

2-е условие:

Возмущение εi есть величина случайная, а Xi – неслучайная.

3-е условие:

Связь между значениями случайной величины в любых двух наблюдениях отсутствует.

4-е условие:

Sεi постоянна для всех наблюдений и равна 1,226.

Оценка является эффективной.

4). Осуществим проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента. Для этого при помощи ППП MS Excel рассчитаем необходимые данные:

t-кр. Стьюд.	2,31
Sa	1,07
ta - рас.	11,41
Sb	0,04
tb-рас.	21,34

tα-расч. > tтабл. следовательно данный параметр уравнения является значимым.

tβ-расч. > tтабл. следовательно коэффициент регрессии является значимым для уравнения регрессии.

6). Рассчитаем эти данные при помощи MS Excel:

R²	0,983
F	7,12
Fтабл	5,32
А	3,19

R² приблизительно равен 1, следовательно качество модели высокое.

Средняя относительная ошибка аппроксимации меньше 7%, значит качество модели хорошее.

Fрасч. > Fтабл. – модель считается значимой.

Следовательно, модель является хорошей, точной, качественной.

 

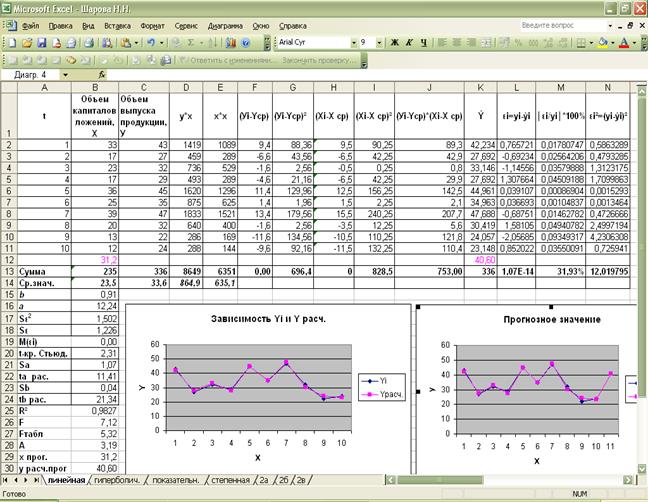
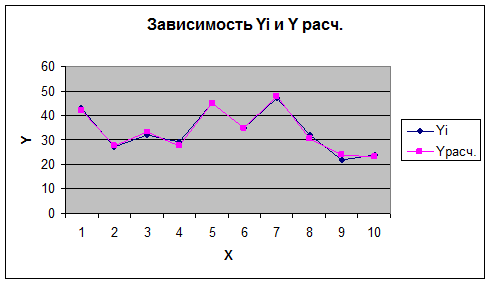
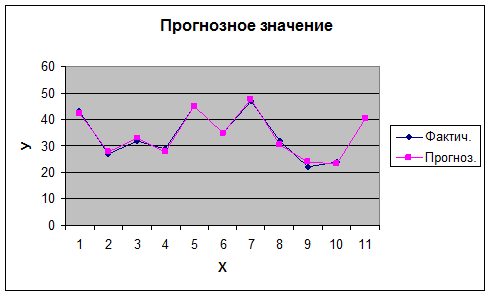
6-7).

Осуществим прогнозирование и построим графики также при помощи MS Excel.

х прог.	31,2
у расч.прог	40,60

Хпрог.= 39*80% : 100%=31,2;

Ур.прог.= 12,24+0,91*31,2=40,6

Представим расчеты в формульном виде:

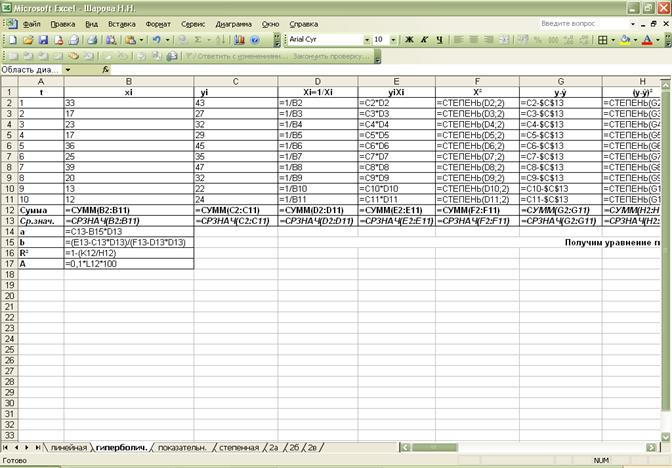
8-9). С помощью ППП MS Excel составим уравнения нелинейной регрессии и найдем для каждого коэффициенты детерминации и средние относительные ошибки аппроксимации, построим графики.

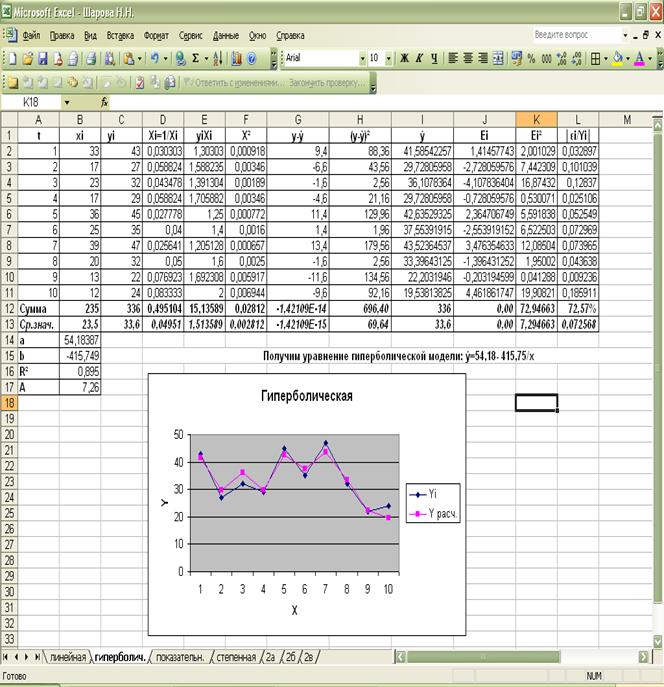
Гиперболическая модель: ŷ=54,18- 415,75/х.

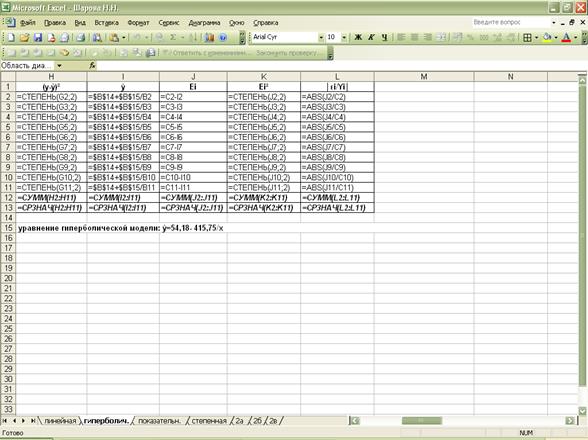
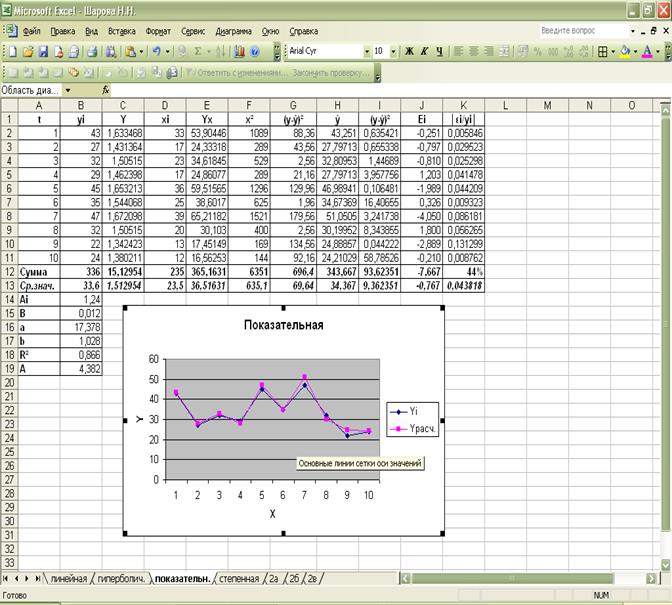
Показательная модель: ŷ=17,38 ∙ 1,028^х.

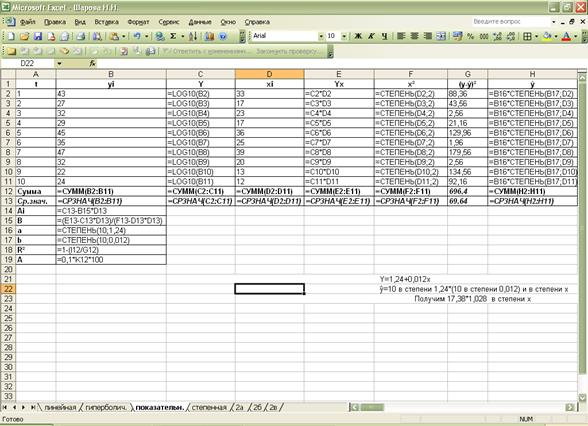
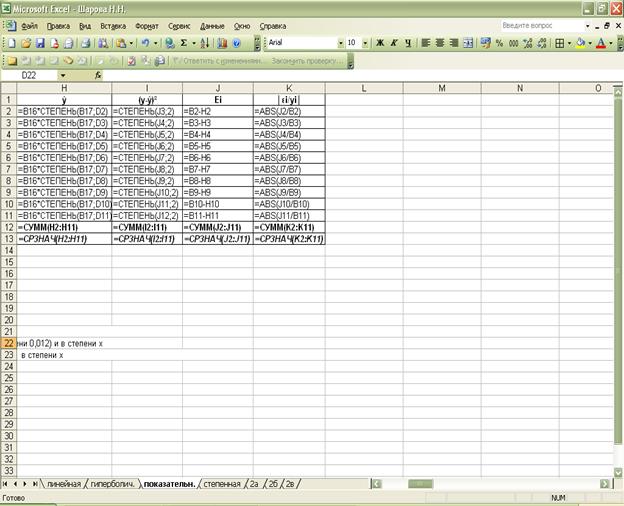
Степенная модель: ŷ=(4,742 ∙ х)^0,625.

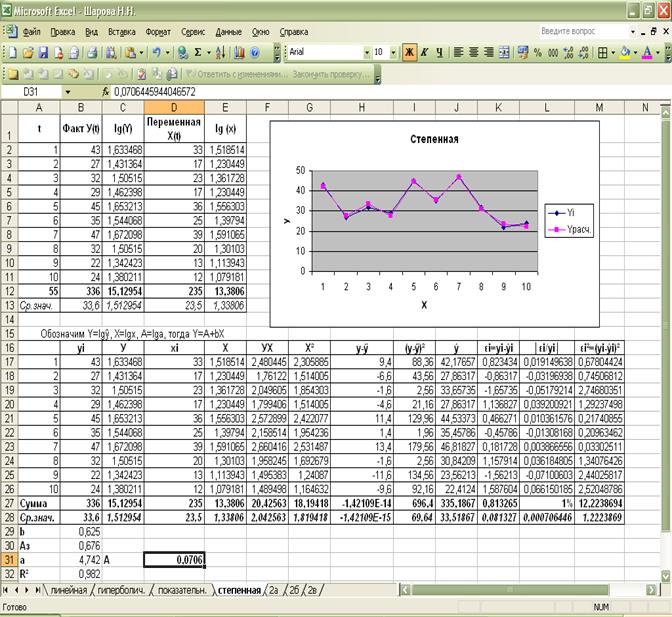
Вывод:

Все модели имеют примерно одинаковые характеристики, однако наибольший коэффициент детерминации имеют две модели степенная и линейная, однако у линейной модели средняя ошибка аппроксимации = 3,19, а у степенной = 0,0706, поэтому степенную модель целесообразнее взять в качестве наилучшей.

Задача №2.

Даны по две СФМ, которые заданы в виде матриц коэффициентов модели. Необходимо записать системы одновременных уравнений и проверить обе системы на идентифицируемость.

2а)

1	-1	b12	b13	a11	a12	0	0
2	b21	-1	b23	a21	0	0	a24
3	0	b32	-1	a31	a32	a33	0

2б).

1	-1	0	b13	a11	a12	0	a14
2	b21	-1	0	a21	0	a23	a24
3	b31	0	-1	a31	a32	0	a34

 

2в). По данным таблицы для своего варианта, используя косвенный метод наименьших квадратов, построить структурную форму модели вида 

y₁= a₀₁  + b₁₂ y₂ +  a₁₁ x₁ + e₁                                                                                                   

y₂= a₀₂  + b₂₁ y₁ + a₂₂ x₂ + e₂

n	у1	у2	х1	х2
1	77,5	70,7	1	12
2	100,6	94,9	2	16
3	143,5	151,8	7	20
4	97,1	120,9	8	10
5	63,6	83,4	6	5
6	75,3	84,5	4	9

Решение:

2а).

Запишем систему одновременных уравнений:

-1y1+b12y2+b13y3+a11x1+a12x2                                                        

b21y1-1y2+b23y3+a21x1+a24x4                                                          

b32y2-1y3+a31x1+a32x2+a33x3

Выражаем из каждого уравнения у:

y1=b12y2+b13y3+a11x1+a12x2                                                           

y2=b21y1+b23y3+a21x1+a24x4                                                           

y3=b32y2+a31x1+a32x2+a33x3

Проверяем данную систему уравнений на необходимое условие идентификации:

1). Н=3; Д=2; 2+1=3, уравнение идентифицируемо                                      

2). Н=3; Д=2; 2+1=3, уравнение идентифицируемо                                      

3). Н=2; Д=1, 1+1=2, уравнение идентифицируемо.

Проверяем систему по достаточному условию идентификации:

1)	№ ур-я	переменные
	х3	х4
	2	0	а24
	3	а33	0
Определитель матрицы = 0*0-а24*а33= -а24*а33, т.е.≠ 0. Ранг матрицы=2, условие выполняется
2)	№ ур-я	переменные
	х2	х3
	1	а12	0
	3	а32	а33
М ≠ 0, ранг =2, т.е. достаточное условие выполняется.
3)	№ур-я	переменные
	у1	х4
	1	-1	0
	2	в21	а24
М ≠ 0, т.е. условие выполняется.

                                                                                                                          Вывод:

Система одновременных уравнений является идентифицируемой, т.к. каждое уравнение этой системы идентифицируемо по необходимому и достаточному условиям идентификации.

        

2б).

1у1+b13y3+a11x1+a12x2+a14x4                                                

b21y1-1y2+a21x1+a23x3+a24x4                                                           

b31y1-1y3+a31x1+a32x2+a34x4  

y1= b13y3+a11x1+a12x2+a14x4            

y2=b21y1+a21x1+a23x3+a24x4                                                            

y3= b31y1+a31x1+a32x2+a34x4                                                                                                                                                                                               Необходимое условие идентификации:

1). Н=2; Д=1, 1+1=2, т.е. уравнение идентифицируемо.

2). Н=2; Д=1, 1+1=2, т.е. уравнение идентифицируемо.

3). Н=2; Д=1, 1+1=2, т.е. уравнение идентифицируемо.

Достаточное условие идентификации:

1).	№ ур-я	переменные
	y2	x3
	2	-1	a23
	3	0	0
M= -1*0-a23*0=0, т.е. уравнение неидентифицируемо
2).	№ ур-я	переменные
	у3	х2
	1	b13	a12
	3	-1	a32
М ≠ 0, ранг матрицы=2, т.е. уравнение идентифицируемо.
3).	№ ур-я	переменные
	у3	х2
	1	0	0
	2	-1	а23
М=0, т.е. уравнение неидентифицируемо. Вывод: Система одновременных уравнений является неидентифицируемым, т.к. два уравнения этой системы неидентифицируемы. 2в) Структурную модель преобразуем в приведенную форму модели: Y1 = δ11X1 + δ12X2 + U1 Y2= δ21X1 + δ22X2 + U2 Для расчета коэффициентов приведенной формы модели применим МНК, используя следующие данные: n у1 у2 х1 х2 у1*х1 х12 х1*х2 у1*х2 у2*х1 у2*х2 х22 1 77,5 70,7 1 12 77,5 1 12 930 70,7 848,4 144 2 100,6 94,9 2 16 201,2 4 32 1609,6 189,8 1518,4 256 3 143,5 151,8 7 20 1004,5 49 140 2870 1062,6 3036 400 4 97,1 120,9 8 10 776,8 64 80 971 967,2 1209 100 5 63,6 83,4 6 5 381,6 36 30 318 500,4 417 25 6 75,3 84,5 4 9 301,2 16 36 677,7 338 760,5 81 Сумма 557,6 606,2 28 72 2742,8 170 330 7376,3 3128,7 7789,3 22801 Ср.знач. 92,9333 101,03 4,667 12               Используем следующую систему нормальных уравнений: ∑Y1X1 = δ11∑ X12 + δ12∑ X1X2 ∑Y1X2 = δ11∑ X1X2 + δ12 ∑X22 2742,8=170δ11+330δ12 7376,3=330δ11+1006δ12 Решение этих уравнений дает значения: δ11 = 5,235 δ12  = 5,615. Используем следующую систему нормальных уравнений: ∑Y2X1 = δ21∑X12 + δ22∑X2X1 ∑Y2X2 = δ21∑ X1X2 + δ22∑ X22 3128,7 =170δ21 + 330 δ22 7789,3= 330δ21+ 1006 δ22 Решение этих уравнений дает значения: δ21 = 9,291 δ22 = 4,695. Y1 = 5,235X1 + 5,615X2 + U1 Y2= 9,291X1 + 4,695X2 + U2 Перейдем к структурной форме модели: Выразим X2 из второго уравнения приведенной формы модели: Х2=Y2 - 9,291Х1 : 4,695. Подставим это выражение в первое уравнение приведенной формы модели. Получим: b12 = 1,196 a11 = -5,877. Выразим X1 из первого уравнения приведенной формы модели: X1 = Y1 –5,615X2 : 5,235 Подставим это выражение  во второе уравнение приведенной формы модели. Получим: b21 = 1,775 a22 = -5,273. Свободные члены структурной формы находим из уравнений: A01 = Y1ср. - b12y2 ср.- a11x1 ср. = 92,933-1,196∙101,033+5,872∙4,667=-0,497. A02 = Y2ср. - b21y1ср. - a22x2 ср.= 101,033-1,775∙92,933+5,273∙12=-0,647. Окончательный вид структурной модели: Y1 = -0,497 + 1,196y2 -5,877x1 + ε1 Y2 = -0,647+ 1,775y1 -5,273x2 + ε2