1. Практическая
задача 1
1.1.
Условие и исходные данные
Вариант выданного задания – 4.
Условие задачи: По предприятиям легкой
промышленности региона получена характеризующая
зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (Х,
млн. руб.).
Таблица 1.1-Исходные данные
|
Y
|
60
|
68
|
74
|
76
|
84
|
86
|
92
|
|
X
|
50
|
54
|
60
|
62
|
70
|
66
|
74
|
Требуется:
1
для характеристики Y
от Х построить следующие модели:
-
линейную;
-
степенную;
-
показательную;
-
гиперболическую.
2.
оценить каждую модель, определив:
-
индекс корреляции,
-
среднюю относительную ошибку,
-
коэффициент детерминации,
-
F-критерий
Фишера.
3.
составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию
рассчитанных характеристик.
4.
рассчитать прогнозные значения результативного признака, если прогнозное значение фактора
увеличится на 10% относительно максимального
уровня.
5.
результаты расчетов отобразить на графике
1.2. Решение задачи
Проводим
корреляционный анализ.
Таблица 1.2- Линейная
модель парной регрессии.
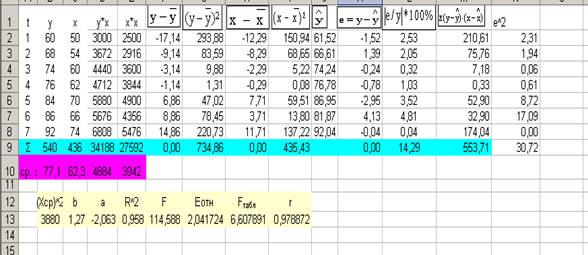
1.2.1 Определим
линейный коэффициент парной корреляции по следующей формуле:
.
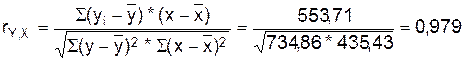Можно
сказать, что связь между объемом капиталовложений Х и объемом выпуска продукции
Y
прямая, достаточно сильная.
Уравнение
линейной регрессии имеет вид: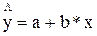 
Значения
параметров a
и b
линейной модели определим, используя данные таблицы 1.2.
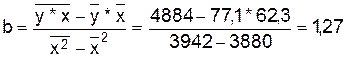
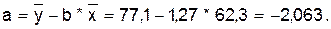
Уравнение
линейной регрессии имеет вид:
.
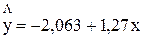С
увеличением объема капиталовложений на 1
млн руб. объем выпускаемой продукции увеличится в среднем на 1270 тыс. руб. Это свидетельствует
о эффективности производства .
1.2.2 Рассчитаем
коэффициент детерминации:
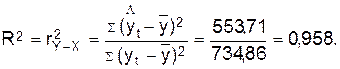
Вариация
результата Y
(объема выпуска продукции) на 95,8%
объясняется вариацией фактора Х (объем капиталовложений).
1.2.3 Оценку значимости
уравнения регрессии проведем с помощью F-критерия Фишера:
.
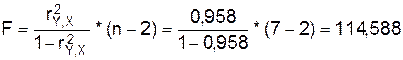F табличное для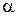 
= 0,05; k1=m=1, k2=n-m-1=5 равно 6,61 =>F>Fтабл.
Уравнение регрессии с
вероятностью 0,95 в целом статистически значимо, т.к. F>Fтабл
1.2.4 Определим среднюю
относительную ошибку:
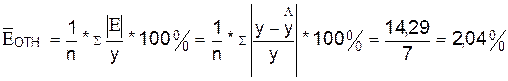
В
среднем расчетные значения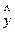 
для линейной модели отличаются от фактических значений на 2,04%.
1.3 Построение степенной модели парной регрессии.
Уравнение степенной имеет вид:
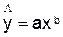
Для
построения этой модели необходимо произвести линеаризацию переменных. Для этого
произведем логарифмирование обеих частей уравнения:
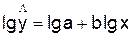
Таблица 1.3- Степенная модель
парной регрессии.
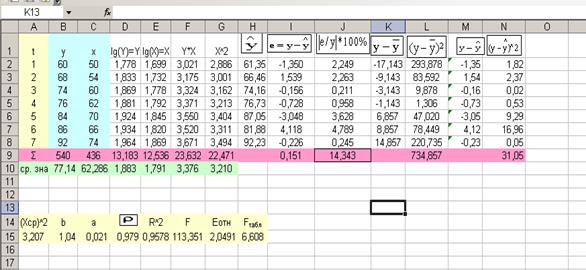
Обозначим
Y=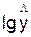 
, Х=
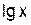, А=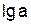
.
1.3.1 Тогда уравнение имеет
вид: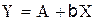 
- линейное уравнение регрессии.
,
.
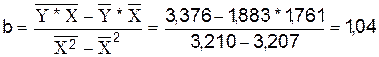1.3.2 Перейдем к исходным
переменным x
и y,
выполнив потенцирование данного уравнения.
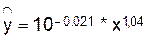
1.3.3 Определим индекс корреляции:
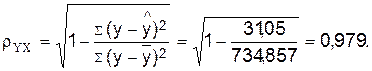
Связь
между показателями y
и фактором х можно считать достаточно сильной.
1.3.4 Рассчитаем индекс
детерминации:
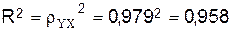
Вариация
результата Y
(объема выпуска продукции) на 95,8% объясняется вариацией
фактора Х (объем капиталовложений).
1.3.5 Оценку значимости
уравнения регрессии проведем с помощью F-критерия Фишера:
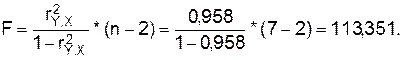
F табличное для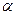 
= 0,05; k1=m=1, k2=n-m-1=5 равно 6,61 =>F>Fтабл.
Уравнение
регрессии с вероятностью 0,95 в целом статистически значимо, т.к. F>Fтабл
1.3.6 Определим среднюю
относительную ошибку:
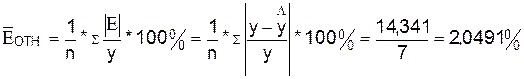
В
среднем расчетные значения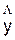 
для линейной модели отличаются от фактических значений на 2,0491%.
1.4 Построение
показательной функции.
Уравнение
степенной имеет вид:
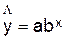
Для
построения этой модели необходимо произвести линеаризацию переменных. Для этого
произведем логарифмирование обеих частей уравнения:
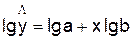
Обозначим
Y=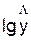 
, B=
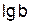, А=.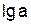
Тогда
уравнение имеет вид: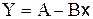 
- линейное уравнение регрессии.
Рассчитаем
его параметры, используя данные таблицы 1.4
Таблица
1.4- Показательная
модель
парной регрессии.
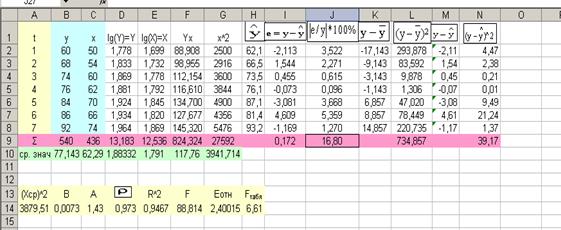
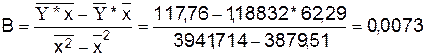
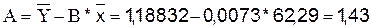
Уравнение будет иметь вид:
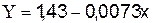
Перейдем
к исходным уравнениям, проведя потенцирование данного уравнения:
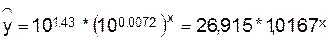
Определим
индекс корреляции:
.
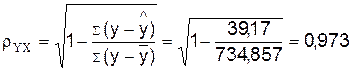Связь
между показателями y
и фактором х можно считать достаточно сильной.
Рассчитаем
индекс детерминации:
Вариация
результата Y
(объема выпуска продукции) на 94,7%
объясняется вариацией фактора Х (объем капиталовложений).
Оценку
значимости уравнения регрессии проведем с помощью F-критерия Фишера:
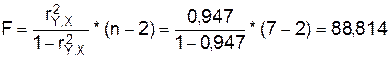
F табличное для 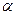= 0,05; k1=m=1, k2=n-m-1=5 равно 6,61 =>F>Fтабл.
Уравнение регрессии с
вероятностью 0,95 в целом статистически значимо, т.к. F>Fтабл
Определим
среднюю относительную ошибку:
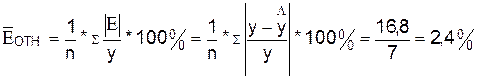
В
среднем расчетные значения 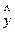для линейной модели отличаются от фактических значений на 2,4%.
1.5 Построение
гиперболической функции.
Уравнение
гиперболической функции:
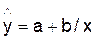
Произведем
линеаризацию модели путем замены X=1/x. В результате получим линейное уравнение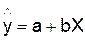 
.
Рассчитаем
его параметры по данным таблицы 1.5.
Таблица 1.5- Гиперболическая функция
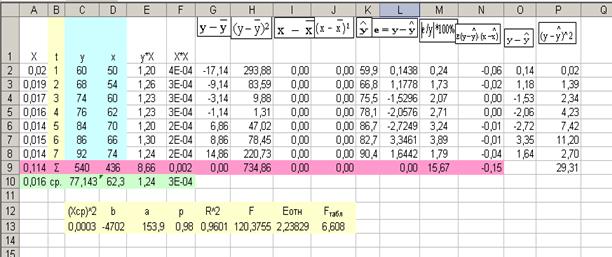
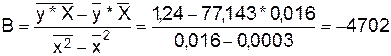
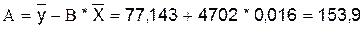
Уравнение
будет иметь вид:
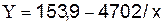
Определим
индекс корреляции:
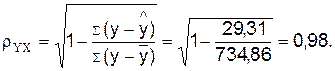
Связь
между показателями y
и фактором х можно считать достаточно сильной.
Рассчитаем
индекс детерминации:
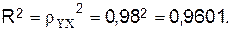
Вариация
результата Y
(объема выпуска продукции) на 96,01%
объясняется вариацией фактора Х (объем капиталовложений).
Оценку
значимости уравнения регрессии проведем с помощью F-критерия Фишера:
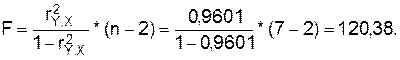
F табличное для 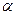= 0,05; k1=m=1, k2=n-m-1=5 равно 6,61 =>F>Fтабл.
Уравнение регрессии с
вероятностью 0,95 в целом статистически значимо, т.к. F>Fтабл
Определим
среднюю относительную ошибку:
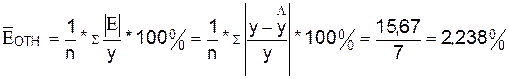
В
среднем расчетные значения 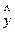для линейной модели отличаются от фактических значений на 2,238%.
1.6 Для
выбора лучшей модели построим
сводную таблицу результатов (таблица 1.6):
Таблица
1.6-Сводная таблица
|
|
R^2
|
f-критерии
|
r
|
Eотн
|
|
линейная
|
0,9582
|
114,588
|
0,805
|
2,042
|
|
степенная
|
0,9578
|
113,351
|
0,9786
|
2,049
|
|
показательная
|
0,9467
|
88,814
|
0,973
|
2,4
|
|
гиперболическая
|
0,9601
|
120,375
|
0,9799
|
2,238
|
Большее
значение F-критерия
Фишера и большее значение коэффициента детерминации R2 имеет гиперболическая
модель. Следовательно, эту модель можно взять в качестве лучшей для построения
прогноза.
Рассчитаем
прогнозное значение результативного признака.
Прогнозное значение
результативного признака (объема выпуска продукции) определим по уравнению
гиперболической модели, подставив в него планируемую величину капиталовложений.
Прогнозное
значение увеличится на 10 % относительно максимального =>74+74*0,1=81,4
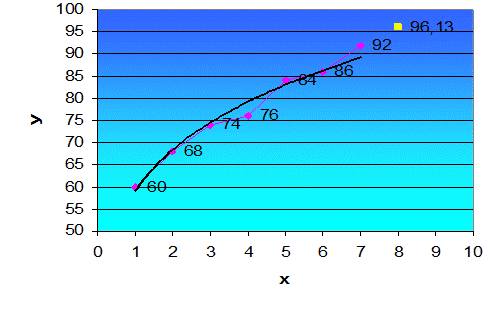
Рисунок 1.1-График результатов расчета
2. Практическая
часть работы
Вариант-9
2.1. По
десяти кредитным учреждениям получены данные, характеризующие зависимость
объема прибыли (Y)
от среднегодовой ставки по кредитам (Х1), ставки по депозитам (Х2)
и размера внутрибанковских расходов (Х3).
Требуется:
1. осуществить
выбор факторных признаков для построения двухфакторной регрессионной модели.
2. рассчитать
параметры модели.
3. для
характеристики модели определить
-
линейный коэффициент множественной корреляции.
-
коэффициент детерминации
-
средние коэффициенты эластичности
-
бета-, дельта- коэффициенты.
Дать
их интерпретацию.
4. осуществить
оценку надежности уровня регрессии.
5. оценить
с помощью t-критерия
Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.
6. построить
точечный и интервальный прогнозы результирующего показателя.
7. отразить
результаты расчетов на графике
Выполнение
задач отразить в аналитической записке, приложить компьютерные распечатки
расчетов.
Таблица 2.1-Исходные данные
|
Y
|
86
|
94
|
100
|
96
|
134
|
114
|
122
|
118
|
130
|
108
|
|
X1
|
60
|
68
|
64
|
72
|
78
|
90
|
82
|
92
|
94
|
68
|
|
X2
|
56
|
48
|
52
|
58
|
66
|
62
|
48
|
66
|
70
|
68
|
|
X3
|
30
|
40
|
44
|
28
|
50
|
56
|
50
|
56
|
60
|
62
|
2.2 Построение
системы показателей (факторов). Выбор факторных признаков для построения
двухфакторной регрессионной модели.
Таблица
2.2- Статистические
данные по всем переменным (n=10,m=3):
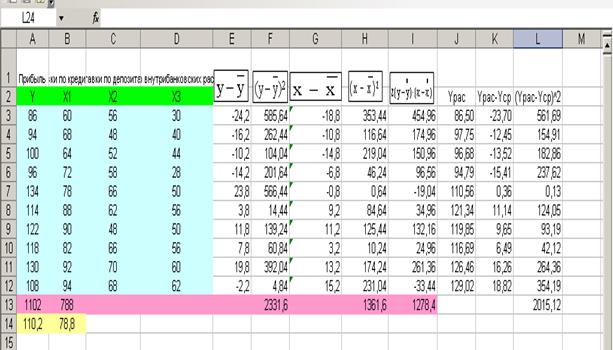
Используя инструмент
корреляция (анализ данных в Excel). Получим следующие результаты:
Таблица 2.3-Результат корреляционного анализа
|
|
Y
|
X1
|
X2
|
X3
|
|
Y
|
1
|
|
|
|
|
X1
|
0,71748854
|
1
|
|
|
|
X2
|
0,53500044
|
0,537046
|
1
|
|
|
X3
|
0,73027393
|
0,842237
|
0,591439
|
1
|
Анализ
матрицы коэффициентов парной корреляции показывает, что зависимая переменная Х1 имеет тесную связь с Х3, отбрасываем Х2. При помощи инструмента
Регрессия (Анализ данных в Excel), получим результаты регрессионного
анализа.
Таблица 2.4-Регрессионный анализ
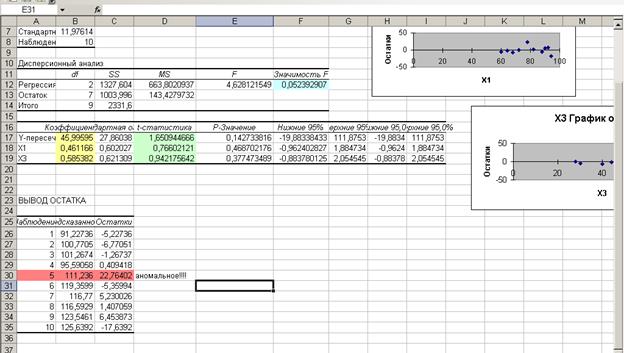
Сравним
полученные значения критерия с табличным.Табличное значение критерия Стьюдента
при 5% уровне значимости и числу степеней свободы равному 7 составляет 2,4496.Ни одно
из расчетных значений t-
критерия Стьюдента на превышает табличного значения, а следовательно, являются
не значимыми. Попробуем отбросить аномальное
наблюдение и проведем еще раз
регрессионный анализ. В нашем случае 5 наблюдение.
Таблица 2.5- Повторное исследование.
Так как имеется аномальное значение -14,8417 отбросив
его, проведем повторный регрессионный анализ.
Таблица 2.6- Повторное исследование.
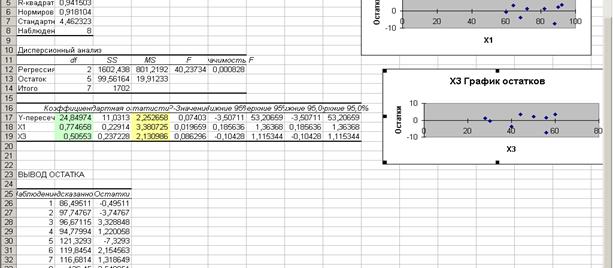
Табличное
значение t
критерия Стьюдента при уровне значимости 5% и 5 степенях свободы составляет 2,57. tрасч>tтабл => коэффициент Х1 значим. Т.о. при
данных значениях 2 фактора удовлетворяют
условиям задачи-модель адекватна.Уравнение регрессии
зависимости объема прибыли от величины внутрибанковских расходов можно записать
в следующем виде: y=24,849+0,7747*x1+0,50563*x3
2.3
Оценка качества модели.
В
таблице 2.7
приведены вычисленные по модели значенияY и значения остаточной
компоненты.
Рисунок 2.1-График остатков
Таблица 2.7-Расчет для оценки d- критерия Дарбина - Уотсона
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
|
|
1
|
61,33
|
-0,50
|
10,58
|
0,25
|
|
2
|
65,52
|
-3,75
|
50,08
|
14,04
|
|
3
|
74,41
|
3,33
|
4,45
|
11,08
|
|
4
|
67,95
|
1,22
|
73,09
|
1,49
|
|
5
|
76,68
|
-7,33
|
89,94
|
53,72
|
|
6
|
84,78
|
2,15
|
0,70
|
4,64
|
|
7
|
86,00
|
1,32
|
4,98
|
1,74
|
|
8
|
89,44
|
3,55
|
12,60
|
12,60
|
|
|
|
|
246,42
|
99,56
|
Оценку
независимости проведем с помощью d- критерия Дарбина - Уотсона
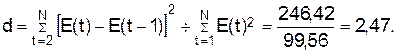
В качестве критических
табличных уровней при N=8, двух объясняющих факторов
при уровне значимости в 5% возьмем величины d1=0.842 d2=1.53.
d’
= 4-2,47=1,53.
Т.к.
d’
лежит в интервале от d2
до 2 (d2<d;<2), что свидетельствует
об отсутствии автокорреляции.
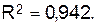
Он
показывает долю вариации результативного признака под воздействием изучаемых
факторов. Следовательно, около 94,2%
вариации зависимой переменной учтено в модели и обусловлено влиянием включенных
факторов.
Оценку
значимости уравнения регрессии проведем с помощью F-критерия Фишера:
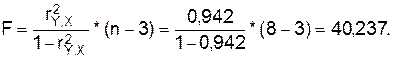
F табличное для 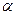= 0,05; k1=m=1, k2=n-m-1=5 равно 5,32 =>F>Fтабл.
Уравнение
регрессии с вероятностью 0,95 в целом статистически значимо, т.к. F>Fтабл .
2.4 Проанализировать
влияние факторов на зависимую переменную
по модели.
Учитывая коэффициент
регрессии не возможно использовать для непосредственной оценки влияния фактора
на зависимую переменную из-за различия единиц измерения, используем коэффициент
эластичности (Э) и бета-коэффициент, которые соответственно рассчитываются по
формулам:
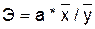
Э1=0,775*77,5/112,25=0,536,
Э1=0,506*48,25/112,25=0,35.
,
.
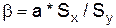
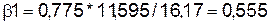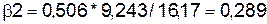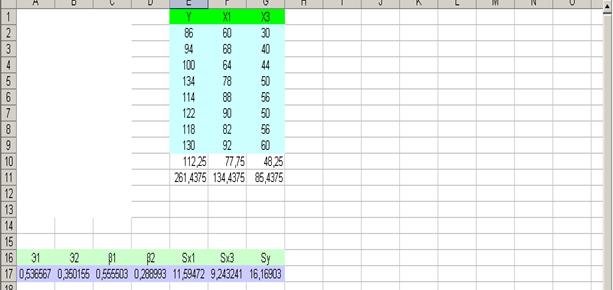
Таблица
2.8-Оценка с помощью t-критерия
Стьюдента
Коэффициент
эластичности показывает, на сколько % изменяется зависимая переменная при
изменении фактора на 1%.
Бета-коэффициент
с математической точки зрения показывает, на какую часть величины
среднеквадратического отклонения меняется среднее значение переменной с
изменением независимой переменной на одно среднеквадратическое отклонение при
фиксированном на постоянном уровне значениях независимых переменных.
2.5 Определить
точечный и интервальный прогнозы многофакторной модели.
Таблица
2.9-Полученные исходные данные
|
Y
|
Х0
|
X1
|
X3
|
|
86
|
1
|
60
|
30
|
|
94
|
1
|
68
|
40
|
|
100
|
1
|
64
|
44
|
|
96
|
1
|
72
|
28
|
|
114
|
1
|
88
|
56
|
|
122
|
1
|
90
|
50
|
|
118
|
1
|
82
|
56
|
|
130
|
1
|
92
|
60
|
Рисунок
2.2-Пргноз показателей ставки по депозитам
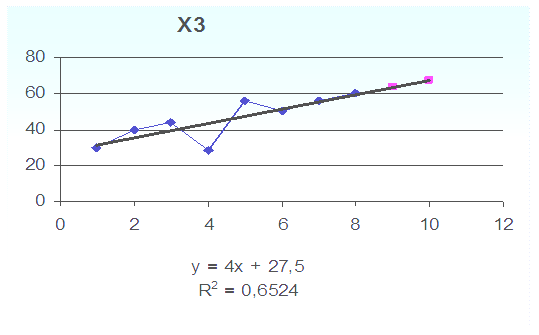
Рисунок 2.3-Пргноз показателей рамера внутрибанковских расходов
Для
получения прогнозных оценок зависимой переменной по модели:
Получим
прогнозные оценки фактора на основе величины его среднего абсолютного прироста Ux
Y=24.85+0.77*X1+0.51*X3,
Y=24.85+0.77*97.785+0.51*63.5=132.5,
Y=24.85+0.77*102.404+0.51*67.5=138.1.
Для получения прогнозных оценок зависимой
переменной воспользуемся следующей формулой:
; 
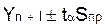
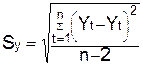
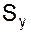- стандартная ошибка - эта
характеристика приведена в таблице
протокола ЕХСЕL и равна 4.462;
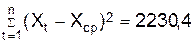
С
помощью матриц рассчитываем недостающие значения
Рисунок
2.3-Расчет матриц
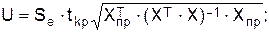
ta -является табличным значением критерия
Стьюдента для уровня значимости a и для числа степеней свободы, равного N-2. В нашем примере t0,5 =
2,57;
Таблица 2.10-Прогноз
(р=95%)
|
Упреждение
|
Нижняя гр-ца
|
Прогноз
|
Верхняя гр-ца
|
|
1
2
|
124,220
129,159
|
132,529
138,126
|
140,839
147,094
|