ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ И НАУКЕ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОУ ВПО

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

ФАКУЛЬТЕТ: Финансово-кредитный

КАФЕДРА: Экономико-математических

методов и моделей

КОНТРОЛЬНАЯ РАБОТА

ПО ДИСЦИПЛИНЕ: «Эконометрика»

Вариант №7

г. Серпухов

2008

Задача

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции , млн. руб. от объема капиталовложений , млн. руб. (таблица 1):

Таблица 1

Исходные данные варианта

х	36	28	43	52	51	54	25	37	51	29
y	85	60	99	117	118	125	56	86	115	68

Требуется:

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков ; построить график остатков.

3. Проверить выполнение предпосылок МНК.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью - критерия Фишера , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

6. Осуществить прогнозирование среднего значения показателя при уровне значимости , если прогнозное значения фактора Х составит 80% от его максимального значения.

7. Представить графически: фактические и модельные значения точки прогноза.

8. Составить уравнения нелинейной регрессии:

· гиперболической;

· степенной;

· показательной.

Привести графики построенных уравнений регрессии.

9. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

Решение:

1. Найти параметры уравнения линейной регрессии, дать экономическую оценку коэффициента регрессии.

Уравнение линейной регрессии имеет вид: .

Для расчёта параметров уравнения линейной регрессии, воспользуемся инструментом анализа данных Регрессия. Для этого в главном меню выбираем Сервис/Анализ данных/ Регрессия (рисунок 1):

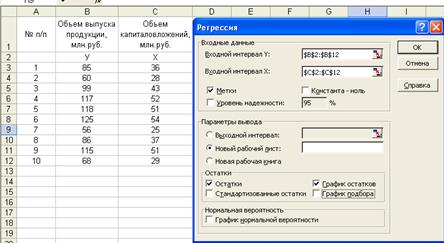
Рис. 1. Диалоговое окно ввода параметров инструмента «Регрессия»

Результаты регрессионного анализа для данных представлены на рисунке 2.

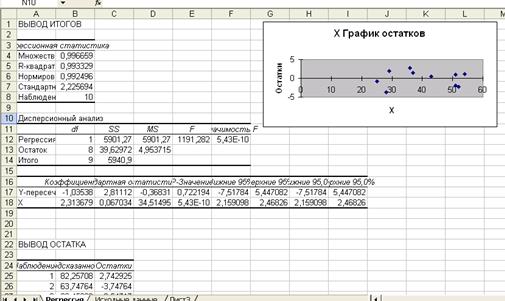
Рис. 2. Результаты применения инструмента «Регрессия»

Отсюда, a=-1,035; b=2,314, тогда уравнение регрессии имеет вид:

у=-1,035+2,314х

Экономическая интерпретация коэффициента регрессии заключается в том, что если объёмы капиталовложений возрастут на 1 млн. руб., то объём выпуска продукции возрастёт на 2,314млн.руб.

2.Для вычисление остатков, остаточной суммы квадратов и оценки дисперсии , построим рабочую таблицу (таблица 2):

Таблица 2

Рабочая таблица


1	85	36	82,2578	-7,9	62,41	2,7422	7,5197
2	60	28	63,7482	-32,9	1082,41	-3,7482	14,049
3	99	43	98,4537	6,1	37,21	0,5463	0,2984
4	117	52	119,277	24,1	580,81	-2,277	5,1847
5	118	51	116,9633	25,1	630,01	1,0367	1,0747
6	125	54	123,9044	32,1	1030,41	1,0956	1,2003
7	56	25	56,8071	-36,9	1361,61	-0,8071	0,6514
8	86	37	84,5715	-6,9	47,61	1,4285	2,0406
9	115	51	116,9633	22,1	488,41	-1,9633	3,8545
10	68	29	66,0619	-24,9	620,01	1,9381	3,7562

Остатки рассчитаны в таблице 2 (столбец 7) по формуле: .

Остаточная сумма квадратов: .

Дисперсия остатков рассчитывается по формуле: , тогда =4,9537. График остатков представлен на рисунке 3:

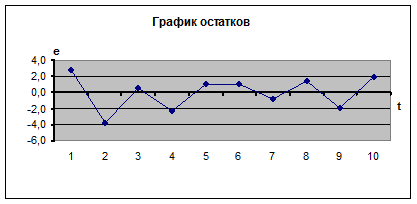
Рис. 3. График остатков

3. Проверим выполнение следующих предпосылок МНК:

Для оценки адекватности модели исследуют остатки

Исследование остатков предполагает проверку наличия у них следующих пяти предпосылок МНК:

а) Случайность характера остатка.

Для проверки случайного характера остатков строится график зависимости остатков от теоретических значений результативного признака (рисунок 4):

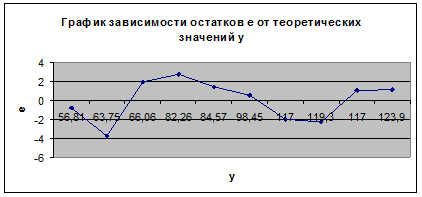
Рис. 4. Зависимость случайных остатков от теоретических значений

Если на графике получена горизонтальная полоса, то остатки представляют собой случайные величины и МНК оправдан. В нашем случае на графике остатков получена горизонтальная полоса, то есть остатки представляют собой случайные величины и МНК оправдан.

б) Нулевая (или близкая к ней) средняя величина остатка.

Для вычисления среднего значения остатка используем функцию СРЗНАЧ (рисунок 5):

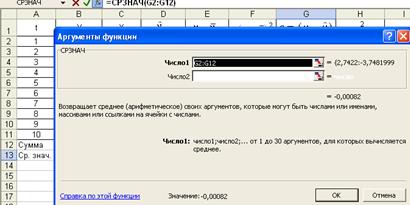
Рис. 5. Диалоговое окно ввода параметров функции СРЗНАЧ

В данной задаче , поэтому вторая предпосылка выполняется.

в) Гомоскедастичность (постоянство) дисперсии остатков. Если это условие не соблюдается, то имеет место гетероскедастичность. Для обнаружения гетероскедастичности используют метод Голдфельда-Квандта. Чтобы оценить нарушение гомоскедастичности по тесту Голдфельда-Квандта необходимо выполнить следующие шаги:

· Упорядочение n наблюдений по мере возрастания переменной х (таблица 3);

Таблица 3

Исходные данные, упорядоченные по мере возрастания переменной х

№ п/п	Объем выпуска продукции, млн.руб.	Объем капиталовложений, млн.руб.
1	56	25
2	60	28
3	68	29
4	85	36
5	86	37
6	99	43
7	118	51
8	115	51
9	117	52
10	125	54

· Разделение совокупности на две группы (соответственно с малыми и большими значениями фактора х), определение по каждой из групп уравнений регрессии. Разделение на две группы по фактору х примет вид (таблица 4, 5):

Таблица 4 Таблица 5

Y, млн. руб.	Х, млн. руб.
56	25
60	28
68	29
85	36
86	37

Y, млн. руб.	X, млн. руб.
99	43
118	51
115	51
117	52
125	54

Выполнив в Excel функцию РЕГРЕССИЯ для первой и второй групп (рисунок 6, 7):

Рис. 6. Результаты применения инструмента регрессии

для группы с малыми значениями фактора х

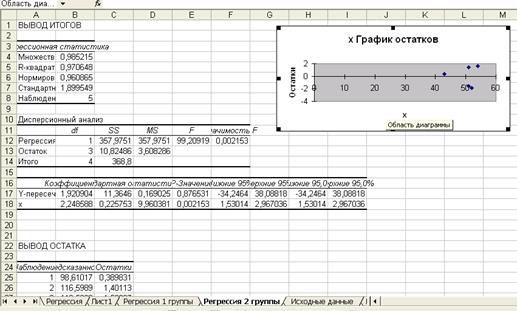
Рис. 7. Результаты применения инструмента регрессии

для группы с большими значениями фактора х

Получим следующие уравнения регрессии:

· Определение остаточной суммы квадратов первой и второй регрессий осуществим с помощью функции СУММКВ (рисунок 8):

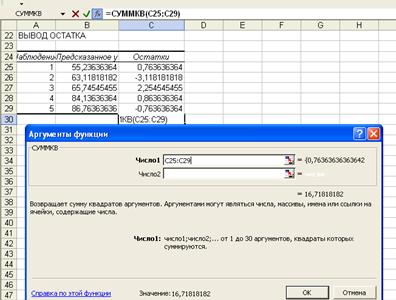
Рис. 8. Диалоговое окно ввода параметров функции СУММКВ

В результате получим для первой регрессии: , для второй 10,825.

· Вычисление отношений (расчетного значения F-критерия): 16,719/10,825= 1,54.

Вычисление табличного значения F-критерия, которое производится при помощи функции FРАСПОБР. , где =0,1. =5, m=2, n=10 (рисунок 9) :

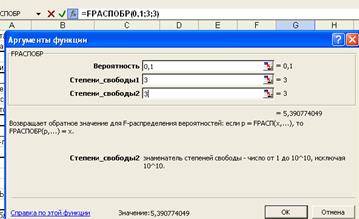
Рис. 9. Определение табличного значения F-критерия

Значение F-расчетного меньше F-табличного, что свидетельствует о том, что гетероскедастичность не обнаружена и, следовательно, выполняются свойства гомоскедастичности остатков.

4) Независимость (отсутствие автокорреляции) остатков проверяют с помощью критерия Дарбина-Уотсона: dw=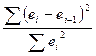, где . Для нахождения коэффициента корреляции построим рабочую таблицу (таблица 6):

Таблица 6

Рабочая таблица

№ п/п	x	y
1	25	56	56,807	-0,807	0,651
2	28	60	63,748	-3,748	14,045	-2,941	8,650
3	29	68	66,061	1,939	3,758	5,686	32,334
4	36	85	82,257	2,743	7,524	0,804	0,647
5	37	86	84,571	1,429	2,043	-1,314	1,726
6	43	99	98,453	0,547	0,299	-0,882	0,778
7	51	115	116,962	-1,962	3,850	-2,509	6,297
8	51	118	116,962	1,038	1,077	3,000	9,000
9	52	117	119,276	-2,276	5,180	-3,314	10,980
10	54	125	123,903	1,097	1,203	3,373	11,375
Итого:					39,630		81,787

Таким образом, dw ==2,064. Перед сравнением с табличным значением преобразую dw критерий по формуле: dw'=4-dw, тогда dw'=4-2,064=1,936. Табличные значения, при уровне значимости α =0,05, соответственно равны . Так как 1,32<1,936<2, тогда ряд остатков не коррелирован, т.е. выполняется свойство независимости остатков.

5) Соответствие ряда остатков нормальному закону распределения определяется при помощи R/S-критерия:

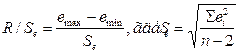
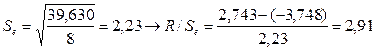Полученное значение этого критерия попадает между табулированными границами (2,67-3,57) с заданным уровнем значимости () и n=10, таким образом, свойство нормальности остатков выполняется.

Все предпосылки МНК выполнены. Построенная модель является адекватной реальному процессу, её можно использовать для построения прогнозных оценок.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента ().

Для оценки статистической значимости параметров полученной модели используем t-критерий. Расчетное значение t-статистики определяется по формулам: . Расчетные значения t-критерия можно найти в протоколе Excel после применения инструмента Регрессия (рисунок 10):

Рис. 10. Результат применения инструмента Регрессия

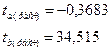
Табличное значение t-критерия (0,05;8)=2,306.

Поскольку , то параметр а является статистически незначимым.

, следовательно, параметр b статистически значим.

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

а) Коэффициент детерминации можно определить по формуле:

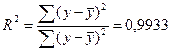
Это означает, что 99,33% вариации объёма выпуска продукции (у) объясняется вариацией фактора х – объёмом капиталовложений.

б) Оценка значимости уравнения регрессии проводится с помощью F-критерия. Расчетное значение F-критерия в нашем случае определяется по формуле:

Табличное значение F-критерия при ,

Поскольку расчетное значение F-критерия Фишера больше табличного, то уравнение регрессии признается статистически значимым.

в) Находим среднюю относительную ошибку аппроксимации :

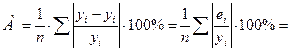2,14%

Качество построенной модели оценивается как хорошее, так как не превышает 8 – 10%. <5%, поэтому модель точна и по ней можно прогнозировать с достаточно высокой вероятностью.

6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости , если прогнозное значение фактора Х составит 80% от его максимально значения.

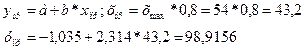
Отклонение от линии регрессии рассчитывается по формуле: 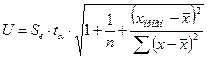, где Se=2,2257 (см. значение «Стандартная ошибка»). Произведём необходимые расчёты (таблица 7):

Таблица 7

Рабочая таблица

№ п/п	x	y
1	25	56	243,36
2	28	60	158,76
3	29	68	134,56
4	36	85	21,16
5	37	86	12,96
6	43	99	5,76
7	51	115	108,16
8	51	118	108,16
9	52	117	129,96
10	54	125	179,56
Итого:	406	929	1102,4
среднее	40,6	92,9

Коэффициент Стьюдента для 8 степеней свободы и на уровне значимости рассчитывается при помощи функции СТЬЮДРАСПОБР(0,1;8)=1,8595.

(43,2-40,6)²=6,76

U_пр=2,2257*1,85*4,33

Следовательно, интервальный прогноз будет выглядеть:

94,58

7. Представить графически: фактические и модельные значения Y, точки прогноза.

Строим график «Фактические и модельные значения У»: скопируем в лист с вычислениями прогнозируемых значений график подбора с листа «Регрессия Y». Соединим точки графика отрезками (активировать курсором точки – тип данных – отрезки).

Переименовываем график подбора в «Фактические значения У». К существующим данным добавляем новые (Исходные данные – Ряд – Добавить): для точечного прогноза, нижней и верхней границ прогноза, указывая соответствующие данные (рисунок 11):

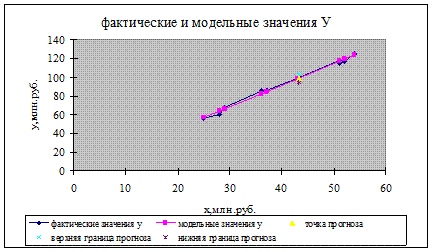
Рис. 11. График фактических и модельных значений у

8. Составить уравнения гиперболической (а), степенной (б), показательной (в) нелинейной регрессий. Построить графики построенных уравнений регрессии.

а) Уравнение гиперболической регрессии имеет вид:

Приведем эту модель к линейному виду осуществив замену переменных: . В результате получим линейное уравнение вида .

Для расчетов используем данные рабочей таблицы 8:

Таблица 8

t	y	x	X	yX	X²	ŷ
1	56	25	0,04	2,24	0,0016	49,42828
2	60	28	0,0357	2,142	0,0013	63,2546
3	68	29	0,0345	2,346	0,0012	67,16526
4	85	36	0,0278	2,363	0,0008	88,77212
5	86	37	0,027	2,322	0,0007	91,35205
6	99	43	0,0233	2,3067	0,0005	103,2842
7	118	51	0,0196	2,3128	0,0004	115,2163
8	115	51	0,0196	2,254	0,0004	115,2163
9	117	52	0,0192	2,2464	0,0004	116,5063
10	125	54	0,0185	2,3125	0,0003	118,7637
Сумма	929		0,2652	22,8454	0,0076
Ср. знач.	92,9		0,02652	2,2845	0,0008

-3224,91;

Получим следующее уравнение гиперболической модели:

ŷ=178,43-3224,91/х

График гиперболической модели представлен на рисунке 11:

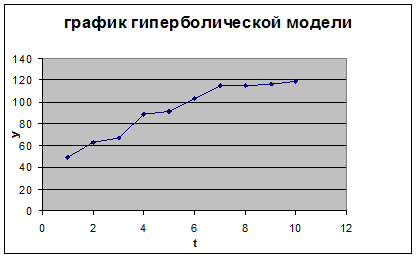
Рис. 11. График гиперболической модели

б) Уравнение степенной модели имеет вид: . Для построения модели произведем линеаризацию переменных, осуществив логарифмирование обеих частей уравнения: lg ŷ =lg a+b lg x. Обозначив Y = lg у, X = lg х, А = lg а, получаем модель вида: Y=A+bX.

Для расчетов параметров уравнения используем данные рабочей таблицы (таблица 8):

Таблица 8

Рабочая таблица

t	y	Y	x	X	YX	X²	ŷ
1	56	1,7482	25	1,3979	2,4438	1,9541	56,5121
2	60	1,7782	28	1,4472	2,5734	2,0944	63,4595
3	68	1,8325	29	1,4624	2,6798	2,1386	65,7792
4	85	1,9294	36	1,5563	3,0027	2,4221	82,0658
5	86	1,9345	37	1,5682	3,0337	2,4593	84,3988
6	99	1,9956	43	1,6335	3,2598	2,6683	98,4262
7	118	2,0719	51	1,7076	3,538	2,9159	117,199
8	115	2,0607	51	1,7076	3,5189	2,9159	117,199
9	117	2,0682	52	1,716	3,549	2,9447	119,5507
10	125	2,0969	54	1,7324	3,6327	3,0012	124,257
Сумма	929	19,5161	406	15,9291	31,2318	25,5145
Ср. знач.	92,9	1,9516	40,6	1,5929	3,1232	2,5515

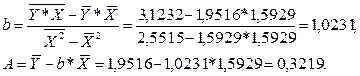
Уравнение регрессии имеет вид: Y=0,3219-1,0231*X.

Перейдем к исходным переменным х и у, выполнив потенцирование данного уравнения: .

График степенной модели представлен на рисунке 12:

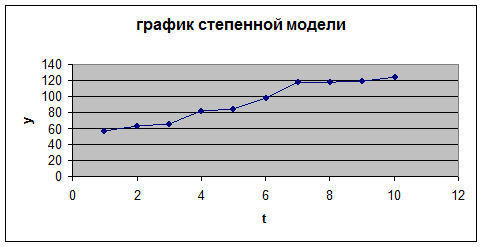
Рис. 12. График степенной модели

в) Уравнение показательной кривой: ŷ =. Для построения модели проведу линеаризацию (логарифмирование) переменных: lg ŷ = lg a + lg x*b.

Обозначим Y = lg ŷ, B = lg b, A = lg a, тогда линейное уравнение регрессии имеет вид: Y = A+ B*x.

Для расчетов параметров уравнения, используем данные рабочей таблицы (таблица 9):

Таблица 9

Рабочая таблица

t	y	Y	x	Yx	x²	ŷ
1	56	1,7482	25	43,705	625	59,1352
2	60	1,7782	28	49,7896	784	64,0183
3	68	1,8325	29	53,1425	841	65,7339
4	85	1,9294	36	69,4584	1296	79,1026
5	86	1,9345	37	71,5765	1369	81,2225
6	99	1,9956	43	85,8108	1849	95,1901
7	118	2,0719	51	105,6669	2601	117,6193
8	115	2,0607	51	105,0957	2601	117,6193
9	117	2,0682	52	107,5464	2704	120,7715
10	125	2,0969	54	113,2326	2916	127,3316
Сумма	929	19,5161	406	805,0244	17586
Ср. знач.	92,9	1,9516	40,6	80,5024	1758,6

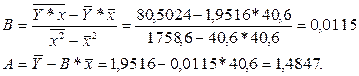
Уравнение имеет вид: Y = 1,4847 + 0,0115*x.

Выполнив потенцирование данного уравнения, получаем:

ŷ = → ŷ =

Найдем теоретическое значение y, построим график степенной регрессии при использовании функции Мастер диаграмм (рисунок 13):

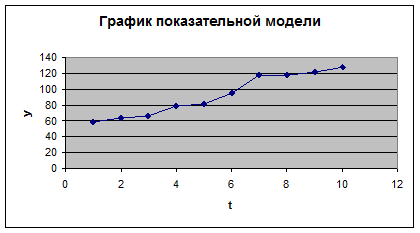
Рис. 13. график показательной функции

а) гиперболическая

Рассчитаем характеристики точности модели, расчеты произведены средствами MS Excel (Приложение 1).

Индекс детерминации: 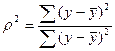=0,7962.

Таким образом, все вариации в объеме выпуска продукции Y на 79,62% обусловлены вариацией в объеме капиталовложений X, т.е. изменениями в факторе X, учтенном в модели.

Средняя относительная ошибка аппроксимации:

=11,7515%.

Таким образом, модельные значения отклоняются от фактических значений Y в среднем на 11,7515%, т.е. получена модель среднего качества.

б) степенная

Рассчитаем характеристики точности модели (Приложение 2).

Индекс детерминации: 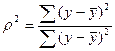=0,9931.

Таким образом, все вариации в объеме выпуска продукции Y на 99,31% обусловлены вариацией в объеме капиталовложений X, т.е. изменениями в факторе X, учтенном в модели.

Средняя относительная ошибка аппроксимации:

=2,1205%

Таким образом, модельные значения отклоняются от фактических значений Y в среднем на 2,12 %, т.е. получена модель хорошего качества, высокой точности.

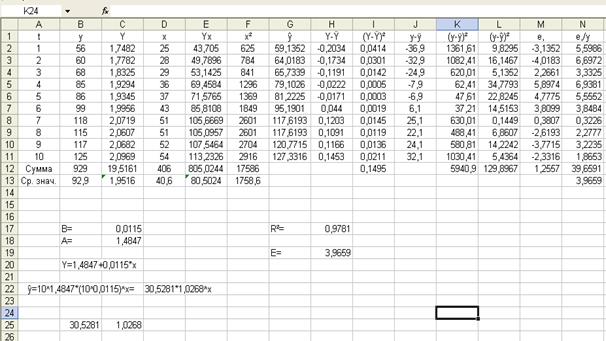
в) показательная

Рассчитаем характеристики точности модели (Приложение 3).

Индекс детерминации: 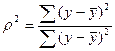=0,9781.

Таким образом, все вариации в объеме выпуска продукции Y на 97,81% обусловлены вариацией в объеме капиталовложений X, т.е. изменениями в факторе X, учтенном в модели.

Средняя относительная ошибка аппроксимации:

= 3,9659 %.

Таким образом, модельные значения отклоняются от фактических значений Y в среднем на 3,97%, т.е. получена модель среднего качества.

Сравнение полученных моделей

Для сравнения моделей используем полученные данные. Построим таблицу (таблица 10):

Таблица 10

	коэффициент детерминации	средняя относительная ошибка
гиперболическая	0,7962	11,7515
степенная	0,9931	2,1205
показательная	0,9781	3,9659

Сравнив модели по этим характеристикам можем сделать вывод:

Степенная модель имеет большее значение коэффициента детерминации R²небольшую относительную ошибку аппроксимации, следовательно, степенная модель лучше остальных оценивает взаимосвязь.

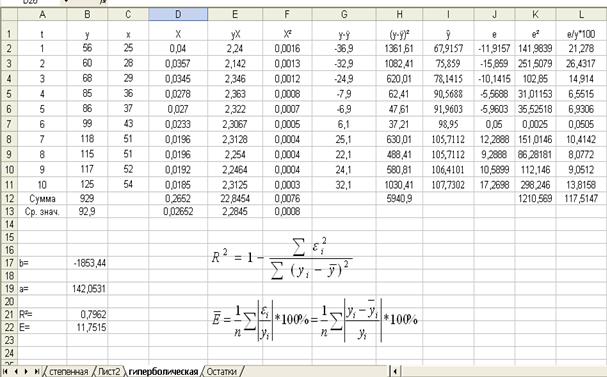
Приложение 1

Расчет параметров гиперболической модели

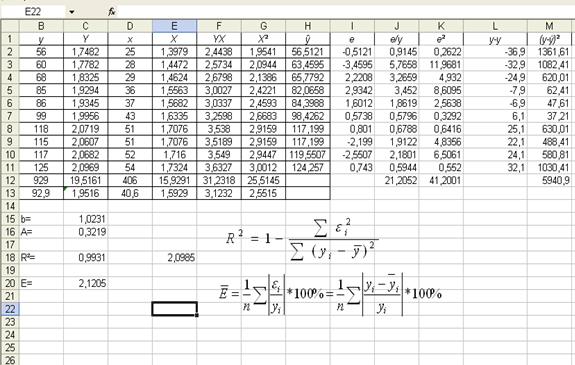
Приложение 2

Расчет параметров степенной модели

Приложение 3

Расчет параметров показательной модели