ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
Лабораторная работа №1
Автоматизированный
априорный анализ статистической совокупности в среде MS Excel
Вариант № 6
Исполнитель: Ржавичева Татьяна Владимировна
Специальность: финансы и
кредит
Группа: дневная III
курс
№ зачетной
книжки: 08ФФД40351
Руководитель:
Леонова Светлана Николаевна
Орел 2009г.
Алгоритмы
выполнения Задания 1
Задача 1. Построение
диаграммы рассеяния изучаемых признаков.
1.
Выделить мышью
исходные данные (табл.1) (В4:С35);
2.

 Вставка Диаграмма Готово.
Вставка Диаграмма Готово.
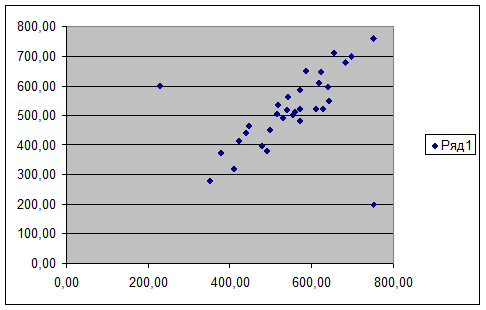
Рис 1. Аномальные
значения признаков на диаграмме рассеяния.
Задача 2. Визуальный
анализ диаграммы рассеяния, выявление и фиксация аномальных значений признаков,
их удаление из первичных данных.
Точки соответствующие аномальным наблюдениям:
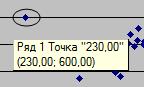
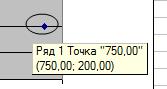
Две единицы наблюдения с аномальными значениями
признаков, имеет следующий вид.
|
|
|
Таблица
2
|
|
Аномальные
единицы наблюдения
|
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
11
|
230,00
|
600,00
|
|
30
|
750,00
|
200,00
|
Алгоритмы выполнения Задания 2
Этап 1. Расчет
описательных параметров выборочной и генеральной совокупностей с использованием
инструмента Описательная статистика
Алгоритм 1.1. Расчет описательных статистик
1. Сервис=>Анализ
данных=>Описательная статистика=>OK;
2. Входной
интервал<= диапазон ячеек таблицы,
выделенный для значений признаков Стоимость основных фондов и
Выпуск продукции (B4:С33);
3. Группирование
=>по столбцам;
4. Итоговая
статистика - Активизировать;
5. Уровень
надежности - Активизировать;
6. Уровень
надежности <= 95,4 (или 95.4);
7. Выходной
интервал <= адрес ячейки заголовка
первого столбца табл.3 (А46);
8. OK;
9.
При появлении
окна с сообщением "Выходной интервал
накладывается на имеющиеся данные" =>ОК.
Результат работы алгоритма 2.1 представлен в табл.3
|
|
|
|
Таблица
3
|
|
Описательные
статистики
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Среднее
|
550
|
Среднее
|
521,7333333
|
|
Стандартная
ошибка
|
17,66404231
|
Стандартная
ошибка
|
21,07168571
|
|
Медиана
|
556
|
Медиана
|
518
|
|
Мода
|
570
|
Мода
|
520
|
|
Стандартное
отклонение
|
96,74994431
|
Стандартное
отклонение
|
115,4143759
|
|
Дисперсия
выборки
|
9360,551724
|
Дисперсия
выборки
|
13320,47816
|
|
Эксцесс
|
-0,344943844
|
Эксцесс
|
-0,205332365
|
|
Асимметричность
|
-0,152503649
|
Асимметричность
|
0,042954448
|
|
Интервал
|
400
|
Интервал
|
480
|
|
Минимум
|
350
|
Минимум
|
280
|
|
Максимум
|
750
|
Максимум
|
760
|
|
Сумма
|
16500
|
Сумма
|
15652
|
|
Счет
|
30
|
Счет
|
30
|
|
Уровень
надежности(95,4%)
|
36,82619052
|
Уровень
надежности(95,4%)
|
43,93048311
|
Этап 2. Оценка предельных ошибок выборки
для различных уровней надежности в режиме Описательная статистика.
Алгоритм 2.1. Расчет предельной ошибки выборки при P=0,683
1.
Сервис=>Анализ данных=>Описательная
статистика=>OK;
2. Входной
интервал<= диапазон ячеек таблицы,
выделенный для значений признаков Стоимость основных фондов и
Выпуск продукции (В4:С33);
3. Итоговая
статистика – НЕ активизировать
(снять флажок);
4. Уровень
надежности – Активизировать;
5. Уровень
надежности<= 68,3 (или 68.3);
6. Выходной
интервал <= адрес ячейки, выделенной для предельной ошибки выборки при P=0,683 (А67);
7. OK;
8.
При появлении
окна с сообщением "Выходной интервал
накладывается на имеющиеся данные" =>ОК.
|
|
|
|
Таблица
4
|
|
Предельные
ошибки выборки
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Уровень
надежности(68,3%)
|
17,98563012
|
Уровень
надежности(68,3%)
|
21,45531235
|
Этап 3. Расчет
описательных параметров выборочной совокупности с использованием инструмента Мастер функций
Алгоритм
3.1. Расчет значений выборочных
параметров 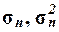
Вычисление показателей для обоих признаков
осуществляется с использованием соответствующих статистических функций СТАНДОТКЛОНП, ДИСПР, СРОТКЛ
инструмента Мастер функций. В макете
табл.5. приведены их имена вместе с адресами аргументов.
1. В ячейках (В83 – В84), выделенных для значений
выборочных показателей признака Среднегодовая
стоимость основных производственных фондов:
1.1. Перед именами функций
поставить знак равенства «=»;
1.2. Enter;
2. В ячейках (D83 – D84), выделенных для значений
выборочных показателей признака Выпуск
продукции:
2.1. Перед именами функций
поставить знак равенства «=»;
2.2. Enter;
|
|
|
|
Таблица
5*
|
|
|
Выборочные показатели вариации
|
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Стандартное
отклонение
|
95,12377901
|
Стандартное
отклонение
|
113,4745003
|
|
Дисперсия
|
9048,533333
|
Дисперсия
|
12876,46222
|
|
Коэффициент
вариации, %
|
B87B83/B48*100
|
Коэффициент
вариации, %
|
D83/D48*100
|
Алгоритм 3.2.
Расчет коэффициентов вариации 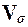 для обоих признаков
для обоих признаков
В макете табл.5. приведены
расчетные формулы коэффициента вариации 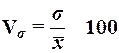 .
.
1. В ячейке В85, выделенной для значений
коэффициента вариации по признаку Среднегодовая стоимость основных производственных
фондов, перед формулой поставить
знак равенства «=»;
2. Enter;
3. В ячейке D85,
выделенной для значений коэффициента вариации по признаку Выпуск продукции, перед формулой
поставить знак равенства «=»;
4. Enter.
В результате работы алгоритмов 3.1-3.2 осуществляется вывод выборочных
параметров 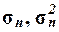 и
и 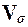 в
соответствующие ячейки рабочего листа. Табл. 5.
в
соответствующие ячейки рабочего листа. Табл. 5.
|
|
|
|
Таблица
5
|
|
|
Выборочные показатели вариации
|
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Стандартное
отклонение
|
95,12377901
|
Стандартное
отклонение
|
113,4745003
|
|
Дисперсия
|
9048,533333
|
Дисперсия
|
12876,46222
|
|
Коэффициент
вариации, %
|
17,29523255
|
Коэффициент
вариации, %
|
21,74952089
|
Задание 3. Построение
и графическое изображение интервального вариационного ряда распределения единиц
совокупности по признаку
Алгоритмы выполнения Задания 3
Этап 1. Построение промежуточной таблицы.
Алгоритм 1.1. Расчет нижних границ интервалов
1. Сервис=>Анализ
данных=>Гистограмма=>ОК;
2. Входной
интервал<= диапазон ячеек,
выделенный для столбца значений первого признака (В4:В33);
3. Интервал
карманов оставить незаполненным;
4. Выходной
интервал <= адрес заголовка
первого столбца первичной промежуточной табл.6 (А90);
5.
OK.
Алгоритм 1.2. Переход от нижних границ к
верхним
1. Выделить курсором верхнюю левую ячейку табл.6 (A91) и нажать
клавишу [Delete];
2. Ввести в последнюю ячейку табл.6 (A96) вместо
"Еще" значение хmax первого признака из табл.3 – Описательные статистики (Термин "Максимум").
|
|
Таблица
6
|
|
Карман
|
Частота
|
|
350
|
1
|
|
430
|
3
|
|
510
|
5
|
|
590
|
11
|
|
670
|
7
|
|
Еще
|
3
|
|
|
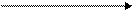
|
|
|
Таблица 6
|
|
Карман
|
Частота
|
|
|
1
|
|
430
|
3
|
|
510
|
5
|
|
590
|
11
|
|
670
|
7
|
|
750
|
3
|
|
|
|
а) первичная Преобразуется
в б) итоговая
Рис.2. Схема
перехода от нижних границ интервалов к верхним
Этап 2. Генерация выходной таблицы и графиков
Алгоритм 2.1.
Построение выходной таблицы, столбиковой диаграммы и кумуляты
1.
Сервис=>Анализ данных=>Гистограмма=>ОК;
2. Входной
интервал<= диапазон ячеек,
выделенный для столбца значений первого признака (В4:В33);
3. Интервал
карманов <= диапазон карманов
итоговой промежуточной табл.6 с верхними границами (А92:А96);
4. Выходной
интервал <= адрес заголовка («Карман») первого столбца выходной табл.7 (А102);
5.
Интегральный процент – Активизировать;
6.
Вывод графика – Активизировать;
7.
ОК;
8.
При появлении
сообщения о наложении данных –
ОК.
Выходная
таблица имеет следующий вид:
|
|
|
Таблица
7
|
|
Интервальный
ряд распределения предприятий
по стоимости основных производственных
фондов
|
|
Группа
предприятий по стоимости основных фондов
|
Число
предприятий в группе
|
Накопленная
частость группы.%
|
|
Карман
|
Частота
|
Интегральный %
|
|
430
|
4
|
13,33%
|
|
510
|
5
|
30,00%
|
|
590
|
11
|
66,67%
|
|
670
|
7
|
90,00%
|
|
750
|
3
|
100,00%
|
|
Еще
|
0
|
100,00%
|
Столбиковая
диаграмма и кумулята приведены ниже:
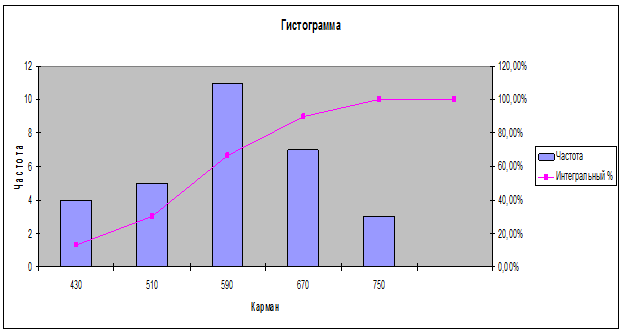
Этап 3. Приведение выходной таблицы
и диаграммы к виду, принятому в статистике.
Алгоритм 3.1. Преобразование выходной
таблицы в результативную
1. Строку 102,
содержащую термин «Карман», выделить мышью (вместе с ее номером);
2. Правка => Удалить;
3. Строку 107,
содержащую термин «Еще», выделить мышью и очистить, нажав клавишу [Delete];
4. Строки первого столбца привести к виду «нижняя
граница интервала - верхняя граница интервала», учитывая
совпадение верхних границ предыдущего интервала с нижней границей последующего
интервала (нижняя граница первого интервала равна хmin первого признака из табл.3 – Описательные статистики – Термин "Минимум").
5. Добавить и заполнить итоговую строку 108 (ячейки
А108:В108).
Excel-формат результативной таблицы выглядит следующим
образом.
|
|
|
Таблица
7
|
|
Интервальный
ряд распределения предприятий
по стоимости основных производственных
фондов
|
|
Группа
предприятий по стоимости основных фондов
|
Число
предприятий в группе
|
Накопленная
частость группы.%
|
|
350-430
|
4
|
13,33%
|
|
430-510
|
5
|
30,00%
|
|
510-590
|
11
|
66,67%
|
|
590-670
|
7
|
90,00%
|
|
670-750
|
3
|
100,00%
|
|
|
0
|
100,00%
|
|
Итого
|
30
|
|
Алгоритм 3.2.
Преобразование столбиковой диаграммы в гистограмму
1. Осуществив «захват мышью», переместить график,
расположив его вслед за табл.7.
2. Исключить зазоры, выполнив следующие действия:
1. Нажать правую кнопку мыши на одном из столбиков
диаграммы;
2. Формат рядов
данных=>Параметры;
3. Ширина зазора<=
0;
4. ОК;
3. Подвести курсор на угол поля графика и, используя прием
"захват мышью", установить визуально соотношение ширины
и высоты фигуры гистограммы в
пропорции 1 : 0,6.
По окончании работы алгоритма 3.2 выполнить настройку диаграммы:
1. Изменить название осей (алгоритм 3.3);
2. Изменить текст легенды (алгоритм 3.4).
Алгоритм 3.3. Изменение названия
осей
1. Выделить мышью построенную
диаграмму;
2. Диаграмма => Параметры диаграммы;
3. В появившемся диалоговом
окне Параметры диаграммы выбрать
вкладку Заголовки и в поле Ось Х ввести заголовок оси – "Среднегодовая стоимость
основных производственных фондов", а
в поле Ось Y – "Число предприятий в группе";
4. ОК.
Алгоритм 3.4. Изменение текста
легенды
1. Выделить мышью построенную
диаграмму;
2. Диаграмма => Исходные данные;
3. В появившемся диалоговом
окне Исходные данные выбрать вкладку
Ряд, в поле Ряд выбрать заголовок "Интегральный %" и в поле Имя
ввести – "Накопленная частость
";
4. ОК.
Гистограмма
и кумулята выглядят следующим образом
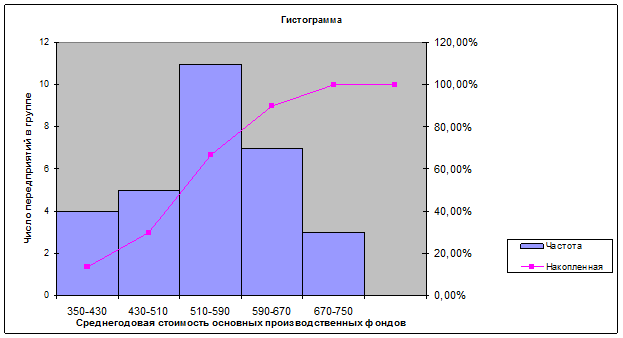
ПРИЛОЖЕНИЕ
табл. 1. Выборочные
исходные данные
|
|
A
|
B
|
C
|
|
3
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
4
|
1
|
422,00
|
412,00
|
|
5
|
2
|
498,00
|
452,00
|
|
6
|
3
|
514,00
|
504,00
|
|
7
|
4
|
542,00
|
560,00
|
|
8
|
5
|
350,00
|
280,00
|
|
9
|
6
|
570,00
|
480,00
|
|
10
|
7
|
586,00
|
648,00
|
|
11
|
8
|
438,00
|
440,00
|
|
12
|
9
|
538,00
|
516,00
|
|
13
|
10
|
622,00
|
644,00
|
|
14
|
11
|
682,00
|
680,00
|
|
15
|
12
|
230,00
|
600,00
|
|
16
|
13
|
518,00
|
536,00
|
|
17
|
14
|
570,00
|
584,00
|
|
18
|
15
|
654,00
|
708,00
|
|
19
|
16
|
750,00
|
760,00
|
|
20
|
17
|
558,00
|
512,00
|
|
21
|
18
|
618,00
|
608,00
|
|
22
|
19
|
490,00
|
380,00
|
|
23
|
20
|
626,00
|
520,00
|
|
24
|
21
|
698,00
|
700,00
|
|
25
|
22
|
478,00
|
396,00
|
|
26
|
23
|
378,00
|
372,00
|
|
27
|
24
|
638,00
|
596,00
|
|
28
|
25
|
570,00
|
520,00
|
|
29
|
26
|
530,00
|
492,00
|
|
30
|
27
|
410,00
|
320,00
|
|
31
|
28
|
554,00
|
500,00
|
|
32
|
29
|
642,00
|
548,00
|
|
33
|
30
|
610,00
|
520,00
|
|
34
|
31
|
750,00
|
200,00
|
|
35
|
32
|
446,00
|
464,00
|
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
Лабораторная работа №2
Автоматизированный
корреляционно-регрессионный анализ взаимосвязи статистических данных в среде MS Excel
Вариант № 6
Исполнитель: Ржавичева Татьяна Владимировна
Специальность: финансы и
кредит
Группа: дневная III
курс
№ зачетной книжки: 08ФФД40351
Руководитель: Леонова Светлана Николаевна
Орел 2009г.
Задание 1 Построение аналитической группировки для выявления
корреляционной зависимости результативного признака от факторного и оценка
тесноты взаимосвязи признаков
Алгоритмы выполнения Задания 1
Задача 1. Построение
аналитической группировки предприятий по признаку Среднегодовая стоимость основных
производственных фондов.
Алгоритм 1.1. Ранжирование исходных данных по факторному
признаку
1. Выделить исходные данные
(вместе с заголовком) табл. 2.1 (А3:С33);
2. Данные => Сортировка;
3. Сортировать по <= заголовок столбца, по которому выполняется сортировка, т.е. Среднегодовая стоимость основных
производственных фондов;
4. По
возрастанию/по убыванию –
устанавливается в положение по
возрастанию;
5. Затем и В последнюю
очередь по – НЕ активизировать;
6. Идентифицировать поля по подписям/обозначениям столбцов листа – устанавливается в положение подписям;
7. ОК.
В результате указанных действий в таблице 2.1
размещаются данные, ранжированные по возрастанию признака Среднегодовая стоимость
основных производственных фондов.
Алгоритм 1.2. Выделение
групп предприятий с помощью заливки контрастным цветом
1. Из всего диапазона отсортированных данных A4:C33
выделить мышью диапазон ячеек первой группы, для чего
необходимо отсчитать в ранжированном ряду количество строк, соответствующее
числу предприятий первой группы (графа 3 табл.2.2);
2. Нажать на панели инструментов кнопку  для выбора цвета заливки;
для выбора цвета заливки;
3.
Выбрать цвет
заливки по собственному усмотрению;
4. Выполнить действия 1–3 для всех групп, выбирая
контрастные цвета для цветовой заливки очередной группы.
Результаты работы алгоритмов 1.1 и 1.2 представлены в табл.2.1(из
приложения)
Алгоритм 1.3. Расчет суммарных групповых значений
результативного признака
1. В ячейке (D41),
выделенной для суммарного значения результативного признака Выпуск продукции первой
группы,
перед формулой поставить знак равенства «=»;
2. В качестве аргумента функции СУММ() указать диапазон ячеек из табл. 2.1 с результативными
значениями уi первой группы (визуально легко
определяется по цвету заливки диапазона);
3. Enter;
4. Выполнить действия 1–3 поочередно для всех
групп, используя цветовые заливки диапазонов.
Алгоритм 1.4. Расчет средних групповых значений
результативного признака
В таблице 2.2 приведены
формулы для расчета средних групповых значений результативного признака Выпуск продукции.
1. В ячейке (Е41), выделенной для среднего значения
результативного признака Выпуск продукции первой группы,
перед формулой поставить знак равенства «=»;
2. Enter;
3. Выполнить действия 1–2 поочередно для всех
групп;
4. В ячейках (C46, D46 и E46), выделенных для расчета
итоговых сумм:
Перед формулой поставить знак равенства «=»;
Enter.
Результаты работы алгоритмов
1.3 и 1.4 приведены в табл. 2.2
|
|
|
|
|
Таблица
2.2
|
|
Зависимость
выпуска продукции от среднегодовой стоимости основных фондов
|
|
Номер группы
|
Группы
предприятий по стоимости основеных фондов
|
Число
предприятий
|
Выпуск
продукции
|
|
Всего
|
В среднем
на одно
предприятие
|
|
1
|
350-430
|
4
|
1384,00
|
346,00
|
|
2
|
430-510
|
5
|
2132,00
|
426,40
|
|
3
|
510-590
|
11
|
5852,00
|
532,00
|
|
4
|
590-670
|
7
|
4144,00
|
592,00
|
|
5
|
670-750
|
3
|
2140,00
|
713,33
|
|
Итого
|
|
30
|
15652,00
|
521,73
|
Задача 2. Оценка тесноты связи изучаемых признаков на основе эмпирического корреляционного
отношения
Задача решается в два этапа:
1. Расчет внутригрупповых
дисперсий результативного признака.
2. Расчет эмпирического
корреляционного отношения.
Алгоритм 2.1. Расчет внутригрупповых дисперсий
результативного признака
1. В ячейке, выделенной для
внутригрупповых дисперсий первой группы (D52),
перед формулой поставить знак равенства «=»;
2. В качестве аргумента функции ДИСПР() указать диапазон ячеек из табл. 2.1 со значениями yi первой группы – визуально легко определяется по цвету заливки диапазона;
3. Enter;
4. Выполнить действия 1–3 поочередно для всех
групп, используя цветовые заливки диапазонов.
5. Для расчета итоговой суммы в табл. 2.3 (в ячейке C57) перед
формулой необходимо поставить знак равенства «=»;
6. Enter.
Результат работы алгоритма 2.1 представлен в табл.2.3
|
|
|
|
Таблица
2.3
|
|
Показатели
внутригрупповой вариации
|
|
Номер группы
|
Группы
предприятий по стоимости основеных фондов
|
Число
предприятий
|
Внутригрупповая
дисперсия
|
|
1
|
350-430
|
4
|
2516,00
|
|
2
|
430-510
|
5
|
1066,24
|
|
3
|
510-590
|
11
|
2170,18
|
|
4
|
590-670
|
7
|
4105,14
|
|
5
|
670-750
|
3
|
1155,56
|
|
Итого
|
|
30
|
|
Алгоритм 2.2. Расчет
эмпирического корреляционного отношения
1. В ячейке, выделенной для
общей дисперсии (А63), перед
формулой поставить знак равенства «=»;
2. Enter;
3. В ячейке, выделенной для
средней из внутригрупповых дисперсий (В63),
перед формулой поставить знак равенства «=»;
4. Enter;
5. В ячейке, выделенной для
значения межгрупповой (факторной) дисперсии (С63), перед формулой поставить знак равенства «=»;
6. Enter;
7. В ячейке, выделенной для
эмпирического корреляционного отношения (D63), перед формулой поставить
знак равенства «=»;
8. Enter.
Результат работы алгоритма
2.2 представлен в табл.2.4.
|
|
|
|
Таблица
2.4
|
|
Показатели
дисперсии и эмпирического корреляционного отношения
|
|
Общая дисперсия
|
Средняя из
внутригрупповых дисперсия
|
Межгрупповая
дисперсия
|
Эмпирическое
корреляционное отношение
|
|
12876,46222
|
2382,328889
|
10494,13333
|
0,902765617
|
Задание 2 Построение однофакторной линейной регрессионной модели связи
изучаемых признаков с помощью инструмента Регрессия
надстройки Пакет
анализа
Алгоритм выполнения Задания 2
Алгоритм 1. Расчет параметров
уравнения линейной регрессии и проверки адекватности модели исходным данным
1.
Сервис => Анализ данных
=> Регрессия => ОК;
2. Входной интервал Y <= диапазон ячеек
таблицы со значениями признака Y – Выпуск продукции (С4:С33);
3. Входной интервал X – диапазон ячеек таблицы со значениями признака X – Среднегодовая стоимость основных
производственных фондов (В4:В33);
4. Метки в первой строке/Метки в первом столбце – НЕ активизировать;
5. Уровень надежности <= 68,3 (или 68.3);
6. Константа–ноль – НЕ
активизировать;
7. Выходной интервал <= адрес ячейки заголовка первого столбца первой
выходной результативной таблицы (А75);
8. Новый рабочий лист и Новая рабочая книга – НЕ
активизировать;
9. Остатки – Активизировать;
10.
Стандартизованные остатки – НЕ
активизировать;
11.
График остатков – НЕ
активизировать;
12.
График подбора – НЕ
активизировать;
13.
График нормальной
вероятности – НЕ активизировать;
14.
ОК.
В результате указанных действий осуществляется вывод
четырех выходных таблиц на Лист 2 Рабочего файла, начиная с
ячейки, указанной в поле Выходной
интервал диалогового окна инструмента Регрессия
(они имеют следующий вид).
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
Регрессионная
статистика
|
|
Множественный
R
|
0,91318826
|
|
R-квадрат
|
0,833912798
|
|
Нормированный
R-квадрат
|
0,827981112
|
|
Стандартная
ошибка
|
47,86829677
|
|
Наблюдения
|
30
|
|
Дисперсионный анализ
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
322135,3993
|
322135,3993
|
140,5861384
|
1,97601E-12
|
|
Остаток
|
28
|
64158,4674
|
2291,373836
|
|
|
|
Итого
|
29
|
386293,8667
|
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 68,3%
|
Верхние 68,3%
|
|
Y-пересечение
|
-77,41201619
|
51,28154579
|
-1,509549195
|
0,142361588
|
-182,4574994
|
27,63346706
|
-129,659926
|
-25,16410641
|
|
Переменная X 1
|
1,089355181
|
0,09187519
|
11,85690257
|
1,97601E-12
|
0,901157387
|
1,277552975
|
0,995748668
|
1,182961694
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД
ОСТАТКА
|
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
1
|
303,8622971
|
-23,86229714
|
|
2
|
334,3642422
|
37,63575779
|
|
3
|
369,223608
|
-49,223608
|
|
4
|
382,2958702
|
29,70412983
|
|
5
|
399,7255531
|
40,27444693
|
|
6
|
408,4403945
|
55,55960549
|
|
7
|
443,2997603
|
-47,2997603
|
|
8
|
456,3720225
|
-76,37202248
|
|
9
|
465,0868639
|
-13,08686392
|
|
10
|
482,5165468
|
21,48345318
|
|
11
|
486,8739675
|
49,12603246
|
|
12
|
499,9462297
|
-7,946229714
|
|
13
|
508,6610712
|
7,338928838
|
|
14
|
513,0184919
|
46,98150811
|
|
15
|
526,0907541
|
-26,09075406
|
|
16
|
530,4481748
|
-18,44817478
|
|
17
|
543,520437
|
-63,52043695
|
|
18
|
543,520437
|
40,47956305
|
|
19
|
543,520437
|
-23,52043695
|
|
20
|
560,9501198
|
87,04988015
|
|
21
|
587,0946442
|
-67,09464419
|
|
22
|
595,8094856
|
12,19051436
|
|
23
|
600,1669064
|
43,83309364
|
|
24
|
604,5243271
|
-84,52432709
|
|
25
|
617,5965893
|
-21,59658926
|
|
26
|
621,95401
|
-73,95400998
|
|
27
|
635,0262722
|
72,97372785
|
|
28
|
665,5282172
|
14,47178278
|
|
29
|
682,9579001
|
17,04209989
|
|
30
|
739,6043695
|
20,39563048
|
Задание 3 Построение однофакторных
нелинейных регрессионных моделей связи признаков с помощью инструмента Мастер
диаграмм и выбор наиболее адекватного нелинейного уравнения регрессии
Алгоритмы выполнения Задания 3
Алгоритм 1. Построение уравнений регрессионных
моделей для различных видов нелинейной
зависимости признаков с использованием средств инструмента Мастер
диаграмм
1. Выделить мышью диаграмму
рассеяния признаков, расположенную начиная с ячейки Е4, и увеличить диаграмму на весь экран, используя прием "захват мышью";
2. Диаграмма => Добавить линию тренда;
3. В появившемся диалоговом
окне Линия тренда выбрать вкладку Тип и задать вид регрессионной модели –
полином
2-го порядка;
4.
Выбрать вкладку Параметры и
выполнить действия:
1. Переключатель Название аппроксимирующей кривой:
автоматическое/другое – установить в положение другое и ввести имя тренда– полином 2-го порядка;
2. Поле Прогноз вперед на – НЕ активизировать;
3. Поле Прогноз назад на – НЕ активизировать;
4. Флажок Пересечение кривой
с осью Y в
точке –
НЕ активизировать;
5. Флажок Показывать уравнение на диаграмме – Активизировать;
6. Флажок Поместить на диаграмму величину достоверности аппроксимации R2 – Активизировать;
7. ОК;
8. Установить курсор на линию
регрессии и щелкнуть правой клавишей мыши;
9. В появившемся диалоговом
окне Формат линии тренда выбрать по
своему усмотрению тип, цвет и толщину линии;
10. ОК;
11. Выделить уравнение регрессии
и индекс детерминации R2
и с помощью приема "захват мышью" вынести их за
корреляционное поле. При необходимости уменьшить размер шрифта.
5. Действия 2 – 4 (в п.4 шаги 1–11) выполнить поочередно для следующих
видов регрессионных моделей:
– полином 3-го порядка,
– степенная функция.
По окончании работы алгоритма 1 выполнить следующие
действия:
1. Присвоить полученной
диаграмме заголовок "Диаграмма 2.1" и удалить
линии сетки по оси Y (алгоритм 2);
2. Снять заливку области
построения (алгоритм 3);
3. При необходимости изменить
масштаб шкалы осей диаграммы (алгоритм 4).
Алгоритм 2. Присвоение
полученной диаграмме заголовка "Диаграмма 2.1" и удаление
линий сетки по оси Y
1. Выделить мышью построенную
диаграмму;
2. Диаграмма => Параметры диаграммы;
3. В появившемся диалоговом
окне Параметры диаграммы выбрать
вкладку Заголовки и в поле Название диаграммы ввести заголовок
диаграммы "Диаграмма 2.1";
4. Выбрать вкладку Линии сетки, в полях Ось Х и Ось Y все флажки – Не активизировать;
5. ОК.
Алгоритм 3. Снятие
заливки области построения
1. Выделить мышью Область построения диаграммы;
2. Формат => Выделенная область построения;
3. В появившемся диалоговом
окне Формат области переключатель Заливка установить в положение Обычная;
4. ОК.
Алгоритм 4. Изменение
масштаба шкалы осей диаграммы
1. Выделить на полученной
диаграмме ось, для которой необходимо изменить масштаб (подвести курсор к
требуемой оси и щелкнуть левой клавишей мыши);
2. Формат => Выделенная ось;
3. В появившемся диалоговом
окне Формат оси выбрать вкладку Шкала;
4. В поле Минимальное значение – ввести минимальное (или несколько ниже)
значение признака, соответствующего форматируемой оси;
5. В поле Максимальное значение – ввести максимальное (или несколько выше)
значение признака, соответствующего форматируемой оси;
6. ОК.
Выделить диаграмму и с помощью приема "захват мышью" переместить ее в конец Рабочего
файла.
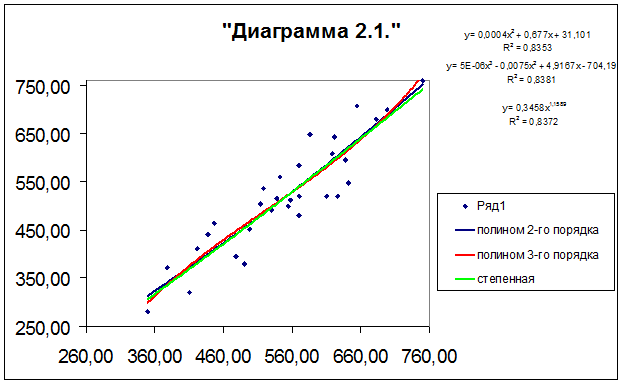
В
результате указанных действий для выбранных видов моделей регрессии
осуществляется вывод на диаграмму рассеяния 3-х уравнений регрессии, их
графиков и значений соответствующих индексов детерминации R2 (Диаграмма 2.1 приведена на рис. 2.1).
ПРИЛОЖЕНИЕ
табл.2.1
|
|
|
Таблица
2.1
|
|
Исходные
данные
|
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
5
|
350,00
|
280,00
|
|
23
|
378,00
|
372,00
|
|
27
|
410,00
|
320,00
|
|
1
|
422,00
|
412,00
|
|
8
|
438,00
|
440,00
|
|
32
|
446,00
|
464,00
|
|
22
|
478,00
|
396,00
|
|
19
|
490,00
|
380,00
|
|
2
|
498,00
|
452,00
|
|
3
|
514,00
|
504,00
|
|
13
|
518,00
|
536,00
|
|
26
|
530,00
|
492,00
|
|
9
|
538,00
|
516,00
|
|
4
|
542,00
|
560,00
|
|
28
|
554,00
|
500,00
|
|
17
|
558,00
|
512,00
|
|
6
|
570,00
|
480,00
|
|
14
|
570,00
|
584,00
|
|
25
|
570,00
|
520,00
|
|
7
|
586,00
|
648,00
|
|
31
|
610,00
|
520,00
|
|
18
|
618,00
|
608,00
|
|
10
|
622,00
|
644,00
|
|
20
|
626,00
|
520,00
|
|
24
|
638,00
|
596,00
|
|
29
|
642,00
|
548,00
|
|
15
|
654,00
|
708,00
|
|
12
|
682,00
|
680,00
|
|
21
|
698,00
|
700,00
|
|
16
|
750,00
|
760,00
|
рис. 2.1
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
Лабораторная работа №3
Автоматизированный
анализ динамики социально-экономических явлений в среде MS Excel
Вариант № 6
Исполнитель: Ржавичева Татьяна Владимировна
Специальность: финансы и
кредит
Группа: дневная III
курс
№ зачетной
книжки: 08ФФД40351
Руководитель: Леонова Светлана Николаевна
Орел 2009г
Задание 1.Расчёт и анализ
показателей ряда динамики выпуска продукции за шестилетний период.
Алгоритмы выполнения Задания 1
Задача 1. . Расчет цепных и базисных показателей динамики: абсолютный прирост
(сокращение); темп роста (снижения); темп прироста (сокращения) и абсолютное
значение 1 % прироста
Алгоритм 1.1. Расчёт цепных и
базисных показателей динамики, характеризующих изменение отдельных уровней ряда
динамики
1. В ячейке, выделенной для значения абсолютного прироста цепного
за первый год (С26), перед формулой
поставить знак равенства «=»;
2. Enter;
3. Установить курсор в правом нижнем углу ячейки (С26) с формулой – образцом (курсор
примет форму черного крестика) и, удерживая левую клавишу мыши в нажатом
состоянии, переместить курсор до нижней клетки графы. Отпустить клавишу мыши
(формула – образец размножилась на всю графу).
4. Выполнить действия 1–2 поочередно для всех
аналитических показателей ряда динамики табл.3.2:
абсолютного
прироста базисного;
темпа
роста цепного и базисного;
темпа
прироста цепного и базисного;
абсолютного
значения 1% прироста.
Результат работы алгоритма 1.1 в табл. 3.2
|
|
|
|
|
|
|
|
|
Таблица
3.2
|
|
Показатели динамики выпуска продукции
|
|
Годы
|
Выпуск продукции, млн. руб.
|
Абсолютный прирост,
млн. руб.
|
Темп роста,
%
|
Темп прироста,
%
|
Абсолютное
значение
1% прироста
|
|
цепной
|
базисный
|
цепной
|
базисный
|
цепной
|
базисный
|
|
1-й
|
3920,00
|
|
|
|
|
|
|
|
|
2-й
|
4160,00
|
240,00
|
240,00
|
106,1
|
106,1
|
6,1
|
6,1
|
39,2
|
|
3-й
|
4550,00
|
390,00
|
630,00
|
109,4
|
116,1
|
9,4
|
16,1
|
41,6
|
|
4-й
|
4430,00
|
-120,00
|
510,00
|
97,4
|
113,0
|
-2,6
|
13,0
|
45,5
|
|
5-й
|
4665,00
|
235,00
|
745,00
|
105,3
|
119,0
|
5,3
|
19,0
|
44,3
|
|
6-й
|
5157,00
|
492,00
|
1 237,00
|
110,5
|
131,6
|
10,5
|
31,6
|
46,65
|
Задача 2. Расчет средних показателей ряда динамики: средний
уровень ряда динамики; средний абсолютный прирост; средний темп роста и средний
темп прироста
Алгоритм 1.2. Расчёт средних показателей ряда динамики
1. В ячейке, выделенной для значения средний уровень ряда динамики (E34), перед формулой поставить
знак равенства «=»;
2. Enter;
3. Выполнить действия 1–2 поочередно для всех
средних показателей ряда динамики табл.3.3:
среднего
абсолютного прироста;
среднего
темпа роста;
среднего
темпа прироста.
Результат работы алгоритма 1.2 в табл. 3.3
|
|
|
|
|
Таблица
3.3
|
|
Средние показатели ряда динамики
|
|
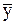
|
Средний уровень ряда
динамики,млн. руб.,
|
|
4480,33
|
|
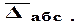
|
Средний абсолютный
прирост,млн. руб.,
|
|
247,40
|
|
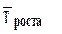 Средний
темп роста, %, Средний
темп роста, %,
|
105,6
|
|
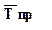 Средний
темп прироста, %, Средний
темп прироста, %,
|
5,6
|
Задание 2.
Прогноз показателя выпуска продукции на 7-ой год методом экстраполяции.
Алгоритмы выполнения Задания 2
Задача 1. Прогнозирование
выпуска продукции предприятием на год вперёд с использованием среднего
абсолютного прироста и среднего темпа роста.
Алгоритм 2.1. Расчёт
выпуска продукции на год вперёд с
использованием среднего абсолютного прироста и среднего темпа роста
1. В ячейке, выделенной для
значений прогнозируемого выпуска продукции по среднему
абсолютному приросту (Е41),
перед формулой поставить знак равенства «=».
2. Enter;
3. Выполнить действия 1–2 для прогнозируемого выпуска
продукции по значению среднего темпа роста (табл.3.4).
Результат работы алгоритма
2.1 в табл. 3.4
|
|
|
|
|
Таблица
3.4
|
|

|
Прогноз выпуска продукции на 7-ой год
|
|
|

|
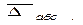 По среднему абсолютному приросту, млню руб., По среднему абсолютному приросту, млню руб.,
|
|
5404,40
|
|
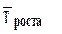 По среднему темпу роста, %, По среднему темпу роста, %,
|
|
5445,79
|
Задача 2. Прогнозирование
выпуска продукции предприятием на год вперёд с использованием аналитического
выравнивания ряда динамики по прямой, параболе и полиному 3-го порядка.
Алгоритм 2.2. Построение
графика динамики выпуска продукции за 6 лет с использованием средств
инструмента МАСТЕР ДИАГРАММ
1. Выделить мышью ячейки,
содержащие выпуск продукции за 6 лет (диапазон ячеек B7:B12);
2. Вставка=>Диаграмма=>Точечная;
3. В появившемся диалоговом
окне Мастер диаграмм (шаг 1 из 4) выбрать
вид точечной диаграммы, на которой значения соединены отрезками;
4. Далее;
5. В появившемся диалоговом
окне Мастер диаграмм (шаг 2 из 4) выбрать
вкладку Ряд и задать имя ряда 1 – «Исходные данные»;
6. Далее;
7. В появившемся диалоговом
окне Мастер диаграмм (шаг 3 из 4) выбрать
вкладку Заголовки и задать названия
диаграммы («Прогнозирование выпуска продукции на 7-ой год») и осей Х («Годы») и У («Выпуск продукции. млн.
руб.»;;
8. Готово;
9. Выделить на полученной
диаграмме ось Y (подвести курсор к
требуемой оси и щелкнуть левой клавишей мыши);
10.
Формат => Выделенная ось;
11.
В появившемся диалоговом окне Формат
оси выбрать вкладку Шкала;
12.
В поле Минимальное значение –
ввести минимальное (или несколько ниже) значение признака «Выпуск продукции»;
13.
ОК.
Выделить диаграмму и с помощью приема "захват мышью" переместить ее в конец Рабочего
файла.
Алгоритм 2.3. Нахождение
тренда ряда динамики выпуска
продукции методом аналитического выравнивания и прогнозирование его на год вперед с помощью инструмента
Мастер диаграмм
1. Выделить мышью диаграмму
«Прогнозирование выпуска продукции на 7-ой год», расположенную в конце Рабочего
файла;
2. Диаграмма => Добавить линию тренда;
3. В появившемся диалоговом
окне Линия тренда выбрать вкладку Тип и задать вид линии тренда – линейная;
4. Выбрать вкладку Параметры и выполнить действия:
1. Переключатель Название аппроксимирующей кривой:
автоматическое/другое – установить в положение другое и ввести имя тренда– Прямая;
2. В поле Прогноз вперед на…едициц ввести значение «1»;
3. Поле Прогноз назад на…единиц – НЕ активизировать;
4. Флажок Пересечение кривой
с осью Y в
точке – НЕ
активизировать;
5. Флажок Показывать уравнение на диаграмме – Активизировать;
6. Флажок Поместить на диаграмму величину достоверности аппроксимации R2 – Активизировать;
7. ОК;
8. Установить курсор на линию
тренда, щелкнуть правой клавишей мыши и выбрать меню Формат линии тренда;
9. В появившемся диалоговом
окне Формат линии тренда выбрать
вкладку Вид и задать по своему
усмотрению тип, цвет и толщину линии;
10. ОК;
11. Выделить уравнение линии
тренда и индекс детерминации R2
и с помощью приема "захват мышью" вынести их за
корреляционное поле. При необходимости уменьшить размер шрифта.
5. Действия 1 – 4 (в п.4 шаги 1–11) выполнить для линии тренда:
парабола;
полином 3-го
порядка.
Результат работы алгоритмов 2.2 – 2.3
представлен на рис.3.1. 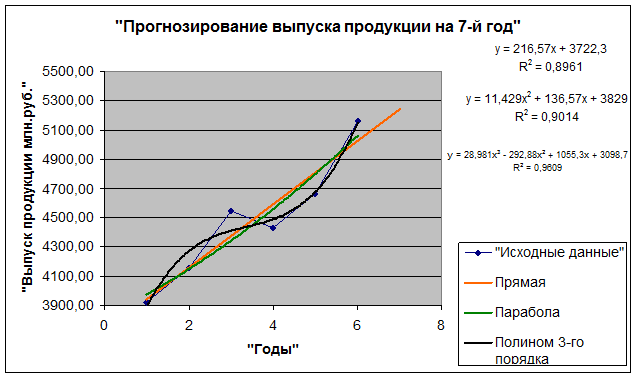
Рис.3.1. График динамики
выпуска продукции за 6 лет и прогноз выпуска на год вперед
Задание 3. Выявление
тенденции развития изучаемого явления (тренда) по данным о выпуске продукции по месяцам за
6-ой год методами скользящей средней и аналитического выравнивания.
Алгоритмы выполнения Задания 3
Алгоритм 3.1. Нахождение
значений скользящей
средней с помощью инструмента СКОЛЬЗЯЩЕЕ СРЕДНЕЕ надстройки ПАКЕТ АНАЛИЗА
1.
Сервис => Анализ данных
=> Скользящее среднее => ОК;
2. Входной интервал <= диапазон ячеек табл. 3.5 со значениями признака –
Выпуск продукции (В47:В58);
3. Метки в первой строке– НЕ
активизировать;
4. Интервал – НЕ активизировать;
5. Выходной интервал <= адрес первой ячейки третьего столбца выходной
результативной таблицы (С47);
6. Новый рабочий лист и Новая рабочая книга – НЕ
активизировать;
7. Вывод графика –Активизировать;
8. Стандартные погрешности – НЕ активизировать;
9. ОК.
Выделить
диаграмму и с помощью приема "захват мышью" переместить ее в конец Рабочего файла.
В
результате указанных действий осуществляется вывод значений скользящей средней,
начиная с ячейки, указанной в поле Выходной
интервал диалогового окна инструмента Скользящее
среднее, и графика. Они представлены
в табл.3.5 и на рис.3.2.
|
|
|
Таблица
3.5
|
|
Выпуск продукции за 6-ой год
|
|
Месяцы
|
Выпуск продукции, млн. руб.
|
Скользящее
среднее
|
|
январь
|
265,00
|
#Н/Д
|
|
февраль
|
331,00
|
#Н/Д
|
|
март
|
390,00
|
328,67
|
|
апрель
|
360,00
|
360,33
|
|
май
|
420,00
|
390,00
|
|
июнь
|
400,00
|
393,33
|
|
июль
|
456,00
|
425,33
|
|
август
|
431,00
|
429,00
|
|
сентябрь
|
510,00
|
465,67
|
|
октябрь
|
531,00
|
490,67
|
|
ноябрь
|
543,00
|
528,00
|
|
декабрь
|
520,00
|
531,33
|
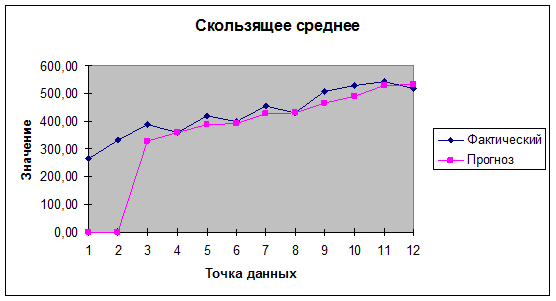
Рис.3.2. График сглаживания ряда динамики выпуска продукции за
6-ой год, сгенерированный в режиме «скользящее среднее» Пакета анализа
Алгоритм 3.2. Приведение выходной таблицы к
виду, принятому в статистике
1. Ячейку С47,
содержащую термин " #Н/Д", выделить мышью и очистить,
нажав клавишу [Delete];
2. Ячейки результативной
таблицы (С49:С58), содержащие значения «Скользящее среднее», вырезать с
помощью инструмента  ;
;
3. Вставить в табл. 3.5, начиная с ячейки С48, с помощью инструмента  ;
;
4. Отформатировать таблицу по образцу с помощью
инструмента  .
.
Полученная
результативная таблица выглядит следующим образом.
|
|
|
Таблица
3.5
|
|
Выпуск
продукции за 6-ой год
|
|
Месяцы
|
Выпуск продукции, млн. руб.
|
Скользящее
среднее
|
|
январь
|
265,00
|
|
|
февраль
|
331,00
|
328,67
|
|
март
|
390,00
|
360,33
|
|
апрель
|
360,00
|
390,00
|
|
май
|
420,00
|
393,33
|
|
июнь
|
400,00
|
425,33
|
|
июль
|
456,00
|
429,00
|
|
август
|
431,00
|
465,67
|
|
сентябрь
|
510,00
|
490,67
|
|
октябрь
|
531,00
|
528,00
|
|
ноябрь
|
543,00
|
531,33
|
|
декабрь
|
520,00
|
|
График сглаживания
ряда динамики выпуска продукции методом скользящей средней представлен на рис. 3.3.
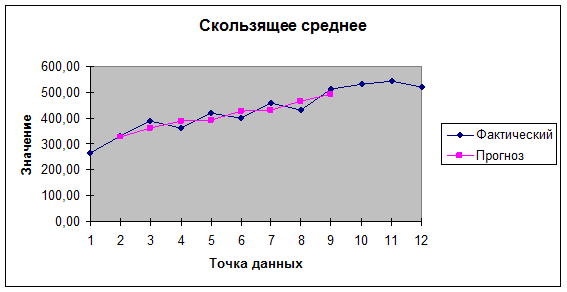
Рис.3.3. График сглаживания скользящей средней ряда динамики
выпуска продукции за 6-ой год
Задача 2. Аналитическое выравнивание по прямой и параболе
Алгоритм 3.3. Построение графика динамики выпуска продукции по
месяцам за 6-ой год с использованием средств инструмента МАСТЕР
ДИАГРАММ
1. Выделить мышью столбец
данных в диапазоне B47:В58 (табл. 3.5);
2. Вставка=>Диаграмма=>Точечная;
3. В появившемся диалоговом
окне Мастер диаграмм (шаг 1 из 4) выбрать
вид точечной диаграммы, на которой значения соединены отрезками;
4. Далее;
5. В появившемся диалоговом
окне Мастер диаграмм (шаг 2 из 4) выбрать
вкладку Ряд и ввести имя ряда «Исходные данные»;
6. Далее;
7. В появившемся диалоговом
окне Мастер диаграмм (шаг 3 из 4) выбрать
вкладку Заголовки и задать названия
диаграммы («Выпуск продукции за 6-ой год
по месяцам») и осей Х («Месяцы») и У («Выпуск продукции. млн. руб.»;
8. Готово.
Выделить диаграмму и с помощью приема "захват мышью" переместить ее в конец Рабочего
файла.
Алгоритм 3.4. Сглаживание ряда динамики выпуска продукции методом
аналитического выравнивания с помощью инструмента
Мастер диаграмм
1. Выделить мышью диаграмму «Выпуск
продукции за 6-ой год по месяцам»,
расположенную в конце Рабочего файла;
2. Диаграмма => Добавить линию тренда;
3. В появившемся диалоговом
окне Линия тренда выбрать вкладку Тип и задать вид линии тренда – линейная;
4.
Выбрать вкладку Параметры и
выполнить действия:
1.
Переключатель Название
аппроксимирующей кривой: автоматическое/другое – установить в положение другое и ввести имя тренда - Прямая;
2.
Поле Прогноз вперед на – НЕ
активизировать;
3.
Поле Прогноз назад на – НЕ
активизировать;
4.
Флажок Пересечение
кривой с осью
Y в точке
– НЕ
активизировать;
5.
Флажок Показывать уравнение на
диаграмме – Активизировать;
6.
Флажок Поместить на диаграмму
величину достоверности аппроксимации R2 – Активизировать;
7.
ОК;
8.
Установить курсор на линию тренда, щелкнуть правой клавишей мыши и
выбрать меню Формат линии тренда;
9.
В появившемся диалоговом окне Формат
линии тренда выбрать вкладку Вид
и задать по своему усмотрению тип, цвет и толщину линии;
10. ОК;
11. Выделить уравнение линии
тренда и индекс детерминации R2
и с помощью приема "захват мышью" вынести их за
корреляционное поле. При необходимости уменьшить размер шрифта.
5. Действия 1 – 4 (в п.4 шаги 1–11) выполнить для линии тренда парабола.
По окончании работы алгоритма
2.4 выполнить следующие действия:
1. Снять заливку области
построения;
2. При необходимости изменить
масштаб шкалы осей диаграммы.
Результат работы алгоритмов 3.3 – 3.4
представлен на рис.3.4.
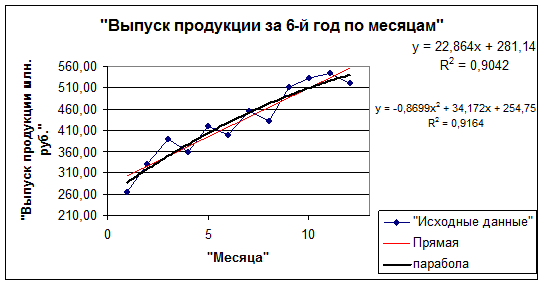
Рис. 3.4. График
сглаживания по прямой и параболе ряда
динамики выпуска продукции за 6-ой год
ПРИЛОЖЕНИЕ
Таблица 3.1
|
|
|
|
|
Таблица
3.1
|
|
Исходные данные
|
|
Годы
|
Выпуск продукции, млн. руб.
|
|
Месяцы
|
Выпуск продукции, млн. руб.
|
|
1
|
3920,00
|
|
январь
|
265,00
|
|
2
|
4160,00
|
|
февраль
|
331,00
|
|
3
|
4550,00
|
|
март
|
390,00
|
|
4
|
4430,00
|
|
апрель
|
360,00
|
|
5
|
4665,00
|
|
май
|
420,00
|
|
6
|
5157,00
|
|
июнь
|
400,00
|
|
|
|
|
июль
|
456,00
|
|
|
|
|
август
|
431,00
|
|
|
|
|
сентябрь
|
510,00
|
|
|
|
|
октябрь
|
531,00
|
|
|
|
|
ноябрь
|
543,00
|
|
|
|
|
декабрь
|
520,00
|
|
|
|
|
Итого
|
5157,00
|