Содержание
Введение. 3
Исходное задание. 5
1. Теоретическая часть. 7
1.1. Процессы и методы принятия решений. 7
1.2. Характеристика экспертных методов
прогнозирования. 8
2. Практическая часть. 13
2.1. Анализ возможности решения проблемы за
указанный срок. 13
2.2. Анализ возможности компании
«Олкрейт» самостоятельно решить свои финансовые проблемы.. 21
2.3. Анализ возможности компании «Олкрейт»
рассчитывать на помощь инвесторов в ближайшие 2-3 года. 23
2.4. Анализ возможности решения главной проблемы
в результате укрепления кадровой политики. 25
2.5. Анализ возможности завода «Петров и Петров»,
являясь заказчиком строительства танкеров, полностью осуществить все платежи по
контрактам. 27
2.6. Анализ возможности ускорения решения
проблемы выпуска танкеров с помощью приоритета не современной судостроительной
техники. 29
2.7. Анализ прогнозов дополнительных затрат. 31
Заключение. 33
Список литературы.. 34
Введение
Принятие решений пронизывает всю
управленческую деятельность, решения принимаются по широкому кругу задач
управления. Ни одна функция управления, независимо от того, какой орган ее
осуществляет, не может быть реализована иначе как посредством подготовки и
исполнения управленческих решений. По существу, вся совокупность видов
деятельности любого работника управления, так или иначе, связана с принятием и
реализацией решений. Этим, прежде всего, определяется значимость деятельности
по принятию решений и определению его роли в управлении. [3, c. 44]
Важность рассмотрения вопроса о
роли принятия решения в управлении определяется также тем, что в литературе
имеет место смешение понятий «решение руководителя (менеджера)» и
«управленческое решение». Оба понятия объединяются единым названием
«управленческое решение». Все-таки следует проводить различие между этими
понятиями. Первое понятие характеризует принятие руководителем любых решений,
вытекающих из характера его деятельности (управленческих, экономических,
производственных и т.п.). Это расширенная трактовка понятия управленческого
решения. Здесь затрагиваются разнообразные сферы деятельности, которыми
управляет руководитель (финансовые, производственные, сбытовые и
др.). Представляется, что такие решения правильнее назвать решениями в бизнесе.
Вторая трактовка предполагает принятие
решений только в разрезе выполнения отдельных функций управления (планирования,
организации, мотивации и контроля). Именно с этих позиций рассматривается
управленческое решение в данной серии статей.
Вышесказанное не означает, что при принятии
управленческих решений не принимаются в расчет финансовые, экономические,
производственные и другие факторы. Важное значение функции принятия
решений для деятельности человека и ее особая роль в процессе управления
определяют необходимость рассмотрения всех аспектов этой функции. При
научном подходе к функции принятия решений все перечисленные аспекты должны
рассматриваться в комплексе. Комплексный подход обеспечивает полноту изучения
этой функции и способствует более глубокому пониманию закономерностей процесса
принятия решений. [5, c. 112]
Характерной особенностью управления любыми
объектами является достижение определенных целей. Эта общая особенность может
быть положена в основу определения процесса управления. Процессом управления
называют целенаправленное воздействие субъекта управления на объект управления
в целях реализации функций управления.
Целью данной работы является изучения
подготовки и принятии управленческих решений с помощью метода экспертных
оценок.
В работе поставлены следующие задачи:
·
Рассмотреть теоретические основы методов
принятия управленческих решений;
·
Проанализировать возможные решения для
анализируемой ситуации с помощью метода экспертных оценок.
Исходное
задание
Компания «Олкрет» с самых первых
дней решила начать осуществление долгосрочной программы развития. В числе
наиболее актуальных задач, поставленных перед собой руководством компании, было
совершенствование транспортной системы России и организации речных и морских
перевозок. Нефть и нефтепродукты в структуре грузопотоков в России составляют
немалую долю. В сложившихся экономических и политических условиях России
лишились своего флота и традиционных перевалочных баз на Черном и Балтийском
морях. Эти факторы определили необходимость строительства флота малотоннажных
судов класса река-море, грузоподъемностью от 3 до 5 тыс. тонн, способных
перевозить нефтепродукты из удаленных районов России в Европу. Перед
руководством фирмы возник серьезный вопрос о возможности решения такой задачи.
Сложность проблемы заключалась в том, что проект действительно грандиозен.
Необходимо было построить 62 танкера водоизмещением 3 тыс. тонн. Собственных
средств на реализацию проекта у «Олкрейт» не хватает,
необходимо привлекать в помощь партнеров или искать инвесторов. Для обеспечения
финансирования строительных судов «Олкрейт» заключило
договор о совместной деятельности по их строительству и эксплуатации с
российским нефтеперерабатывающим заводом «Петров и Петров».
Вопросы:
1.
Возможно ли за короткий срок решить указанную проблему?
2.
Сможет ли компания «Олкрейт»
самостоятельно решить свои финансовые проблемы?
3.
Можно ли рассчитывать на помощь инвесторов в ближайшие
2-3 года?
4.
Решится ли главная проблема в результате укрепления
кадровой политики?
5.
Сможет ли завод «Петров и Петров», являясь заказчиком
строительства танкеров, полностью осуществить все платежи по контрактам?
6.
Поможет ли приоритет не современной судостроительной
техники ускорению решения проблемы выпуска танкеров?
Варианты ответов экспертов по основным вопросам приведены в
табл. 1.
Таблица 1
Варианты ответов экспертов по основным вопросам
|
Вопросы
|
1
|
2
|
3
|
4
|
5
|
6
|
|
Эксперты
|
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
|
2
|
1
|
0
|
0
|
1
|
1
|
1
|
|
3
|
0
|
1
|
0
|
0
|
1
|
1
|
|
4
|
1
|
1
|
0
|
0
|
0
|
1
|
|
5
|
1
|
0
|
0
|
1
|
0
|
0
|
|
6
|
0
|
0
|
0
|
1
|
1
|
0
|
|
7
|
0
|
1
|
1
|
1
|
1
|
1
|
|
Ваше мнение 8
|
0
|
0
|
1
|
1
|
1
|
1
|
Варианты прогнозов дополнительных затрат представлены в
табл. 2.
Таблица 2
Варианты прогнозов
дополнительных затрат
|
Эксперты
|
Вариант I (Kmin)
|
Вариант II (Kmax)
|
|
1
|
3,0
|
3,5
|
|
2
|
2,5
|
3,0
|
|
3
|
3,2
|
3,3
|
|
4
|
3,0
|
3,3
|
|
5
|
2,4
|
2,8
|
|
6
|
2,5
|
3,0
|
|
7
|
2,8
|
3,0
|
|
8
|
2,8
|
3,2
|
1. Теоретическая часть
1.1. Процессы и методы принятия решений
Процессы принятия
решений, понимаемые как выбор человеком одной из нескольких альтернатив его
дальнейшего поведения, сопровождает всю человеческую жизнь. Большинство решений
мы принимаем не задумываясь, так как существует автоматизм поведения,
выработанный практикой. Но возможны и ситуации, когда человек испытывает
мучительные раздумья. Это случается, когда он сталкивается либо с новым
объектом выбора, либо с новой обстановкой, в которой совершается выбор.
Принятие решений
представляет собой сознательный выбор одного из имеющихся вариантов
(альтернатив) действий, сокращающих разрыв между настоящим и будущим желательным состоянием - целью.
Сам процесс принятия решений включает множество различных элементов, но
непременно в нем присутствуют такие элементы, как цели, средства, альтернативы. Принятие решений – это
"центр", вокруг которого вращается жизнь как отдельного человека, так
и организации. Решение в организации можно рассматривать как продукт
управленческого труда, а его принятие – как процесс, ведущий к появлению этого
продукта. [4, c. 38]
Таким образом,
принятие управленческих решений отражается на всех аспектах деятельности
организации, и этот процесс является основной частью ежедневной работы любого
руководителя (менеджера). [2,c. 110]
Принятие решений в
организации это:
–
сознательная и целенаправленная деятельность, осуществляемая
людьми - руководителями,
менеджерами,
–
поведение людей, основанное как на фактах, так и на их
ценностных ориентациях,
–
процесс, базирующийся на осознанном взаимодействии
членов организации,
–
выбор лучшей из ряда альтернатив в рамках состояния
внешней и внутренней организационной среды.
Принятие решений –
это и наука, и искусство.
Для принятия управленческих решений, таким
образом, должны быть определены:
–
мотивирующие цели,
–
допустимые альтернативные способы достижения поставленных
целей – стратегии,
–
возможные состояния внешней (неопределенной) среды,
–
ожидаемые результаты реализации стратегий при различных
состояниях среды – исходы.
Затем альтернативы
должны быть оценены, согласно выбранному критерию решения, для выбора лучшей из
них. Хорошо, если этот выбор может быть каким-либо образом формализован. К
этому необходимо стремиться, однако в любом случае окончательное решение всегда
остается за руководителем. [8, c. 98]
Формализованные
методы обоснования принятия управленческих решений в мировой практике носят
название ''исследование операций'', где
под операцией понимают любой вид деятельности человека.
1.2. Характеристика экспертных методов прогнозирования
Экспертные методы
применяются для оценки объектов и процессов, не поддающихся непосредственному
измерению, т. е. характеризующихся лишь качественно.
Экспертные методы - это
совокупность специальных методик обработки экспертных оценок, позволяющих
свести ошибку прогнозирования к минимуму.
Экспертные оценки – это субъективные
суждения специалистов в данной области, высказанные ими открыто или скрыто,
индивидуально, независимо от других, или коллективно.
Обоснование
объективности результатов экспертной оценки, кроме высокой квалификации
экспертов, обусловлено следующим предположением: неизвестная характеристика
оцениваемого (прогнозируемого) процесса трактуется как случайная величина, а индивидуальные оценки экспертов - как множество ее
реализаций, отражающее закон и параметры распределения этой случайной величины.
Предполагается, что истинное значение прогнозируемой характеристики
находится внутри диапазона оценок, полученных от экспертов.
Недостатки
экспертных методов неизбежно связаны с их природой.
Для недостаточно
исследованных областей истинное значение прогнозируемой характеристики может
находиться вне диапазона данных экспертами оценок, т. е. один из экспертов,
давший крайнюю оценку, может оказаться наиболее близким к истине.
Даже для достаточно
исследованных областей экспертные оценки могут нести в себе не только
субъективные черты отдельных специалистов, но и коллективные субъективные черты,
рассматриваемые как "общественное мнение", "общественная точка
зрения", "научная школа" и т. п.
Они не исчезают при обработке результатов по специальным методикам, а
иногда могут даже усиливаться. [6, c. 44]
При коллективной
экспертной оценке, а иногда даже и при индивидуальной, на результат может
заметно влиять мнение одного человека: руководителя, самого авторитетного
специалиста, "сильной личности".
Наиболее известны
следующие экспертные методы.
1.
Метод "мозговой атаки", при котором
все мнения, высказанные экспертами, тотчас же обсуждаются до тех пор, пока все
они не придут к общему мнению. При этом приветствуется свободное высказывание
самых необычных и оригинальных мнений.
2.
Метод Дельфи - итеративный групповой метод - самый старый из методов, пришедший к нам из древней Греции.
3.
Метод индивидуальной разовой экспертной оценки - классический, хорошо формализованный метод.
Индивидуальная
разовая экспертная оценка проводится в четыре этапа:
1)
подбор группы экспертов, взаимная оценка их компетентности;
2)
формирование списка факторов, по которым будет оцениваться
объект, и оценка их значимости;
3)
оценка объектов анализа (прогнозирования) с учетом
значимости выделенных факторов и компетентности экспертов;
4)
ранжирование объектов с учетом полученных ими
обобщенных оценок; выводы.
Процедуру
экспертизы проводит группа менеджеров. Вначале они подбирают группу экспертов
так, чтобы минимизировать возможные недостатки метода, отмеченные ранее. Затем
устанавливается и доводится до экспертов шкала балльных оценок, которая будет
использоваться в дальнейшем. Экспертов собирают вместе фактически или
виртуально, и первое, что они делают, – оценивают компетентность друг друга.
Результат – квадратная матрица оценок Кij ,
данных i-м экспертом j-у (i =
1, 2,…, n, j = 1, 2,…, n), где n -
общее количество экспертов. [10 ,c. 78]
Менеджеры
обрабатывают матрицу и рассчитывают коэффициенты компетентности экспертов: 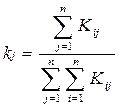 , j = 1, 2, …, n.
, j = 1, 2, …, n.
Эксперты,
получившие минимальную оценку, могут быть исключены из группы.
На втором этапе
эксперты независимо друг от друга составляют перечни факторов оценки объектов.
Все факторы сводятся в единый список, который передается им для оценки.
Результат оценки – матрица размерности n´m, где m – число оцениваемых
факторов, а Fij – оценка, данная i-м
экспертом j-у фактору.
[10, c. 80 ]
Менеджеры
обрабатывают матрицу и рассчитывают коэффициенты значимости факторов: 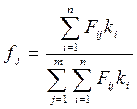 , j = 1, 2, …, m.
, j = 1, 2, …, m.
Факторы ранжируются
в порядке убывания их значимости и наименее значимые по решению менеджеров
могут быть отброшены для сокращения объема работ на следующем этапе. После
такого отбрасывания расчет коэффициентов значимости должен быть повторен, но
уже без учета оценок, полученных исключенными из рассмотрения факторами. В
любом случае должно выполняться условие:
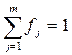 . Аналогичное условие
выдвигается по отношению к коэффициентам компетентности экспертов.
. Аналогичное условие
выдвигается по отношению к коэффициентам компетентности экспертов.
На третьем,
основном, этапе эксперты оценивают объекты с учетом выделенных факторов.
Результат оценки – Р матриц
размерностью n´ m, где Р – число
оцениваемых объектов, а Wijр – оценка, данная i-м
экспертом р-у
объекту с учетом j-го фактора.[10,c. 81]
Менеджеры
обрабатывают информацию и рассчитывают обобщенные оценки всех объектов:  , р = 1, 2, …, Р.
, р = 1, 2, …, Р.
На четвертом этапе
объекты располагаются в порядке убывания (возрастания) значений обобщенной
оценки, таким образом из них отбираются лучшие. На любом этапе по результатам
выставления экспертами оценок можно определить коэффициент согласованности их
мнений: 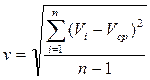 . Здесь V – любая из выставляемых
экспертами оценок (K, F, W). В случае значительного расхождения мнений группа может
быть распущена. [10, c. 83]
. Здесь V – любая из выставляемых
экспертами оценок (K, F, W). В случае значительного расхождения мнений группа может
быть распущена. [10, c. 83]
Для целей
разработки простейшего прогноза может быть использована усеченная процедура, в
которой опущены выбор и оценка значимости факторов, прогнозируется состояние
одного объекта, балльная оценка может быть заменена оценкой процентной
вероятности.
2. Практическая часть
Варианты ответов экспертов
по основным вопросам
|
Вопросы
Эксперты
|
1
|
2
|
3
|
4
|
5
|
6
|
р
|
q
|
σ2
|
|
I
|
0
|
0
|
0
|
0
|
1
|
1
|
0,33
|
0,67
|
0,22
|
|
11
|
1
|
0
|
0
|
1
|
1
|
1
|
0,66
|
0,34
|
0,22
|
|
III
|
0
|
1
|
0
|
0
|
1
|
1
|
0,5
|
0,5
|
0,25
|
|
IV
|
1
|
1
|
0
|
0
|
0
|
1
|
0,5
|
0,5
|
0,25
|
|
V
|
1
|
0
|
0
|
1
|
0
|
0
|
0,33
|
0,67
|
0,22
|
|
VI
|
0
|
0
|
0
|
1
|
1
|
0
|
0,33
|
0,67
|
0,22
|
|
VII
|
0
|
1
|
1
|
1
|
1
|
1
|
0,83
|
0,17
|
0,14
|
|
Ваше мнение (VIII)
|
0
|
0
|
1
|
1
|
1
|
1
|
0,67
|
0,33
|
0,22
|
Вопросы анкет могут быть как
альтернативного (да, нет; 1,0), так и оценочного(от 0 до 1) характера. В первом
случае удобно использовать элементы дисперсионного анализа, во втором - таксономии.
При использовании дисперсионного анализа положительный ответ эксперта
оценивается 1, отрицательный -О.
Основными
характеристиками являются значения P,g, σ.
Р
= M/N,
где М - число единиц
(положительные ответы); N - общее число параметров.
G=L/N,
где L - число нулей (отрицательные ответы)
p+g = 1
Средняя величина,
характеризующая число положительных ответов х=Р Дисперсия, характеризующая отклонение от
средней величины определяется:
σ 2= P*g
Проведем классификацию
ответов экспертов, используя приемы таксономии, Для этого определяем
коэффициент близости между ответами. Существует несколько формул при
определении этих значений. Воспользуемся формулой Роджерса
и Танимото
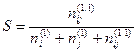
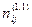 - число совпадающих единиц между сравниваемыми рядами;
- число совпадающих единиц между сравниваемыми рядами;
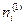 - число всех единиц в i-том сравниваемом ряду;
- число всех единиц в i-том сравниваемом ряду;
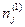 - число единиц в j-том сравниваемом ряду.
- число единиц в j-том сравниваемом ряду.
Сравнивается первый ряд
последовательно со всеми остальными, заполняется первая строка матрицы, затем
вторая строка со всеми остальными и т. д. В результате получим матрицу (табл. 3).
Таблица 3
Определение коэффициентов
близости между ответами экспертов
|
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII
|
∑
|
|
I
|
-
|
0,25
|
0,29
|
0,2
|
0,14
|
0,25
|
0,2
|
0,25
|
1,58
|
|
II
|
0,25
|
-
|
0,29
|
0,2
|
0,2
|
0,25
|
0,2
|
0,25
|
1,64
|
|
III
|
0,29
|
0,29
|
-
|
0,25
|
0,2
|
0,2
|
0,25
|
0,2
|
1,68
|
|
IV
|
0,2
|
0,2
|
0,25
|
-
|
0,2
|
0,07
|
0,14
|
0,07
|
1,13
|
|
V
|
0,14
|
0,2
|
0,2
|
0,2
|
-
|
0,25
|
0,07
|
0,14
|
1,2
|
|
VI
|
0,25
|
0,25
|
0,2
|
0,07
|
0,25
|
-
|
0,2
|
0,25
|
1,47
|
|
VII
|
0,2
|
0,2
|
0,25
|
0,14
|
0,07
|
0,2
|
-
|
0,29
|
1,35
|
|
VIII
|
0,25
|
0,25
|
0,2
|
0,07
|
0,14
|
0,25
|
0,29
|
-
|
1,45
|
Для ее обработки существуют
разные алгоритмы, возьмем простейший. Выделим произвольно какое-либо число в
матрице (лучше одно из наибольших), например 0,29 ( III строка,
I столбец), Теперь по I столбцу ищем наибольшие числа - это 0,25 на пересечении со
второй строкой. Затем ищем наибольшие числа по II строке
(использованные числа не применяются) берем значение 0,29 по III столбцу и т. д. Если встречаются одинаковые числа, то
получаемый граф разделяется и каждая ветвь рассматривается отдельно. В нашем
случае получается следующий граф (рис. 1).


 0.29 (I, III)
0.29 (I, III) 

 Рис. 1
Рис. 1


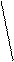
0,25 (I, VIII)
0,25 (I, IV)
0,29 (II, III)
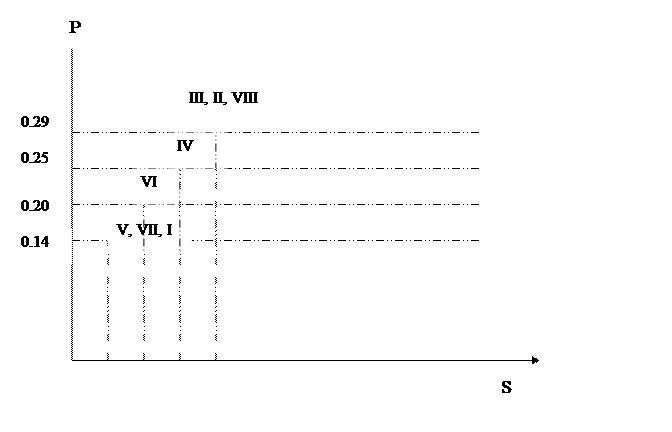
Итак, мнение экспертов можно
представить следующим образом,
S (коэффициент близости)
0, 29 – III, II, VIII,
0,25- IV
0.14- V, VII, I
0,2-
VI,
Чтобы определить, насколько существенные различия между мнениями
экспертов и сгруппировать эти мнение в таксоны составим матрицу коэффициентов
Фишера (табл. 3).
Коэффициент Фишера
определяется через отношение дисперсий,
т. е. F = σ2/σ2
(большее значение дисперсии всегда берется в
числителе).
Матрица коэффициентов Фишера
получена следующим образом: берется отношение дисперсий ответов на вопросы
анкет первого эксперта последовательно к дисперсиям ответов всех остальных
(заполняется первая строка матрицы), затем дисперсии мнений второго ко
всем остальным и т. д.
Таблица 4
Коэффициенты Фишера по
вариантам определения мнений экспертов
|
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII
|
|
I
|
-
|
1
|
1.13
|
1.13
|
1
|
1
|
1.57
|
1
|
|
II
|
1
|
-
|
1.13
|
1.13
|
1
|
1
|
1.57
|
1
|
|
III
|
1.13
|
1.13
|
-
|
1
|
1.13
|
1.13
|
1.57
|
1.13
|
|
IV
|
1.13
|
1.13
|
1
|
-
|
1.13
|
1
|
1.57
|
1.57
|
|
V
|
1
|
1
|
1.13
|
1.13
|
-
|
1
|
1.57
|
1
|
|
VI
|
1
|
1
|
1.13
|
1
|
1
|
-
|
1.57
|
1
|
|
VII
|
1.57
|
1.57
|
1.57
|
1.57
|
1.57
|
1.57
|
-
|
1.57
|
|
VIII
|
1
|
1
|
1.13
|
1.57
|
1
|
1.57
|
1
|
-
|
Данные этой матрицы сравним
с критическим значением, F (табл. приложение I). В нашем случае степени свободы к1 и к2 равны
семи (степени свободы определяются как п-1, где n - число параметров), значения пограничных показателей
достоверности F (критерий Фишера) берем при
вероятности Р' =0,8, Fкр =
1,945. Сравнивая коэффициенты Фишера из матрицы с его критическим значением
видим, что эти показатели меньше, следовательно, отличия в мнениях экспертов
несущественными при классификации их можно объединить в один таксон. Чтобы
выработать далее единую точку зрения на вопрос можно использовать метод
"мозговой атаки" или метод Дельфи и прийти
к единому мнению.
Ознакомившись с проектной
документацией по представленной проблеме эксперты предложили свои варианты
расчетов основываясь на благоприятном (Kmin) и неблагоприятном (Кmax) прогнозах. Результаты их прогнозов представлены в табл. 4.
Проведем анализ полученных
данных, определим меры близости мнений экспертов. В случае, когда ответы
экспертов имеют числовое значение, для нахождения коэффициентов близости
используется евклидово расстояние.
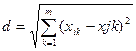
Таблица 5
Варианты прогнозов дополнительных
затрат для обеспеченbz выхода из кризиса
|
Эксперты
|
Значения характеристик
дополнительных капиталовложений по вариантам (млрд.руб.)
|
|
Вариант I (Кmin)
|
Вариант II (Кmax)
|
|
I
|
3,0
|
3,5
|
|
11
|
2,5
|
3,0
|
|
III
|
3,2
|
3,3
|
|
IV
|
3,0
|
3,3
|
|
V
|
2,4
|
2,8
|
|
VI
|
2,5
|
3,0
|
|
VII
|
2,8
|
3,0
|
|
VIII
|
2,8
|
3,2
|
Результаты расчетов
представлены в матрице коэффициентов близости мнений экспертов (табл. 6).
Таблица 6
Коэффициенты близости мнений экспертов
|
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII
|
|
1
|
-
|
0,22
|
0,1
|
0,64
|
0,36
|
0,45
|
0,57
|
0,22
|
|
II
|
0,22
|
-
|
0,32
|
0,41
|
0,14
|
0,3
|
0,36
|
0,14
|
|
III
|
0,1
|
0,32
|
-
|
0,71
|
0,45
|
0,6
|
0,64
|
0,28
|
|
IV
|
0,64
|
0,41
|
0,71
|
-
|
0,32
|
0,22
|
0,1
|
0,42
|
|
V
|
0,36
|
0,14
|
0,45
|
0,32
|
-
|
0,22
|
0,22
|
0,2
|
|
VI
|
0,45
|
0,3
|
0,6
|
0,22
|
0,22
|
-
|
0,2
|
0,22
|
|
VII
|
0,57
|
0,36
|
0,64
|
0,1
|
0,22
|
0,2
|
-
|
0,36
|
|
VIII
|
0,22
|
0,14
|
0,28
|
0,42
|
0,2
|
0,22
|
0,36
|
-
|
Каждая строка матрицы
рассчитывается следующим образом, от значения Kmin (I эксперт) вычитается
значение Kmin (II эксперт), разность возводится
в квадрат, затем от значения Кmax(I эксперт) вычитается
значение Кmax (II эксперт), разность возводится в квадрат. Из суммы полученных
величин извлекается квадратный корень. Таким же образом находится величина
коэффициентов близости между показателями первого и третьего экспертов, первого
и четвертого и т. д. Вторая строка матрицы определяется подобными операциями
для второго и последующих экспертов.
Обработка матрицы проводится
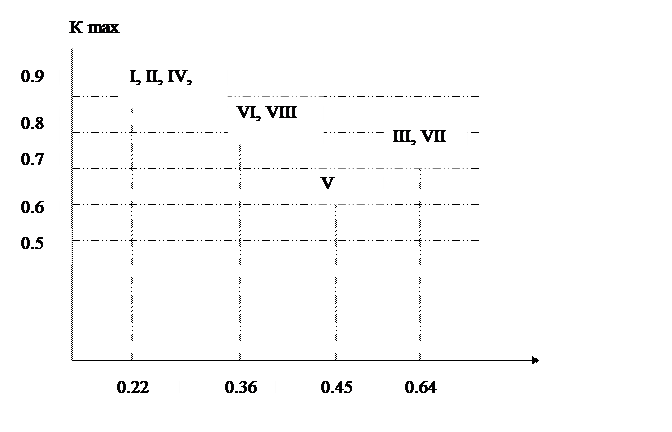
аналогично обработке матрицы (табл. 2). Получается граф (рис. 3), с помощью
которого строятся таксоны, изображенные на графике (рис. 4). По оси ординат
указываются значения дополнительных капиталовложений на расширение системы
водоснабжения, а по оси абсцисс - коэффициенты близости мнений экспертов
(величину, диаметр таксона задает исследователь).
Таксоны формировались по
коэффициентам близости, получилось два таксона. Это говорит о наличии двух
групп мнений. Для их "примирения" возможно дальнейшее
применение методики системной) анализа, в частности, методов, направленных на
активизацию использования интуиции и опыта специалистов, метода Дельфи, когда постепенно, накапливая информацию,
конкретизируя рассматриваемые факты, можно находить пути решения отдельных
задач и прийти к общему мнению в целом по проблеме.
 0.07
0.07
 0.25 0.22 0.14 0.2 0.29 0.2
0.25 0.22 0.14 0.2 0.29 0.2
Рис. 2 0.29
2.1. Анализ возможности решения проблемы за
указанный срок
Ответы экспертов на данный вопрос приведены в табл. 7
Таблица 7
Варианты экспертных
оценок ответа на вопрос «Возможно ли решить проблему за указанный срок»
|
Эксперты
|
«Возможно ли решить проблему за
указанный срок»
|
|
1
|
0
|
|
2
|
1
|
|
3
|
0
|
|
4
|
1
|
|
5
|
1
|
|
6
|
0
|
|
7
|
0
|
|
Ваше
мнение 8
|
0
|
Цифра «0» в ответах экспертов соответствует ответу «Нет»,
цифра «1» - ответу «Да», интервал от 0 до 1 соответствует вероятности
возможности наступления данного события от 0 до 100 %.
Найдем среднюю арифметическую и отклонение экспертных оценок
от среднего значения (табл. 8.):
Таблица 8
Среднее
арифметическое и отклонение от среднего значения экспертных оценок
|
Эксперты
|
«Возможно ли решить проблему за
указанный срок» (x)
|
Отклонение от среднего значения, (х-хср)
|
Квадрат отклонений
(х-хср)2
|
|
1
|
0
|
-0,375
|
0,1406
|
|
2
|
1
|
0,625
|
0,3906
|
|
3
|
0
|
-0,375
|
0,1406
|
|
4
|
1
|
0,625
|
0,3906
|
|
5
|
1
|
0,625
|
0,3906
|
|
6
|
0
|
-0,375
|
0,1406
|
|
7
|
0
|
0,625
|
0,3906
|
|
Ваше
мнение 8
|
0
|
0,625
|
0,3906
|
|
Сумма
баллов
|
3
|
|
2,37
|
|
Среднее
|
0,375
|
|
|
S2
= ∑(Х – Хср)2
/n-1 = 2,37/7 = 0,338
S = √
S2 = 0, 58
V = S/ Хср * 100
= 0, 58 /0,375*100 = 154, 67 %
Коэффициент вариации равный 154,67 % характеризует низкую степень
согласованности экспертов.
Таким образом, можно сделать вывод, что вероятность возможности решения
данной проблемы за указанный срок составляет 0,375 или 37,5 % из 100, т.е по
мнению экспертов, данное событие скорее всего не произойдет.
2.2.
Анализ возможности компании «Олкрейт» самостоятельно решить свои финансовые
проблемы
Ответы экспертов на данный вопрос приведены в табл. 9
Таблица 9
Варианты экспертных оценок ответа на вопрос «Сможет ли
компания «Олкрейт» самостоятельно решить свои
финансовые проблемы?»
|
Эксперты
|
«Сможет
ли компания «Олкрейт» самостоятельно решить свои
финансовые проблемы?»
|
|
1
|
0
|
|
2
|
0
|
|
3
|
1
|
|
4
|
1
|
|
5
|
0
|
|
6
|
0
|
|
7
|
1
|
|
Ваше
мнение 8
|
0
|
Цифра «0» в ответах экспертов соответствует ответу «Нет»,
цифра «1» - ответу «Да», интервал от 0 до 1 соответствует вероятности
возможности наступления данного события от 0 до 100 %.
Найдем среднюю арифметическую и отклонение экспертных оценок
от среднего значения (табл. 10.):
Таблица 10
Среднее
арифметическое и отклонение от среднего значения экспертных оценок
|
Эксперты
|
«Сможет ли компания «Олкрейт» самостоятельно решить свои финансовые проблемы?»
(x)
|
Отклонение от среднего значения, (х-хср)
|
Квадрат отклонений
(х-хср)2
|
|
1
|
0
|
-0,375
|
0,3906
|
|
2
|
0
|
-0,375
|
0,3906
|
|
3
|
1
|
0,625
|
0,1406
|
|
4
|
1
|
0,625
|
0,1406
|
|
5
|
0
|
-0,375
|
0,3906
|
|
6
|
0
|
-0,375
|
0,3906
|
|
7
|
1
|
0,625
|
0,1406
|
|
Ваше
мнение 8
|
0
|
-0,375
|
0,3906
|
|
Сумма
баллов
|
3
|
|
2,37
|
|
Среднее
|
0,375
|
|
|
S2
= ∑(Х – Хср)2
/n-1 = 2,37/7 = 0,338
S = √
S2 = 0, 58
V = S/ Хср * 100
= 0, 58 /0,375*100 = 154, 67 %
Коэффициент вариации равный 154,67 % характеризует низкую степень
согласованности экспертов.
Таким образом, можно сделать вывод, что вероятность компании
«Олкрейт» самостоятельно решить свои финансовые
проблемы составляет 0,375 или 37,5 % из 100, т.е по мнению экспертов, данное
событие скорее всего не произойдет.
2.3. Анализ возможности компании «Олкрейт» рассчитывать на помощь инвесторов в
ближайшие 2-3 года
Ответы экспертов на данный вопрос приведены в табл. 11
Таблица 11
Варианты экспертных оценок ответа на вопрос «Сможет ли
компания «Олкрейт» самостоятельно решить свои
финансовые проблемы?»
|
Эксперты
|
«Сможет
ли компания «Олкрейт рассчитывать на помощь
инвесторов в ближайшие 2-3 года»?»
|
|
1
|
0
|
|
2
|
0
|
|
3
|
0
|
|
4
|
0
|
|
5
|
0
|
|
6
|
0
|
|
7
|
1
|
|
Ваше
мнение 8
|
1
|
Цифра «0» в ответах экспертов соответствует ответу «Нет»,
цифра «1» - ответу «Да», интервал от 0 до 1 соответствует вероятности
возможности наступления данного события от 0 до 100 %.
Найдем среднюю арифметическую и отклонение экспертных оценок
от среднего значения (табл. 12):
Таблица 12
Среднее
арифметическое и отклонение от среднего значения экспертных оценок
|
Эксперты
|
«Сможет ли компания «Олкрейт рассчитывать на помощь инвесторов в ближайшие 2-3
года» (x)
|
Отклонение от среднего значения, (х-хср)
|
Квадрат отклонений
(х-хср)2
|
|
1
|
0
|
-0,375
|
0,3906
|
|
2
|
0
|
-0,375
|
0,3906
|
|
3
|
0
|
-0,375
|
0,3906
|
|
4
|
0
|
-0,375
|
0,3906
|
|
5
|
0
|
-0,375
|
0,3906
|
|
6
|
0
|
-0,375
|
0,3906
|
|
7
|
1
|
0,625
|
0,1406
|
|
Ваше
мнение 8
|
1
|
0,625
|
0,1406
|
|
Сумма
баллов
|
2
|
|
2,62
|
|
Среднее
|
0,25
|
|
|
S2
= ∑(Х – Хср)2
/n-1 = 2,62/7 = 0,37
S = √
S2 = 0, 61
V = S/ Хср
* 100 = 0, 61/0,375*100 = 163, 14 %
Коэффициент вариации равный 163,14% характеризует низкую
степень согласованности экспертов. Таким образом, можно сделать вывод, что
вероятность компании «Олкрейт» рассчитывать на помощь
инвесторов в ближайшие 2-3 года составляет 0,25 или 25,0 % из 100, т.е по
мнению экспертов, данное событие скорее всего не произойдет.
2.4. Анализ возможности решения главной
проблемы в результате укрепления кадровой политики
Ответы экспертов на данный вопрос приведены в табл. 13
Таблица 13
Варианты экспертных оценок ответа на вопрос «Решится ли
главная проблема в результате укрепления кадровой политики?»
|
Эксперты
|
«Решится
ли главная проблема в результате укрепления кадровой политики?»
|
|
1
|
0
|
|
2
|
1
|
|
3
|
0
|
|
4
|
0
|
|
5
|
1
|
|
6
|
1
|
|
7
|
1
|
|
Ваше
мнение 8
|
1
|
Цифра «0» в ответах экспертов соответствует ответу «Нет»,
цифра «1» - ответу «Да», интервал от 0 до 1 соответствует вероятности
возможности наступления данного события от 0 до 100 %.
Найдем среднюю арифметическую и отклонение экспертных оценок
от среднего значения (табл. 14.):
Таблица 14
Среднее
арифметическое и отклонение от среднего значения экспертных оценок
|
Эксперты
|
«Решится
ли главная проблема в результате укрепления кадровой политики?» (x)
|
Отклонение от среднего значения, (х-хср)
|
Квадрат отклонений
(х-хср)2
|
|
1
|
0
|
-0,375
|
0,3906
|
|
2
|
1
|
0,625
|
0,1406
|
|
3
|
0
|
-0,375
|
0,3906
|
|
4
|
0
|
-0,375
|
0,3906
|
|
5
|
1
|
0,625
|
0,1406
|
|
6
|
1
|
0,625
|
0,1406
|
|
7
|
1
|
0,625
|
0,1406
|
|
Ваше
мнение 8
|
1
|
0,625
|
0,1406
|
|
Сумма
баллов
|
5
|
|
1,87
|
|
Среднее
|
0,625
|
|
|
S2
= ∑(Х – Хср)2
/n-1 = 1,87/7 = 0,267
S = √
S2 = 0, 516
V = S/ Хср * 100 =
0, 516/0,375*100 = 82,69 %
Таким образом, можно сделать вывод, что степень
согласованности экспертов по данному вопросу заметно выше. Степень вероятности
решения проблем в результате укрепления кадровой политики «Олкрейт»
также довольно высокая и составляет, по мнению экспертов, 62,5 %.
2.5. Анализ возможности завода «Петров и
Петров», являясь заказчиком строительства танкеров, полностью осуществить все
платежи по контрактам
Ответы экспертов на данный вопрос приведены в табл. 15
Таблица 15
Варианты экспертных оценок ответа на вопрос «Сможет ли завод
«Петров и Петров», являясь заказчиком строительства танкеров, полностью
осуществить все платежи по контрактам?»
|
Эксперты
|
«Сможет
ли завод «Петров и Петров», являясь заказчиком строительства танкеров, полностью
осуществить все платежи по контрактам?»
|
|
1
|
0
|
|
2
|
1
|
|
3
|
0
|
|
4
|
0
|
|
5
|
1
|
|
6
|
1
|
|
7
|
1
|
|
Ваше
мнение 8
|
1
|
Цифра «0» в ответах экспертов соответствует ответу «Нет»,
цифра «1» - ответу «Да», интервал от 0 до 1 соответствует вероятности
возможности наступления данного события от 0 до 100 %.
Найдем среднюю арифметическую и отклонение экспертных оценок
от среднего значения (табл. 16.):
Таблица 16
Среднее
арифметическое и отклонение от среднего значения экспертных оценок
|
Эксперты
|
«Сможет
ли завод «Петров и Петров», являясь заказчиком строительства танкеров,
полностью осуществить все платежи по контрактам?» (x)
|
Отклонение от среднего значения, (х-хср)
|
Квадрат отклонений
(х-хср)2
|
|
1
|
1
|
0,625
|
0,1406
|
|
2
|
1
|
0,625
|
0,1406
|
|
3
|
1
|
0,625
|
0,1406
|
|
4
|
0
|
-0,375
|
0,3906
|
|
5
|
0
|
-0,375
|
0,3906
|
|
6
|
1
|
0,625
|
0,1406
|
|
7
|
1
|
0,625
|
0,1406
|
|
Ваше
мнение 8
|
1
|
0,625
|
0,1406
|
|
Сумма
баллов
|
6
|
|
1,62
|
|
Среднее
|
0,75
|
|
|
S2
= ∑(Х – Хср)2
/n-1 = 1,62/7 = 0,2314
S = √
S2 = 0, 481
V = S/ Хср * 100
= 0, 481/0,75*100 = 64,13%
В данном случает также можно сделать вывод, что степень
согласованности экспертов по данному вопросу заметно выше. Степень вероятности
решения данной проблемы довольно высокая и составляет, по мнению экспертов,
75,0 %, что означает, что завод «Петров и Петров» являясь заказчиком
строительства танкеров, скорее всего, сможет полностью осуществить все платежи
по контрактам.
2.6. Анализ возможности ускорения решения
проблемы выпуска танкеров с помощью приоритета не современной судостроительной
техники
Ответы экспертов на данный вопрос приведены в табл. 17
Таблица 17
Варианты экспертных оценок ответа на вопрос «Сможет ли завод
«Петров и Петров», являясь заказчиком строительства танкеров, полностью
осуществить все платежи по контрактам?»
|
Эксперты
|
«Поможет
ли приоритет не современной судостроительной техники ускорению решения
проблемы выпуска танкеров?»
|
|
1
|
1
|
|
2
|
1
|
|
3
|
1
|
|
4
|
1
|
|
5
|
0
|
|
6
|
0
|
|
7
|
1
|
|
Ваше
мнение 8
|
1
|
Цифра «0» в ответах экспертов соответствует ответу «Нет»,
цифра «1» - ответу «Да», интервал от 0 до 1 соответствует вероятности
возможности наступления данного события от 0 до 100 %.
Найдем среднюю арифметическую и отклонение экспертных оценок
от среднего значения (табл. 18.):
Таблица 18
Среднее
арифметическое и отклонение от среднего значения экспертных оценок
|
Эксперты
|
«Поможет
ли приоритет не современной судостроительной техники ускорению решения
проблемы выпуска танкеров» (x)
|
Отклонение от среднего значения, (х-хср)
|
Квадрат отклонений
(х-хср)2
|
|
1
|
1
|
0,625
|
0,1406
|
|
2
|
1
|
0,625
|
0,1406
|
|
3
|
1
|
0,625
|
0,1406
|
|
4
|
1
|
0,625
|
0,3906
|
|
5
|
0
|
-0,375
|
0,3906
|
|
6
|
0
|
-0,375
|
0,3906
|
|
7
|
1
|
0,625
|
0,1406
|
|
Ваше
мнение 8
|
1
|
0,625
|
0,1406
|
|
Сумма
баллов
|
6
|
|
1,87
|
|
Среднее
|
0,75
|
|
|
S2
= ∑(Х – Хср)2
/n-1 = 1,87 /7 = 0,267
S = √
S2 = 0, 516
V = S/ Хср * 100
= 0, 516/ 0,75*100 = 68,8 %
Степень вероятности возможности ускорения решения проблемы
выпуска танкеров с помощью приоритета не современной судостроительной техники
довольно высока и составляет, по мнению экспертов, 75,0 %.
2.7. Анализ прогнозов дополнительных затрат
Варианты прогнозов дополнительных затрат приведены в табл. 19.
Таблица 19
Варианты прогнозов
дополнительных затрат
|
Эксперты
|
Вариант I (Kmin)
|
Вариант II (Kmax)
|
|
|
1
|
3,0
|
3,5
|
|
|
2
|
2,5
|
3,0
|
|
|
3
|
3,2
|
3,3
|
|
|
4
|
3,0
|
3,3
|
|
|
5
|
2,4
|
2,8
|
|
|
6
|
2,5
|
3,0
|
|
|
7
|
2,8
|
3,0
|
|
|
8
|
2,8
|
3,2
|
|
|
Сумма
|
22,2
|
25,1
|
47,3
|
|
КОВ
|
46,9
|
53,1
|
|
Как видно из табл. 19, согласно экспертным оценкам ожидаемые
дополнительные затраты будут минимальны.
Таким образом, анализируя представленную ситуацию, можно
сделать следующие выводы.
Рассматриваемую проблему – привлечение партнеров и инвесторов для обеспечения
финансирования строительных судов компании «Олкрейт» по мнению экспертов, скорее
всего не удастся решить в указанный срок.
По мнению экспертов, компания «Олкрейт»,
скорее всего не сможет самостоятельно решить свои финансовые проблемы.
Вероятность компании «Олкрейт» рассчитывать
на помощь инвесторов в ближайшие 2-3 года составляет 0,25 или 25,0 % из 100,
т.е по мнению экспертов, данное событие скорее всего не произойдет.
Степень вероятности решения проблем в результате укрепления
кадровой политики «Олкрейт» довольно высокая и
составляет, по мнению экспертов, 62,5 %.
Завод «Петров и Петров» являясь заказчиком строительства
танкеров, скорее всего (с вероятностью 75 %), сможет полностью осуществить все
платежи по контрактам.
Степень вероятности возможности ускорения решения проблемы
выпуска танкеров с помощью приоритета не современной судостроительной техники
довольно высока и составляет, по мнению экспертов, 75,0 %.
Заключение
Таким образом, в работе рассмотрен вариант принятия
управленческих решений с помощью метода экспертных оценок.
В результате анализа проблемы были сделаны следующие выводы:
Рассматриваемую проблему – привлечение партнеров и инвесторов для обеспечения
финансирования строительных судов компании «Олкрейт» по мнению экспертов, скорее
всего не удастся решить в указанный срок.
По мнению экспертов, компания «Олкрейт»,
скорее всего не сможет самостоятельно решить свои финансовые проблемы.
Вероятность компании «Олкрейт» рассчитывать
на помощь инвесторов в ближайшие 2-3 года составляет 0,25 или 25,0 % из 100,
т.е по мнению экспертов, данное событие скорее всего не произойдет.
Степень вероятности решения проблем в результате укрепления
кадровой политики «Олкрейт» довольно высокая и
составляет, по мнению экспертов, 62,5 %.
Завод «Петров и Петров» являясь заказчиком строительства танкеров,
скорее всего (с вероятностью 75 %), сможет полностью осуществить все платежи по
контрактам.
Степень вероятности возможности ускорения решения проблемы
выпуска танкеров с помощью приоритета не современной судостроительной техники
довольно высока и составляет, по мнению экспертов, 75,0 %.
Список литературы
1. Блаубеpг И.В., Юдин Э.Г. Становление и
сущность системного подхода. М.: Дело, 2000.
2. Бреддик У. Менеджмент в организации. -
М.:Инфра-М, 2001 -344с.
3. Карданская Н.Л. Основы принятия управленческих решений.
-М.: Русская деловая литература, 1998.
4. Комаров
И. Принятие решений: методы и
модели // Менеджмент в России и за рубежом, 2001, №7
5. Лаpичев О.И. Hаука и искусство принятия
pешений. М.: Hаука, 2000.
6. Ларичев
О.И. Теория и методы принятия решений. –М.: Логос, 2000
7. Литвак
Б.Г. Разработка управленческого решения. –М.: Дело, 2000.
8. Майталь Ш. Экономика для менеджеров.-
М.:"Дело",1999.-416 с.
9. Мескон М. Х., Альберт М., Хедоури
Ф. Основы
менеджмента. М:. Дело, 2002 – 702 с.
10.
Надина Ю.А. Принятие решений в бизнес-
процессах // Менеджмент в России и за рубежом, 2000,
№4.
11.
Планкетт Л., Хейл Г. Выработка и принятие управленческих решений.-М., 1984.
12.
Фатхутдинов Р.А. Разработка
управленческого решения. – М.: ЗАО «Бизнес-школа» Интел-синтез», 1998.
13.
Цыгичко В.Н. Руководителю о
принятии решений. -М.: ИНФРА-М, 1996.
14.
Юкаева В.С. Управленческие
решения. -М.: Издательский дом «Дашков и Ко», 1999.
Приложение