1.
Понятие «Экономический факторный анализ», исходная и
конечная факторные системы
Экономический
анализ – это прежде всего факторный анализ. История факторного
анализа начинается с 1919 года, когда впервые была предложена детерминированная
модель Дюпона (The DuPont System of Analysis)
для расчета коэффициента рентабельности совокупного капитала (ROA).
Под
экономическим факторным анализом понимаются степенной переход от исходной
факторной системы (результативный показатель) к конечной факторной системе (или
наоборот), раскрытие полного набора прямых, количественно измеримых факторов,
оказывающих влияние на изменение результативного показателя.
Факторный
анализ – анализ влияния факторов на изменение результативного показателя,
является одним из сильнейших методических решений в анализе хозяйственной
деятельности компаний для принятия решений. Для руководителей - дополнительный аргумент, дополнительный "угол
зрения".
Однако
на практике он применяется редко в силу нескольких причин:
1. Реализация этого метода требует некоторых усилий и специфического
инструмента (программного продукта);
2. У компаний есть другие «вечные» первоочередные задачи.
Как
известно, анализировать можно все и до бесконечности. Целесообразно на первом
этапе реализовать анализ по отклонениям, а там где это необходимо и оправдано -
применить факторный метод анализа. Во многих случаях простого анализа по
отклонениям достаточно, чтобы понять, что отклонение «критическое», и когда
совсем не обязательно знать степень его влияния.
Методы
факторного анализа используются в тех случаях, когда поставлена задача
рассчитать влияние отдельных факторов на изменение результативного показателя.
Основными
задачами факторного анализа являются:
1. Постановка цели анализа.
2. Отбор факторов, которые определяют
динамику результативных показателей;
3. Классификация и систематизация
факторов с целью обеспечения возможностей системного подхода;
4. Определение вида зависимости и
моделирование взаимосвязей между факторами и результативным показателем;
5. Расчет влияния факторов и оценка роли
каждого из них в изменении величины результативного показателя;
6. Принятие управленческих решений на
основе результатов факторного анализа (практическое ее использование для
управления экономическими процессами).
Отбор
факторов для анализа того или иного показателя осуществляется на основе теоретических и
практических знаний в конкретной отрасли. При этом обычно исходят из принципа:
чем больший комплекс факторов исследуется, тем точнее будут результаты анализа.
Вместе с тем необходимо иметь в виду, что если этот комплекс факторов
рассматривается как механическая сумма, без учета их взаимодействия, без
выделения главных, определяющих, то выводы могут быть ошибочными. В анализе
хозяйственной деятельности взаимосвязанное исследование влияния факторов на
величину результативных показателей достигается с помощью их систематизации,
что является одним из основных методологических вопросов этой науки.
Важным методологическим
вопросом в факторном анализе является определение
формы зависимости между факторами и результативными показателями:
функциональная она или стохастическая, прямая или обратная, прямолинейная или
криволинейная. Здесь используется теоретический и практический опыт, а также
способы сравнения параллельных и динамичных рядов, аналитических группировок
исходной информации, графический и др.
Моделирование
экономических показателей
также представляет собой сложную проблему в факторном анализе, решение которой
требует специальных знаний и навыков.
Расчет
влияния факторов -
главный методологический аспект в анализе хозяйственной деятельности. Для
определения влияния факторов на конечные показатели используется множество
способов.
Последний этап факторного
анализа - практическое использование
факторной модели для подсчета резервов прироста результативного
показателя, для планирования и прогнозирования его величины при изменении
ситуации.
Различают два основных
вида факторного анализа – детерминированный
и стохастический.
Суть стохастического
метода – измерение влияния стохастических зависимостей с неопределенными и
приблизительными факторами. Стохастический метод целесообразно применять для
экономических исследований с неполной (вероятностной) корреляцией: например,
для задач маркетинга.
Детерминированный
факторный анализ представляет
собой методику исследования влияния факторов, связь которых с результативным
показателем носит функциональный характер, т. е. когда результативный
показатель факторной модели представлен в виде произведения, частного или
алгебраической суммы факторов.
2.
Этапы моделирования экономических процессов
Одной из задач факторного
анализа является моделирование взаимосвязей между результативными показателями
и факторами, которые определяют их величину. Моделирование - это один из
важнейших методов научного познания, с помощью которого создается модель
(условный образ) объекта исследования. Сущность его заключается в том, что
взаимосвязь исследуемого показателя с факторными передается в форме конкретного
математического уравнения.
Процесс моделирования
можно условно подразделить на три этапа:
1. Анализ теоретических закономерностей,
свойственных изучаемому явлению или процессу, и эмпирических данных о его
структуре и особенностях. На основе такого анализа формируются модели;
2. Определение методов, с помощью
которых можно решить задачу;
3. Анализ полученных результатов.
При
экономико-математическом моделировании часто возникает ситуация, когда
изучаемая система имеет слишком сложную структуру, не разработаны
математические методы, схемы, которые охватывали бы все основные особенности и связи
этой системы. Такой экономической системой, например, является экономика
предприятия в целом, в ее динамике развитии. Возникает необходимость упрощения
изучаемого объекта, исключения и анализа некоторых его второстепенных
особенностей с тем, чтобы подвести эту упрощенную систему под класс уже
известных структур, поддающихся математическому описанию и анализу. При этом
степень упрощения должна быть такой, чтобы все существенные для данного
экономического объекта черты в соответствии с целью исследования были включены
в модель.
Важным моментом первого
этапа моделирования является четкая формулировка конечной цели построения
модели, а также определение критерия, по которому будут сравниваться различные
варианты решения. В экономическом анализе такими критериями могут быть:
наибольшая прибыль, наименьшие издержки производства, максимальная загрузка
оборудования, производительность труда и другие. В задачах математического
программирования такой критерий отражается целевой функцией.
При постановке задач математического
программирования обычно предполагается ограниченность ресурсов, которые
необходимо распределить на производство продукции. Поэтому очень важно
определить, какие ресурсы являются для изучаемого процесса решающими и в то же
время лимитирующими, какой запас. Если все виды производственных ресурсов, к
которым относятся сырье, трудовые ресурсы, мощность оборудования и другие,
используются для выпуска продукции, то необходимо знать расход каждого вида
ресурса на единицу продукции.
Все ограничения, отражающие
экономический процесс должны быть непротиворечивыми, т. е. должно существовать
хотя бы одно решение задачи, удовлетворяющее всем ограничениям.
В качестве ограничений
при построении экономико-математической модели выступает система неравенств,
имеющая следующий вид:
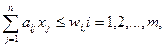 (1)
(1)
где aij –
норма расхода i-го
производственного ресурса на производство единицы j-го вида продукции;
wi – запасы i-го вида
производственного ресурса на рассматриваемый период времени.
Объединяя уравнение целевой функции и
систему ограничений в единую модель, получим линейную экономико-математическую
модель ассортиментной задачи:
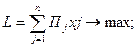 (2)
(2)
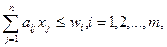 (3)
(3)
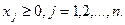 (4)
(4)
Не для всякой
экономической задачи нужна собственная модель. Некоторые процессы с
математической точки зрения однотипны и могут описываться одинаковыми моделями.
Например, в линейном программировании теории массового обслуживания и других
существуют типовые модели, к которым приводится множество конкретных задач.
Вторым этапом
моделирования экономических процессов является выбор наиболее рационального
математического метода для решения задачи. Например, для решения задач
линейного программирования известно много методов: симплексный, потенциалов и
другие. Лучшей моделью является не самая сложная и самая похожая на реальное
явление или процесс, а та, которая позволяет самое рациональное решение и
наиболее точные экономические оценки. Излишняя детализация затрудняет
построение модели, часто не дает каких-либо преимуществ в анализе экономических
взаимосвязей и не обогащает выводов. Излишнее укрупнение модели приводит к
потере существенной экономической информации и иногда даже неадекватному
отражению реальных условий.
Третьим этапом
моделирования является всесторонний анализ результата, полученного при изучении
экономического явления или процесса. Окончательным критерием достоверности и
качества модели являются: практика, соответствие полученных результатов и
выводов реальным условиям производства, экономическая содержательность
полученных оценок. Если полученные результаты не соответствуют реальным
производственным условиям, то необходим экономический анализ причин
несоответствия. Такими причинами могут быть: недостаточная достоверность
информации, а также несоответствие используемых математических средств и схем особенностям и сущности изучаемого
экономического объекта. После того, как причина определена, в модель должны
быть внесены соответствующие коррективы, и решение задачи повторяется.
Таким образом,
экономико-математическое моделирование работы предприятия должно быть основано
на анализе его деятельности и, в свою очередь, обогащать этот анализ
результатами и выводами, полученными после решения соответствующих задач.
При моделировании
детерминированных факторных систем необходимо выполнять ряд требований.
1. Факторы, включаемые в
модель, и сами модели должны иметь определенно выраженный характер, реально
существовать, а не быть придуманными абстрактными величинами или явлениями.
2. Факторы, которые
входят в систему, должны быть не только необходимыми элементами формулы, но и
находиться в причинно-следственной связи с изучаемыми показателями. Иначе
говоря, построенная факторная система должна иметь познавательную ценность.
Факторные модели, которые отражают причинно-следственные отношения между
показателями, имеют значительно большее познавательное значение, чем модели,
созданные при помощи приемов математической абстракции.
3. Все показатели
факторной модели должны быть количественно измеримыми, т.е. должны иметь
единицу измерения и необходимую информационную обеспеченность.
4. Факторная модель
должна обеспечивать возможность измерения влияния отдельных факторов, это
значит, что в ней должна учитываться соразмерность изменений результативного и
факторных показателей, а сумма влияния отдельных факторов должна равняться
общему приросту результативного показателя.
3. Классификация
задач экономического факторного анализа: прямой и обратный факторный анализ;
детерминированный и стохастический; одноступенчатый и цепной; статистический,
пространственный и динамический; пространственный и временной; ретроспективный,
оперативный и перспективный анализ
При прямом факторном анализе исследование
ведется дедуктивным способом - от общего к частному. Обратный факторный анализ осуществляет исследование
причинно-следственных связей способом логичной индукции - от частных, отдельных
факторов к обобщающим. Задачи прямого и обратного факторного анализа могут быть
детерминированными и стохастическими.
Примерами прямого, детерминированного, факторного анализа
являются: анализ влияния производительности труда и численности работающих на
объем произведенной продукции; анализ влияния величины прибыли, стоимости
основных производственных фондов и нормируемых оборотных средств на уровень
рентабельности.
Если в случае прямого
детерминированного факторного анализа исходные данные для анализа имеются в
форме конкретных чисел, то в случае прямого стохастического факторного анализа
заданы выборкой. Решения задач стохастического факторного анализа требуют
глубокого экономического исследования для выявления основных факторов, влияющих
на результативный показатель; подбора вида регрессии, который бы наилучшим
образом отражал действительную связь изучаемого показателя с набором факторов;
разработки метода, позволяющего определить влияние каждого фактора на
результативный показатель. Примером прямого стохастического факторного анализа
является регрессионный анализ производительности труда и других экономических
показателей.
Примерами задачи
обратного детерминированного факторного анализа являются задачи комплексной
оценки производственно-хозяйственной деятельности, а также задачи
математического программирования, в том числе и линейного.
Примером задачи обратного
стохастического факторного анализа могут служить производственные функции,
которыми устанавливаются зависимости между величиной выпуска продукции и
затратами производственных факторов.
Детерминированный
факторный анализ представляет
собой методику исследования влияния факторов, связь которых с результативным
показателем носит функциональный характер, т. е. когда результативный
показатель факторной модели представлен в виде произведения, частного или
алгебраической суммы факторов.
Данный вид факторного
анализа наиболее распространен, поскольку, будучи достаточно простым в
применении (по сравнению со стохастическим анализом), позволяет осознать логику
действия основных факторов развития предприятия, количественно оценить их
влияние, понять, какие факторы и в какой пропорции возможно и целесообразно
изменить для повышения эффективности производства.
Стохастический
анализ представляет
собой методику исследования факторов, связь которых с результативным
показателем в отличие от функциональной является неполной, вероятностной
(корреляционной). Если при функциональной (полной) зависимости с изменением
аргумента всегда происходит соответствующее изменение функции, то при
корреляционной связи изменение аргумента может дать несколько значений прироста
функции в зависимости от сочетания других факторов, определяющих данный
показатель. Стохастическое моделирование является в определенной степени
дополнением и углублением детерминированного факторного анализа.
Факторный анализ может
быть одноступенчатым и цепным (многоступенчатым). Первый тип
используется для исследования факторов только одного уровня (одной ступени)
подчинения без их детализации на составные части. Например, 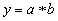 . При
цепном факторном анализе проводится детализация факторов a
и b на составные элементы с целью изучения
их поведения. Детализация факторов может быть продолжена и дальше. В этом
случае изучается влияние факторов различных уровней соподчиненности.
. При
цепном факторном анализе проводится детализация факторов a
и b на составные элементы с целью изучения
их поведения. Детализация факторов может быть продолжена и дальше. В этом
случае изучается влияние факторов различных уровней соподчиненности.
Необходимо также
различать статический и
динамический факторный
анализ. Первый вид применяется при изучении влияния факторов на результативные
показатели на соответствующую дату. Другой вид представляет собой методику
исследования причинно-следственных связей в динамике.
Экономический факторный
анализ может быть направлен на выяснение действия факторов, формирующих результаты
хозяйственной деятельности, по различным источникам пространственного и
временного происхождения.
Анализ динамических
(временных) рядов показателей хозяйственной деятельности, расщепление уровня
ряда на его составляющие (основную линию развития – тренд, сезонную или периодическую составляющую, циклическую
составляющую, связанную с воспроизводственными явлениями, случайную
составляющую) – задача временного факторного анализа.
И, наконец, факторный анализ может быть ретроспективным, который изучает причины прироста
результативных показателей за прошлые периоды, перспективным, который исследует поведение факторов и
результативных показателей в перспективе, и оперативным, который осуществляет постоянный
контроль рациональности функционирования хозяйственной системы, за выполнением
плановых заданий, процессами и реализацией продукции, а также своевременное
выявление и использование текущих внутрипроизводственных резервов с целью
обеспечения выполнения и перевыполнения бизнес-плана.
Классификация задач
факторного анализа упорядочивает постановку многих экономических задач,
позволяет выявить общие закономерности их решения. При исследовании сложных
экономических процессов возможна комбинация постановки задач, если последние не
относятся к какому-либо типу, указанному в классификации.
Укрупненная схема
классификации задач экономического факторного анализа представлена ниже на
рисунке 1:







|
Статический пространственный анализ
|
|
Рис. 1 Укрупненная схема
классификации задач экономического факторного анализа
4. Классификация
факторов в экономическом анализе
Классификация факторов
представляет собой распределение их по группам в зависимости от общих
признаков. Она позволяет глубже разобраться в причинах изменения исследуемых
явлений, точнее оценить место и роль каждого фактора в формировании величины
результативных показателей.
Исследуемые в анализе
факторы могут быть классифицированы по разным признакам.
По своей природе факторы
подразделяются на природные, социально-экономические и производственно-экономические.
Природные факторы
оказывают большое влияние на результаты деятельности в сельском хозяйстве, в
лесном хозяйстве и других отраслях. Учет их влияния дает возможность точнее
оценить результаты работы субъектов хозяйствования.
К социально-экономическим
факторам относятся жилищные условия работников, организация оздоровительной
работы на предприятиях с вредным производством, общий уровень подготовки кадров
и др. Они способствуют более полному использованию производственных ресурсов
предприятия и повышению эффективности его работы.
Производственно-экономические
факторы определяют полноту и эффективность использования производственных
ресурсов предприятия и конечные результаты его деятельности.
По степени воздействия на
результаты хозяйственной деятельности факторы делятся на основные и
второстепенные. К основным относятся факторы, оказывающие решающее воздействие
на результативный показатель. Второстепенными считаются те, которые не
оказывают решающего воздействия на результаты хозяйственной деятельности в
сложившихся условиях. Необходимо отметить, что в зависимости от обстоятельств
один и тот же фактор может быть и основным, и второстепенным. Умение выделить
из всего множества факторов главные обеспечивает правильность выводов по
результатам анализа.
Факторы подразделяются на
объективные, не зависящие от
воли и желаний людей, и субъективные,
подверженные влиянию деятельности юридических и физических лиц.
По степени
распространенности факторы делятся на общие и специфические. Общие факторы
действуют во всех отраслях экономики. Специфические факторы действуют в
пределах отдельной отрасли или конкретного предприятия.
В процессе работы
организации одни факторы оказывают воздействие на изучаемый показатель
непрерывно на протяжении всего времени. Такие факторы называются постоянными. Факторы, воздействие
которых проявляется периодически, называются переменными (это, например, внедрение новой технологии, новых
видов продукции).
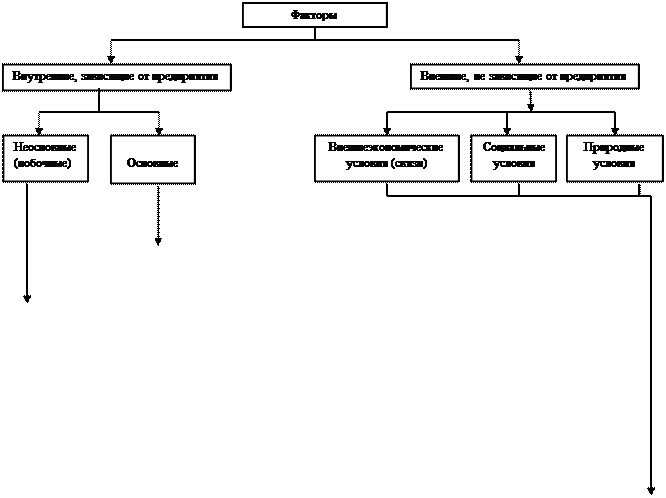
Исходя из задач анализа
хозяйственной деятельности важное значение имеет классификация (рис.2), в
которой факторы делятся на внутренние, или контролируемые предприятием (они, в
свою очередь, подразделяются на основные и неосновные),
и внешние, малоконтролируемые или вообще
неконтролируемые. Внутренними основными называются факторы, теоретически
определяющие результаты работы предприятия. Внутренние неосновные
факторы хотя и влияют на обобщающие показатели, но не связаны непосредственно с
сущностью рассматриваемого показателя, например нарушения хозяйственной и
технологической дисциплины. Внешние факторы не зависят от деятельности
предприятия, но количественно определяют уровень использования производственных
и финансовых ресурсов данного предприятия.

|
Нарушения
хозяйственной дисциплины и др.
|
|
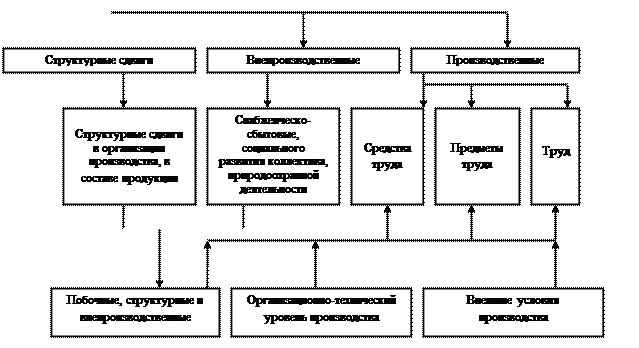
Рис 2. Классификация факторов для анализа результатов
деятельности предприятия
Большое значение для
оценки деятельности предприятий имеет деление факторов по характеру их действия
на интенсивные и экстенсивные. К экстенсивным
относятся факторы, которые связаны с изменением количественных, а не
качественных характеристик функционирования предприятия. В качестве примера
можно привести увеличение объема производства продукции за счет увеличения
числа рабочих. Интенсивные факторы характеризуют качественную сторону процесса
производства. Примером может служить увеличение объема производства продукции
за счет повышения уровня производительности труда.
Большинство изучаемых
факторов по своему составу являются сложными, состоят из нескольких элементов.
Однако есть и такие, которые не раскладываются на составные части. В связи с
этим факторы делятся на сложные
(комплексные) и простые
(элементные). Примером сложного фактора является
производительность труда, а простого - количество рабочих дней в отчетном
периоде.
По уровню соподчиненности
(иерархии) различают факторы первого, второго, третьего и последующего уровней
подчинения. К факторам первого уровня
относятся те, которые непосредственно влияют на результативный показатель.
Факторы, влияющие на результативный показатель косвенно, при помощи факторов
первого уровня, называют факторами
второго уровня и т. д.
Классификация факторов и
совершенствование методики их анализа позволяют решить важную проблему –
очистить основные показатели от влияния внешних и побочных факторов с тем,
чтобы показатели, принятые для оценки эффективности деятельности предприятия,
объективнее отражали его достижения.
5. Систематизация
факторов в экономическом анализе, их взаимосвязь и соподчиненность
Системный подход в
анализе хозяйственной деятельности вызывает необходимость взаимосвязанного
изучения факторов с учетом их внутренних и внешних связей, взаимодействия и
соподчиненности, что достигается с помощью систематизации. Систематизация в
целом – это размещение изучаемых явлений или объектов в определенном порядке с
выявлением их взаимосвязи и подчиненности.
Одним из способов
систематизации факторов является создание детерминированных факторных систем.
Создать факторную систему - значит представить изучаемое явление в виде алгебраической
суммы, частного или произведения нескольких факторов, определяющих его величину
и находящихся с ним в функциональной зависимости.
Развитие
детерминированной факторной системы достигается, как правило, за счет
детализации комплексных факторов. Элементные не раскладываются на сомножители,
так как по своему содержанию они однородны. С развитием системы комплексные
факторы постепенно детализируются на менее общие, те в свою очередь еще на
менее общие, постепенно приближаясь по своему аналитическому содержанию к
элементным (простым).
Однако необходимо
заметить, что развитие факторных систем до необходимой глубины связано с
некоторыми методологическими трудностями и, прежде всего с трудностью
нахождения факторов общего характера, которые можно было бы представить в виде
произведения, частного или алгебраической суммы нескольких факторов. Поэтому
обычно детерминированные системы охватывают наиболее общие факторы. Между тем
исследование более конкретных факторов в анализе хозяйственной деятельности имеет
существенно большее значение, чем общих.
Отсюда следует, что
совершенствование методики факторного анализа должно быть направлено на
взаимосвязанное изучение конкретных факторов, которые находятся, как правило, в
стохастической зависимости с результативными показателями.
Большое значение в
исследовании стохастических взаимосвязей имеет структурно-логический анализ
связи между изучаемыми показателями. Он позволяет установить наличие или
отсутствие причинно-следственных связей между исследуемыми показателями, изучить
направление связи, форму зависимости и т.д., что очень важно при определении
степени их влияния на изучаемое явление и при обобщении результатов анализа.
Анализ структуры связи
изучаемых показателей в анализе хозяйственной деятельности осуществляется с
помощью построения структурно-логической блок-схемы, которая позволяет
установить наличие и направление связи не только между изучаемыми факторами и
результативным показателем, но и между самими факторами.
Построив блок-схему,
можно увидеть, что среди изучаемых факторов имеются такие, которые более или
менее непосредственно воздействуют на результативный показатель, и такие,
которые воздействуют не столько на результативный показатель, сколько друг на
друга.
Таким образом,
систематизация факторов позволяет более глубоко изучить взаимосвязь факторов
при формировании величины изучаемого показателя, что имеет очень важное
значение на следующих этапах анализа, особенно на этапе моделирования
исследуемых показателей.
Все явления и процессы
хозяйственной деятельности предприятий находятся во взаимозависимости. Связь экономических явлений - это
совместное изменение двух или более явлений. Среди многих форм закономерных
связей важную роль играет причинно-следственная (детерминистская), при которой
одно явление порождает другое.
В хозяйственной
деятельности предприятия некоторые явления непосредственно связаны между собой,
другие - косвенно. Например, на величину валовой продукции непосредственное
влияние оказывают такие факторы, как численность рабочих и уровень
производительности их труда. Множество других факторов косвенно воздействует на
этот показатель.
Кроме того, каждое
явление можно рассматривать как причину и как следствие. Например,
производительность труда можно рассматривать, с одной стороны, как причину
изменения объема производства, уровня ее себестоимости, а с другой - как
результат изменения степени механизации и автоматизации производства,
усовершенствования организации труда и т. д.
Количественная
характеристика взаимосвязанных явлений осуществляется с помощью показателей.
Показатели, характеризующие причину, называются факторными (независимыми), а
показатели, характеризующие следствие, называются результативными (зависимыми).
Совокупность факторных и результативных признаков, связанных причинно-следственной
связью, называется факторной системой.
Моделирование какого-либо явления - это построение
математического выражения существующей зависимости. Моделирование - это один из
важнейших методов научного познания. Существуют два типа зависимостей, изучаемых
в процессе факторного анализа: функциональные и стохастические.
Связь называется
функциональной, или жестко детерминированной, если каждому значению факторного
признака соответствует вполне определенное неслучайное значение результативного
признака.
Связь называется
стохастической (вероятностной), если каждому значению факторного признака
соответствует множество значений результативного признака, т. е. определенное
статистическое распределение.
Чем детальнее исследуется
зависимость результативного показателя от тех или иных факторов, тем точнее
результаты анализа и оценка качества работы предприятий. Без глубокого и
всестороннего изучения факторов нельзя сделать обоснованные выводы о
результатах деятельности, выявить резервы производства, обосновать планы и
управленческие решения.
6.
Детерминированное моделирование факторных систем: типы, приемы и способы
Детерминирование – определять, обуславливать. С
помощью детерминанта находятся решения линейных систем уравнений. При его
исследовании величина влияния факторов рассчитывается умножением абсолютного
прироста исследуемого фактора на базовую (плановую) величину факторов
Детерминированный факторный анализ представляет собой методику исследования
влияния факторов, связь которых с результативным показателем носит
функциональный характер.
Основные свойства
детерминированного подхода к анализу: построение детерминированной модели путем
логического анализа; наличие полной (жесткой) связи между показателями;
невозможность разделения результатов влияния одновременно действующих факторов,
которые не поддаются объединению в одной модели; изучение взаимосвязей в
краткосрочном периоде.
Различают 4 типа
детерминированных моделей:
─
аддитивные
модели представляют собой алгебраическую сумму показателей. К таким моделям,
например, относятся показатели себестоимости во взаимосвязи с элементами затрат
на производство и со статьями затрат, показатель объема производства продукции
в его взаимосвязи с объемом выпуска отдельных изделий или объема выпуска в
отдельных подразделениях;
─
мультипликативные
модели – эта модель применяется, когда результативный показатель является
произведением нескольких факторов;
─
кратные
модели – эта модель применяется, когда результативный показатель является
частным от деления одного фактического показателя на другую величину;
─
смешанные
модели представляют собой комбинацию перечисленных выше моделей.
Одним из важнейших
методологических вопросов анализа хозяйственной деятельности является
определение величины влияния отдельных факторов на прирост результативных
показателей.
В детерминированном
анализе для этого используются следующие способы:
─ цепных подстановок - заключается в
определении ряда промежуточных значений обобщающего показателя путем
последовательной замены базисных значений факторов на отчетные.
Недостаток метода состоит
в том, что, в зависимости от выбранного порядка замены факторов, результаты
факторного разложения имеют разные значения. Это связано с тем, что в
результате применения этого метода образуется некий неразложимый остаток, который
прибавляется к величине влияния последнего фактора. На практике точностью
оценки факторов пренебрегают, выдвигая на первый план относительную значимость
влияния того или иного фактора. Однако существуют определенные правила,
определяющие последовательность подстановки: при наличии в факторной модели
количественных и качественных показателей в первую очередь рассматривается
изменение количественных факторов; если модель представлена несколькими
количественными и качественными показателями, последовательность подстановки
определяется путем логического анализа;
─ индексный - основан на относительных
показателях динамики, пространственных сравнениях, выполнении плана, выражающих
отношение фактического уровня анализируемого показателя в отчетном периоде к его
уровню в базисном периоде;
─ абсолютных разниц
- является модификацией способа цепной подстановки. Изменение результативного
показателя за счет каждого фактора способом разниц
определяется как произведение отклонения изучаемого фактора на базисное или
отчетное значение другого фактора в зависимости от выбранной последовательности
подстановки;
─ относительных разниц
- применяется для измерения влияния факторов на прирост результативного
показателя в мультипликативных и смешанных моделях вида у = (а – в) * с. Он
используется в случаях, когда исходные данные содержат определенные ранее
относительные отклонения факторных показателей в процентах. Чтобы рассчитать
влияние второго фактора нужно к плановой величине результативного показателя
прибавить изменения за счет 1-го фактора, затем полученную сумму умножить на
относительный прирост второго фактора (дней в %) и разделить на 100% ;
─ интегральный метод - при его
использование исходят, из того что факторы изменяются независимо друг от друга,
на самом же деле они изменяются совместно, взаимосвязано и от этого
взаимодействия получается дополнительный прирост результативного показателя,
который при применение способов элиминирования присоединяется к одному из
факторов, как правило, к последнему.
Первые 4 способа основываются
на методе элиминирования. Элиминировать - это означает устранить, отклонить,
исключить воздействие всех факторов на величину результативного показателя
кроме одного. Этот метод исходит из того, что изменяется один, а все другие
остаются без изменения, потом изменяются 2, затем три так далее, при
неизменности остальных. Это позволяет определить влияние каждого фактора на
величину исследуемого показателя в отдельности.
Применительно к классу
детерминированных факторных систем различают следующие основные приемы
моделирования:
1. Прием удлинения факторной системы - предусматривает
удлинение числителя исходной модели путем замены одного или нескольких факторов
на сумму однородных показателей;
2. Прием расширения факторной системы - предусматривает
расширение исходной факторной модели за счет умножения числителя и знаменателя
дроби на один или несколько новых показателей;
3. Прием сокращения факторной системы - представляет
собой создание новой факторной модели путем деления числителя и знаменателя
дроби на один и тот же показатель;
4. Прием формального разложения
факторной системы - предусматривает удлинение знаменателя исходной факторной
модели путем замены одного или нескольких факторов на сумму или произведение
однородных показателей.
Таким образом,
результативные показатели могут быть разложены на составные элементы (факторы)
различными способами и представлены в виде различных типов детерминированных
моделей. Выбор способа моделирования зависит от объекта исследования,
поставленной цели, а также от профессиональных знаний и навыков исследователя.
Процесс моделирования
факторных систем - очень сложный и ответственный момент в анализе хозяйственной
деятельности. От того, насколько реально и точно созданные модели отражают
связь между исследуемыми показателями, зависят конечные результаты анализа.
7. Стохастическое моделирование
факторных систем
Стохастический анализ
направлен на изучение косвенных связей, т. е. опосредованных факторов (в случае
невозможности определения непрерывной цепи прямой связи). Из этого вытекает
важный вывод о соотношении детерминированного и стохастического анализа: так
как прямые связи необходимо изучать в первую очередь, то стохастический анализ
носит вспомогательный характер. Стохастический анализ выступает в качестве
инструмента углубления детерминированного анализа факторов, по которым нельзя
построить детерминированную модель.
Стохастическое
моделирование факторных систем взаимосвязей отдельных сторон хозяйственной
деятельности опирается на обобщение закономерностей варьирования значений
экономических показателей -
количественных характеристик факторов и результатов хозяйственной
деятельности. Количественные параметры связи выявляются на основе сопоставления
значений изучаемых показателей в совокупности хозяйственных объектов или
периодов. Таким образом, первой предпосылкой стохастического моделирования
является возможность составить совокупность наблюдений, т. е. возможность
повторно измерить параметры одного и того же явления в различных условиях.
В стохастическом анализе,
где сама модель составляется на основе совокупности эмпирических данных,
предпосылкой получения реальной модели является совпадение количественных
характеристик связей в разрезе всех исходных наблюдений. Это означает, что
варьирование значений показателей должно происходить в пределах однозначной
определенности качественной стороны явлений, характеристиками которых являются
моделируемые экономические показатели (в пределах варьирования не должно
происходить качественного скачка в характере отражаемого явления). Значит,
второй предпосылкой применяемости стохастического
подхода моделирования связей является качественная однородность совокупности
(относительно изучаемых связей).
Изучаемая закономерность
изменения экономических показателей (моделируемая связь) выступает в скрытом
виде. Она переплетается со случайными с точки зрения исследования (неизучаемыми) компонентами вариации и ковариации показателей.
Закон больших чисел гласит, что только в большой совокупности закономерная
связь выступает устойчивее случайного совпадения направления варьирования
(случайной к - вариации).
Из этого вытекает третья
предпосылка стохастического анализа -
достаточная размерность (численность) совокупности наблюдений,
позволяющая с достаточной надежностью и точностью выявить изучаемые
закономерности (моделируемые связи). Уровень надежности и точности модели
определяется практическими целями использования модели в управлении
производственно-хозяйственной деятельностью.
Четвертая предпосылка
стохастического подхода - наличие методов, позволяющих выявить количественные
параметры экономических показателей из массовых данных варьирования уровня
показателей. Математический аппарат применяемых методов иногда предъявляет
специфические требования к моделируемому эмпирическому материалу. Выполнение
данных требований является важной предпосылкой применяемости методов и
достоверности полученных результатов.
Основная особенность
стохастического факторного анализа заключается в том, что при стохастическом
анализе нельзя составлять модель путем качественного (теоретического) анализа,
необходим количественный анализ эмпирических данных.
В отличие от жестко
детерминированного стохастический подход для реализации требует ряда
предпосылок:
─ наличие совокупности;
─ достаточный объем наблюдений;
─ случайность и независимость
наблюдений;
─ однородность;
─ наличие распределения признаков,
близкого к нормальному;
─ наличие специального математического
аппарата.
Основными методами
стохастического факторного анализа являются:
1. Способ парной корреляции - метод
корреляционного и регрессионного (стохастического) анализа широко используется
для определения тесноты связи между показателями, не находящимися в
функциональной зависимости, т.е. связь проявляется не в каждом отдельном
случае, а в определенной зависимости.
С помощью корреляции
решаются две главные задачи:
─ составляется модель действующих
факторов (уравнение регрессии);
─ дается количественная оценка тесноты
связей (коэффициент корреляции).
2. Матричные модели - представляют собой схематическое отражение
экономического явления или процесса с помощью научной абстракции. Наибольшее
распространение здесь получил метод анализа «затраты - выпуск», строящийся по
шахматной схеме и позволяющий в наиболее компактной форме представить
взаимосвязь затрат и результатов производства.
3. Математическое программирование - это основное средство решения задач по
оптимизации производственно-хозяйственной деятельности.
4. Метод исследования операций - направлен на изучение экономических систем, в
том числе производственно-хозяйственной деятельности предприятий, с целью
определения такого сочетания структурных взаимосвязанных элементов систем,
которое в наибольшей степени позволит определить наилучший экономический
показатель из ряда возможных.
5. Теория игр - это теория
математических моделей принятия оптимальных решений в условиях неопределенности
или конфликта нескольких сторон, имеющих различные интересы.
8. Практическое
применение результатов факторного анализа
Созданный в начале века
для нужд психологии (предпринимались попытки выделить основной фактор,
определяющий интеллект), факторный анализ впоследствии получил большое
распространение в экономике, медицине, социологии и других науках,
располагающих огромным количеством переменных, из которых обычно необходимо
выделить ведущие.
С помощью факторного
анализа не просто устанавливается связь изменения одной переменной с изменением
другой переменной, а определяется мера этой связи, и обнаруживаются основные
факторы, лежащие в основе указанных изменений. Факторный анализ особенно
продуктивен на начальных этапах научных исследований, когда необходимо выделить
какие-либо предварительные закономерности в исследуемой области. Это позволяет
последующий эксперимент сделать более совершенным по сравнению с экспериментом
на переменных, выбранных произвольно или случайно.
Как метод факторный анализ имеет определенные
слабые стороны, в частности отсутствует однозначное математическое решение
проблемы факторных нагрузок, т.е. влияния отдельных факторов на изменения
различных переменных.
Методы факторного анализа
нашли применение главным образом в психологии. Причиной этому был тот факт, указанный
ранее, что факторный анализ зародился в психологии и формализм этой дисциплины
тесно связан с психологической концепцией ментальных факторов, даже
специалисту-статистику трудно заметить и установить связь между методами
факторного анализа и методами обычной математической статистики.
Решение, полученное
методами факторного анализа, может послужить основой при формулировании
некоторой научной гипотезы; возможно и обратное: методами факторного анализа
ищется подтверждение существующей гипотезы.
Спирмен показал, что если между парными
корреляциями имеются определенные взаимосвязи, то может быть выписана система
линейных уравнений, связывающих все рассматриваемые параметры, генеральный
фактор и по одному дополнительному характерному фактору на каждый параметр. Эти
взаимосвязи и позволяют дать статистическое обоснование двухфакторной теории.
Если набор психологических параметров не удовлетворяет условиям существования
указанных взаимосвязей, то может быть постулирована более сложная гипотеза,
требующая уже несколько генеральных факторов для адекватного статистического
описания системы параметров.
Одна из наиболее ранних
работ, связанных с расширением сферы приложения факторного анализа, была
проделана в 1950 г.
Т.Келли. В ней предлагался метод достижения
максимальной социальной полезности каждого индивидуума при сохранении
индивидуальных свобод и прав. Во время второй мировой войны факторный анализ
широко применялся различными военными службами США в связи с решением проблем
классификационных проверок, классификации и распределения личного состава.
Разумеется, психологи и по сей день продолжают развивать и применять методы
факторного анализа.
Столь же широкое
применение, как и при исследовании интеллекта, факторный анализ получил и в
других областях психологии, в частности при изучении темперамента, создании
клинической терапии и т.д.
За последние годы
факторный анализ все более широко начал применяться и в других областях знания:
в социологии, метеорологии, медицине, географии, экономике и других.