Задача 1.
|
Показатель
|
Идентификатор
|
Отчетный
год
|
Предыдущий
год
|
Отклонение
|
|
Выручка от реализации продукции,
тыс. руб.
|
N
|
1000
|
1020
|
-20
|
|
Материальные затраты, тыс. руб.
|
IОА
|
460
|
510
|
-50
|
|
Материалоемкость продукции
|
γМ
|
0,46
|
0,5
|
-0,04
|
Построим двухфакторную
мультипликативную модель типа y=ab.
Алгоритм ее расчета интегральным
методом следующий:
ΔуОА=ΔОА*
IОА0+1/2ΔОА*ΔIОА
ΔуIоа= Δ IОА* ОА0+1/2ΔОА*ΔIОА
ΔуОА
= -0,5*50+1/2*50*0,04 = - 24 – влияние изменения 1 фактора
ΔуIоа = -0,04*510+1/2*50*0,04
= -19,4 – влияние изменения 2 фактора
Задача 2.
|
Показатель
|
Предыдущий год
|
Отчетный год
|
Отклонение
|
|
Прибыль отчетного года, тыс. руб.
|
8500
|
7300
|
1200
|
|
Среднегодовая стоимость
внеоборотных активов, тыс. руб., ВА
|
55600
|
56300
|
-700
|
|
Среднегодовая стоимость оборотных
активов, тыс. руб., ОА
|
46400
|
41800
|
4600
|
|
Среднегодовая стоимость всех
активов, тыс. руб., А
|
102000
|
98100
|
3900
|
|
Рентабельность активов, Ра, %
|
8,33
|
7,44
|
0,89
|
Рассчитаем
среднегодовую стоимость как среднее значение между ВА и ОА.
Рассчитаем
отклонение как разницу между отчетным годом и предыдущим годом.
Рентабельность
определяется отношением прибыли к среднегодовой стоимости активов. Данные
занесем в таблицу.
Определим
долю прироста ВА: -700/3900*100%=-17,95%;
Определим
долю прироста ОА: 4600/3900*100%=117,95%.
Таким
образом, уменьшение стоимости ВА увеличило бы рентабельность на 11,75%, а
увеличение стоимости АО уменьшило рентабельность на 77,24%.
Мы
видим, что изменения в среднегодовой стоимости по-разному влияют на
рентабельность, т.е. уменьшение среднегодовой стоимости оборотных активов
уменьшает ее, тогда как увеличение среднегодовой стоимости внеоборотных активов увеличивает.
Рассчитаем
влияние отклонения по каждому показателю:
По ВА: 5400:1100*1,48=7,27%
По ОА: 2900:1100*1,48=3,9%
Задача 3.
Способ
относительных разниц (его еще называют индексным методом или методом разниц в %), как и
предыдущий, применяется в мультипликативных моделях, а также в комбинированных
- типа Y = (a-b)*c. Он значительно проще цепных подстановок, что в
некоторых случаях делает его очень эффективным (например, когда исходные данные
уже содержат определенные ранее относительные отклонения факторных
показателей). Сущность данного метода рассмотрим на предыдущей модели.
Сначала
необходимо рассчитать относительные отклонения факторных показателей.
|
Торговый портфель
|
Предыдущий
год
|
Следующий
год
|
Относит.
отклонение, %
|
Относит.
отклонение, %
|
|
Доход на
1 ЦБ
|
Кол-во ЦБ в портфеле , шт.
|
Доход на
1 ЦБ
|
Кол-во ЦБ в портфеле , шт.
|
|
Акции
|
15
|
1000
|
18
|
950
|
20
|
-5
|
|
Облигации
|
200
|
100
|
220
|
90
|
10
|
-10
|
Тогда
отклонение результативного показателя за счет каждого фактора определяется
следующим образом:
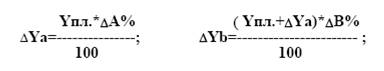
Акции
ΔуА1= 15*20/100=3
Δуb1=(1000+20)*-5/100=-51
Облигации
ΔуА2= 200*10/100=20
Δуb2=(100-5)*-10/100=-9,5
Задача 4.
Дано:
Сумма долга D=18000000 руб.
r=34%
T=2 года
Sинф= S0*(1 +it)
Отсюда S0=18000000/(1+0,34) 2= 10024504 руб.
Задача 5.
S=600 000 руб.
r= 36%
h=4
t=12
Наращенная сумма определяется по
следующей формуле.
Sинф=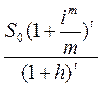
Sинф= 600000*(1+(0,36/12)4)/(1+0,04)4=577253,8
ЭК= Sинф - S0
ЭК=577253,8-600 000= - 22746 руб.
Задача 6.
|
год
|
1
|
2
|
3
|
4
|
|
поступления
|
250
|
250
|
110
|
110
|
I=600
K=19%
T=4
Общая сумма поступлений
за 4 лет составит: 250*2+110*5=1050 млн. руб.
Общая сумма инвестиций с
учетом дисконтирования составит: 1050*1,19=1249,5