Задача. Дан временной
ряд:
|
t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
yt
|
10
|
14
|
21
|
24
|
33
|
41
|
44
|
47
|
49
|
Необходимо:
1. Определить наличие тренда 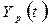 ;
;
2. Построить линейную модель 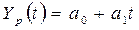 ;
;
3. Построить точечный и интервальный
прогнозы на два шага вперед (для вероятности Р=70%).
Отобразить
на графике фактические данные, результаты расчетов и программирования.
Решение
1. Определение
наличия тренда 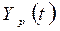
Гипотезу
о равенстве дисперсий проверим с помощью Двухвыборочного
F-теста для дисперсий, который можно найти среди инструментов Анализа данных (рис. 1.1)
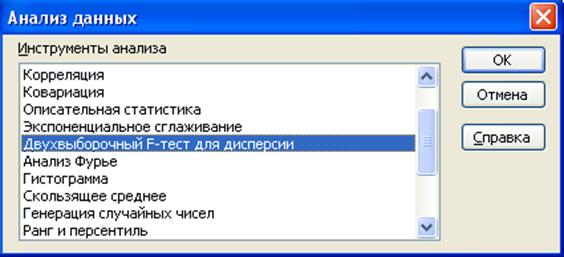
Рис. 1.1 Вызов надстройки Excel Анализ данных
Вводим данные для выполнения F-теста, указывая интервал для
первой и второй переменных (рис. 1.2).
Результат выполнения F-теста приведен на рис. 1.3. Анализируя результаты
выполнения двухвыборочного F-теста для проверки гипотезы о равенстве дисперсий,
приходим к выводу, что исправленные выборочные дисперсии 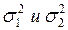 различаются, но
различие не больше F критического 6,56<9,12, следовательно,
различие незначимо.
различаются, но
различие не больше F критического 6,56<9,12, следовательно,
различие незначимо.
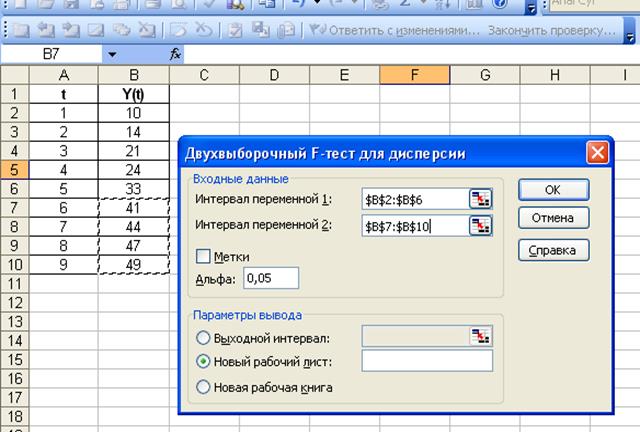
Рис. 1.2 Введение данных для двухвыборочного F-теста
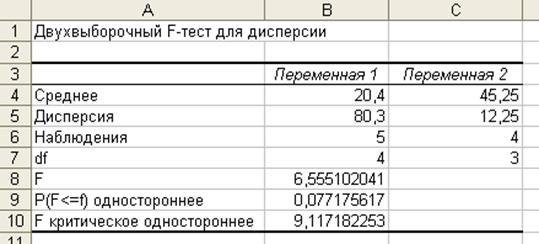
Рис. 1.3. Результат выполнения для дисперсии
Выбираем инструмент анализа Двухвыборочный
t-тест с одинаковыми дисперсиями (рис. 1.4). Вводим данные. Результат выполнения t-теста приведен
на рис. 1.5, анализируя который
убеждаемся, что тренд есть (5,18>2,36).
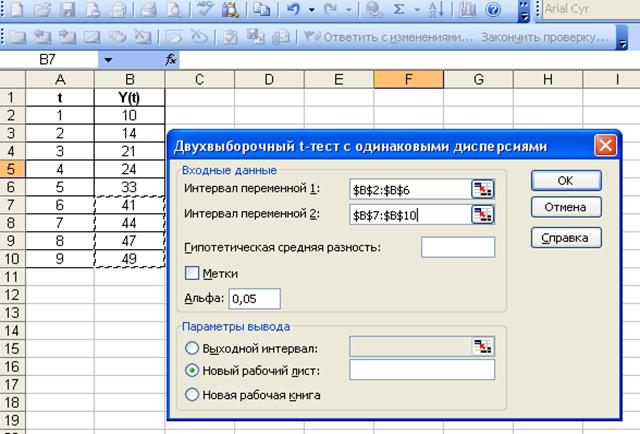
Рис. 1.4. Ввод данных для двухвыборочного t-теста с одинаковыми дисперсиями.
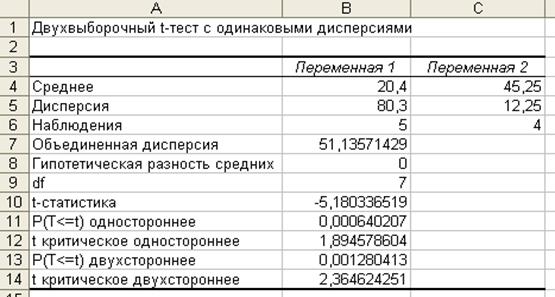
Рис. 1.5. Результат выполнения t-теста
2. Построение линейной модели 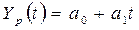
Оценка
параметров модели с помощью надстройки Excel Анализ данных. Построим линейную модель регрессии Y от t. Для проведения регрессионного
анализа выполним следующие действия:
·
Выберем
Сервис  Анализ данных
Анализ данных
·
В
диалоговом окне Анализ данных
выберем инструмент Регрессия;
·
В
диалоговом окне Регрессия в поле Входной интервал Y введем адрес
диапазона ячеек $B$2:$B$10,
который представляет зависимую переменную;
·
В
поле Входной интервал X введем адрес
диапазона $A$2:$A$10;
·
Выберем
параметры Вывода – Новый рабочий лист;
·
В
поле график подбора поставим флажок;
·
В
поле остатки поставим флажки (рис. 1.6)
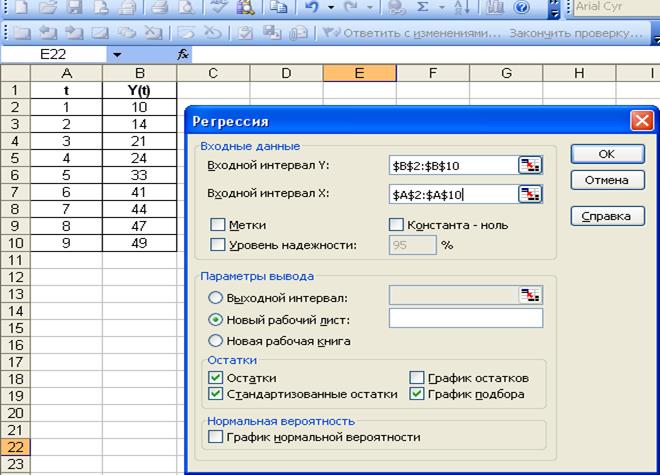
Рис. 1.6 Ввод данных в окно Регрессия
Результат регрессионного анализа приведен на
рис.
1.7. и 1.8.
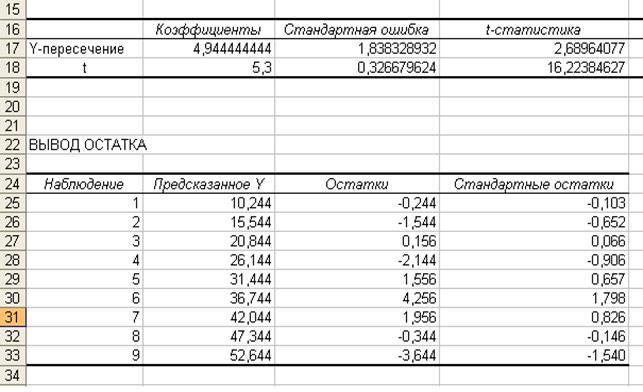
Рис. 1.7 Результат регрессионного анализа и вывод
остатков
На основе данных таблицы можно
утверждать, что 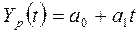 имеет вид:
имеет вид: 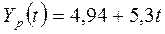
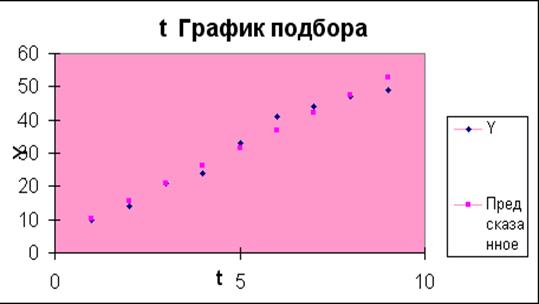
Рис. 1.8 График подбора
1. Построим линию тренда. Для этого
2. Кликнем правой кнопкой мыши на одном
из рядов диаграммы.
3.
Выберем команду Добавить линию тренда из
контекстного меню.
4.
Выберем тип регрессии:
- линейный
- полиномиальный 2 степени
- полиномиальный 3 степени
- степенной
- экспоненциальный
Вкладке Параметры установим флажки в полях:
-
показывать уравнение на диаграмме
-
поместить на диаграмме величину доверительной аппроксимации R2 (рис.1.9)
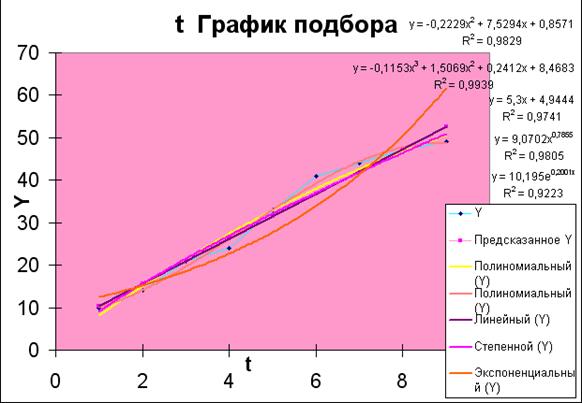
Рис. 1.9 Уравнения регрессии и их графики
Выбор наиболее адекватного уравнения регрессии
определяется максимальным значением коэффициента аппроксимации R2: чем ближе значение R2 к единице, тем более
точно регрессионная модель соответствует фактическим данным.
Вывод: Максимальное
значение коэффициента детерминации R2 =0,9939
присуще полиномиальному уравнению регрессии 3 степени.
Это уравнение регрессии и его график приведены на
отдельной диаграмме рассеяния (рис. 1.10):
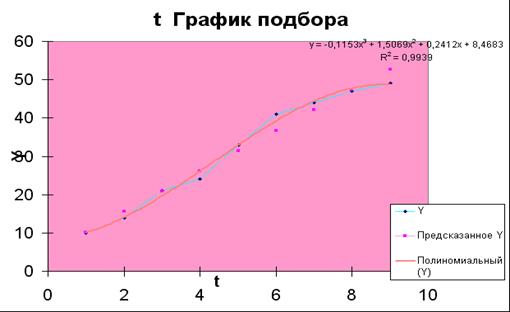
Рис. 1.10 График полиномиальной зависимости 3 степени.
Рассчитать параметры
уравнения можно вручную с помощью компьютера по формулам: 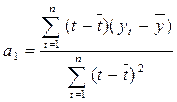
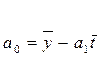 (рис. 1.11)
(рис. 1.11)
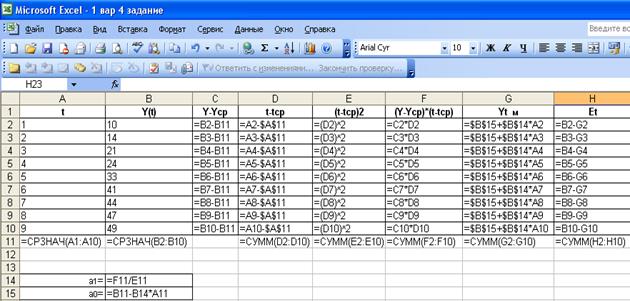
Рис. 1.11 Формульный вид расчета вспомогательных величин
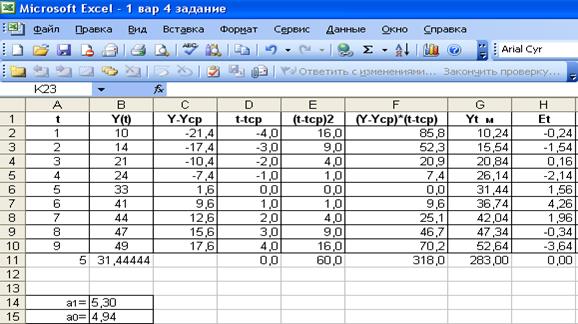
Рис. 1.12 Результат расчета вспомогательных величин
3. Построение точечного и интервального
прогнозов на два шага вперед.
Для
вычисления точечного прогноза на 2 шага вперед в построенную модель подставляем
соответствующие значения фактора t = n+k:
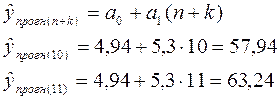
Для построения интервального прогноза
рассчитаем доверительный интервал. Примем значение уровня значимости 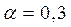 , доверительная вероятность равна 70 %, а критерий Стьюдента
при
, доверительная вероятность равна 70 %, а критерий Стьюдента
при 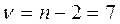 по таблице
t-статистики Стьюдента равен 1,12.
по таблице
t-статистики Стьюдента равен 1,12.
Ширину доверительного интервала вычислим по формуле:
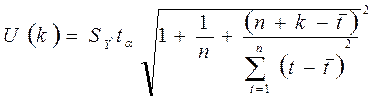 , где
, где
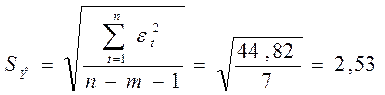
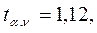
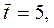
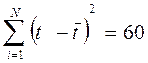
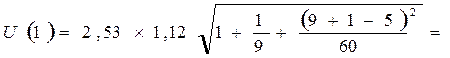 3,502,
3,502,
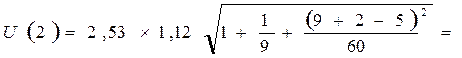 3,707.
3,707.
Далее вычислим верхнюю и нижнюю
границы прогноза:
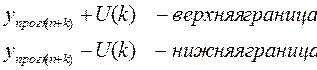
В результате получаем таблицу:
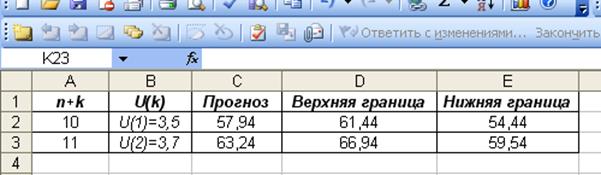
Рис. 1.13 Построение интервального прогноза
Отобразим на графике фактические данные, результаты расчетов и
прогнозирования.
- Построим
первый ряд «Фактические данные» и второй ряд «Сглаживание» с помощью
инструмента Мастер диаграмм:
- Тип
диаграммы – график;
- В
строку «Диапазон» введем диапазон ячеек: =Лист1!$B$2:$B$10 (рис.1.14).
Получаем график фактических данных (рис.
1.15).
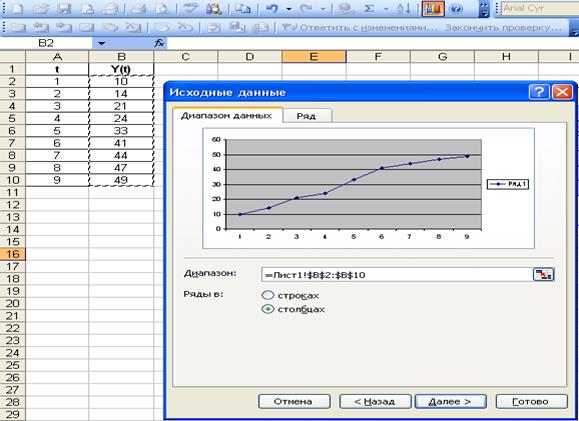
Рис. 1.14 Ввод данных в строку «Диапазон»
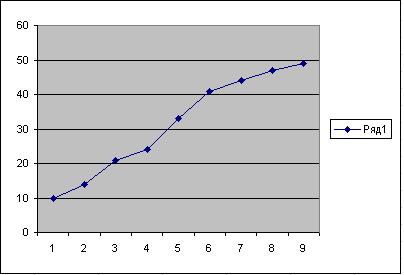
Рис. 1.15 График фактических данных
Построим
график простой скользящей средней, при помощи которой сгладим значения y(t). Значения простой скользящей
средней могут быть найдены так: Сервис Анализ данных
Анализ данных Скользящее среднее. Заполним строки (рис.1.16):
Скользящее среднее. Заполним строки (рис.1.16):
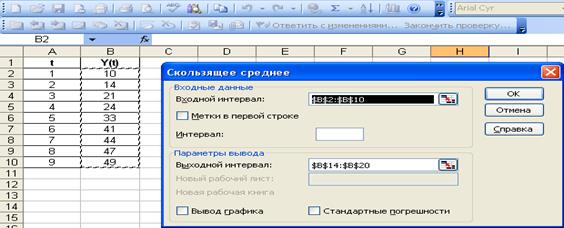
Рис. 1.16 Заполнение строк для нахождения скользящей
средней
Значения
простой скользящей средней отображены на рис. 1.17 они располагаются в ячейках В14:В20.
В области графика кликнем правой кнопкой мыши.
Из появившегося меню выберем параметр Исходные
данные (рис. 1.17). В поле Имя введем название Ряда1 «Фактические
данные».
В этом
же окне нажмем кнопку Добавить для
добавления еще одного Ряда, для построения графика скользящей средней:
В поле Имя введем: «Сглаживание»
В поле Значения введем: =Лист1!$B$14:$B$20 (рис. 1.17)
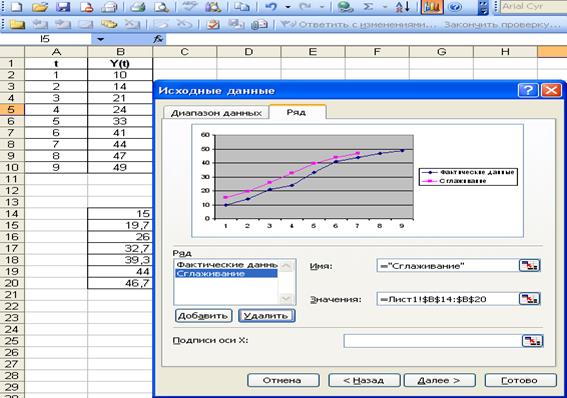
Рис. 1.17
Построение рядов
Построим линию точечного прогноза по данным
из рис.
1.13:
Для этого аналогичным образом добавим
ряд 3, заполним строки:
В поле Имя введем: «Прогноз»
В поле Значения введем: =Лист1!$С$2:$B$12
Построим линии интервального прогноза:
Добавим Ряд 4:
В поле Имя введем: «Прогноз верхние границы»
В поле Значения введем: =Лист1!$D$2:$D$12
Добавим Ряд 5:
В поле Имя введем: «Прогноз нижние границы»
В поле Значения введем: =Лист1!$E$2:$E$12 (рис. 1.18)
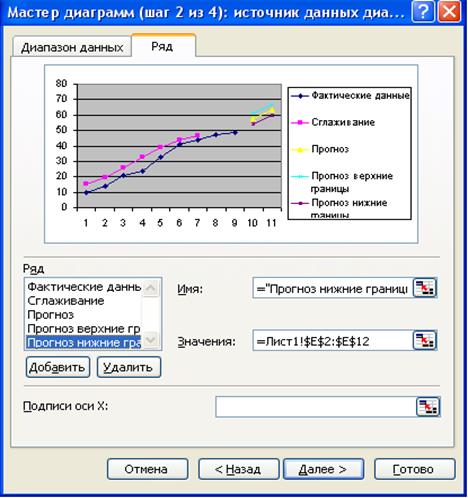
Рис. 1.18 Построение границ прогноза
Таким образом, графический результат
моделирования и прогнозирования нашей модели 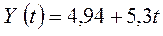 представлен на рис. 1.19:
представлен на рис. 1.19:
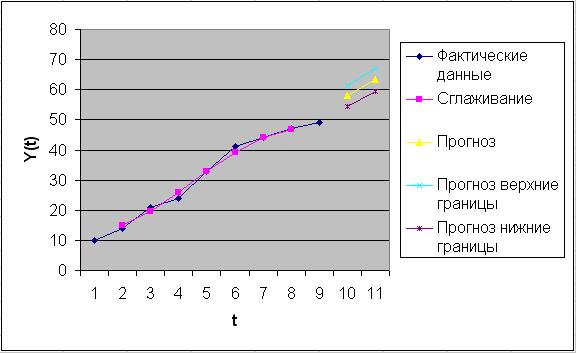
Рис. 1.19
Результаты моделирования и прогнозирования