1. Отбор факторов для включения в многофакторную регрессионную модель

В ряде случаев на величину того или иного технико-эксплуатационного или экономического показателя влияет не один, а несколько различных факторов. Каждый из них может не оказывать большого воздействия, но их совокупное влияние окажется решающим, и тогда по изменению этих факторов можно определить и изменение самого показателя. В этих случаях для измерения совместного влияния нескольких факторов на величину результативного показателя у строят модели множественной корреляции. При этом у рассматривается как функция не одного, а нескольких факторов х, т. е..

y=f(x₁, x₂, . . . , x_i, . . . , x_n),

где i - порядковый номер фактора-показателя (i=l, 2,..., п).

В многофакторных корреляционных моделях выбор уравнения связи еще более сложен, чем при парных зависимостях, так как не представляется возможным проследить действие различных факторов на искомый показатель с помощью построения графиков. Поэтому качественный анализ характера связей каждого фактора с искомым результативным показателем здесь приобретает весьма важное значение.

Если эта связь может быть принята линейной или близкой к ней, то применяется линейное уравнение множественной корреляции:

y = a₀+a₁x₁+a₂x₂+...+a_nx_n

Для нахождения параметров a₀; a₁; a₂; ... a_n, так же как и при парной корреляции используется метод наименьших квадратов и решение на его основе системы нормальных уравнений.

Например, если имеется линейная связь между у и двумя факторами х₁ и x₂, то уравнение связи записывается следующим образом:

y_x_1,_x2 = a₀+a₁x₁+a₂x₂,

а параметры этого уравнения находятся с помощью решения соответствующей системы нормальных уравнений.

В случаях, когда в уравнении множественной корреляции имеется значительное количество факторов, расчеты становятся очень трудоемкими и их следует проводить с помощью ЭВМ по стандартным программам. Если воздействие каких-либо факторов на результативный показатель не может считаться прямолинейным, то соответствующие переменные х; включаются в уравнение не только в первой степени, но и в более высоких степенях.

Предположим, что на среднюю заработную плату шоферов грузовых автомобилей у влияют только два фактора — выработка на одну списочную автомобиле-тонну х₁ и средняя грузоподъемность подвижного состава х₂. При сдельной оплате труда шоферов их заработная плата прямо пропорциональна росту выработки, но уменьшается с ростом грузоподъемности подвижного состава, т. е. криволинейно связана с фактором x₂. При этом можно предположить, что кривая приближенно соответствует обычной параболе. В этом случае целесообразно провести расчеты по следующему уравнению множественной корреляции:

y = a₀+a₁x₁+a₂x₂+...+a₃x₂

Для оценки тесноты связи между результативным показателем и всеми факторами, включенными в модель, используется коэффициент множественной корреляции R, который характеризует силу совместного влияния учтенных факторов на величину результативного показателя. Чем ближе R к единице, тем выше теснота связи между результативным показателем и учтенными факторами.

При построении многофакторных корреляционных моделей обычно вначале делается предположение, что на у влияет значительное число факторов х. Однако оказывается, что некоторые из этих факторов являются несущественными, т. е. их влияние на величину у значительно меньше других. Поэтому используется пошаговый процесс решения, когда на каждом шаге из уравнения исключается одна из переменных x_i. При этом все время сравнивается значение R на предыдущем шаге с его значением на последующем. Если при исключении очередного фактора R уменьшается незначительно, то это означает, что данный фактор является несущественным и можно отказаться от его учета при определении значения результативного признака.

В последние годы построение многофакторных регрессионных моделей находит все большее применение при анализе и планировании работы автомобильного транспорта. Следует подчеркнуть, что конкретные модели корреляционного анализа должны использоваться только для тех хозяйственных объектов, по данным которых они были рассчитаны.

2. Применение скользящих средних в экономическом прогнозировании

Часто ряды динамики характеризуются резкими колебаниями показателей по годам. Такие ряды, как правило, имеют слабую связь со временем и не обнаруживают четкой тенденции изменения. В этом случае методы аналитического выравнивания и экспоненциального сглаживания малоэффективны, так как достоверность расчетов резко падает. Доверительные границы прогноза порой оказываются шире колебаний показателя в ряду динамики.

При прогнозировании урожайности сельскохозяйственных культур на основе сильно колеблющихся временных рядов можно использовать метод скользящих средних. Выравнивать по скользящим средним можно также ряды динамики, имеющие тесную и умеренную связь со временем. При этом появляется возможность определять среднее прогнозное значение для планового периода в целом.

Метод скользящих средних позволяет отвлечься от случайных колебаний временного ряда, что достигается путем замены значений внутри выбранного интервала средней арифметической величиной. Интервал, величина которого остается постоянной, постепенно сдвигается на одно наблюдение. Величина интервала скольжения Р может принимать любое значение от минимального (Р= 2) до максимального (Р= N— 1, где N— длина рассматриваемого временного ряда). Сглаженный ряд короче первоначального на Р— 1 наблюдение.

При использовании метода скользящих Средних прежде всего определяют величину интервала скольжения, обеспечивающую взаимное погашение случайных отклонений во временном ряду. Выбор величины интервала должен осуществляться с учетом особенностей динамики урожайности сельскохозяйственных культур, а также с учетом периодов развития сельскохозяйственного производства (до Великой Отечественной войны, после войны и т.д.). Если наблюдается определенная цикличность изменения показателей, интервал скольжения должен быть равен продолжительности цикла. При отсутствии цикличности в изменении показателей рекомендуется производить многовариантный расчет при изменяющемся параметре сглаживания. Лучший вариант Р определяется на основании последующей оценки выравненных рядов (по коэффициентам, темпам роста и т.д.). Найденный таким образом параметр скольжения затем используется для прогнозирования показателей урожайности.

Для любого интервала скользящая средняя исчисляется по формуле:

При явной или скрывающейся за резкими колебаниями тенденции к снижению урожайности (или продуктивности) выравнивание динамических рядов по скользящим средним, как правило, не дает желаемых результатов. В таких случаях использование приемов экстраполяции оказывается нецелесообразным. Следует отметить, что наибольшая достоверность прогнозов обеспечивается при одновременном использовании различных приемов и методов (экстраполяции, экспертных оценок и т.д.).

Метод гармонических весов очень близок по сущности к методу экспоненциального сглаживания, он основывается на тех же принципах. В этом методе в отличие от метода экспоненциального сглаживания вместо скользящей средней используется идея скользящего тренда. Экстраполяцию показателя проводят по скользящему тренду, отдельные точки ломаной линии взвешиваются с помощью гармонических весов, т.е. более поздним наблюдениям придается больший вес. Метод был разработан польским ученым Э. Хельвигом.

Уравнение авторегрессии выражается переменной у( через ее значения в моменты времени (/— 1), (t—2), (t— 3),..., (t— p). В линейной форме оно имеет вид:

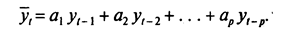
Уравнения классифицируют по количеству элементов, включенных в правую часть выражения: первого порядка, второго порядка и т.д. Эти уравнения могут быть широко использованы в имитационном прогнозировании.

3. Задача

Практический расчёт осуществляется по шагам в следующей последовательности:

Шаг 1. Проверить гипотезу о существовании тенденции в динамическом ряду.

Шаг 2. Оценить существенность коэффициента парной корреляции.

Шаг 3. Выбрать функцию, описывающую развитие технико-эконо-мнческого показателя во времени.

Шаг 4. Определить параметры тренда и получить экономико-математическую модель.

Шаг 5. Оценить точность и надежность модели, применяемой для прогнозирования.

Шаг 6. Найти точечный и интервальный прогноз.

Шаг 7. Изобразить результаты расчётов графически, сделать выводы.

Решение:

Выберем модель регрессии для отображения связи между фондом начисленной заработной платы (у) и численностью работников списочного состава на конец отчетного периода (х_сс), среднемесячной заработной платой работника (х_сзпл), числом принятых работников (х_чпр) и числом выбывших работников (х_чвыб).

1. Построим линейную модель для отображения связи между фондом начисленной заработной платы (у) и численностью работников списочного состава на конец отчетного периода (х_сс).

Определим линейный коэффициент парной корреляции по следующей формуле.

Можно сказать, что связь между факторами обратная, но не очень сильная.

Уравнение линейной регрессии имеет вид:

Определим значения параметров линейной модели.

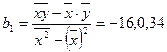, а = 2050921,174

Уравнение регрессии имеет вид:

у=2050921,174-16,034*х_сс

Рассчитаем коэффициент детерминации:

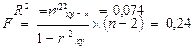Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера.

F< Fтабл=10,13 для α=0,05; k₁=m=1;k₂=n-m-1=3

Уравнение регрессии с вероятностью 0,95 в целом статистически не значимое, т.к. F < Fтабл.

Определим среднюю ошибку:

В среднем расчетные значения ý для линейной модели отличаются от фактических значений на 13,44%.

Построим точечный и интервальный прогнозы на два шага вперед по модели регрессии с надежностью Р=0.9

В качестве параметра для вычисления прогноза воспользуемся средним абсолютнымм приростом.

Затем по формуле рассчитываем прогнозные значения x (k – шаг прогноза):

X₆=x₅+kDx_cp=23981+1*(-892,25)= 23088,75

X₇=x₅+ kDx_cp=23981-2*892,25=22196,5

Для получения прогнозных значений y прогнозные значения х подставляем в модель:

У=2050921,174-16,034*х_сс

И получаем точечный прогноз y: y₆=1680716; y₇=1695022

Рассчитаем доверительынй интервал прогноза с надежностью Р_д=0,9

Значение t cтатистики определяем по таблице: t_табл=2,5706

Вычислим среднее значение ошибки прогноза:

S_e=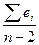=18,312/3=6,104

m₆=6,104*2,5706*1,11=17,42

m₇ = 22,52

Вычисляем границы доверительного интервала, соответственно:

нижняя граница=y₆-m₆=1680716-17,42=1680698,58;

y₇-m₇=1695022-22,52=1695044,52

верхняя граница= y6+m6=1680716+17,42=1680733,42;

y₇₊m₇=1695022+22,52=1695044,52

Построим линейную модель для отображения связи между фондом начисленной заработной платы (у) и среднемесячной заработной платой работника (х_сзпл).

Определим линейный коэффициент парной корреляции.

Можно сказать, что связь между факторами обратная, но не очень сильная.

Уравнение линейной регрессии имеет вид:

Определим значения параметров линейной модели.

b=-72,101, а = 1904485,203

Уравнение регрессии имеет вид:

у=2050921,174-16,034*х_сзпл

Рассчитаем коэффициент детерминации:

Определим среднюю ошибку:

В среднем расчетные значения ý для линейной модели отличаются от фактических значений на 13,87%.

Построим точечный и интервальный прогнозы на два шага вперед по модели регрессии с надежностью Р=0.9

В качестве параметра для вычисления прогноза воспользуемся средним абсолютным приростом.

Затем по формуле рассчитываем прогнозные значения x (k – шаг прогноза):

X₆=x₅+kDx_cp=5870+1*994,5= 6864,5

X₇=x₅+ kDx_cp=5870+2*994,5=7859

Для получения прогнозных значений y прогнозные значения х подставляем в модель:

у=2050921,174-16,034*х_сзпл

И получаем точечный прогноз y: y₆=1940856; y₇=1924910

Рассчитаем доверительынй интервал прогноза с надежностью Р_д=0,9

Значение t cтатистики определяем по таблице: t_табл=2,5706

Вычислим среднее значение ошибки прогноза:

S_e=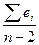=1,222

m₆=18,16083931

m₇ = 20,35531641

Вычисляем границы доверительного интервала, соответственно:

нижняя граница=y₆-m₆=1680697,839;

y₇-m₇=1695042,355

верхняя граница= y6+m6=1680734,1619;

y₇₊m₇=1695042,355

3. Построим линейную модель для отображения связи между фондом начисленной заработной платы (у) и числом принятых работников (х_чпр).

Определим линейный коэффициент парной корреляции.

Можно сказать, что связь между факторами прямая, но не очень сильная.

Значения параметров линейной модели определим, используя данные таблицы 1.

b=-18,236, а = 1481128,615

Уравнение регрессии имеет вид:

у=1481128,615-18,236*х_пр

Рассчитаем коэффициент детерминации:

Определим среднюю ошибку:

В среднем расчетные значения ý для линейной модели отличаются от фактических значений на 6,046%.

Построим точечный и интервальный прогнозы на два шага вперед по модели регрессии с надежностью Р=0.9

В качестве параметра для вычисления прогноза воспользуемся средним абсолютным приростом.

Затем по формуле рассчитываем прогнозные значения x (k – шаг прогноза):

X₆=x₅+kDx_cp=8505+1*310,5= 8815,5

X₇=x₅+ kDx_cp=8505+2*310,5=9126

Для получения прогнозных значений y прогнозные значения х подставляем в модель:

у=1481128,615-18,236*х_пр

И получаем точечный прогноз y: y₆=1320369,157; y₇=1314706,879

Рассчитаем доверительный интервал прогноза с надежностью Р_д=0,9

Значение t cтатистики определяем по таблице: t_табл=2,5706

Вычислим среднее значение ошибки прогноза:

S_e=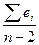=0,148

m₆=19,47175072

m₇ = 17,57888057

Вычисляем границы доверительного интервала, соответственно:

нижняя граница=y₆-m₆=1320369,157-19,47175072=1320349,685;

y₇-m₇=1314706,879-17,57888057=1314689,3

верхняя граница= y6+m6=1320388,629;

y₇₊m₇=1314724,458

Построим линейную модель для отображения связи между фондом начисленной заработной платы (у) и числом выбывших работников (х_чвыб).

Определим линейный коэффициент парной корреляции.

Можно сказать, что связь между факторами обратная, но не очень сильная.

Уравнение линейной регрессии имеет вид:

Определим значения параметров линейной модели определим.

b=-13,798, а = 1741417,527

Уравнение регрессии имеет вид:

у=1741417,527-13,798*х_выб

Рассчитаем коэффициент детерминации:

Определим среднюю ошибку:

В среднем расчетные значения ý для линейной модели отличаются от фактических значений на 14,178%.

Построим точечный и интервальный прогнозы на два шага вперед по модели регрессии с надежностью Р=0.9

В качестве параметра для вычисления прогноза воспользуемся средним абсолютным приростом.

Затем по формуле рассчитываем прогнозные значения x (k – шаг прогноза):

X₆=x₅+kDx_cp=10942+1*1078,25= 12020,25

X₇=x₅+ kDx_cp=10942+2*1078,25=13098,5

Для получения прогнозных значений y прогнозные значения х подставляем в модель:

у=1741417,527-13,798*х_выб

И получаем точечный прогноз y: y₆=1575562,118; y₇=1560684,424

Рассчитаем доверительный интервал прогноза с надежностью Р_д=0,9

Значение t cтатистики определяем по таблице: t_табл=2,5706

Вычислим среднее значение ошибки прогноза:

S_e=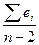=6,1

m₆=18,08370689

m₇ = 21,79757676

Вычисляем границы доверительного интервала, соответственно:

нижняя граница=y₆-m₆=1575544,034;

y₇-m₇=1560662,626

верхняя граница= y6+m6=1575580,202;

y₇₊m₇=1560706,222

Из вышеуказанных факторов наиболее сильная связь между фондом начисленной заработной платы и среднемесячной заработной платой работника, в связи с чем прогнозные значения фонда заработной платы на 2004-2005 г.г. примем по данной модели. Представим итого расчета в таблице 1:

Таблица 1

Прогноз численности, заработной платы и движения работников

год

Численность работников списочного состава на конец отчетного периода Человек.

Фонд начисленной заработной платы включая выплаты социального характера

Тыс. руб.

Средне месячная зарплата работника Рублей.

Принято работников (без внешних совмес тителей)

Выбыло работников без внешних совместителей

2004

23088,75

1940856

6864,5

8815,5

12020,25

2005

22196,5

1924910

7859

9126

13088,5

Список литературы

1.                Алексеева М.М. Планирование деятельности фирмы: Учебно-методическое пособие. М.: Финансы и статистика, 2002.

2.                Глущенко В. В., Глущенко И. И. Разработка управленческого решения. Прогнозирование — планирование. Теория проектирования экспериментов. М.: ТОО НПЦ «Крылья», 2004.

3.                Денисов В. В. Основы экономического прогнозирования в пищевой промышленности: Учебное пособие. М.: Колос, 2003.

4.                Идрисов А.Б., Картышев С.В., Постников А. В. Стратегическое планирование и анализ эффективности инвестиций. 2-е изд. М.: Филинъ, 2003.

5.                Личко К. П. Планирование и прогнозирование развития сельскохозяйственной сферы АПК. (Опыт и проблемы). М.: МСХА, 2004.

6.                Личко К.Л. Теоретические основы системы планирования аграрной сферы АПК в условиях формирования нового экономического механизма хозяйствования: Лекция. М.: МСХА, 2002.

7.                Личко К. П., Абельдяев Н.Ф. Прогнозирование урожайности сельскохозяйственных культур (экстраполяционные приемы). 2-е изд. М.: МСХА, 2002.

8.                Серков А. Ф. Индикативное планирование в сельском хозяйстве. М.: Информа-гробизнес, 2002. 162с.