Задача 1.

Производственной функции Y = 40 (KL)^0,4, где К – затраты капитала,

L – затраты труда, Y – объём выпуска продукции, К_min = 10, К_max = 27, L_min = 13, L_max = 32, L_баз = 24, Y_баз = 439, р_к = 14, р_i = 11, С = 77.

Решение.

1.     Графики

а) К = 0,5 (К_min + К_max) = 18,5

Y = 40 (18,5 L)^0,4

L	13	15	20	25	30	32
Y	359	380	426	466	501	514

L

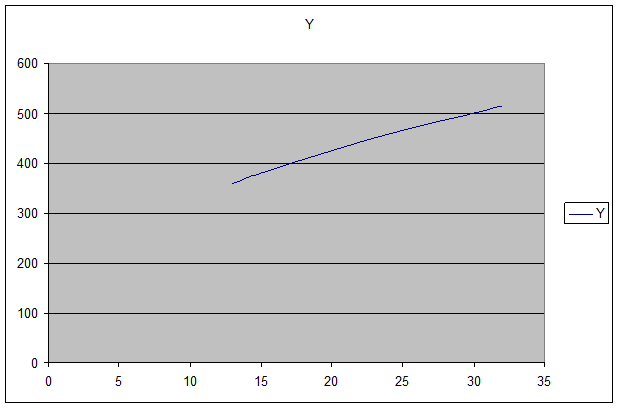
б) L = 0,5 (13 + 32) = 22,5

Y = 40 (22,5 К)^0,4

K	10	15	20	25	27
Y	349	411	461	504	519

К

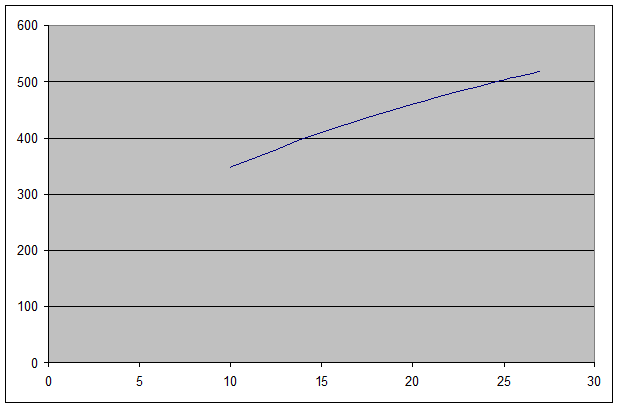
2. Функции среднего и предельного продукта

а) функции среднего продукта

А_к =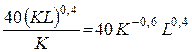

При L = 22,5 получаем

А_к = 139/К^0,6

К	10	15	20	25	27
Ак	34,9	27,4	23	20,1	19,2

К

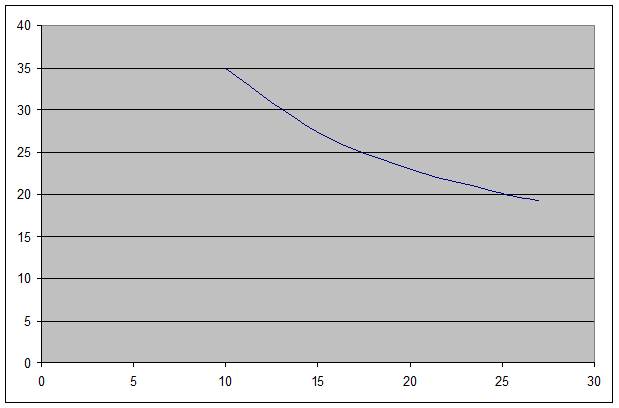
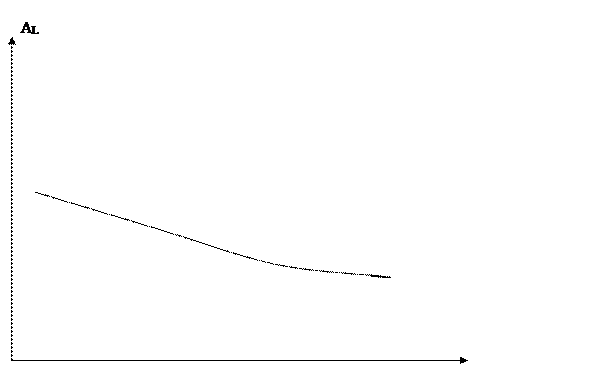
А_L = 40 К^0,4 / L^0,6

При К = 18,5 получаем А_L = 128,5 / L^0,6

30 20 10 0

10                             20                           30

L

б) Функции  предельного продукта

М_к =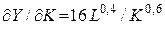

При L = 22,5 получаем М_к = 55,6 / К^0,6

К	10	20	27
Мк	14	9,2	7,7

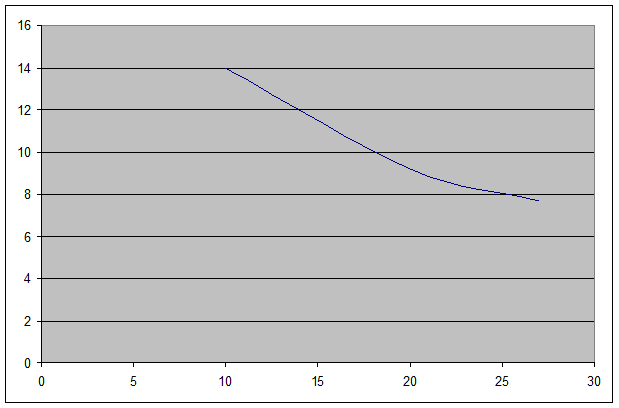
М_L =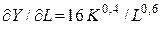

При К = 18,5 получаем М_L = 5 / L^0,6

L	13	25	32
МL	1,1	0,7	0,6

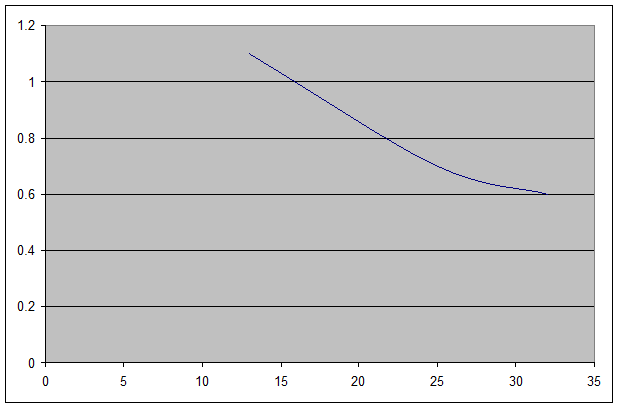
Средняя производительность ресурса – это отношение значения объёма выпуска к объёму ресурса.

Предельная производительность ресурса – это частная эластичность по этому ресурсу.

При увеличении ресурса соответствующие величины убывают.

В методических указаниях написано, что их графики – гиперболы. Скорее всего, они походят на гиперболы, поскольку в математике под гиперболой понимается график зависимости у = а / х, а не у = а / х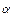. В нашей задаче гиперболами будут изокванты.

3. Изокванты

Если у = const, то изоквантой называется линия 40 (КL)^0,4 = у или просто KL = (у / 40)^2,5 – гипербола.

Нам нужно нарисовать их при у = 129,6; 399; 864.

40 30 20 Y = 280 10

L

К

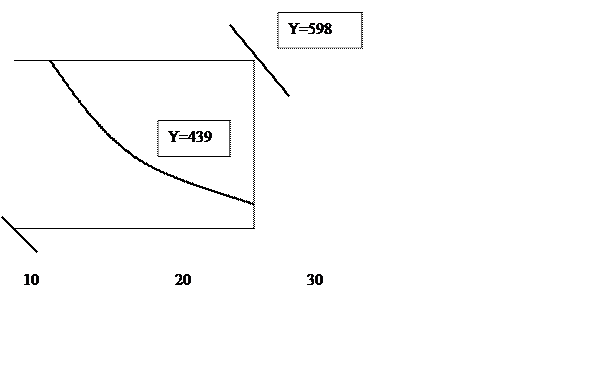
Через весь прямоугольник 10 ≤ К ≤ 27,   13 ≤ L ≤ 32

Проходит только центральная изокванта, а две другие задевают этот прямоугольник только в двух противоположных вершинах.

4. Предельные нормы замещения и эластичности. Эластичность производства

R_KL = M_K / M_L = L / K

R_KL (10; 13) = 1,3;           R_LK = 1 / R_KL

R_LK (10; 13) = 0,91

R_KL (27; 32) = 1,19;         R_LK (27; 32) = 0,84

Например, R_KL (10; 13) = 1,3 означает, что на соответствующей изокванте при уменьшении затрат ресурса К на одну единицу затраты ресурса L должны увеличиться ≈ на 1,3 единиц.

Эластичности

Е_к = М_к / А_к = 0,4;

Е_L = М_L / А_L = 0,4.

Эластичность производства

Е = Е_к + Е_L = 0,8

При малых изменениях ресурсов (по отдельности) увеличение объёма составит 0,4 увеличения ресурса.

5. Расчёт потребности в ресурсах

у_баз = 439

L_баз = 24

А) Определить К_план по двум условиям:

∆Y / Y_баз * 100% = 10%

∆L / L_баз * 100% = 5%

Решение.

∆у = 0,1 у_баз = 43,9

у_план = 482,9

KL =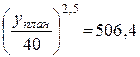

∆L ≤ 0,05 L_баз = 24 * 0,05 = 1,2

К = 506,4 / L на изокванте

Если L возрастает от 24 до 25,2, то К убывает от 21,1 до 20,1

В) Определить К_план по двум условиям:

∆у / у_баз = 0,08

L = L_баз

Решение.

∆у = 0,08 * 439 = 35,12

у_план ^{= 474, 12}

KL = 483,7

К_план = 483,7 / 24 = 20,2.

6. Оптимизационная задача

р_к = 14, р_i = 11, С = 77

Y (K,L) = 40 (KL)^0,4 → max

При условии 14 К + 11 L ≤ 77. Условный экстремум укажет функция Лагранжа.

F = (К, L, 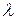) = 40 (KL)^0,4 -  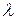(14 К + 11 L – 77)

Необходимые условия    экстремума

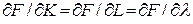
принимают вид

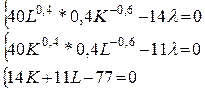
откуда находим

К^* = 11 / 4

L^* = 7 / 2

Y_max = 99

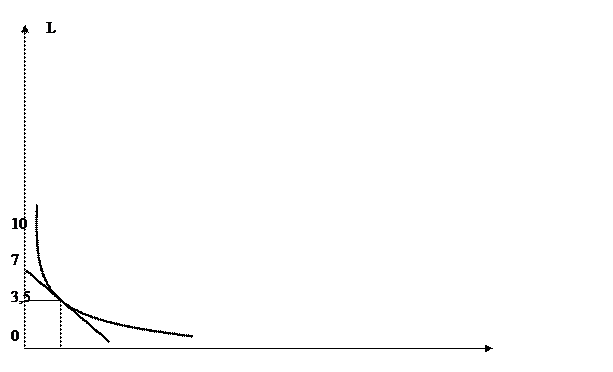
7. Геометрическая интерпретация

KL = (у / 40)^2,5

У = 99

L = 9,64 / К

К^* = 2,75

L^* = 3,5

К

2,75            5,5             10

Задача 2. (вариант 26)

Понадобилась фиктивная работа R нулевой продолжительности

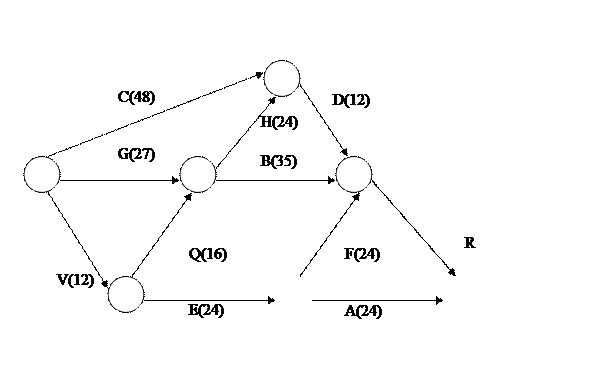
Критические пути:

1) V, Q, B, R;       2) V, Q, H, D, R.

Стоимость всего комплекса работ  при нормальных условиях 1210,5 млн. р.

Т_кр = 64.

Сократить срок работы можно на 4 дня за счёт работ критических путей. Найдём нормы ускорения.

V	Q	B	H	D
12	11,7	9,6	2,5	10,2

Если В и Н сократить на 4 дня каждую, то плана за ускорение 9,6 + 2,5 = 12,1 (млн. руб.)

12,1 * 4 = 48,4 (млн. руб.)

Если сократить общую работу Q на 4 дня, то  плана за ускорение 11,7 * 4 = 46,8 (млн. руб.)

Это выгоднее!

Итоговая стоимость всех работ  1210,5 + 46,8 = 1257, 3 (млн. руб.)

Задача 3.

Оптимизация заказа запасов и их хранения.

а = 6900,  в = 28 руб., с = 70 руб., d = 3, р% = 11%.

Решение.

С_h = р / 100 * в = 3,08

1. Оптимальный размер одного запаса

 

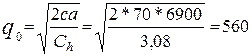
Годовая стоимость запасов

ТС (560) = с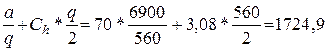

Общая стоимость годового заказа

 = ТС (560) + ав = 1724,9 + 6900*28 = 194924,9

Стоимость запасов составляет от общей стоимости годового заказа часть:

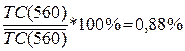
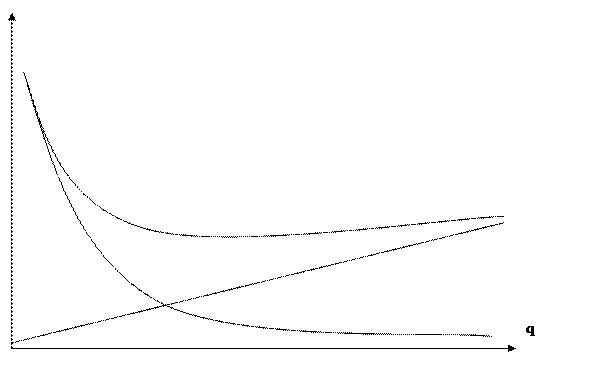
Графики функций: подачи заказа, издержек хранения, общей годовой стоимости запасов изображаем на одном рисунке.

483000 / q – гипербола.

1,54q – прямая линия,   ТС (q) = 483000 / q + 1,54q – сложный график

q	100	500	1000	2000	3000
C*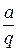	4830	862.5	483	241.5	161
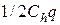
	154				4628

5000

0                        1000                    2000                      300

2. Повторение заказов

Магазин работает 300 дней в году N = a/q = 6900/560 = 12,32 заказов

Интервал повторного заказа

t = a/q (лет) = q/a * 300 (дней) = 25

За время поставки реализовано единиц продукции:

d*a/300 = 3*6900/300 = 69

Это и есть уровень запасов при повторном заказе

3. Экономия при заказах

n = 390 – объём заказываемой партии товара

ТС(390) = 483000/390 + 1,5*390 = 1823,46

Если заказы проводить по оптимальному плану q₀ = 560, то величина экономии

∆ = ТС(390) – ТС(560) = 98,6

При этом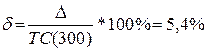 

4. Скидки при заказах    

q ≥ Т = 400, но q ≤ 2Т = 800

предполагает скидку 2%, q ≥ 2Т – даёт скидку 3%.

Общая годовая стоимость запасов

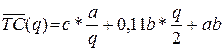
b₁ = 28; b₂ = 27,44; b₃ = 27,16.

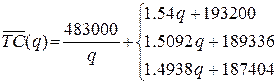
соответственно при 0 ≤ q < 400,  400 ≤ q < 800,  800 ≤ q < ∞.

q₀ = q₀(b) =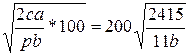

q₀ (b₁) = 560 – уже известно

q₀ (b₂) = 565.72

q₀ (b₃) = 568.63

Точка внутреннего локального минимума придётся на второй участок. Поэтому минимальное значение 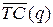 на первом участке принимается в точке q = 400, 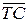  (400) = 195023,5.

На втором участке минимальное значение принимается в точке 565,72.

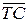 (565,72) = 191043,6.

На третьем участке минимальное значение принимается в точке 800.

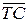 (800) = 189202, 8.

Для точек разрыва, например, 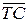 (400+0) = 191147,2.

Далее, 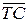 (100) = 4830 + 154 + 193200 = 198184.

 

200000 190000 180000

                                                  

Задача 4.

Линейная корреляция

1. Поле рассеяния

Гипотеза: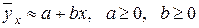 

 

2. Линейная модель регрессии

Вычисляем необходимые суммы:

∑х = 29,25                      ∑у = 23,61

∑х² = 61,6263                 ∑у² = 39,5377

∑ух = 49,0489                n = 15

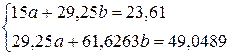
Решая систему, получаем:

а = 0,2948;              b = 0,656

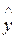 = 0,295 + 0,656 х

График этой прямой построен на фоне поля рассеяния.

3. Коэффициент парной корреляции

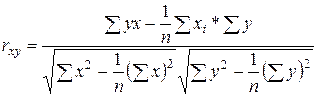
Подставляя уже найденные значения для сумм, получаем

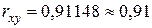
Значение 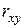 близко к единице, корреляционная зависимость сильная.

Тем не менее проверим значимость этого коэффициента.

Сначала вычисляем

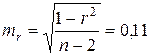
Согласно теории, дробь t_r = 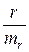 ориентирована на рапределение Стьюдента, t_r = 7,99.

При уровне значимости 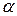 = 0,05 табличное значение t_табл = 1,987.

Так как t_r > t_табл, коэффициент 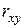 считается значимым.

Есть ещё коэффициент детерминации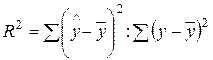

Есть и совсем простая формула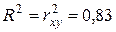 

4. Значимость уравнения регрессии в целом

Рассчитаем значения 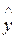= 0,295 + 0,656 х для всех 15 значений аргумента.

1,21	1,15	1,44	1,38	1,55
1,47	1,06	1,33	1,76	1,60
1,80	1,90	1,61	2,60	1,74

После этого находим дисперсии

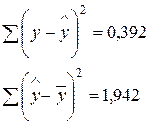
Согласно теории математической статистики, дробь

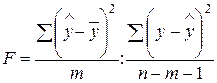
Ведёт себя как распределение Фишера-Снедекора со степенями свободы m и n-m-1.

У нас n = 15, m = 1.

Расчётное значение

F_расч = 1,942*13/0,3920316 = 64,4

Табличное значение при уровне значимости 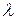 = 0,05 равно F_табл = 4,67 с большим запасом F_расч > F_табл. Значит, вся линейная модель значимая.

5. Точечный и интервальный прогноз

По условию х_n = 1,99*1,3 = 2,587

По уравнению регрессии находим у_n = 1,99. Это точечный прогноз.

Для интервального прогноза понадобится

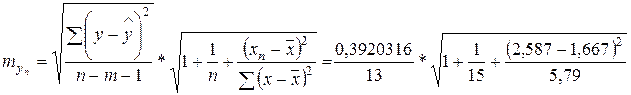
= 0,1736554 * 1,3831365 = 0,24.

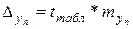
а) 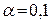         t_табл = 1,771

б) 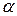 = 0,05     t_табл = 2,15

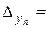
Сначала 0,425 и   1,565 < y_n < 2,415

Затем 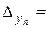 0,52 и    1,47 < y_n < 2,51

При уменьшении уровня значимости рамки доверительного интервала расширились.

Какого-то специального экономического смысла у параметров в этой задаче нет. Номинально х - размер ОФ предприятия, у – величина прибыли. В уравнении регрессии 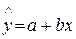  коэффициент «b» выступает как эластичность линейной зависимости. И всё. Гораздо более интересный экономический смысл во всех других задачах контрольной работы.

Задача 5.

Кредит при покупке товара D = 20000, j% = 22%, n = 4 месяца.

1. Структура кредита

Ежемесячный  платёж

Y =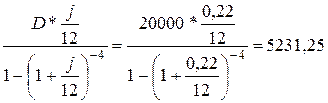

Общие расходы S = nY = 4*5231,25 = 20925

Сумма выплаченных  процентов

J = S – D = 925 (денежных единиц)

2. План погашения кредита

D₀ = 20000    I₁ = D₀*j/12=366,67

D₁ = D₀ – R₁, сначала ищем

R₁ = Y – I₁ = 5231,25 – 366,67 = 4864,58

Затем D₁ = 15135,42

Повторяем эти действия

I₂ = D₁*j/12 = 277,48

R₂ = Y – I₂ = 4953,77

D₂ = D₁ – R₂ = 10181,65

Ещё раз повторяем этот цикл

I₃ = D₂ * j/12 = 186,66

R₃ = Y – I₃ = 5044,59

D₃ = D₂ – R₃ = 5137,06

И последний раз

I₄ = D₃*j/12=94,18

R₄ = Y – I₄ = 5137,07 – последняя выплата

Месяц	Остаток долга на начало месяца	Ежемесячные расходы по займу	Проценты за месяц, ден. ед.	Погашение основного долга
t	Dt-1	Y	It	Rt
1	20000	5231,25	366,67	4864,58
2	15135,42	5231,25	277,48	4953,77
3	10181,65	5231,25	186,66	5044,59
4	5137,06	5231,25	94,18	5137,07

3. Эффективная годовая ставка

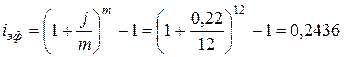 - это 24,36%.

4. Простая годовая ставка

D = 20000, n = 4, j = 0,22 (простая)

Задолженность D*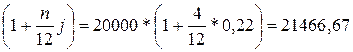

Ежемесячные выплаты

Y_потр = 5366,67

Сумма выплаченных процентов

I_потр = nY_потр – D = 1466,67

Какова доходность для магазина?

Нужно найти ставку i_м такую, чтобы 20000 =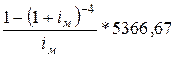

Это уравнение пятой степени для i_м преобразуется к виду

3,7267 i_м +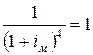

Решить его можно без обращения к пакету EXCEL, используя метод итераций, i_м = 0,029 (это 2,9%).

Доходность составит

I_эф (потр) = (1 + i_м)¹² – 1 = 0,409

В процентах получается 40,9%.

5. Сравнение результатов

По первому виду кредита доходность составляет 24,36% - эффективная годовая ставка сложных процентов.

По второму виду кредита аналогичная ставка j = 22% одна и та же. Потребительский кредит выгоден магазину.

6. Учёт темпа инфляции

h (%) = 2% - ежемесячный темп инфляции, h = 0,02.

При первом виде кредита i_эф = 0,2436.

Значит, (1 + 0,2436) = (1 + i_реал)*(1,02)¹²

Получаем отрицательную доходность i_реал = -1,9%

При втором виде кредита i_эф (потр) = 0,409

Уравнение (1 + 0,409) = (1 + i_реал)*(1,02)¹² даёт значение i_реал (потр) = 1,1% (уже знак плюс)

В нашей задаче первый вид кредита приводит, в случае инфляции, к убыткам, а доходность потребительского кредита с учётом инфляции положительна.