ОГЛАВЛЕНИЕ
Введение............................................................................................ 5
1. МЕТОДЫ СЕТЕВОГО ПЛАНИРОВАНИЯ И
УПРАВЛЕНИЯ.................................................................................... 6
1.1. Сетевая модель и ее основные элементы.................................. 6
1.2. Параметры сетевой модели с учетом временных
характеристик…………………...................................................... 12
1.3. Методы расчета параметров сетевой модели......................... 18
2 Вероятностные модели
систем................................. 26
2.1. Ориентированный граф состояния системы.
Марковские
процессы........................................................................................... 26
2.2. Уравнения Колмогорова для вероятностей состояний.......... 30
2.3. Системы массового обслуживания (СМО)............................. 33
2.3.1. Общая характеристика СМО............................................. 33
2.3.2. Математическая модель однофазной СМО и показатели ее эффективности.............................................................................. 36
2.3.3. СМО с конечной очередью................................................ 40
2.3.4. СМО с отказами.................................................................. 43
2.3.5. Чистая СМО с ожиданием................................................. 43
2.3.6. Смешанные системы массового обслуживания.............. 46
2.3.7. Особенности применения моделей массового
обслуживания................................................................................ 48
3 Управление запасами........................................................ 51
3.1. Системы управления запасами................................................ 51
3.2. Управление запасами при детерминированном
стационарном
спросе…………………..................................................................... 59
3.2.1. Мгновенная поставка, возникновение дефицита не
допускается. 60
3.2.2.Мгновенная
поставка, возникновение дефицита .............. допускается……………………… 62
3.2.3. Поставка с постоянной интенсивностью......................... 64
3.3. Однокаскадные СУЗ при вероятностном дискретном
спросе……………………………… 66
4 МЕТОДЫ ПРИНЯТИЯ ТЕХНИЧЕСКИХ
РЕШЕНИЙ....... 73
4.1. Основная формальная структура принятия решений............ 73
4.1.1. Матрица решений............................................................... 73
4.1.2. Оценочная функция............................................................ 76
4.1.3. Особые случаи..................................................................... 83
4.2. Классические критерии принятия решений........................... 84
4.2.1. Минимаксный критерий.................................................... 84
4.2.2. Критерий Байеса — Лапласа............................................. 85
4.2.3. Критерий Сэвиджа.............................................................. 86
4.2.4. Расширенный минимаксный критерий............................ 87
4.2.5. Применение классических критериев.............................. 88
4.3. Производные критерии............................................................. 91
4.3.1. Критерий Гурвица.............................................................. 91
4.3.2. Критерий Ходжа-Лемана................................................... 92
4.3.3. Критерий Гермейера.......................................................... 93
4.3.4. BL (MM)-критерий............................................................. 94
4.3.5. Критерий произведений..................................................... 97
4.3.6. Принятие решений согласно производным критериям.. 98
Литература............................................................................... 102
Введение
Современные промышленные, научно-производственные, экономические
и другие комплексы, включающие оборудование, людей, транспорт и объединенные в
административные и хозяйственные подразделения, а также потребителей и среду,
образуют сложную разветвленную схему взаимодействующих друг с другом факторов.
Это неизбежно приводит к формированию системного подхода к
решению задач оптимального планирования, задач определения структур систем управления
и нахождения оптимальных алгоритмов управления.
Этим вопросам и посвящено настоящее учебное пособие. Его
основная цель – развить у студентов системное мышление и научить применять
процедуры и методы построения моделей и получения с их помощью управленческих
решений.
Рассматриваются задачи следующих классов: управления запасами,
массового обслуживания, сетевого планирования и управления, упорядочения и
распределительные.
1 МЕТОДЫ СЕТЕВОГО ПЛАНИРОВАНИЯ
И УПРАВЛЕНИЯ
1.1.СЕТЕВАЯ
МОДЕЛЬ И ЕЕ ОСНОВНЫЕ ЭЛЕМЕНТЫ
При управлении разработками сложных программ и системами
возникает задача рационального планирования и координации большого комплекса
различных работ (операций, действий).
Характерным для сложных комплексов связанных между собой
работ является то, что отдельные работы не могут быть выполнены независимо
друг от друга, выполнение ряда работ не может быть начато раньше, чем
завершены другие.
Системы сетевого планирования и управления (СПУ) обеспечивают
системный подход к решению вопросов организации управления, то есть
рассмотрение всего комплекса работ как единого неразрывного комплекса
взаимосвязанных работ, направленных на достижение общей конечной цели.
Логико-математическое описание, формирование планов и управляющих воздействий
осуществляется на базе использования особого класса моделей, называемых
сетевыми моделями. Поэтому естественно начать изложение с установления понятия
сетевой модели.
Ориентированный граф, в котором существует лишь одна вершина,
не имеющая входящих дуг, и лишь одна вершина, не имеющая выходящих дуг,
называется сетью. Сеть, моделирующая комплекс работ, называется его сетевой
моделью или сетевым графиком. Дуги, соединяющие вершины графа, ориентированы в
направлении достижения результата при осуществлении комплекса работ.
Наиболее распространен способ представления моделируемого
комплекса работ в понятиях работ и событий.
Понятие «работа» имеет следующие значения:
– «действительная
работа» – процесс, требующий затрат времени и ресурсов;
– «фиктивная
работа» – логическая связь между двумя или несколькими работами, указывающая на
то, что начало одной работы зависит от результатов другой. Фиктивная работа не
требует затрат времени и ресурсов, продолжительность ее равна нулю.
На сетевых моделях работам соответствуют дуги, причем действительные
работы изображаются сплошными линиями, а фиктивные – пунктирными.
Понятие «событие» означает факт получения результата вследствие
завершения одной или нескольких работ. Каждая работа заключена между двумя
событиями, так как с события, завершающего одну или несколько работ,
начинаются другие работы. Событие может наступить только тогда, когда окончатся
все предшествующие ему работы.
Событие, с которого начинается выполнение всех работ комплекса,
называется исходным. Исходное событие не имеет предшествующих ему работ и
событий.
Событие, которым заканчивается весь комплекс работ, называется
завершающим. Завершающее событие не имеет последующих работ и событий.
Событие, непосредственно предшествующее работе (с которого
начинается работа), называется начальным, а непосредственно следующее за ней (которым
заканчивается работа) – конечным.
На сетевой модели событиям соответствуют вершины графа.
Любая последовательность работ в сетевой модели, в которой
конечное событие одной работы совпадает с начальным событием следующей за ней
работы, называется путем. Путь от исходного события до завершающего называется
полным путем.
Каждой дуге сетевой модели приписывают число, которое называется
длиной дуги. Соответственно длиной пути называется сумма длин
последовательности дуг, составляющих данный путь. Длина дуги выражает время,
необходимое для выполнения работы, представленной данной дугой. Поэтому длина
пути (или продолжительность пути) есть суммарная продолжительность работ, составляющих
данный путь.
Начальная информация, необходимая для построения сетевой
модели, должна содержать перечень всех работ и последовательность их
выполнения, то есть отношения непосредственного предшествования между работами
комплекса.
Пусть информация о комплексе работ задана табл. 1.1, в которой
работы условно обозначены символами а1, a2, . . . . Из таблицы видно, что работы а1, а5, а6 не имеют предшествующих,
поэтому в сетевой модели дуги, соответствующие этим работам, будут выходить из
исходного события комплекса. Работы а12, a13, a14 не предшествуют никаким другим работам, и поэтому
дуги, соответствующие этим работам, будут входить в завершающее событие комплекса.
Конечное событие работы а1
является начальным событием для работ a2,
a2, a2; конечное событие для работы a2 является начальным для работы a14 и так далее Сетевой график комплекса изображен на
рис. 1.1.
Работы (дуги) на сетевых графиках обозначают символом (i, j), где i – номер начального события работы, а j – номер конечного события. События должны быть пронумерованы
так, чтобы для любой работы (в том числе и фиктивной) всегда i < j. Для получения такой нумерации применяется метод разделения событий
на ранги. Сущность метода заключается в следующем.
Таблица
1.1
Комплекс
работ
|
Работа
|
Каким
работам непосредственно предшествует
|
Работа
|
Каким
работам непосредственно предшествует
|
|
a1
|
a2, a3, a4
|
a8
|
a12
|
|
a2
|
a14
|
a9
|
a11, a13
|
|
a3
|
a11, a13
|
a10
|
a12
|
|
a4
|
a9, a10
|
a11
|
a14
|
|
a5
|
a9, a10
|
a12
|
–
|
|
a6
|
a7, a8
|
a13
|
–
|
|
a7
|
a9, a10
|
a14
|
–
|
Исходному событию присваивается нулевой ранг. Вычеркнув все
дуги, выходящие из исходного, получим несколько (или, по крайней мере, одно)
событий без входных дуг. Этим событиям присваивается первый ранг. Вычеркнув все
дуги, выходящие из событий первого ранга, снова получим события без входящих
дуг, которым присваивается второй ранг. Вычеркнув далее все дуги, выходящие из
событий второго ранга, получим события без входящих дуг, которым присваивается
третий ранг, и так далее
Легко видеть, что событие любого ранга связано с событием
предшествующего ранга одной дугой. Следовательно, событие k-го ранга обязательно связано с исходным событием путем, состоящим
из k дуг; хотя, кроме того, событие k-го
ранга может быть соединено с исходным событием и путем, состоящим из меньшего
числа дуг. Так, например, событие 6 на сетевом графике рис. 1.1 связано с
исходным событием тремя путями: 1) путем, состоящим из дуг (0, 1), (1, 6); 2)
путем, состоящим из дуг (0, 3), (3, 4), (4, 6) и 3) путем, состоящим из дуг (0,
1), (1, 3), (3, 4), (4, 6). Ранг события 6 равен 4, так как последний путь
содержит максимальное число дуг, равное 4.
Событию присваивается ранг k, если максимальное число дуг пути, соединяющего его с исходным,
равно k.
После распределения всех событий по рангам нумерация осуществляется
следующим образом. Исходное событие нулевого ранга получает номер 0. Событиям
первого ранга в произвольном порядке присваивают номера 1, 2, . . ., n1, где п1 – число
событий первого ранга; события второго ранга получают номера n1+1, n1+2, . . ., n1+ n2 где п2 – число
событий второго ранга, и так далее
Так как события одного ранга между собой не соединены, а события
меньшего ранга имеют меньший номер, то для любой дуги (i, j) всегда i < j.
Рассмотренный метод нумерации событий также называют методом
последовательного вычеркивания дуг.
Заметим, что нумерация событий, при которой для любой дуги (i, j) всегда i < j обязательна при
машинных методах расчета параметров сетевых моделей.
В зависимости от задач управления в системах СПУ применяют
различные типы сетевых моделей, отличающиеся составом информации о комплексе
работ. Среди них можно выделить два основных типа: модели с учетом только
временных характеристик (ограничения на ресурсы не накладываются) и модели с
учетом временных и ресурсных характеристик.
Модели первого типа не являются оптимизационными. Но, несмотря
на это, их применение в системах СПУ позволяет эффективно решать существенные
проблемы управления, а именно – найти минимальное время, в течение которого
может быть выполнен весь комплекс, и определить календарные сроки начала и
окончания каждой работы комплекса, обеспечивающих выполнение всего комплекса
в найденное минимальное время.
Модели второго типа относятся к задачам распределения ресурсов.
Эти задачи являются оптимизационными и встречаются в разных постановках. В
зависимости от принятого критерия оптимальности и характера ограничений их
можно разбить на две основные группы:
– задачи
минимизации сроков наступления завершающего события при соблюдении заданных
ограничений на использование ресурсов;
– задачи
оптимизации некоторого показателя качества использования ресурсов при заданных
сроках выполнения комплекса. К этой группе относится, в частности, задача
минимизации ресурсов при заданном времени выполнения комплекса.
Основной временной характеристикой комплекса работ и каждой
отдельной работы является их продолжительность. Оценки продолжительности
выполнения отдельных работ могут быть детерминированными и вероятностными.
Первые используются в тех случаях, когда предполагаемая продолжительность работ
может быть оценена точно с относительно небольшой ошибкой. Если же продолжительность
работы не поддается точному определению и представляет собой случайную
величину, используются вероятностные оценки. В первом случае сетевая модель
называется детерминированной, во втором – вероятностной.
Сетевые модели могут быть также смешанными, поскольку для
некоторых работ могут существовать детерминированные оценки, а для некоторых
вероятностные.
Продолжительность работы (i, j) обозначают через tij. Оценка величины tij может производиться:
– по действующим нормативам;
– по накопленным данным с достаточно высоким процентом повторяемости
работ;
– методом экспертных оценок;
– на основе вероятностных оценок.
На основании статистических данных установлено, что распределение
случайной величины tij
определяется так называемым бета-распределением. Это распределение имеет место
в тех случаях, когда случайная величина зависит от большого числа случайных
факторов, оказывающих незначительное влияние, и от нескольких существенно
влияющих факторов.
В системах СПУ используются три вероятностные оценки:
aij –
минимальное время, необходимое для выполнения работы при наиболее благоприятных
условиях;
bij –
максимальное время, необходимое для выполнения работы при наименее
благоприятных условиях;
mij –
наиболее вероятное время выполнения работы при нормальных, наиболее часто
встречающихся условиях.
Все эти оценки даются ответственными исполнителями или экспертами.
Величины aij,
bij и mij используются для вычисления ожидаемого значения
продолжительности работы 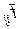 , представляющего собой математическое ожидание случайной
величины tij, и дисперсии Dij. Полученные значения
, представляющего собой математическое ожидание случайной
величины tij, и дисперсии Dij. Полученные значения 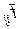 и Dij являются характеристиками случайной величины tij, распределенной по закону
бета-распределения. Кривая бета-распределения изображена на рис. 1.2.
и Dij являются характеристиками случайной величины tij, распределенной по закону
бета-распределения. Кривая бета-распределения изображена на рис. 1.2.
Вследствие различного подхода к учету возможного отклонения реального закона
распределения от принятого бета-распределения и ошибок в определении исходных
величин aij, bij и mij, а также некоторых других факторов создано несколько
формул для вычисления 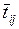 и Dij. Из них в системах СПУ наиболее широко
применяются следующие:
и Dij. Из них в системах СПУ наиболее широко
применяются следующие:

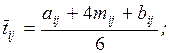 (1.1)
(1.1)

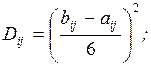 (1.2)
(1.2)
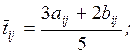 (1.3)
(1.3)
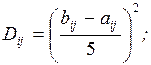 (1.4)
(1.4)
По степени охвата работ различают первичные, частные и комплексные
сетевые модели.
Первичные сетевые модели представляют собой детализированные
изображения частей комплекса и составляются ответственными исполнителями
работ. Частные сетевые модели строятся на основе первичных. Сшивание частной
модели заключается в объединении первичных моделей в одну общую модель,
завершающее событие (события) которой соответствует заданной частной цели
(целям). Для сшивания частной модели необходимо строго установить идентичность
граничных событий в первичных сетевых моделях.
Комплексная (сводная) сетевая модель охватывает все работы
комплекса. Сшивание комплексной модели производится аналогично сшиванию
частных моделей.
На высоких уровнях управления неудобно пользоваться детализированными
сетевыми моделями, поэтому производится их укрупнение. При укрупнении модели
должны соблюдаться следующие правила:
– участок модели (группа взаимосвязанных работ) может быть
заменен одной укрупненной работой, если этот участок имеет одно исходное и одно
завершающее событие. Продолжительность такой укрупненной работы равна
продолжительности критического пути данной группы работ;
– нельзя вводить в укрупненную модель события, которых нет в
детализированной модели;
– исходное и завершающее события в детализированной и укрупненной
моделях должны иметь одинаковый смысл:
– объединять в одну работу следует только такие группы работ,
которые закреплены за одним ответственным исполнителем.
1.2. ПАРАМЕТРЫ
СЕТЕВОЙ МОДЕЛИ С УЧЕТОМ
ВРЕМЕННЫХ ХАРАКТЕРИСТИК
Исходная информация для модели включает сеть, продолжительности
tij всех работ (i, j), момент начала выполнения комплекса
Т0, а также может
содержать (но не обязательно) директивный срок Тдир наступления завершающего события. Продолжительности
работ задаются как детерминированные неотрицательные величины.
Одна из основных задач управления состоит в составлении плана
выполнения комплекса работ. Параметрами плана, определяемыми с помощью сетевой
модели, являются лишь временные характеристики: моменты начала и окончания
каждой работы и всего комплекса работ. Их называют параметрами сетевой модели.
Важнейшим параметром является критическое время Tкр – минимальное
время, за которое может быть выполнен весь комплекс. Критическому времени
соответствует критический путь Lкр,
то есть полный путь, продолжительность которого и составляет критическое
время: t(Lкр)=Ткр.
Очевидно, что продолжительность любого другого полного пути равна или меньше
критического времени Ткр,
поэтому критический путь можно определить как путь, имеющий максимальную
продолжительность.
Работы, лежащие на критическом пути, называются критическими
работами. Именно они определяют время выполнения комплекса в целом, поэтому
ход их выполнения имеет особую важность при управлении выполнением всего
комплекса.
В плане выполнения всего комплекса, естественно, должны быть
определены моменты наступления всех событий, начала и окончания работ. Как
правило, эти моменты устанавливаются не однозначно, а располагаются в некотором
диапазоне. При анализе сетевой модели определяются параметры, ограничивающие
эти диапазоны. Такими параметрами для каждого k-го события являются ранний срок наступления события 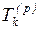 и поздний срок наступления
события
и поздний срок наступления
события 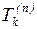 . Используя эти параметры, можно вычислить и другие
параметры, в том числе критическое время Tкр
и критический путь Lкр, на
основании которых составляется план выполнения комплекса. Поэтому начнем с
рассмотрения параметров
. Используя эти параметры, можно вычислить и другие
параметры, в том числе критическое время Tкр
и критический путь Lкр, на
основании которых составляется план выполнения комплекса. Поэтому начнем с
рассмотрения параметров 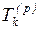 и
и 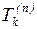 .
.
Предварительно заметим, что все временные параметры сетевой
модели можно определять как календарные (при этом момент начала выполнения
комплекса Т0 должен быть
задан календарной датой) и как относительные (при этом принимают Т0=0). В последующем изложении
принято Т0==0.
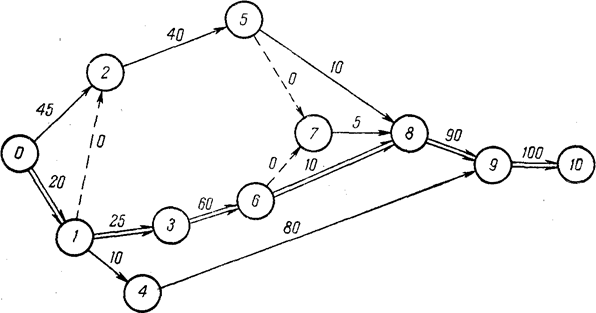
На рис. 1.3 изображена сетевая модель, используемая далее
при изложении методики расчета параметров сетевых моделей.
Ранний срок наступления события 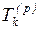 – это самый ранний
из возможных моментов наступления данного k-го
события, и определяется он временем, необходимым для выполнения всех предшествующих
ему работ. Под предшествующими работами понимают работы, составляющие все пути,
связывающие данное событие с исходным. Очевидно, что событие может наступить
только тогда, когда будут выполнены все работы максимального по продолжительности
пути. Поэтому значение
– это самый ранний
из возможных моментов наступления данного k-го
события, и определяется он временем, необходимым для выполнения всех предшествующих
ему работ. Под предшествующими работами понимают работы, составляющие все пути,
связывающие данное событие с исходным. Очевидно, что событие может наступить
только тогда, когда будут выполнены все работы максимального по продолжительности
пути. Поэтому значение 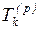 и определяется как
продолжительность максимального из путей, ведущих от основного события к k-му:
и определяется как
продолжительность максимального из путей, ведущих от основного события к k-му:
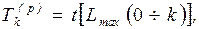 (1.5)
(1.5)
где нулем обозначен номер исходного
события.
Например, к событию 7 (рис.1.3) ведут три пути: 0–1–3–6–7,
продолжительность которого равна 105 единицам времени;
0–1–2–5–7 с продолжительностью 60 ед. и 0–2–5–7 с продолжительностью
85 ед. Очевидно, что событие 7 может наступить не раньше, чем через 105 ед.
времени после исходного события, поэтому 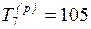 ед.
ед.
Напишем формулу для вычисления 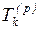 . Обозначим через
. Обозначим через 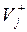 множество дуг (i,j), входящих в j-ю вершину (событие), и допустим, что все значения для
j-х событий, которыми начинается
каждая из этих дуг (работ), нами уже вычислены. Тогда на основании формулы
(1.5) можем написать
множество дуг (i,j), входящих в j-ю вершину (событие), и допустим, что все значения для
j-х событий, которыми начинается
каждая из этих дуг (работ), нами уже вычислены. Тогда на основании формулы
(1.5) можем написать
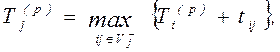 (1.6)
(1.6)
где 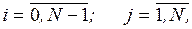 N – номер завершающего события, причем
N – номер завершающего события, причем 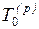 = 0.
= 0.
Вычисляя с помощью формулы (1.6) значения 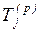 (вычисления ведутся последовательно от
исходящего события к завершающему), найдем для нашей сетевой модели (рис. 1.3)
(вычисления ведутся последовательно от
исходящего события к завершающему), найдем для нашей сетевой модели (рис. 1.3)
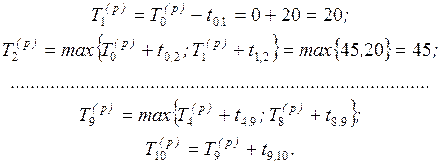
Вычислив все значения 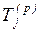 получим
получим 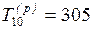 . Ранний срок наступления завершающего события определяет
продолжительность критического пути
. Ранний срок наступления завершающего события определяет
продолжительность критического пути
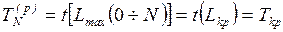 (1.7)
(1.7)
Поздний срок наступления события 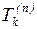 – это самый поздний из
допустимых моментов наступления данного k-го
события, при котором еще возможно выполнение всех последующих работ без превышения
критического времени. Превышение позднего срока на некоторую величину приводит
к аналогичному увеличению критического времени. Значение
– это самый поздний из
допустимых моментов наступления данного k-го
события, при котором еще возможно выполнение всех последующих работ без превышения
критического времени. Превышение позднего срока на некоторую величину приводит
к аналогичному увеличению критического времени. Значение 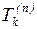 определяется как
разность между критическим временем и продолжительностью максимального пути,
ведущего от данного события к завершающему:
определяется как
разность между критическим временем и продолжительностью максимального пути,
ведущего от данного события к завершающему:
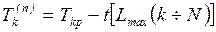 . (1.8)
. (1.8)
Например, от события 6 (рис. 1.3) к завершающему событию ведут
два пути: 6–7–8–9–10 с продолжительностью 195 ед. и 6–8–9–10, продолжительность
которого равна 200 ед. Согласно формуле (1.8) 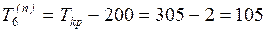 . Очевидно, что если событие 6 наступит в момент
. Очевидно, что если событие 6 наступит в момент 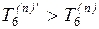 (тo есть позднее
(тo есть позднее 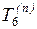 ), а на выполнение
работ, составляющих путь 6–8–9–10, требуется 200 ед., то в результате
завершающее событие наступит в момент, превышающий Ткр на столько,
на сколько
), а на выполнение
работ, составляющих путь 6–8–9–10, требуется 200 ед., то в результате
завершающее событие наступит в момент, превышающий Ткр на столько,
на сколько 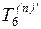 больше
больше 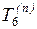 . Действительно, вычислим поздний срок наступления события 6
как разность между Ткр и продолжительностью
первого пути:
. Действительно, вычислим поздний срок наступления события 6
как разность между Ткр и продолжительностью
первого пути: 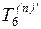 = Ткр–195
= 305–195 = 110 ед. С этого момента требуется еще 200 ед. времени на выполнение
работ второго пути, следовательно, завершающее событие наступит через
110+200=310 ед. после начала работ, то есть Tкр будет превышено на 5 ед.
= Ткр–195
= 305–195 = 110 ед. С этого момента требуется еще 200 ед. времени на выполнение
работ второго пути, следовательно, завершающее событие наступит через
110+200=310 ед. после начала работ, то есть Tкр будет превышено на 5 ед.
Правило вычисления значения 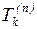 по выражению (1.8)
можно сформулировать более полно следующим образом: если от данного k-го события к завершающему ведут несколько
путей, то значение
по выражению (1.8)
можно сформулировать более полно следующим образом: если от данного k-го события к завершающему ведут несколько
путей, то значение 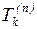 определяется как
разность между критическим временем и продолжительностью максимального пути
или, что то же самое, как минимальная из разностей между критическим временем
и продолжительностью каждого из путей.
определяется как
разность между критическим временем и продолжительностью максимального пути
или, что то же самое, как минимальная из разностей между критическим временем
и продолжительностью каждого из путей.
Из сформулированных понятий раннего и позднего сроков наступления
событий следует, что для завершающего события
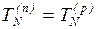 = Tкр. (1.9)
= Tкр. (1.9)
Напишем формулу для вычисления 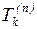 . Обозначим через
. Обозначим через  множество дуг (i,j), выходящих из i-й вершины, и допустим, что все значения
множество дуг (i,j), выходящих из i-й вершины, и допустим, что все значения 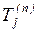 для j-х событий, которыми заканчивается
каждая из дуг, уже вычислены. Тогда на основании формул (1.8) и (1.9) можно
написать
для j-х событий, которыми заканчивается
каждая из дуг, уже вычислены. Тогда на основании формул (1.8) и (1.9) можно
написать
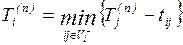 (1.10)
(1.10)
где 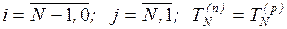 .
.
Вычисляя с помощью формулы (1.10) значения 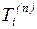 (вычисления ведутся
последовательно от завершающего события к исходному), получим для нашей
сетевой модели (рис. 1.3)
(вычисления ведутся
последовательно от завершающего события к исходному), получим для нашей
сетевой модели (рис. 1.3)
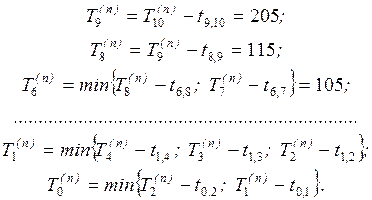
Зная ранние и поздние сроки наступления событий, можно вычислить
для каждой работы (i,j):
– ранний
срок начала 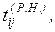
– ранний
срок окончания 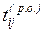 ,
,
– поздний
срок начала 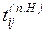 ,
,
– поздний
срок окончания 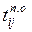 .
.
Первые два параметра – это самые ранние из возможных моментов
начала и окончания данной работы. Очевидно, что ранний срок начала работы
совпадает с ранним сроком наступления ее начального события, а ранний срок
окончания превышает его на величину продолжительности работы (i, j):
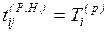 ; (1.11)
; (1.11)
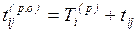 . (1.12)
. (1.12)
Вторые два параметра обозначают самые поздние из допустимых
моментов начала и окончания данной работы, при которых еще возможно выполнение
всех следующих работ без превышения критического времени. Поздний срок
окончания работы совпадает с поздним сроком наступления ее конечного события, а
поздний срок начала — меньше на величину tij
:
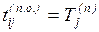 ; (1.13)
; (1.13)
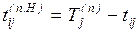 . (1.14)
. (1.14)
Важными параметрами сетевой модели являются резервы времени
событий и работ. Резервы времени существуют в сетевой модели во всех случаях,
когда имеется более одного пути разной продолжительности.
Резерв времени события R
– это такой промежуток времени, в пределах которого может меняться момент
наступления события без превышения критического времени. Величина Rk определяется как разность:
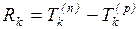 , (1.15)
, (1.15)
где k – номер
события.
Исходное, завершающее событие, а также все события, лежащие
на критическом пути, резервами времени не располагают. Отсюда простой способ
нахождения критического пути: определить события, не имеющие резерва времени,
через них и пройдет критический путь.
Для работ можно рассматривать различные виды резервов, из
которых наиболее важными являются:
– полный резерв
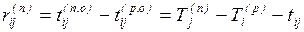 , (1.16)
, (1.16)
представляющий максимальное время,
на которое можно отсрочить начало или увеличить продолжительность работы (i,j), не изменяя срок наступления
завершающего события;
– свободный резерв
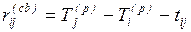 , (1.17)
, (1.17)
представляющий собой максимальное
время, на которое можно отсрочить начало или увеличить продолжительность
работы, не изменяя при этом ранние сроки наступления всех следующих событий.
Полный резерв времени работы принадлежит всему пути, на котором
эта работа лежит. Если этот резерв использовать полностью для увеличения
длительности данной работы или какой-либо другой работы данного пути, то
остальные работы пути останутся без резервов.
Работа может принадлежать нескольким путям одновременно.
Полный резерв времени этой работы принадлежит не только ей, а всем работам,
лежащим на проходящих через нее путях. При использовании этого резерва целиком
для одной работы резервы времени остальных работ, лежащих на пути максимальной
продолжительности, будут полностью исчерпаны, а резервы времени работ на
других путях соответственно сократятся.
Работы, у которых полный резерв отличается от полного резерва
критических работ (то есть от  ) не более чем на заданную величину d, называются
подкритическими. При небольших отклонениях в сроках выполнения подкритические
работы становятся критическими, поэтому при управлении комплексом нужно наряду
с критическими уделять особое внимание и подкритическим работам.
) не более чем на заданную величину d, называются
подкритическими. При небольших отклонениях в сроках выполнения подкритические
работы становятся критическими, поэтому при управлении комплексом нужно наряду
с критическими уделять особое внимание и подкритическим работам.
Множество всех критических и подкритических работ называют
критической зоной комплекса.
1.3. МЕТОДЫ
РАСЧЕТА ПАРАМЕТРОВ СЕТЕВОЙ МОДЕЛИ
Для расчета параметров сетевых моделей применяют следующие
три метода:
– метод
вычислений непосредственно на сетевом графике;
– матричный
метод,
– табличный
метод.
Все эти методы основываются на формулах (1.6), … (1.10) и отличаются
только процедурами вычислений.
Метод вычислений на
сетевом графике. Предварительно каждый кружок, изображающий вершину
графика (событие), делится на четыре сектора: в верхний сектор записывается
номер события k, в левый – значение Тk(p), в правый – Tk(n), а в нижний
– Rk = Tk(n) –Тk(p) (рис. 1.4).
Согласно формуле (1.6) ранний срок наступления данного события
определяется как сумма раннего срока непосредственно предшествующего события и
длины дуги (продолжительности работы), которая их соединяет. Если к событию
подходят две или большее число дуг, то вычисляют указанные суммы для каждой из
входящих дуг; максимальная из сумм и есть ранний срок наступления данного
события, который записывается в левый сектор. Расчет ведется последовательно от
исходящего события к завершающему.
Обратимся к рис. 1.4, на котором изображена та же сетевая модель,
что и на рис. 1.3. В левый сектор исходящего события сразу записывается
значение T0(p) = 0. Далее находим: к
событию 1 подходит одна дуга (0, 1), поэтому
T1(p) = 0+20 = 20; к событию 2
подходят две дуги (0, 2) и (1, 2), поэтому T2(p) = max{0+45; 20+0}=45, и
так далее Каждое вычисленное значение Tk(p)сразу
записывается в соответствующий сектор.
Поздний срок наступления данного события согласно формуле
(2.10) определяется как разность между поздним сроком непосредственно
следующего события и длиной дуги, которая их соединяет. Если из события выходят
две или большее число дуг, вычисляют указанные разности для каждой из выходящих
дуг; минимальная из разностей и есть поздний срок наступления данного события,
который записывается в правый сектор.
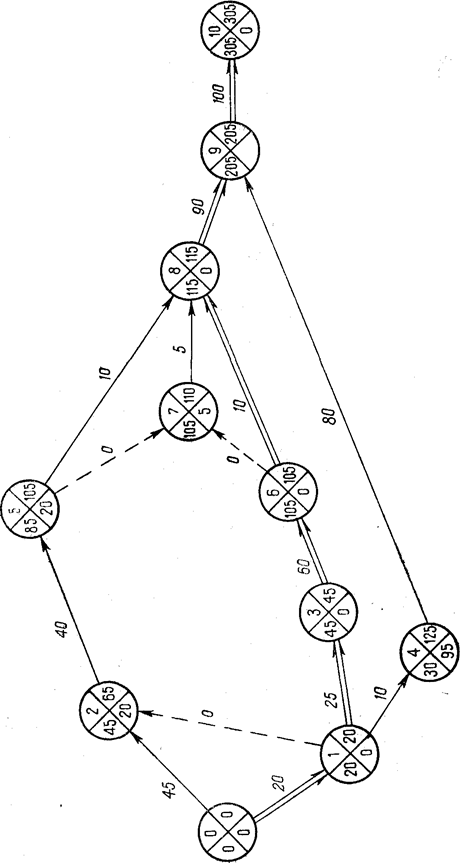
Поздний срок наступления завершающего события согласно
формуле (1.9) равен раннему сроку, эту величину записывают в правый сектор и
далее ведут расчет последовательно от завершающего события к исходящему.
Для нашего сетевого графика имеем T10(n)
= T10(p) =305. Далее находим: из событий 9, 8, 7 выходит по
одной дуге, поэтому T9(n) = 305–100 =205;
T8(n) =205–90=115; T7(n) =115–5=110;
из события 6 выходят две дуги (6,
7) и (6, 8), поэтому T6(n) = min{110–0; 115–10} =105
и так далее.
После того, как рассчитаны все значения Tk(n) вычисляют резервы времени событий как
разности между величинами, записанными в левых и правых секторах, и записывают
их в нижние секторы. Остальные параметры сетевой модели вычисляют, по формулам
(1.11)–(1.17). Результаты всех расчетов удобно представить в виде табл. 1.2.
Таблица 1.2.
|
Начальное
событие i
|
Конечное
событие j
|
Tij
|
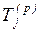
|
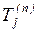
|
Rij
|
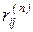
|
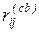
|
|
0
|
1
|
20
|
20
|
20
|
0
|
0
|
0
|
|
0
|
2
|
45
|
45
|
65
|
20
|
20
|
0
|
|
1
|
2
|
0
|
45
|
65
|
20
|
45
|
25
|
|
1
|
3
|
25
|
45
|
45
|
0
|
0
|
0
|
|
1
|
4
|
10
|
30
|
125
|
95
|
95
|
0
|
|
2
|
5
|
40
|
85
|
105
|
20
|
20
|
0
|
|
3
|
6
|
60
|
105
|
105
|
0
|
0
|
0
|
|
4
|
9
|
80
|
205
|
205
|
0
|
95
|
95
|
|
5
|
7
|
0
|
105
|
110
|
5
|
25
|
20
|
|
5
|
8
|
10
|
115
|
115
|
0
|
20
|
20
|
|
6
|
7
|
0
|
105
|
110
|
5
|
5
|
0
|
|
6
|
8
|
10
|
115
|
115
|
0
|
0
|
0
|
|
7
|
8
|
5
|
115
|
115
|
0
|
5
|
5
|
|
8
|
9
|
90
|
205
|
205
|
0
|
0
|
0
|
|
9
|
10
|
100
|
305
|
305
|
0
|
0
|
0
|
Критический путь проходит через события, для которых Rj=0
(0–3–6–8–9–10).
При расчете параметров сетевой модели непосредственно на
графике можно не нумеровать события так, чтобы выполнялось условие i<j
для любой дуги (i, j).
Матричный метод. Метод сводится к простым формальным операциям
над величинами tij без
необходимости обращаться к графику. Процедуру расчета рассмотрим на примере
сетевой модели, изображенной на рис. 1.3.
Представим сетевой график в виде матрицы смежности, но вместо
единиц запишем соответствующие значения tij.
В результате получим табл. 1.3 (в таблицу также записаны величины Ti(p) и Tj(n), которые еще
нужно вычислить).
Таблица 1.3
|
 j
j
i
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Ранний
срок
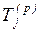
|
|
0
|
|
20
|
45
|
|
|
|
|
|
|
|
|
0
|
|
1
|
|
|
0
|
25
|
10
|
|
|
|
|
|
|
20
|
|
2
|
|
|
|
|
|
40
|
|
|
|
|
|
45
|
|
3
|
|
|
|
|
|
|
60
|
|
|
|
|
45
|
|
4
|
|
|
|
|
|
|
|
|
|
80
|
|
30
|
|
5
|
|
|
|
|
|
|
|
0
|
10
|
|
|
85
|
|
6
|
|
|
|
|
|
|
|
0
|
10
|
|
|
105
|
|
7
|
|
|
|
|
|
|
|
|
5
|
|
|
105
|
|
8
|
|
|
|
|
|
|
|
|
|
90
|
|
115
|
|
9
|
|
|
|
|
|
|
|
|
|
|
100
|
205
|
|
10
|
|
|
|
|
|
|
|
|
|
|
|
305
|
|
Поздний
срок 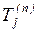
|
0
|
20
|
65
|
45
|
125
|
105
|
105
|
110
|
115
|
205
|
305
|
|
Таблица может быть составлена как по сетевому графику, так и
по упорядоченному перечню событий и работ.
Правило определения раннего срока событий вытекает из выражения
(1.6) и формулируется следующим образом: ранний срок события с номером j,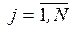 равен сумме элемента
матрицы tij с ранним
сроком предшествующего события, причем, если предшествующих событий несколько,
то берется максимальная из сумм, результат записывается в строку с номером i=j.
равен сумме элемента
матрицы tij с ранним
сроком предшествующего события, причем, если предшествующих событий несколько,
то берется максимальная из сумм, результат записывается в строку с номером i=j.
Так как ранний срок нулевого события равен нули, то сразу записывают
в нулевую строку значение T0(p) =0. Дальше последовательно
просматриваются столбцы (последующие события), начиная с первого (j=1). Из матрицы видим, что событие 1
связано только с одним предшествующим событием, а именно – с нулевым, причем t0,1=20. Складываем t0,1 со значением Т0(p) = 0, записанным в столбце Тi(p) по нулевой строке, а результат t0,1+T0(p) =
20 записываем в первую строку в столбец Тi(p).
Это и будет значение T1(p).
Переходим ко второму столбцу (j=2). Событие 2 связано с двумя предшествующими событиями: 0 и 1,
причем t0,2=45; t1,2=0.
Составляем две суммы t0,2+
Т0(p) = 45+0=45; t1,2+T1(p) =
0+20 = 20 и большую записываем во вторую строку в столбец Тi(p).
Рассмотрим еще восьмой столбец (j=8). Событие 8 связано с тремя предшествующими событиями 5, 6 и 7.
Составляем суммы 10+85=95; 10+105=115; 5+105=110 и в восьмую строку в столбец Тi(p) записываем наибольшую, равную 115.
Правило вычисления позднего срока события следует из выражения
(2.10) и формулируется следующим образом: поздний срок события с номером i, 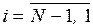 определяется путем вычитания элемента матрицы tij из позднего срока
последующего события, причем, если последующих событий несколько, то берется
минимальная из разностей; результат записывается в столбец с номером j=i.
определяется путем вычитания элемента матрицы tij из позднего срока
последующего события, причем, если последующих событий несколько, то берется
минимальная из разностей; результат записывается в столбец с номером j=i.
Вычисления начинают с завершающего события и сразу записывают
в столбец для j=N величину TN(n)= ТN(p).
В нашем случае в столбец для j=10 записывают
Т10(n) =305. Теперь просматриваем последовательно строки,
начиная с N–1 (в нашем случае девятой).
Из таблицы видно, что событие 9 связано с одним последующим событием 10,
причем t9,10=100. Вычитаем
согласно правилу из T10(n)=305 величину t9,10=100 и разность, равную
205, записываем в девятый столбец в строку Тj(n).
Это и будет величина T9(n)=205.
Переходим к следующей, восьмой строке (i=8). Событие 8, как видно из матрицы, связано с одним последующим
событием 9, причем t8,9=90.
Составим разность 205–90=115 и результат запишем в восьмой столбец в строку Tj(n).
Рассмотрим пятую строку. Событие 5 связано с двумя последующими
событиями 7 и 8, а соответствующие элементы матрицы t5,7=0 и t5,8=10. Составляем две разности 110–0=110;
115–10=105 и меньшую из них запишем в пятый столбец в строку Tj(n). Это и будет
T5(n)=105
Остальные параметры вычисляют по формулам (1.11) – (1.17),
записывают их в табл. 1.2 и определяют критический путь.
Табличный метод в принципе не отличается от изложенных методов
и преимуществ перед ними не имеет.
Теперь обратимся к сетевым моделям, у которых продолжительности
работ являются случайными величинами. В этом случае продолжительность
критического пути также является случайной величиной; сохраним за ней
обозначение Ткр. Исходная
информация таких моделей содержит сеть, законы распределения вероятностей величин
tij (или вероятностные
оценки aij, bij,
mij) и (но не обязательно)
директивный срок наступления завершающего события Тдир.
Основными задачами анализа этих моделей являются:
– определение среднего значения и дисперсии критического
времени Tкр;
– определение закона распределения величины Tкр;
– определение таких сроков наступления событий, которые с заданной
вероятностью не будут превышены;
– определение законов распределения для моментов наступления
событий;
– определение вероятности прохождения критического пути через
данную работу или совокупность работ.
Существующие аналитические методы решения перечисленных
задач весьма громоздки и не нашли практического применения. Более широкое применение
получил метод статистических испытаний.
Далее излагается практически удобный для расчетов метод вероятностной
оценки наступления завершающего события. Необходимо подчеркнуть, что
вероятностный анализ для завершающего события особенно важен, поскольку для
продолжительности выполнения комплекса, как правило, устанавливается
директивный срок и характер распределения случайного реального завершения комплекса
работ по отношению к директивному сроку может существенно влиять на принятые
решения при управлении выполнением комплекса.
Рассмотрим следующие задачи вероятностного анализа свершения
завершающего события:
– определить вероятность того, что продолжительность критического
пути (выполнения комплекса работ) Tкр
лежит в заданных пределах 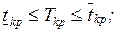
– определить вероятность того, что продолжительность критического
пути не превысит заданный директивный срок;
– определить такой директивный срок, который с заданной вероятностью
не будет превышен.
В методе приняты некоторые допущения, из которых выделим два
основных:
1. Дисперсия Dкр
величины критического времени зависит только от дисперсий работ, лежащих на
критическом пути.
2. Величина Tкр
распределена по нормальному закону. Это допущение основывается на предположении,
что число работ критического пути достаточно велико и что продолжительности
этих работ являются независимыми случайными величинами. Согласно центральной
предельной теореме сумма достаточно большого числа независимых случайных
величин, сравнимых по дисперсии, приближенно распределена по нормальному закону.
Расчет для всех задач начинается с вычисления
математических ожиданий 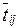 продолжительностей tij для всех работ комплекса
по формуле (1.1) или (1.3). Затем, оперируя величинами
продолжительностей tij для всех работ комплекса
по формуле (1.1) или (1.3). Затем, оперируя величинами 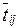 как детерминированными:
как детерминированными:
– вычисляют продолжительность критического пути 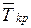 , представляющую собой математическое ожидание случайной
величины Tкр;
, представляющую собой математическое ожидание случайной
величины Tкр;
– определяют критический путь Lкр;
– вычисляют
дисперсии Dij
продолжительностей работ, лежащих на критическом пути, по формуле (1.2) или
(1.4);
– на основании известной теоремы, что дисперсия
суммы независимых величин равна сумме дисперсий слагаемых, находят дисперсию продолжительности
критического пути
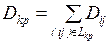 . (1.18)
. (1.18)
Теперь при сделанных допущениях можно решить первую из
перечисленных выше задач, а именно – определить вероятность того, что продолжительность критического пути лежит в заданных
пределах 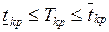 : |
: |
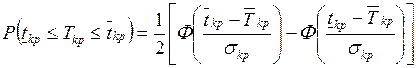 , (1.19)
, (1.19)
где 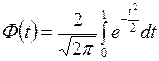 – функция Лапласа ;
– функция Лапласа ;
t – аргумент
функции Лапласа ;
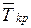 – математическое
ожидание случайной величины Ткр;
– математическое
ожидание случайной величины Ткр;
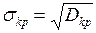 .
.
Перейдем ко второй задаче. Согласно принятому допущению случайная
величина Ткр распределена
по нормальному закону, поэтому на основании правила трех сигм можно написать
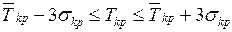 . (1.20)
. (1.20)
Очевидно, что директивный срок должен лежать в тех же пределах:
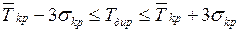 . (1.21)
. (1.21)
Действительно, если  то вероятность выполнения
комплекса работ равна нулю; если же взять
то вероятность выполнения
комплекса работ равна нулю; если же взять 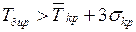 то без оснований будет
растянут срок выполнения комплекса.
то без оснований будет
растянут срок выполнения комплекса.
Кроме того, должно выполняться условие
Ткр < Тдир. (1.22)
Из неравенств (1.20), (1.21), (1.22) следует, что
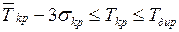 (1.23)
(1.23)
Теперь можно найти решение второй задачи – определить вероятность
того, что продолжительность критического пути не превысит заданный директивный
срок. Искомую вероятность получим из выражения
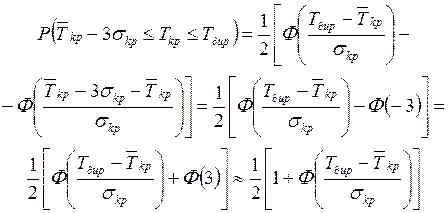 (1.24)
(1.24)
так как Ф(3) =0,9973.
Третью задачу можно решить следующим образом. С учетом заданной
вероятности Р3 перепишем выражение (1.24) в виде
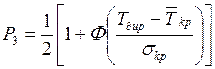 . (1.25)
. (1.25)
По известным величинам Р3, 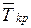 и sкр
можно определить с помощью таблиц функции Лапласа величину Тдир, удовлетворяющую уравнению (1.25).
и sкр
можно определить с помощью таблиц функции Лапласа величину Тдир, удовлетворяющую уравнению (1.25).
Недостаток метода состоит в том, что анализ проводится лишь
для одного критического пути. Но при случайных длительностях tij совокупность работ,
составляющих критический путь, также является случайной и может не совпадать с
совокупностью работ анализируемого критического пути. Возможность таких
несовпадений возрастает, если имеются полные пути, продолжительность которых
незначительно отличается от продолжительности критического пути. Поэтому для
принятия эффективных решений необходимо иметь надежные вероятностные оценки длительности
работ комплекса.
2 Вероятностные модели систем
2.1.
ОРИЕНТИРОВАННЫЙ ГРАФ СОСТОЯНИЯ СИСТЕМЫ.
МАРКОВСКИЕ ПРОЦЕССЫ.
Вероятностные (стохастические) модели используются
для исследования таких систем, процесс функционирования которых определяется
случайными факторами. Учет случайных факторов является обязательным при
исследовании процессов применения, эксплуатации, ремонта и обеспечения
технических комплексов, при оценке их эффективности, разработке
автоматизированных систем управления, обосновании технических требований к системам и так
далее.
Мощным средством разработки и исследования вероятностных
моделей является аппарат теории марковских случайных процессов в развитие
которого внесли большой вклад русские и советсткие ученые А.А.Марков,
А.Я.Хинчин, А.Н.Колмогоров, Б.В.Гнеденко, И.Н.Коваленко, Н.П.Бусленко,
Ю.В.Прохоров и многие другие.
В данной главе рассматриваются дискретные системы с непрерывным
временем. Возможные состояния такой системы S0, S1, S2, … можно перечислить (перенумеровать), а переход ее
из одного состояния в другое возможен в любой, наперед неизвестный, случайный
момент времени, причем этот переход осуществляется скачком (мгновенно). Число
состояний системы может быть как конечным, так и бесконечным (но счетным).
Множество S={S0, S1, S2,
…} возможных состояний системы и множество возможных ее переходов из одного
состояния в другое удобно представлять в виде ориентированнного графа (рис
2.1.), вершинам которого соответствуют состояния системы, а дугам – возможные
переходы, причем направление дуги указывает, из какого состояния и в какое
возможен переход системы. Процесс функционирования системы в данном случае
можно представить как случайное перемещение (блуждание) точки, изображающей
систему, по графу состояний. Характерной особенностью стохастических систем
является то, что для любого момента времени t
нельзя однозначно указать, в каком из состояний находится система, а можно
определить только распределение вероятностей для состояний, то есть определить
значения вероятностей Pk(t) того, что в момент времени система
находится в состоянии Sk..
Так как в любой момент времени t система обязательно находится в одном из возможных ее состояний,
то при t любом справедливо нормировочное
условие:
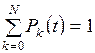 , (2.1)
, (2.1)
где N+1 – число возможных
состояний системы.
 Совокупность
функциональных соотношений и логических условий, позволяющих вычислить значение
вероятностей Pk(t) для k=0,N, и представляет собой
вероятностную модель системы.
Совокупность
функциональных соотношений и логических условий, позволяющих вычислить значение
вероятностей Pk(t) для k=0,N, и представляет собой
вероятностную модель системы.
Из изложенного следует, что при разработке модели системы
необходимо прежде всего определить
множество S ее возможных состояний
и дать описание законов, в соответствии с которыми она переходит из одного
состояния в другое.
Множество S можно определить, во-первых, как множество допустимых
комбинаций возможных состояний элементов системы. Важным при этом является
анализ и учет взаимосвязей между элементами системы.
Во-вторых, каждое состояние системы можно
охарактеризовать численными значениями одного или нескольких ее параметров,
т.е. множество возможных комбинаций численных значений параметров системы. Этот
подход более целесообразен, так как набор параметров, характеризующих состояние
системы, определяют не только исходя из природы системы, но и с учетом цели
проводимого исследования.
Оба указанных подхода не исключают, а наоборот, дополняют
друг друга, так как на основе анализа возможных состояний элементов системы
можно определить ее параметры.
Чтобы выявить и описать закономерности перехода системы из
одного состояния в другое, каждый переход удобно рассматривать как результат
воздействия на систему некоторого случайного потока событий.
Поток – это последовательность однородных событий, следующих
одно за другим в случайные моменты времени (например, поток отказов технических
систем, поток сообщений, поступающих в АСУ, и тому подобные).
Наиболее важными свойствами потоков являются : стационарность,
ординарность и отсутствие последействия.
Стационарность
потока означает, что его вероятностные характеристики не зависят от времени.
Важнейшей характеристикой потока является его интенсивность l – среднее число событий в единице времени. Для
стационарного потока l=const,
а для нестационарного l=l(t) – функция
времени.
Ординарность
потока означает практическую невозможность появления двух и более событий в
один и тот же момент времени.
Отсутствие
последействия означает, что события появляются в потоке независимо
друг от друга, т.е. вероятность появления определенного числа событий за
некоторый произвольно выбранный промежуток времени не зависит от того, сколько событий произошло раньше (не
зависит от предыстории изучаемого потока).
Поток событий, обладающий всеми тремя свойствами, называется
простейшим или стационарным пуассоновским потоком. Число событий пуассоновского
потока, попадающих на любой участок, распределено по закону Пуассона, то есть
вероятность попадания ровно k событий на участок (t0, t0+t)
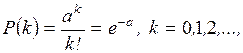 (2.2)
(2.2)
где а – среднее
число событий, приходящихся на участок t.
Для простейшего потока а=lt,
а для нестационарного пуассоновского
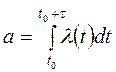 .
.
Определим закон распределения F(t) интервала времени
между событиями. Так как F(t) – вероятность того, что на участок
длительности t попадает хотя бы одно
событие, то
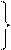 F(t)=
1–P(0)=1–e-lt (2.3)
F(t)=
1–P(0)=1–e-lt (2.3)
f(t) = F’(t)=
le-lt, t ³ 0.
Таким
образом, закон распределения интервалов времени между событиями простейшего
потока является экспоненциальным (показательным).
Математическое
ожидание Mt (средняя
длительность интервала между событиями), дисперсия Dt и среднее квадратическое отклонение st случайной величины, распределенной по показательному закону,
определяются соотношениями
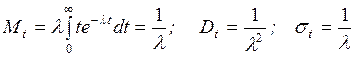 . (2.4)
. (2.4)
Экспоненциальное распределение обладает замечательным
свойством «не помнить о прошлом»: если рассматриваемый промежуток времен уже
«длился» некоторое время, то это никак не влияет на закон распределения
оставшейся части этого промежутка. Это означает, что вероятность появления
события в течение некоторого интервала времени не зависит от того, сколько
времени прошло после появления предыдущего события, а среднее время ожидания
этого события также не зависит от того, с какого момента времени мы его
ожидаем.
Простейшие потоки событий довольно часто встречаются на
практике, так как суммарный поток, образующийся при взаимном наложении
достаточно большого числа стационарных и ординарных потоков с последействием
(что часто имеет место на практике), является простейшим.
Из сказанного следует: если переход системы из состояния Si в состояние Sj происходит под
воздействием L простейших потоков интенсивности 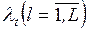 , то
, то
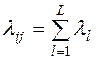 .
.
Таким образом, каждой дуге (i,j) графа состояний можно поставить в соответствие интенсивность
суммарного потока событий lij.
Такой граф называется размеченным, и ему соответствует квадратная матрица
интенсивностей переходов 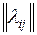 порядка (N+1, N+1),
причем
порядка (N+1, N+1),
причем 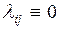 . Для размеченного графа состояний (рис 2.1) имеем
. Для размеченного графа состояний (рис 2.1) имеем
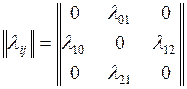 .
.
Можно
доказать следующее утверждение : если все потоки событий, переводящие систему
из состояния в состояние, пуассоновские, то процесс функционирования системы
представляет собой марковский процесс с непрерывным временем. Отличительной особенностью
марковского процесса является то, что вероятность любого состояния системы в
будущем зависит только от ее состояния в настоящем и не зависит от того, когда
и каким образом система пришла в это состояние. Понятие «марковский процесс»
ввел советский математик А.Н.Колмогоров в честь русского ученого А.А.Маркова
(1856–1922), внесшего большой вклад в теорию случайных процессов.
2.2. Уравнения
Колмогорова для вероятностей
состояний
Введем
обозначения:
Pk(t) – вероятность того, что система в
момент времени t находится в состоянии
Sk(k=0, 1, 2, …, N);
Pik(Dt) – условная вероятность того, что система, будучи в момент t в состоянии Si, за время перейдет в состояние Sk(k¹i).
Так как Pik(Dt) – вероятность появления хотя бы
одного события за время Dt, то
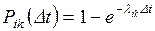 ,
,
где lik
– интенсивность потока событий, под воздействием которого система переходит из
состояния Si в состояние Sk .
Разлагая
показательную функцию в ряд Тейлора, имеем:
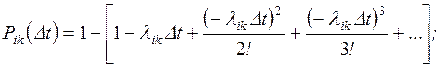
 . (2.5)
. (2.5)
Пусть
в момент времени t система находится
в одном из возможных состояний. Определим вероятность Pk(t+) того,
что в момент t+Dt
она будет находиться в состоянии Sk
(k=0,1,…,N).
Предположим,
что за время Dt
система может только один раз изменить свое состояние. Это означает, что
система может попасть в состояние Sk двумя способами.
1.
В момент t
система находилась в одном из состояний Si(i¹k),
которое соединено дугой (i, k) с состоянием Sk , а за время Dt
перешла в состояние Sk .
Вероятность этого события
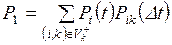 ,
где
,
где 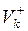 – множество дуг, заходящих в вершину Sk . Например, для состояния S1 (рис. 2.1)
– множество дуг, заходящих в вершину Sk . Например, для состояния S1 (рис. 2.1) 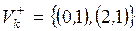 ,
P1=P0(t)P01(Dt)+P2(t)P21(Dt) .
,
P1=P0(t)P01(Dt)+P2(t)P21(Dt) .
2.
В момент t
система находилась в состоянии Sk и за время Dt
не вышла из него ни по одной из дуг, исходящих из вершины Sk.. Вероятность этого события
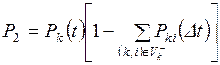 ,
где
,
где 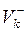 – множество дуг, исходящих из вершины Sk . Для
состояния S1 (рис. 2.1)
– множество дуг, исходящих из вершины Sk . Для
состояния S1 (рис. 2.1) 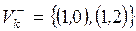 ,
P2=P1(t)[1–P10(Dt)–P12(Dt)]
,
где [P10(Dt)+P12(Dt)] – вероятность того, что система, будучи в момент
t в состоянии S1, за время Dt перейдет из него в состояние S0 или S2.
,
P2=P1(t)[1–P10(Dt)–P12(Dt)]
,
где [P10(Dt)+P12(Dt)] – вероятность того, что система, будучи в момент
t в состоянии S1, за время Dt перейдет из него в состояние S0 или S2.
Так как оба способа несовместны, то
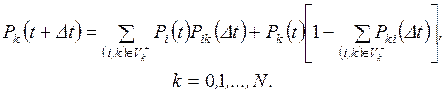 (2.6)
(2.6)
Перенесем
Pk(t) в левую часть и разделим все члены уравнения (2.6) на Dt, получим
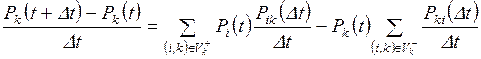 .
.
В
результате предельного перехода при Dt®0 с
учетом выражения (2.5) получим систему дифференциальных уравнений Колмогорова
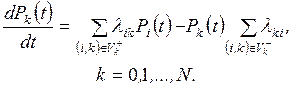 (2.7)
(2.7)
Уравнение (2.7) в отличие от
уравнения (2.6) является точным, так как члены, соответствующие двум и более
переходам системы за время Dt
и опущенные в выражении (2.6), в результате предельного перехода обращаются в
нуль. Действительно, пусть за время Dt
система может перейти из состояния Si
в состояние Sk через состояние
Sj. Условная вероятность
этого события с учетом формулы (2.5)
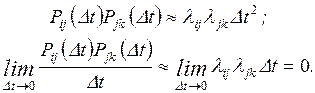
При записи правой части уравнения (2.7) целесообразно руководствоваться
мнемоническим правилом : «то, что втекает, прибавляется, а что вытекает –
вычитается».
Для рассматриваемого примера (рис 2.1) уравнения Колмогорова
имеют вид (читателю рекомендуется записать их самостоятельно)
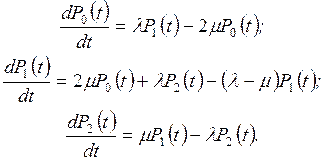
Интегрируя систему линейных дифференциальных уравнений (2.7)
с учетом условия нормировки (2.1) при заданных начальных условиях (например, Pk(0)=1, а для всех i ¹
k
Pi(0)=0 – в начальный момент система находится в
состоянии Sk), можно
определить распределение для вероятностей состояний системы в любой момент
времени.
На практике часто наибольший интерес представляет поведение
системы в установившемся режиме при t®¥.
Здесь сразу же возникает вопрос, как поведут себя вероятности Pk(t) при t®¥,
стремятся ли они к каким либо пределам, существует ли в системе некоторый установившийся
(стационарный) режим.
Предельные вероятности 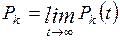 существуют и не зависят
от начального состояния системы, если граф ее состояний конечен и существует
маршрут между любой парой его вершин, то есть система может перейти из каждого
состояния в любое другое за конечное число шагов. Такие системы называют
эргодическими.
существуют и не зависят
от начального состояния системы, если граф ее состояний конечен и существует
маршрут между любой парой его вершин, то есть система может перейти из каждого
состояния в любое другое за конечное число шагов. Такие системы называют
эргодическими.
Предельная вероятность Pk – это
средняя доля времени, в течение которого система находится в состоянии Sk . Если, например, Pk=0,3, то это означает, что в состоянии Sk система времени ее функционирования.
Для вычисления предельных вероятностей в уравнениях (2.7)
производные приравнивают нулю и получают систему линейных алгебраических
уравнений
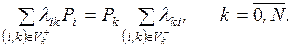 (2.8)
(2.8)
Так
как система (2.8) однородна, то при вычислении вероятностей Pk одно из уравнений (2.8) заменяют нормировочным
условием
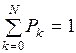 .
.
При
аналитическом исследовании удобно использовать следующий способ решения системы
(2.8): сначала все предельные вероятности выражают через какую-либо одну, а
затем их подставляют в условие нормировки.
2.3. Системы массового обслуживания
(СМО)
2.3.1. Общая характеристика СМО
Основными признаками реальной системы, позволяющими рассматривать
ее как своеобразную СМО, являются :
– наличие
объектов, нуждающихся в случайные моменты времени в обслуживании (в выполнении
некоторых работ над собой или для себя); эти объекты порождают так называемый
входящий поток заявок (требований) на обслуживание;
– наличие
объектов, которые производят обслуживание и называются обслуживающими приборами
(каналами);
– возникновение
задержек в обслуживании (образование очереди).
В качестве своеобразных СМО могут рассматриваться: системы
связи и ремонта; пункты технического обслуживания; вычислительные центры и
отдельные ЭВМ: автоматизированные производственные цехи, поточные линии; транспортные
системы; системы материального обеспечения.
Для задания СМО необходимо указать: входящий поток заявок,
множество обслуживающих приборов и дисциплину обслуживания.
При аналитическом исследовании СМО чаще всего предполагают,
что входящий поток – простейший поток событий интенсивности l. Часто заявку отождествляют с ее материальным
носителем : поток приборов, агрегатов, машин, поступающих на ремонт; поток
отчетов, поступающей в вычислительный центр и так далее
Обслуживающий прибор (канал) – это материальный объект или
совокупность объектов, одновременно участвующих в обслуживании заявки. В каждый
момент времени прибор может обслуживать только одну заявку.
Основным параметром обслуживающего прибора является среднее
время обслуживания одной заявки 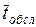 или производительность
прибора
или производительность
прибора 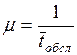 . Под временем обслуживания tобсл всегда будем понимать время от момента начала
обслуживания заявки до момента готовности прибора к обслуживанию очередной
заявки.
. Под временем обслуживания tобсл всегда будем понимать время от момента начала
обслуживания заявки до момента готовности прибора к обслуживанию очередной
заявки.
При аналитическом исследовании СМО обычно полагают, что tобсл – случайная величина,
распределенная по показательному закону, то есть
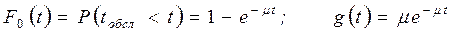 .
.
Таким образом, каждый обслуживающий прибор при непрерывной
работе порождает поток обслуженных заявок интенсивности m.
Отсутствие последействия в данном случае означает, что вероятность
завершения обслуживания заявки в любой момент времени не зависит от того,
сколько времени оно уже продолжалось.
В зависимости от числа обслуживающих приборов и характера взаимосвязи между ними
в процессе обслуживания заявок различают одноканальные и многоканальные,
однофазные и многофазные системы.
Обобщенная схема однофазной многоканальной СМО изображена на
рис. 2.2, где.сплошной стрелкой показан
входящий поток, кружками – заявки,
ожидающие обслуживания в очереди, а штриховыми стрелками – возможные пути движения заявок. В этой системе все обслуживающие
приборы (П1, П2.,. . ., Пn.) выполняют однородные операции обслуживания и
работают параллельно. Заявка считается обслуженной системой, если она обслужена
одним из ее приборов.
Если обслуживание заявки должно осуществляться последовательно
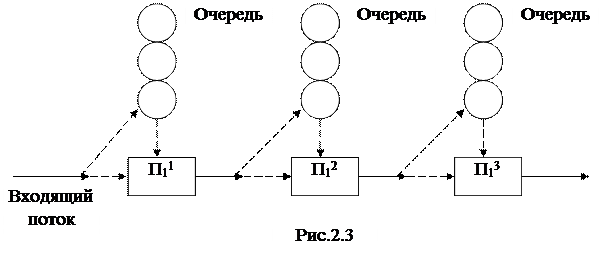
несколькими приборами, то такие системы называются многофазными. Схема
одноканальной многофазной (трехфазной) СМО изображена на рис. 2.3. Заявка считается обслуженной системой,
если она прошла все фазы обслуживания. Типичными примерами многофазных СМО
являются технологические потоки сборки (ремонта) приборов, агрегатов или машин.
Дисциплина обслуживания – это
совокупность правил поведения заявки от момента ее поступления в систему до
момента прекращения обслуживания. К основным правилам обслуживания относятся:
выбор свободного прибора, назначение очередной заявки на обслуживание и дисциплина
очереди.
Выбор свободного прибора может осуществляться:
– случайным образом (например, с равной вероятностью);
– в порядке нумерации
(наибольший или наименьший номер);
– в зависимости от
времени нахождения прибора в состоянии «свободен» (наименьшее или наибольшее
время).
В основе правил назначения очередной заявки на обслуживание
лежит или фактическое время ожидания, или остающаяся часть времени ожидания.
Частными случаями .являются:
– равновероятное поступление на обслуживание любой заявки из
очереди;
– строгая очередность – заявки к обслуживанию назначаются в порядке
поступления;
– обратная очередность – «последним
пришел – первым обслуживается».
Иногда назначение на обслуживание происходит по некоторой
системе приоритетов, (пенсионеры обслуживаются в первую очередь).
Дисциплина очереди определяет, в каких случаях заявка становится
в очередь и когда она покидает систему, и задается в виде ограничений,
накладываемых на параметры СМО: длина очереди (максимально допустимое число
заявок в очереди т), время ожидания
заявки в очереди tож или время
пребывания заявки в системе tc(tc= tож+tобсл).
Ограничение времени ожидания (пребывания) означает, что заявка
может ожидать обслуживания (находиться в СМО) какое-то время, не превышающее
некоторой случайной величины tож(tс).
Эти ограничения определяют поток заявок, уходящих из очереди
(системы) необслуженными. Обычно предполагают, что этот поток – простейший поток событий интенсивности
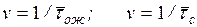 ,
,
где 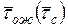 – среднее
допустимое время ожидания (пребывания). Следует подчеркнуть, что дисциплина
очереди не является чем-то внешним по отношению к заявкам. Наоборот, чаще всего
указанные ограничения определяются характером заявок.
– среднее
допустимое время ожидания (пребывания). Следует подчеркнуть, что дисциплина
очереди не является чем-то внешним по отношению к заявкам. Наоборот, чаще всего
указанные ограничения определяются характером заявок.
В зависимости от совокупности ограничений, накладываемых на
параметры СМО, различают:
– СМО с отказами – образование очереди не допускается; заявка,
заставшая все приборы занятыми, покидает систему;
– чистая СМО с ожиданием – любая заявка, поступившая в систему,
будет рано или поздно обслужена (на параметры СМО ограничения не накладываются);
– смешанные СМО – накладывается ограничение на один из параметров:
т – СМО
с конечной очередью; tож(tс)
– СМО с ограниченным временем
ожидания (пребывания) или одновременно на параметры т и tож(tс).
Главная задача исследования СМО – установление связи между параметрами системы (n – число каналов, m, l, m, v) и показателями
ее эффективности.
Для решения этой задачи прежде всего необходимо построить
математическую модель системы.
2.3.2. Математическая модель однофазной СМО
и показатели ее эффективности.
1. Математическая модель
Состояние однофазной СМО с абсолютно надежными обслуживающими
приборами в любой момент времени полностью определяется числом заявок k, находящихся в ней. Действительно, если k £ п, то k заявок
находятся на обслуживании, очереди нет; k приборов заняты обслуживанием
заявок, а n – k
приборов свободны. Если k > n, то все
приборы заняты (n заявок обслуживается), а k–п
заявок находится в очереди.
Величина k может принимать значения k=0, 1, 2, . . ., N, где N = n+m, причем для СМО с отказами m=0, а для систем с неограниченной очередью т и N ®¥.
Увеличение числа заявок в системе (переход из состояния Sk в состояние Sk+1) происходит под
воздействием потока заявок интенсивности l,
которая не зависит от k, то есть
lk,k+1 = l.
(2.9)
Уменьшение числа заявок в системе (переход из состояния Sk в состояние Sk–1)
происходит в общем случае под воздействием потока обслуживании интенсивности m и потока уходов заявок из очереди (системы)
интенсивности v, причем lk,k+1= f(k, n,
m, v),
а вид этой функции определяется типом СМО.
Из сказанного следует, что однофазной СМО соответствует граф
состояний (рис. 2.4), вершины которого (S0, S1, S2, . . .)
образуют последовательную цепочку и любые две соседние вершины соединены двумя
встречно направленными дугами, а процесс ее функционирования представляет собой
так называемый процесс «гибели и размножения» (уменьшение и увеличение числа
заявок).
Определим предельные вероятности состояний Рk, для СМО с конечным числом состояний. Для СМО Pk, – это
вероятность того, что в произвольный момент времени в системе находится ровно k заявок.
В СМО с конечным числом состояний всегда имеет место стационарный
режим, так как между любыми двумя вершинами графа существует маршрут.
Уравнения Колмогорова имеют вид:
– состояние S0
l10P1=l01P0 (2.10)
– состояние S1
l01P0+l21P2=l10P1+l12P1;
учитывая выражение (2.10),
получим
l21P2=l12P1 (2.11)
– состояние S2
l12P1+l32P3=l21P2+l23P2;
учитывая формулу (2.11),
имеем
l32P3=l23P2 (2.12)
— состояние Sk-1 (по аналогии)
lk,k-1Pk=lk-1,kPk-1
(2.13)
– состояние SN-1
lN-1,NPN-1=lN,N-1PN . (2.14)
Для состояния SN непосредственно по графу находим
уравнение
lN-1,NPN-1=lN,N-1PN ,
которое совпадает с уравнением (2.14).
Поэтому последнее уравнение исключаем из /рассмотрения, а
вместо него используем условие нормировки
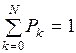 . (2.15)
. (2.15)
Для решения системы уравнений
(2.10) – (2.15) выразим все вероятности 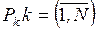 через Р0 и получим
через Р0 и получим
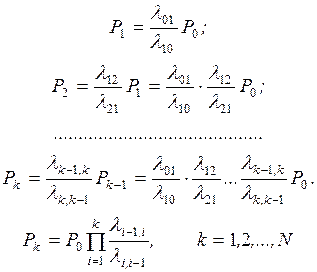 (2.16)
(2.16)
Подставляя значения Рд в формулу (2.15), получим
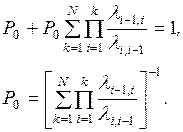 (2.17)
(2.17)
Обратим внимание на структуру формул (2.16) и (2.17). В формуле (2.16) имеем произведение отношений
интенсивностей перехода слева направо к интенсивностям перехода справа налево
для всех переходов между начальной и рассматриваемой вершинами графа состояний.
В формуле (2.17) имеем сумму этих
произведений, вычисленных для всех вершин графа 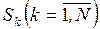 .
.
Подставляя в формулы (2.16)
и (2.17) значения интенсивностей
переходов li,i-1 и li-1,i для
СМО любого типа, можно рассчитать вероятности ее состояний и определить
показатели, эффективности.
2. Показатели эффективности.
Эффективность СМО характеризует ее приспособленность к выполнению
задач по обслуживанию заявок. Показатель эффективности – это количественная мера эффективности, определяющая степень
соответствия результатов функционирования СМО целям (задачам), стоящим перед
системой.
Рассмотрим наиболее часто используемые показатели эффективности
СМО.
1. Вероятность отказа
в обслуживании Ротк – вероятность того, что поступившая в систему
заявка не будет обслужена. Это очень важный показатель для СМО.
Абсолютная пропускная способность СМО Q – это среднее число заявок, обслуживаемых
системой в единицу времени. Для оценки потенциальных возможностей СМО по
обслуживанию заявок используется номинальная пропускная способность системы
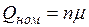 .
.
3. Относительная
пропускная способность q – это средняя доля заявок,
обслуживаемых системой:
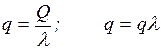 . (2.18)
. (2.18)
Величину q можно определить и
через Ротк. Действительно,
Ротк – средняя доля времени, в течение которого
заявки получают отказ, а следовательно, и средняя доля заявок, не принимаемых
системой на обслуживание, то есть.
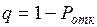 . (2.19)
. (2.19)
4. Среднее число занятых приборов
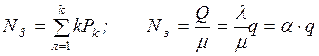 , (2.20)
, (2.20)
где 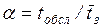 – параметр
обслуживания (среднее необходимое число обслуживающих приборов).
– параметр
обслуживания (среднее необходимое число обслуживающих приборов).
Производными от данного показателя являются коэффициент занятости
(загрузки) приборов Kз и коэффициент их простоя
Kп:
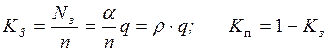 , (2.21)
, (2.21)
где r – номинальный коэффициент загрузки приборов.
5. Средняя длина очереди L – математическое
ожидание числа заявок, ожидающих обслуживания. Производным от показателей Nз и L является среднее число заявок,
находящихся в системе,
Y=Nз+L. (2.22)
6. Среднее время ожидания обслуживания 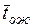 – математическое ожидание времени пребывания заявки в
очереди.
– математическое ожидание времени пребывания заявки в
очереди.
7. Среднее время
пребывания заявки в системе
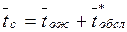 , (2.23)
, (2.23)
где
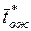 – среднее время от момента начала обслуживания до
момента окончания обслуживания (
– среднее время от момента начала обслуживания до
момента окончания обслуживания (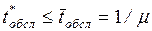 ).
).
8. Экономическая
эффективность СМО может быть оценена средней прибылью, получаемой в единицу
времени при функционировании системы :
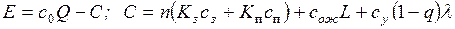 ; (2.24)
; (2.24)
где c0 – прибыль, получаемая при обслуживании заявки;
c – функция стоимости
потерь; cз – стоимость эксплуатации
прибора в единицу времени; сп — стоимость единицы времени простоя прибора; сож – стоимость потерь, связанных с простаиванием заявка в очереди в
единицу времени; сy – стоимость убытков, связанных с уходом
заявки из системы.
Выбор показателя для оценки эффективности конкретной СМО определяется
как особенностями системы (ее типом) и ее назначением, так и задачами проводимого
исследования.
Определим показатели эффективности для СМО рассматриваемых
типов, при этом сначала рассмотрим систему с конечной очередью, а затем
полученные результаты используем при анализе других систем.
2.3.3. СМО с конечной очередью
СМО с конечной очередью длины т характеризуется тем, что при поступлении очередной заявки
возможны три исхода:
– заявка немедленно
принимается на обслуживание, если в системе в данный момент находится k заявок и k<n;
– заявка становится в очередь, если п £ k<n+m;
– заявка получает отказ и покидает систему, если k=n+m. Следовательно,
в любой момент времени система может находиться в одном из п+т+1 состояний, то есть множество
состояний 
Увеличение числа заявок в системе происходит только под воздействием
потока заявок интенсивности l, а уменьшение числа заявок в системе — только в результате завершения обслуживания
одной из заявок, то есть
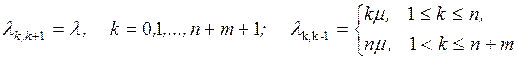
(k
занятых приборов порождают поток обслуженных заявок интенсивности k m).
Размеченный граф состояний СМО с конечной очередью для п=3, т=2 изображен на
рис. 2.5.
Для определения вероятностей состояний системы в формулы (2.16) и (2.17)
подставим значения
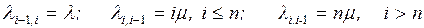
и получим:
–
для k£n
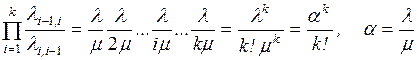 ;
;
–
для k<n
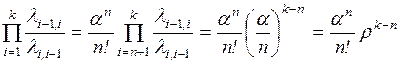 .
.
Полагая в уравнении (2.17)
N=n+m, находим
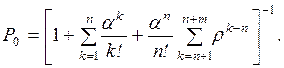 (2.25)
(2.25)
Учитывая, что a0/0!=1
и вычисляя сумму т членов геометрической
прогрессии со знаменателем r,
находим
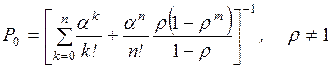 (2.26)
(2.26)
Из уравнения (2.16)
находим вероятности состояний
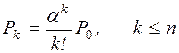 ; (2.27)
; (2.27)
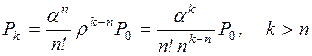 (2.28)
(2.28)
На основании формул (2.25) –
(2.28) определим основные показатели эффективности системы.
1. Вероятность отказа
в обслуживании – это вероятность того, что в СМО имеется п+т заявок, то есть
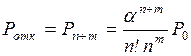 (2.29)
(2.29)
Зная Ротк
по формулам (2.19) – (2.21), можно
вычислить абсолютную и относительную пропускную способность системы, среднее
число занятых приборов, коэффициенты их загрузки и простоя.
2. Вероятность того,
что поступившая в систему заявка застанет все каналы занятыми (не будет
немедленно принята на обслуживание),
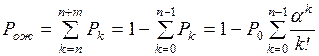 . (2.30)
. (2.30)
3. Средняя длина
очереди
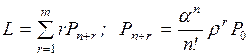 ,
,
где Pn+r – вероятность того, что в очереди
находится ровно r заявок (k=n+r).
Подставляя в полученное выражение Pn+r,
находим
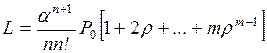 ; (2.31)
; (2.31)
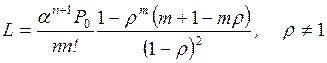 . (2.32)
. (2.32)
4. Среднее время
ожидания в очереди определяется как математическое ожидание. Если к моменту
поступления заявки в очереди находится r=0, 1, . . ., т–1
заявок, то она поступит на обслуживание после завершения обслуживания r+1 заявок, то есть
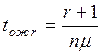 ;
;
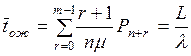 . (2.33)
. (2.33)
Среднее время ожидания
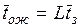 – это среднее
время накопления очереди длиной L.
– это среднее
время накопления очереди длиной L.
Среднее число заявок, находящихся в СМО, и среднее время
пребывания заявки в системе определяются по формулам (2.22) и (2.23) с учетом
формул (2.31) – (2.33).
Из полученных соотношений следует, что показатели Ротк, q, Nз, L, Y не зависят от конкретных значений l
и m, а только от их соотношения
a. Показатели 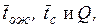 напротив,
чувствительны к изменению не только параметра a,
но и к изменению l при a=const.
Так, например, при увеличении l
и m в два раза Ротк, q, nз и L не изменяются, Q увеличивается, а
напротив,
чувствительны к изменению не только параметра a,
но и к изменению l при a=const.
Так, например, при увеличении l
и m в два раза Ротк, q, nз и L не изменяются, Q увеличивается, а 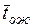 уменьшается в два
раза, то есть при одновременном увеличении плотности потоков заявок и
обслуживании характеристики процесса обслуживания улучшаются.
уменьшается в два
раза, то есть при одновременном увеличении плотности потоков заявок и
обслуживании характеристики процесса обслуживания улучшаются.
2.3.4. СМО с отказами
СМО с отказами является частным случаем СМО с конечной
очередью при m=0. Полагая в формулах (2.25) – (2.29) т=0, найдем показатели
эффективности СМО с отказами:
– вероятность простоя
всех обслуживающих приборов из выражения (2.26)
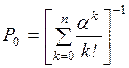 ; (2.34)
; (2.34)
– вероятность того,
что в системе находится k заявок, из формулы (2.27)
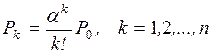 ; (2.35)
; (2.35)
– вероятность отказа в обслуживании из выражения (2.29)
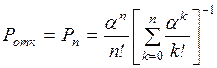 ; (2.36)
; (2.36)
– абсолютная и относительная пропускная способность системы
и среднее число занятых приборов
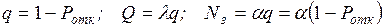 (2.37)
(2.37)
Зависимости (2.34) – (2.36)
были впервые получены датским инженером А.К.Эрлангом и поэтому известны как
формулы Эрланга.
Советский ученый Б.А.Севастьянов доказал, что формулы Эрланга
справедливы при любом законе распределения времени обслуживания, но при
конечном и постоянном значении его математического ожидания. Это позволяет
использовать соотношения (2.34) – (2.37)
для решения широкого класса практических задач.
2.3.5. Чистая СМО с ожиданием.
Чистая СМО с ожиданием характеризуется тем, что любая заявка,
поступившая в систему, будет обязательно обслужена (Ротк=0).
Вероятности состояний для этой системы можно получить из уравнений (2.25) – (2.28) в результате предельного перехода
при т®¥.
Так как сумма 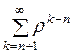 в формуле (2.25) сходится только при r<1, то в рассматриваемой системе стационарный
режим имеет место только при r<1;
если r£1, то очередь неограниченно возрастает. Так как
в формуле (2.25) сходится только при r<1, то в рассматриваемой системе стационарный
режим имеет место только при r<1;
если r£1, то очередь неограниченно возрастает. Так как
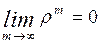 при r<1, то из выражения (2.26) находим
при r<1, то из выражения (2.26) находим
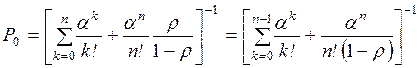 , (2.38)
, (2.38)
Вероятности состояний системы Рk, рассчитываются по формулам (2.27) и
(2.28), где Р0
вычисляется по формуле (2.38).
Показатели эффективности чистой СМО с ожиданием:
– относительная и
абсолютная пропускная способность системы из формулы (3.19) при Ротк=0
q=1; Q=l; (2.39)
– среднее число занятых каналов
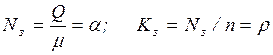 ; (2.40)
; (2.40)
– вероятность того, что заявка, поступившая в систему, будет
ожидать обслуживания, из формул (2.30) и (2.38)
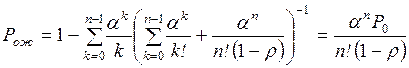 ; (2.41)
; (2.41)
– средняя длина очереди, как следует из формулы (3.32) при т®¥,
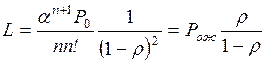 ; (2.42)
; (2.42)
– среднее время ожидания
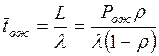 ; (2.43)
; (2.43)
– вероятность пребывания заявки в очереди более t единиц времени
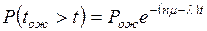 . (2.44)
. (2.44)
Методику вычисления рассмотренных показателей эффективности
СМО поясним на примере.
На пункте технического обслуживания (ПТО) оборудованы две линии
по обслуживанию техники. Время обслуживания одной единицы техники распределено
по показательному закону с параметром  Число единиц техники,
одновременно находящихся на ПТО, не должно превышать четырех единиц. Поток
техники на обслуживание простейший поток
заявок интенсивности l=0,5ед./ч. Определить показатели эффективности
работы ПТО.
Число единиц техники,
одновременно находящихся на ПТО, не должно превышать четырех единиц. Поток
техники на обслуживание простейший поток
заявок интенсивности l=0,5ед./ч. Определить показатели эффективности
работы ПТО.
Решение. Анализ
задачи показывает, что ПТО можно рассматривать как СМО с конечной очередью,
параметры которой n=2, m=2, l=0,5
ед./ч, m=0:5 ед./ч, a= 1, r=0,5.
Результаты вычислений для различных значений п и т
(различных вариантов организации ПТО) приведены в табл. 2.1.
Расчет показателей СМО целесообразно производить в последовательности,
указанной в таблице. Если r=1
(для п=1, m=3), то Р0 и L рассчитывают непосредственно по формулам (2.25) и (2.31).
Из полученных данных видно, что уменьшение п при постоянном значении п+т=4
позволяет значительно (в 1,7 раза)
повысить коэффициент загрузки линий Kз Однако
эффективность обслуживания техники значительно снизилась: при п=1 каждая пятая машина (Ротк=0,2) уходит с ПТО
необслуженной, а при n=2 только одна из 25 машин (Ротк=0,044)
получает отказ; среднее время пребывания машины на ПТО при n=1  , а при п=2
, а при п=2 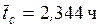 .
.
Таблица
2.1
|
Показатели
|
п=2, т= 2
|
п=1, т= 3
|
п=2, т=0
|
п=2, т®¥
|
|
Р0
|
0,348
|
0,2
|
0,4
|
0,333
|
|
Pож
|
0,304
|
0,8
|
–
|
0,333
|
|
Ротк
|
0,044
|
0.2
|
0,2
|
0
|
|
q =
1–Ротк
|
0,956
|
0,8
|
0,8
|
1,0
|
|
Q (ед./ч)
|
0,478
|
0,4
|
0,4
|
0,5
|
|
Nз (ед.)
|
0,956
|
0,8
|
0,8
|
1,0
|
|
Кз (%)
|
47,8
|
80
|
40
|
50
|
|
L (ед.)
|
0,174
|
1,2
|
–
|
0,333
|
|
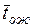 (ч) (ч)
|
0.348
|
2,4
|
–
|
0.666
|
Исключение очереди на ПТО (п=2,т=0) приводит к значительному возрастанию вероятности отказа
(с 0,044 до 0,2). Отсутствие ограничения на длину очереди (п=2, m®¥) несколько повышает
загрузку линий, однако приводит к увеличению времени ожидания почти в два раза
(с 0,348 до 0,666 ч). Для этого случая целесообразно определить вероятность
того, что число машин, одновременно находящихся на ПТО, превышает 4:
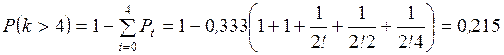 ,
,
то есть пятую часть времени на ПТО находится более четырех
машин одновременно.
Приведенный пример наглядно показывает важность сравнения
различных вариантов организации СМО и учета при синтезе СМО экономических
показателей.
2.3.6. Смешанные системы массового обслуживания
СМО с ограниченным временем ожидания характеризуется
тем, что уменьшение числа заявок в ней происходит как в результате завершения
обслуживания одной из заявок, так и в результате ухода заявок из очереди с
интенсивностью v.
Если число заявок в системе k<n, то lk,k-1= km..
Если в очереди имеется r заявок (k=n+r), то переход из состояния Sk в состояние Sk-1 осуществляется или в результате завершения
обслуживания одной из п заявок, или в
результате ухода из очереди одной из r
заявок, то есть
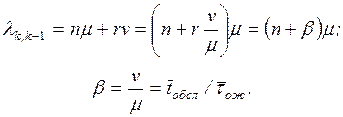
Таким образом, для СМО с ограниченным временем ожидания
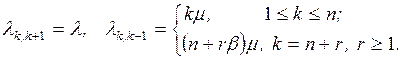 (2.45)
(2.45)
Граф состояний системы изображен на рис. 2.6 (п=2).
Подставляя выражения (2.45)
в формулы (2.16) и 2.17), как и в случае СМО с конечной очередью, получим
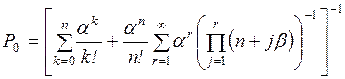 (2.46)
(2.46)
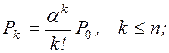 (2.47)
(2.47)
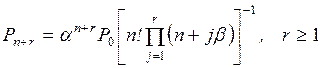 . (2.48)
. (2.48)
Определим основные показатели эффективности системы. Средняя
длина очереди
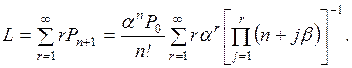 (2.49)
(2.49)
На каждую из L заявок, находящихся в
очереди, действует поток уходов интенсивности v, то есть
в среднем в единицу времени из очереди уходит Lv заявок.
Следовательно, абсолютная пропускная способность
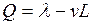 ; (2.50)
; (2.50)
относительная пропускная способность
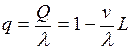 (2.51)
(2.51)
вероятность отказа в обслуживании
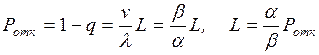 ; (2.52)
; (2.52)
среднее число занятых приборов
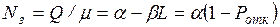 ; (2.53)
; (2.53)
вероятность того, что любая заявка будет обслужена,

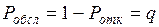 (2.54)
(2.54)
При вычислениях в формулах
(2.46) и (2.49) в качестве приближенного
значения для бесконечных сумм берется сумма конечного числа l–1
членов, а остаток оценивается следующим образом
:
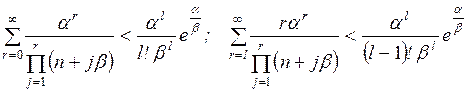 .
.
Из выражений (2.50) – (2.54)
следует, что основные показатели СМО можно вычислить через Ротк, причём для определения Ротк используют таблицы с
тремя входами: n, a, b.
СМО с ограниченным временем пребывания
характеризуется тем, что заявка может уйти необслуженной как из очереди, так и
после начала обслуживания. Интенсивность перехода данной системы из состояния Sk в Sk-1
(уменьшения числа заявок)
Подставляя выражения (2.9)
и (2.55) в формулы (2.16) и (2.17), можно
определить вероятности состояний данной системы.
Если одновременно накладывается ограничение на время ожидания
(пребывания) и длину очереди, то число состояний системы конечно и равно п+т+1,
а интенсивности переходов определяются формулами (2.45) или (2.55), в которых
r = 1,
2, . . ., т. Типичным
примером системы данного типа является вычислительное устройство, которое может
одновременно обрабатывать п сообщений
и имеет буферную память для хранения т
сообщений. Поток сообщений – простейший
поток интенсивности l,
время обработки одного сообщения 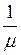 , информация теряет свою ценность через время
, информация теряет свою ценность через время 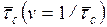 . Граф состояний для случая n=2, m=3 изображен на рис.
. Граф состояний для случая n=2, m=3 изображен на рис.  2.7.
2.7.
2.3.7. Особенности применения моделей массового обслуживания
Рассмотренные модели массового обслуживания находят широкое
применение при исследовании надежности технических систем, организации их
эксплуатации и использования по назначению, а также при анализе и синтезе
автоматизированных систем управления. Достаточно подробно вопросы практического
применения моделей СМО рассмотрены в работе
[1].
При решении прикладных задач необходимо прежде всего правильно
определить, насколько аппроксимирующие предположения, принятые при разработке
математических моделей СМО, приемлемы для реальной системы и каким образом ее
специфические особенности можно учесть в типовой модели.
Основными аппроксимирующими предположениями при разработке
моделей СМО были предположения о том, что все потоки событий являются
простейшими. Широкое использование указанных предположений обусловливается
следующими факторами.
1. Простейший поток
событий, как уже отмечалось, носит предельный характер и поэтому часто
встречается в практических задачах. Так, например, Н. М. Седякин показал, что
поток отказов элементов технических систем сводится к простейшему, если
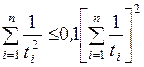 , (2.56)
, (2.56)
где ti – среднее время наработки i-го
элемента данного типа на отказ, а п – число
элементов. Если n>10, то это
условие выполняется и тогда, когда каждый из элементов отказывает через постоянные
интервалы времени.
2. Простейший поток
заявок ставит СМО в наиболее тяжелые условия. И. Н. Коваленко показал, что
система, рассчитанная на обслуживание простейшего потока, будет обслуживать
любой другой поток с одинаковой интенсивностью более надежно.
3. При простейшем
потоке заявок показатели эффективности СМО с отказами и ограниченным временем
ожидания практически не зависят от вида закона распределения времени
обслуживания, а определяются его средним значением. Показатели эффективности
реальной СМО при простейшем потоке заявок не хуже значений этих показателей,
вычисленных в предположении об экспоненциальном распределении времени обслуживания.
4. При указанных
предположениях можно получить аналитическую модель системы и на основе ее
исследования найти ее оптимальные параметры. Простая модель позволяет
разобраться в основных закономерностях явления, наметить «ориентиры» для построения
статистической модели системы, позволяющей учесть те особенности реальной
системы, которые трудно (или невозможно) учесть при аналитическом исследовании.
Сочетание простых аналитических моделей и статистического моделирования
вероятностных систем на ЭВМ — один из
основных методов современного научного исследования.
При решении прикладных задач всегда необходимо учитывать
возможность использования результатов исследования стационарного режима для
оценки эффективности системы на конечных интервалах времени. Характеристики
стационарного режима с достаточной для практики точностью можно использовать
для процессов длительностью (3¸4)×1/m [1].
При исследовании СМО предполагалось, что обслуживающие приборы
абсолютно надежны. Если вероятность успешного обслуживания заявки Р<1, то ее влияние на эффективность
СМО можно учесть через Pотк В этом случае
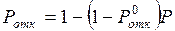 ,
,
где Р0отк — вероятность отказа для системы с
абсолютно надежными приборами (Р=1).
Все рассмотренные модели СМО относятся к классу так называемых
разомкнутых систем, в которые поступает неограниченный поток заявок и его
параметры не зависят от процесса обслуживания. Однако на практике часто
встречаются системы, когда поток заявок ограничен и его параметры зависят от
процесса обслуживания (замкнутые системы).
Типичным примером замкнутой системы является следующая
система. Имеется п ремонтных
мастерских, которые предназначены для обслуживания и ремонта т технических систем. Технические
системы отказывают только в период эксплуатации с интенсивностью l (в период ремонта l=0),
производительность каждой мастерской m.
Число возможных состояний данной системы
m+1 (k=0, 1, 2, ..., т – число технических систем, требующих
ремонта). Граф состояний данной системы для п=2, т=5
(рис. 2.8) свидетельствует о том, что
для ее исследования нельзя использовать ни одну из рассмотренных моделей СМО.
При ее исследовании необходимо непосредственно использовать выражения (2.16) и (2.17)
для процесса «гибели и размножения».
 Приведенный пример показывает, что при выборе модели СМО для решения конкретной
задачи ошибки можно исключить, если построить размеченный граф состояний. На
основе анализа размеченного графа состояний в некоторых случаях можно
установить, что для исследования системы, по формальным признакам не относящейся
к системам массового обслуживания, можно использовать одну из известных
моделей СМО.
Приведенный пример показывает, что при выборе модели СМО для решения конкретной
задачи ошибки можно исключить, если построить размеченный граф состояний. На
основе анализа размеченного графа состояний в некоторых случаях можно
установить, что для исследования системы, по формальным признакам не относящейся
к системам массового обслуживания, можно использовать одну из известных
моделей СМО.
При решении прикладных задач следует также всегда отличать
показатели эффективности L, 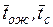 от ограничений,
накладываемых на параметры СМО: т,
от ограничений,
накладываемых на параметры СМО: т, 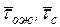 . Показатели
L,
. Показатели
L, 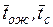 используются
для оценки эффективности СМО, а параметры т,
используются
для оценки эффективности СМО, а параметры т,
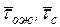 определяются
спецификой процесса обслуживания и физическими свойствами заявок (например,
емкость хранилищ в ремонтном органе, время старения информации и так далее).
определяются
спецификой процесса обслуживания и физическими свойствами заявок (например,
емкость хранилищ в ремонтном органе, время старения информации и так далее).
Задачи, решаемые с помощью моделей СМО, можно разделить на
два основных класса. К первому классу относятся задачи анализа эффективности
систем и определения числа обслуживающих приборов, обеспечивающих требуемые
значения показателей ее эффективности. Ко второму классу относятся задачи
определения числа и типа (производительности) обслуживающих приборов.
3 Управление запасами
3.1. Системы управления запасами
Важнейшим условием успешного функционирования экономических,
технических систем различного назначения является своевременное обеспечение их
соответствующими материальными ресурсами (товарами, сырьем, комплектующими
элементами, горюче-смазочными материалами, транспортными средствами и так
далее). Качественное решение этой задачи предполагает создание запасов. Это
обусловливается тем, что в большинстве случаев либо физически невозможно, либо
экономически нецелесообразно полностью совмещать объем и сроки поставки
материальных ресурсов с моментами возникновения потребности в них. Первый
случай имеет место тогда, когда расход ресурса носит случайный характер, а
пополнение возможно только в дискретные моменты времени или длительность интервала
между моментом подачи заявки на материальные ресурсы и моментом их поступления
представляет случайную величину. Второй случай имеет место тогда, когда затраты
на поставки ресурсов соизмеримы с затратами на создание запасов, их хранение и
обслуживание.
Создание запасов связано с дополнительными затратами и поэтому
вступает в противоречие с требованием своевременного обеспечения потребителей
материальными ресурсами. Необходимость разрешения этого противоречия и
стимулировала развитие теории управления запасами, которая изучает системы,
связанные с накоплением, расходованием и пополнением материальных ресурсов и
называемые системами управления запасами (СУЗ).
СУЗ – это совокупность баз сосредоточения запасов (складов,
пунктов хранения) и обслуживающих организации подразделений, связанных между
собой линиями связи и транспортными средствами. При анализе и синтезе СУЗ
необходимо учитывать: структуру системы и ее параметры, свойства предметов
запаса, характер спроса и характер пополнения.
Структура СУЗ –
это совокупность взаимосвязей и отношений между ее элементами. Она определяется
числом уровней, характером взаимосвязи между складами и организацией
управления.
По числу уровней различают однокаскадные и эшелонированные
(многокаскадные) системы. В однокаскадных системах непосредственно обслуживают
потребителе все склады, а в эшелонированных – только склады первого уровня.
Запас склада k-го уровня предназначен
для пополнения запасов склада k-1-го
уровня и может использоваться для обслуживания потребителей, если отсутствуют
запасы на складах низших уровней. Пополнение склада старшего уровня производится
из источника снабжения, который обладает неограниченным
запасом.
По характеру взаимосвязи между складами различных уровней различают системы с
линейной и пирамидальной (разветвленной структурой. В линейных системах (рис
3.1.) склад k-го уровня обслуживает
один склад уровня, а в пирамидальных (рис 3.2.) – несколько складов k-1-го уровня.
По характеру взаимосвязи между складами одного уровня различают
системы с разрешенным и запрещенным обменом запасами.
Управление в
СУЗ может быть децентрализованным и централизованным. В первом случае заказы
подаются в направлении, обратном движению запасов, а во втором – вся информация
о наличии запасов, их расходовании и пополнении сосредоточиваются в едином
центре управления, из которого поступают указания о перемещении запасов.
Централизованное управление характерно для автоматизированных СУЗ.
Предметы запасов.
В зависимости от количества хранимых на складах номенклатур различают
однономенклатурные и многономенклатурные системы. В последнем случае необходимо
учитывать наличие «взаимосвязи» между номенклатурами (изделия разных типов
могут заменять друг друга, дополнять друг друга и так далее). Своеобразной
формой «взаимосвязи» между номенклатурами является наличие в СУЗ предметов
запаса в различной степени готовности к удовлетворению заказов потребителей
(сырье, полуфабрикаты, частично собранные узлы, готовые к использованию
предметы запаса).
Важной характеристикой предметов запаса является стабильность
из свойств (параметров). Различают системы с наличием и отсутствием
естественной убыли запасов. Например, запасные элементы для технических систем
могут отказывать в период их хранения.
Спрос
характеризуется моментами времени, в которые он возникает и объемом. Каждая из
этих величин может быть либо детерминированной, либо случайной.
Детерминированность спроса определяется ролью случайных факторов в процессе
расходования материальных ресурсов. Если роль случайных факторов относительно невелика
(например, для завода с жесткой производственной программой), то спрос можно
считать детерминированным. В противном случае имеет место вероятностный спрос.
Как детерминированный, так и вероятностный спрос может быть стационарным или
нестационарным, непрерывным или дискретным.
Характер пополнения.
Системы, в которых предусматривается пополнение запасов, называют системами с
неограниченным запасом (источник снабжения неисчерпаем). Если пополнение не
предусматривается, имеем систему с ограниченным запасом.
При анализе процессов пополнения запасов необходимо учитывать
задержки поставки во времени относительно момента подачи заказа, способ
ликвидации недостач и тип стратегии управления запасами.
По первому признаку различают системы с мгновенной поставкой
(задержка отсутствует или пренебрежимо мала), с задержкой на фиксированный срок
и с задержкой на случайный интервал времени.
Недостачи ликвидируются или путем экстренной поставки из
уровня, в котором имеются требуемые предметы запаса, или источника снабжения,
или путем накопления заявок до очередной поставки.
Стратегия управления
запасами – это совокупность правил, в соответствии с которыми
определяется момент подачи заказа и его объем.. Определение стратегии
управления запасами и ее параметров является основной задачей теории управления
запасами.
По правилу определения момента заказа различают периодические
стратегии и стратегии с критическим уровнем. В первом случае заказ подается
через равные промежутки времени T
(период пополнения), а во втором – он подается, если в момент контроля объема
запасов текущий объем запаса
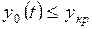 , где yкр –
минимально допустимый уровень запаса на складе.
, где yкр –
минимально допустимый уровень запаса на складе.
Объем заказа S
может быть постоянным или определяется по правилу
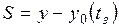 , (3.1)
, (3.1)
где y –
максимальный уровень запаса на складе; y0(t) – объем запаса на складе в момент tз подачи заказа
(отрицательные значения y0(tз) имеют смысл накопленного
дефицита).
Возможные комбинации этих правил определения момента заказа
и его объема дают четыре типа простейших стратегий.
Стратегия (T, S) –
периодическая с постоянным объемом заказа – не содержит элемента обратной связи
(ее параметры T и S не изменяются при изменении параметров
спроса). Нечувствительность к спросу определяет применимость данной стратегии
только в условиях стабильного спроса. Она соответствует нормативному снабжению.
 Стратегия
(T, S) – периодическая с пополнением
до максимального уровня. Объем заказа определяется правилом (3.1.) для tз
=T, 2T, 3T, … Эта стратегия
содержит элемент обратной связи (ее параметр S учитывает действительный расход
запасов). Реализация функции y0(t) для случая мгновенной поставки
отображена на рис. 3.3.
Стратегия
(T, S) – периодическая с пополнением
до максимального уровня. Объем заказа определяется правилом (3.1.) для tз
=T, 2T, 3T, … Эта стратегия
содержит элемент обратной связи (ее параметр S учитывает действительный расход
запасов). Реализация функции y0(t) для случая мгновенной поставки
отображена на рис. 3.3.
Недостатком данной стратегии является излишняя
чувствительность к спросу и повышенный средний объем запаса. Поэтому ее
целесообразно использовать в системах, где высок штраф из-за возникновения
дефицита, а также в многономенклатурных системах, где может быть достигнута
экономия за счет совмещения моментов заказа и поставки по нескольким
номенклатурам. В последнем случае
применяется стратегия (T,Y) в
векторной форме, то есть 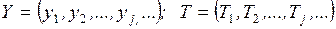 , когда значения Tj
кратны некоторому базовому периоду (система кратных периодов).
, когда значения Tj
кратны некоторому базовому периоду (система кратных периодов).
Стратегия (yкр,
S) характеризуется тем, что заказ
объема S подается в момент контроля
при снижении объема запаса ниже yкр.
На рис. 3.4, а изображен график изменения текущего объема запаса при мгновенной
поставке и контроле с периодом tк.
Стратегия (yкр, S) реагирует на спрос более медленно,
чем (T, y). Ее недостатком является
возрастание частоты заказов при стабилизации спроса на высоком уровне.
 Стратегия
(yкр,, y) – стратегия двух
уровней – является наиболее гибкой, так как в ней спрос определяет и момент
подачи заказа, и его объем. Реализация функции y0(t) для этой
стратегии при мгновенной поставке и непрерывном контроле отображена на рис.
3.4. б. Данная стратегия позволяет
поддерживать средний объем запаса вблизи
yкр при достаточно редких поставках.
Можно показать, что для однономенклатурных систем стратегия (yкр,, y) является наилучшей.
Это стратегия удобна в автоматизированных СУЗ.
Стратегия
(yкр,, y) – стратегия двух
уровней – является наиболее гибкой, так как в ней спрос определяет и момент
подачи заказа, и его объем. Реализация функции y0(t) для этой
стратегии при мгновенной поставке и непрерывном контроле отображена на рис.
3.4. б. Данная стратегия позволяет
поддерживать средний объем запаса вблизи
yкр при достаточно редких поставках.
Можно показать, что для однономенклатурных систем стратегия (yкр,, y) является наилучшей.
Это стратегия удобна в автоматизированных СУЗ.
Совокупность рассмотренных классификационных признаков определяет
тип системы управления запасами, объем задач, решаемых при их синтезе, и
математические методы исследования.
Из общей характеристики основных компонентов СУЗ (структура,
предметы запаса, спрос, пополнение запасов) следует, что при их создании
необходимо определить структуру системы (число уровней, число и места
расположения складов, способ управления и характер взаимосвязи между складами),
способы пополнения запасов и ликвидации недостач, тип стратегии управления
запасами и ее параметры.
Структуру системы и ее параметры, а также способ ликвидации
недостач определяют, как правило, на основе накопленного опыта функционирования
подобных СУЗ с учетом взаимосвязей между потребителями запасов и важности
решаемых ими задач.
В настоящее время в теории управления запасами наиболее
полно разработаны вопросы определения параметров стратегии управления запасами
для заданных условий спроса и пополнения. Решение этой задачи включает два
основных этапа. На первом этапе определяют функцию затрат, связанных с
реализацией данной стратегии, а на втором – выбирают такие значения параметров
стратегии, при которых функция затрат достигает минимума, то есть находят оптимальные
параметры стратегии.
Функция затрат представляет собой затраты, связанные с функционированием
СУЗ в течение некоторого периода или в единицу времени, и имеет три
составляющие:
С=сп+си+сд (3.2)
где сп – стоимость поставок; си – издержки
хранения, сд – штрафы из-за
дефицита (несвоевременного обеспечения потребителей).
При определений сп
учитывают постоянную составляющую и составляющие, пропорциональные суммарному
объему заказа и количеству заказываемых номенклатур.
При определении издержек хранения учитывают стоимость
складских помещений, расходы на содержание обслуживающего персонала, потери от
естественной убыли запасов, убытки от снижения потребительских качеств запасов,
потери от омертвления средств, вложенных в запасы. В большинстве случаев при
аналитическом исследовании предполагают, что издержки хранения пропорциональны
среднему запасу и времени его существования.
Величина штрафа зависит от самого факта возникновения недостачи,
величины дефицита и времени его существования. Характер зависимости величины
штрафа от указанных параметров может быть самым разнообразным.
Функция затрат является показателем экономической эффективности
СУЗ. Однако, во-первых, показатель экономической эффективности не всегда
является определяющим, а во-вторых, в некоторых случаях через функцию затрат
невозможно достаточно полно учесть все факторы, связанные с созданием запасов и
возникновением дефицита.
Указанные обстоятельства являются типичными для медицинских
СУЗ, когда величина ущерба, связанного с недостачей материальных ресурсов, связана
со здоровьем людей. Поэтому для оценки эффективности СУЗ используют и такие
показатели как вероятность возникновения дефицита, величина возможного дефицита
или среднее время его существования. В этих случаях задача оптимального
управления запасами заключается в определении стратегии (или ее параметров),
минимизирующей затраты на создание и функционирование СУЗ при заданном значении
одного из указанных показателей.
Возможна также постановка и обратной задачи – определить стратегию управления запасами и
ее параметры так, чтобы при ограниченном количестве средств, выделенных на
создание и функционирование СУЗ, вероятность возникновения дефицита (объем
дефицита или среднее время его существования) была минимальной.
Следует отметить, что определение допустимых
(требуемых) значений указанных показателей представляет самостоятельную, достаточно
сложную задачу. В некоторых случаях эти величины можно определить исходя из
требуемой эффективности систем, которые используют создаваемые запасы.
При решении задач оптимального управления запасами необходимо
также учитывать возможные ограничения на максимальный объем запасов, их вес,
стоимость, общий объем поставки, число поставок в заданном интервале времени и
так далее.
Таким образом, решение задачи оптимального управления запасами
предполагает разработку математической модели функционирования СУЗ с целью
установления зависимости между показателями ее эффективности и параметрами. На
этом этапе широко используются модели массового обслуживания, метод динамики
средних и метод статистических испытаний. На втором этапе при выборе
оптимальных параметров СУЗ используют методы математического программирования.
Методику разработки математических моделей СУЗ и типовые
задачи оптимального управления запасами рассмотрим на примере исследования
простейших однокаскадных и эшелонированных систем.
Функция затрат представляет собой затраты, связанные с функционированием
СУЗ в течение некоторого периода или в единицу времени, и имеет три
составляющие:
С=сп+си+сд (3.2)
где сп – стоимость поставок; си – издержки
хранения, сд – штрафы
из-за дефицита (несвоевременного обеспечения потребителей).
При определений сп
учитывают постоянную составляющую и составляющие, пропорциональные суммарному
объему заказа и количеству заказываемых номенклатур.
При определении издержек хранения учитывают стоимость
складских помещений, расходы на содержание обслуживающего персонала, потери от
естественной убыли запасов, убытки от снижения потребительских качеств запасов,
потери от омертвления средств, вложенных в запасы. В большинстве случаев при
аналитическом исследовании предполагают, что издержки хранения пропорциональны
среднему запасу и времени его существования.
Величина штрафа зависит от самого факта возникновения недостачи,
величины дефицита и времени его существования. Характер зависимости величины
штрафа от указанных параметров может быть самым разнообразным.
Функция затрат является показателем экономической эффективности
СУЗ» Однако, во-первых, показатель экономической эффективности не всегда является
определяющим, а во-вторых, в некоторых случаях через функцию затрат невозможно
достаточно полно учесть все факторы, связанные с созданием запасов и
возникновением дефицита.
Для оценки эффективности СУЗ используют и такие показатели
как вероятность возникновения дефицита, величина возможного дефицита или
среднее время его существования. В этих случаях задача оптимального управления
запасами заключается в определении стратегии (или ее параметров),
минимизирующей затраты на создание и функционирование СУЗ при заданном значении
одного из указанных показателей.
Возможна также постановка и обратной задачи – определить стратегию управления запасами и
ее параметры так, чтобы при ограниченном количестве средств, выделенных на
создание и функционирование СУЗ, вероятность возникновения дефицита (объем
дефицита или среднее время его существования) была минимальной.
Следует отметить, что определение допустимых (требуемых)
значений указанных показателей представляет самостоятельную, достаточно сложную
задачу. В некоторых случаях эти величины можно определить исходя из требуемой
эффективности систем, которые используют создаваемые запасы.
При решении задач оптимального управления запасами необходимо
также учитывать возможные ограничения на максимальный объем запасов, их вес,
стоимость, общий объем поставки, число поставок в заданном интервале времени и
так далее.
Таким образом, решение задачи оптимального управления запасами
предполагает разработку математической модели функционирования СУЗ с целью
установления зависимости между показателями ее эффективности и параметрами. На
этом этапе широко используются модели массового обслуживания, метод динамики
средних и метод статистических испытаний. На втором этапе при выборе
оптимальных параметров СУЗ используют методы математического программирования.
Методику разработки математических моделей СУЗ и типовые
задачи оптимального управления запасами рассмотрим на примере исследования
простейших однокаскадных и эшелонированных систем.
3.2. УПРАВЛЕНИЕ ЗАПАСАМИ ПРИ
ДЕТЕРМИНИРОВАННОМ СТАЦИОНАРНОМ СПРОСЕ
Рассмотрим задачу управления запасами по одной номенклатуре
на одиночном складе при детерминированном стационарном спросе l единиц запаса в единицу времени. Для управления
запасами используется стратегия типа (Т,
у) —
периодическая с пополнением до максимального уровня: Необходимо определить
оптимальные параметры стратегии Т* и
у* и на их основе установить момент
подачи заказа t3 и его объем S.
При определении параметров Т* и у* необходимо
учитывать характер пополнения и допустимость возникновения дефицита. В практике
управления запасами чаще всего имеют место следующие случаи:
– поставка
осуществляется мгновенно, а возникновение дефицита не допускается;
– поставка
осуществляется мгновенно, допускается возникновение дефицита;
–  поставка
осуществляется с постоянной интенсивностью m допускается
возникновение дефицита;
поставка
осуществляется с постоянной интенсивностью m допускается
возникновение дефицита;
– поставка
осуществляется с постоянной интенсивностью m возникновение
дефицита не допускается.
Фиксированную или случайную задержку поставки можно учесть
при определении точки заказа t3.
Во всех случаях при определении параметров стратегии управления
запасами будем предполагать, что стоимость поставки не зависит от объема
заказа, то есть сп =с0 издержки хранения пропорциональны
среднему объему запаса на складе и времени его хранения (с1 – стоимость
хранения единицы запаса в единицу времени), величина штрафа за дефицит
пропорциональна среднему дефициту и времени его существования (с2— величина штрафа за
дефицит единицы запаса в единицу времени).
Рассмотрим эти случаи.
3.2.1. Мгновенная поставка, возникновение дефицита не допускается.
Этот случай имеет место тогда, когда 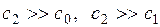 .
.
Так как интенсивность спроса постоянна, то текущий объем запаса
(рис. 3.5) изменяется в пределах одного
периода по линейному закону
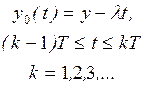 ,
,
Функция затрат за период определяется выражением
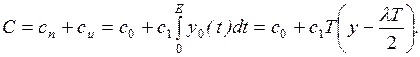 (3.3)
(3.3)
Интеграл определяет произведение среднего объема запаса на
время его существования [площадь фигуры, ограниченной осями координат и линией y0(t)]. Средние затраты в единицу времени
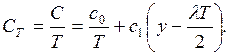
Так как возникновение дефицита не допускается, то объем запаса
в начале периода должен быть равен спросу за период, то есть y=lT . Учитывая, что 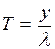 находим
находим
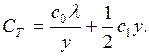 (3.4)
(3.4)
Приравнивая нулю производную этой функции по у, находим
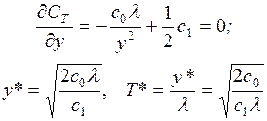 (3.5)
(3.5)
Подставляя у* из формулы (3.5) в выражение (3.4),
определим минимальные затраты на пополнение и хранение запасов в единицу времени:
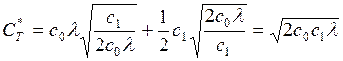 (3.6)
(3.6)
Формулы (3.5) и (3.6) известны как формулы Уилсона, причем
у*
– это экономический размер заказа.
Если пополнение осуществляется мгновенно, то заказ подается
в моменты времени tз=T*, объем
заказа S=y'*.
При задержке поставки на фиксированное время т заказ необходимо
подавать в момент снижения объема запасов до величины
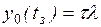 ,
,
где tl – спрос за
время поставки. В этом случае поставка будет поступать на склад в момент
исчерпания запаса.
При случайной задержке поставки точку заказа определяют по
правилу
 ,
,
где 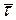 и
и 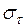 – математическое
ожидание и среднее квадратическое отклонение времени задержки поставки.
Коэффициент k определяет резервный запас,
который «демпфирует» случайные колебания времени задержки поставки. Значениям k=1, 2, 3 соответствуют вероятности возникновения
дефицита q=0,17; 0,025; 0,005 – для нормального; q=0,13; 0,05; 0,018 – для экспоненциального и q= 0,211; 0,067; 0 – для равномерного закона
распределения времени задержки поставки.
– математическое
ожидание и среднее квадратическое отклонение времени задержки поставки.
Коэффициент k определяет резервный запас,
который «демпфирует» случайные колебания времени задержки поставки. Значениям k=1, 2, 3 соответствуют вероятности возникновения
дефицита q=0,17; 0,025; 0,005 – для нормального; q=0,13; 0,05; 0,018 – для экспоненциального и q= 0,211; 0,067; 0 – для равномерного закона
распределения времени задержки поставки.
Если требуемое значение q не соответствует
указанным значениям, то коэффициент k рассчитывают следующим образом.
Очевидно, что дефицит отсутствует, если время задержки поставки
в данном периоде не превышает величины 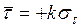 , то есть
, то есть
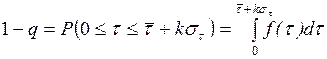 ,
,
где 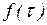 – плотность
распределения времени задержки поставки. Для экспоненциального распределения
– плотность
распределения времени задержки поставки. Для экспоненциального распределения
Аналогично точку заказа определяют, если имеют место
случайные колебания как времени задержки поставки, так и спроса.
Следует подчеркнуть, что такой подход к определению параметров
стратегии управления запасами при случайной задержке поставки и (или)
вероятностном спросе является приближенным. Для определения оптимальных параметров стратегии управления запасами необходимо
исследовать вероятностную модель СУЗ.
3.2.2.Мгновенная
поставка, возникновение дефицита
допускается.
График изменения текущего объема запаса показан на рис. 3.6, где y1 – максимальный уровень запаса, Т1 – период пополнения.
Начальный запас в
каждом периоде будет исчерпан к моменту времени t1, то есть  .
.
На интервале [0, t] y0(t)>0 и имеют место издержки хранения
На интервале [t1, T1] y0(t)<0 (имеет место
дефицит), и склад выплачивает штраф в размере
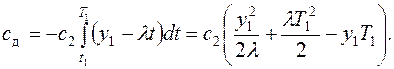
Знак «минус» перед интегралом учитывает, что дефицит равен
объему запаса с противоположным знаком.
Функция затрат в единицу времени
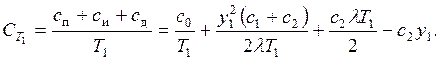 (3.7)
(3.7)
Для определения оптимальных параметров стратегии управления
запасами приравниваем производные функции (3.7)
по у1 и T1 нулю,
то есть
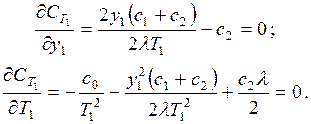
Из первого уравнения находим
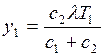 (3.8)
(3.8)
и, подставляя его во второе
уравнение, получим
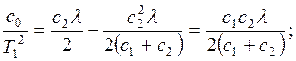
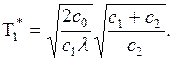 (5.9)
(5.9)
Подставляя выражение (3.9)
в уравнение (3.8), находим
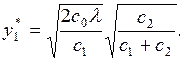 (3.10)
(3.10)
Из формулы (3.7) с
учетом выражений (3.9) и (3.10) находим минимальные затраты в единицу
времени на пополнение, хранение запасов и выплату штрафов:
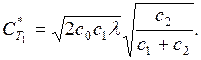 (3.11)
(3.11)
Из выражений (3.9) – (3.11)
и формул Уилсона (3.5) и (3.6) следует, что задалживание спроса (то
есть ликвидация недостач путем накопления требований до очередной поставки и
выплаты штрафов) позволяет в 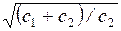 раз уменьшить
максимальный уровень запаса, минимальное значение функции затрат и частоту
заказов (увеличить период пополнения) по сравнению со случаем отсутствия дефицита.
Если c2>>c1, то
раз уменьшить
максимальный уровень запаса, минимальное значение функции затрат и частоту
заказов (увеличить период пополнения) по сравнению со случаем отсутствия дефицита.
Если c2>>c1, то 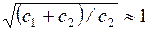 и формулы (3.9) – (3.11) совпадают с формулами Уилсона.
и формулы (3.9) – (3.11) совпадают с формулами Уилсона.
Объем заказа при наличии дефицита
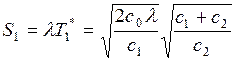 (3.12)
(3.12)
превышает объем заказа при
отсутствии дефицита в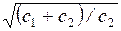 раз.
раз.
При фиксированной задержке на время t
заказ подается в момент t3 снижения
объема запаса до уровня
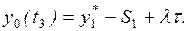
Учитывая выражения (5.10)
и (5.12), находим
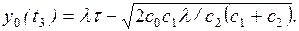
Если t =
0, то в момент подачи заказа на складе имеет место максимальный дефицит объемом
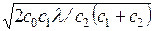 .
.
3.2.3. Поставка с постоянной интенсивностью
Характерна для заводского склада, когда продукция производится
партиями и с момента запуска ее в производство поступает на склад с постоянной
интенсивностью m >l (если m < l, то система не работает).
Запуск производства вызывает фиксированные затраты c0 на переналадку оборудования, которые не зависят от
объема партии.
 График изменения текущего объема запаса изображен на рис. 3.7.
График изменения текущего объема запаса изображен на рис. 3.7.
Период времени между поставками содержит четыре интервала:
[0, t1] – интервал накопления
запасов с интенсивностью (m –l), максимальный уровень запаса у2 будет накоплен за время t1, то есть
 ;
;
[t1, t2] – интервал расходования запаса с интенсивностью
l, весь запас будет
израсходован к моменту времени t2,
то есть
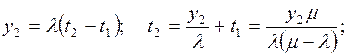 (3.13)
(3.13)
[t2, t3] – интервал накопления дефицита, за время (t3–t3) будет
накоплен максимальный дефицит
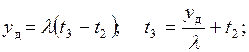 (3.14)
(3.14)
[tз, Т2] —интервал ликвидации
дефицита с интенсивностью (m –l), дефицит будет ликвидирован за время T2 – t3, то есть
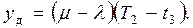
Подставляя в это уравнение t3
из выражения (3.14) и t2 из формулы
(3.13), находим
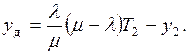
Затраты на хранение запасов в течение периода имеют место на
интервале [0, t2] и пропорциональны
площади треугольника 0AВ, то есть
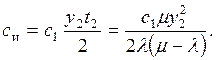
На интервале [t2, Т2]склад выплачивает штраф,
размер которого пропорционален площади треугольника BCD, то есть

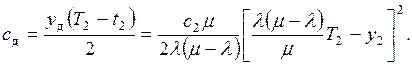
Функция затрат в единицу времени
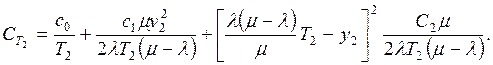
Приравнивая производные этой функции по у2 и Т2. нулю и решая полученную систему
уравнений, находим
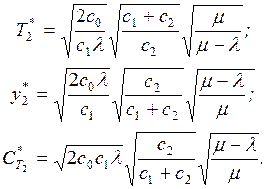 (3.15)
(3.15)
Если возникновение дефицита не допускается (рис. 5.8), то
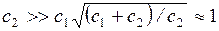 и параметры Стратегии
управления запасами
и параметры Стратегии
управления запасами
 (3.16)
(3.16)
Сравнивая выражения (3.15)
с (3.9) – (3.11) и (3.16) с (3.5) – (3.6),
можно установить, что при поставке с постоянной интенсивностью максимальный
объем запаса, минимальное значение функции затрат и частота заказов уменьшаются
в 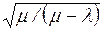 раз. Если
раз. Если 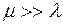 , то
, то 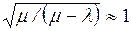 и из формул (3.15) получаем выражения (3.9) – (3.11), а из (3.16) – (3.5) и (3.6).
и из формул (3.15) получаем выражения (3.9) – (3.11), а из (3.16) – (3.5) и (3.6).
Рассмотренные модели управления запасами могут использоваться
для определения ориентировочных значений параметров стратегии управления
запасами при вероятностном спросе.
3.3. ОДНОКАСКАДНЫЕ СУЗ ПРИ ВЕРОЯТНОСТНОМ
ДИСКРЕТНОМ СПРОСЕ
Главной особенностью управления запасами при вероятностном
спросе является то, что теоретически исключить дефицит невозможно, а можно
только обеспечить требуемое значение вероятности возникновения дефицита.
Поэтому прежде всего рассмотрим методику определения этого показателя для
однокаскадной системы управления многономенклатурными запасами при следующих
предположениях:
– дискретный вероятностный стационарный спрос представляет
простейший поток требований на предметы запаса интенсивности 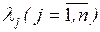 , п – число номенклатур;
, п – число номенклатур;
– стратегия управления
запасами типа (Т, уj) – периодическая с пополнением объема запаса
по каждой номенклатуре до максимального уровня уj; пополнение запаса по всем
номенклатурам осуществляется одновременно;
– поставка осуществляется
мгновенно, а ликвидация дефицита – накоплением
требований до очередной поставки.
Эффективность управления запасами по каждой номенклатуре
будем характеризовать вероятностью возникновения дефицита q(уj) или вероятностью
его отсутствия 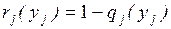 в течение периода
между поставками.
в течение периода
между поставками.
Дефицит по j-й номенклатуре в
течение периода между поставками отсутствует, если число требований k на предметы запаса данной номенклатуры за период Т не превысит величины уj, то есть  – вероятность того, что за время Т в СУЗ поступит не более yj требований.
– вероятность того, что за время Т в СУЗ поступит не более yj требований.
Так как спрос представляет простейший поток требований, то
вероятность Рjk того, что
за время Т в систему поступит ровно k требований на предметы запаса j-й номенклатуры, определяется по формуле
Пуассона, то есть
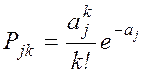 , (3.17)
, (3.17)
где 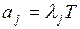 – среднее ожидаемое
число требований на предметы запаса за время Т. Для нестационарного пуассоновского потока
– среднее ожидаемое
число требований на предметы запаса за время Т. Для нестационарного пуассоновского потока
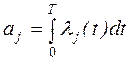
Дефицит отсутствует при k = 0, 1,2,. . ., уj, то есть
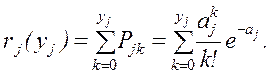 (3.19)
(3.19)
Эффективность СУЗ в целом можно оценить вероятностью достаточности
объема запасов Y = (y1, у2, . . ., yn) на период Т, которая представляет собой
вероятность отсутствия дефицита по всем номенклатурам
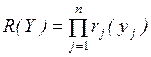 , (3.20)
, (3.20)
или вероятностью возникновения дефицита хотя бы по одной номенклатуре
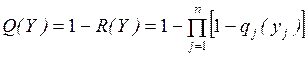 . (3.20)
. (3.20)
Выполнив умножение в выражении (3.20) и пренебрегая членами, содержащими произведение двух и
более величин qj(yj)
находим
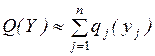 (3.21)
(3.21)
Абсолютная погрешность вычисления Q(Y) по формуле (3.21) не
превышает 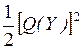 и поэтому ее можно
использовать при
и поэтому ее можно
использовать при 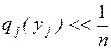 При
определении оптимальных параметров стратегии управления запасами необходимо
учитывать и такие характеристики СУЗ, как общая стоимость запасов C(Y), их вес G(Y), требуемая емкость склада V(Y):
При
определении оптимальных параметров стратегии управления запасами необходимо
учитывать и такие характеристики СУЗ, как общая стоимость запасов C(Y), их вес G(Y), требуемая емкость склада V(Y):
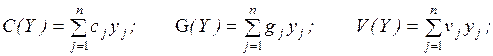 (3.22)
(3.22)
где cj
– стоимость; Gj –
вес предмета запаса j-й номенклатуры; Vj – требуемая емкость склада (объем или площадь)
для его хранения.
Полученные зависимости
(3.19), (3.21) и (3.22) позволяют
сформулировать ряд задач оптимизации объема запасов Y для заданного
периода пополнения Т.
Задача 1. Определить объем запасов 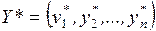 так, чтобы их
стоимость была минимальной то есть
так, чтобы их
стоимость была минимальной то есть
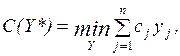 (3.23)
(3.23)
а вероятность его достаточности R(Y) была не ниже заданной Rд, то есть
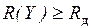 , или
, или 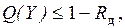 (3.24)
(3.24)
и выполнялись ограничения по суммарному весу запасов и требуемой
емкости склада
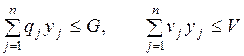 , (3.25)
, (3.25)
где G — допустимый вес запасов; V — ограничение на емкость склада.
Задача 2. Определить объем запасов V* так, чтобы
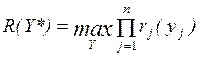 (3.26)
(3.26)
или
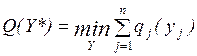 , (3.27)
, (3.27)
и выполнялись условия
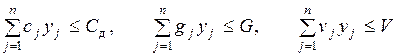 (3.28)
(3.28)
где Сд — объем средств, выделяемых на создание
запасов в каждом периоде.
Если ограничение на вес запасов и (или) емкость склада не накладывается,
то соответствующие неравенства в (3.25)
или (3.28) не учитываются.
Рассмотренная математическая модель управления запасами
широко используется при определении состава комплектов ЗИПа для технических
систем. В этом случае уj – количество
запасных элементов j-го типа, a R(Y) – вероятность достаточности комплекта
ЗИПа или вероятность нормального функционирования технической системы (без
простоев из-за недостачи запасных элементов) .
Рассмотрим пример. Техническая система состоит из n=10 типов элементов, суммарная
интенсивность потока отказов элементов каждого типа 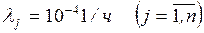 ,
интенсивность потока отказов системы
,
интенсивность потока отказов системы 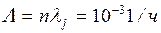 . Определить состав комплекта ЗИПа, необходимого для
обеспечения нормального функционирования системы в течение времени T=1000 ч с вероятностью Rд ==0,95.
. Определить состав комплекта ЗИПа, необходимого для
обеспечения нормального функционирования системы в течение времени T=1000 ч с вероятностью Rд ==0,95.
Оптимальный состав комплекта ЗИПа можно определить в результате
решения задачи (3.23) – (3.25), если
заданы стоимостные, весовые и габаритные характеристики элементов системы, а
также требования к стоимостным (минимум стоимости), весовым G и габаритным V характеристикам комплекта ЗИПа.
Если указанные характеристики не заданы, то рациональный состав
комплекта ЗИПа определяют из условия обеспечения равной вероятности
достаточности запасных элементов каждого типа («равнопрочный» ЗИП). Решение
задачи производится в следующем порядке.
1. Определить
требуемые значения вероятности достаточности rj(yj) или недостаточности qj(уj) из условия
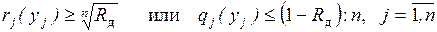 .
.
Для рассматриваемого примера
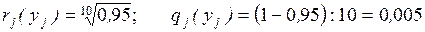 .
.
2. Вычислить среднее
ожидаемое число требований на элементы каждого типа
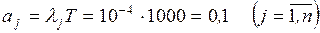 .
.
3. По формуле (3.18) методом последовательных приближений
определить минимальное количество запасных элементов каждого типа, необходимых
для обеспечения требуемого значения rj (уj).
Так, для рассматриваемого примера 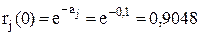 ;
; 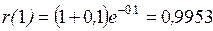 , то есть в состав комплекта ЗИПа достаточно включить
по одному элементу каждого типа (всего 10
элементов).
, то есть в состав комплекта ЗИПа достаточно включить
по одному элементу каждого типа (всего 10
элементов).
Рассчитаем состав группового комплекта ЗИПа, необходимого
для эксплуатации W=5 одинаковых
систем для условий рассматриваемого примера. В этом случае 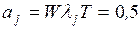 . Для обеспечения
. Для обеспечения 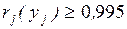 в состав комплекта
ЗИПа необходимо включить по три запасных элемента каждого типа (всего 30
элементов). Следовательно, создание группового комплекта позволяет уменьшить
объем запаса в расчете на одну систему в 10:(30:5)=1,67
раза.
в состав комплекта
ЗИПа необходимо включить по три запасных элемента каждого типа (всего 30
элементов). Следовательно, создание группового комплекта позволяет уменьшить
объем запаса в расчете на одну систему в 10:(30:5)=1,67
раза.
Пусть за счет применения однотипных элементов удалось сократить
количество типов элементов до n=5, интенсивность потока
отказов системы осталась прежней, то есть 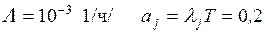 .
.
Для обеспечения вероятности 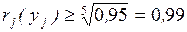 в состав
индивидуального комплекта необходимо включить по два элемента каждого типа
(всего 10 элементов), так как
в состав
индивидуального комплекта необходимо включить по два элемента каждого типа
(всего 10 элементов), так как
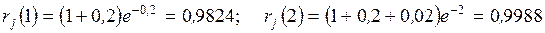 ,
,
а в состав группового комплекта на W=5 систем – по четыре
элемента каждого типа (всего 20 комплектов). Групповой комплект эффективнее
индивидуального в 10:(20:5)=2,5 раза. Уменьшение
числа типов элементов позволило сократить объем запаса в групповом комплекте в
30:20=1,5 раза. Таким образом, при простейшем потоке требований на предметы
запаса целесообразно увеличение количества потребителей, обслуживаемых одним
складом (создание групповых комплектов ЗИПа), и уменьшение числа используемых
номенклатур (числа ЗИПов элементов в технических системах).
При управлении запасами
дорогостоящих предметов (стоимость предметов запаса значительно превышает стоимость поставки) целесообразно
использовать стратегию двух уровней (T,
y) при S= y – yкр=1.
В этом случае заказ подается каждый раз после выдачи потребителю предмета запаса,
то есть пополнение является непрерывным.
Рассмотрим случай, когда поток требований на предметы запаса
– простейший поток интенсивности λ; время пополнения
– случайная величина, распределенная по экспоненциальному со средним значением 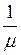 (μ – интенсивность пополнения), а величина дефицита не может
превысить единицу. Этот случай типичен при обеспечении технических систем
дорогостоящими запасными элементами (приборами, агрегатами). Если в момент отказа
системы в комплекте ЗИПа нет требуемого элемента, то она простаивает и ее
элементы не отказывают (дефицит не может превысит единицы). Пополнение комплекта
ЗИПа происходит или за счет поставки из органа снабжения или путем ремонта отказавшего
прибора.
(μ – интенсивность пополнения), а величина дефицита не может
превысить единицу. Этот случай типичен при обеспечении технических систем
дорогостоящими запасными элементами (приборами, агрегатами). Если в момент отказа
системы в комплекте ЗИПа нет требуемого элемента, то она простаивает и ее
элементы не отказывают (дефицит не может превысит единицы). Пополнение комплекта
ЗИПа происходит или за счет поставки из органа снабжения или путем ремонта отказавшего
прибора.
Для определения вероятности возникновения дефицита построим
граф состояний СУЗ по одной номенклатуре. При заданном у состояние СУЗ в любой момент времени полностью определяется числом
заявок k на предметы запаса, поданных в источник снабжения.
Действительно, если СУЗ находится в состоянии Sд (k = 0, 1, . . ., у, у+1), то это означает, что подано k заявок на предметы запаса, а
на складе имеется у – k предметов запаса (при k = y +1
имеет место дефицит). Переход СУЗ из состояния Sk
в состояние Sk+1 (k = 0, 1,
. . ., у) происходит под
воздействием потока требований интенсивности λ, а переход из Sk в Sk-1 (k=1, 2, . . .,y+1)
под воздействием потока поступлений предметов запаса на склад интенсивности kμ..
 Размеченный
граф состояний изображен на рис. 3.9 и соответствует (y+1)-канальной
СМО с отказами. Следовательно, вероятность возникновения дефицита есть
вероятность попадания СУЗ в состояние Sу+1 а стационарное значение этой
вероятности определяется формулами Эрланга (2.36), то есть
Размеченный
граф состояний изображен на рис. 3.9 и соответствует (y+1)-канальной
СМО с отказами. Следовательно, вероятность возникновения дефицита есть
вероятность попадания СУЗ в состояние Sу+1 а стационарное значение этой
вероятности определяется формулами Эрланга (2.36), то есть
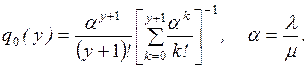 (3.29)
(3.29)
Стационарная вероятность достаточности предметов запаса
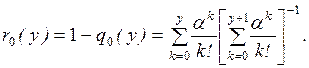 (3.30)
(3.30)
Физически q0(у) – это
средняя доля времени, в течение которого на складе имеет место дефицит, а r0(у) – доля времени, в течение которого он
отсутствует. Для случая обеспечения технических систем запасными элементами r0(у) – составляющая
коэффициента готовности технической системы, характеризующая своевременность
обеспечения ее запасными элементами.
Эффективность многономенклатурной СУЗ можно оценить вероятностью
отсутствия дефицита по всем номенклатурам R0(Y) или вероятностью
возникновения дефицита хотя бы по одной номенклатуре Q0(Y) в стационарном режиме
функционирования системы
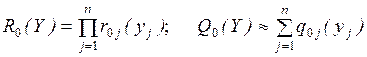 . (3.31)
. (3.31)
Оптимальные параметры стратегии управления запасами 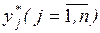 можно определить в
результате решения задачи (3.23)–(3.25)
или (3.26) – (3.28), где вместо R(Y) и Q(Y) используют R0(Y) и Q0(Y) из формул (3.31). Требуемое значение показателя
вероятности отсутствия дефицита Rд
можно определить исходя из физических особенностей предметов запаса и важности
задач, решаемых их потребителями. Так, для случая обеспечения технических
систем запасными элементами величину Rд
можно определить из условия
можно определить в
результате решения задачи (3.23)–(3.25)
или (3.26) – (3.28), где вместо R(Y) и Q(Y) используют R0(Y) и Q0(Y) из формул (3.31). Требуемое значение показателя
вероятности отсутствия дефицита Rд
можно определить исходя из физических особенностей предметов запаса и важности
задач, решаемых их потребителями. Так, для случая обеспечения технических
систем запасными элементами величину Rд
можно определить из условия
Kг= Rд Kг0
где Кг – требуемое значение коэффициента готовности; Кг0 – значение коэффициента готовности, вычисленное при условии, что
дефицит на запасные элементы не возникает.
4 МЕТОДЫ
ПРИНЯТИЯ ТЕХНИЧЕСКИХ РЕШЕНИЙ
4.1. ОСНОВНАЯ
ФОРМАЛЬНАЯ СТРУКТУРА ПРИНЯТИЯ
РЕШЕНИЙ
4.1.1. Матрица решений
Принятие решения представляет собой выбор одного из некоторого
множества рассматриваемых вариантов: 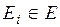 . В дальнейшем мы будем изучать наиболее часто
встречающийся на практике случаи когда имеется лишь конечное, число вариантов
. В дальнейшем мы будем изучать наиболее часто
встречающийся на практике случаи когда имеется лишь конечное, число вариантов 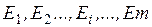 , причем обычно небольшое, хотя принципиально мыслимо
и бесконечное множество вариантов
, причем обычно небольшое, хотя принципиально мыслимо
и бесконечное множество вариантов 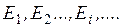 При необходимости наше рассмотрение без труда
переносится на этот наиболее общий случай.
При необходимости наше рассмотрение без труда
переносится на этот наиболее общий случай.
Условимся прежде всего, что каждым вариантом Ei
однозначно определяется некоторый результат еi. Эти результаты должны допускать количественную
оценку, и мы будем для простоты отождествлять эти оценки с соответствующими
результатами, обозначая их одним и тем же символом еi.
Мы ищем вариант с наибольшим значением результата, то есть
целью нашего выбора является 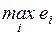 . При этом мы
считаем, что оценки еi характеризуют такие величины, как, например, выигрыш,
полезность или надежность. Противоположную ситуацию с оценкой затрат или потерь
можно исследовать точно так же путем минимизации оценки или, как это делается
чаще, с помощью рассмотрения отрицательных величин полезности.
. При этом мы
считаем, что оценки еi характеризуют такие величины, как, например, выигрыш,
полезность или надежность. Противоположную ситуацию с оценкой затрат или потерь
можно исследовать точно так же путем минимизации оценки или, как это делается
чаще, с помощью рассмотрения отрицательных величин полезности.
Таким образом, выбор оптимального варианта производится с
помощью критерия
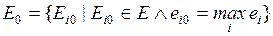 (4.1)
(4.1)
Это правило выбора читается следующим образом: множество E0 оптимальных вариантов состоит из тех вариантов Ei0, которые принадлежат множеству Е всех вариантов и оценка еi0 которых максимальна среди всех оценок еi (логический знак
/\ читается как «и» и требует, чтобы оба связываемых им утверждения были
истинны).
Выбор оптимального варианта в соответствии с критерием (4.1)
не является, вообще говоря, однозначным, поскольку максимальный результат 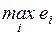 может достигаться в
множестве всех результатов многократно. Необходимость выбирать одно из
нескольких одинаково хороших решений на практике обычно не создает
дополнительных трудностей. Поэтому в дальнейшем мы лишь упоминаем об этой возможности,
не занимаясь ею более подробно.
может достигаться в
множестве всех результатов многократно. Необходимость выбирать одно из
нескольких одинаково хороших решений на практике обычно не создает
дополнительных трудностей. Поэтому в дальнейшем мы лишь упоминаем об этой возможности,
не занимаясь ею более подробно.
Только что рассмотренный случай принятия решений, при котором
каждому варианту решения соответствует единственное внешнее состояние (и тем самым
однозначно определяется единственный результат) и который мы называем случаем
детерминированных решений, с точки зрения его практических применений является
простейшим и весьма частным. Разумеется, такие элементарные структуры лежат в
основании реальных процедур принятия решений. В более сложных структурах
каждому допустимому варианту решения Еi вследствие различных внешних условий могут соответствовать
различные внешние условия (состояния) F, и результаты еij решений.
Следующий пример иллюстрирует это положение.
Пусть из некоторого материала требуется изготовить
изделие, долговечность которого при допустимых затратах невозможно определить.
Нагрузки считаются известными. Требуется решить, какие размеры должно иметь
изделие из данного материала.
Варианты решений таковы:
Е1 – выбор размеров из соображений
максимальной долговечности, т. е. изготовление изделия с минимальными
затратами в предположении, что материал будет сохранять свои характеристики в
течение длительного времени;
Еm – выбор размеров в предположении минимальной долговечности;
Еi – промежуточные решения.
Условия, требующие рассмотрения, таковы:
F1 – условия, обеспечивающие максимальную долговечность;
Fn– условия,
обеспечивающие минимальную долговечность;
Fj – промежуточные
условия.
Под результатом решения еij здесь можно понимать оценку, соответствующую
варианту Еi
и условиям Fj
и характеризующую экономический эффект (прибыль), полезность или надежность
изделия. Мы будем называть такой
результат полезностью решения.
Семейство решений описывается некоторой матрицей (табл. 4.1). Увеличение объема семейства по сравнению
с рассмотренной выше ситуацией детерминированных решений связано как с недостатком
информации, так и с многообразием технических возможностей.
Конструктор и в этом случае старается выбрать решение с наилучшим
результатом, но, так как ему неизвестно, с какими
Основная
формальная структура принятия решений
Таблица 4.1.
Матрица решений ||eij||
|
|
F1
|
F2
|
F3
|
…
|
Fj
|
…
|
Fn
|
|
E1
|
e11
|
e12
|
e13
|
…
|
e1j
|
…
|
e1n
|
|
E2
|
e21
|
e22
|
e23
|
…
|
e2j
|
…
|
e2n
|
|
E3
|
e31
|
e32
|
e33
|
…
|
e3j
|
…
|
e3n
|
|
.
.
.
|
.
.
.
|
.
.
.
|
.
.
.
|
.
.
.
|
.
.
.
|
.
.
.
|
.
.
.
|
|
Ej
|
ej1
|
ej2
|
ej3
|
…
|
eij
|
…
|
emn
|
|
.
.
.
|
.
.
.
|
.
.
.
|
.
.
.
|
.
.
.
|
.
.
.
|
.
.
.
|
.
.
.
|
|
Em
|
Em1
|
em2
|
em3
|
…
|
emj
|
…
|
emn
|
условиями он столкнется, он вынужден
принимать во внимание все оценки eij,
соответствующие варианту Еi. Первоначальная задача максимизации 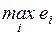 согласно критерию (4.1)
должна быть теперь заменена другой, подходящим образом учитывающей все
последствия любого из вариантов решения Ei.
согласно критерию (4.1)
должна быть теперь заменена другой, подходящим образом учитывающей все
последствия любого из вариантов решения Ei.
4.1.2. Оценочная функция
Чтобы прийти к однозначному и по возможности наивыгоднейшему
варианту решения даже в том случае, когда каким-то вариантам решений Ei
могут соответствовать различные условия Fj, можно ввести
подходящие оценочные (целевые) функции. При этом матрица решений ||eir||сводится к одному столбцу. Каждому варианту Ei
приписывается, таким образом, некоторый результат eir,
характеризующий, в целом, все последствия этого решения. Такой результат мы
будем в дальнейшем обозначать тем же символом eir.
Процедуру выбора можно теперь представить по аналогии с
применением критерия (4.1). Возникает,
однако, проблема, какой вложить смысл в результат eir.
Если, например, последствия каждого из альтернативных решений характеризовать
комбинацией из его наибольшего и наименьшего результатов, то можно принять
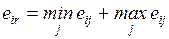 . (4.2)
. (4.2)
Из сказанного вытекает способ
построения оценочных функций, приводимый в табл. 4.2. Наилучший в этом смысле результат имеет вид
 . (4.3)
. (4.3)
Теперь решение можно снова искать в
соответствии с критерием (4.1). Формируя
таким образом желаемый результат, конструктор исходит из компромисса между
оптимистическим и пессимистическим подходами.
Рассмотрим теперь некоторые:
другие оценочные функции, которые в данном примере мог бы выбрать конструктор,
а также соответствующие им исходные позиции.
Таблица 4.2.
Построение оценочных функций
|
E1
|
e1n
|
|
E2
|
e2n
|
|
E3
|
e3n
|
|
.
.
.
|
.
.
.
|
|
Ej
|
emn
|
|
.
.
.
|
.
.
.
|
|
Em
|
emn
|
Оптимистическая позиция:
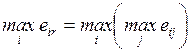 . (4.4)
. (4.4)
Из матрицы результатов решений еij (табл. 4.1) выбирается вариант (строка), содержащий в
качестве возможного следствия наибольший из всех возможных результатов. Наш
конструктор становится на точку зрения азартного игрока. Он делает ставку на
то, что. выпадет наивыгоднейший случай, и исходя из этого выбирает размеры изделия.
Позиция нейтралитета:
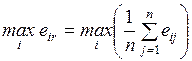 . (4.5)
. (4.5)
Конструктор
исходит из того, что все встречающиеся отклонения результата решения от
«среднего» случая допустимы, и выбирает размеры, оптимальные с этой точки
зрения.
Пессимистическая позиция:
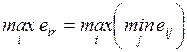 . (4.6)
. (4.6)
Конструктор исходит из того, что надо ориентироваться на наименее
благоприятный случай и приписывает каждому из альтернативных вариантов
наихудший из возможных результатов. После этого он выбирает самый выгодный
вариант, то есть ожидает наилучшего результата в наихудшем случае. Для каждого
иного внешнего состояния результат может быть только равным этому или лучшим.
Позиция относительного пессимизма:
 . (4.7)
. (4.7)
Для каждого варианта решения конструктор оценивает потери в
результате по сравнению с определенным по каждому варианту наилучшим
результатом, а затем из совокупности наихудших результатов выбирает наилучший
согласно представленной оценочной функции.
Таблица 4.3.
Влияние вида оценочных функций на выбор размеров кабеля
|
Уравнение
|
Оценочная функция
|
Результат
|
|
(4.6)
|
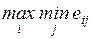
|
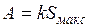
|
|
(4.5)
|
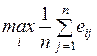
|
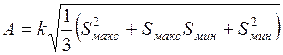
|
|
(4.7)
|
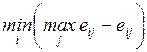
|
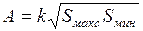
|
|
(4.4)
|
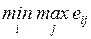
|
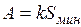
|
Ряд таких оценочных функций можно было бы продолжить. Некоторые
из них получили широкое распространение в хозяйственной деятельности. Так, если
условия эксплуатации заранее не известны, ориентируются обычно на наименее
благоприятную ситуацию. Это соответствует оценочной функции (4.6). Нередко используются также функции (4.6) и (4.7).
В табл. 4.3 показан
пример выбора сечения А кабеля при
неизвестной токовой нагрузке S с
использованием всех четырех вышеназванных оценочных функций. Константа k здесь одна и та же для всех четырех случаев. Отметим, что
результаты зависят только от Sмакс и Sмин, т. е. от максимальной и
минимальной токовых нагрузок.
Приведенные результаты существенно различаются. Они
упорядочены таким образом, что влияние минимальной токовой нагрузки Sмин нарастает от строки к
строке, т. е. получающиеся сечения становятся все меньше и меньше. Решение при
этом становится все более оптимистичным. При этом выбор критерия определяется
исключительно позицией конструктора. Поясним эти положения.
Влияние исходной позиции конструктора на эффективность результата
решения можно интерпретировать, исходя из наглядных представлений. Простейшим
здесь является графическое изображение на плоскости, для чего мы временно
ограничимся случаем с двумя (п =2)
внешними состояниями при т вариантах
решения. Полезно, разумеется, чтобы мы уяснили для себя и, руководствуясь
дальнейшими построениями, рассмотрели самостоятельно, как обобщается изложенное
на случай большего, чем два, числа состояний, особенно на случай п=3,
графически труднее представимый, но хорошо интерпретируемый в пространстве.
Введем теперь прямоугольную систему координат, откладывая по
оси абсцисс значения результата решения еi1,
соответствующие внешнему состоянию F1 а по оси
ординат – значения еi2,
соответствующие состоянию F2,
i=1, ..., т. В этом случае каждый вариант решения Ei,
соответствует точке (ei1, ei2), i=1, ... т, на плоскости.
Точку с координатами 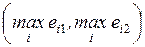 мы назовем утопической
точкой (УТ). Смысл этого названия в том, что координаты всех точек
мы назовем утопической
точкой (УТ). Смысл этого названия в том, что координаты всех точек 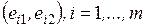 , соответствующих
вариантам решений
, соответствующих
вариантам решений  не могут быть больше,
чем у точки УТ, и что УТ встречается среди этих т точек только в том редком, идеальном случае, когда существует вариант
решения, дающий максимальный результат для каждого из (двух) возможных внешних
состояний. Аналогичное значение имеет и так называемая антиутопическая точка
(АУТ), имеющая координаты
не могут быть больше,
чем у точки УТ, и что УТ встречается среди этих т точек только в том редком, идеальном случае, когда существует вариант
решения, дающий максимальный результат для каждого из (двух) возможных внешних
состояний. Аналогичное значение имеет и так называемая антиутопическая точка
(АУТ), имеющая координаты 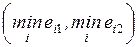 координаты всех точек
координаты всех точек 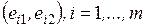 , соответствующих вариантам решений
, соответствующих вариантам решений  , не могут быть меньше, чем у точки АУТ. Отсюда следует, что
все m точек
, не могут быть меньше, чем у точки АУТ. Отсюда следует, что
все m точек  лежат внутри прямоугольника, стороны которого параллельны
координатным осям, а противоположные вершины – точки УТ и АУТ; мы называем этот прямоугольник полем полезности решений (рис. 4.1).
лежат внутри прямоугольника, стороны которого параллельны
координатным осям, а противоположные вершины – точки УТ и АУТ; мы называем этот прямоугольник полем полезности решений (рис. 4.1).
Теперь, чтобы сравнить варианты решений с точки зрения их
качества, назовем вариант Ei не худшим,
чем вариант Еj
если для соответствующих точек  и
и 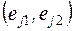 выполняются неравенства
выполняются неравенства 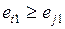 и
и 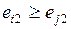 . Причем Ei считается лучшим,
чем Ej, если хотя
бы одно из этих двух неравенств является строгим.
. Причем Ei считается лучшим,
чем Ej, если хотя
бы одно из этих двух неравенств является строгим.
Очевидно, что при таком определении не любые два варианта
решений допускают сравнение в том смысле, что один из них оказывается лучше
другого. (Может случиться, что для точек 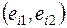 и
и 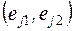 , соответствующих вариантам Ei
и Ej выполняются, например,
неравенства
, соответствующих вариантам Ei
и Ej выполняются, например,
неравенства 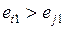 и
и 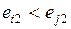 ). На математическом языке это означает, что на
множестве вариантов решений установлено так называемое отношение частичного порядка. Это отношение
частичного порядка обладает рядом свойств, хорошо усматриваемых на рис. 4.1. Выберем в поле полезности произвольную
точку, которую будем называть. рассматриваемой (РТ). С помощью прямых,
параллельных координатным осям, разобьем плоскость на четыре части и обозначим
их I, II, III и IV. В рассматриваемом нами двумерном случае каждая из этих частей
имеет вид (бесконечного) прямоугольника; в случае произвольной размерности они
превращаются в так называемые конусы.
). На математическом языке это означает, что на
множестве вариантов решений установлено так называемое отношение частичного порядка. Это отношение
частичного порядка обладает рядом свойств, хорошо усматриваемых на рис. 4.1. Выберем в поле полезности произвольную
точку, которую будем называть. рассматриваемой (РТ). С помощью прямых,
параллельных координатным осям, разобьем плоскость на четыре части и обозначим
их I, II, III и IV. В рассматриваемом нами двумерном случае каждая из этих частей
имеет вид (бесконечного) прямоугольника; в случае произвольной размерности они
превращаются в так называемые конусы.
Рассматривая положение точек поля полезности относительно
этих четырех .конусов, можно в общем случае сказать следующее. Все точки из
конуса I в смысле введенного выше частичного
порядка лучше, чем рассматриваемая точка РТ. Поэтому мы называем конус I конусом
предпочтения. Соответственно все точки из конуса III хуже точки РТ, и мы будем называть область III антиконусом.
Таким образом, оценка качества точек из этих двух конусов в сравнении с точкой
РТ проста и однозначна. Оценка же
точек в отмеченных штриховкой конусах II
и IV является неопределенной, вследствие
чего их называют областями
неопределенности. Для этих точек оценка получается только с помощью
выбранного критерия принятия решения. В случае m вариантов
решений  и п внешних состояний Fi,...,Fn критерий
принятия решения можно представить в виде
и п внешних состояний Fi,...,Fn критерий
принятия решения можно представить в виде
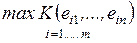
или
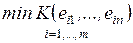 .
.
Функция п переменных К. характеризует соответствующий критерий и задает одновременно
оценочную функцию. Для анализа критерия рассмотрим, полагая ei1=x1, еi2=х2, ..., еin=хп,
функцию К на всем n-мерном пространстве Rn.
Тогда каждому значению действительного параметра k
посредством равенства
K(x1,...,xп)=k
ставится в
соответствие некоторая гиперповерхность в пространстве Rn, называемая нами поверхностью
уровня, соответствующей значению k. В двумерном случае,
интересующем нас ввиду его наглядности, мы специально полагаем ei1=x1=u, и еi2=х2=v, отождествляя тем самым еi1-ось
с u-осью, а еi2-ось с v-осью, и с помощью
равенства
K(u,v)=k .
Получаем в этом
случае на плоскости (и, v) кривую, называемую линией
уровня, соответствующей значению k. При фиксированном уровне k
уравнение K(и,v)=k определяет функциональную зависимость
между переменными и и v, называемую функцией
предпочтения; так же называют и соответствующую кривую на плоскости (u, v).
Рассмотрим, например, оценочную функцию (4.5). При еi1=и
и еi2=v получаем для т=2 семейство функций предпочтения,
зависящих от параметра k:
(u+v)/n=k .
При графическом изображении это выражение дает прямые, параллельные
биссектрисе второго и четвертого квадрантов плоскости (и,v). Поскольку рассматриваемому критерию, в соответствии с которым
путем оптимального выбора решения максимизируется среднее значение всех
возможных результатов, отвечает нейтральная в известном смысле позиция принимающего
решение, мы приписываем название «нейтральной» и соответствующей функции
предпочтения (рис. 4.2). Выберем теперь
на какой-либо линии уровня этого критерия произвольную точку РТ и проведем
через нее «осевой крест», разбивающий плоскость на описанные выше четыре квадранта
– конус предпочтения, антиконус и конусы неопределенности.
|
|
 |
Все точки из областей неопределенности, лежащие справа и выше этой линии
уровня, в смысле нашего критерия лучше точек, лежащих слева и ниже. Сказанное
справедливо и для функций предпочтения любого другого критерия. Всякая функция
(кривая) предпочтения объединяет все точки фиксированного уровня; оправа и
выше ее располагаются все лучшие точки, то есть точки более высокого уровня, а
слева и ниже – худшие, то есть точки
более низкого уровня. Если на основе какого-либо критерия получается кривая
предпочтения типа штриховой (рис. 4.2),
то мы называем такую кривую вогнутой, подразумевая под этим, что в
соответствующих ей областях неопределенности имеется меньшее число лучших
точек, чем при нейтральном критерии (4.5).
Отметим, что такая вогнутая кривая предпочтения характеризует пессимистическую
исходную позицию. Кривые предпочтения типа сплошной на рис. 4.2 соответствуют оптимистическому подходу,
поскольку на этот раз в сравнении с нейтральным критерием больше точек из
областей неопределенности принадлежит к числу лучших; мы называем такие кривые
выпуклыми. Предельный случай пессимистического подхода образуют, очевидно,
граничные прямые квадранта I, а
оптимистического—граничные прямые квадранта III, и чем ближе подходит кривая предпочтения
к этим граничным прямым, тем в большей степени соответствующий критерий
представляет пессимистическую или, соответственно, оптимистическую точку
зрения. Если выбор оценочной функции отдается на усмотрение лица, принимающего
решение, то, как показывают табл. 4.3 и
рис. 4.2, приходится считаться с
возможностью различных результатов для одного и того же решения. Таким образом,
принятие решения не есть чисто рациональный процесс. Опасность возникает в тех
случаях, когда оценочные функции выбираются интуитивно, иногда даже без
выяснения исходной позиции принимающего решение.
Всякое техническое или экономическое решение в условиях неполной
информации – сознательно или неосознанно
– принимается в соответствии с какой-либо оценочной функцией описанного выше
типа. Как только это бывает признано явно, следствия соответствующих решений
становятся лучше обозримыми, что позволяет улучшить их качество. При этом
выбор оценочных функций всегда должен осуществляться с учетом количественных
характеристик ситуации, в которой принимаются решения.
Таблица 4.4.
(m´2)-матрица решений
|
 F F
E
|
F1
|
F2
|
|
E1
|
E11
|
E12
|
|
E2
|
E21
|
E22
|
|
E3
|
E31
|
E32
|
|
.
.
.
|
.
.
.
|
.
.
.
|
|
Ei
|
ei1
|
ei2
|
|
.
.
.
|
.
.
.
|
.
.
.
|
|
Em
|
em1
|
em2
|
Таблица 2.5.
Фатальная ситуация в принятии решений
|
|
F1
|
F2
|
F3
|
…
|
Fj
|
…
|
Fn
|
|
E1
|
E11
|
E12
|
E13
|
…
|
e1j
|
…
|
e1n
|
4.1.3. Особые случаи
Схематическое сопоставление всех возможных полезностей eij различных решений в матрице табл. 4.1 облегчает поначалу их обозрение, не требуя
при этом формальной оценки. Эта матрица может быть меньшего объема (табл. 4.4) и даже выродиться в единственный
столбец, если будет представлена полная информация о том, с каким внешним
состоянием Fj следует считаться. Это
соответствует элементарному сравнению различных технических решений. Матрица
решений может, однако, свестись и к единственной строке (табл. 4.5). В этом случае мы имеем дело с так
называемой фатальной ситуацией принятия решений, когда в силу ограничений
технического характера, внешних условий и других причин остается единственный
вариант Ei,
хотя его дальнейшие последствия зависят от внешнего состояния Fj, и поэтому результат решения оказывается
неизвестным.
Случается и так, что некоторый вариант решения, например Ek, оказывается настолько удачным, что для другого
варианта El из матрицы решений
выполняются неравенства еkj ³ еlj для j = 1, ..., п.
Тогда говорят, что вариант Ek доминирует
над вариантом El. Вариант Ek в этом случае с
самого начала оказывается лучшим, а вариант El, напротив, не
представляет далее интереса. Более подробно понятие доминирования будет рассмотрено
в конце раздела 4.5.
Ради возможности графической интерпретации вернемся еще раз
к решениям с двумя только внешними состояниями F1
и F2. Все
варианты, доминирующие над точкой РТ, лежат на рис. 4.1 в конусе предпочтения (то есть в I квадранте), а варианты, над которыми РТ доминирует, расположены
в антиконусе (в III квадранте). Следовательно,
для формального оценивания остаются точки из II
и IV квадрантов, первоначально названных
областями неопределенности. Этими областями мы займемся в следующей главе. В
этих квадрантах будут найдены варианты, оптимальные в смысле различных
критериев, и даны их количественные оценки. Для этого соответствующие функции предпочтения
должны быть в обеих областях разумным образом упорядочены.
4.2. КЛАССИЧЕСКИЕ
КРИТЕРИИ ПРИНЯТИЯ РЕШЕНИЙ
4.2.1. Минимаксный
критерий
Минимаксный критерий (ММ)
[10] использует оценочную функцию (2.6),
соответствующую позиции крайней осторожности.
При
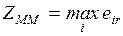 (4.8)
(4.8)
и
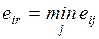 (4.9)
(4.9)
справедливо соотношение
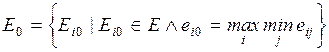 (4.10)
(4.10)
где zmm — оценочная функция ММ-критерия.
Поскольку в области технических задач построение множества Е вариантов уже само по себе требует
весьма значительных усилий, причем иногда возникает необходимость в их рассмотрении
с 'различных точек зрения, условие 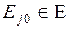 включается во все
критерии. Оно должно напоминать о том, что совокупность вариантов необходимо
исследовать возможно более полным образом, чтобы была обеспечена оптимальность
выбираемого варианта.
включается во все
критерии. Оно должно напоминать о том, что совокупность вариантов необходимо
исследовать возможно более полным образом, чтобы была обеспечена оптимальность
выбираемого варианта.
Правило выбора решения в соответствии с ММ-критерием можно
интерпретировать следующим образом:
Матрица решений ||еij|| дополняется еще одним столбцом из наименьших
результатов еir
каждой строки. Выбрать надлежит те варианты Еi0, в строках которых стоят наибольшие
значения еir
этого столбца.
Выбранные таким образом варианты полностью исключают риск.
Это означает, что принимающий решение не может столкнуться с худшим
результатом, чем тот, на который он ориентируется. Какие бы условия Fj
ни встретились, соответствующий результат не может оказаться ниже Zмм. Это свойство заставляет считать
минимаксный критерий одним из фундаментальных. Поэтому в технических задачах он
применяется чаще всего, как сознательно, так и неосознанно. Однако положение об
отсутствии риска стоит различных потерь. Продемонстрируем это на небольшом
примере (табл. 4.6).
Хотя вариант E1 кажется
издали более выгодным, согласно ММ-критерию оптимальным следует считать E0={E2}. Принятие решения по этому критерию может,
однако, оказаться еще менее разумным, если
– состояние F2 встречается чаще,
чем состояние f1,
и
– решение реализуется
многократно.
Таблица 4.6.
Пример
вариантов решения без учета риска
|
|
F1
|
F2
|
eir
|
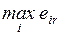
|
|
E1
|
1
|
100
|
1
|
|
|
E2
|
1,1
|
1,1
|
1,1
|
1,1
|
Выбирая вариант Ei, .предписываемый
ММ-критерием, мы, правда, избегаем неудачного значения 1, реализующегося в варианте E1 при внешнем
состоянии F1, получая вместо него при этом состоянии немного лучший результат 1,1, зато в состоянии F2
теряем выигрыш 100, получая всего только 1,1. Этот пример показывает, что в
многочисленных практических ситуациях пессимизм минимаксного критерия может
оказаться очень невыгодным.
Применение ММ-критерия бывает оправданно, если ситуация, в
которой принимается решение, характеризуется следующими обстоятельствами:
– о возможности появления внешних состояний fj ничего не известно;
– приходится считаться
с появлением различных внешних состояний Fj;
– решение реализуется лишь один раз;
– необходимо исключить
какой бы то ни было риск, то есть ни при каких условиях Fj
не допускается получать результат, меньший, чем zmm.
4.2.2. Критерий Байеса — Лапласа
При построении оценочной функции ZMM (согласно
ММ-критерию) каждый вариант Ei представлен лишь одним
из своих результатов 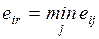 . Критерий Байеса—Лапласа (BL), напротив, учитывает каждое из
возможных следствий.
. Критерий Байеса—Лапласа (BL), напротив, учитывает каждое из
возможных следствий.
Пусть qj – вероятность появления внешнего состояния
Fj; тогда для
BL-критерия
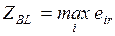 , (4.11)
, (4.11)
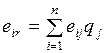 , (4.12)
, (4.12)
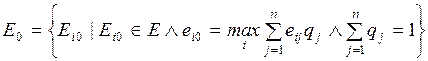 (4.13)
(4.13)
Соответствующее правило выбора можно интерпретировать
следующим образом:
Матрица решений ||еij|| дополняется еще одним столбцом, содержащим
математическое ожидание значений каждой из строк. Выбираются те варианты Еi0, в строках которых стоит наибольшее значение eir
этого столбца.
При этом предполагается, что ситуация, в которой
принимается решение, характеризуется следующими обстоятельствами:
– вероятности
появления состояний Fj известны и не зависят
от времени;
– решение реализуется
(теоретически) бесконечно много раз;
– для малого числа
реализации решения допускается некоторый риск.
При достаточно большом количестве реализации среднее значение
постепенно стабилизируется. Поэтому при полной (бесконечной) реализации
какой-либо риск практически исключен.
Исходная позиция применяющего
BL-критерий оптимистичнее, чем в случае ММ-критерия, однако она
предполагает более высокий уровень информированности и достаточно длинные реализации.
4.2.3. Критерий Сэвиджа
Рассмотрим более подробно критерий Сэвиджа, введенный выше
соотношением (4.7). С помощью обозначений
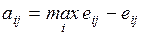 (4.14)
(4.14)
и
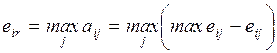 (4.15)
(4.15)
формируется оценочная функция
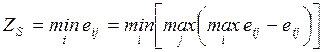 (4.16)
(4.16)
и строится множество оптимальных
вариантов решения

E0= 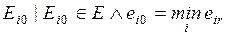 . (4.17)
. (4.17)
Для понимания этого критерия определяемую соотношением (4.14)
величину 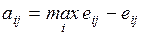 можно трактовать как
максимальный дополнительный выигрыш, который достигается, если в состоянии Fj вместо варианта Ei выбрать другой,
оптимальный для этого внешнего состояния вариант. Мы можем, однако,
интерпретировать аij, и как потери (штрафы), возникающие в состоянии Fj
при замене оптимального для него варианта на вариант Ei. Тогда
определяемая соотношением (4.15) величина
eir представляет собой – при интерпретации аij в качестве потерь – максимальные
возможные (по всем внешним состояниям Fj, (j=1, ..., n) потери в случае выбора варианта Ei.
Теперь, согласно (4.16) и (4.17), эти максимально возможные потери
минимизируются за счет выбора подходящего варианта Ei.
можно трактовать как
максимальный дополнительный выигрыш, который достигается, если в состоянии Fj вместо варианта Ei выбрать другой,
оптимальный для этого внешнего состояния вариант. Мы можем, однако,
интерпретировать аij, и как потери (штрафы), возникающие в состоянии Fj
при замене оптимального для него варианта на вариант Ei. Тогда
определяемая соотношением (4.15) величина
eir представляет собой – при интерпретации аij в качестве потерь – максимальные
возможные (по всем внешним состояниям Fj, (j=1, ..., n) потери в случае выбора варианта Ei.
Теперь, согласно (4.16) и (4.17), эти максимально возможные потери
минимизируются за счет выбора подходящего варианта Ei.
Соответствующее S-критерию правило выбора теперь
интерпретируется так:
Каждый элемент матрицы решений ||еij|| вычитается из наибольшего
результата 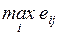 соответствующего
столбца.
соответствующего
столбца.
Разности aij образуют
матрицу остатков ||aij||. Эта матрица пополняется
столбцом наибольших разностей еir. Выбираются те варианты Еi0, в строках которых стоит наименьшее для
этого столбца значение.
По выражению (4.16)
оценивается значение результатов тех состояний, которые, вследствие выбора
соответствующего распределения вероятностей, оказывают одинаковое влияние на
решение. С точки зрения результатов матрицы ||еij|| S-критерий связан с риском,
однако, с позиций матрицы ||aij||, он от
риска свободен. В остальном к ситуации принятия решений предъявляются те же
требования, что и в случае ММ-критерия.
4.2.4. Расширенный
минимаксный критерий
Рассмотрим в заключение еще один метод, допускающий интерпретацию
в качестве расширенного минимаксного критерия. В нем используются понятия
теории вероятностей, а также теории игр. В технических приложениях этот
критерий до сего времени применяется мало.
Основным здесь
является предположение о том, что каждому из n возможных состояний Fj приписана вероятность
его появления qj: 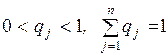 .
.
Сформируем из n вероятностей qj вектор q =
(q1, …, qn) и обозначим
через W(n) множество
всех n-мерных
вероятностных векторов. Выбор какого-либо варианта решения Ei
приводит при достаточно долгом применении Ei к среднему
результату 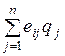 . Если же теперь случайным образом с распределением
вероятностей p=(p1,…,pm)ÎW(m) смешать m вариантов
решений Ei, то в результате получим среднее
значение
. Если же теперь случайным образом с распределением
вероятностей p=(p1,…,pm)ÎW(m) смешать m вариантов
решений Ei, то в результате получим среднее
значение
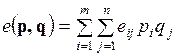 .
.
В
реальной ситуации вектор q=(q1,
…, qn), относящийся к состояниям Fj, бывает, как правило, неизвестен. Ориентируясь применительно
к значению e(p, q) на наименее
выгодное распределение q состояний Fj и добиваясь, с другой
стороны, максимального увеличения e(p, q)
за счет выбора наиболее удачного распределения p вариантов решения Ei,
получают в результате значение, соответствующее расширенному ММ-критерию.
Обозначим теперь E(p) обобщенный вариант решения, определяемый
с помощью выбора вероятностного вектора 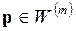 , а через
, а через  – множество всех таких
критериев.
– множество всех таких
критериев.
E(p0) = {E(p0)| E(p0)Î Ù e(p0,
q0) =
Ù e(p0,
q0) =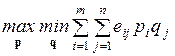 },
},
где p – вероятностный вектор для Ei,
а q – вероятностный вектор для Fj.
Таким
образом, расширенный ММ-критерийзадается целью найти наивыгоднейшее
распределение вероятностей на множестве вариантов Ei, когда в многократно воспроизводящейся ситуации ничего
не известно о вероятностях состояний Fj.
Поэтому предполагается, что Fj распределены наименее выгодным образом.
4.2.5. Применение
классических критериев
Из требований, предъявляемых рассмотренными критериями к анализируемой ситуации, становится ясно,
что вследствие их жестких исходных
позиций они применимы только для идеализированных практических решений. В
случаях, когда требуется слишком сильная идеализация, можно одновременно
применять поочередно различные критерии. После этого среди нескольких
вариантов, отобранных таким образом в качестве оптимальных, приходится все-таки
волевым образом выделять некоторое
окончательное решение. Такой подход позволяет, во-первых, лучше
проникнуть во все внутренние связи проблемы принятия решений и, во-вторых,
ослабляет влияние субъективного фактора.
Выбор решения по классическим критериям проиллюстрируем следующим
примером.
Пусть некоторую машину (технологическую установку, конвейер,
станок и тому подобные) требуется подвергнуть проверке с приостановкой,
естественно, ее эксплуатации. Из-за этого приостанавливается выпуск продукции.
Если же эксплуатации машины помешает не обнаруженная своевременно
неисправность, то это приведет не только к приостановке работы, но и
дополнительно к поломке.
Варианты решения таковы:
E1 – полная проверка;
Е2 – минимальная проверка;
Е3 – отказ от проверки.
Машина может находиться в следующих состояниях:
F1 – неисправностей нет;
F2 – имеется
незначительная неисправность;
F3 – имеется серьезная
неисправность.
Результаты включают затраты на проверки и устранение неисправности,
а также затраты, связанные с потерями в продукции и с поломкой. Они приведены в
таблице 4.7.
Таблица 4.7
Варианты
решения о проверках машины и их оценки (в 103)
согласно
ММ- и BL-критериям для qi = 0,33
|
|
F1
|
F2
|
F3
|
ММ-критерий
|
BL- критерий
|
|
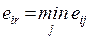
|
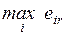
|
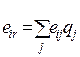
|
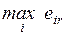
|
|
E1
|
–20,0
|
–22,0
|
–25,0
|
–25,0
|
–25,0
|
–22,33
|
|
|
Е2
|
–14,0
|
–23,0
|
–31,0
|
–31,0
|
|
–22,67
|
|
|
Е3
|
0
|
–24,0
|
–40,0
|
–40,0
|
|
–21,33
|
–21,33
|
Согласно ММ-критерию
(4.103.3), следует проводить полную проверку (E0={Е1}). BL-критерий
в предположении, что все состояния машины равновероятны (qi = 0,33), рекомендует отказаться от проверки (E0={Е1}). Табл. 4.8 иллюстрирует применение S-критерия. Им в качестве оптимальной
рекомендуется минимальная проверка.
Наш пример сознательно выбран так, что каждый критерий
предлагает новое решение. Неопределенность состояния, в котором проверка
застает машину, превращается теперь в отсутствие ясности, какому же критерию
следовать. Таким образом, мы вроде бы мало что выиграли. Самое большее, можно
было бы проверить после этого, не принимают ли величины eir
для какого-нибудь критерия приблизительно |равные значения, как, например, e2r = 14,0·103 и e3r = 15,0·103
в табл. 4.8;
Таблица 4.8
Матрица
остатков для примера «Решения о проверках машины»
и их
оценка (в103) согласно S-критерию
|
|
F1
|
F2
|
F3
|
S-критерий
|
|
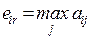
|
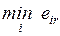
|
|
E1
|
+20,0
|
0
|
0
|
+20,0
|
|
|
Е2
|
+14,0
|
+1,0
|
+6,0
|
+14,0
|
+14,0
|
|
Е3
|
0
|
+2,0
|
+15,0
|
+15,0
|
|
рекомендации такого критерия
выглядят менее убедительными. Поскольку различные критерии связаны с
различными же аспектами ситуации, в которой принимается решение, лучше всего
для сравнительной оценки рекомендаций тех или иных критериев получить дополнительную
информацию о самой ситуации. Если принимаемое решение относится к сотням машин
с одинаковыми параметрами, то целесообразно придерживаться BL-критерия. Если же число реализации
невелико, то больший вес приобретают более осторожные рекомендации S- или ММ-критериев.
В области технических задач различные критерии часто приводят
к одному результату. Предположим, что в рассматриваемом примере серьезная
неисправность (состояние F3) встречается вдвое чаще, чем любое
другое состояние (q1 = q2;
q3 = 0,5); тогда ВL-критерий, как и ММ-критерий,
рекомендует полную проверку (Eo ={E1}).
Бывают и такие ситуации, когда все критерии дают одинаковые
результаты. Если для нашего примера (табл. 4.7)
с помощью соответствующих мероприятий удастся так снизить затраты на полную проверку,
что в соответствующей строке мы будем иметь е11=18,0.103,
e12= –20,0·103 и e13=22,0·103, то все три применявшихся
критерия предпишут полную проверку.
Всякий вариант, избираемый в данном случае всеми рассмотренными
критериями, является слабо доминирующим. Сильное доминирование имеет место,
когда для всех результатов е11 одного
из рассматриваемых вариантов справедливо
e1j £ eij для j=1, .... п
и
e1j < eij хотя
бы для одного j.
Над указанным вариантом Е1 остальные варианты
доминируют. Его можно исключить из матрицы решений, так как для всякого Fj он дает худший результат, чем другие.
Если какой-либо вариант Е1
доминирует сильно, то есть выполняются условия
e1j ³eij для всех j=1, .... п
и
e1j > eij хотя бы для одного j,
то даже при отсутствии информации о возможных внешних состояниях
Fj никакой проблемы относительно принимаемого
решения нет. Для всякого Fj вариант Е1 – наилучший.
4.3. ПРОИЗВОДНЫЕ КРИТЕРИИ
4.3.1. Критерий Гурвица
Стараясь занять наиболее уравновешенную позицию, Гурвиц [4] предложил критерий (HW), оценочная функция которого
находится где-то между точками зрения предельного оптимизма (4.4) и крайнего пессимизма (4.6):
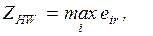 (4.18)
(4.18)
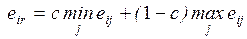 (4.19)
(4.19)
Тогда
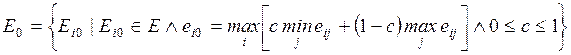 ,
,
где с – весовой множитель.
Правило выбора согласно
HW-критерию формулируется нами следующим образом:
Матрица решений ||eij||
дополняется столбцом, содержащим средние взвешенные наименьшего и наибольшего
результатов для каждой строки (4.19).
Выбираются те варианты Eij, в строках которых
стоят наибольшие элементы eir
этого столбца.
Для с=1 HW-критерий превращается в ММ-критерий. Для с=0 он превращается в критерий азартного
игрока. Отсюда ясно, какое значение имеет весовой множитель с. В технических приложениях правильно
выбрать этот множитель бывает так же трудно, как 'правильно выбрать критерий. Вряд
ли возможно найти количественную характеристику для тех долей оптимизма и
пессимизма, которые присутствуют при принятии решения. Поэтому чаще всего
весовой множитель с=0,5 без возражений принимается в качестве
некоторой «средней» точки зрения. При обосновании выбора применяют обратный
порядок действий. Для приглянувшегося решения вычисляется весовой множитель с, и он интерпретируется как показатель
соотношения оптимизма и пессимизма. Таким образом, позиции, исходя из которых
принимаются решения, можно рассортировать по крайней мере задним числом.
В табл. 4.9
представлена матрица решений, из которой хорошо видно, что выбор в соответствии
с HW-критерием может, несмотря на вполне
уравновешенную точку зрения, приводить к нерациональным решениям. Пример построен
так, что оптимальное (согласно HW-критерию)
решение Е0 есть Е1 независимо от весового
множителя.
Таблица 4.9
Пример
матрицы решений в соответствии
с HW-критерием
|
|
f1
|
f2
|
f3
|
f4
|
…
|
fn-1
|
fn-2
|
|
E1
|
10000
|
1
|
1
|
1
|
…
|
1
|
1
|
|
E2
|
9999
|
9999
|
9999
|
9999
|
…
|
9999
|
0,99
|
HW-критерий
предъявляет к ситуации, в которой принимается решение, следующие требования:
– о вероятностях
появления состояний Fj, ничего не известно;
– с появлением
состояний Fj необходимо считаться;
– реализуется лишь
малое количество решений;
– допускается
некоторый риск.
4.3.2. Критерий
Ходжа-Лемана
Критерий Ходжа-Лемана
(HL) опирается
одновременно на ММ-критерий (4.10) и
ВL-критерий (4.13). С помощью параметра v выражается степень доверия к используемому распределению
вероятностей. Если это доверие велико, то акцентируется ВL-критерий, в противном случае
предпочтение отдается ММ-критерию.
Оценочная функция определяется равенством
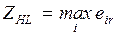 , (4.20)
, (4.20)
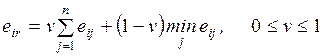 , (4.21)
, (4.21)
а множество HL-оптимальных
решений записывается в виде
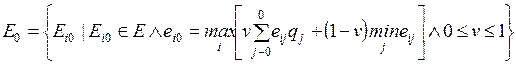 . (4.22)
. (4.22)
Правило выбора, соответствующее HL-критерию, формулируется следующим образом: ;
Матрица решений ||eij||
дополняется столбцом, составленным из средних взвешенных (с постоянными весами)
математического ожидания и наименьшего результата каждой строки (4.21). Отбираются те
варианты решений Еi0,
в строках которых стоит наибольшее значение этого столбца.
Для v=l HL-критерий переходит в BL-критерий, а для v=0превращается в ММ-критерий.
Степень уверенности в какой-либо функции распределения
практически не поддается оценке. Сам критерий тоже не дает для этого точки опоры. Таким образом, выбор
параметра v подвержен
влиянию субъективизма. Кроме того, без внимания остается и число реализации.
Поэтому HL-критерий не применяется при
принятии технических решений.
Следующие свойства ситуации, в которой принимается решение,
предполагаются рассматриваемым критерием:
– вероятности появления состояний Fj
неизвестны, но некоторые предположения о распределениях вероятностей возможны;
– принятое решение теоретически допускает бесконечно, много реализации;
– при малых числах реализации допускается некоторый риск.
4.3.3. Критерий Гермейера
Отправляясь от подхода Гермейера к отысканию эффективных и
пригодных к компромиссу решений в области полиоптимизации – то есть всех решений, которые не считаются
заведомо худшими, чем другие, – можно
предложить еще один критерий [4],
обладающий в некотором отношении определенной эластичностью. Он с самого начала
ориентирован на величины
потерь, то есть на отрицательные значения всех еij.
В качестве оценочной функции выступает
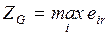 , (4.23)
, (4.23)
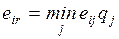 . (4.24)
. (4.24)
Сам критерий гласит, таким образом,
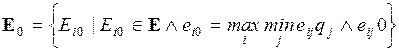 . (4.25)
. (4.25)
Поскольку в хозяйственных задачах преимущественно имеют дело
с ценами и затратами, условие eij<0
обычно выполняется. В случае же, когда среди величин eij
встречаются и положительные значения, можно перейти к строго отрицательным
значениям с помощью преобразования еij–a при подходящим образом подобранном а>0. (Следует, однако, иметь в виду,
что оптимальный вариант решения зависит от а.)
Правило выбора согласно критерию Гермейера (G) формулируется теперь следующим
образом:
Матрица решений ||еij||
дополняется еще одним столбцом, содержащим в каждой строке наименьшее
произведение имеющегося в ней результата на вероятность соответствующего
состояния Fj. Выбираются те
варианты Еi0, в строках которых находится наибольшее
значение eir этого столбца.
В известном отношении
G-критерий обобщает ММ-критерий. В случае равномерного распределения 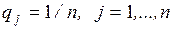 они становятся
идентичными.
они становятся
идентичными.
Условия его применимости таковы:
– вероятности появления состояний Fj известны;
– с появлением тех или
иных состояний, отдельно или в комплексе, необходимо считаться;
– допускается
некоторый риск;
– решение может
реализоваться один или много раз.
Если функция распределения известна не очень надежно, а числа
реализации малы, то, следуя G-критерию,
получают, вообще говоря, неоправданно большой риск. Таким образом, здесь остается
некоторая свобода для субъективных действий.
4.3.4. BL (MM)-критерий
Стремление получить критерии, которые бы лучше приспосабливались
к имеющейся ситуации, чем все до сих пор рассмотренные, привело к построению
так называемых составных критериев. В качестве примера критериев,
сформированных с этой целью, приведем критерий
IV из работы [4].
Исходным для построенного был
BL-критерий (см. (4.11) и (4.12)). Вследствие того, что распределение 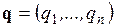 устанавливается
эмпирически и потому известно неточно, происходит, с одной стороны, ослабление
критерия, а с другой, напротив, с помощью заданных границ для риска и
посредством ММ-критерия (см. (4.8) и (4.9)) обеспечивается соответствующая свобода
действий. Точные формулировки состоят в следующем.
устанавливается
эмпирически и потому известно неточно, происходит, с одной стороны, ослабление
критерия, а с другой, напротив, с помощью заданных границ для риска и
посредством ММ-критерия (см. (4.8) и (4.9)) обеспечивается соответствующая свобода
действий. Точные формулировки состоят в следующем.
Зафиксируем прежде всего задаваемое ММ-критерием опорное
значение:
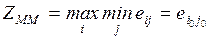 ,
,
где i0
и j0 – оптимизирующие
индексы для рассматриваемых вариантов решений и, соответственно, состояний.
Посредством некоторого заданного или выбираемого уровня допустимого
риска 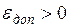 определим некоторое
множество согласия, являющееся подмножеством множества индексов {1, …, т}:
определим некоторое
множество согласия, являющееся подмножеством множества индексов {1, …, т}:
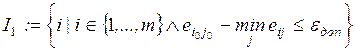 . (4.26)
. (4.26)
Величина 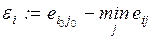 , для всех
, для всех 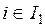 характеризует
наибольшие возможные потери в сравнении со значением
характеризует
наибольшие возможные потери в сравнении со значением 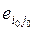 задаваемым
ММ-критерием. С другой стороны, в результате такого снижения открываются и
возможности для увеличения выигрыша по сравнению с тем, который обеспечивается
ММ-критерием. Поэтому мы рассматриваем также (опять-таки как подмножество
множества {1,...,m})
некоторое выигрышное множество
задаваемым
ММ-критерием. С другой стороны, в результате такого снижения открываются и
возможности для увеличения выигрыша по сравнению с тем, который обеспечивается
ММ-критерием. Поэтому мы рассматриваем также (опять-таки как подмножество
множества {1,...,m})
некоторое выигрышное множество
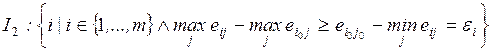 (4.27)
(4.27)
Тогда в множество-пересечение 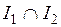 мы соберем только такие варианты
решений, для 'которых, с одной стороны, в определенных состояниях могут иметь
место потери по сравнению с состоянием, задаваемым ММ-критерием, но зато в
других состояниях имеется по меньшей мере такой же прирост выигрыша. Теперь
оптимальными в смысле BL
(ММ)-критерия будут решения из множества
мы соберем только такие варианты
решений, для 'которых, с одной стороны, в определенных состояниях могут иметь
место потери по сравнению с состоянием, задаваемым ММ-критерием, но зато в
других состояниях имеется по меньшей мере такой же прирост выигрыша. Теперь
оптимальными в смысле BL
(ММ)-критерия будут решения из множества
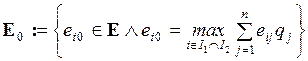 . (4.28)
. (4.28)
Правило выбора для этого критерия формулируется следующим
образом.
Матрица решений ||eij||
дополняется еще тремя столбцами, В первом из них записываются математические
ожидания каждой из строк, во втором – разности между опорным значением 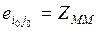 и наименьшим значением
и наименьшим значением 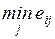 соответствующей
строки. В третьем столбце помещаются разности между наибольшим значением
соответствующей
строки. В третьем столбце помещаются разности между наибольшим значением 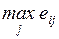 каждой строки и
наибольшим значением
каждой строки и
наибольшим значением 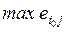 той строки, в
которой находится значение
той строки, в
которой находится значение 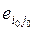 . Выбираются те варианты
. Выбираются те варианты
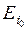 строки которых (при
соблюдении приводимых ниже соотношений между элементами второго и третьего
столбцов) дают наибольшее математическое ожидание. А именно, соответствующее
значение
строки которых (при
соблюдении приводимых ниже соотношений между элементами второго и третьего
столбцов) дают наибольшее математическое ожидание. А именно, соответствующее
значение  из второго
столбца должно быть меньше или равно некоторому заранее заданному уровню риска
из второго
столбца должно быть меньше или равно некоторому заранее заданному уровню риска 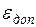 . Значение же из третьего столбца должно быть больше значения
из второго столбца.
. Значение же из третьего столбца должно быть больше значения
из второго столбца.
Применение этого критерия обусловлено следующими признаками
ситуации, в которой принимается решение:
– вероятности появления состояний Fj
неизвестны, однако имеется некоторая априорная информация в пользу какого-либо
определенного распределения;
– необходимо считаться
с появлениями различных состояний как по отдельности, так и в комплексе;
– допускается
ограниченный риск;
– принятое решение
реализуется один раз или многократно.
Таким образом, спектр применимости нашей теории распространяется
далеко за пределы предыдущих критериев. Особо следует подчеркнуть, что действие
новых критериев остается вполне обозримым, хотя функция распределения может
играть лишь подчиненную роль.
BL
(ММ)-критерий хорошо приспособлен для построения практических решений прежде
всего в области техники и может считаться достаточно надежным. Однако задание
границы риска 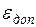 и, соответственно,
оценок риска
и, соответственно,
оценок риска  не учитывает ни число
применений решения, ни иную подобную информацию. Влияние субъективного фактора
хотя и ослаблено, но не исключено полностью.
не учитывает ни число
применений решения, ни иную подобную информацию. Влияние субъективного фактора
хотя и ослаблено, но не исключено полностью.
Условие 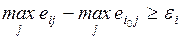 существенно в тех
случаях, когда решение реализуется только один или малое число раз. В этих случаях
недостаточно ориентироваться на риск, связанный лишь с невыгодными внешними
состояниями и средними значениями. Из-за этого, правда, можно понести некоторые
потери в удачных внешних состояниях. При большом числе реализации это условие
перестает быть таким уж важным. Оно даже допускает разумные альтернативы. В
вышеизложенном не видно, однако, четких количественных указаний, в каких
случаях это условие следовало бы опустить.
существенно в тех
случаях, когда решение реализуется только один или малое число раз. В этих случаях
недостаточно ориентироваться на риск, связанный лишь с невыгодными внешними
состояниями и средними значениями. Из-за этого, правда, можно понести некоторые
потери в удачных внешних состояниях. При большом числе реализации это условие
перестает быть таким уж важным. Оно даже допускает разумные альтернативы. В
вышеизложенном не видно, однако, четких количественных указаний, в каких
случаях это условие следовало бы опустить.
В заключение, не вдаваясь в детали, опишем некоторую комбинацию
критерия Байеса–Лапласа с критерием Сэвиджа, называемую нами по аналогии с
изложенным BL(S)-критерием; для этого
сравним соотношения (4.11), (4.12) и (4.13) с (4.14)
– (4.17). За опорную величину примем
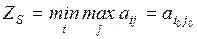 ,
,
где 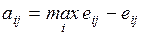 . Через
. Через 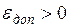 вновь определим
допустимую границу риска. При этом уравнения
(4.26) и (4.27) приобретают вид
вновь определим
допустимую границу риска. При этом уравнения
(4.26) и (4.27) приобретают вид
где  – допустимая граница
риска.
– допустимая граница
риска.
Для
Е0 имеем:
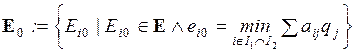 .
.
4.3.5. Критерий
произведений
Критерий произведений (Р) до сего времени в теории принятия
решений не применялся. В теории нечетких множеств эта П-операция служит для
фильтрации информации. С самого начала этот критерий ориентирован на величины
выигрышей, то есть на положительные значения eij.
Определим оценочную функцию:
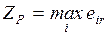 , (4.29)
, (4.29)
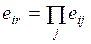 . (4.30)
. (4.30)
Тогда
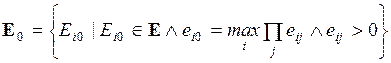 . (4.31)
. (4.31)
Правило выбора в этом случае формулируется так.
Матрица решений ||eij||дополняется
новым столбцом, содержащим произведения всех результатов каждой строки.
Выбираются те варианты Еi0, в
строках которых находятся наибольшие значения этого столбца.
Применение этого критерия обусловлено следующими обстоятельствами:
– вероятности появления состояний Fj неизвестны;
– с появлением каждого
из состояний Fj по отдельности необходимо
считаться;
– критерий применим и при малом числе реализации решения;
– некоторый риск
допускается.
Как уже упоминалось, Р-критерий приспособлен в первую очередь
для случаев, когда все eij положительны. Если
указанное условие нарушается, а Р-критерий приходится применять и в этом
случае, то следует выполнить некоторый сдвиг eij+a с некоторой константой  . Разумеется, результат применения критерия существенно
зависит от этого значения а. На
практике в качестве значения а охотно
используют величину
. Разумеется, результат применения критерия существенно
зависит от этого значения а. На
практике в качестве значения а охотно
используют величину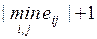 . Если же никакая константа не может быть признана имеющей
смысл, то к таким проблемам Р-кри-терий не применим.
. Если же никакая константа не может быть признана имеющей
смысл, то к таким проблемам Р-кри-терий не применим.
Выбор оптимального решения согласно Р-критерию оказывается
значительно менее пессимистическим, чем, например, выбор в соответствии с
ММ-критерием. Его тесная связь с нейтральным критерием (4.5) усматривается, например, из следующего рассуждения. Из
строгой монотонности логарифмической функции следует, что значение 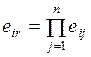 , рассматриваемое в зависимости от i,
максимально в точности тогда, когда максимален
, рассматриваемое в зависимости от i,
максимально в точности тогда, когда максимален 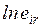 причем мы
предполагаем здесь, что eij>0 для всех i
и j.
причем мы
предполагаем здесь, что eij>0 для всех i
и j.
Теперь имеем 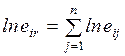 , и эта величина, очевидно, достигает максимума
одновременно
, и эта величина, очевидно, достигает максимума
одновременно 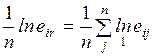 . Последнее же выражение
в точности соответствует нейтральному BL-критерию
(4.5), если только величины еij – в нем заменить на логарифмы
. Последнее же выражение
в точности соответствует нейтральному BL-критерию
(4.5), если только величины еij – в нем заменить на логарифмы 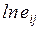 .
.
Таким образом, в результате применения Р-критерия происходит
некоторое выравнивание между большими и малыми значениями eij,
и, устанавливая оптимальный вариант решения с помощью Р-критерия, мы можем при
фиксированных состояниях Fj
получить большую выгоду, чем при использовании ММ-критерия, но при этом должна
учитываться возможность появления и худших результатов. Следует отметить, что
при использовании этого критерия ни число реализации, ни информация о
распределении вероятностей не принимаются во внимание.
Если оптимальный результат, полученный согласно Р-кри-терию,
определяется преимущественно малыми значениями результатов, это указывает на
довольно-таки пессимистический подход, аналогичный ММ-критерию. При возрастании
полезного эффекта пессимистический акцент снижается и по существу происходит
все большее сближение данного критерия с нейтральным. Тем самым достигается,
правда, определенное выравнивание между пессимистической и нейтральной точками
зрения, однако это выравнивание не есть результат какой-либо определенной
характеристики ситуации, в которой принимаются решения, а скорее объясняется
более или менее случайным набором возможных результатов.
4.3.6. Принятие решений
согласно производным критериям
Для построения оптимальных вариантов решения согласно производным
критериям вновь рассмотрим матрицу решений о проведении проверок из разд. 4.2.5, табл.
4.7. Табл. 4.10 показывает применение HW-критерия (4.12) при с=0,5.
Таблица 4.10
Построение
оптимального решения для матрицы решений о проверках по HW-критерию при с =0,5 (данные в 103)
|
|
||eij||
|
|
|
|
eir
|
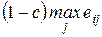
|
|
–20,0
|
–22,0
|
–25,0
|
–12,5
|
–10,0
|
–22,5
|
|
|
–14,0
|
–23,0
|
–31,0
|
–15,5
|
–7,0
|
–22,5
|
|
|
0
|
–24,0
|
–40,0
|
–20,0
|
0
|
–20,0
|
–20,0
|
Таблица 4.11
Построение
оптимального решения для матрицы решений
о
проверках по HL-критерию при qi=0,33
и v=0,5 (данные в 103)
|
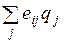
|
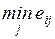
|
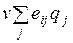
|
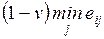
|
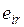
|
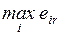
|
|
–22,33
|
–25,0
|
–11,17
|
–12,5
|
–23,67
|
–23,67
|
|
–22,67
|
–31,0
|
–11,34
|
–15,5
|
–26,84
|
|
|
–21,33
|
–40,0
|
–10,67
|
–20,0
|
-30,76
|
|
Таблица 4.12
Построение
оптимального решения для матрицы решений
о
проверках по G-критерию при qj=0,33 (данные в
103)
|
|
||eij||
|
|
|
||eijqj||
|
|
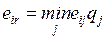
|
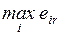
|
|
–20,0
|
–22,0
|
–25,0
|
–6,67
|
–7,33
|
–8,33
|
–8,33
|
–8,33
|
|
–14,0
|
–23,0
|
–31,0
|
4,67
|
–7,67
|
–10,33
|
–10,33
|
|
|
0
|
–24,0
|
–40,0
|
0
|
–8,0
|
–13,33
|
–13,33
|
|
Таблица 4.13
Построение
оптимального решения для матрицы решений
о
проверках по BL
(ММ)-критерию при qj=0,33 (данные в 103)
|
|
|
|
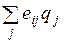
|
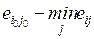
|
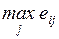
|
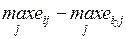
|
|
–20,0
|
–22,0
|
–25,0
|
–22,33
|
0
|
–20,0
|
0
|
|
–14,0
|
–23,0
|
–31,0
|
–22,67
|
+6,0
|
–14,0
|
+6,0
|
|
0
|
–24,0
|
–40,0
|
–21,33
|
+15,0
|
0
|
+20,0
|
В рассматриваемом примере у решения имеется поворотная точка
относительно весового множителя с.
Вплоть до с=0,57 в качестве оптимального выбирается вариант E3,
а при больших значениях –Е1.
Для применения HL-критерия
(4.22) сначала из разд. 4.2.5, табл. 4.7, переносятся построенные там столбцы 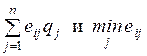 . Табл. 4.11 содержит результаты расчетов для
. Табл. 4.11 содержит результаты расчетов для  и
и 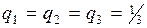
В этом случае HL-критерий
рекомендует вариант Е1
(полную проверку) – так же как и
ММ-критерий. Смена рекомендуемого варианта происходит только при v=0,94. Поэтому равномерное распределение состояний
рассматриваемой машины должно распознаваться с довольно высокой вероятностью,
чтобы его можно было выбрать по большему математическому ожиданию. При этом
число реализации решения всегда остается произвольным.
Табл. 4.12
иллюстрирует выбор оптимального варианта согласно G-критерию (4.25) при 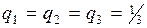 .
.
В качестве оптимального выбирается вариант Е1. Сравнение вариантов с помощью величин еir показывает, что способ
действия G-критерия является даже более
гибким, чем у ММ-критерия.
Табл. 4.13
иллюстрирует выбор решения в соответствии с BL (ММ)-критерием (4.12)
при 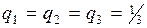 . Вариант Е3 (отказ от проверки) принимается
этим критерием только тогда, когда риск приближается к eвозм=15·103. В противном случае оптимальным оказывается Е1. Во многих технических или хозяйственных задачах допустимый риск
бывает намного ниже, составляя обычно лишь незначительный процент от общих
затрат. В подобных случаях бывает особенно ценно, если неточное знание
распределения вероятностей сказывается не очень сильно. Если при этом
оказывается невозможным установить допустимый риск eдоп заранее,
независимо от принимаемого решения, то помочь может вычисление ожидаемого риска
eвозм.
Тогда становится возможным подумать, оправдан ли подобный риск. Такое
исследование обычно дается легче.
. Вариант Е3 (отказ от проверки) принимается
этим критерием только тогда, когда риск приближается к eвозм=15·103. В противном случае оптимальным оказывается Е1. Во многих технических или хозяйственных задачах допустимый риск
бывает намного ниже, составляя обычно лишь незначительный процент от общих
затрат. В подобных случаях бывает особенно ценно, если неточное знание
распределения вероятностей сказывается не очень сильно. Если при этом
оказывается невозможным установить допустимый риск eдоп заранее,
независимо от принимаемого решения, то помочь может вычисление ожидаемого риска
eвозм.
Тогда становится возможным подумать, оправдан ли подобный риск. Такое
исследование обычно дается легче.
Выбор решения согласно Р-критерию (4.29) иллюстрирует табл.4.14.
Условие еij>0
для данной матрицы не выполнено. Поэтому к элементам матрицы добавляется (по
внешнему произволу) сначала а=41·103,
а затем а=200·103.
Дальнейшее показано в табл. 4.14. Для а=41·103 оптимальным
оказывается вариант E1, а для 200·103 – вариант Е3, так что
здесь снова видна зависимость оптимального варианта от значения а.
В табл. 4.15 сведены
воедино рекомендации всех критериев.
Таблица 4.14
Построение
оптимального решения для матрицы решений
о
проверках по Р-критерию при а=41·103
и а=200·103 (данные в 103)
|
|
|
||eij+a||
|
|
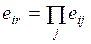
|
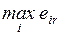
|
|
a = 41
|
+21
|
+19
|
+16
|
638
|
6384
|
|
+27
|
+18
|
+10
|
4680
|
|
|
+41
|
+17
|
+1
|
697
|
|
|
a = 200
|
+180
|
+178
|
+175
|
5607
|
|
|
+186
|
+177
|
+169
|
5563
|
|
|
+200
|
+176
|
+160
|
5632
|
5632
|
Таблица 4.15
Оптимальные
варианты для задачи о проверках, полученные
с
помощью различных критериев и разных значений
характеристических
параметров
|
|
Критерии
|
|
|
ММ
|
BL
|
S
|
HW
|
HL
|
G
|
BL(MM)
|
P
|
|
E1
|
+
|
|
+
|
c³0,57
|
v£0,94
|
qj=0,33
|
eдоп<15·103
|
a=41·103
|
|
E2
|
|
|
|
|
|
|
|
|
|
E3
|
|
qj=0,33
|
|
c<0,57
|
v>0,94
|
|
eдоп³15·103
|
a=200·103
|
Видно, что применение производных критериев повышает надежность
решения. Вариант Е2
оказывается невыгодным с различных точек зрения. Критерии G и BL(MM)
выделяют вариант Е1. Критерий BL(MM) устанавливает уровень риска, который следует превысить, чтобы
выбрать Е3. Если число
реализации нашего решения не слишком велико, то следует предпочесть вариант Е1, хотя классические
критерии не высказываются единогласно в пользу какого-либо из вариантов.
Литература
1. Мушик
Э., Мюллер П. Методы принятия технических решений. Пер. с нем. –М.: Мир, 1990.
2. Таха
Х. Введение в исследование операций. В 2-х книгах. Кн. 2. Пер. с англ. –М.:
мир, 1985.
3. Управление
в системах РАВ: Учебник. –Л.: Воениздат, 1980.
Л.Р.№
020308 от 14.02.97
Евгений Сергеевия Голик
Математические методы
системного анализа и
теории принятия решений
Часть II
Учебное пособие
Редактор .
Подписано в печать Формат 60´84
Б..кн.-журн. П.л. 1,5
Б.Л. 0,75 РТП РИО СЗПИ
Тираж
100 Заказ
Редакционно-издательский отдел
Северо-Западного заочного
политехнического института
191186, Санкт-Петербург, ул.
Миллионная, 5