Содержание
Тема
1. Предмет и значение логики. 3
Тема
2. Логика и язык. 6
Тема
3. Основные методологические принципы логики. 7
Тема
4. Суждение. 8
Тема
5. Выражение суждений на языке логики предикатов. 11
Тема
6. Логическая характеристика вопросов. 13
Тема 7. Норма. 14
Тема
8. Умозаключение. Дедуктивные умозаключения. 16
Тема
9. Категорический силлогизм.. 17
Тема
11. Индуктивные умозаключения. 18
Тема
13. Аналогия. 19
Тема
14. Понятие. 20
Тема
15. Отношения между понятиями. 22
Теме
16. Виды определений. 26
Тема17.
Правила определения. Ошибки. 27
Тема
18. Деление и его виды. Ошибки. 29
Тема
19. Классификация. 32
Тема
20. Аргументация и доказательство. 35
Тема
21. Стратегия и тактика аргументации и критики. 37
Тема
22. Правила построения логических правил. 38
Тема
23. Проблема и гипотеза. 40
Тема
24. Теория. 43
Тема
25. Управленческое решение. 46
Тема 1. Предмет и
значение логики
Для того чтобы определить, что
такое логика, мы должны предварительно выяснить, в чём заключается цель
человеческого познания. Цель познания заключается в достижении истины при
помощи мышления, цель познания есть истина. Логика же есть наука, которая
показывает, как должно совершаться мышление, чтобы была достигнута истина;
каким правилам мышление должно подчиняться для того, чтобы была достигнута
истина. При помощи мышления истина иногда достигается, а иногда не достигается.
То мышление, при помощи которого достигается истина, должно быть названо
правильным мышлением. Таким образом, логика может быть определена как наука о
законах правильного мышления, или наука о законах, которым подчиняется правильное
мышление.
Из этого определения видно, что
логика исследует законы мышления. Но так как исследование законов мышления как
известного класса психических процессов является также предметом психологии, то
предмет логики выяснится лучше в том случае, если мы рассмотрим отличие логики
от психологии в исследовании законов мышления.
На мышление мы можем смотреть с
двух точек зрения. Мы можем на него смотреть прежде всего как на известный
процесс, законы которого мы исследуем. Это будет точка зрения психологическая.
Психология изучает, как совершается процесс мышления. С другой стороны, мы
можем смотреть на мышление, как на средство достижения истины. Логика
исследует, каким законам должно подчиняться мышление, чтобы оно могло привести
к истине.
Итак, разница между психологией и
логикой в отношении к процессу мышления может быть выражена следующим образом.
Психология рассматривает безразлично всевозможные роды мыслительной
деятельности: рассуждение гения, бред больного, мыслительный процесс ребёнка,
животного — для психологии представляют одинаковый интерес, потому что она
рассматривает только, как осуществляется процесс мышления; логика же
рассматривает условия, при которых Мысль может быть правильной. В этом
отношении логика сближается с грамматикой. Подобно тому, как грамматика
указывает правила, которым должна подчиняться речь, чтобы быть правильной, так
логика указывает нам законы, которым должно подчиняться наше мышление для того,
чтобы быть правильным.
Для того чтобы понять
утверждение, что существуют известные правила, которым должно подчиняться
мышление, рассмотрим, в чём заключается задача логики.
Есть положения или факты,
истинность которых усматривается непосредственно, и есть положения или факты,
истинность которых усматривается посредственно, именно через посредство других
положений или фактов. Если я скажу: «я голоден», «я слышу звук», «я ощущаю
тяжесть», «я вижу, что этот предмет большой», «я вижу, что этот предмет
движется» и т. п., то я выражу факты, которые должны считаться непосредственно
познаваемыми. Такого рода факты мы можем назвать также непосредственно очевидными,
потому что они не нуждаются ни в каком доказательстве: их истинность очевидна
без доказательств. В самом деле, разве я нуждаюсь в доказательстве, что передо
мной находится предмет, имеющий зелёный цвет? Неужели, если бы кто-нибудь стал
доказывать, что этот предмет не зелёный, а чёрный, я поверил бы ему? Этот факт
для меня непосредственно очевиден. К числу непосредственно очевидных положений
относятся, прежде всего, те положения, которые являются результатом
чувственного восприятия.
Все те факты, которые совершаются
в нашем отсутствии (например, прошедшие явления, а также и будущие), могут быть
познаваемы только посредственно. Я вижу, что дождь идёт, — это факт
непосредственного познания; что ночью шёл дождь, есть факт посредственного
познания, потому что я об этом узнаю через посредство другого факта, именно
того факта, что почва мокрая. Факты посредственного познания или просто
посредственное познание является результатом умозаключения, вывода. По
развалинам я умозаключаю, что здесь был город. Если бы я был на этом месте
тысячу лет назад, то я непосредственно воспринял бы этот город. По следам я
заключаю, что здесь проехал всадник. Если бы я был здесь час назад, то я
непосредственно воспринял бы самого всадника.
Посредственное знание
доказывается, делается убедительным, очевидным при помощи знаний
непосредственных. Этот последний процесс называется доказательством.
Таким образом, есть положения,
которые не нуждаются в доказательствах, и есть положения, которые нуждаются в
доказательствах и очевидность которых усматривается посредственно, косвенно.
Если есть положения, которые
нуждаются в доказательствах, то в чём же заключается доказательство?
Доказательство заключается в том, что мы положения неочевидные стараемся свести
к положениям или фактам непосредственно очевидным или вообще очевидным. Такого
рода сведение положений неочевидных к положениям очевидным лучше всего можно
видеть на доказательствах математических; Если возьмём, например, теорему Пифагора,
то она на первый взгляд совсем не очевидна.
Но если мы станем её доказывать,
то, переходя от одного положения к другому, мы придём в конце концов к аксиомам
и определениям, которые имеют непосредственно очевидный характер. Тогда и самая
теорема сделается для нас очевидной. Таким образом, познание посредственное
нуждается в доказательствах; познание непосредственное в доказательствах не
нуждается и служит основой для доказательства познаний посредственных.
Заметив такое отношение между
положениями посредственно очевидными и положениями непосредственно очевидными,
мы можем понять задачи логики. Когда мы доказываем что-либо, т. е. когда мы
сводим неочевидные положения к непосредственно очевидным, то в этом процессе
сведения мы можем сделать ошибку: наше умозаключение может быть ошибочным. Но
существуют определённые правила, которые показывают, как отличать умозаключения
правильные от умозаключений ошибочных. Эти правила указывает логика. Задача
логики поэтому заключается в том, чтобы показать, каким правилам должно
следовать умозаключение, чтобы быть верным. Если мы эти правила знаем, то мы
можем определить, соблюдены ли они в том или другом процессе умозаключения.
Из такого определения задач
логики можно понять значение логики.
Для выяснения значения логики
обыкновенно принято исходить из определения её. Мы видели, что логика
определяется как наука о законах правильного мышления. Из этого определения
логики, невидимому, следует, что стоит изучить законы правильного мышления и
применять их в процессе мышления, чтобы можно было мыслить вполне правильно.
Многим даже кажется, что логика может указывать средства для открытия истины в
различных областях знания.
Но в действительности это
неверно. Логика не поставляет своею целью открытие истин, а ставит своею целью
доказательство уже открытых истин. Логика указывает правила, при помощи которых
могут быть открыты ошибки. Вследствие этого, благодаря логике можно избежать
ошибок. Поэтому становится понятным утверждение английского философа Д.С. Милля, что польза логики главным образом отрицательная. Её
задача заключается в том, чтобы предостеречь от возможных ошибок. Вследствие
этого практическая важность логики чрезвычайно велика. «Когда я принимаю в
соображение, — говорит Д. С. Милль, — как проста теория умозаключения, какого
небольшого времени достаточно для приобретения полного знания её принципов и
правил и даже значительной опытности
в их применении, я не нахожу никакого извинения для тех, кто, желая заниматься
с успехом каким-нибудь умственным трудом, упускает это изучение. Логика есть
великий преследователь тёмного и запутанного мышления; она рассеивает туман,
скрывающий от нас наше невежество и заставляющий нас думать, что мы понимаем
предмет, в то время когда мы его не понимаем. Я убеждён, что в современном
воспитании ничто не приносит большей пользы для выработки точных мыслителей,
остающихся верными смыслу слов и предложений и находящихся постоянно настороже
против терминов неопределённых и двусмысленных, как логика».
Многие часто ссылаются на так
называемый здравый смысл и говорят: «Да ведь ошибки можно находить без помощи
логики, посредством лишь одного здравого смысла». Это, конечно, справедливо, но
часто бывает недостаточно найти ошибку, нужно ещё объяснить её, уметь точно
охарактеризовать и даже обозначить её. Иной знает, что в том или другом
умозаключении есть ошибка, но он не в состоянии сказать, почему это
умозаключение нужно считать ошибочным. Это часто возможно сделать только
благодаря знанию правил логики.
Логика имеет также значение для
определения взаимного отношения между науками. Различие между науками, например
математическими, физическими и историческими, может стать ясным только в том
случае, если мы рассмотрим различие методов познания с логической точки зрения.
Творцом логики как науки следует
считать Аристотеля (384—322). Логика
Аристотеля имела господствующее значение не только в древности, но также и в
средние века, в эпоху так называемой схоластической философии. Заслуживает
упоминания сочинение последователей философа Декарта (1596—1650), которое
называлось: La logique ou lart de penser
(1662). Эта логика, которая называется логикой Port, которая, принадлежит к так
называемому формальному направлению. В Англии Бэкон (1561—1626) считается основателем особого направления в логике,
которое называется индуктивным, наилучшими выразителями которого в современной
логике являются Д.С. Милль
(1806—1873) и Л. Бэн (1818—1903).
Тема 2. Логика и язык
Поскольку
логика изучает формы мышления и способы их выражения в языке, постольку логика
является также наукой о языке. В логике исследуются отдельные аспекты естественных
языков (языков, которые возникли и развиваются в основном стихийно), а также
создаются искусственные языки — специальные языки логики. Одним из таких языков
является язык логики предикатов, широко используемый при выявлении
связей между мыслями по их логическим формам. Основное достоинство этого языка
заключается в том, что его выражения однозначны. В нем нет омонимов и нет
неясных выражений. Это позволяет строго фиксировать ход рассуждений и точно
решать вопрос об их правильности или неправильности, а также ряд других
вопросов.
Лри
логическом анализе язык рассматривается как знаковая система.
Знак
— это
материальный объект, используемый в процессе познания или общения в качестве
представителя какого-либо объекта.
Можно
выделить знаки следующих трех типов: знаки-индексы, знаки-образы,
знаки-символы.
Знаки-индексы
связаны с
представляемыми ими объектами как следствия с причинами. Так, дым говорит о
наличии огня, повышенная температура человека — о заболевании, изменение цвета
ногтей человека — о заболевании внутренних органов, изменение высоты ртутного
столба — об изменении атмосферного давления.
Знаками-образами
являются те
знаки, которые сами по себе несут информацию о представляемых ими объектах
(карта местности, картина, чертеж), поскольку они находятся в отношении подобия
с обозначаемыми объектами.
Знаки-символы
не связаны причинно
и не сходны с представляемыми ими объектами.
Логика
исследует знаки последнего вида.
Как
правило, знаки имеют предметные и смысловые значения. Предметным значением является
тот объект, который представляется (или обозначается) знаком. Смысловое
значение — это выражаемая знаком характеристика объекта, представителем
которого является знак (информации об этом объекте). Предметное значение часто
называют просто значением, а смысловое значение — смыслом.
Некоторые
знаки не имеют значения, т.е. представляют несуществующие объекты (например,
«вечный двигатель»), а некоторые не имеют смысла, т.е. обозначают какие-то
объекты, но не несут о них информации, до крайней мере такой, которая
позволяла бы однозначно выделять предметы, обозначаемые знаком.
Роль
знаков в дознании исследовал еще Аристотель. Этой проблемой занимались Лейбниц
и другие ученые. Особенно актуальным стало развитие учения о знаках в XIX в. в связи с запросами
лингвистики и символической логики. Американский философ Чарльз Пирс
(1839-1914) заложил основы особой науки о знаках — семиотики. В этой
науке выделяют три раздела — синтаксис, семантику и прагматику, что
связано с наличием трех аспектов языка.
Синтаксис
— раздел
семиотики, в котором исследуются отношения между самими знаками (правила
построения и преобразования выражений языка и т.д.). В процессе этого исследования
отвлекаются от смыслов и значений знаков.
Семантика
— раздел
семиотики, в котором прежде всего исследуются отношения знаков к представляемым
ими объектам, а также смыслы знаков, поскольку они являются одним из средств
установления связи знаков и их значений.
Прасматика
изучает
отношение человека к знакам, а также отношения между людьми в процессе
знакового общения.
Тема 3. Основные
методологические принципы логики
Основные методологические принципы формальной логики: тождество,
непротиворечия, исключенного третьего и достаточного основания. Эти принципы
выражают наиболее общие требования, которым должны удовлетворять наши
рассуждения и логические операции с мыслями, если мы ставим перед собой цель
достигать истину рациональными методами.
Принцип тождества
устанавливает требование определенности мышления – в процессе рассуждения,
употребляя некоторый термин, мы должны употребить его в одном и том же смысле,
понимать под ним нечто определенное. Хотя предметы, существующие в объективной
действительности, непрерывно изменяются, в понятиях об этих предметах
выделяется нечто неизменное. В процессе рассуждения нельзя изменять понятия без
специальной оговорки. По-другому принцип тождества можно назвать принципом
оговорок: если изменяешь смысл термина, то оговори это, иначе будешь понят
неправильно.
Принцип непротиворечия
требует, чтобы мышление было последовательным. Он требует, чтобы, утверждая
нечто о чем-то, мы не отрицали того же о том же в том же самом смысле в то же
самое время, т.е. запрещает одновременно принимать некоторое утверждение и его
отрицание.
Противоречия в языковых контекстах иногда
являются неявными. Так, известное утверждение Сократа «Я знаю, что я ничего не
знаю» скрывает в себе противоречие. В самом деле, если Сократ знает, что он ничего
не знает, то он и этого не знает.
Принцип исключенного
третьего требует не отвергать одновременно высказывание и его отрицание.
Высказывания А и
ù А нельзя отвергнуть
одновременно, так как одно из них обязательно истинно, поскольку произвольная
ситуация либо имеет, либо не имеет места в действительности.
Согласно этому принципу нужно уточнять наши
понятия так, чтобы можно было давать ответы на альтернативные вопросы.
Например: «Является ли это деяние преступлением или оно не является
преступлением?». Если бы понятие «преступление» не было точно определено, то в
некоторых случаях на этот вопрос невозможно было бы ответить. Другой вопрос:
«Солнце взошло или не взошло?». Представим себе такую ситуацию: Солнце
наполовину вышло из-за горизонта. Как ответить на этот вопрос? Принцип
исключенного третьего требует, чтобы понятия уточнялись для возможности давать
ответы на такого рода вопросы. В случае с восходом Солнца мы можем, например,
договориться считать, что Солнце взошло, если оно чуть-чуть показалось из-за
горизонта. В противном случае считать, что оно не взошло.
Уточнив понятия, мы можем сказать о двух
суждениях, одно из которых является отрицанием другого, что одно из них
обязательно истинно, т.е. третьего не дано.
Принцип достаточного
основания требует, чтобы всякое утверждение было в какой-то мере
обосновано, т.е. истинность утверждений нельзя принимать на веру.
Суждения, из которых выводится утверждение при
его обосновании (если считать правила логики данными), называются основаниями,
поэтому рассматриваемый принцип называется принципом достаточного основания,
что означает: оснований должно быть достаточно для выведения из них
рассматриваемого утверждения.
Если требование принципа достаточного
основания не выполняется, то утверждения оказываются необоснованными,
голословными.
Тема 4. Суждение
В зависимости от того, что
утверждается или отрицается в суждениях, — принадлежность признака предмету,
отношение между предметами или факт существования предмета,— они делятся на
1) атрибутивные суждения, 2)
суждения с отношениями и 3) суждения существования (экзистенциальные).
1. Атрибутивным (от латинского
attributio — «свойство», «признак») называется суждение о признаке предмета. В
нем отражается связь между предметом и его признаком, эта связь утверждается
или отрицается. Например: «Сроки аренды определяются договором», «Никто из
судей не вправе воздержаться от голосования».
Атрибутивные суждения называют
также категорическими (от греческого kategorikos — «ясный», «безусловный», «не
допускающий иных толкований»),
Атрибутивное, или категорическое,
суждение состоит из субъекта, предиката и связки; его логическая схема S—Р, где
S — субъект суждения, Р — предикат суждения, «—» — связка.
Субъектом суждения называется
понятие о предмете суждения. Понятие о признаке предмета называется предикатом
суждения. Связка выражает отношение между субъектом и предикатом.
Субъект и предикат называются
терминами суждения. Каждый из них играет особую познавательную роль. Субъект
суждения отражает то, о чем мы судим, т.е. предмет суждения. Он содержит
исходное знание. В предикате отражается признак предмета, то, что говорится о
предмете суждения; он содержит новое знание о нем. Например, в суждении «Россия
(S) — суверенное государство (Р)» знание о России выражено в предикате, раскрывающем
один из ее признаков. Поэтому основную смысловую нагрузку несет предикат.
Субъект и предикат образуют
суждение посредством связки. Устанавливая принадлежность или не принадлежность
признака предмету, связка объединяет термины суждения в единое целое. Благодаря
этой функции связка является необходимым элементом суждения.
Рассмотренные до сих пор примеры
атрибутивных суждений включали в свой состав субъект, отражающий один предмет
или класс предметов. Однако в рассуждениях иногда используются суждения,
предикат которых относится не к одному, а к нескольким субъектам, например:
«Права авторов, рационализаторов и изобретателей охраняются государством». Это
суждение является сложным, состоящим из трех простых: «Права авторов охраняются
государством»; «Права рационализаторов охраняются государством»;
«Права изобретателей охраняются
государством» (S1есть Р; S2 есть Р; S3 есть
Р). Но так как все три суждения имеют один и тот же предикат, оно может
рассматриваться как простое со сложным субъектом:
S (S1, S2,S3) есть Р.
Некоторые суждения отражают
принадлежность (или непринадлежность) предмету нескольких признаков. В этом
суждении субъект имеет не один, а два или больше предикатов. Например: «Никто
(S) не может быть подвергнут произвольному аресту (Pi), задержанию (Р2)
или изгнанию (Рз)». Это суждение является сложным, состоящим из трех простых,
но оно может быть рассмотрено как простое с одним сложным предикатом:
S есть Р (P1, Р2,
Рз).
Интерпретация суждений со сложным
субъектом или предикатом как простых позволяет использовать эти суждения в
умозаключениях, посылками которых являются простые суждения.
Атрибутивному суждению может быть
дана объемная интерпретация. В этом случае оно рассматривается не как связь
между предметом и его признаком, а как включение объема одного понятия в объем
другого или исключение из него. Например, в суждении «Россия (S) — суверенное
государство (Р)» субъект (понятие «Россия») включается в объем предиката
(понятие «суверенное государство») — рис. 1а. В суждении «Никто из судей (S) не
вправе воздержаться от голосования (Р)» субъект («судьи») исключается из объема
предиката («лица, имеющие право воздержаться от голосования») — рис.1б.
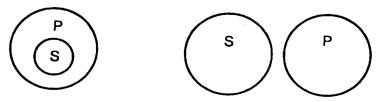
а) б)
Рис.1
Круговые схемы позволяют наглядно
представить отношение между терминами суждения, они широко используются в
анализ( умозаключений, построенных из атрибутивных суждений.
2. Суждением с отношением
называется суждение об отношении между предметами. Это могут быть отношения
равенства, неравенства, родства, пространственные, временные,
причинно-следственные и другие отношения. Например: «А равно В», «С больше D»,
«Семен — отец Сергея», «Казань восточнее Москвы», «Мораль
возникла раньше права», «Пьянство
— причина многих преступлений».
Принята следующая запись суждения
с отношениями: xRy, где х и у — члены отношения, они обозначают понятия о
предметах, R — отношение между ними (R — первая буква латинского слова
relati-vus — «относительный»). Запись читается: х находится в отношении R к у.
Запись отрицательного суждения Ч (xRy) (неверно, что х находится в отношении R
к у).
Суждение с отношениями имеют
структуру, отличающуюся от структуры атрибутивных суждений. Тем не менее они
могут быть преобразованы в атрибутивные. Например, суждение «А равно В»
рассматривается как суждение, где А — субъект суждения, «равно В» — его
предикат; при такой интерпретации равенство предмету В выступает как признак
предмета А. Суждение «Семен — отец Сергея» рассматривается так: «Семен (S) —
отец Сергея (Р)», отец Сергея — признак Семена.
3. В суждениях существования
(экзистенциальных суждениях; от латинского existentia — «существование»)
выражается сам факт существования или несуществования предмета суждения.
Например: «Существуют статистические законы»; «На Земле уже нет многих видов
животных»; «Суждения без предложения не существует». Предикатами этих суждений
являются понятия о существовании или несуществовании предмета; связка, как
правило, в языке не выражается, но путем преобразования грамматической формы
суждения она может быть выражена словами «есть», «не есть», «является» и т.п.
Например: «Статистические законы (S) есть (связка) то, что существует (Р)».
Тема 5. Выражение
суждений на языке логики предикатов
На языке логики предикатов
суждения А, Е, I, О записывают
следующим образом:
А (Все S суть Р): V х (S(x) ->
Р(х))
читается: для всех х, если х
присуще свойство S, то х присуще свойство Р.
Е (Ни одно S не есть Р): V х
(S(x) -> -1 Р(х)) читается: ни одному х, которому присуще свойство S, не
присуще свойство Р.
I (Некоторые S суть Р): Э x(S(x)
л Р(х))
читается: существуют х, которым
присуще свойство S и свойство Р.
О (Некоторые S не суть Р): 3
x(S(x) л 1 Р(х)) читается: существуют х, которым присуще свойство S и не
присуще свойство Р.
Выделяющие и исключающие суждения
Особое место в классификации
суждений занимают 1) выделяющие и 2) исключающие суждения.
1) Количественная характеристика
суждений устанавливает объем субъекта, а что касается предиката, то его объем
остается неопределенным. В самом деле, из суждения «Зимин — свидетель
происшествия» нельзя установить, является ли Зимин единственным или одним из
свидетелей происшествия.
Выделяющие суждения устраняют эту
неопределенность; они выражают тот факт, что признак, выраженный предикатом,
принадлежит (или не принадлежит) только данному, и никакому другому, предмету.
Выделяющие суждения могут быть
единичными, частными и общими. Например: «Только Зимин является свидетелем
происшествия» (S, и только S, есть Р — единичное выделяющее суждение. Оно
выражает знание о том, что Зимин является единственным свидетелем происшествия.
Субъект и предикат этого суждения имеют одинаковый объем.
«Некоторые города — столицы
государств» — пример частного выделяющего суждения (некоторые S, и только S,
суть Р). Столицами государств могут быть только города, и притом только
некоторая их часть. Предикат частного выделяющего суждения полностью входит в
объем субъекта. Другие примеры частных выделяющих суждений: «Некоторые
приговоры суда являются оправдательными»;
«Некоторые преступники —
рецидивисты».
Частные выделяющие суждения не
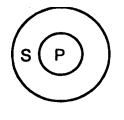
следует смешивать с определенными частными суждениями. Если в определенном
частном суждении уточняется объем субъекта, то в частных выделяющих суждениях
уточняется объем предиката. Так, в суждении «Только некоторые свидетели дали показания»
отношение предиката к субъекту остается неопределенным: показания дают не
только свидетели, но также потерпевший, обвиняемый. Это определенное частное
суждение (рис. 2). В частном выделяющем суждении определено отношение не только
субъекта к предикату, но и предиката к субъекту: некоторые преступники (и
только преступники) — рецидивисты (рис.3).
 «Все преступления, и только преступления, —
предусмотренные законом общественно опасные деяния» — пример общего выделяющего
суждения (Все S, и только S, суть Р). Объемы субъекта и предиката общего
выделяющего суждения полностью совпадают.
«Все преступления, и только преступления, —
предусмотренные законом общественно опасные деяния» — пример общего выделяющего
суждения (Все S, и только S, суть Р). Объемы субъекта и предиката общего
выделяющего суждения полностью совпадают.
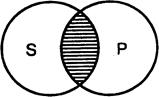
Рис.2 Рис. 3
Слова «только», «лишь», входящие
в состав предложений, выражающих выделяющие суждения, могут находиться как
перед субъектом, так и перед предикатом (например, «Уголовное наказание
применяется только по приговору суда»). Но они могут и вообще отсутствовать. В
этих случаях установить, что данное суждение является выделяющим, помогает
логический анализ.
2) Исключающим называется
суждение, в котором отражается принадлежность (или непринадлежность) признака
всем предметам, за исключением некоторой их части. Например: «Все студенты
нашей группы, кроме Волкова, сдали экзамены», включающие суждения выражаются
предложениями со словами «кроме», «за исключением», «помимо», «не считая» и
т.п. (Все S, за исключением S1,суть Р).
Значение выделяющих и исключающих
суждений состоит в том, что положения, выраженные в форме этих суждений,
характеризуются точностью и определенностью, что исключает их неоднозначное
понимание. Именно поэтому ряд научных положений, а также статей международных
документов, законов государства, статей уголовного, уголовно-процессуального и
других кодексов выражен в форме выделяющих или исключающих суждений. Например,
в Конституции Российской Федерации статьи 118 (часть 1) и 123 (часть 2) гласят:
«Правосудие в Российской Федерации осуществляется только судом», «Заочное
разбирательство уголовных дел в судах не допускается, кроме случаев,
предусмотренных федеральными законами».
Тема 6. Логическая
характеристика вопросов
Вопросы задают в тех случаях, когда
есть познавательная неопределенность.
Характеризуя вопросы с логической точки зрения, следует рассматривать
вопросно-ответные ситуации, включающие предпосылки вопросов.
Благодаря последним вопросы
могут ис пользоваться
для неявной передачи информации. Например, в вопросе «С кем окажется армия, если
будет предпринята попытка государственного переворота?» содержится
информация, что такая попытка возможна и возможно выступление армии на стороне
как организаторов, так и противников переворота.
пользоваться
для неявной передачи информации. Например, в вопросе «С кем окажется армия, если
будет предпринята попытка государственного переворота?» содержится
информация, что такая попытка возможна и возможно выступление армии на стороне
как организаторов, так и противников переворота.
Тот факт, что вопросы имеют предпосылки, используется для
совершения уловки, называемой сокрытие необоснованности
утверждения. Необоснованное утверждение выражается не явно, а в
виде предпосылки вопроса. Например, вместо того чтобы обосновать целесообразность
снижения налогов, властям задают вопрос: «Когда вы начнете снижать
налоги?»
Как реагировать на данную уловку? Нужно явно сформулировать
предпосылку вопроса и сказать, что она является необоснованной,
а также заметить, что совершена уловка «сокрытие необоснованности утверждения».
Другая уловка, связанная с предпосылками вопросов, имеет название подмена
вопроса. Она заключается в следующем. Пользуясь тем, что одним и тем же
вопросительным предложением могут быть выражены разные вопросы из-за различия
в подразумеваемых или содержащихся в контекстах предпосылках,
заданный вопрос заменяют другим или же ответ па один вопрос выдают за ответ на другой.

 Так, в ходе дискуссии о гуманизации уголовных
наказаний противникам отмены смертной казни задавались вопросы:
Так, в ходе дискуссии о гуманизации уголовных
наказаний противникам отмены смертной казни задавались вопросы:
1)
Вы за неотвратимость наказаний или за их ужесточение?
2)
Вы лично, сейчас,
здесь, готовы привести
в исполнение
смертный приговор? На эти вопросы не было
получено ответов.
Как следует отвечать на такие вопросы? Отвечая на первый
вопрос, нужно отметить, что вопрос является логически некорректным,
провокационным, поскольку его предпосылка «Человек должен выступать или за
неотвратимость наказания, или за ужесточение наказания» есть ложное
утверждение. Затем целесообразно предложить исправить вопрос, например,
«разбив его на два вопроса: «Вы за неотвратимость наказания или против
неотвратимости?», «Вы за смягчение наказания или за ужесточение, или за то, чтобы
оставить действующие меры наказания?*
При ответе на второй вопрос тоже нужно сказать, что он является
провокационным, и указать предпосылку: «Если человек не исключает возможность
смертной казни в качестве высшей меры наказания, то он должен быть готов
привести такой приговор в исполнение в любое время, в любом месте». Эта
предпосылка является ложной.
Тавтологичные вопросы. На вопрос данного типа нельзя дать ответа,
снижающего познавательную неопределенность, поскольку таковой нет. Различают
вопросы логически тавтологичные и фактически тавтологичные.
Вопрос является логически тавтологичным, если
запрашиваемая информация выражается его логической формой. Пример:
«Является Сидоров тем человеком, которым он действительно является?» На такие вопросы
нельзя дать ложного ответа, не являющегося логически противоречивым.
Вопрос является фактически тавтологичным, если запрашиваемая
информация выражается всеми терминами, входящими в его формулировку, а не только
логической формой. Пример : «Между кем и кем была русско-японская война?»
Трудные и легкие вопросы. По степени
неопределенности, которую
требуется устранить, вопросы делятся на трудные и легкие. Например, одному студенту, стоящему около боевой машины пехоты (БМП), был задан вопрос: «Где находится
дверь БМП?», а другому: «Где
находится выхлопная труба БМП?» Второй не смог ответить. (Труба находится на крыше БМП.)
Открытые и закрытые вопросы. К вопросам первого
типа относятся те, на которые не существует определенного числа ответов.
Закрытые вопросы требуют определенного числа ответов. Эти вопросы
важно различать при проведении социологических исследований посредством
анкетирования. В большинстве случаев в анкеты должны включаться лишь
закрытые вопросы.
Тема 7. Норма
Нормы говорят, что некто обязан что-то сделать (или воздержаться
от некоторого действия) или что кому-то разрешено (запрещено) определенное
действие (или воздержание от действия).
Примеры предложений, выражающих нормы: «Гражданин России
обязан соблюдать российские законы, где бы он ни находился — в России или за границей»,
«Запрещено проводить пропаганду войны».
Одно и то же предложение в зависимости от контекста может выражать
как норму, так и утверждение о норме.
Пример. В рассуждении «Гражданин России обязан соблюдать
российские законы, где бы он ни находился — в России или за
границей. Петров — гражданин России. Следовательно, Петров обязан
соблюдать российские законы, где бы он ни находился — в России или за границей» первое
из предложении выражает утверждение о
норме. Его можно истолковать
так: «Гражданин России в соответствии
с Конституцией обязан соблюдать российские законы, где бы он ни находился — в России или за границей». Или
так: «Законодатель установил и не отменил, что гражданин России обязан соблюдать российские законы, где бы
он ни находился — в России или за границей».
Утверждения о нормах являются суждениями и оцениваются как
истинные или ложные.
Рассмотрим далее, истинна ли норма кодекса «Запрещено проводить
пропаганду войны». Эта норма не является истинной или ложной в смысле соответствия
или несоответствия объективной реальности.
В
связи с этим возникает вопрос, каково отношение нормы к социальной реальности,
является ли она «картиной, образом действительности»? Для ответа на
вопрос о применимости к нормам характеристики «картина, образ действительности»
необходимо уточнить объект, с которым соотносится норма.
О какой-то норме можно сказать, что она является картиной, образом
действительности, если под действительностью понимать расстановку классовых сил в
обществе; о другой норме этого сказать нельзя, так как она входит в
действующие кодексы государств с различным социальным строем. По первой
можно в определенной мере судить о социальном строе, о том, чьим
интересам служит норма, по второй — нельзя.
Из того факта, что некоторая норма более чем другая характеризует
социальное устройство, нельзя сделать вывод о том, что она истинна, а другая ложна
(конечно, имеются в виду нормы, запрещающие или разрешающие одно и то же деяние и
рассматриваемые в контексте с другими нормами). С точки зрения
выражения нормой интересов определенной социальной группы, вторая может оказаться
более приемлемой.
Норма не является картиной, образом, если ее соотносить, например, с
запросами объективной необходимости общественного
развития. В этом случае вводятся другие оценки — нормативная
истина и нормативная ложь. Норма, соответствующая запросам объективной необходимости
общественного развития, является нормативно-истинной, а не соответствующая —
нормативно-ложной.
Понятия «соответствие» и «несоответствие» нормы запросам объективной
необходимости общественного развития имеют следующий смысл. В силу объективной
закономерности общественного развития общество, находящееся на определенном этапе
развития, движется к определенной цели. Совершая одни деяния (назовем их «деяния первого
рода»), мы способствуем приближению общества к этой цели, совершая другие (второго
рода), препятствуем этому приближению. Нормы, обязывающие выполнять деяния
первого рода, соответствуют запросам объективной необходимости
общественного развития, являются нормативно-истинными, а
нормы, разрешающие или обязывающие выполнять деяния второго рода, не соответствуют
запросам объективной необходимости общественного развития, являются нормативно-ложными.
Норма, соответствующая запросам объективной необходимости на
одной стадии общественного развития, может им не соответствовать на другой стадии, если
она перестанет способствовать в должной мере развитию общества в данном направлении. Кроме
того, объективная необходимость развития общества и наше знание этой необходимости
— не одно и то же. С течением времени наше знание необходимости уточняется,
а уточненное знание требует изменения действующих норм.
Таким образом, согласно точке зрения, в соответствии с которой
признается объективная необходимость общественного развития,
нормы требуют совершенствования, во-первых, вследствие развития общества,
во-вторых, в результате уточнения нашего знания объективной необходимости
общественного развития.
В соответствии с концепциями, в которых не признается объективная необходимость
общественного развития, разрабатываемые нормы тоже можно оценивать как
нормативно-истинные или нормативно-ложные, если они отвечают или не
отвечают целям, которые ставит законодатель, например, максимально служить
интересам определенного класса или общим интересам нескольких или всех
социальных групп, способствовать экономическому развитию общества и т.д.
Тема 8. Умозаключение.
Дедуктивные умозаключения
Дедукция - пер. с лат. выведение. В широком смысле слова это такая
форма мышления, когда новая мысль выводится чисто логическим путем из некоторых
данных мыслей-предпосылок.
В
узком смысле слова это:
а) как дедуктивное умозаключение,
например, все ароматические вещества имеют особый вкус, ваниль - ароматическое
вещество, значит у нее должен быть особый вкус.
Такое
умозаключение применяется человеком всякий раз, когда требуется рассмотреть
какое -либо явление на основании уже известного нам общего положения, и вывести
из этого заключение. Этим методом выводятся все законы, гипотезы, теории, он
используется различными науками.
Впервые
дедукция как теория была обстоятельно разработана Аристотелем, именно он
составил основные правила дедуктивного умозаключения.
б) сущность дедукции как метода
исследования заключается в следующем:
для
того чтобы найти новое знание о предмете, надо найти ближайший род, куда входят
эти предметы или явления, и затем применить к ним закон, присущий всему данному
классу предметов - это есть переход от более общих к менее общим знаниям.
в) дедукция есть форма расположение
материала в художественной литературе, научном докладе.
Тема 9. Категорический
силлогизм
Силлогизм
есть такая форма умозаключения, в которой из двух суждений необходимо вытекает
третье, причём одно из двух данных суждений является обще-утвердительным или
обще-отрицательным.
Силлогизм, таким образом, представляет собой умозаключение от общего.
Полученное суждение ни в коем случае не будет более общим, чем суждения, из
которых оно выводится.
Например, нам даются два суждения:
Все растения суть организмы. ,
Сосны суть растения.
Из них следует, что «сосны суть организмы».
Этот пример показывает, что, если нам даются
два суждения, из них необходимо получается новое суждение. Мы не входим в
рассмотрение того, истинны ли эти суждения или нет, но раз только мы допустим
их, то тотчас же необходимо следует новое суждение.
Части
силлогизма. Данные суждения
называются предпосылками или посылками (praemissae), а новое суждение, которое получается из
сопоставления посылок, называется
заключением (conclusio).
Те понятия, которые входят в заключение и предпосылки, называются терминами (termini). Подлежащее заключения («сосны») называется меньшим термином (terminus minor), сказуемое заключения («организмы»)
называется большим термином (terminus major), а термин («растение»), который не входит в
заключение, называется средним термином
(terminus medius).
Обозначение, терминов большими или меньшими находится зависимости от того, какой объём им присущ в
одном из типичных случаев силлогистического вывода, как в только что
приведённом. Самый больший объём приходится на долю сказуемого («организмы»),
самый меньший — на долю меньшего термина, подлежащего заключения («сосны»), а
средний — на долю среднего термина («растения»), который не входит в
заключение. Это наглядно обнаруживается, если изобразить отношение между
терминами схематически. На рис. 19 S
обозначает меньший термин, М —
средний, Р — больший.
Средний термин называется средним также
потому, что он служит посредствующим связующим элементом между большим и
меньшим терминами. Средний термин служит для сравнения большего термина с
меньшим. Сами по себе эти термины не могут быть сравниваемы. Сравнение может
происходить через посредство среднего термина. Мы не могли бы связать термин
«сосны» с термином «организмы», если бы у нас не было термина «растения»,
который связывается, с одной стороны, с термином «организмы», с другой стороны,
с термином «сосны» и, таким образом, служит связующим звеном между термином
«сосны» и термином «организмы».
Суждение, в которое входит больший термин,
называется большей посылкой;
суждение, в которое входит меньший термин, называется меньшей посылкой.
Тема 11. Индуктивные
умозаключения
Индукция - ( наведение ) - это
форма мышления, посредством которой мысль наводится на какое-либо общее
правило, общее положение, присущее всем единичным предметам какого-либо класса.
Индуктивное
умозаключение сложилось в результате длительной многовековой практики
человечества. Человек замечал, фиксировал в памяти, а затем приходил к общим выводам - как сохранить огонь? Познание большего всегда
начинается с познания его частей - какой металл пригоден для ножа? Как Менделеев
делал общие выводы? Первым начал исследовать индуктивный прием мышления
древнегреческий философ Сократ, затем Аристотель. Этот метод позволяет
предсказывать и прогнозировать возможные изменения процессов, он позволяет
осуществлять поиск. Индукция как метод исследования наиболее полно реализуется
системой статистических методов.
В
узком смысле слова термин "индукция" имеет три следующие значения:
а) индуктивное умозаключение,
когда на основании данных об отдельных предметах данного класса получается
общий вывод, содержащий знания о всех предметах класса:
круг
пересекается прямой в двух точках
эллипс пересекается прямой в двух точках
парабола
пересекается прямой в двух точках
гипербола
пересекается прямой в двух точках
Это все (других нет) виды
конических сечений, отсюда вывод: все
конические сечения пересекаются прямой в двух точках
б) индукция - это метод исследования,
который заключается в следующем:
для
того чтобы получить общие знания о каком-либо классе предметов, необходимо
исследовать дельные предметы этого класса, найти в них существенные признаки,
которые и послужат основой для знания об общем.
Главное - это идет переход от
знаний менее общих положений к знанию более общих.
в) индуктивный прием как метод
изложения материала в художественной книге, научном докладе.
Возможны
две типичные ошибки в индуктивном умозаключении:
-поспешность, возникающая из-за
того, что не учтены все обстоятельства, все причины явления;
-смещение понятий из-за
чередования их во времени: после того это еще не значит, что по причине этого.
Тема 13. Аналогия
Умозаключение по аналогии (или
просто аналогия) – индуктивное умозаключение, когда на основе сходства двух
объектов по каким-то одним параметрам делается вывод об их сходстве также по
другом параметрам.
Например, планеты Марс и Земля во
многом сходны: они расположены рядом в Солнечной системе, на обеих есть вода и
атмосфера и т.д.; на Земле есть жизнь; поскольку Марс похож на Землю с точки
зрения условий, необходимых для существования живого, можно сделать вывод, что
на Марсе также имеется жизнь. Это заключение является, конечно, только
правдоподобным.
Общая схема умозаключения по
аналогии:
Объект А имеет признаки а, b, с.
Объект B сходен с A в том, что
имеет признаки а и b.
Значит, объект В имеет, вероятно, и признак с.
Сопоставление двух объектов, как
бы далеко оно не шло, способно дать только предположительное знание, гипотезу,
нуждающуюся в дальнейшей проверке.
Не всегда аналогия выступает в
такой прозрачной форме, как в приведенных примерах.
У книгопечатника Д.Дантона был
счастливый, но очень, короткий брак: молодая жена его рано скончалась. Спустя
всего полгода он, однако, вновь женился. В истории своей жизни Дантон
оправдывал столь скорое утешение тем, что вторая жена была всего лишь
повторением первой: "Я поменял только лицо, женские же добродетели в моем
домашнем круге остались те же. Моя вторая жена – не что иное, как первая, но
лишь в новом издании, исправленном и расширенном, и я бы сказал: заново
переплетенном".
Здесь отношение новой жены к
предыдущей уподобляется отношению второго издания книги к первому ее изданию.
Какое значение имеет то, что второе издание вышло сразу же вслед за первым?
Любопытно заметить, что, как истинный любитель книги, Дантон ценит именно
первое издание, даже несмотря на то, что оно утрачено.
Аналогия может выступать в форме,
напоминающей популярную индукцию.
К примеру, человек прочел
"Записки Пиквикского клуба" Ч.Диккенса – понравилось, прочел
"Оливера Твиста" – тоже понравилось. На этом основании он заключает,
что и роман Диккенса "Домби и сын", к чтению которого он только
приступил, окажется интересным.
В начале этого и подобных ему
рассуждений констатируется, что каждый из встречавшихся ранее предметов
некоторого рода имел определенное свойство. В заключении выражается
предположение, что и следующий встреченный предмет этого рода также будет
обладать данным свойством. Если бы, прочитав два-три произведения Диккенса и
найдя их интересными, кто-то пришел к мысли, что все произведения этого
классика интересны, – это была бы популярная индукция. В примере же с романом
"Домби и сын" от знания об отдельных объектах совершается переход к
знанию еще об одном, опять-таки индивидуальном объекте.
Другой пример – уже из астрономии
– позволит яснее понять различие между аналогией и популярной индукцией.
И.Кеплер нашел, что Марс описывает вокруг Солнца траекторию в форме эллипса.
Зная также, что имеется много общего между Марсом и Меркурием, Венерой, Землей,
Юпитером и Сатурном, Кеплер заключил, что все планеты Солнечной системы
движутся по эллиптическим орбитам. В этом рассуждении комбинируются аналогия и
популярная индукция. Форма траектории Марса известна, значит, и похожий на него
Меркурий описывает такую же траекторию. Это верно также для Венеры, Земли,
Юпитера и Сатурна. Получив посредством аналогии знание об орбитах отдельных
планет, можно выдвинуть индуктивное обобщение: не только рассмотренные, но и
вообще все планеты Солнечной системы движутся по эллипсам.
Итак, в обычном мышлении
умозаключение по аналогии редко встречается в ясной, не требующей размышления и
реконструкции форме. Чаще всего аналогия оказывается свернутой, какие-то части
умозаключения опускаются. Иногда она протекает так, что ее можно спутать с
популярной индукцией.
Умозаключение по аналогии
— это умозаключение от частного к частному. Сущность умозаключения по аналогии
состоит в том, что на основании сходства двух предметов в некоторых отношениях
делается вывод о сходстве этих предметов и в других отношениях. Умозаключение
по аналогии лежит в основе создания многих гипотез, догадок.
Тема 14. Понятие
Понятия в психологии получаются из сравнений
сходных представлений. Представления в свою очередь складываются из отдельных
элементов. Составные элементы представления или понятия принято называть
признаками. Признаки есть то, чем одно представление или понятие отличается от
другого. Например, признаками золота мы считаем «металл», «драгоценный»,
«имеющий определённый удельный вес» и т. п. Это всё то, чем золото отличается
от других вещей, от не-металлов, от недрагоценных металлов и т. п.
Не все признаки нужно считать равноценными.
Каждое понятие имеет множество различных признаков, но при мышлении о нём мы
прежде всего по преимуществу мыслим только известные признаки. Эти признаки
являются как бы основными, около которых группируются другие признаки. Первые
признаки называются существенными, или основными, а остальные — второстепенными.
Основные признаки — это такие признаки, без которых мы не можем мыслить
известного понятия и которые излагают природу предмета. Например, для ромба
существенным является тот признак, что он есть четырёхугольник с параллельными
и равными сторонами и т. п.; несущественным для понятия ромба является тот признак,
что он имеет ту или другую величину сторон, ту или другую величину углов.
Признаки понятий со времени Аристотеля
принято делить на следующие 5 классов:
1. Родовой признак. Если мы скажем, что химия
есть наука, то наука будет родовым признаком для понятия «химия»; в числе
других признаков, присущих понятию «химия», есть и признак «наука»; этот
признак отличает химию от всего, что не есть наука. Род (genus) или родовой признак есть понятие класса, в
который мы вводим другое рассматриваемое нами понятие.
2. Видовое различие. Если мы скажем, что
химия есть наука, занимающаяся изучением строения вещества, то прибавление
признака — «занимающаяся изучением строения вещества» будет служить для обозначения
того, чем эта наука отличается от других наук. Такой признак, который служит
для того, чтобы выделять понятие из ряда ему подобных понятий, называется видовым
различием (differentia specifica). Возьмём понятия «моряк русский», «моряк
французский», «моряк английский». В этом случае «русский», «французский»,
«английский» есть видовое различие; оно служит для того, чтобы выделить моряка
одной нации от моряков всех прочих наций.
3. Вид (species). Если к родовому признаку присоединить видовое
различие, то получится вид. Например, «здание для склада оружия» == арсенал;
«здание для склада хлеба» = амбар. В этом случае «здание» есть род, «для
хранения оружия» есть видовое различие; присоединение к роду видового различия
даёт вид «арсенал». Присоединение к понятию «здание» видового признака
«служащее для хранения хлеба» даёт вид «амбар». Вид может быть Признаком,
потому что его можно приписать понято. Например, «эта наука есть химия».
4. Собственный признак (proprium). Собственный признак — это такой признак,
который присущ всем вещам данного класса, который не содержится в числе
существенных признаков, но который может быть выведен из них. Например,
существенным признаком человека является его «разумность». Из этого свойства
вытекает его способность владеть речью. Этот последний признак есть
собственный признак. Основной признак треугольника — это прямолинейная плоская
фигура с тремя сторонами. Что же касается того признака треугольника, что
сумма углов его равняется двум прямым, то это есть его собственный признак,
потому что вытекает или выводится из основных признаков.» Мы этого признака не
мыслим, когда думаем о треугольнике, поэтому он является выводным.
5. Несобственный признак (accidens). Несобственный пригнан — это такой
признак, который не может быть выведен из существенного признака, хотя и может
быть присущ всем вещам данного класса. Например, чёрный цвет ворона есть accidens. Если бы чёрный цвет ворона был выводим из
основных свойств то, то он мог бы быть назван proprium, но он не выводим, так как бы не знаем, по
какой причине вороны имеют чёрный цвет юрьев. Он есть, следовательно, accidens.
Несобственные признаки делятся на две группы:
на неотделимые несобственные признаки (accidens inseparable)
и отделимые несобственные признаки (accidens separabile). Последние суть те признаки, которые присущи только некоторым вещам
того или другого класса, но не всем, а первые присущи всем вещам данного
класса. Например, чёрный цвет ворона есть accidens inseparabile. Чёрный цвет волос для человека есть
accidens separabile, потому что
есть люди, которые не имеют чёрного цвета волос. По отношению к отдельным
индивидуумам несобственный признак также может быть отделимым и неотделимым.
Отделимые — это такие признаки, которые одно время имеются налицо, а в другое
время не имеются. Например, Бальфур—первый министр Англии. Через некоторое
время он может не быть первым министром. Это есть признак отделимый. «Лев
Толстой родился в Ясной Поляне». В этом предложении признак «родился в Ясной
Поляне» есть неотделимый признак.
Содержание и объём понятий. Понятия могут
быть рассматриваемы с точки зрения содержания и объёма.
Содержание понятия—это то, что мыслится в
понятии. Например, в понятии «сахар» мыслятся признаки: сладкий, белый,
шероховатый, имеющий тяжесть и т. д.; эти признаки в совокупности и составляют
содержание понятия «сахар». Содержание понятия, другими словами, есть сумма
признаков его; поэтому каждое понятие можно разложить на ряд присущих ему
признаков. Содержание понятия может быть весьма изменчивым в зависимости от
принятой точки зрения, от размера знания и т. п. Например, в понятии «сахар»
химик мыслит одно содержание, а нехимик— другое.
Объём понятия есть то, что мыслится
посредством понятия, т. е. объём понятия есть сумма тех классов, групп, родов,
видов и т.п., к которым данное понятие может быть приложено. Например, объём
понятия «животное»: птица, рыба, насекомое, человек и т. д.; объем понятия
«элемент»: кислород, водород, углерод, азот и т. д.; объём понятия
«четырёхугольник»: квадрат, прямоугольник, ромб, трапеция;
Таким образом, различие между объёмом понятия и содержанием понятия
сводится к следующему: объём понятия означает ту совокупность предметов, к
которым должно прилагаться данное понятие, а содержание обозначает те признаки,
которые приписываются тому или другому понятию.
Тема 15. Отношения между
понятиями
Рассмотрим логические
отношения, существующие между понятиями.
1. Подчинение понятий (subordinatio notionurn) мы имеем в том случае, когда одно понятие
относится к другому, как вид к своему роду, когда одно понятие входит в объём другого как часть его
объема. Для примера возьмём понятие «дерево» А и понятие «берёза» В.
Последнее понятие входит в объём первого. (Символ подчинения понятий см. на
рис. 4.) Другие примеры: «духовная деятельность», «ощущение вкуса», «человек»,
«математик».
2. Соподчинение понятий (coordinatio notionum) мы имеем в том случае, если а объём одного
и того же более широкого понятия входят два иди несколько одинаково подчинённых
ему низших понятий. Эти низшие понятия называются соподчинёнными
(координированными). Например, «мужество» В,
«умеренность» С, «добродетель» А. Оба первых понятия входят в объём
последнего (рис. 5).
|
|
3. Понятия
равнозначащие (notiones aequipollentes). Для
разъяснения этого отношения возьмём два понятия: «английский народ» и «первые
мореплаватели в мире». Когда мы произносим слова «английский народ» и при этом
имеем в уме понятие «английский народ», мы думаем об англичанах. Когда мы
произносим слова «первые мореплаватели», мы также думаем об англичанах;
следовательно, объём этих двух понятий один и тот же. Раскроем теперь
содержание этих понятий. В понятии «английский народ» мы мыслим известное
политическое устройство, известную территорию, известную культуру и т. д., в
понятии же «первые мореплаватели» — известное искусство в постройке кораблей и
управлении ими, известное развитие морской торговли, многочисленность флота и
т. д.; следовательно, содержание этих понятий различно. Если у нас есть два
понятия с различным содержанием, но одинаковым объёмом, то такие понятия
называются равнозначащими. Другие примеры: «христианин — крещёный», «органический
— смертный», «величайший писатель—автор «Войны и мира». Равнозначащие понятия
можно символизировать при помощи двух кругов, сливающихся в один, подобно тому
как сливаются объёмы указанных понятий; различие же содержания символизируется
двумя различными буквами, стоящими в этом круге (рис. 6).
 рис 6
рис 6
4. Противные и противоречащие понятия. На эти
два различных класса понятий, очень сходных по своим внешним свойствам, но в то
же время совершенно различных по существу, следует обратить особенное внимание
и хорошенько продумать их различие, .так как при оперировании с ними легко
впасть в ошибку.
Если мы возьмём объём какого-нибудь понятия и
будем распределять по степени сходства виды, входящие в него, таким образом,
что после каждого вида мы будем брать следующий, наименее от него отличный, то
в конце концов из этих понятий-видов получится ряд, в котором первый и
последний члены очень сильно отличаются друг от друга. Эти-то два понятия, первое
и последнее, во взятом нами ряде видов находятся в отношении противности или
противоположности. Будем, например, указанным способом распределять виды
понятия «цвет». В его объём входят различные оттенки всевозможных цветов:
красного, зелёного, чёрного, белого, серого и т. п. Если мы указанным выше
способом будем размещать виды в ряд по мере сходства их, то можем получить
приблизительно следующий ряд: белый, беловатый, светло-серый, серый,
темно-серый, черноватый, чёрный.
Рис. 7.
 Рис. 8.
Рис. 8.
Как видно из этого, наибольшее различие здесь
между понятиями «белый» и «чёрный»; они-то и суть противоположные или
противные понятия. Итак, понятия, входящие в один и тот же объём, но очень
отличающиеся друг от Друга, называются противными (contrariae). Схема: в круге, символизирующем объём
какого-нибудь понятия, двумя линиями отделены два крайних отрезка, один против
другого (рис. 7). Другие примеры: «добрый», «злой»; «высокий», «низкий»;
«красивый», «уродливый»; «громкий», «тихий»; «глубокий», «мелкий». Надо заметить,
что не все понятия имеют противные им понятия. Например, понятие «голубой» не
имеет противного ему понятия.
Если мы имеем какое-нибудь понятие А и другое понятие В, относительно которого известно только то, что оно не есть А, то такие понятия называются
противоречащими (contradictoriae). Например, понятия «белый» и «небелый» суть понятия противоречащие.
Итак, два термина, из которых один получен путём прибавления отрицательной
частицы «не» к другому, относятся между собой, как противоречащие.
Символически отношение между противоречащими понятиями выражается следующим
образом (рис. 8). Кругом символизируется какое-нибудь одно понятие А, и вне его ставится другое понятие В, которое есть не-А, причём это понятие В может
быть поставлено где угодно, лишь бы не внутри круга, не в его объёме; это второе понятие по своим
свойствам называется понятием отрицательным или нёопредёленным (notio negativa seu indefinita).
Если мы возьмём для сравнения
два понятия противоположные и два противоречащие: «белый» — «чёрный»
(противоположные), «белый» -
«небелый» (противоречащие), то мы можем наглядно убедиться, что разница между
этими двумя логическими отношениями огромная: тогда как второй член первой пары
(чёрный) имеет вполне определённое содержание, которое можно представить,
второй член второй пары (небелый) такого определённого содержания не имеет. Его
содержание отличается неопределённостью, т. е., употребляя слово «небелый», мы
можем под ним понимать и красный, и зелёный, и синий, и даже большой,
красивый, добрый и т. п.
5. Скрещивающиеся понятия (notiones
inter se convenientes). Если мы
имеем два понятия, содержание которых различно, но объёмы некоторыми своими
частями совпадают, то такие два понятия называются скрещивающимися. Возьмём
два понятия, например А — «писатели»
и В — «учёные». В объёме понятия
«писатели» заключается часть объёма понятия «учёные», ибо некоторые писатели
суть учёные, и, с другой стороны, в объёме понятия «учёные» заключается
некоторая часть объёма понятия «писатели», ибо некоторые из учёных суть
писатели. Это мы могли бы изобразить при помощи схемы на рис. 9.
Так как та часть объёма понятия «писатели», которая
состоит из учёных, и та часть объёма понятия «учёные», которая состоит из
писателей, логически между собой равны, то символически их можно представить
равными частями двух кругов, которые при наложении могли бы совпасть. Поэтому
схемой скрещивающихся понятий могут служить два скрещивающихся круга, причём
круги символизируют объёмы данных понятий, а место их скрещивания — совпадающие, логически равные
части этих объёмов. Другой пример —
прямоугольные фигуры и параллелограммы, ибо некоторые прямоугольные фигуры суть
параллелограммы и некоторые параллелограммы суть прямоугольные фигуры.
6. Понятия несравнимые (notiones disparatae). Возьмём два понятия: «душа» и
«треугольник». Для этих двух понятий нет общего ближайшего родового понятия, в
объём которого они могли бы оба войти как координированные. Между ними нет
ничего такого общего, что могло бы для них явиться посредствующим, связывающим
элементом, на основании которого их можно было бы сравнить. Такие два понятия
находятся в логическом отношении несравнимости. Для того чтобы можно было
сравнить два понятия, необходимо нечто третье, что объединяло бы эти понятия, —
это именно ближайшее общее понятие, в объём которого они входили бы. Это
третье понятие называется tertium comparationis.
Сюда же относятся понятия, которые вообще получены неотрицательным путём,
например «бесконечный», «бесспорный» и т. п., если эти понятия могут быть
символизированы только что указанным способом.
Теме 16. Виды
определений
Цель определения. Когда мы произносим
какое-либо слово, соответствующее известному понятию, и хотим сделать его понятным
для всех, то мы должны раскрыть содержание понятия, соответствующего
указанному слову, а так как содержанием понятия называется совокупность его
признаков, то раскрытие содержания понятия можно обозначить как перечисление
признаков, присущих данному понятию. Какое-либо понятие А содержит признаки а, Ь, с, d; если мы перечислим эти признаки, то тем самым точно обозначим,
раскроем содержание понятия А; это
значит, другими словами, что мы определим его.
Следует заметить, что не все понятия могут
быть определены. Понятия по своему содержанию бывают весьма различны:
содержание одних понятий больше, других —меньше. Такие понятия, которые имеют
сложное содержание, т. е. такие, которые имеют много признаков, могут быть
определены. Но есть понятия, которые имеют настолько простое содержание, что не
могут быть определены, потому что, как было сказано, для определения необходимо
раскрытие содержания понятия; если же содержание понятия не может быть
раскрыто, то оно не может быть и определено. Такие понятия называются
простыми. Например, понятие «пунцовый цвет» не подлежит определению: цвет этот
нужно видеть, чтобы знать, что он такое. Всё же определения, которые мы
попытались бы дать в данном случае, были бы ложными в логическом отношении.
Точно так же определять, что такое тон известной высоты, бесполезно; это
усваивается, понимается непосредственным восприятием этого тона. Сюда же
относятся такие понятия, как, например, понятия «равенство», «тождество»,
«тяжесть», «протяжение», «сознание» и т. п. Точно так же не могут быть
определяемы индивидуальные понятия, потому что при определении их пришлось бы
перечислить бесконечное множество признаков. Например: «этот бриллиант».
Итак, определить то или иное понятие значит перечислить его признаки.
Но это представляется иногда задачей трудной, потому что количество признаков
того или другого понятия может быть очень велико; поэтому перечислить даже
большинство этих признаков не окажется возможным. Если бы, например, определяя
понятие «прямоугольник», мы сказали, что прямоугольник есть геометрическая
фигура, плоская, ограниченная прямыми линиями, четырёхугольная, с прямыми
углами и т. д., то это определение было бы правильно, но практически оно
неудобно, потому что перечисляется целый ряд признаков. Вследствие этого
принят другой способ определения понятий, который имеет целью избежать полного
перечисления признаков.
Тема17. Правила
определения. Ошибки
Если нам нужно определить какое-либо понятие,
то мы выражаем наше определение при помощи суждения, содержащего подлежащее и
сказуемое. Подлежащее этого суждения называется определяемым (definiendum), сказуемое называется определяющим (definiens). Эти термины важны потому, что благодаря им
мы можем указать те правила, при соблюдении которых получается правильное
определение. Таких правил четыре.»
Другие в этой формуле прибавляют к genus термин proximum: «definitro fit per genus proximum et differentiam speoificam» («определение совершается при помощи ближайшего рода и видового различия»),
желая этим указать на то, что следует пользоваться ближайшим родовым понятием.
1.
Определение должно быть соразмерным, т. е; таким, в котором объёмы определяемого и определяющего тождественны,
т. е. одинаково велики. Если правило это нарушено, то определение неадекватно,
или несоразмерно. В таком случае определение делается или слишком широким или
слишком узким, именно, если объём определяющего становится слишком широким или
слишком узким в сравнении с объёмом определяемого. Возьмём в пример
определение лошади. Если сказать, что «лошадь есть домашнее животное», то это
определение будет слишком широким; в нём объём определяющего будет более
широким, чем объём определяемого понятия (в объём домашнего животного, кроме
лошади, входят ещё коровы, собаки и т. п.). Относительно такого определения
можно также сказать, что в него не входит указание существенного признака
данного понятия. Если в определении опущены существенные признаки понятия, тогда
оно окажется слишком широким, как в только что приведённом примере.
Возьмём определение, которое
погрешает в противоположном направлении. Если бы мы сказали, что «треугольник
есть плоская прямолинейная фигура, имеющая три равные стороны», то это определение
было бы слишком узким. В нём объём определяющего понятия меньше объёма
определяемого понятия. Именно: в объём определяющего понятия входят только
равносторонние треугольники, а в объём определяемого понятия входят как равносторонние,
так и неравносторонние треугольники.
2.
Определение не должно делать круга. Это правило требует, чтобы определяемое понятие не определялось
посредством понятия, которое само делается понятным только посредством
определяемого. Возьмём, например, определение «вращение есть движение вокруг
оси». Это определение понятия «вращение» посредством понятия «ось» делает круг,
ибо само понятие «ось» определяется только через понятие «вращение» (как
известно, ось — это прямая, вокруг которой происходит вращение). Таким
образом, ясно, что в нашем определении получается круг: понятие «вращение»
определяется посредством понятия «ось», а понятие «ось»— посредством понятия
«вращение».
В определении определяющее и определяемое
должны быть двумя различны ми и притом самостоятельными понятиями. Если это не
соблюдается, то получается ошибка, которая называется idem per idem, или тавтологией, именно: в определении
получается только повторение того же слова, т. е. употребляются слова, имеющие
то же самое значение. Например: «свет есть то, чему присущ свет»; «величина
есть то, что способно уменьшаться и увеличиваться». Последнее определение
представляет собой тавтологию, потому что уменьшение есть убавление величины,
увеличение же есть прибавление величины, а потому, если мы определяем величину
посредством того, что способно увеличиваться или уменьшаться, то очевидно, что
в определяющем понятии содержится определяемое понятие.
3.
Определение не должно быть отрицательным, оно должно указывать признаки, присущие данному понятию, а не чуждые
ему, ибо эти последние для нас неважны и, кроме того, их можно указать очень
много. Например, возьмём определение «театр есть здание, не служащее для
жилья». Если А будет здание, служащее
для жилья, то не-А, или зданий, не служащих для жилья, будет бесчисленное множество.
Таким образом, это определение делается для нас непригодным. К числу
определений, которые вследствие своего отрицательного характера непригодны,
нужно отнести следующие: «жидкость есть то, что не твердо и не газообразно»,
«точка есть то, что не имеет частей и не имеет никакой величины». Отрицательные
определения не раскрывают содержания понятия, они оставляют содержание понятия
неопределённым. Поэтому отрицательные определения не отвечают главной цели
определения — раскрыть содержание определяемого понятия, сделать содержание
понятия определённым..
Отрицательные определения могут быть
употребляемы только тогда, когда определяемое понятие имеет отрицательный
характер. Например, «чужестранец»—это человек, не принадлежащий к данной
стране, д.
4.
Определение должно быть ясным,
т. е. в определении нельзя пользоваться выражениями двусмысленными,
метафорическими и вообще мало понятными. Нарушение этого правила приводит к
попытке сделать понятным неизвестное через посредство ещё менее известного (ignotum per ignotius). Например, выражения «архитектура есть
застывшая музыка» и «нужда есть мать изобретения» — это есть образные
выражения, которые не объясняют значения термина. Если же сказать, что
«эксцентричность есть своеобразная идиосинкразия», то мы непонятное пытаемся
объяснить посредством непонятного же.
Тема 18. Деление и его
виды. Ошибки
От процесса определения отличается процесс
деления (divisio). Различие между
ними заключается в том, что определение раскрывает содержание понятия, а
деление раскрывает его объём. Задача деления заключается в том, чтобы указать
все виды, совокупность которых составляет объём данного понятия. Так,
например, понятие «треугольник» мы могли делить следующим образом: Треугольник
(А) –Прямоугольный (B)
-Остроугольный (C)
- Тупоугольный (D)
У нас было понятие
«треугольник» (Л), и мы перечислили все частные понятия: В, С и D, входящие в объём этого более общего понятия, которое
относится к ним, как род к своим видам.
То понятие, объём которого мы
раскрываем, называется делимым (totum dividendum), а те виды, которые получаются от деления,
называются членами деления (membra divisionis).
Основание деления.
Когда мы производим деление рода на виды, то мы обращаем внимание на те
признаки, которыми обладают одни виды и не обладают другие. Тот признак,
который даёт нам возможность разделить род на виды, называется основанием деления (fundamentum divisionis). Основанием вышеприведённого деления
понятия «треугольник» была величина углов в треугольнике. Но можно, это же
самое понятие делить по какому-нибудь другому основанию, например положить в
основание деления отношение сторон треугольника по величине. Тогда деление
представится в следующем виде: треугольник (A): равносторонний
(B) равнобедренный (C) разносторонний
(D)
Процесс несколько усложняется, если
полученные от деления виды в свою очередь делить на подвиды (этот процесс
называется подразделением). Так,
например, вид понятия «треугольник», именно тупоугольный треугольник (или
какой-нибудь другой),. можно в свою очередь подразделить на подвиды:
равнобедренный и разносторонний; разумеется, деление и подразделение будут
относиться к одному понятию: дихотомия. В процессе деления иногда употребляется
приём, который называется дихотомией и который заключается в деления данного
понятия Л на противоречащие понятия В
и не-В. Берём какое-нибудь понятие, которое нам надо разделить, например
понятие «человек»; выделяем в одну группу какой-нибудь из видов, заключающихся
в этом понятии, например вид «славянин», а в другую группу — «не-славянин» —
относим все прочие виды. Затем с этим вторым отрицательным понятием поступаем
точно таким же образом: подразделяем понятие «не-славянин» на две группы; в
одну из них относим, например, подвид «германец», а в другую — все прочие
остающиеся подвиды, соединяя их в одно понятие «не-германец»; затем с этим
понятием поступаем точно так же, как и с предыдущим, и продолжаем наше деление
до тех пор, пока оно не окажется исчерпанным.
Человек:
Славянин
Не-славянин:
Германец
Не-германец И
т. д.
Этот приём имеет тот недостаток, что
оставляет каждый раз крайне неопределённой часть объёма делимого понятия,
именно ту часть, которая обозначается частицей не, но, с другой стороны,
значительно облегчает самый процесс деления, потому что придаёт ему исчерпывающий
характер, почему его иногда называют исчерпывающим делением. Что оно имеет исчерпывающий
характер, можно объяснить при помощи следующего примера. Если мы разделим всех
обитателей Европы и Азии на расы — белую и жёлтую, то может оказаться, что некоторые
племена не подойдут ни под одну из этих рас и мы не будем в состоянии поместить
их в нашем делении, но этого не будет в том случае, если мы будем делить
дихотомически.
Обитатели
земного шара: Белые
Не-белые:
Желтые
Не-желтые
При таком делении всякое новое
племя должно будет войти в последнюю группу, которая не будет ни белой, ни
жёлтой. В этом заключаются преимущества дихотомического деления.
Правила деления.
Деление должно подчиняться следующим правилам:
1. Деление должно
быть адекватно, или соразмерно. Это
значит, что если мы перечисляем по какому-нибудь основанию или принципу виды
данного родового понятия, то мы должны точно перечислить все виды, не уменьшая
и не увеличивая их количества, т. е. сумма видов должна равняться делимому
роду.
Если при делении мы не
перечислим всех видов, т. е. если эта сумма будет меньше, то у нас получится деление неполное; если же мы в объём делимого
понятия введём виды, которые в нём на самом деле не содержатся, то у нас
получится деление слишком обширное, т. е. указанная сумма будет больше. Например,
положив в основание деления понятия «треугольник» величину его углов, мы могли
бы получить такое деление:
Треугольник: Остроугольный, Тупоугольный
Ясно, что это деление неполное,
ибо здесь не хватает одного члена деления, потому что в объёме понятия
«треугольник» находится ещё один вид, который при делении нами пропущен,
именно прямоугольный треугольник.
Неполным было бы деление людей
на порочных и добродетельных, деление научных теорий на истинные и ложные,
потому что в этих делениях упускаются промежуточные ступени. Кроме людей
порочных и добродетельных есть люди, о которых нельзя сказать, что они порочны,
но нельзя также сказать, что они добродетельны; кроме истинных и ложных теорий
существуют еще теории частью истинные и частью ложные.
Обратная ошибка будет
получаться в том случае, если мы, деля какое-либо понятие, вводим в его объём
такой вид, который не входит в действительности в его объём. Если бы мы,
например, разделили понятие «дерево» на «дуб», «ель», «фиалка», то очевидно,
что вид «фиалка» относится к объёму совсем другого понятия и что при делении
понятия «дерево» он попал в число членов его неправильно.
2.
Члены деления должны исключать друг друга. Это требование станет ясным, если мы возьмём
для примера, следующее деление:
Книги:
Французские
Немецкие
Словари и т. д.
Это деление неправильно, ибо понятие,
например, «французские книги» и понятие «словари» не исключают друг друга:
книга может быть и французской и словарём в одно и то же время. Или возьмём в
пример также другое деление понятия «книги»:
Книги: Полезные, Понятные, Интересные и т. д.
Здесь один вид книг не исключает из своего
объёма других видов: полезная книга может быть в одно и то же время и понятной
и интересной. Ошибки, как в первом, так и во втором из приведённых примеров
деления произошли потому, что не было выдержано третье требование правильного
деления, а именно:
3.
Деление должно иметь одно основание. При делении понятий чаще всего повторяется ошибка, заключающаяся в
том, что в процессе деления меняется
основание деления.
Произведём деление народов
Европы:
Народы Европы: Магометане, Христиане, Французы, Немцы и т.д.
Это деление неправильно, ибо мы, взяв сначала
основанием деления понятие «религия», затем меняем это основание на другое,
именно на понятие «национальность».
Или другой пример:
Прямолинейные фигуры:
Треугольники, Параллелограммы, Прямоугольники, Многоугольники
Это деление также неправильно,
так как у нас здесь скрещиваются такие различные основания деления, как число
сторон, направление сторон, величина углов. Такое деление называется
перекрёстным;
Итак, третье условие
правильности деления заключается в том, чтобы при последовательном перечислении
видов делимого понятия было выдержано одно основание деления. Но следует
заметить, что одно основание деления должно быть выдержано только при первом
делении понятия; уже при вторичном делении, т. е. при подразделении, основание
деления должно измениться. Так, например, если мы разделили понятие
«треугольник», взяв основанием деления величину углов, на такие виды, как
остроугольный, прямоугольный и тупоугольный, то, желая далее продолжать
деление какого-нибудь из этих членов деления, мы уже должны основание деления
изменить. Так, понятие «остроугольный треугольник» мы можем делить ещё далее,
если возьмём основанием деления уже не
величину углов, а отношение сторон по величине.
Треугольник: 1) Тупоугольный
2) Прямоугольный
3) Остроугольный: а) равносторонний
б) равнобедренный
в) разносторонний
4.
Деление должно быть непрерывным,
т. е. при делении какого-либо понятия нужно переходить к ближайшему низшему
роду, в противном случае будет получаться то, что называется скачком в делении.
Если бы мы понятие «природа» разделили на 1) «животные», 2) «растения», 3)
«минералы», то в этом делении был бы слишком внезапный переход от понятия «природа»
к понятиям «минералы», «животные». Чтобы исправить ошибку, следует вставить
между понятием «природа» и членами вышеприведённого деления ещё два
посредствующих звена.
Именно: понятия «мир неорганический» и «мир
органический». Тогда деление приняло бы следующий вид:
Природа:
Мир органический: животные
растения
Мир неорганический: минералы и проч.
Тема 19. Классификация
Определение классификации. В этом разделе мы
рассмотрим процесс классификации, потому что он служит вспомогательным
средством для индукции; с другой стороны, как мы сейчас увидим, классификация
возможна только благодаря индукции. Классификацией мы называем распределение
вещей по классам согласно сходству между ними. Так, например, мы можем отнести
зарево, кровь, вишни в один класс, потому что все они при всём различии имеют
то общее, что они суть красного цвета. Классификация вещей, или распределение
их по классам, преследует свои определённые задачи, которые можно формулировать
так:
задача классификации заключается в том, чтобы
распределить вещи по группам в таком порядке, который наиболее полезен для
припоминания вещей и для определения свойств их.
Первое требование хорошей классификации
заключается в том, чтобы пункты сходства, на основании которых мы составляем
классы, были важны в практическом отношении.
Второе требование хорошей классификации
состоит в том, чтобы она давала нам возможность сделать наибольшее число
утверждений. Та классификация наилучшая, в которой предметы сходны друг с
другом в возможно большем числе признаков.
Из этого становится ясной связь классификации
с индукцией. Именно классификация предполагает индукцию, потому что эта
последняя определяет те общие признаки, которые дают возможность относить
предметы в общий класс. Только что указанный признак классификации отличает
естественную классификацию от искусственной. Чтобы понять это, возьмём пример
какой-нибудь искусственной классификации. Мы можем распределить фамилии
каких-либо авторов по первым буквам их фамилий. Это иногда очень важно потому,
что .мы можем в случае надобности отыскивать те или иные фамилии. Но такая
классификация допускает чрезвычайно мало утверждений. В самом деле, что мы
можем утверждать относительно того или иного автора только на том основании,
что фамилия его начинается с буквы А
или с буквы Б?.
Естественная классификация. Для того чтобы мы
могли делать большое число утверждений, мы должны брать за основание
классификации такие признаки, которые влекут за собой большое число других
признаков. Это бывает в том случае, когда мы соединяем предметы в классы по признакам
существенным, выражающим природу вещей. Если мы имеем такую классификацию, то
для нас вполне достаточно знать название класса, чтобы судить о свойствах
вещей, принадлежащих к этому классу.
Возьмём пример для пояснения этого. Рожь,
ячмень, овёс и другие сорта растений относятся к семейству злаков. Всякий, кто
знаком с ботаникой, легко может определить, принадлежит ли данное растение к
злакам или нет. В пищу как людям, так и животным главным образом идёт
какой-нибудь род злаков, и поэтому следует предположить, что ни одно из
растений, принадлежащих к этому семейству, не ядовито. Предположим, что
путешественник попал в какую-нибудь необитаемую страну и нуждается в пище. Если
он увидит какой-либо злак, он станет питаться его семенами, так как ему
известно, что злаки не ядовиты. Следовательно, по принадлежности известного
растения к известному классу можно умозаключать о ядовитости или неядовитости
его.
Таким образом, естественная классификация
имеет в виду раскрыть истинные свойства вещей и основывается вследствие этого
на признаках важных и существенных. Так, людей можно классифицировать по
религии, речи, государственному устройству и т. п. Если бы мы стали делить
людей на классы, смотря по тому, как они изготовляют пищу или как они одеваются,
то это было бы искусственной классификацией.
Искусственная классификация. Искусственная
классификация кладёт в основу классификации какие-либо произвольные признаки.
Так, например, известная Линнеевская система классификации растений может
служить примером искусственной классификации. Шведский ботаник Линней разделил
все растительное царство на 24 класса на основании числа тычинок, их
прикрепления, срастания между собой и т. п. В искусственной классификации
вследствие того, что она имеет в своей основе более или менее случайный
признак, всегда возможно, что совершенно несходные предметы могут очутиться в
одной группе, между тем как очень родственные предметы могут очутиться в очень
отдалённых группах. В Линнеевской классификации очень родственные группы
растений, например злаки, относятся в различные, очень несходные классы, между
тем как очень несходные, например дуб и один вид осоки, соединяются в один
класс. Это происходит вследствие того, что в основе этой классификации лежит
только такой признак, как строение цветка. Этого не может быть в естественной
классификации, в которой для выяснения родства между растительными формами
обращают внимание на всю совокупность признаков, свойственных изучаемым
организмам. Другой пример. Семейство губоцветных характеризуется четырёхгранным
стеблем, супротивными листьями, двугубым зевообразным венчиком и четырьмя
тычинками. Но есть растение (шалфей), которому присущи все указанные черты, но
в котором всего две тычинки. Вследствие этого его приходится отнести в другое
семейство, если пользоваться искусственной классификацией, хотя родство его с
губоцветными не подвергается никакому сомнению.
В связи с классификацией следует упомянуть о
научной номенклатуре и научной терминологии.
Номенклатура. Номенклатура самым теснейшим
образом связана с классификацией. Группы естественные или искусственные, на
которые распределяются предметы, не могут быть нами запоминаемы, не могут быть
сообщаемы другим, если только эти группы не фиксируются определёнными
названиями. Для этого именно существует номенклатура. Номенклатура может быть
определена как собрание названий всех реальных родов, классов, например в
ботанике, зоологии, химии и т. п. В минералогии названия отдельных минералов,
каковы, например, гематит, топаз, амфибоз, составляют номенклатуру. В химии мы
имеем названия, например, для органических соединений: этил, ацетил, бензол и
т. п. Число естественных групп в природе настолько велико, что почти невозможно
запомнить имена отдельных групп. Так, известные науке виды растений значительно
превосходят 60 тысяч, но если мы примем в соображение разновидности и
подразновидности, то число групп будет значительно больше. Поэтому только при
помощи названий и возможно оперировать с таким огромным числом предметов. Мы
можем не помнить подгруппы, но если мы помним группу, то этого вполне
достаточно для оперирования с ними. В пример можно привести номенклатуру,
введённую Линнеем в ботанику. Эта номенклатура была в состоянии обозначить
около 10 тысяч видов растений 1 700 родовыми названиями, которым придавались
видовые признаки. Так, например, в ботанике каждое растение обозначается
двойным названием: одно из них есть родовое, т. е. Указывает род, другое
видовое. Например, в названии Betula alba—Betula есть название всего рода берёз, alba есть название вида. Может быть десять видов
герани; эти виды каждый в отдельности нам нет надобности запоминать, достаточно
помнить только род. Всякая хорошая номенклатура предполагает хорошую систему
классификации. Только те науки, которые имеют полную классификацию, имеют и
выработанную номенклатуру, например ботаника и химия.
Тема 20. Аргументация и
доказательство
Человек разумный есть
человек аргументирующий. Независимо от того, осознает он это или нет, человек
вовлечен в аргументационную деятельность. В установлении научной истины, в
решении политических проблем, в судебных разбирательствах, в обсуждении
вопросов обыденной жизни - во всем этом значительное место занимает
аргументация. Ответ студента на экзамене или защита им дипломного проекта - вид
аргументационной деятельности.
Словом "аргументация" называют: 1) процедуру приведения
аргументов в пользу какого-либо положения; 2) саму совокупность таких
аргументов; 3)обоснование - в той или иной степени - истинности некоторого
суждения.
Краткий
Оксфордский словарь описывает аргументацию как
-
методическое
доказывание, дебаты;
-
довод,
выдвинутый за или против;
-
процесс
доказывания.
Для аргументации характерны следующие черты:
-
аргументация
всегда выражена в языке, имеет форму произнесенных или написанных утверждений;
-
аргументация
является целенаправленной деятельностью, цель аргументационного воздействия -
убеждение;
-
аргументация
- это социальная деятельность, поскольку направлена на человека, предполагает
диалог и активную реакцию другой стороны на приводимые доводы.
-
аргументация
предполагает разумность тех, кто ее воспринимает, их способность рационально
взвешивать аргументы, принимать их или оспаривать.
В аргументационной деятельности два главных действующих лица:
аргументатор и реципиент. Термином "аргументатор" обозначается лицо,
осуществляющее аргументацию. Термином "реципиент" (адресат) - лицо,
которому она адресована.
Аргументация относится к гуманным средствам воздействия на человека.
Реципиент обладает свободой воли, он может принять аргументы или отвергнуть их.
В аргументационной деятельности реципиент не является объектом жесткого
управления. Цель этой деятельности - внутреннее принятие тезиса аргументатора
реципиентом.
На убеждения человека можно воздействовать насилием, пыткой, гипнозом,
внушением, подсознательной стимуляцией, психотропными средствами, наркотиками.
Эти методы воздействия явно выходят за рамки аргументационных. К
неаргументационным средствам относятся также приказы, угрозы, все виды
физического воздействия, "промывание мозгов".
Аргументация предполагает наличие доказательства, однако не сводится к
нему. Доказательство - логическая основа аргументации. При этом для
аргументации требуется наряду с доказательством еще и убеждающее воздействие.
Вынуждающий, механический характер доказательства, его безличность составляют
главное отличие доказательства от аргументации. Аргументация имеет
невынуждающий характер, ее правильность не может быть установлена механическим
путем. Сравнивая результаты аргументации и доказательства иногда говорят:
"доказал, но не убедил".
Доказательство - это
логическая операция обоснования истинности какого-либо суждения с помощью других истинных и связанных с ним
суждений. В доказательстве выделяют три элемента: 1) доказываемое положение -
тезис; 2) суждения, с помощью которых обосновывается истинность тезиса, -
аргументы, или доводы, или основания доказательства; 3) логическая связь тезиса
с аргументами - демонстрация.
В качестве аргументов в логике могут быть использованы: 1)
удостоверенные факты; 2) законы науки; 3) ране доказанные теоремы; 4) аксиомы и
постулаты; 5) определения.
Правила доказательства
Для того, чтобы доказательство достигало своей цели, нужно соблюдать
некоторые правила, или требования, относящиеся к элементам доказательства.
Требования к тезису
1) Тезис должен нуждаться в доказательстве.
Бессмыленно пытаться доказывать очевидные вещи, определения понятий,
констатации фактов, аксиомы и постулаты.
2)
Тезис должен
быть ясным и точным. Многие слова естественного языка являются многозначными и
расплывчатыми, что обусловливает неясность тезиса. Кроме того, следует иметь в
виду, что в качестве тезиса лучше брать частные суждения, а не общие. Частное
суждение легче доказать и труднее опровергнуть.
3) Тезис должен оставаться одним и тем же на
протяжении всего доказательства. Распространенная ошибка - подмена тезиса.
Менее распространенная - потеря тезиса.
Требования к аргументам
1) Аргументы
должны быть истинными суждениями, причем их истинность должна быть доказана. Нарушение этого требования, связанное с
использованием ложного аргумента, называется "основным заблуждением".
Ошибка, связанная с использованием, может быть и истинного, но еще не
доказанного аргумента носит наименование "предвосхищение основания".
2) Истинность аргументов должна устанавливаться
автономно, т. е. независимо от тезиса. При нарушении этого требования мы имеем
дело с ошибкой, известной как "круг в обосновании" или "круг в
доказательстве".
3)
Совокупность аргументов должна быть непротиворечива.
Если аргументы противоречат друг другу, то по крайней мере один из них ложен, а
ложные аргументы ничего не доказывают.
4)
Совокупность аргументов должна быть достаточной для
вывода тезиса. Один аргумент почти никогда не дает обоснование тезиса, его
доказательная сила мала. Но несколько аргументов, находящихся во взаимной
связи, способны создать прочную логическую основу для вывода тезиса. Однако не
следует злоупотреблять количеством аргументов. Иногда полагают, что чем больше
доводов привлекут к обоснованию своего тезиса, тем лучше. Это не так. Среди
неряшливо подобранных аргументов могут оказаться ложные, необоснованные,
противоречащие друг другу и даже доказываемому тезису. В таком случае
доказательство может рассыпаться. Аргументов должно быть достаточно для вывода
тезиса и не более того. Каждый лишний аргумент ослабляет доказательство. Важно
не количество аргументов, а их весомость.
Требования к демонстрации
Это
обычные требования к умозаключениям. В повседневной жизни часто случается так,
что, высказав некоторые аргументы, человек присоединяет к ним свой тезис с
помощью слов: "таким образом", "отсюда можно заключить",
"поэтому" и т. п. Однако сами по себе эти слова не создают логической
связи между аргументами и тезисом, нужно еще показать, что тезис действительно
связан с аргументами определенными видами умозаключений и эти умозаключения
корректны. Ошибки, связанные с нарушением правил умозаключений, носят общее
название "не следует": тезис логически не вытекает, не следует из
аргументов.
Тема 21. Стратегия и
тактика аргументации и критики
Проблемное совещание может
включать такую форму групповой принятия решений, как дискуссия, которая
предполагает общение на основе доводов и аргументов с целью найти истину путем
всестороннего сопоставления различных мнений. Суть действий в дискуссии состоит
в защите или опровержении тезиса. Напомним, что при выдвижении тезиса участники
дискуссии обязаны соблюдать ряд правил: тезис должен быть четко сформулирован и
ясен оппоненту, он должен оставаться неизменным в ходе всего диалога и не
должен содержать в себе логических противоречий.
Использование дискуссии в
проблемном совещании ставит перед руководителем три группы взаимосвязанных
задач: задачи по отношению к проблеме, задачи по отношению к группе участников
дискуссии, задачи по отношению к каждому отдельному участнику. В соответствии с
этим функции ведущего дискуссии определяются типом решаемых задач.
Задачи по отношению к проблеме:
1) сформулировать цель и тему
дискуссии. Следить за регламентом, направлять дискуссию в русло намеченной
цели;
2) собрать максимум предложений
по обсуждаемой проблеме, стараясь осветить все ее аспекты; анализировать
поступающие предложения и высказываемые мнения;
3) подвести итоги дискуссии,
сопоставив ее цели с полученными результатами.
На качество решения, принятого
группой, заметное влияние оказывает последовательность шагов в рассмотрении
поставленного вопроса. В теории управления используется модель «рефлексивной
рамки», которая представляет собой схему принятия группового решения, состоящую
из нескольких взаимосвязанных блоков вопросов. Ответы на эти вопросы позволяют
группе увеличить эффективность принимаемого решения. К базовым категориям
вопросов относятся следующие:
• В чем суть проблемы? Ясно ли она определена и понятно ли она
сформулирована? Есть ли понимание общей ситуации, в которой эта проблема имеет
место?
• Какова фактическая сторона дела? Какова история проблемы? В чем ее
причины? Почему это важно? На кого она влияет и как?
• Каким критериям должно соответствовать принимаемое решение? По
каким или чьим стандартам должно оцениваться решение? Каковы принципиальные
требования к решению: в какую сумму оно должно уложиться, чьи интересы нельзя
затрагивать?
• Каковы возможные решения проблемы ?
• Какое решение является
наилучшим?
• Каким образом можно исполнить
решение? Какие этапы необходимы для проведения решения в жизнь? Какова их
последовательность? Кто несет ответственность?
Задачи по отношению к участникам совещания в целом:
1) поддерживать высокий уровень
активности всей группы. Сопоставляя различные мнения, вычленять противоречия,
спорные вопросы, формулировать противоречие как проблему;
2) поддерживать деловую
атмосферу, не допуская личной конфронтации участников, препятствовать
некорректным действиям;
3) помочь группе прийти к
согласованному мнению.
Задачи по отношению к каждому участнику:
1) уделять внимание каждому
участнику;
2) активизировать пассивных;
3) подчеркнуть вклад каждого в
общий итог, поблагодарить всех членов группы за участие в дискуссии
Тема 22. Правила
построения логических правил
Готовя выступление, следует
учитывать основные логические законы.
1. Закон тождества. Всякая
мысль в процессе рассуждения должна быть тождественна самой себе. Этот закон
требует, чтобы в выступлении данная мысль о каком-либо предмете, событии должна
иметь определенное устойчивое содержание, сколько бы раз и в какой бы форме к
ней ни возвращались.
2. Закон непротиворечия.
Два несовместимых друг с другом суждения не могут быть одновременно истинными:
по крайней мере одно из них необходимо ложно.
3. Закон исключенного
третьего. Утверждение и его отрицание не могут быть одновременно ни
истинными, ни ложными, одно из них необходимо истинно, другое — необходимо
ложно. Если в выступлении сформулировано какое-то положение в виде
высказывания, а затем — его отрицание, то одно из этих высказываний будет
истинным, а другое — ложным.
4. Закон достаточного
основания. Всякая мысль признается истинной, если она имеет достаточное
основание. Поскольку наши суждения, высказывания могут быть истинными или
ложными, то, утверждая истинность высказывания, следует дать обоснование этой
истинности.
На основе
логических законов, которые носят формальный характер, фиксируют формальную
правильность различных интеллектуальных операций в чистом виде, складываются
конкретные правила, рекомендации, инструкции, предусматривающие достижение
вполне определенного необходимого результата в практической деятельности. Так,
на основе закона непротиворечия может быть сформулировано правило: не
использовать противоречивые высказывания. Поэтому говорят не просто о законах
логики, а о законах и правилах логики.
Следует иметь в виду, что логика
выступления является лишь составной частью более общей системы приемов,
называемой системой аргументации, которая используется в воздействующей,
убеждающей речи. Система аргументации включает в себя «способы обоснования и
опровержения убеждений, зависимость этих способов от аудитории и обсуждаемой
проблемы, своеобразие обоснования в разных областях мышления и деятельности,
начиная с естественных и гуманитарных наук и кончая идеологией, пропагандой и
искусством и др.». Типовые ситуации в ораторском выступлении порождают типовые
схемы аргументации. Не все из них в логическом отношении являются верными.
Укажем на наиболее часто встречающиеся ошибки:
а) Неполная аналогия. Приводя
умозаключение по аналогии, помните, что аналогия не всегда бывает полной.
Утверждение «процесс работы над текстом устного выступления аналогичен процессу
написания статьи» верно лишь отчасти: есть много общего между написанием статьи
и созданием текста устного выступления, но есть и существенные различия. Полной
аналогии здесь нет.
б) Отождествление временной
последовательности событий с их причинной связью: временная последовательность
событий не всегда подразумевает наличие между ними причинно-следственных
отношений. Если предприятие оказалось банкротом после внесения изменений в
налоговое законодательство, это не означает, что они оказались причиной
банкротства: такая зависимость может быть, но может и отсутствовать.
• Квазилогические рассуждения: «Я не против, когда кто-то решает служебные
дела поличному телефону, значит, они тоже не должны быть против, когда я .звоню
им домой по служебному делу.
• Ошибки объединения: «Эта газета для бездомных, следовательно, се
выпускают лица без определенного места жительства».
• Ошибки разъединения: «Совет
директоров компании исчерпал свои возможности, следовательно, люди, в него
входящие, тоже исчерпали свои возможности.
Тема 23. Проблема и
гипотеза
Важную роль в гуманитарных науках играют учение логики не только о понятии, суждении, умозаключении и
аргументации, но и о таких формах развития знания, как проблема, гипотеза и теория.
Однако представители гуманитарных наук часто не имеют достаточного
представления об этих формах развития знания и говорят о проблемах и т.д. в тех
случаях, когда таковых нет. Недостаточное знакомство с формами развития знания
затрудняет ведение научно-исследовательской, практической и преподавательской
работы.
Проблемами называют важные в практическом или теоретическом отношении
задачи, способы решения которых неизвестны или известны не полностью. Различают
проблемы двух видов: неразвитые и развитые.
Неразвитая проблема — это задача, которая характеризуется следующими
чертами.
Во-первых, это нестандартная
задача, т.е. задача, для решения которой нет алгоритма (алгоритм неизвестен или
даже невозможен). Чаще всего это трудная
задача.
Во-вторых, это задача, которая возникла на базе определенного знания (теории, концепции и т.д.), т.е. задача,
которая возникла как закономерный результат процесса познания.
В-третьих, это задача, решение которой направлено на устранение противоречия, возникшего в познании (противоречия между
отдельными положениями теории или концепции, положениями концепции и фактами,
положениями теории и более фундаментальными теориями, между кажущейся
завершенностью теории и наличием фактов, которые теория не может объяснить), а
также на устранение несоответствия между потребностями и наличием средств для
их удовлетворения.
В-четвертых, это задача, путей
решения которой не видно.
Чтобы подчеркнуть незавершенный характер неразвитых проблем, их иногда
называют пред проблемами.
Задача, которая характеризуется тремя первыми из указанных выше черт, а
также содержит более или менее конкретные указания на пути решения, называется развитой проблемой, или собственно проблемой. Собственно проблемы делятся
на виды по степени конкретности указаний на пути их решения.
Таким образом, развитая проблема — это «знание о некотором незнании», дополненное более или менее
конкретным указанием путей устранения этого незнания.
Формулировка проблемы включает в себя, как правило, три части: систему утверждений (описание исходного
знания — того, что дано); вопрос или побуждение (как установить то-то и то-то,
найти то-то и то-то); систему указаний на возможные пути решения. В
формулировке неразвитой проблемы последняя часть отсутствует.
Проблемой называется не только знание указанных видов, но и процесс
познания, который заключается в формировании неразвитой проблемы, превращении
последней в развитую, а затем развитой проблемы первой степени в развитую
проблему второй степени и т.д. вплоть до решения проблемы.
Проблема как процесс развития знания состоит из ступеней:
формирования неразвитой проблемы (предпроблемы);
развития проблемы — формирования развитой проблемы первой степени, затем
второй и т.д. путем постепенной конкретизации путей ее разрешения;
разрешения (или установления неразрешимости) проблемы.
Почти всегда, когда человек начинает какое-либо исследование, он
выдвигает предположение о его результатах, т.е. как бы видит желаемый результат
в начале исследования. Такое предварительное решение вопроса в большинстве
случаев идет на пользу делу, поскольку позволяет разработать план исследования.
Если бы в своей работе ученые не пользовались предположениями, то они
превратились бы лишь в собирателей фактов, в регистраторов событий.
Предположения, позволяющие разработать план исследования, называются гипотезами.
Они науке и особенно ее изучению необходимы. Они дают стройность и
простоту, каких без их допущения достичь трудно. Вся история наук это
показывает. А потому можно смело сказать: лучше держаться такой гипотезы,
которая может оказаться со временем неверною, чем никакой. Гипотезы облегчают и
делают правильною научную работу — отыскания истины, как плуг земледельца
облегчает выращивание полезных растений.
Слово «гипотеза» греческого происхождения. Оно означает «предположение ».
В научной литературе не
любое предположение называют гипотезой. Гипотеза — это предположение особого
рода. Гипотезой называют также процесс познания, который заключается в
выдвижении этого предположения. Таким образом, в научной литературе слово
«гипотеза» употребляется в двух смыслах. Гипотезой называют особого рода
знание, а также особый процесс развития знания.
Гипотеза в первом смысле слова — это обоснованное (не полностью)
предположение о причинах явления, о ненаблюдаемых связях между явлениями и т.д.
Гипотеза во втором смысле слова — это сложный процесс познания,
заключающийся в выдвижении предположения, его обосновании (неполном) и
доказательстве или опровержении.
В этом процессе выделяют две ступени: развитие предположения;
доказательство или опровержение предположения.
Развитие предположения
Здесь можно выделить два этапа. Первый этап —выдвижение предположения.
Предположения выдвигаются на основе аналогии, неполной индукции, методов
Бэкона—Милля и т.д. Например, по аналогии с Солнечной системой была создана
планетарная модель атома. Выдвинутое таким образом предположение, чаще всего
еще не гипотеза. Это скорее догадка, чем гипотеза, поскольку оно, как правило,
не является хотя бы частично обоснованным.
В гуманитарных науках гипотезами неправомерно называют догадки, не
являющиеся в какой-либо мере обоснованными.
Второй этап — объяснение с помощью выдвинутого предположения всех
имеющихся фактов, относящихся к предметной области гипотезы (фактов, которые
гипотеза призвана объяснить, предсказать и т.д.), — тех фактов, которые были
известны до выдвижения предположения, но еще не принимались в учет, а также тех
фактов, которые были открыты после выдвижения предположения.
Так, предположение о планетарном строении атома из догадки превратилось в
гипотезу лишь после того, как на его основе удалось объяснить ряд известных
фактов, в частности периодическую систему химических элементов Менделеева. До
того времени эта система являлась эмпирическим законом химии. Менделеев
расположил химические элементы в определенном порядке на основе их атомных
весов и закономерностей в изменении химических и физических свойств. Создание
планетарной модели атома позволило придать физический смысл расположению
элементов в таблице. Оказалось, что порядковый номер элемента в таблице равен
числу положительных зарядов его ядра.
Кроме прохождения этих двух этапов в своем развитии предположение, чтобы
быть гипотезой, должно удовлетворять следующим требованиям.
Первое требование — предположение не должно быть логически противоречивым
(самопротиворечивым) и не должно противоречить фундаментальным положениям
науки.
Противоречивыми могут оказаться гипотезы, выдвинутые даже крупными
мыслителями. Так, К. Маркс пишет об Адаме Смите по поводу его гипотезы,
объясняющей природу стоимости и ценообразования, что у него можно найти «не
только два, но и целых три, а говоря совсем точно — даже четыре резко
противоположных взгляда на стоимость, которые мирно располагаются у него рядом
или переплетаются друг с другом».
По поводу требования «предположение не должно противоречить
фундаментальным положениям науки» следует заметить, что оно не является
абсолютным. Если гипотеза противоречит каким-то из таких положений, в некоторых
случаях полезно подвергнуть сомнению сами эти положения, особенно если речь
идет об исследованиях в социальной сфере.
Положения естествознания тоже не являются незыблемыми. Так, в прошлом
веке Французская академия наук приняла решение не рассматривать исследования о
камнях, падающих с неба, так как падать им неоткуда.
Если же фундаментальные положения науки, которым противоречит выдвигаемое
предположение, не поддаются опровержению, под сомнение берется предположение.
Второе требование — предположение должно быть принципиально проверяемым.
Различают два рода проверяемости — практическую и принципиальную. Предположение
является практически проверяемым, если оно может быть проверено в данное время
или в относительно недалекий период времени. Предположение является
принципиально проверяемым, когда оно может быть проверено (если и не в
ближайшее время, то когда-нибудь).
В качестве гипотез не признаются догадки, которые в принципе нельзя
проверить (обосновать или опровергнуть).
Тема 24. Теория
В науке выделяют два уровня познания — эмпирический и теоретический.
На первом уровне производится сбор фактов (накопление информации об исследуемых
объектах) и осуществляется их первичная систематизация в форме таблиц, схем,
графиков и т.д. На этом уровне могут
даже формулироваться законы, которые носят гипотетический характер, т.е.
требуют объяснения и логического обоснования.
На втором уровне
действительность отражается в форме теорий. Слово «теория», как и многие другие
слова естественного языка, употребляется в разных смыслах; в частности, говорят
о теории в широком и узком смыслах слова.
Когда хотят разграничить мыслительную и предметно-практическую деятельность,
говорят о теории и практике. В этих случаях теорией (в широком смысле) называют мышление
вообще.
Что понимают под теорией в узком смысле, являющейся предметом нашего
рассмотрения? Есть много определений теории. Например, теорию определяют как
множество предложений, связанных отношением выводимости. Это определение и
неточно, и неполно. Почему неточно? Не все предположения теории связаны этим
отношением. Почему неполно? Здесь выделяется лишь один аспект теории —
формально-логический. Другое определение: теория — это множество предложений,
замкнутых относительно выводимости. Это определение не выделяет многих
существенных свойств теории. Иногда прибегают к остенсивному определению теории
(теория — это, например, теория относительности, учение о происхождении видов
Дарвина и т.д.). В остенсивных определениях не раскрываются отличительные
признаки теории.
Конечно, любое определение не выражает всей сущности предмета. Однако
основные из существенных черт в определении все же можно выделить. Дадим
следующее определение теории.
Теория — это достоверное (в
диалектическом смысле) знание об определенной области действительности,
представляю-щее собой систему понятий и утверждений и позволяющее объяснять и
предсказывать явления из данной области.
Какие же признаки теории мы включаем в определение?
Теория — достоверное знание (в диалектическом смысле). Хотя теория и не
является полной и окончательной истиной о какой-то области действительности,
она все же в своей основной части обоснована. В ней есть содержание, которое в
дальнейшем не будет опровергнуто.
Не все философы считают, что достоверность — это необходимый признак
теории.
В этом вопросе нужно разграничить два подхода. Представители первого
подхода если и относят к теориям концепции, которые могут оказаться
недостоверными, то все же считают, что задача науки — создание достоверных
теорий.
Представители второго подхода утверждают, что теории не являются
отражением реальной действительности. Теорию они понимают как инструмент
познания. Одна теория лучше другой, если она является более удобным
инструментом познания. Например, система мира Коперника, по мнению некоторых из
них, является более удобным инструментом познания, чем система мира Птолемея.
Говорить о достоверности одной из них нельзя.
Принимая достоверность (обоснованность) за отличительную черту теории, мы
стремимся отделить этот вид знания от гипотезы.
В теориях действительность отражается посредством моделей. Моделями здесь
служат системы идеализированных и некоторых других объектов. Идеализированные объекты образуются при
помощи особого приема познания, называемого идеализацией.
В процессе идеализации на основе знания о существующих объектах создаются
понятия об объектах, которые в действительности не существуют, да и не могут
существовать, но которые в то же время в определенных отношениях сходны со
своими прообразами. В процессе идеализации происходит отвлечение от некоторых
признаков предметов и приписывание им признаков, которые им в действительности
не могут принадлежать. В основе идеализации чаще всего лежит способность
некоторых признаков изменяться по степеням.
Так, тело может изменять размеры, интенсивность цвета и т.д. На основе
мысленного изменения таких свойств до некоторых, невозможных в
действительности, пределов образуются понятия тел, не имеющих размеров, тел,
являющихся, например, абсолютно черными и т.д.
Примеры идеализированных объектов: точка в геометрии (в реальном мире нет
объектов, которые не имеют ни длины, ни высоты, ни ширины); точка в механике.
Н.Е.Жуковский так поясняет последнее понятие:
«Это — как бы шарик, наполненный материей, радиус которого уменьшился до
бесконечно малой величины, а масса сохранилась та же. Хотя это представление —
чисто фиктивное, так как беспредельное сжатие не согласно с непроницаемостью
материи, но в механическом смысле существуют точки, имеющие тождественное
значение с материальной точкой конечной массы.
Такой точкой, например, является центр тяжести твердого тела».
Следовательно, объектами
теоретической механики фактически являются центры тяжести тел.
Идеализированные объекты широко используются в общественных науках,
например в политической экономии.
В физике как полезнейшие орудия познания природы применяются абстракции
идеального газа и идеальной жидкости. Реальные газы и жидкости не ведут себя «идеально»
или ведут себя так лишь при некоторых определенных условиях. Однако имеет
большой смысл абстрагироваться от этих нарушений, чтобы изучать явления «в
чистом виде». Нечто подобное представляет собой в политической экономии
абстракция «экономического человека» и свободной (совершенной) конкуренции.
Реальный человек не может быть сведен к своекорыстному интересу. Точно так же
при капитализме никогда не было и не может быть абсолютно свободной
конкуренции. Однако наука не смогла бы изучать массовидные экономические
явления и процессы, если бы она не делала известных допущений, которые
упрощают, моделируют бесконечно сложную и разнообразную действительность,
выделяют в ней важнейшие черты.
В понятиях теории обобщаются и выделяются идеализированные и некоторые
другие объекты, а утверждения теории описывают системы таких объектов,
выступающих в качестве моделей реально существующих объектов (оригиналов).
Свойства моделей переносятся на системы реальных объектов.
Идеализированные объекты специфичны для теоретического уровня познания,
поэтому их называют теоретическими объектами науки в отличие
от неидеализированных объектов, называемых эмпирическими.
Эмпирические объекты являются фрагментами действительности,
рассматриваемыми, возможно, с тех или иных сторон. Теоретические объекты в
действительности не существуют.
В противоположность эмпирическим объектам теоретические объекты уже не
просто фрагменты действительности, а ее логические реконструкции. Так, точка,
«абсолютно твердое тело» суть теоретические объекты, тогда как «стол»,
«расстояние между Землей и Луной» — эмпирические.
В связи с выделением двух типов объектов науки различают два типа терминов языка науки —
эмпирические и теоретические: первые из них называются чаще всего терминами наблюдения. Термины наблюдения
обозначают наблюдаемые объекты, а теоретические термины — объекты, которые не
являются наблюдаемыми. Исходя из представления о двух видах терминов, различают
два вида предложений — эмпирические и
теоретические. Первые — те, в которые
не входят теоретические термины. Вторые содержат теоретические термины.
Особенностью теории является то, что она обладает предсказательной силой. В теории имеется множество исходных
утверждений, из которых логическими средствами выводятся другие утверждения,
т.е. в теории возможно получение одних знаний из других без непосредственного
обращения к действительности. Это одно из условий предсказательной
ценности теории.
Теория не только описывает определенный круг явлений, но и дает объяснение этим явлениям.
Теория является средством
дедуктивной и индуктивной систематизации
эмпирических фактов.
Посредством теории можно установить определенные отношения между
высказываниями о фактах, законах и т.д. в тех случаях, когда вне рамок теории
такие отношения не наблюдаются. Частными случаями таких отношений являются
отношения дедуктивного следования и подтверждения (индуктивного следования).
Теория «...объединяет и обобщает эмпирические законы и гипотезы. Такая
систематизация формально сводится к тому, что известные эмпирические законы,
так же как и многие новые законы, выводятся в качестве логических следствий из
более общих теоретических законов, принципов и допущений».
В социальной теории можно выделить следующие составные части:
— исходную эмпирическую базу (звание
фактов, зафиксированных наукой);
— исходную теоретическую основу, представляющую собой систему исходных утверждений, понятий, законов и принципов
теории;
—
множество
следствий, выведенных из исходных теоретической основы и эмпирической базы
теории.
Тема 25. Управленческое
решение
Процессы принятия управленческих
решений занимают в управленческой деятельности центральное место. Не всякое
решение является управленческим, а только такое, которое, во-первых, является
результатом выбора между несколькими альтернативами, в большинстве случаев
приблизительно равноценными с точки зрения принимающего решение, а во-вторых,
когда результат выбора как социальное явление влияет на других людей и
воспринимается ими в качестве обязательного к исполнению.
Процесс
принятия решений является циклической последовательностью действий субъекта
управления, направленных на разрешение проблем организации и заключающихся в
анализе ситуации, генерации альтернатив, принятии решения и организации его
выполнения.
Наиболее
целостное и наглядное представление о процессе принятия решений дает рис. 2,
отражающий его основные стадии и порядок их следования.
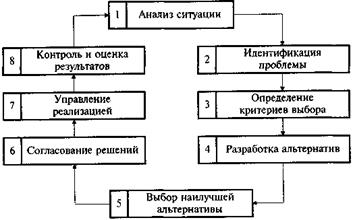
Рис. 2 Состав и последовательность процедур
процесса принятия управленческих решений
Рассмотрим
содержание каждой из основных процедур процесса принятия решения.
1.
Анализ ситуации. Для возникновения необходимости принять управленческое решение
нужен сигнал о внешнем или внутреннем воздействии, вызвавшем или способном
вызвать отклонение от заданного режима функционирования системы, т.е. наличие
управленческой ситуации. Поэтому одним из важнейших условий принятия
правильного решения является анализ ситуации.
Анализ управленческой ситуации требует сбора и обработки
информации. Этот этап выполняет функцию восприятия организацией внешней и
внутренней среды. Данные о состоянии основных факторов внешней среды и
положении дел в организации поступают к менеджерам и специалистам, которые
классифицируют, анализируют информацию и сравнивают реальные значения
контролируемых параметров с запланированными или прогнозируемыми, что в свою
очередь позволяет им выявить проблемы, которые следует решать.
2.
Идентификация проблемы. Первый шаг на пути решения проблемы – ее определение
или диагноз, полный и правильный. Как принято говорить, правильно
сформулировать проблему – значит наполовину решить ее.
Существуют два взгляда на сущность проблемы. Согласно
одному, проблемой считается ситуация, когда поставленные цели не достигнуты или
существует отклонение от заданного уровня, например, мастер может установить,
что производительность труда или качество изделий на его участке ниже нормы. В
соответствии с другим, как проблему следует рассматривать также и потенциальную
возможность повышения эффективности. Объединяя оба эти подхода, будем понимать
под проблемой расхождение между желаемым и реальным состоянием управляемого
объекта.
Выявление и формулировка проблемы – весьма сложная
процедура. Дело в том, что в момент своего возникновения многие важнейшие
проблемы слабо структурированы, т.е. не содержат очевидных целей, альтернативных
путей их достижения, представления о затратах и эффекте, связанных с каждым из
вариантов, и доведение этих проблем до количественной определенности
(структурирование) требует от руководителей не только знаний и опыта, но и
таланта, интуиции, творческого подхода.
Пользуясь медицинской терминологией, первый шаг в
диагностировании сложной проблемы – установление симптомов. Общими симптомами
болезни организации являются: низкие – прибыль, объем продаж,
производительность труда, качество товаров и услуг; высокие – издержки,
текучесть кадров, многочисленные конфликты. Выявление симптомов помогает
определить проблему в общем виде, однако подобно тому, как различные болезни
нередко имеют общие симптомы (головная боль может быть вызвана и обычным
переутомлением и гипертонией), различные причины могут вызывать сходные
организационные проблемы (низкое качество товара может быть следствием как
изношенности оборудования, так и недостаточной квалификации рабочих). Поэтому
менеджеры должны более глубоко исследовать причины возникшей проблемы и не
спешить устранять только ее симптомы.
Нельзя также забывать, что все элементы и работы в
организации взаимосвязаны и решение какой-либо проблемы в одной части
организации может вызвать появление проблем в других. Поэтому, определяя
решаемую проблему, следует стремиться к тому, чтобы число вновь возникающих при
этом проблем было минимальным.
3. Определение критериев выбора. Прежде чем рассматривать
возможные варианты решения возникшей проблемы, руководителю необходимо
определить показатели, по которым будет производиться сравнение альтернатив и
выбор наилучшей. Эти показатели принято называть критериями выбора. Например,
принимая решение о приобретении нового оборудования, можно ориентироваться на
критерии цены, производительности, эксплуатационных расходов, эргономичности и
т.п., а в случае принятия решения о приеме на работу нового сотрудника,
критериями выбора среди кандидатов могут быть: образование, опыт работы,
возраст, личные качества.
4.
Разработка альтернатив. Следующий этап – разработка набора альтернативных
решений проблемы. В идеале желательно выявить все возможные альтернативные пути
решения проблемы, только в этом случае решение может быть оптимальным. Однако
на практике руководитель не располагает (и не может располагать) такими
запасами знаний и времени, чтобы сформулировать и оценить каждую возможную
альтернативу. Менеджеры хорошо понимают, что поиск оптимального решения очень
труден, занимает много времени и дорого стоит, поэтому они ищут не оптимальный,
а достаточно хороший, приемлемый вариант, позволяющий снять проблему и
помогающий отсечь заранее непригодные альтернативы, критерии выбора,
определенные на предыдущем этапе.
Наряду
с положением, когда варианты решения проблемы заранее известны или
обнаруживаются без особых трудностей, часто бывают ситуации, при которых
решаемая проблема не встречалась раньше, т.е. возможные альтернативы неизвестны
и их необходимо предварительно сформулировать. В таких случаях весьма полезным
может оказаться коллективное обсуждение проблемы и генерирование альтернатив.
5.
Выбор альтернативы. Разработав возможные варианты решения проблемы, их
необходимо оценить, т.е. сравнить достоинства и недостатки каждой альтернативы
и объективно проанализировать вероятные результаты их реализации. Для сопоставления
вариантов решения необходимо иметь стандарты или критерии, по которым их можно
сравнивать. Такие критерии выбора были установлены на третьем этапе. С их
помощью и производится выбор наилучшей альтернативы.
Поскольку выбор осуществляется, как правило, на основе
нескольких критериев, а не одного, он всегда носит характер компромисса. Кроме
того, при оценке возможных вариантов решения руководитель фактически имеет дело
с прогнозными оценками сравниваемых величин, а они всегда вероятностные. Поэтому
очень важно учитывать фактор риска, т.е. определять вероятность осуществления
каждой альтернативы. Учет фактора риска приводит к пересмотру самого понятия
наилучшего решения: им является не тот вариант, который максимизирует или
минимизирует некоторый показатель, а тот, который обеспечивает его достижение с
наиболее высокой степенью вероятности.
6.
Согласование решения. В современных системах управления в результате разделения
труда сложилось положение, при котором подготавливают, разрабатывают решение одни
работники организации, принимают или утверждают – другие, а выполняют – третьи.
Иначе говоря, руководитель часто утверждает и несет ответственность за решение,
которого не разрабатывал, специалисты, готовившие и анализировавшие решение, не
участвуют в его реализации, а исполнители не принимают участия в подготовке и
обсуждении готовящихся решений. Принятие управленческих решений в организации
довольно часто ошибочно рассматривается как индивидуальный, а не групповой
процесс. Между тем, хотя основные этапы ППР организациями и отдельными людьми
совпадают, формирование решений в организации существенно отличается от
индивидуального принятия решения. Именно организация, а не отдельный
руководитель должна реагировать на возникающие проблемы. И не один руководитель,
а все члены организации должны стремиться к повышению эффективности ее работы.
Конечно, менеджеры выбирают курс для организации, но чтобы решение было
реализовано, необходимы совместные действия всех членов организации. Поэтому в
групповых процессах принятия решений весьма существенную роль играет стадия
согласования.
В идеальном случае исполнители будут действовать в
соответствии с решениями менеджеров, однако практика далека от идеала и так
происходит не всегда. Признание решения редко бывает автоматическим, даже если
оно явно хорошее. Поэтому руководитель должен убеждать в правильности своей
точки зрения, доказывать работникам, что его решение несет выгоды и
организации, и отдельным ее членам. Практика показывает, что вероятность
быстрой и эффективной реализации значительно возрастает, когда исполнители
имеют возможность высказать свое мнение по поводу принимаемого решения, внести
предложения, замечания и т.п. Тогда принятое решение воспринимается как свое, а
не навязанное «сверху». Поэтому лучший способ согласования решения –
привлечение работников к процессу его принятия. Разумеется, этот способ не надо
абсолютизировать: встречаются ситуации, когда это невозможно или не рационально
и менеджер вынужден принимать решение единолично, не прибегая к обсуждениям и
согласованиям, но надо помнить, что систематическое игнорирование мнения
подчиненных ведет к авторитарному стилю руководства.
7. Управление реализацией. Процесс решения проблемы не
заканчивается выбором альтернативы: для получения реального эффекта принятое
решение должно быть реализовано. Именно это и является главной задачей данного
этапа.
Для успешной реализации решения прежде всего необходимо
определить комплекс работ и ресурсов и распределить их по исполнителям и
срокам, т.е. предусмотреть, кто, где, когда и какие действия должен предпринять
и какие для этого необходимы ресурсы. Если речь идет о достаточно крупных
решениях, это может потребовать разработки программы реализации решения. В ходе
осуществления этого плана руководитель должен следить за тем, как выполняется
решение, оказывать в случае необходимости помощь и вносить определенные
коррективы.
8. Контроль и оценка результатов. Даже после того как
решение окончательно введено в действие, процесс принятия решений не может
считаться полностью завершенным, так как необходимо еще убедиться, оправдывает
ли оно себя. Этой цели и служит этап контроля, выполняющий в данном процессе
функцию обратной связи. На этом этапе производятся измерение и оценка
последствий решения или сопоставление фактических результатов с теми, которые
руководитель надеялся получить.
Решение всегда носит временный
характер. Срок его эффективного действия можно считать равным периоду
относительного постоянства проблемной ситуации. За его пределами решение может
перестать давать эффект и даже превратиться в свою противоположность – не
способствовать решению проблемы, а обострять ее. В связи с этим основная задача
контроля – своевременно выявлять убывающую эффективность решения и
необходимость в его корректировке или принятии нового решения. Кроме того,
осуществление этого этапа является источником накопления и систематизации опыта
в принятии решений.
Таким образом, под процессом принятия
управленческих решений понимается состав и последовательность процедур,
приводящих к решению проблем предприятия, в комплексе с методами разработки и
анализа альтернатив.
Принятие решения – не одномоментный
акт, а результат процесса, имеющего определенную продолжительность и структуру.
Процесс принятия решений – циклическая последовательность действий субъекта
управления, направленных на разрешение проблем организации и заключающихся в
анализе ситуации, генерации альтернатив, выборе из них наилучшей и ее
реализации. Одна из сложнейших процедур процесса принятия решения –
идентификация решаемой проблемы, поскольку в момент своего возникновения многие
важные проблемы слабо структурированы, т.е. не содержат очевидных целей,
альтернативных путей их достижения и представлений о затратах и эффекте,
связанных с каждым из возможных вариантов. Прежде чем анализировать возможные
альтернативы решения, менеджеру необходимо определить показатели, по которым
будут сравниваться варианты.