Лекция 4,5. Физические основы термодинамики
Термодинамика как и молекулярная физика занимается
изучением физических процессов, происходящих в макроскопических системах, т.е.
в телах, содержащих огромное число микрочастиц, взаимодействующих друг с другом
и внешними телами.
Задачей термодинамического метода изучения состояний
макроскопических систем является установление связей между непосредственно
наблюдаемыми величинами, такими, как давление, объем, температура, концентрация
раствора, напряженность электрического или магнитного поля, световой поток и
т.д. Никакие величины, связанные с атомно-молекулярной структурой вещества (
размеры атома или молекулы, их масса, количество и т.д.), не входят в
рассмотрение при термодинамическом подходе к решению задач.
Термодинамический метод, не связанный с модельными
представлениями, обладает большей общностью, отличается простотой и ведет,
после ряда простых математических процедур, к решению целого ряда конкретных
задач, не требуя никаких сведений о свойствах атомов или молекул.
Однако при термодинамическом рассмотрении остается
нераскрытым внутренний (атомно-молекулярный) механизм явлений. По этой причине
в термодинамике, как правило, бессмысленны вопросы " почему" ?
Например, почему
при быстром растяжении медная проволока охлаждается, а
резиновый жгут нагревается? Мы должны удовлетворить этим результатам, а
механизм, ведущий к нему, остается скрытым от нас.
В основе термодинамики лежат принципы, являющиеся
обобщение опытных данных: принцип температуры (часто называемый нулевым началом
термодинамики), принцип энергии (I начало), принцип энтропии (II начало) и
постулат Нернста (III начало термодинамики).
- Термодинамические
системы. Равновесные состояния и равновесные процессы
Будем называть термодинамической системой любое
макроскопическое тело, находящееся в равновесном или близком к равновесному
состоянию.
Состояния любой термодинамической системы могут быть
заданы с помощью ряда параметров, например, для газа P, V, T , для жидкости - a (коэффициент поверхностного натяжения), s (поверхность
пленки), Т и.т.д.
Следует заметить, что не в любом состоянии системы все
ее параметры имеют определенный смысл. Например, представим себе сосуд,
разделенный на две половины перегородкой с краном, и пусть вначале в левой
половине находится газ, а в правой - вакуум. Если мы откроем кран, то из него
вырвется струя газа, и в первые моменты этого процесса объем газа будет
неопределенным - плотность газа в правой половине сосуда будет меняться от
точки к точке по какому-то сложному закону и указать границы объема, в котором
находится газ, невозможно.
Можно, например, представить себе систему, температура
которой меняется от точки к точке, или газ, в разных точках которого давление
различно. Такие состояния называются неравновесными.
Обычно по прошествии некоторого времени
устанавливается состояние, в котором каждый такой параметр имеет одно и то же
значение во всех точках системы и остается неизменным сколь угодно долго, если
не меняются внешние условия. Такие состояния называются равновесными.
Процесс перехода термодинамической системы из
неравновесного состояния в равновесное называется процессом релаксации, он
характеризуется временем релаксации.
Представим себе процесс, протекающий в
термодинамической системе со скоростью, значительно меньшей скорости
релаксации; это значит, что на любом этапе этого процесса значения всех
параметров будут успевать выравниваться и такой процесс будет представлять
собой последовательность бесконечно близких друг к другу равновесных состояний.
Такие достаточно медленные процессы принято называть равновесными или
квазистатическими. Ясно, что все реальные процессы являются неравновесными и
могут лишь в большей или меньшей степени приближаться к равновесным.
Заметим, что равновесный процесс может идти как в
прямом, так и в противоположном направлениях. В связи с этим равновесные
процессы называют также обратимыми. В дальнейшем мы будет рассматривать только
равновесные процессы.
Для каждой термодинамической системы существует
состояние термодинамического равновесия, которое она при фиксированных внешних
условиях достигает.
Например, чайник, снятый с плиты, сам остывает до
комнатной температуры.
Сформулированный признак термодинамических систем
настолько важен, что он получил название нулевого начала термодинамики. (Это
начало имеет такой странный номер потому, что лишь после того как были открыты
первое и второе начала термодинамики, ученые осознали, что этот практически
очевидный постулат нужно поставить впереди.) По существу, нулевое начало
термодинамики постулирует существование температуры.
2. Внутренняя энергия идеального газа. Число степеней
свободы молекулы. Закон равномерного распределения энергии по степеням свободы
Важной характеристикой термодинамической системы
является ее внутренняя энергия U - энергия хаотического (теплового) движения
микрочастиц системы (молекул, атомов, электронов, ядер и т.д.) и энергия
взаимодействия этих частиц. К внутренней энергии не относятся кинетическая
энергия движения системы как целого и потенциальная энергия системы во внешних
полях.
В курсе физики уже встречалось понятие числа степеней
свободы i: это число независимых координат, полностью
определяющих положение тела ( материальной точки, системы материальных точек) в
пространстве. Так, например, положение материальной точки определяется тремя
координатами (x, y, z), следовательно, i=3. Тонкий стержень имеет 5 степеней
свободы (x, y, z, a, b), т.е. 3 поступательные и 2
вращательные, твердое тело имеет 6 степеней свободы (x,
y, z, a, b, g), т.е. 3 поступательные и 3
вращательные.
С учетом этого для одноатомных молекул газа (He, Ne, Ar)
i=3, для двухатомных молекул газа (H2, O2, N2)
с жесткой связью атомов i=5, для трех- и более атомных молекул газа с жесткой
связью атомов (CO2, NH3) i=6.
Естественно, что жесткой связи между атомами не
существует - атомы могут совершать колебания. С учетом этого полное число
степеней свободы iå=i+2iколеб. В классической теории
рассматривают молекулы с жесткой связью атомов, для них iколеб.=0.
Итак, независимо от числа степеней свободы молекул три
степени свободы всегда поступательные. Ни одна из них не имеет преимущества
перед другими, поэтому на каждую из них приходится в среднем одинаковая
энергия, равная 1/3 значения <Wk>
[см.(16) в лекции 1,2], т.е.
<Wk>/3 = kT/2.
Важнейший закон классической статистической физики -
закон равномерного распределения энергии по степеням свободы - утверждает: на
каждую степень свободы молекулы в среднем приходится одинаковая кинетическая
энергия, равная kТ/2.
Следовательно, средняя кинетическая энергия молекулы,
имеющей i степеней свободы, <Wk>
= 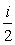 kT .(1)
kT .(1)
Так как в идеальном газе взаимная потенциальная
энергия молекул равна нулю (т.е. молекулы между собой не взаимодействуют), то
внутренняя энергия U представляет собой кинетическую энергию его молекул.
Для одного моля
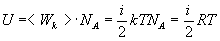 ,(2)
,(2)
для произвольной массы m
газа
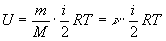 , (3)
, (3)
где М - масса моля, n=m/M - число молей.
Таким образом, внутренняя энергия идеального газа
пропорциональна температуре газа и зависит от числа степеней свободы его
молекул.
3. Работа и теплота
Рассмотрим термодинамическую систему, для которой
механическая энергия не изменяется, а изменяется лишь ее внутренняя энергия.
Внутренняя энергия закрытой системы (т.е. системы, которая не обменивается
веществом с внешней средой; в 4,5 лекциях мы изучаем только закрытые системы)
может изменяться качественно различными способами:
1. Путем совершения работы внешними телами над
системой, например, при сжатии газа температура его повышается и,
следовательно, изменяется (увеличивается) его внутренняя энергия.
2. Путем теплообмена, т.е. процесса обмена внутренними
энергиями при контакте тел с различными температурами. Энергию, передаваемую от
одних тел к другим в процессе теплообмена, называют теплотой.
Таким образом, можно говорить о двух формах передачи
энергии от одних тел к другим: работе и теплоте. Энергия механического движения
может превращаться в энергию теплового движения и наоборот. При этих
превращениях соблюдается закон сохранения и превращения энергии. Применительно
к термодинамическим процессам этим законом и является первое начало
термодинамики, установленное в результате обобщения многовековых опытных
данных.
4. Первое начало термодинамики (ПНТ)
Допустим, что некоторая термодинамическая система
(например, газ, заключенный в цилиндр под поршнем), обладая внутренней энергией
U1, получила некоторое количество теплоты Q и, перейдя в новое
состояние, характеризующееся внутренней энергией U2, совершила
работу А над внешней средой, т.е. против внешних сил. В этом случае Q=U2-U1+A
или
Q=DU+A.(4)
Уравнение (4) выражает ПНТ: теплота, сообщаемая
системе, расходуется на изменение ее внутренней энергии и на совершение ею
работы против внешних сил.
Для бесконечно малых процессов выражение (4)
записывают в дифференциальной форме dQ=dU+dA или в
более корректной форме
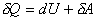 ,(5)
,(5)
поскольку только dU является
полным дифференциалом, а dQ и dА полными дифференциалами не
являются.
Из формулы (5) следует, что в СИ количество теплоты
выражается в тех же единицах, что работа и энергия, т.е. в джоулях (Дж).
Если система периодически возвращается в
первоначальное состояние, то изменение ее внутренней энергии DU=0. Тогда, согласно (4) А= Q , т.е. вечный двигатель первого рода,
который совершал бы большую работу, чем сообщенная ему извне энергия, не
возможен. Это одна из формулировок первого начала термодинамики.
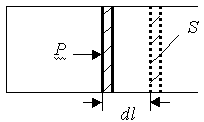
5. Работа газа при изменении его объема
|
|
Найдем работу, совершаемую газом при изменении его
объема, 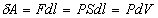 , где S
- площадь поршня, Sdl =dV
- изменение объема газа. Таким образом, , где S
- площадь поршня, Sdl =dV
- изменение объема газа. Таким образом,
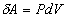 . (6) . (6)
|
Полная работа при расширении газа от объема V1
до объема V2
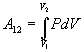 (7)
(7)
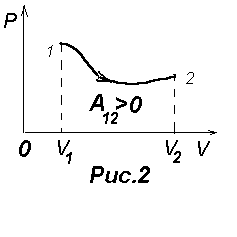
И графически она изображается площадью фигуры, лежащей
под кривой P(V) (Рис.2). Таким образом, работа не определяется только начальным
и конечным состояниями газа,
|
|
а зависит от всего хода процесса. Следовательно,
криволинейный интеграл (7) зависит от пути интегрирования и поэтому
подынтегральное выражение 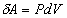 не
является полным дифференциалом какой-либо функции состояния газа. не
является полным дифференциалом какой-либо функции состояния газа.
С учетом (6) ПНТ можно представить в другой форме
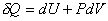 .(8) .(8)
|
6. Теплоемкость
Удельная теплоемкость вещества - величина, равная
количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:
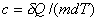 , Дж/(кгК). (9)
, Дж/(кгК). (9)
Молярная теплоемкость - величина, равная количеству
теплоты, необходимому для нагревания 1 моля вещества на 1 К:
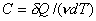 , Дж/(мольК). (10)
, Дж/(мольК). (10)
где n=m/M -
количество молей вещества.
7. Применение ПНТ к изопроцессам
7.1. Изохорический процесс
|
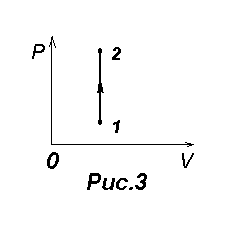
|
Для него V=const.
Диаграмма этого процесса (изохора) изображена на рис.3. Процесс 1-2
соответствует нагреванию, а процесс 2-1 - охлаждению газа. При изохорическом
процессе газ не совершает работы: 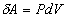 =0 и вся
теплота, сообщаемая газу, идет на увеличение его внутренней энергии, т.е. dQ=dU.
(11) =0 и вся
теплота, сообщаемая газу, идет на увеличение его внутренней энергии, т.е. dQ=dU.
(11)
|
Согласно формуле (3) для произвольной массы газа 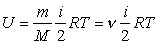 и поэтому
и поэтому 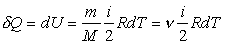 , (12)
, (12)
и молярная теплоемкость при постоянном объеме
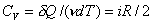 . (13)
. (13)
Таким образом, 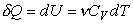 . (14)
. (14)
7.2.Изобарический процесс
|

|
Для него P=const.
Диаграмма этого процесса (изобара) изображена на рис.4. Практически он
осуществляется, например, при нагревании (процесс 1-2) или охлаждении
(процесс 2-1) газа, находящегося в цилиндре с подвижным поршнем, на который
действует постоянное внешнее давление.
Учитывая, что для произвольной массы газа U=(i/2)nRT,
|
PV=nRT, запишем ПНТ в
дифференциальной форме для изобарического процесса:
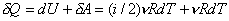 , (15)
, (15)
Молярная теплоемкость при постоянном давлении
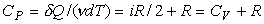 . (16)
. (16)
Выражение 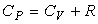 (17)
(17)
называется уравнением Майера; оно показывает, что CP
всегда больше CV на величину универсальной газовой постоянной R. Это
объясняется тем, что для нагревания газа при постоянном давлении требуется еще
дополнительное количество теплоты на совершение работы расширения газа.
Таким образом, физический смысл универсальной газовой
постоянной R: она численно равна работе, совершаемой одним молем идеального
газа при его изобарическом нагревании на 1 К.
С учетом (16) первое начало термодинамики для
изобарического процесса имеет вид 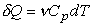 , (18)
, (18)
кроме того, 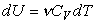 ,
,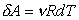 .
.
7.3. Изотермический процесс
Для него Т-const.
Например, процессы кипения, конденсации, плавления и кристаллизации химически
чистых веществ происходят при постоянной температуре, если внешнее давление
постоянно.
|
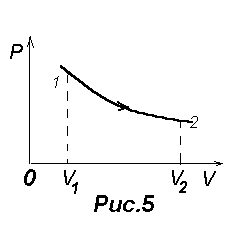
|
Для идеального газа при Т=const
выполняется закон Бойля-Мариотта PV=const.
Диаграмма изотермического процесса (изотерма) изображена на рис.5. Процесс
1-2 соответствует нагреванию газа, а процесс 2-1 - охлаждению его.
Внутренняя энергия идеального газа в изотермическом
процессе не изменяется, т.е. 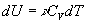 =0, так
как Т=const и dT=0. Таким образом из
ПНТ ( =0, так
как Т=const и dT=0. Таким образом из
ПНТ (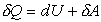 )
следует, что )
следует, что 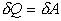 , т.е.
вся теплота, сообщаемая газу, расходуется на , т.е.
вся теплота, сообщаемая газу, расходуется на
|
совершение им работы против внешних сил:
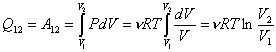 , (19)
, (19)
гдеn=m/M - число
молей.
Процесс 1-2 (см.рис.5) соответствует изотермическому
расширению газа, в этом случае Q12>0 и A12>0.
Обратный процесс 2-1 соответствует изотермическому сжатию газа, для него Q12<0
и A12<0.
7.4. Адиабатический процесс
Это процесс, при котором отсутствует теплообмен (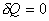 ) между
системой и окружающей средой. К адиабатическим можно отнести все
быстропротекающие процессы.
) между
системой и окружающей средой. К адиабатическим можно отнести все
быстропротекающие процессы.
Из ПНТ (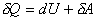 ) для
адиабатического процесса следует, что
) для
адиабатического процесса следует, что
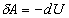 ,(20)
,(20)
т.е. внешняя работа совершается за счет уменьшения
внутренней энергии системы. Учитывая, что 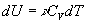 , найдем
работу адиабатического расширения газа от объема V1 до V2
( при этом температура газа уменьшается от Т1 до Т2):
, найдем
работу адиабатического расширения газа от объема V1 до V2
( при этом температура газа уменьшается от Т1 до Т2):
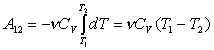 . (21)
. (21)
Можно показать, что для адиабатического процесса
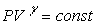 . (22)
. (22)
Это уравнение называют уравнением Пуассона или
уравнением адиабаты, g=СP/CV=(i+2)/i - показатель адиабаты (коэффициент Пуассона), i - число степеней свободы молекулы газа.
|
|
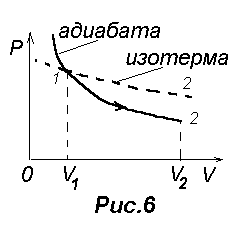
На диаграмме PV линия, изображающая адиабатический
процесс, называется адиабатой (рис.6.). Так как g>1, то адиабата идет круче, чем изотерма, уравнение которой PV=const. Процесс 1-2 соответствует
адиабатическому расширению газа. В этом случае 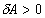 , dU>0. Обратный процесс 2-1 соответствует
адиабатическому сжатию газа. В этом случае , dU>0. Обратный процесс 2-1 соответствует
адиабатическому сжатию газа. В этом случае 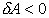 , dU<0. , dU<0.
|