ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Кафедра статистики

Курсовая работа

по дисциплине «Статистика»

на тему

«Статистические методы изучения инвестиций»

Исполнитель: Дибаева А.И.

Специальность: Финансы и кредит

Группа: 1

№ зачетной книжки: 03ФФБ 3351

Руководитель: Орлович Ж.Б.

Уфа 2005

СОДЕРЖАНИЕ

Введение  3

1. Теоретические аспекты статистики инвестиций  4

1. Экономическая сущность инвестиций  4

1.2. Группировка инвестиций  7

1.3. Доходность инвестиций  10

1.4. Источники статистической информации об инвестициях  13

Расчетная часть. Вариант 2  54

Аналитическая часть 

Заключение 

Список использованной литературы  

Введение

Актуальность и практическая значимость таких проблем, как формирование портфеля инвестиций, управление эффективностью инвестиций обусловлены развитием рыночных отношений. Для любого предприятия важна разумная и целенаправленная инвестиционная деятельность.

Инвестор, вкладывая средства в проект, прежде всего проводит оценку проекта, которая предполагает определение рыночной стоимости актива. Однако, если оцениваемый объект финансируется за счет собственных и заемных средств инвестора, возникает проблема определения рыночной стоимости собственного капитала инвестора и рыночной стоимости привлекаемого ипотечного кредита.

Проблема принятия инвестиционных решений традиционно находится в центре внимания как ученых-теоретиков, так и хозяйственников-практиков.

И это объяснимо: инвестирование играет ключевую роль в фундаментальных экономических процессах, протекающих как на уровне всей экономики, так и на уровне отдельных предприятий. От качественных и количественных характеристик инвестиций зависят производственный потенциал страны, эффективность его функционирования. Решение многих социальных проблем, таких как безработица, условия труда, уровень жизни населения, связано с масштабами инвестиционного процесса и его эффективностью. Но, несмотря на значительное количество публикаций по данной проблеме, для российской экономики она не решена.

В связи с этим высока роль статистики как фактора формирования общественного сознания, помогающее расширить гласность и доступность сводной статистической информации при сохранении принципа конфиденциальности индивидуальных данных.

 

 

 

 

 

1. Теоретические аспекты сТАТИСТИКи ИНВЕСТИЦИЙ

1. Экономическая сущность инвестиций

Одной из основных особенностей формирования рыночных отношений в экономике страны является развитие инвестиционной деятельности.

Под инвестиционной деятельностью понимается «вложение инвестиций и осуществление практических действии в целях получения прибыли и (или) достижения иного полезного эффекта».

В условиях командно-административной системы экономическая категория «инвестиции» подменялась понятием «капитальные вложе­ния», под которыми понимались все денежные затраты, направляе­мые на воспроизводство и ремонт основных фондов.

В широком смысле инвестиции - это денежные средства, ценные бумаги, иное имущество, в том числе имущественные права, иные права, имеющие денежную оценку, вкладываемые в объекты предпри­нимательской и (или) иной деятельности в целях получения прибыли и (или) достижения иного полезного характера. Понятие инвестиций гораздо шире понятия капитальных вложений.

В Федеральном законе «Об инвестиционной деятельности в Российской Федерации, осуществляемой в форме капитальных вложений» указано: «капитальные вложения - инвестиции в основной капитал (основные средства), в том числе затраты на новое строительство, расширение, реконструкцию и техническое перевооружение действующих предприятий, приобретение машин, оборудования, инструмента, инвентаря, проектно-изыскательские работы и другие затра­ты». Используя общепринятое деление инвестиций на реальные и фи­нансовые, можно сказать, что реальные инвестиции - это капитальные вложения в основной производственный капитал.

В статистической практике под реальными инвестициями понимают инвестиции в нефинансовые активы, которые осуществляет предприятие.

Инвестиции в нефинансовые активы включают:

инвестиции в основной капитал;

инвестиции в нематериальные активы;

инвестиции в объекты природопользования (водоемы, леса и т. д.) и землю;

инвестиции в пополнение запасов материальных оборотных средств;

затраты на капитальный ремонт зданий, сооружений, машин и оборудования.

Инвестиции в основной капитал подразделяются на:

инвестиции в основной материальный капитал;

инвестиции в основной нематериальный капитал.

Инвестиции в основной нематериальный капитал складываются из затрат на новое строительство, расширение, реконструкцию, техни­ческое перевооружение, приобретение и капитальный ремонт зданий, сооружений, машин, оборудования, приобретение многолетних насаж­дений, рабочего скота и т. д.

Под новым строительством следует понимать строительство но­вых зданий и сооружений, осуществленное на новых площадках.

К расширению действующих предприятий относится строительст­во дополнительных производств, цехов и объектов на территории действующего предприятия с целью создания дополнительных мощ­ностей, а также строительство филиалов, которые будут находиться на самостоятельном балансе.

Реконструкция действующих предприятий обязательно связана с переустройством существующих производств и цехов с учетом дости­жений научно-технического прогресса для получения более совершен­ных мощностей производства.

Техническое перевооружение действующих предприятий - это комплекс мероприятий по повышению технико-экономического уров­ня отдельных производств.

Инвестиции в основной нематериальный капитал могут включать затраты на создание и приобретение программных продуктов, опыт­но-конструкторских разработок и т. д. Инвестиции в нематериальные активы — это затраты на приобретение лицензии, патентов, авторских прав, разработку торговых марок и т. д.

Инвестиции на пополнение запасов материальных оборотных средств складываются из изменения стоимости готовой продукции и товаров, незавершенного производства, производственных запасов.

Затраты на капитальный ремонт зданий и сооружений - это за­траты на смену изношенных конструкций и деталей, кроме полной замены основных конструкций (стен, фундаментов, межэтажных пе­рекрытий и др.). Капитальным ремонтом машин и оборудования считается такой вид ремонта, при котором производятся полная разборка агрегата, замена или ремонт всех изношенных деталей и узлов, их сборка и испытания.

Финансовые инвестиции представляют собой вложения денежных средств, материальных и иных ценностей в акции, облигации и дру­гие ценные бумаги юридических лиц.

Финансовые инвестиции представляют собой:

банковские вклады (депозиты), которые отражают денежные сум­мы, помещаемые на хранение в банк клиентом банка;

облигации - долговые обязательства перед их владельцами по вы­плате определенного дохода в форме процента и полного погашения их стоимости по истечении установленного срока;

акции - ценные бумаги, которые удостоверяют вклад акционера в имущество предприятия;

кредит - денежные средства, временно привлекаемые юридиче­ским лицом и подлежащие возврату;

дебиторскую задолженность - денежные средства, которые получа­ет юридическое лицо по итогам взаимоотношений с дебиторами;

ссуду - денежные средства, которые получает заемщик в собствен­ность и обязуется возвратить, как правило, с процентами;

пай - часть определенных имущественных прав и обязанностей предприятия, предусмотренных в положении или уставе соответствую­щего предприятия.

На практике существует понятие «чистые финансовые инвести­ции», которые представляют собой разницу между приобретением финансовых активов и погашением финансовых обязательств.

1.2. Группировка инвестиций

Реальные и финансовые инвестиции можно сгруппировать по формам собственности, по отраслям экономики, по источникам финансирования и т. д.

Группировка инвестиций по формам собственности предполагает следующее их распределение: государственная и негосударственная форма собственности. Государственная собственность включает собственность, принадлежащую полностью федеральным, региональным, муниципальным органам управления. Негосударственная форма собственности включает частную собственность, собственность общественных организаций и смешанную собственность. Частная собственность может предполагать долевую или совместную собственность. Смешанная собственность представляет собой собственность хозяйст­вующих субъектов, действующих на основе объединения частной, государственной собственности и собственности общественных организаций. Смешанная форма собственности может предполагать и иностранную собственность, т. е. собственность иностранных юридических или физических лиц, государств и международных организаций.

Группировка инвестиций по отраслям экономики производится в соответствии с действующим ОКОНХ.

По источникам финансирования инвестиции распределяются на собственные и привлеченные средства. Собственные средства включа­ют прибыль, остающуюся в распоряжении предприятий; амортизационные отчисления; денежные накопления юридических лиц и сбережения физических лиц;. денежные суммы, выплачиваемые страховыми организациями в виде возмещения потерь от стихийных бедствий, аварий и т. п.; другие средства.

Привлеченные средства включают: кредиты банков, средства от продажи акций, благотворительные и иные взносы, средства, выделяе­мые вышестоящими холдинговыми и акционерными компаниями, промышленно-финансовыми группами на безвозмездной основе; различные формы заемных средств, в том числе кредиты, предоставляемые государством на возвратной основе, кредиты иностранных инвесторов, облигационные займы, кредиты инвестиционных фондов и компаний, страховых обществ и др.; средства из федерального бюд­жета и бюджетов субъектов Федерации; средства внебюджетных фон­дов; иностранные инвестиции, предоставляемые в форме финансово­го или иного участия в уставном капитале совместных предприятий, а также в форме прямых вложений финансовых институтов, государств, международных организаций и др.

Наряду с перечисленными существует ряд других общепринятых группировок. Например, Государственный комитет Российской Феде­рации по статистике использует технологическую группировку инве­стиций в основной материальный капитал. Инвестиции по технологической структуре подразделяются на стоимость всех видов строительных работ; работ по монтажу оборудования; оборудования (требующего и не требующего монтажа), предусмотренного в сметах на строительство; инструмента и инвентаря, включаемых в сметы на строительство; машин и оборудования, не входящих в сметы на строительство; прочих капитальных работ и затрат.

Финансовые инвестиции в зависимости от срока погашения под­разделяются на краткосрочные и долгосрочные. Краткосрочные фи­нансовые инвестиции осуществляются на срок не более одного года. Долгосрочными считаются инвестиции, осуществленные с намерением получения дохода по ним сроком более одного года.

В финансовых инвестициях особо выделяются иностранные инве­стиции, которые могут быть как от конкретного юридического лица (резидента) в экономику «остального мира», так и от нерезидента в данное предприятие. Эти инвестиции делятся на прямые, портфель­ные и прочие.

Прямые инвестиции - это инвестиции, сделанные прямыми инвесторами, т. е. юридическими или физическими лицами, полностью владеющими предприятием или контролирующими не менее 10% акций или акционерного капитала предприятия, что дает право на участие в управлении предприятием.

Из прямых инвестиций выделяются:

взносы в уставный капитал, фактически внесенные зарубежными совладельцами предприятия. Эти взносы включают материальные и нематериальные активы, сделанные в виде недвижимости, оборудова­ния, товаров и т. п., а также взносы в виде денежных средств;

финансовый лизинг (в форме предоставления услуг по финансовому лизингу имущества российским организациям);

кредиты, полученные от зарубежных совладельцев предприятий;

прочие прямые инвестиции (дополнительная покупка акций соуч­редителями, оборудование, переданное прямым инвестором предприятию, и т. п.).

Портфельные инвестиции представляют собой покупку акций, не дающих вкладчикам права влиять на работу предприятий и состав­ляющих менее 10% в общем акционерном капитале предприятия, а также облигаций, векселей и других долговых ценных бумаг собствен­ного и заемного капитала.

В портфельные инвестиции входят акции, долговые ценные бума­ги предприятий, включающие векселя, долгосрочные и краткосроч­ные государственные ценные бумаги.

Прочие иностранные инвестиции включают:

торговые кредиты (оплата импорт или экспорт и предоставление кредитов для этих целей);

прочие кредиты, кроме торговых, полученные не от прямых инвесторов.

Сюда включаются кредиты, полученные от международных фи­нансовых организаций: Мирового банка, Международного валютного фонда, Международного банка реконструкции и развития, Европейского банка реконструкции и развития и т. д.;

кредиты правительств иностранных государств под гарантии пра­вительства Российской Федерации;

банковские вклады (счета иностранных юридических лиц в рос­сийских банках);

прочие,

1.3. Доходность инвестиций

Инвестиции осуществляются с целью получения прибыли (дохо­да).

Доход от инвестирования представляет собой выгоду, получаемую от вложений средств в экономические активы. При этом вид дохода определяется  формой  экономического  актива,  в который  производится инвестирование.

Состав инвестиционного дохода по видам экономических активов выглядит следующим образом:

1.  Доход от инвестиций в нефинансовые активы

1.1.  Прибыль

1.2.  Рента

2.  Доход от инвестиций в финансовые активы

2.1.  Проценты по депозитам

2.2.  Проценты (дисконт, индексация суммы долга) по ценным бумагам, кроме, акций

2.3.  Проценты по ссудам

2.4.  Дивиденды по акциям

2.5.  Проценты по товарному кредиту

Инвестирование в некоторые виды активов (например, ценности, наличные деньги и др.) не связано с получением дохода,

Доход от инвестиций в нефинансовые (реальные) активы — это доход от реализации произведенных с их помощью товаров и услуг за вычетом расходов на производство (заработная плата, стоимость использованных материалов и иные затраты). Таким образом, по эко­номическому содержанию этот показатель аналогичен прибыли.

Если реальные инвестиции осуществлены с целью расширения или модернизации производственного потенциала хозяйственных объ­ектов, то инвестиционный доход представляет собой дополнительную прибыль, получаемую в результате дополнительного ввода мощностей, реконструкции действующего предприятия, повышения произво­дительности оборудования.

Если реальные активы используются владельцем для предоставле­ния в пользование другим экономическим единицам, то доход от инвестирования в эти виды активов определяется:

а) для произведенных активов (здания, сооружения, машины и оборудование) - в размере чистой прибыли от деятельности по сдаче в аренду;

б) для непроизведенных активов (земля, недра и т. п.) - в размере чистой ренты, получаемой их владельцем.

Инвестиционный доход от вложений в финансовые активы пред­ставляет собой доход от собственности, получаемый в результате пре­доставления этих активов в пользование другим экономическим еди­ницам. Вид получаемого дохода от собственности определяется ви­дом предоставляемых финансовых активов.

Инвестиционный доход по депозитам и ссудам измеряется сум­мой процентов, начисляемых исходя из установленной в соответст­вующем договоре процентной ставки. К категории ссуд относятся также соглашения о продаже ценных бумаг с последующим их выкупом. Инвестиционный доход по ним определяется как разница между ценой выкупа и ценой продажи ценных бумаг.

Инвестиционный доход по ценным бумагам, кроме акций, измеряется в зависимости от их вида суммой процентов, дисконта или индексации суммы долга. Так, владельцы облигаций и депозитных сертификатов получают проценты. Для владельцев индексируемых ценных бумаг инвестиционный доход складывается из процентов и величины индексации основной суммы долга. По бескупонным обли­гациям и казначейским векселям инвестиционный доход определяет­ся в размере дисконта (скидки с номинальной стоимости, т. е. разни­цы между ценой выкупа и ценой реализации), а по облигациям с глубоким дисконтом к сумме дисконта добавляются также проценты. Проценты по векселям определяются как разница между суммой, выплаченной держателю векселя (кредитору) при наступлении срока платежа, и суммой, выплаченной кредитором при покупке векселя у дебитора (должника).

Инвестиционный доход по акциям и другим видам участия в ка­питале (паи различного вида) определяется в размере начисляемых дивидендов. Дивиденды могут выплачиваться не только в денежной форме, но и акциями, облигациями, товарами, В этом случае величи­на дивиденда определяется в размере их рыночной стоимости.

К инвестиционному доходу по дебиторской задолженности отно­сятся проценты за товарный кредит.

Показатель, характеризующий доходность инвестиций в общем виде, определяется нормой процента (дохода) на вложенные средст­ва, которая рассчитывается по следующей формуле:

Д=П/И,

где Д - доход инвестиций (норма процента);

П - годовой доход от инвестиций;

И - инвестиции.

Структура доходности инвестиций по видам экономических акти­вов выглядит следующим образом:

1. Доходность инвестиций в нефинансовые активы

1.1. Норма прибыли на стоимость нефинансовых активов (или их отдельных видов)

1.2. Норма прибыли на инвестиции в нефинансовые  активы, произведенные в отчетном или ином периоде

2. Доходность инвестиций в финансовые активы

2.1. Норма процента по депозитам

2.2. Норма процента по ценным бумагам, кроме акций

2.3. Норма процента по ссудам

2.4. Норма дивидендов по акциям

2.5. Норма процента по товарному кредиту

Доходность от вложений в нефинансовые активы измеряется нор­мой прибыли на инвестиции в реальные активы, используемые в про­изводстве. При этом если прибыль, полученная в отчетном периоде, рассматривается как результат инвестиций всех предыдущих периодов, то доходность инвестиций определяется как отношение нормы прибыли к стоимости реальных активов или их отдельных компонентов (основной капитал, запасы материальных оборотных средств, непроизводственные нефинансовые активы).

Др = ЧП/СР,

где Др - доходность инвестиций в реальные активы;

ЧП - чистая прибыль в отчетном периоде после уплаты процентов за кредит;

СР- средняя стоимость реальных активов или их компонентов.

Если же прибыль, полученная в отчетном периоде, рассматривается как результат инвестиций какого-либо предыдущего периода, определенного с учетом временного лага между вложением средств и получением отдачи, то при относительно равномерном развитии экономики прибыль отчетного периода может быть соотнесена с инвестициями этого же периода.

Др = ЧП/ИР,

где Др -инвестиции в реальные активы в отчетном или другом периоде (валовое накопление основного капитала, изменение запасов материальных средств, чистое приобретение непроизводственных нефинансовых активов).

Доходность инвестиций в ценные бумаги измеряется отношением суммы полученных в отчетном периоде процентов, дивидендов и ана­логичных доходов к стоимости приобретенных ценных бумаг.

Доходность ценных бумаг, кроме акций, определяется как отношение процентов, полученных в отчетном периоде, к покупной стоимости ценных бумаг.

Доходность акций определяется как отношение дивидендов, полу­ченных в отчетном периоде, к покупной стоимости акций.

1.4. Источники статистической информации об инвестициях. Ряды динамики

Основным источником статистической информации об инвести­циях является форма № П-2 «Сведения об инвестициях», которую представляют все юридические лица (как коммерческие, так и некоммерческие организации), их филиалы или представительства, осуществляющие инвестирование или получившие инвестиции от других юридических лиц. Начиная с отчета за январь 1999 г. эту форму не представляют субъекты малого предпринимательства.

Форма состоит из:

раздела 1  «Финансовые вложения»;

раздела 2 «Инвестиции в нефинансовые активы, осуществленные данным предприятием»;

раздела 3 «Источники инвестиций».

Государственный комитет по статистике сбор сведений об инве­стициях осуществляет ежеквартально. Дополнительно к ежекварталь­ной форме №П-2 представляются ежемесячно сведения по форме N° П-2 (краткая) об инвестициях в основной капитал с выделением вложений в машины, инструменты и инвентарь. Наряду с ежемесяч­ной формой представляется и годовая форма, приложение к форме №П-3 «Сведения об инвестициях 8 основной капитал». В этой форме предусмотрено два раздела:

раздел  1  «Структура инвестиций»;

раздел 2 «Источники финансирования инвестиций в основной ка­питал по отраслям и видам экономической деятельности».

Ряд динамики представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение  общественных явлений во времени. В каждом ряду динамики имеются два  основных элемента: время t  и конкретное значение показателя (уровень ряда)  y.

Выявление основной  тенденции  в изменении уровней, именуемой трендом, является одной из главных задач анализа рядов динамики. Во  времени, отраженному в динамических рядах, они разделяются на моментные и интервальные. Моментным рядом динамики называется такой ряд, уровни которого характеризуют состояние явления на определенные даты (моменты времени). Примером моментного ряда могут служить  следующие данные об общих денежных ресурсах государства (см. табл.1).

Этот ряд характеризует динамику денежных ресурсов государства России в на 01.07. 2002-2004гг.

Таблица 1

Общие денежные ресурсы государства (млрд. руб.)

Показатели	01.07.2002	01.07.2003	01.07.2004
Средства Правительства РФ и Банк России	227,4	384,7	611,4
Фонд обязательных резервов кредитных организаций	177,3	238,8	25 1,2
Средства государственных организаций в банках	102,3	103,3	130,2
Валютные резервы	1 249,1	1 879,9	2 551,8
lice го	1 756,1	2 606,7	3 544,6

            Источник: Caвин М. О состоянии инвестиционного климата...// Наша власть: дела и лица. 2003. - № 6. – с. 30

Поскольку в каждом  последующем  уровне содержится полностью или частично значение предыдущего  уровня, суммировать уровни моментного ряда не следует, так как это приводит к повторному счету.

Интервальным  (периодическим) рядом динамики называется такой ряд, уровни которого  характеризуют размер явления за конкретный период времени (год, квартал, месяц).  Примером такого ряда могут служить данные о инвестициях в основной капитал в Российской Федерации (см. табл.2).

Таблица 2

Динамика инвестиций в основной капитал в Российской Федерации

Инвестиции	2000 г.	2001 г.	2002 г.	2003 г.	2004 г.
Валовые инвестиции в основной капитал, млрд. руб., текущие цены	1 165	1 505	1 301	1775	2130,2
Валовые инвестиции в основной капитал, годовые индексы	118,1	110,2	102,6	112,9	110,9
Валовые инвестиции в основной капитал в текущих ценах как доля поминального ВВП, %	15,9	16,8	12,0	13,4	12,70

Источник: Без малого бизнеса и теневой экономики.// Официальный Интернет-сайт Госкомстата России. - www. gks. ru

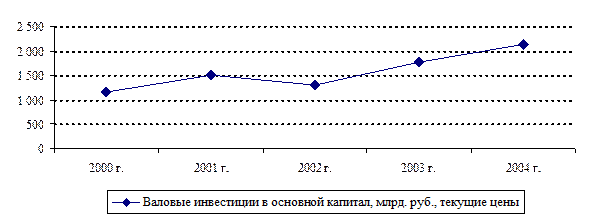
Рис.1. Динамика инвестиций в основной капитал в Российской Федерации

Таблица 3

Отраслевая структура инвестиций в основной капитал

Отрасль	2000 г.	2001 г.	2002 г.	2003 г.	2004 г.
Нефтегазовая	18,5	19,2	20,5	20,5	26,2
Электроэнергетика	3,7	3,6	4,9	5,2	8,3
Транспорт	21,1	20,7	19,4	18,0	19,1
Связь	2,6	2,9	4,0	5,4	6,4
Жилищно-коммунальное хозяйство	18,0	16,5	15,4	14,3	13,9

Источник: Без малого бизнеса и теневой экономики.// Официальный Интернет-сайт Госкомстата России. - www. gks. ru

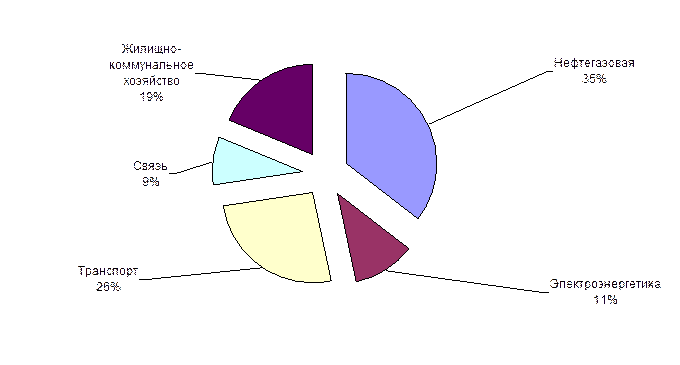
Рис.2. Отраслевая структура инвестиций в основной капитал

Отраслями, традиционно получившими наи­большую долю инвестиций, являлись нефтегазо­вая, жилищно-коммунальное хозяйство, транс­порт, связь, а также электроэнергетика.

Значение уровней интервального ряда в отличие от уровней моментного ряда не содержатся в предыдущих или последующих показателях, их можно просуммировать, что позволяет  получать ряды динамики более укрупненных периодов. Например, суммирование уровней инвестиций за каждый год по данным, приведенным выше, позволяет определить его  уровень за все пять лет в целом и в среднем за год.

Интервальный ряд, где последовательные уровни могут суммироваться, можно представить  как ряд с нарастающими итогами. При построении таких рядов производится последовательное  суммирование уровней смежных уровней. Этим достигается суммарное обобщение результата развития изучаемого  явления с начала отчетного периода (месяца, квартала, года и т.д.)

Абсолютные и относительные величины

Уровни в динамическом ряду, могут быть представлены абсолютными, средними или относительными величинами. Так, в рассмотренных рядах динамики уровни выражены абсолютными статистическими величинами. Средними величинами могут выражаться уровни, характеризующие динамику средней реальной заработной платы в промышленности, динамику урожайности зерновых культур (ц/га). Относительными величинами характеризуются, например динамика доли городского и сельского населения (%) и уровня безработицы.

По расстоянию между уровнями ряды динамики подразделяются на ряды с равностоящими и неравностоящими уровнями по времени.

Если в рядах динамики прерывающиеся и неравномерные интервалы времени, то такие ряды являются неравностоящими.

Ряды динамики могут быть изображены графически. Графически. Графическое изображение позволяет наглядно представить развитие явления во времени и способствует  проведению анализа уровней. Наиболее распространенным видом графического изображения для аналитических целей является линейная диаграмма, которая сроится в прямоугольной системе координат: на оси абсцисс отмечается время, а на оси ординат – урони ряда.

Наряду с линейной диаграммой для графического изображения рядов динамики в целях популяризации широко используются столбиковая диаграмма, секторная диаграмма и другие виды диаграмм (фигурные, квадратные, полосовые).

 Показатели анализа ряда динамики

При изучении динамики общественных явлений возникает проблема описания интенсивности изменения и расчета средних показателей динамики.

Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней, к таким показателям относятся: абсолютный прироста, темп прироста, абсолютное значения одного процента прироста.

Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп прироста.

Показатели анализа динамики могут вычисляться на постоянной и переменных базах сравнения. При этом принято называть сравнимый уровень отчетным, а уровень, с которым производится сравнение, - базисным.

Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень с которого начинается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными.

Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными.

Важнейшим статистическим анализа показателем динамики является абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за определенный промежуток времени с переменной  базой называют скоростью роста.

Абсолютный прирост (цепной)     Абсолютный прирост (базисный)

y^ц =y_i – y_i-1                                                 y^б = y_i – y₀

где     y_i – уровень сравниваемого периода;

y_i-1 – уровень предшествующего периода

y₀ -  уровень базисного периода.

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени: (  y^ц =  y^б).

Для оценки интенсивности, т.е. относительного изменения уровня динамического ряда за какой-либо период времени исчисляют темпы роста (снижения).

Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному.

Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста. Эти показатели интенсивности изменения отличаются только единицами измерения.

Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение  составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.

Коэффициент роста (цепной):                 Коэффициент роста (базисный):

К = ,                                                                   К  = .

Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены  по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу росту.

Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели  темпа прироста (сокращения).

Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения.

Темп прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах и долях единицы (коэффициент прироста).

Темп пророста (цепной):                                  Темп пророста (базисный):

Е  =  * 100                                                      Е =   * 100

Темп прироста (сокращения) можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием из коэффициента роста:

Т_пр = Т_р – 100;                                                    К_пр = К_р – 1.

При анализе динамики развития следует  также знать, какие  абсолютные значения  скрываются за темпами роста и прироста.

Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что  при снижении (замедлении) темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают  показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %:

А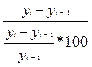_% = = == 0,01y_i-1

Абсолютное значение одного процента прироста равно сотой части предыдущего (или базисного) уровня. Оно показывает, какое абсолютное значение  скрывается за относительным показателем – одним процентом прироста.

В тех случаях, когда сравнение производится с отдалением периода времени, принятого за базу сравнения, рассчитывают так называемые пункты роста, которые представляют собой разность базисных темпов роста, %, двух смежных периодов.

В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно суммировать, в результате получаем темп прироста соответствующего периода по сравнению с базисным.

Для более глубокого понимания характера явления необходимо показатели динамики анализировать комплексно, совместно.

Для обобщающей характеристики динамики исследуемого явления определяет средние показатели: средние уровни ряда и средние показатели изменения уровней ряда. Средний уровень ряда характеризует обобщенную величину абсолютных уровней. Он рассчитывается по средней хронологической, т.е. по средней исчисленной из значений, изменяющихся во времени.

Методы расчета среднего уровня интервального и моментного рядов динамики различны.

Для интервальных рядов динамики из абсолютных уровней средний уровень за период времени определяется по формуле средней арифметической.

При равных интервалах применяется  средняя арифметическая простая:

=

Средний уровень моментного  ряда динамики с равностоящими уровнями определяется по формуле средней хронологической моментного ряда:

= =

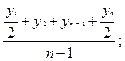
где     y1, yn – уровни  периода, за который делается расчет;

n - число уровней;

n-1 – длительность периода времени.

Средний уровень моментных рядов с неравностоящими уровнями определяются по формуле средней хронологической взвешенной:

=;

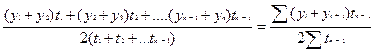где     yi, yn – уровни рядов динамики:

t – интервал времени между смежными уровнями.

Обобщающий показатель скорости изменения уровней во времени – средний абсолютный  прирост (убыль),  представляющий собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний абсолютный прирост как среднюю арифметическую простую:

=,

где     m – число уровней ряда динамики в изучаемом периоде, включая базисный.

Сводной обобщающей  характеристикой интенсивности изменения уровней ярда динамики служит средний темп прироста (снижения), показывающий, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.

Средний темп роста (снижения) – обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления  среднего темпа роста (снижения) применяется определяющий показатель – произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Следовательно, если значение признака образуется как произведение отдельных вариантов, то согласно общему правилу нужно применять среднюю геометрическую.

Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах (=*100), то для равностоящих  рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):

= = =

где n – число цепных коэффициентов роста;

 - цепные коэффициенты роста;  - базисный коэффициент роста за весь период.

Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста, вычитанием из последних 100%, то средний темп прироста – отрицательной величиной. Отрицательный  темп прироста представляет собой средний  темп сокращения  и характеризует  среднюю относительную скорость снижения уровня.

Сравнительные характеристики направления к интенсивности роста одновременно развивающихся во времени  явлений определяются приведением рядов динамики к общему (единому) основанию и расчетом коэффициентов опережения (отставания).

Ряды динамики (в которых возникают, например, проблемы сопоставимости цен сравниваемых стран, методики расчета  сравниваемых показателей и т.п.) обычно приводят к одному основанию, если они не могут  быть решены другими методами. По исходным уровням нескольких рядов динамики определяют относительные величины – базисные темпы роста или прироста. Принятый при этом за базу сравнения период времени (дата) выступает в качестве постоянной базы расчетов темпов роста для каждого из изучаемых рядов динамики. В зависимости от целей исследования базой     сожжет быть начальный, средний или другой уровень ряда.

Сравнение интенсивности  изменений уровней рядов во времени  возможно с помощью коэффициентов опережения (отстаивания), представляющих собой отношение базисных темпов роста (или прироста) двух рядов динамики за одинаковые отрезки времени:

Коп=                               Коп=

где ,, - базисные темпы роста и прироста первого и второго рядов динамики (соответственно).

Коэффициент опережения (отстаивания) показывает, во сколько раз быстрее растет (остает) уровень одного ряда динамики по сравнению с другим. При  этом сравнении темпы должны характеризовать тенденцию одного направления.

Показатели динамических рядов имеют большое практическое  значение  и находят самое широкое применение  в анализе общественных явлений  и процессов.

4.Методы анализа основной тенденции развития в рядах динамики

Одной из важных задач статистики является определение в рядах динамики общей тенденции развития явления.

Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня  явления во времени , свободное от случайных колебаний.

Задача состоит в том, чтобы выявить  общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов. С этой целью ряды динамики подвергаются обработке методами укрупнения интервалов, скользящей средней и аналитического выравнивания.

Одним из наиболее простых методов изучения основной тенденции в рядах динамики является укрупнение интервалов. Он основан на укрупнении  периодов времени, к которым относятся уровни ряда динамики. Например, ряд ежесуточного выпуска продукции и т.д. Средняя, исчисленная по укрупненным интервалам, позволяет выявлять  направление и характер (ускорение или замедление роста) основной тенденции развития.

Например, применение метода укрупнения интервалов на ежемесячных данных о выпуске продукции на предприятии. Различные направления изменений уровней ряда по отдельным месяцам затрудняет выводы  об основной тенденции  производства. Если соответствующие месячные уровни объединить в квартальные и вычислить среднемесячный выпуск продукции по кварталам, те.е укрупним интервал, то решение задачи упрощается. Выявление основной тенденции может осуществляться также методом скользящей (подвижной) средней.  Сущность заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного  (3, 5, 7 и т.д.), первых по счету  уровней ряда, затем из такого же  числа уровней, на начиная со второго по счету, далее  - начиная с третьего  и т.д. Таким образом, средняя  как бы «скользит» по ряду  динамики, передвигаясь  на один срок.

Недостатком сглаживания ряда является «укорачивание» сглаженного  ряда по сравнению  с фактическим, а следовательно, потеря  информации.

Для  того чтобы дать количественную модель, выражающую основную тенденции изменения уровней динамического ряда во времени, используется  аналитического  выравнивание ряда динамики.

Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается как функция времени:

где   - уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.

Определение теоретических (расчетных) уровней , производится на основе   так называемой адекватной математической модели, которая наилучшим образом  отображает (аппроксимирует) основную тенденцию ряда динамики.

Выбор типа модели зависит от цели исследования и должен быть  основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображения ряда динамики (линейной диаграмме).

Например, простейшими моделями (формулами), выражающими тенденцию развития являются:

Линейная функция – прямая

 = а₀ +а₁t,

где    а0, а1 – параметры уравнения ,

t – время;

Показательная  функция  = а₀а;

Степенная функция – кривая второго порядка (парабола)

 = а₀ +а₁t+ а₂t^2.

В тех случаях, когда требуется особо точное изучение тенденции развития (например, модели тренда для прогнозирования), при выборе вида адекватной функции можно использовать  специальные критерии математической статистики.

Расчет  параметров функции обычно производится  методом наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теретическими и эмпирическими уровнями:

где      - выравнивание (расчетные) уровни;

 - фактические уровни.

Параметры уравнения, а_i, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выровненные уровни. Таким образом, выравнивание ряда динамики заключается в замене фактических уровней y_i, плавно изменяющимися уравнениями , наилучшим образом аппроксимирующими статистические данные.

Выравнивание по прямой используется, как правило,  в тех случаях, когда  абсолютные  приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии (или близко  к ней).

Выравнивание по показателям функции используется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т.е. когда  цепные коэффициенты роста практически постоянны.

Расчетная часть

Задание 1

По исходным данным таблицы 1:

1.     Построить статистический ряд распределения организаций по признаку инвестиции в основные фонды образовав четыре группы с равными интервалами.

2.     Построить графики полученного ряда распределения. Графически определить значения моды и медианы.

3.     Рассчитать характеристики интервального ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.

4.     Вычислить среднюю арифметическую по исходным данным (таблица 1), сравнить ее с аналогичным показателем, рассчитанным в п. 3 настоящего задания, для интервального ряда распределения. Объяснить причину их расхождения.

Сделать выводы по результатам выполнения задания.

Задание 2

По исходным данным таблицы 1:

1.       Установить наличие и характер связи между признаками нераспределенная прибыль и инвестиции в основные фонды, образовав четыре группы с равными интервалами по обоим признакам, методами:

- аналитической группировки;

- корреляционной таблицы.

2.       Измерить тесноту корреляционной связи между названными признаками с использованием коэффициента детерминации и эмпирического корреляционного отношения. Сделать выводы.

Таблица 1

№ п/п	Инвестиции в ОФ млн.руб.(У)	Нераспредел. прибыль млн.руб. (Х)
1	0,37	2,7
2	0,90	4,8
3	0,96	6,0
4	0,68	4,7
5	0,60	4,4
6	0,61	4,3
7	0,65	5,0
8	0,51	3,4
9	0,35	2,3
10	0,70	4,5
11	0,80	4,7
12	0,74	5,4
13	0,92	5,8
14	0,58	3,9
15	0,57	4,2
16	0,78	5,6
17	0,65	4,5
18	0,59	3,8
19	0,16	2,0
20	0,72	4,8
21	0,63	5,2
22	0,24	2,2
23	0,45	3,6
24	0,57	4,1
25	0,45	3,3

Задание 3

По результатам выполнения задания 1 с вероятностью 0,954 определите:

1.     Ошибку выборки среднего размера инвестиций и границы, в которых он будет находиться в генеральной совокупности.

2.     Ошибку выборки доли предприятий с инвестициями в основной капитал 0,76 млн. руб. и более и границы, в которых будет находиться генеральная доля.

Задание 4

Динамика инвестиций в отрасли промышленности города характеризуется следующими данными:

Год	Темпы роста к предыдущему году, %
2001	102
2002	104
2003	103
2004	106

Определите:

1.            Базисные темпы роста и прироста к 2000 г. Результаты расчетов представьте в таблице.

2.            Среднегодовой темп роста и прироста.

Определите прогноз базисных темпов роста инвестиций на 2005, 2006 гг., при условии сохранения среднегодового темпа роста.

Сделайте выводы.

Задание1 . Исследование структуры совокупности

Для построения ряда распределения необходимо определить признак -  инвестиции в основные фонды (таблица 2.1.).

Таблица 2.1.

Исходные и отсортированные данные

№ п/п	Инвестиции в ОФ млн.руб.(У)
исходные	отсортированные
1	0,37	0,16
2	0,90	0,24
3	0,96	0,35
4	0,68	0,37
5	0,60	0,45
6	0,61	0,45
7	0,65	0,51
8	0,51	0,57
9	0,35	0,57
10	0,70	0,58
11	0,80	0,59
12	0,74	0,60
13	0,92	0,61
14	0,58	0,63
15	0,57	0,65
16	0,78	0,65
17	0,65	0,68
18	0,59	0,70
19	0,16	0,72
20	0,72	0,74
21	0,63	0,78
22	0,24	0,80
23	0,45	0,90
24	0,57	0,92
25	0,45	0,96

Ряд распределения – это простейшая группировка, представляющая собой распределение численности единиц совокупности по значению какого-либо признака, в настоящем случае по признаку – инвестиции в основные фонды. Если ряд построен по количественному признаку, его называют вариационным. При построении вариационного ряда с равными интервалами определяют число групп (n) и величину интервала (h). По условию задачи необходимо образовать четыре группы (n=4). Величина равного интервала рассчитывается по формуле:

 млн. руб.

где y_max и y_min – максимальное и минимальное значения признака.

Величина интервала равна 0,2. Отсюда путем прибавления величины интервала к минимальному уровню признака в группе получим следующие группы организаций по признаку инвестиции в основные фонды (таблица 2.3.).

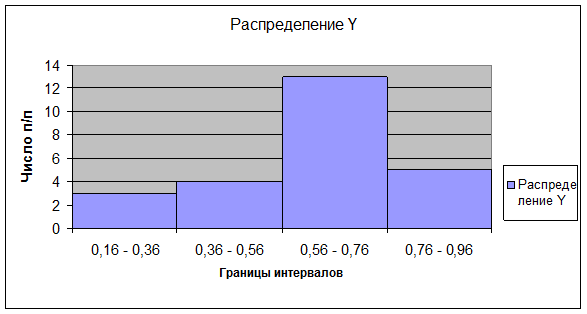
Таблица 2.3.

№ интервала	Группа организаций	Число п/п
в абсолютном выражении	в относительном выражении
1	0,16 - 0,36	3	12,0%
2	0,36 - 0,56	4	16,0%
3	0,56 - 0,76	13	52,0%
4	0,76 - 0,96	5	20,0%
Итого		25	100,0%

Данные группировки показывают, что 80,0% организаций имеют инвестиции в основные фонды менее 0,76 млн. руб.

Мода (Мо) – это значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду – это вариант, имеющий наибольшую частоту. В интервальном вариационном ряду мода вычисляется по формуле:

где y₀ – нижняя граница модального интервала;

h – размер модального интервала;

f_Mo – частота модального интервала;

f_Mo-1 – частота интервала, стоящего перед модальной частотой;

f_Mo+1 – частота интервала, стоящего после модальной частоты.

Отсюда:  млн. руб.

         Графическое нахождение моды:

Медиана (Ме) – это величина признака, который находится в середине ранжированного ряда, то есть расположенного в порядке возрастания или убывания.

Для интервального вариационного ряда Ме рассчитывается по формуле: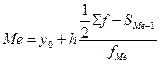

где y₀ – нижняя граница медианного интервала;

h – размер медианного интервала;

 - половина от общего числа наблюдений;

S_Me-1 – сумма наблюдений, накопленная до начала медианного интервала;

f_Me – частота медианного интервала.

         Определяем медианный интервал, в котором находится порядковый номер медианы (n).

         В графе «Сумма накопленных наблюдений» таблицы 2.4. значение 12,5 соответствует интервалу №3, то есть 0,56 – 0,76. Это и есть медианный интервал, в котором находится медиана.

         Отсюда: 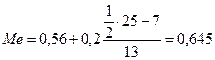 млн. руб.

Таблица 2.4.

№ интервала	Группа п/п	Число п/п	Сумма накопленных наблюдений (S)	Середина интервала, Yi
в абсолютном выражении	в относительном выражении
1	0,16 - 0,36	3	12,0%	3	0,3
2	0,36 - 0,56	4	16,0%	7	0,5
3	0,56 - 0,76	13	52,0%	20	0,7
4	0,76 - 0,96	5	20,0%	25	0,9
Итого		25	100,0%

Графическое нахождение медианы:

Рассчитаем характеристики ряда распределения.

Средняя арифметическая взвешенная определяется по формуле:

,

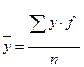где y – варианты или середины интервалов вариационного ряда;

f – соответствующая частота;

n – количество вариантов в вариационном ряду ().

Для расчета необходимо определить середины интервалов распределения инвестиции в основные фонды (таблица 2.5.).

Таблица 2.5.

Группа организаций	Середина интервала, Yi	Число п/п Ni	Yi * Ni	Yi - Ycp	(Yi - Ycp)2 * Ni
0,16 - 0,36	0,26	3	0,780	-0,360	0,389
0,36 - 0,56	0,46	4	1,840	-0,160	0,102
0,56 - 0,76	0,66	13	8,580	0,040	0,021
0,76 - 0,96	0,86	5	4,300	0,240	0,288
Итого		25	15,500		0,800

 млн. руб.

Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и равно:

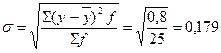млн. руб.

То есть в среднем инвестиции в основные фонды по предприятиям колеблется в пределах ± 0,179 млн. руб. от ее среднего значения 0,620 млн. руб.

Коэффициент вариации представляет собой процентное отношение среднего квадратического отклонения к средней арифметической:

На основании полученного коэффициента вариации можно сделать вывод, что по уровню инвестиций в основные фонды предприятия являются   однородными, так как коэффициент не превышает 33 %.

Вычислим среднюю арифметическую по исходным данным таблицы 1. Средняя арифметическая простая равна сумме значений признака, деленной на их число:

,

где y – значение признака;

n – число единиц признака.

 млн. руб.

Расхождения между арифметической средней простой и взвешенной возникли из-за того, что арифметическая средняя взвешенная считалась по сгруппированным данным.

Задание 2. Выявление корреляционной связи между признаками, установление направления связи и измерение ее тесноты.

Необходимо определить связь между признаками – инвестициями и нераспределенной прибылью.

Таблица 2.6.

Исходные данные

№ п/п	Инвестиции в ОФ млн.руб. (У)	Нераспред. прибыль млн.руб.(Х)
1	0,37	2,7
2	0,90	4,8
3	0,96	6,0
4	0,68	4,7
5	0,60	4,4
6	0,61	4,3
7	0,65	5,0
8	0,51	3,4
9	0,35	2,3
10	0,70	4,5
11	0,80	4,7
12	0,74	5,4
13	0,92	5,8
14	0,58	3,9
15	0,57	4,2
16	0,78	5,6
17	0,65	4,5
18	0,59	3,8
19	0,16	2,0
20	0,72	4,8
21	0,63	5,2
22	0,24	2,2
23	0,45	3,6
24	0,57	4,1
25	0,45	3,3

Таблица 2.7.

Отсортированные данные

№ п/п	Инвестиции в ОФ млн.руб. (У)	Нераспред. прибыль млн.руб.(Х)
1	0,16	2,0
2	0,24	2,2
3	0,35	2,3
4	0,37	2,7
5	0,45	3,3
6	0,45	3,4
7	0,51	3,6
8	0,57	3,8
9	0,57	3,9
10	0,58	4,1
11	0,59	4,2
12	0,60	4,3
13	0,61	4,4
14	0,63	4,5
15	0,65	4,5
16	0,65	4,7
17	0,68	4,7
18	0,70	4,8
19	0,72	4,8
20	0,74	5,0
21	0,78	5,2
22	0,80	5,4
23	0,90	5,6
24	0,92	5,8
25	0,96	6,0

Построим интервальный ряд, характеризующий распределение предприятий по нераспределенной прибыли, образовав четыре группы с равными интервалами (таблица 2.8.).

Таблица 2.8.

Группа организаций	Число п/п в абсолютном выражении	Сумма накопленных наблюдений (S)	Середина интервала, Yi
2 - 3	4	4	2,5
3 - 4	5	9	3,5
4 - 5	10	19	4,5
5 - 6	6	25	5,5
Итого	25

Корреляционная таблица – это специальная комбинационная таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному и результативному. Необходимо определить, существует ли зависимость между инвестициями в основные фонды и нераспределенной прибылью. Построим корреляционную таблицу, образовав четыре группы по факторному и результативному признакам (таблица 2.9.).

Таблица 2.9.

Центр.значение, Ycp(j)	0,26	0,46	0,66	0,86		Nj	Ycp(j) * Nj	Ycp(i)	(Ycp(i) - Ycp)2 * Nj
Группы по Х	Группы по У	0,16	0,36	0,36	0,56	0,56	0,76	0,76	0,96
2,0	3,0	3	1	0	0		4	1,2	0,3	0,38
3,0	4,0	0	3	2	0		5	2,7	0,5	0,03
4,0	5,0	0	0	8	2		10	7,0	0,7	0,06
5,0	6,0	0	0	3	3		6	3,7	0,7	0,12
							25	15,5	0,6	0,62

Как видно из данных таблицы 2.9, распределение числа предприятий произошло вдоль диагонали, проведенной из левого верхнего угла в правый нижний угол таблицы, то есть увеличение признака «Инвестиции в основные фонды» сопровождалось увеличением признака «Нераспределенная прибыль». Характер концентрации частот по диагонали корреляционной таблицы свидетельствует о наличии прямой тесной корреляционной связи между изучаемыми признаками.

Аналитическая группировка позволяет изучать взаимосвязь факторного и результативного признаков. Установим наличие и характер связи между инвестициями в основные фонды и нераспределенной прибылью  методом аналитической группировки (таблица 2.10.).

Таблица 2.10.

Группа п/п	Число п/п	Инвестиции в ОФ	Нераспред прибыль
Всего по группе	В среднем	Всего по группе	В среднем
0,16 - 0,36	3	0,75	0,25	6,5	26,0
0,36 - 0,56	4	3,50	0,88	25,2	28,8
0,56 - 0,76	13	7,35	0,57	52,2	92,3
0,76 - 0,96	5	3,58	0,72	21,3	29,7
Итого	25	15,18	0,61	105,2	173,3

Данные таблицы 2.10. показывают, что с ростом инвестиций в основные фонды нераспределенная прибыль увеличивается. Следовательно, между исследуемыми признаками существует прямая корреляционная связь.

Вычислим коэффициент детерминации и эмпирическое корреляционное отношение, для чего выполним некоторые расчеты (таблица 2.11.).

Таблица 2.11.

Исходные данные и расчет коэффициента корреляции

Инвестиции в ОФ млн.руб.	Нераспределенная прибыль млн.руб.	d = (Х - Хср)	d2 = (Х-Хср)2	z = (У - Уср)	z2 = (У-Уср)2	d * z
0,16	2,0	-2,2	4,9	-0,447	0,200	0,987
0,24	2,2	-2,0	4,0	-0,367	0,135	0,737
0,35	2,3	-1,9	3,6	-0,257	0,066	0,491
0,37	2,7	-1,5	2,3	-0,237	0,056	0,358
0,45	3,6	-0,6	0,4	-0,157	0,025	0,096
0,45	3,3	-0,9	0,8	-0,157	0,025	0,143
0,51	3,4	-0,8	0,7	-0,097	0,009	0,079
0,57	4,2	0,0	0,0	-0,037	0,001	0,000
0,57	4,1	-0,1	0,0	-0,037	0,001	0,004
0,58	3,9	-0,3	0,1	-0,027	0,001	0,008
0,59	3,8	-0,4	0,2	-0,017	0,000	0,007
0,60	4,4	0,2	0,0	-0,007	0,000	-0,001
0,61	4,3	0,1	0,0	0,003	0,000	0,000
0,63	5,2	1,0	1,0	0,023	0,001	0,023
0,65	5,0	0,8	0,6	0,043	0,002	0,034
0,65	4,5	0,3	0,1	0,043	0,002	0,012
0,68	4,7	0,5	0,2	0,073	0,005	0,036
0,70	4,5	0,3	0,1	0,093	0,009	0,027
0,72	4,8	0,6	0,4	0,113	0,013	0,067
0,74	5,4	1,2	1,4	0,133	0,018	0,158
0,78	5,6	1,4	1,9	0,173	0,030	0,241
0,80	4,7	0,5	0,2	0,193	0,037	0,095
0,90	4,8	0,6	0,4	0,293	0,086	0,173
0,92	5,8	1,6	2,5	0,313	0,098	0,498
15,180	105,200		29,1		0,944	4,905
0,607	4,208

Коэффициент детерминации

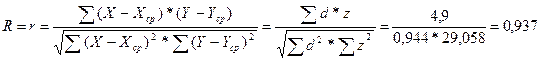
Межгрупповая дисперсия

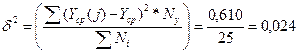
Общая дисперсия

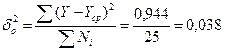
Эмпирическое корреляционное отношение

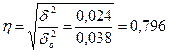
Коэффициент детерминации показывает, что на 93,7% фактор Х обусловлен фактором Y. Расчетное показывает сильную линейную связь между Х и Y. Эмпирическое корреляционное отношение показывает общую тесноту связи между Х и Y. Расчетное значение показывает сильную тесноту связи.

Проведем корреляционно-регрессионный анализ данных, представленных в данной задаче.

Рассчитаем коэффициент линейной корреляции между переменными:

 

Значение r = 0,937 показывает, что связь между Y и X заметная.

Значение r > 0 показывает, что связь между Y и X прямая: с ростом Х (нераспределенная прибыль) наблюдается рост У (инвестиции в ОФ).

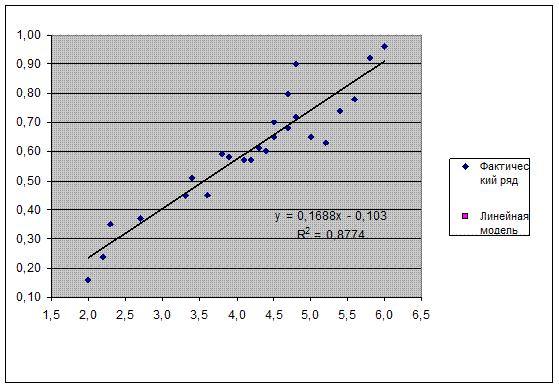
Построим линейную модель регрессии: Y^ = а₀ + а₁ *X

Параметры линейной регрессии найдем по методу наименьших квадратов

 

Итак, линейное уравнение регрессии имеет вид Y^ = -0,103 + 0,169 *X

Значение "а₁" = 0,169 показывает, что с ростом Х (нераспределенная прибыль) на 0,103 наблюдается рост У (инвестиции в ОФ) на 0,169.

Задание 3

Известен процент выборки m = 0,10

Исправленное среднее квадратическое отклонение

Средняя ошибка выборки

Известна вероятность Р = Ф(t) = 0,954; тогда t (из таблицы Лапласа) = 2,00

Предельная ошибка выборки

Тогда искомые границы для ср. значения

Искомая доля

Тогда средняя ошибка выборки для доли

Предельная ошибка выборки для доли

Тогда искомые границы для доли

Генеральная доля находится в границах (0,480 ; 0,352)

Задание 4

Таблица исходных и расчетных данных
Среднегодовой оборот
Абсолютный прирост
Темп роста
Темп прироста
Среднегодовые значения:
Темпа роста
Темпа прироста

Решение представим в виде таблицы

Решение представим в виде таблицы

Инвестиции в промышленности	2001	2002	2003	2004	прогноз 2005	прогноз 2006
t	1	2	3	4	5	6
Темп роста	цепной	102,0	104,0	103,0	106,0	105,0	105,0
базисный	102,0	106,1	109,3	115,8	121,6	127,7
Темп прироста	цепной	2,0	4,0	3,0	6,0	5,0	5,0
базисный	2,0	6,1	9,3	15,8	21,6	27,7

Решение представим в виде таблицы

Динамика инвестиций в промышленности характеризуется постоянной положительной динамикой.

В итоге в 2004г. темп прироста к 2000г. достигает 15,8%.

Исходя из таких темпов к 2006г. темп прироста к 2000г. достигает 27,7%.

Таким образом, в промышленности наблюдается благоприятный инвестиционный климат в течение нескольких лет.

аналитическая часть

Динамика инвестиций в отрасли с/х города (по данным  ж-ла «Экономика сельского хозяйства» №6 2003 г.) характеризуется следующими данными:

		1998г.	1999г.	2000г.	2001г.	2002г.
t	1	2	3	4	5
Инвестиции в с/х	263	218	214	221	230

Определите:

1.     Значения цепных и базисных абсолютных приростов

2.     Цепные и базисные темпы роста и прироста к 2000 г.

3.     Результаты расчетов представьте в таблице.

4.     Среднегодовой темп роста и прироста.

Решение:

Статистические расчеты анализа динамики можно представить с использованием прикладных программ обработки электронных таблиц MS Excel. Для этого сначала представим формулы, необходимые для внесения для обработки электронных таблиц.

 

Среднегодовой объем
Абсолютный прирост
Темп роста
Темп прироста
Абсолютное значение 1% прироста
Среднегодовые значения:
Абсолютного прироста
Темпа роста
Темпа прироста

Составим таблицу исходных и расчетных данных в формулах:

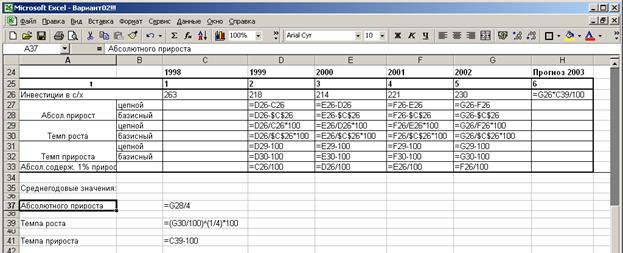
Получи следующую таблицу.

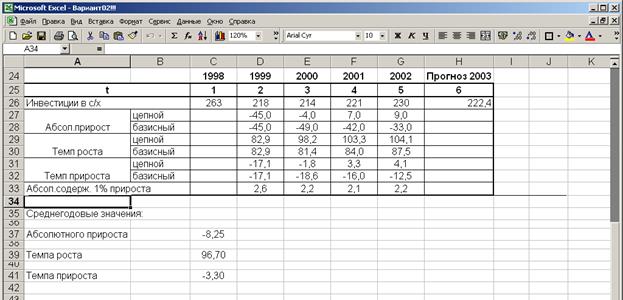
За указанные годы наблюдается снижение объемов инвестиций в с/х: ежегодное снижение составляет 8,25 млн.руб. или 3,3%. В итоге, за период с 1998г. по 2002г. снижение объемов инвестиций в с/х: составило 33 млн.руб. или 12,5%. Прогнозный объем инвестиций в с/х в 2003г. составит 222,4 млн.руб. с учетом среднегодовых значений абсолютного прироста.

Графически изобразим динамику объемов инвестиций в с/х:

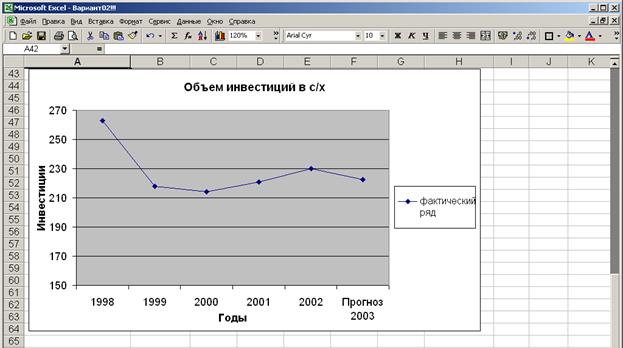
Графическое изображение фактического ряда и темпов роста демонстрирует, что отрицательная тенденция наблюдалась лишь в 1999г.- 2000г., но с 2000г. наблюдается положительная динамика инвестиций (оживление).

Проведем корреляционно-регрессионный анализ по данным за период с 1998 по 2002 г.г. Целью анализа является выявление зависимости между объемом инвестиций в с/х (до официальным городским данным) и рентабельностью с/х.  Данная зависимость имеет существенное значение, поскольку является основой для работы по привлечению инвестиций в с/х.

Рассчитаем коэффициент линейной корреляции между переменными: Х – объем инвестиций в с/х, У - рентабельностью с/х:

Для чего создадим форму для расчета необходимых показателей:

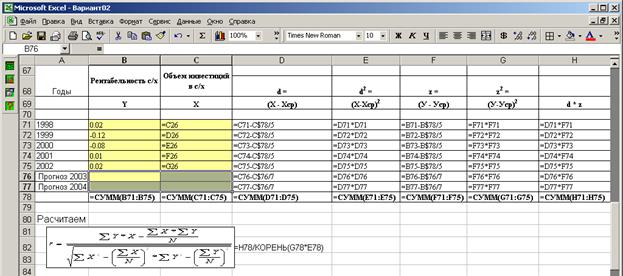
В итоге получим:

 

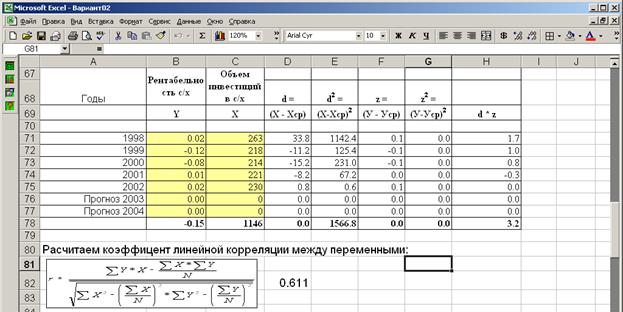
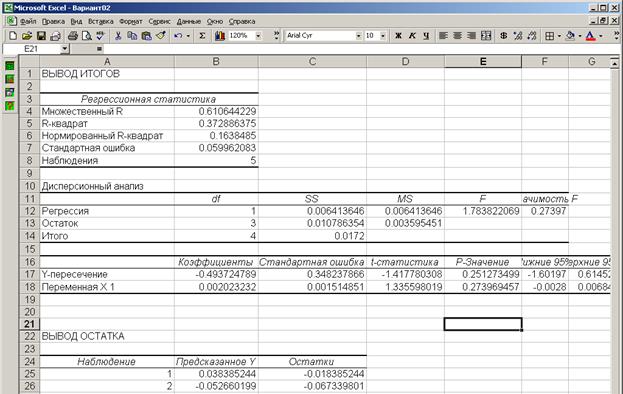
Значение r = 0,611 показывает, что связь между Y и X заметная.  

Значение r > 0 показывает, что связь между Y и X прямая: с ростом Х (инвестиций в с/х) наблюдается рост У (рентабельность с/х).                                               

Примечание: значение "r" можно взять из РЕГРЕССИОННОЙ СТАТИСТИКИ (об этом речь пойдет ниже) строка "Множественный R"                       

Построим линейную модель регрессии: Y* = b₀ + b₁ *X

Параметры линейной регрессии найдем по методу наименьших квадратов.

Итак, линейное уравнение регрессии имеет вид

Y* = -0,494 + 0,002 * X

Значение "b₁" = 0,002 показывает, что с ростом Х (инвестиций в с/х) на

1 млн.руб. наблюдается рост У (рентабельность с/х) на 0,002 или на 0.2%.

Для расчета силы влияния фактора Х на фактор У рассчитаем дополнительно коэффициент эластичности:

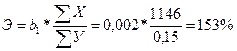
Значение "Э" = 153 показывает, что с ростом Х (инвестиций в с/х) на

1 % наблюдается рост У (рентабельность с/х) на 153%.

Для расчета коэффициента корреляции и уравнения линейной регрессии используем возможности Excel:

«Сервис» => «Анализ данных» => «Регрессия»:

В диалоговом окне зададим необходимые параметры:

Получим таблицы типа:

Построим график фактических данных и результатов вычислений.

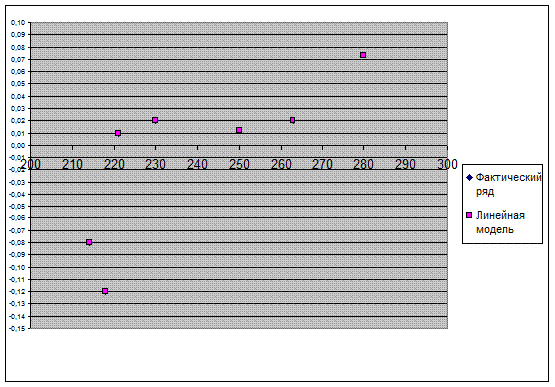
Графически очевидна прямая зависимость объема инвестиций в с/х, и рентабельности с/х, что говорит о возможностях эффекта инвестиций в с/х.

Более того, прогнозируя по линейному уравнению регрессии, получим:

·        в 2003г. Y2003 = -0,494 + 0,002 * 250 = 0,01 (положительная рентабельность с/х в 1%)

·        в 2004г. Y2004 = -0,494 + 0,002 * 280 = 0,07 (положительная рентабельность с/х в 7%)

Таким образом, речь об инвестициях вести необходимо, поскольку уже через год они способны давать рентабельность, сравнимую с рентабельностью в промышленности.

Заключение.

Инвестиции - денежные средства, ценные бумаги, иное имущество, в том числе имущественные права, иные права, имеющие денежную оценку, вкладываемые в объекты предпринимательской и (или) иной деятельности в целях получения прибыли и (или) достижения иного полезного эффекта.                    Инвестиции - сравнительно новая категория для российской экономики. В рамках централизованной плановой системы использовалось понятие “валовые капитальные вложения”, под которыми понимались все затраты на воспроизводство основных фондов, включая затраты на их полное восстановление. Они и рассматривались как понятие, тождественное инвестициям. В настоящее время идет активный процесс развития теории инвестиционных проектов и прежде всего статистического оценивания финансовых и капитальных вложений. Для точного анализа необходимо создание обширной информационной базы.  Основными источниками статистической информации об инвестициях являются данные государственного статистического наблюдения, бухгалтерской отчетности организации, административные данные (например, сведения о государственной регистрации операций с недвижимостью).               Статистическое наблюдение позволяет получить следующую информацию:

·        о потоке финансовых инвестиций за отчетный период и их накопленной величине на конец этого периода (как по инвестициям, направленным данной организацией в другие хозяйственные единицы, так и по инвестициям, вложенным в данную организацию);

·        о потоке инвестиций, направленных организацией на создание и приобретение нефинансовых активов (в разрезе их видов);

·        об источниках средств для инвестиций.

На основании этих данных рассчитываются статистические показатели, характеризующие структуру инвестиций и  главный критерий осуществления инвестиционных процессов -  определение их доходности.

В расчетной части в Задании 1 был построен статистический ряд распределения организаций по признаку инвестиции в основные фонды и проанализированы полученные результаты группировки, в результате чего выяснили, что львиная доля предприятий имеет значительные инвестиции в основные фонды.

В расчетной части в Задании 2 установили наличие и характер связи между признаками нераспределенная прибыль и инвестиции в основные фонды, образовав группы по обоим признакам различными методами, а также измерили тесноту корреляционной связи между названными признаками с использованием коэффициента детерминации и эмпирического корреляционного отношения. Полученные результаты показали высокую тесноту корреляционной связи между названными признаками (93,7% изменения инвестиций в основные фонды обусловлен изменениями нераспределенной прибыли), а также прямую форму связи между ними.

Аналитическая часть работы была посвящена корреляционно-регрессионному анализу инвестиций в с/х, в ходе которого выявилось, что За указанные годы наблюдается снижение объемов инвестиций в с/х: ежегодное снижение составляет 8,25 млн.руб. или 3,3%. В итоге, за период с 1998г. по 2002г. снижение объемов инвестиций в с/х: составило 33 млн.руб. или 12,5%. Прогнозный объем инвестиций в с/х в 2003г. составит 222,4 млн.руб. с учетом среднегодовых значений абсолютного прироста.

Регрессионный анализ показал, что сила влияния фактора Х на фактор У достаточно сильна: значение коэффициента эластичности показал, что с ростом Х (инвестиций в с/х) на 1 % наблюдается рост У (рентабельность с/х) на 153%.

Список использованной литературы

1.     Гусаров В.М. Теория статистики. – М:. ЮНИТИ, 2001. – 463 с.

2.     Елисеева И.И. Общая теория статистики. – М.:Финансы и Статистика, 1998г.

3.     Ильенкова С.Д., Н.Д. Ильенков. Экономико-статистический анализ. Уч.пос.-М.,2002. – 215с.

4.     Общая теория статистики / Под ред. А.С.Спирина. – М.:Финансы и Статистика, 2000г.

5.     Практикум по статистике. Учебное пособие / под ред. В. М. Симчеры. – М.:ФинанСтатинформ, 1999г.

6.     Практикум по статистике. Учебное пособие / под ред. Р.А. Шмайловой. – М.: Финансы и Статистика, 2004г.

7.     Спирин А.А. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности-М.: Финансы и статистика, 1997г.