1.
Классификация случайных событий.
Классическое определение вероятности. Свойства вероятности события,
непосредственный подсчет вероятности. Примеры.
Классификация случайных событий.
Событие – исход
нек. опыта (или к-л природного явления).
Соб-е наз-ся достоверным,
если в рез-те испытания оно произойдет.
Соб-е наз-ся невозможным, если в данных усл-ях оно
не может произойти.
Соб-е наз-ся случайным,
если в рез-те испытания оно как может произойти, так и не может.
Соб-я наз-ся равновозможными, если появление 1 из
них не предпочтительнее появления другого. 2 соб-я наз-ся несовместимыми, если 1 соб-е исключает появление другого.
Неск-ко соб-ий наз-ся
попарно несовместимыми, если появл-е
любого из этих соб-ий исключает появление других. 2 соб-я наз-ся независимыми, если появл-е 1-го из них
не влияет на возможность появл-я другого. Неск-ко соб-ий образуют единственно возможную систему соб-ий,
если в рез-те испытания хотя бы 1 из них произойдет.
Полной системой
соб-ий наз-ся единственно возможная система соб-ий, состоящая из соб-ий несовместимых.
Соб-я образуют полную систему соб-ий, если в рез-те испытания обязательно
произойдет 1 из этих соб-ий и только 1.
Суммой 2-х соб-ий
наз-ют соб-е, состоящее в том, что хотя бы 1 из этих соб-ий произойдет. Произведением 2-х соб-ий наз-ют соб-е,
состоящее в том, что оба соб-я произойдут.
Вероятность события
– числовая характеристика возможности появления соб-я. Исход, при кот. соб-е
появляется, будем наз-ть благоприятствующим этим соб-ям.
Классической вероятностью события А называют отношение числа исходов в
кот соб имеет место к общему числу равновозможных и попарно несовместимых
исходов. Р(А)=ma\n, ma – исходы благоприятствующие
исходу событий, n – полное
число возм-х исходов
Сочетанием из n элементов по m наз-ся всякое неупорядочное
подмножество содержащее m
элементов, выбранных из данных n
элементов. Число сочетаний обозначается 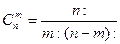
n: =
1*2*…*n (n: фактором) 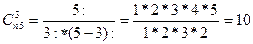
Пример: 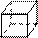 Попарная несовместимость озн невозможность
совместного осущ-я исходов в 1 испытании. Соб А – при бросании кубика выпало 1
очко; ma=1 соб; n=6 граней. P(A)=1\6
Попарная несовместимость озн невозможность
совместного осущ-я исходов в 1 испытании. Соб А – при бросании кубика выпало 1
очко; ma=1 соб; n=6 граней. P(A)=1\6
Свойства вероятности
события: 1) Вер-ть любого соб заключена между 0 и 1, 0≤P(A)≤1
2) Вер-ть
достоверного соб =1; 3) Вер-ть
невозможного соб =0.
2.
Статистическое определение
вероятности события и условия его применимости. Пример.
Стат вер-ю соб А наз-ся
относительная частота появления этого события в n произведённых испытаниях P(A)=w(A)=m\n, где P(A)-стат вер соб А; w(A) – относительная частота соб А; m – число испытаний в кот появилось соб А; n – общее число испытаний.
Стат-ое определение вер-ти
применимо к тем событиям с неопределённым исходом, кот обладают свойствами:
1) Расм-ые
события д\б исходами только тех испытаний, кот м\б воспроизведены
неограниченное число раз при одном и том же комплексе условий. (появление войн,
иск шедевров – бессмысленно)
2) События
должны обладать стат-й устойчивостью, те в различных сериях испытаний относит
частота события изменяется незначительно, колеблясь ок постоянного числа.
3) Число
испытаний, в рез-те кот появл соб А д\б достаточно велико, тк только в этом
случае можно считать вер соб А
приближённо равной её частоте.
Свойства вер, вытекающие
из классического определения сохраняются и при статистическом опр-ии вер-ти: 1) Вер-ть любого соб заключена между
0 и 1, 0≤P(A)≤1 2) Вер-ть достоверного соб =1; 3) Вер-ть невозможного соб =0.
3.
Несовместимые и совместимые
события. Сумма событий. Теорема сложения вероятностей с доказательством.
Пример.
Два соб-я наз-ся несовместимыми,
если 1 соб-е исключает появление другого. Неск-ко соб-ий наз-ся попарно
несовместимыми, если появл-е любого из этих соб-ий исключает появление
других.
Сложение вероятностей зависит от совместности и
несовместности событий.
Несовместные события. Вер-ть суммы двух несовм соб
А и В равна сумме вер-ей этих соб-й. Это вытекает из того, что множество С = А+В включает подмножества А и В, не
имеющие общих точек, и Р(А+В) = Р(А)+Р(В) по опр вер-ти на основе меры. По
частотному опр-ю вер-ти в силу несовместности соб-й имеем: P(A+B) = 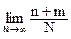 =
= 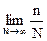 +
+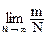 = P(A) + P(B), где n и m - число случаев появления соб-й А и В
соответственно при N испытаниях.
= P(A) + P(B), где n и m - число случаев появления соб-й А и В
соответственно при N испытаниях.
Противоположные
события также являются несовместными и образуют полную группу. Отсюда, с учетом:
P(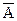 ) = 1 - Р(А). В общем
случае для группы несовместных событий: P(A+B+...+N) = P(A) + P(B) + ... + P(N), если все подмножества принадлежат одному множеству соб-й и
попарно несовм. А если эти подмножества образуют полную группу соб-й, то с
учетом: P(A) + P(B) + ... + P(N) = 1
) = 1 - Р(А). В общем
случае для группы несовместных событий: P(A+B+...+N) = P(A) + P(B) + ... + P(N), если все подмножества принадлежат одному множеству соб-й и
попарно несовм. А если эти подмножества образуют полную группу соб-й, то с
учетом: P(A) + P(B) + ... + P(N) = 1
Совместные события. Вероятность появления хотя бы одного из двух совместных событий
равна сумме вероятностей этих событий без вероятности их совместного появления:
P(A+B) = P(A) +
P(B) - P(A×B).
Разобьем события А и В каждое на два множества, не имеющие общих точек:
А', A'' и B', B''. Во множества А'' и B'' выделим события, появляющиеся
одновременно, и объединим эти множества в одно множество С. Для этих множеств
действительны выражения:
С = A''×B''
º
А'' º
В'' º
А×В, P(C) = P(A'') = P(B'') = P(A×B).
P(A) = P(A')+P(A''), P(A') = P(A)-P(A'') = P(A)-P(A×B).
P(B) = P(B')+P(B''), P(B') = P(B)-P(B'') = P(B)-P(A×B).
Множества A', B' и С попарно несовм : P(A+B) = P(A'+B'+C) = P(A') + P(B') + P(С).
В общем случае, для m различных событий А1, А2,
..., Аm:
P(A1+...+ Am) =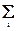 P(Ai)
-
P(Ai)
-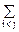 P(Ai×Aj) +
P(Ai×Aj) +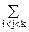 P(Ai×Aj×Ak) -...+(-1)m+1P(A1×A2× ... ×Am).
P(Ai×Aj×Ak) -...+(-1)m+1P(A1×A2× ... ×Am).
Теорема сложения:
Вер-ть суммы двух несовм-х соб-й = сумме вер-тей этих соб. P(A+B+…+К)=P(A)+P(B)+…+Р(К)
Доказательство: Пусть
в рез-те испытания из общего числа n равновозможных и несовм-х исходов испытания соб-ю А
благоприятствует m1 случаев,
а соб-ю В – m2 случаев.
Согласно классич определению P(A)=m1\n,
P(В)=m2\n. Т.к соб А и В несовм-е, то ни 1 из случаев, благоприят-х 1
из этих соб-й, не благоприят-т другому. Поэтому событию А+В будет
благоприятств-ть m1+m2 случаев, следовательно: 
Следствие 1: Сумма вер-ей событий, образующих полную
группу, равна 1: P(A)+P(B)+…+Р(К)=1, Если события А,В,…,К
образуют полную группу, то они единственно возможные и несовместимые.
ТК события А,В,…,К
– единственно возможные, то событие А+В+…+К, состоящее в появлении в рез-те
испытания хотя бы одного из этих событий, явл-ся достоверным, его вер-ть = 1 : Р(А+В+…+К)=1 В силу т\ч события А,В,…,К
– несовместимые, к ним применима теорема сложения: Р(А+В+…+К)=Р(А)+Р(В)+…+Р(К)=1
Следствие 2: Сумма
вер-ей противоположных событий = 1 Р(А)+Р(`А )=1 Это следует из т\ч противоположные
события образуют полную группу.
Пример 1.
В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления
цветного шара. Решение. Появление
цветного шара означает появление либо красного, либо синего шара.
Вероятность появления красного шара (событие А) Р (А) = 10 /
30 = 1 / 3. Вероятность появления синего шара (событие В) Р (В) = 5 / 30 = 1 /
6. События А и В несовместны (появление шара одного цвета исключает появление
шара другого цвета), поэтому теорема сложения применима. Искомая вероятность P
(A + B) = P (A) + P (B) = l / 3 + l / 6 = l / 2.
4.
Полная группа событий.
Противоположные события. Соотношения между вероятностями противоположных
событий (с выводом). Пример.
Несколько событий образуют полную группу событий если в результате
опыта обязательно появится хотя бы одно из них. Это означает, что в рез
испытания должно произойти 1 и только 1 из этих событий.
Частным случаем событий , образующих полную группу, явл
противоположные события. 2 несовместимых соб из кот-х 1 должно обяз-но
произойти наз-ся противоположными. Событие
противоположное соб А ->  . (появление герба и решки у монеты)
. (появление герба и решки у монеты)
Доказательство
теоремы о полной группе событий
Так как появление одного из
событий полной группы достоверно, а вероятность достоверного события равна
единице, то Р (A1 + A2 + ... + An) = 1.
(*)
Любые два события полной группы
несовместны, поэтому можно применить теорему сложения: Р (А1 +
А2 + ... + Аn) = Р (A1)
+ Р (A2) + ... + Р (Аn). (**)
Сравнивая (*) и (**), получим Р (А1) + Р (А2)
+ ... + Р (Аn) = 1.
Пример: Консультационный
пункт института получает пакеты с контрольными работами из городов А, В и С.
Вероятность получения пакета из города А равна 0,7, из города В — 0,2. Найти
вероятность того, что очередной пакет будет получен из города С.
Решение. События
"пакет получен из города А", "пакет получен из города В",
"пакет получен из города С" образуют полную группу, поэтому сумма
вероятностей этих событий равна единице: 0,7 + 0,2 + p =1. Отсюда искомая
вероятность р = 1 — 0,9 = 0,1.
Пример 2. Попадание и промах при выстреле по
цели — противоположные события. Если А — попадание, то противоположное событие
— промах.
5.
Зависимые и независимые события.
Произведение событий. Понятие условной вер-ти. Теорема умножения вер-тей с
док-вом. Пример.
События А, Б, В... называют зависимыми друг
от друга, если вероятность появления хотя бы одного из них изменяется в
зависимости от появления или непоявления других событий. Примером зависимых событий являются события, происходящие при
отборе единиц из совокупности по схеме невозвращенного шара, когда от появления
годного или бракованного изделия при первом испытании зависит вероятность
появления годного изделия при втором испытании.
События называются независимыми, если вероятности появления каждого из них не зависят от
появления или непоявления прочих из них.
Произведением двух событий
А и В называют событие АВ, состоящее в совместном появлении (совмещении)
этих событий. Например, если А — деталь годная, В — деталь окрашенная, то АВ —
деталь годна и окрашена.
Произведением нескольких
событий называют событие, состоящее в совместном появлении всех этих
событий. Например, если А, В, С — появление «герба» соответственно в первом,
втором и третьем бросаниях монеты, то АВС — выпадение «герба» во всех трех
испытаниях.
Условной
вероятностью (РA
(В)-усл вер-ть соб В относительно А) называют вероятность события В,
вычисленную в предположении, что событие А уже наступило. пример
условной вероятности Исходя из классического определения вероятности,
формулу РA (В) = Р (АВ) / Р (А) (Р (А) > 0 можно доказать. Это
обстоятельство и служит основанием для следующего общего (применимого не только
для классической вероятности) определения. Условная вер-ть события В при
условии, что событие А уже наступило, по определению, равна РA (В) = Р (АВ) / Р (А)
(Р(A)>0).
Теорема
умножения вероятностей зависимых событий. Вероятность совместного появления двух событий равна произведению
вероятности одного из них на условную вероятность другого, вычисленную в
предположении, что первое событие уже наступило:
Р (АВ) = Р (А) РA (В)
Доказательство
З а м е ч ан и е.
Применив формулу (*) к событию ВА, получим
Р (ВА) = Р (В) Рв (А), или, поскольку событие ВА не отличается от
события АВ, -> Р(АВ) = Р (В) Рв (А)
Сравнивая формулы
Р (АВ) = Р (А) РA
(В) и Р(АВ) = Р (В) Рв (А),
заключаем о справедливости равенства
Р (А) Ра (В) = Р
(В) Рв (А)
С л е д с т в и е. Вероятность
совместного появления нескольких событий равна произведению вероятности одного
из них на условные вероятности всех остальных, причем вероятность каждого последующего
события вычисляется в предположении, что все предыдущие события уже появились:
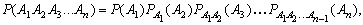 где
где 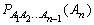 явл вероятностью события An, вычисленной в предположении, что события А1,А2,...,
Аn — 1 наступили. В частности, для трех событий Р (AВС) = Р (А) РA
(В) РAB (С). Порядок, в котором расположены события, может быть
выбран любым, т. е. безразлично какое событие считатьпервым, вторым и т. д.
явл вероятностью события An, вычисленной в предположении, что события А1,А2,...,
Аn — 1 наступили. В частности, для трех событий Р (AВС) = Р (А) РA
(В) РAB (С). Порядок, в котором расположены события, может быть
выбран любым, т. е. безразлично какое событие считатьпервым, вторым и т. д.
Пример 1. У сборщика имеется 3 конусных и 7 эллиптических валиков.
Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из
взятых валиков — конусный, а второй — эллиптический.
Р е ш е н и е.
Вероятность того, что первый валик окажется конусным (событие A), Р (А) = 3 /
10. Вероятность того, что второй валик окажется эллиптическим (событие В),
вычисленная в предположении, что первый валик — конусный, т. е. условная
вероятность РA (В) = 7 / 9.
По теореме умножения, искомая вероятность Р (АВ) = Р (А) РA
(В) = (3 / 10) * (7 / 9) = 7 / 30. Заметим, что, сохранив обозначения, легко
найдем: Р (В) = 7 / 10, РB (А) = 3 / 9, Р (В) РB (А) = 7 / 30, что
наглядно иллюстрирует справедливость равенства (***).
6.
Формулы полной
вер-ти и Байеса с док-вом. Примеры.
Формула полной вер-ти. Теорема.
Если событие F может произойти только при условии появления
одного из событий (гипотез) А1,А2,…,Аn, образующих полную группу, то вер-ть соб
F =сумме произведений вероятностей каждого из этих событий на соответствующие
условные вер-и события F. 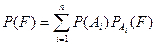
По условию гипотезы А1,А2,…,Аn образуют полную группу,
->, они единственно возможные и несовместные. Т.к А1,А2,…,Аn - единственно
возможные, а соб F может произойти только вместе с 1 из гипотез, то 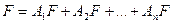 . В силу
т\ч А1,А2,…,Аn несовместны, можно применить теорему сложения вер-ей:
. В силу
т\ч А1,А2,…,Аn несовместны, можно применить теорему сложения вер-ей: 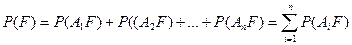
По теореме умножения вер-ей 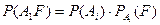 .Следствием
Т умножения и формулы полной вер-ти явл формула Байеса.
.Следствием
Т умножения и формулы полной вер-ти явл формула Байеса.
Формула Байеса:
Пусть Н1, Н2 …— полная группа событий и A — некоторое событие положительной
вероятности. Тогда условная вероятность того, что имело место событие Нk, если
в результате эксперимента наблюдалось событие A, может быть вычислена по
формуле:
Доказательство: По определению условной вероятности,
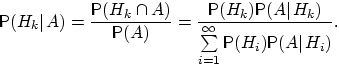
Пример: Два стрелка подбрасывают монетку и выбирают, кто из них стреляет
по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1,
второй стрелок — с вероятностью 0,00001. Можно сделать два предположения
об эксперименте: 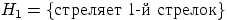 и
и 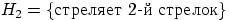 .
.
Априорные вер-ти этих
гипотез одинаковы: 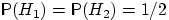 .
.
Рассмотрим событие 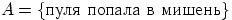 . Известно,
что
. Известно,
что 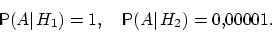
Поэтому вероятность
пуле попасть в мишень 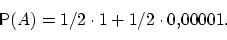
Предположим, что событие 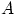 произошло.
Какова теперь апостериорная ( «после опыта») вероятность
каждой из гипотез
произошло.
Какова теперь апостериорная ( «после опыта») вероятность
каждой из гипотез 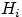 ? Очевидно,
что первая из этих гипотез много вероятнее второй (а именно, в
? Очевидно,
что первая из этих гипотез много вероятнее второй (а именно, в 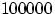 раз).
Действительно,
раз).
Действительно,
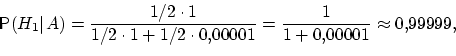
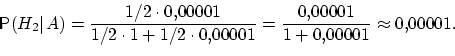
7.
Повторные независимые испытания.
Формула Бернулли с выводом. Примеры
Если вер-ть наступления события А
в каждом испытании не меняется в завис-ти от исходов других, то такие испытания
наз-ся независ-ми относит-но события А. Если
независ-е повторные испытания проводятся при одном и том же комплексе условий,
то вер-ть наступления соб-я А в каждом испытании одна и та же.
Последовательность испытаний, в
кот 1 и те же события происходят с одинаковой вер-ю, наз последовательностью независ-х испытаний.
А соб, кот может иметь место с
вер-ю Р(А) в любом из n
испытаний.
А ->P(A)
P(A)=P –
вер-ть осущ-я события в каждом отдельном событии
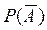 - вер-ть неоосущ-я событий;
- вер-ть неоосущ-я событий; 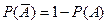 ;
; 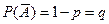 ;
; 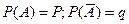
Поставим задачу опр-я вер-ти m-кратного осуществл-я
события А в серии из n
испытаний. Pm,n – вер-ть m-кратного осуществл-я события в серии n испытаний.
Условно рез-ты послед-ти
независ-х испытаний м\б представлены: 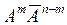 , тк в послед-ти независ-х испытаний, каждое из соб независимо
и для m-кратного
осуществл события они должны произойти совместно, соотв-я вер-ть опр-ся по ф-ле
вер-ти произведения
, тк в послед-ти независ-х испытаний, каждое из соб независимо
и для m-кратного
осуществл события они должны произойти совместно, соотв-я вер-ть опр-ся по ф-ле
вер-ти произведения 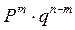 . Предполагая, что возможен и др порядок следования А и
. Предполагая, что возможен и др порядок следования А и 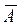 на множестве n испытаний, а кол-во
комбинаций =
на множестве n испытаний, а кол-во
комбинаций = 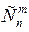 , получим ф-лу m-кратного осуществ-я соб А в серии из n испытаний:
, получим ф-лу m-кратного осуществ-я соб А в серии из n испытаний: 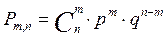 àФормула Бернулли. Используется
при усл, что соб происх-т многократно.
àФормула Бернулли. Используется
при усл, что соб происх-т многократно.
Теорема: Если вер-ть А в
каждом испытании постоянна, то вер-ть Pm,n того, что событие А наступит m раз в n независимых испытаниях,
равна
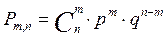 , где q=1-p ф
Бернулли применяется в тех случаях, когда число опытов невелико, а вероятности
появления достаточно велики.
, где q=1-p ф
Бернулли применяется в тех случаях, когда число опытов невелико, а вероятности
появления достаточно велики. 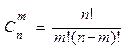
8.
Локальная теорема
Муавра-Лапласа, условия её применимости. Св-ва ф-ии f(x). Пример.
Аналогом ф Бернулли является локальная ф Муавра-Лапласа, она
асимптотическая (ф-ла, точность кот при оценке расм-го параметра возрастает с
увеличением аргумента). Локальная
теорема Муавра – Лапласа Вероятность
того, что в n независимых испытаниях, в каждом из
которых вероятность появления события равна р (0<p<1),
событие наступит ровно m раз, приближенно равна (тем
точнее, чем больше n). 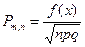 , где Р-вер-ть
осущ-я события в отдельном испытании, q -
вер-ть неосущ-я события в отдельном испытании, n – кол-во испытаний,
, где Р-вер-ть
осущ-я события в отдельном испытании, q -
вер-ть неосущ-я события в отдельном испытании, n – кол-во испытаний, 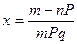 , m – кол-во испытаний, в
кот данное событие имеет место.
, m – кол-во испытаний, в
кот данное событие имеет место. 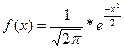 ф-я
ф-я 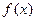 явл-ся табличной функцией. Использование таблиц предполагает
правила: 1.
явл-ся табличной функцией. Использование таблиц предполагает
правила: 1. ; 2.
; 2.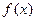 - убывающая; 3.Четность
- убывающая; 3.Четность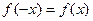 ; 4.Для всех х>5
à
; 4.Для всех х>5
à 
Пример Заявки,
расм-ые фирмой удовлетв-ся в 30% случаях. Представлено 200 заявок. Найти в-ть
т\ч не будет удовлетв-но 130 заявок из 200. Условие: n=200; m=130; P=0,7(70%); q=0,3(30%). 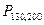 -?
-?
Решение В
лок ф Муавра-Лапласа 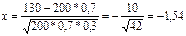 , тогда подставляем -1,54 в ф-лу
, тогда подставляем -1,54 в ф-лу 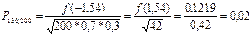 (1,54 ищем по таблице)
(1,54 ищем по таблице)
9.
Асимптотическая ф-ла
Пуассона и условия её применимости. Пример.
Ф-ла Пуассона характеризует вер-ть
m-кратного осуществ-го события в серии из n испытаний, при условии, когда кол-во испытаний велико, а
в-ть осуществ-я события в каждом из испытаний весьма мала, но т\о что np<10. При этом условии имеет место табличная формула
Пуассона: 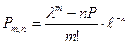 , где n-велико, p-мало,
, где n-велико, p-мало, 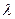 =np, np<10. Ф-я Рm,n
опред-ая ф Пуассона явл-ся табличной ф-ей, позволяющая находить значение вер-ей
по заданным значениям m,
n, p.
=np, np<10. Ф-я Рm,n
опред-ая ф Пуассона явл-ся табличной ф-ей, позволяющая находить значение вер-ей
по заданным значениям m,
n, p.
Пример: Электронная
система состоит из 2000 эл-в, вероятность отказа каждого из кот сост 0,001. Найти:
а) Вер-ть отказа любых 2х Эл-в системы б) вер-ть отказа более 2х Эл-в.
Решение: Поскольку кол-во испытаний(число Эл-в системы) в
д\сл велико(2000), а в-ть наступления события (отказ Эл-в) мало (0,001) р=0,001
(вер-ть отказа 1 эл-та); nр=2000;
0,001=2<10, то для нахождения вер-ти ипольз-м ф Пуассона.
а) m=2; 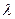 =np=2;
=np=2; 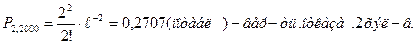
Чем больше множество, тем больше вер-ть.
б) 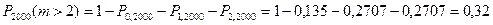
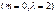
10. Интегральная теорема Муавра-Лапласа и условия её
применимости. Функция Лапласа f(x) и её свойства. Пример.
Предельная теорема
Муавра — Лапласа: Пусть событие А может произойти в любом из n независимых
испытаний с одной и той же вероятностью Р и пусть 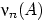 — число
осуществлений события А в n испытаниях. Тогда
— число
осуществлений события А в n испытаниях. Тогда 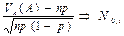 при n à∞
т.е. для любых вещественных x<y имеет место
сходимость
при n à∞
т.е. для любых вещественных x<y имеет место
сходимость 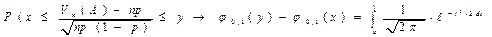
Доказательство:
Величина 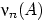 есть сумма независимых, одинаково распределённых
случайных величин,
имеющих распределение Бернулли
с параметром, равным вероятности успеха
есть сумма независимых, одинаково распределённых
случайных величин,
имеющих распределение Бернулли
с параметром, равным вероятности успеха 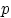 :
: 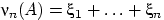 , где
, где 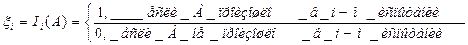 ;
; 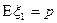 ;
; 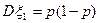
Особый вид асимпт-х формул представляет интегральная функ Муавра-Лапласа, а
также следствия из неё. Инт ф М-Л позволяет
находить вер-ть т\ч число повторений события m в серии из n испытаний не выдет за границы заданного интервала 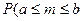 . Данная вер-ть выр-ся формулой:
. Данная вер-ть выр-ся формулой: 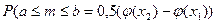 , где
, где 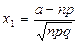 ;
; 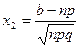
Интегр. Функция
Лапласа: 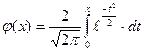 ; Интегральная функция Лапласа явл-ся табличной. Структура
аналогична структуре локальной ф-ии Муавра-Лапласа. Осн свойства: С1: Ф(0)=0˚; С2: Ф(х)↑ - возрастающая; С3: Ф(-х)= - Ф(х) – нечетная; С4:
при х≥5 Ф(х)=1
; Интегральная функция Лапласа явл-ся табличной. Структура
аналогична структуре локальной ф-ии Муавра-Лапласа. Осн свойства: С1: Ф(0)=0˚; С2: Ф(х)↑ - возрастающая; С3: Ф(-х)= - Ф(х) – нечетная; С4:
при х≥5 Ф(х)=1
Пример: Вер-ть
т\ч покупателю нужна обувь 36 размера =0,3. Найти в-ть т\ч среди 2000
покупателей нуждающихся в обуви 36 размера окажется не менее 575.
Решение: m – покуп, кот купят 36 р; n=2000; 575≤m≤2000; Р=0,3; q=0,7 (обрат 0,3);
Р(575≤m≤2000)
- ?
Для реш задачи посредством интегр фМ-Л определим х1 и х2
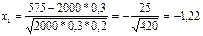 ;
; 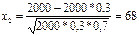 ; х1 и х2 подставляем в интегр ф-лу:
; х1 и х2 подставляем в интегр ф-лу:
Р(575≤m≤2000)=0,5(Ф(68)-Ф(-1,22))=0,5(Ф(68)+Ф(1,22))=0,5(1+0,775)=0,89 (по С4).
11. Следствия из интегральной теоремы Муавра-Лапласа с
выводом. Примеры.
Частными случаями инт т М-Л явл-ся
следствием из неё:
След1: Если в\ть
наступления события в каждом отдельном испытании постоянно и отлично от 0 и 1,
а число испыт велико, то событие имело место от np
на величину непревосходящую r по абсолютной величине,
нах по ф-ле: 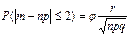 ;
; 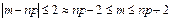 ; (
; (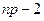 =
= ;
;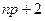 =
=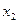 )
)
След2: Если в\ть
наступления события в каждом отдельном испытании постоянно и отлично от 0 и 1,
а число испыт велико, то событие имело место отклонение частности осуществл-я
события от в\ти на величину
непревосходящую дельта 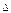 по абсолютной величине, нах по ф-ле:
по абсолютной величине, нах по ф-ле: 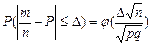
Пример: Всхожесть
семян сост-т 80%, найти в\ть т\ч из 2500 семян, кол-во взошедших не выдет за границы
интервала [1900; 2100].
Решение: n=2500-посев; p=0,8-в\ть всхода 80%; q=0,2-в\ть невхода; 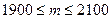 ; m-np, тогда
; m-np, тогда
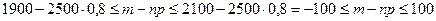 ;
; 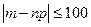 , в следствии r
=100, подставляем в ф-лу:
, в следствии r
=100, подставляем в ф-лу: 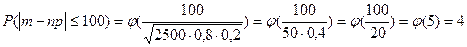 (по С4)
(по С4)
12. Понятие случайной величины и её описание. Дискретная сл\в
и её закон (ряд) распределения. Независимые сл\в. Примеры.
Испытания
связ-е с осущ-ем события сопровожд-ся появлением некоторого численного значения
- случайной величины. Случайной наз вел, предсказать значение кот
заранее невозможно. Случайные величины принято обозначать (X,Y,Z), а
соответствующие им значения (x,y,z)
Сл/в наз-ся
дискретной, если она принимает конечное множество значений. Пусть Х={Х1;
Х2;…Хn}- множество
значений дискретной сл\вел.
Мерой возм-ти появления каждого из данных знач явл
соответствие вер\ти, т\о, способом описание сл\в явл соответ-ием м\у значениями
сл\в и вер-ми, с кот она принимает указ-е значения. Закон распределения может быть задан аналитически, в виде таблицы
или графически. Таблица соответствия знач-й сл\в и их вер-ей называется рядом распределения
|
Xi
|
X1
|
X2
|
…
|
Xk
|
|
Pi
|
P1
|
P2
|
…
|
Pk
|
Графическое представление этой табл наз-ся многоугольником распределения.
При этом сумма всех ординат многоугольника распределения предст-т собой в\ть
всех возможных значений сл\в, а, след, =1.
Следствие: Из
определения закона распределения следует что события (Х=х),…, (Х=хк) –образуют
полн. систему. => Р(Х=х1)+…+Р(Х=хк)=1
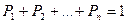 ßосновное св-во
закона распределения. Сл\в наз-ся
независимыми, если закон распределения одной из них не зависит от того,
какое знач принимает другая сл\в. Условные распределения независ-х сл\в-н = их
безусловным распределениям. Для т\ч сл\в Х и Y были независимы, необх, чтобы
плотность совместного распределения системы (X, Y) была = произведению
плотностей распределения составляющих.
f(x,y)=f1(x)*f2(x)
ßосновное св-во
закона распределения. Сл\в наз-ся
независимыми, если закон распределения одной из них не зависит от того,
какое знач принимает другая сл\в. Условные распределения независ-х сл\в-н = их
безусловным распределениям. Для т\ч сл\в Х и Y были независимы, необх, чтобы
плотность совместного распределения системы (X, Y) была = произведению
плотностей распределения составляющих.
f(x,y)=f1(x)*f2(x)
Для дискретных сл\в используются формулы: 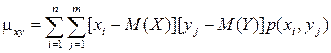
Пример. Последовательно
послано 4 радиосигнала. Вер-ти приема каждого из них не зависят от того,
приняты ли остальные сигналы, или нет. Вер-ти приема сигналов = соотв-но 0,2,
0,3, 0,4, 0,5. Определить вер-ть приема 3х радиосигналов. Решение:Событие приема 3х сигналов из 4х возможно в 4х случаях: 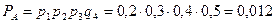 ;
; 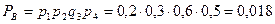
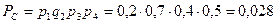 ;
; 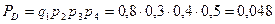
Для приема 3х сигналов необходимо совершение одного из
событий А, В, С или D. Т.о, находим искомую в-ть: 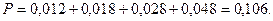
13. Математические операции над дискретными сл\велечинами. Приведите пример
построения закона распределения сл\вел Z=X+Y или Z=XY по заданным распределениям X и Y.
|
Вид операции
|
Выражение
знач. Сл\в
|
Выр знач
вер-ти
|
|
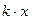
|
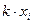
|
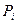 не изм-ся не изм-ся
|
|
x²
|
x²
|
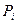 не изм-ся не изм-ся
|
|
x+y
|
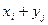
|

|
|
xy
|
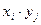
|

|
Над сл\вел можно выполнять
действия, кот состоят в действиях над значениями сл\в и соотв-х операциях над
вер-ми. Соответствие действий наз значениями и вер-ми выражается таблицей ß.
Пример: Законы
распределения числа бракованных деталей выпускаемые 2мя разными станками выр-ся
таблицами:
|
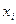
|
0
|
1
|
2
|
|
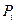
|
0,1
|
0,3
|
0,6
|
|
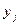
|
0
|
1
|
|
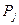
|
0,8
|
0,2
|
Построить сл\в Z=X+Y
Решение:

|
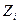
|
0
|
1
|
2
|
3
|
|
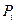
|
0,08
|
0,26
|
0,54
|
0,12
|
à 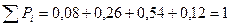
14. Математическое ожидание дискретной случ\вел и его свойства с выводом.
Примеры.
Матем ожиданием дискретной сл\в наз сумма произведений
всех возможных значений сл\в на их вероятности. 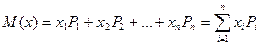
Матем ожид сущ-т, если ряд, стоящий в правой части
равенства, сходится абсолютно. С точки зрения вер-ти можно сказать, что матем
ожид приближенно равно среднему арифм-му наблюд-х значений сл\в.
Свойства
математического ожидания:
1) Мат ожид постоянной
величины равно самой постоянной. 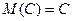
2) Постоянный
множитель можно выносить за знак мат-го ожид. 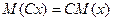
3) Мат ожид
произведения 2х независ-х сл\в-н = произведению их матем-х ож-й. 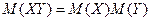
Это свойство справедливо для произвольного числа сл\в.
4) Мат ожид суммы
2х сл\в = сумме мат ожид-й слагаемых. 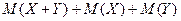
Это свойство также справедливо для произвольного числа сл\в.
Пусть производится п независимых испытаний, вероятность
появления события А в которых равна р.
Теорема. Мат ожид
М(Х) числа появления события А в п независимых испытаниях = произведению числа
испытаний на вер-ть появления события в каждом испытании. 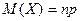 Однако, мат
ожид не может полностью характеризовать случайный процесс. Кроме мат-го ожид
надо ввести величину, которая хар-т отклонение значений сл\в от мат-го ожидания.
Однако, мат
ожид не может полностью характеризовать случайный процесс. Кроме мат-го ожид
надо ввести величину, которая хар-т отклонение значений сл\в от мат-го ожидания.
Это отклонение равно разности между сл\в и ее мат-м ожид.
При этом мат-е ожид отклонения = 0. Это объясняется тем, что одни возможные
отклонения положительны, другие отрицательны, и в результате их взаимного
погашения получается 0.
15. Дисперсия дискретной случ\вел и её свойства с выводом. Примеры.
Дисперсией
(рассеиванием) дискретной сл\в наз мат ожид квадрата отклонения сл\в от ее
мат ожид. 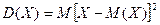
Теорема.
Дисперсия равна разности между мат-м ожид квадрата сл\в Х и квадратом ее мат-го
ожид.
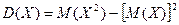
Доказательство. С
учетом того, что мат ожид М(Х) и квадрат мат-го ожид М2(Х) – величины постоянные,
можно записать:
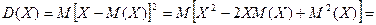
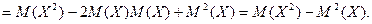
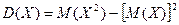
Свойства дисперсии
С1. Дисперсия постоянной величины равна нулю. 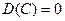
С2. Постоян множитель можно выносить за знак дисперсии, возводя
его в квадрат. 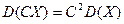
С3.Дисперсия суммы 2х независимых сл\в = сумме дисперсий этих
величин.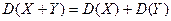
С4. Дисперсия разности 2х независимых сл\в = сумме дисперсий
этих величин. 
Справедливость этого равенства вытекает из свойства 2.
С5. Дисперсия = мат ожид квадрата сл\в без квадрата мат ожид. 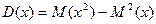
Доказательство С5:
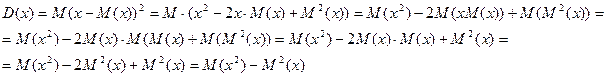
Использовние С5, значит-но упрощает процесс нахожд-я
дисперсии по отнош-ю использ-я опр-я, поэтомк,
в кач ф-лы нахожднеия дисперсии, использ-ся С5 дисперсии.
Теорема.
Дисперсия числа появления события А в п независимых испытаний, в каждом
из кот вер-ть р появления события постоянна, = произведению числа испытаний на
вер-ти появления и не появления события в каждом испытании. 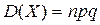
16. Математическое ожидание и дисперсия числа m и частности m\n наступлений события в n-повторных независимых испытаниях, с выводом.
Дискретная сл\в Х имеет гипергеометрическое распределение,
если она принимает значения 1,2,3,,…min (n,M)с вер-ми 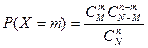 , где m=0,1,2,…min (n;M),
, где m=0,1,2,…min (n;M), 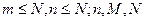 - натуральные числа. Гипергеометрическое распр имеет сл\в Х=m – число объектов,
обладающих заданным св-м, среди n
объектов, случайно извлечённых из совокупности N объектов, M из кот-х обладают этим свойством.
- натуральные числа. Гипергеометрическое распр имеет сл\в Х=m – число объектов,
обладающих заданным св-м, среди n
объектов, случайно извлечённых из совокупности N объектов, M из кот-х обладают этим свойством.
Теорема. Мат\ожидание
сл\в Х, имеющей гипергеометрическое рапр-е с параметрами n,M,N, есть
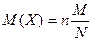 , а её дисперсия
, а её дисперсия 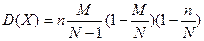 .
.
Сл\в Х=m, распределённую по биномиальному закону, можно интерпретировать
как число m объектов, обладающих данным св-м, из
общего числа n объектов, случайно извлечённых из
некоторой воображаемой бесконечной совокупности, доля p объектов
которой обладает этим св-м. Поэтому гипергеометричесоке рапр можно расм-ть как
модификацию биномиального распр-я для случая конечной совокупности, состоящей
из N объектов, М из кот обладают этим св-м.
17. Случайная величина, распределённая по биномиальному закону, её
математическое ожидание и дисперсия. Закон распределения Пуассоана.
Биномиальным
наз-ся распределение сл\в, в кот она принимает последовательность целых неотрицательных
значений с вер-ми определяемыми по формуле Бернулли. 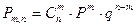
мат\о 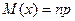 и дисперсия
и дисперсия 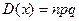 биномиально распределённой
сл\величины.
биномиально распределённой
сл\величины.
Законом распределения
Пуассона наз распр-е сл\в, в кот она принимает последовательность целых
неотрицательных значений с вер-ми определ-ся по формуле Пуассона. Если имеет
место распределение Пуассона заданного распр-я 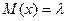 , то мат\о находится
, то мат\о находится 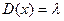
Распределение
Пуассона. Пусть производится n независимых испытаний, в кот появление соб А имеет в-ть р. Если число испытаний n достаточно велико,
а в-ть появления соб А в каждом испытании мало, то для
нахождения в-ти появления события А k раз находится след образом: Произведение
np сохраняет
постоянное значение: 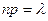 , это означает, что
среднее число появления соб в различных сериях испытаний (при разном n) остается
неизменным.
, это означает, что
среднее число появления соб в различных сериях испытаний (при разном n) остается
неизменным.
По формуле Бернулли получаем:
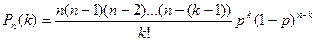 ;
; 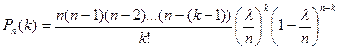
Найдем предел этой вероятности при n à
∞.
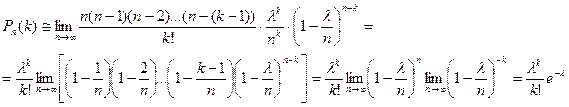
Получаем формулу распределения Пуассона: 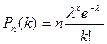
18. Функция и распределения случайной величины, её определение, свойства и
график.
Функцией
распределения сл\в Х наз-ся ф-я F(x), выражающая для каждого х вер-ть т\ч сл\в Х примет значение, меньшее х. 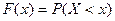
ФР также наз интегральной
ф-ей распр-я. ФР любой дискретной сл\в есть разрывная ступенчатая ф-я, скачки кот происходят в точках, соотв-х
возможным значениям сл\в и равны вер-м этих значений. Сумма всех скачков ф F(X) =1. Она полностью характеризует сл\в
и явл-ся одной из форм закона распределения.
Для дискретной сл\в ф-я распр-я имеет вид: 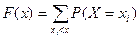
Знак неравенства под знаком суммы показывает, что
суммирование распр-ся на те возможные знач сл\в, кот меньше аргумента х. Ф-я
распр-я дискретной сл\в Х разрывна и возрастает скачками при переходе через каждое
значение хi.
Свойства функции
распределения
1) ФР сл\в есть неотрицательная ф-я, заключенная м\у 0 и 1: 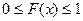
2) ФР сл\в есть неубывающая ф-я на всей числовой оси. 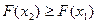 при
при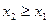
3) На минус бесконечности ФР = нулю, на плюс бесконечности ФР
= единице.
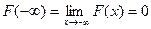 ;
; 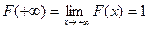
4) Вер-ть попадания сл\в в интервал 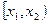 (включая
(включая 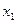 ) равна приращению её ФР на этом интервале, т.е.
) равна приращению её ФР на этом интервале, т.е. 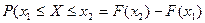
19. Непрерывная случайная величина (НСВ). Вероятность отдельного
взятого значения НСВ. Математическое
ожидание и дисперсия НСВ. Функция распределения НСВ.
Сл\в Х наз-ся непрерывной, если её Функция Распределения
непрерывна в любой точке и дифференцируемая
во всюду, кроме отдельных точек (точки излома).
Мат\ожиданием
дискретной сл\в называется сумма произведений всех возможных значений сл\в
на их вероятности.
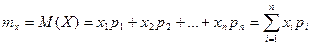 Мат\о
существует, если ряд, стоящий в правой части равенства, сходится абсолютно. С
точки зрения вер-ти можно сказать, что м\о приближенно = среднему
арифметическому наблюдаемых значений сл\в.
Мат\о
существует, если ряд, стоящий в правой части равенства, сходится абсолютно. С
точки зрения вер-ти можно сказать, что м\о приближенно = среднему
арифметическому наблюдаемых значений сл\в.
Пусть НСВ Х задана ФР F(x). Допустим, что все возможные значения сл\в принадлежат
отрезку [a,b].
Мат\ож-м НСВ
Х, возможные значения которой
принадлежат отрезку [a,b], наз-ся определенный интеграл 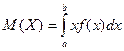 . Если возможные значения сл\в рассм-ся на всей числовой оси,
то мат\о нах по формуле:
. Если возможные значения сл\в рассм-ся на всей числовой оси,
то мат\о нах по формуле: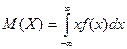 , при этом предпол-ся, что несобственный интеграл сходится.
, при этом предпол-ся, что несобственный интеграл сходится.
Дисперсией НСВ
наз мат\ож квадрата ее отклонения. 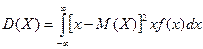 . По аналогии с дисперсией, дискретной сл\в, для
практического вычисления дисперсии используется формула:
. По аналогии с дисперсией, дискретной сл\в, для
практического вычисления дисперсии используется формула: 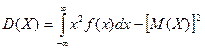 .
.
Функция распределения
НСВ:
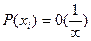 , в качестве способа задания НСВ используется функция распределения НСВ.
, в качестве способа задания НСВ используется функция распределения НСВ.
ФРНСВ наз вер-ть
т\ч она примет значение меньшее
заданного. 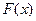 -обознач ф-ии распр в-тей
-обознач ф-ии распр в-тей
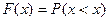 à
à
Основные свойства
ф-ии распределения НСВ:
С1. 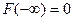
С2. 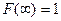
С3. 
С4. Вер-ть т\ч
НСВ примет значение из интервала, равна приращению ф-ии на этом интервале 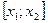
1)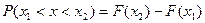

2) 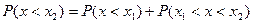
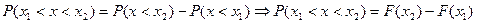
20. Плотность вероятности НепрерывныхСВ, её определение, свойства. Кривая
распределения. Связь между функцией распределения и плотностью вероятности НСВ.
Математическое ожидание и дисперсия НСВ.
Скорость изменения функции распределения хар-ся плотностью
распр-я. Обозначается символом 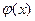 . Плотностью вер-ти (плотностью распр-я)
. Плотностью вер-ти (плотностью распр-я) 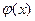 НСВ Х наз-ся производная её ф-ии распр-я
НСВ Х наз-ся производная её ф-ии распр-я 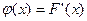
Свойства плотности
распр-я (ПР):
С1. ПР –
неотрицательная функция.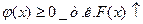 ;
;
С2. Вер-ть
попадания НСВ в интервал [a,b] равна определённому
интегралу от её плотности вер-ти в пределах от a до b, т.е. 
С3. Ф-я распр НСВ
м\б выражена через плотность вер-ти по формуле: 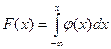
С4. Несобственный
интеграл в бесконечных пределах от плотности вер-ти НСВ =1. 
Из выражений,
связывающих плотность и функцию распределения следует, что м\у ними существует
взаимно однозначное соответствие, те каждое из них определяет выражение другой.
Плотность вер-ти, как
и ф-ция рапр-я явл-ся одной из форм закона распределения, но в отличии от ф-ции
рапр, она существует только для НСВ. Плотность вер-ти называют и
дифференциальной функцией. График плотности вер-ти называется кривой распределения.
ПР составляет
основания определения хар-к сл\в: мат\о и дисперсии.
Мат\ожиданием НСВ
Х, возможные значения которой принадлежат отрезку [a,b], называется определенный
интеграл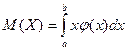 . Если возможные значения сл\в рассматриваются на всей
числовой оси, то м\о находится по формуле:
. Если возможные значения сл\в рассматриваются на всей
числовой оси, то м\о находится по формуле: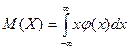 . При этом предполагается, что несобственный интеграл
сходится.
. При этом предполагается, что несобственный интеграл
сходится.
Дисперсией НСВ
называется мат\о квадрата ее отклонения. 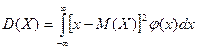
По аналогии с дисперсией дискретной сл\в, для практического вычисления дисперсии
используется формула: 
Мат\о определяется:

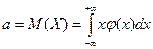 ,если интеграл
абсолютно сходится и
,если интеграл
абсолютно сходится и 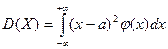 , если интеграл сходится. С3 дисперсии имеет вид:
, если интеграл сходится. С3 дисперсии имеет вид: 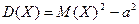 или
или 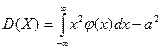
21. Определение нормального закона
распределения. Теорико-вероятный смысл его параметров. Нормальная кривая и
зависимость её положения и формы от параметров.
Нормальным называется
распределение вероятностей непрерывной случайной величины, которое описывается
плотностью вероятности 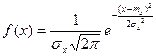 .Нормальный закон
распр также называется законом Гаусса. НЗР
занимает центральное место в теории вероятностей. Это обусловлено тем, что этот
закон проявляется во всех случаях, когда сл\в является результатом действия
большого числа различных факторов. К НЗ
приближаются все остальные законы распределения.
.Нормальный закон
распр также называется законом Гаусса. НЗР
занимает центральное место в теории вероятностей. Это обусловлено тем, что этот
закон проявляется во всех случаях, когда сл\в является результатом действия
большого числа различных факторов. К НЗ
приближаются все остальные законы распределения.
Можно легко показать, что параметры 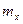 и
и  , входящие в плотность распределения являются соответственно мат\ожиданием и средним квадратическим
отклонением сл\в Х.
, входящие в плотность распределения являются соответственно мат\ожиданием и средним квадратическим
отклонением сл\в Х.
Найдем функцию распределения F(x).
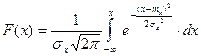
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.
Нормальная кривая
обладает следующими свойствами:
1) Функция определена на всей числовой оси.
2) При всех х ф-я
распр принимает только положительные
значения.
3) Ось ОХ является горизонтальной асимптотой графика
плотности вер-ти, т.к. при неограниченном возрастании по абсолютной величине
аргумента х, значение функции стремится к
нулю.
4) Найдем экстремум функции:
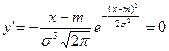 ;
;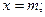 Т.к. при y’ > 0 при x < m и y’ < 0 при
x > m , то в точке х = т функция имеет максимум, равный
Т.к. при y’ > 0 при x < m и y’ < 0 при
x > m , то в точке х = т функция имеет максимум, равный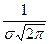
5) Функция является симметричной
относительно прямой х = а, т.к.
разность (х – а) входит в
функцию плотности распределения в квадрате.
6) Для нахождения
точек перегиба графика найдем вторую производную функции плотности:
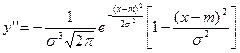
При x = m + s и x = m - s вторая производная равна
нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция
имеет перегиб. В этих точках значение
функции равно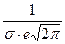
Построим график функции плотности
распределения.
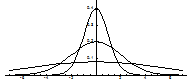 Построены
графики при т =0 и трех возможных значениях среднего квадратичного отклонения s = 1, s = 2 и s = 7. При увеличении знач среднего квадратичного отклонения
график становится более пологим, а максимальное значение уменьшается..
Построены
графики при т =0 и трех возможных значениях среднего квадратичного отклонения s = 1, s = 2 и s = 7. При увеличении знач среднего квадратичного отклонения
график становится более пологим, а максимальное значение уменьшается..
Если а > 0, то
график сместится в положительном направлении, если а < 0 – в отрицательном. При а = 0 и s = 1 кривая
называется нормированной. Уравнение
нормированной кривой: 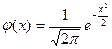
22. Функция распределения нормальной распределённой сл\величины и её
выражение через функцию Лапласа.
Функция Лапласа
Найдем в-ть попадания сл\в, распределенной по нормальному
закону, в заданный интервал.
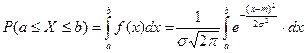 Обозначим
Обозначим 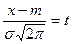 ;
; 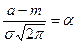 ;
;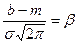 Тогда
Тогда 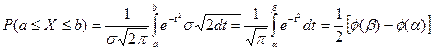 . Т.к. интеграл
. Т.к. интеграл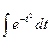 не выражается через элементарные функции, то вводится в
рассмотрение функция
не выражается через элементарные функции, то вводится в
рассмотрение функция 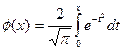 , кот наз ф-ей Лапласа
или интегралом вероятностей. Значения этой ф-ии при различных знач х посчитаны и приводятся в специальных
таблицах. График функции Лапласа.
, кот наз ф-ей Лапласа
или интегралом вероятностей. Значения этой ф-ии при различных знач х посчитаны и приводятся в специальных
таблицах. График функции Лапласа.
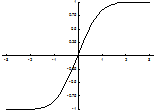 Ф-я
Лапласа обладает следующими свойствами:
Ф-я
Лапласа обладает следующими свойствами:
1) Ф(0) = 0;
2) Ф(-х) = - Ф(х);
3) Ф(¥) = 1.
Ф-ю Лапласа также называют ф-ей ошибок и обозначают erf x.
23. Формулы для определения вероятности: а)попадания нормально
распределённой сл\вел в заданный интервал; б) её отклонения от математического
ожидания. Правило «трёх сигм».
а) Найдем в-ть
попадания сл\в, распределенной по нормальному закону, в заданный интервал.
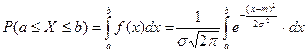 Обозначим
Обозначим 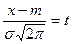 ;
; 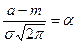 ;
;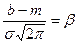 Тогда
Тогда 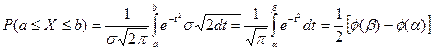 . Т.к. интеграл
. Т.к. интеграл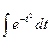 не выражается через элементарные функции, то вводится в
рассмотрение функция
не выражается через элементарные функции, то вводится в
рассмотрение функция 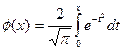 , кот наз ф-ей Лапласа
или интегралом вероятностей. Значения
этой ф-ии при различных знач х
посчитаны и приводятся в специальных таблицах.
, кот наз ф-ей Лапласа
или интегралом вероятностей. Значения
этой ф-ии при различных знач х
посчитаны и приводятся в специальных таблицах.
б) В-ть того что
отклонение сл\в от её мат\ожидания по абсолютной величине превзойдёт 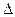 не больше дроби, числ
кот – дисперсия сл\в, а знаменатель – квадрат
не больше дроби, числ
кот – дисперсия сл\в, а знаменатель – квадрат 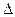 .
.
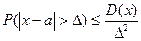 или
или 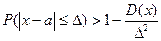
Правило трёх сигм
При рассм нормального закона распределения выделяется важный
частный случай, известный как правило трех сигм. Запишем в-ть т\ч отклонение
нормально распр сл\в от мат\ожидания меньше заданной величины D:
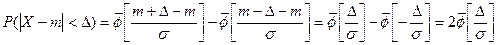 Если принять D = 3s,
то получаем с использованием таблиц значений функции Лапласа:
Если принять D = 3s,
то получаем с использованием таблиц значений функции Лапласа: 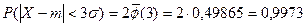
Т.е. в-ть т\ ч сл\в отклонится от своего мат\о на величину,
большую чем утроенное среднее квадратичное отклонение, практически равна нулю. Это
правило называется правилом трех сигм.На
практике считается, что если для какой – либо сл\в выполняется правило трех
сигм, то эта сл\в имеет нормальное распределение.
Пример.
Нормально распределенная сл\в Х задана своими параметрами – а =2 – мат\о и s =
1 – среднее квадратическое отклонение. Требуется написать плотность вер-ти и
построить ее график, найти в-ть того, Х примет значение из интервала (1; 3),
найти вероятность того, что Х отклонится (по модулю) от математического
ожидания не более чем на 2. Плотность распределения имеет вид: 
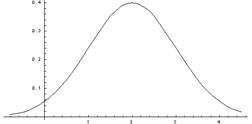 Построим график:
Построим график:
Найдем в-ть попадания
случайной величины в интервал (1; 3). 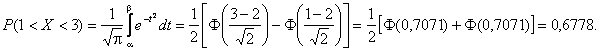
Найдем в-ть
отклонения сл\в от мат\о на величину, не большую чем 2. 
Тот же результат может быть получен с использованием
нормированной функции Лапласа. 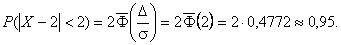
24. Центральная предельная теорема. Понятия о теореме Ляпунова и её
значение. Пример.
Теорема. Если сл\в Х представляет собой сумму очень
большого числа взаимно независимых сл\в, влияние каждой из которых на всю сумму
ничтожно мало, то Х имеет распр, близкое к нормальному.
На практике для большинства сл\в выполняются условия теоремы
Ляпунова.
25. Понятие двумерной (n-мерной)
сл\вел. Примеры. Таблица её распределения. Условные распределения и их
нахождение по таблице распределения.
Существуют сл\в, которые определяются двумя, тремя и т.д.
числами. Такие сл\в называются двумерными,
трехмерными и т.д. В зависимости от типа, входящих в систему сл\в, системы
могут быть дискретными, непрерывными или смешанными, если в систему входят
различные типы сл\в.
Рассм системы двух сл\в.
Законом
распределения системы сл\в называется соотношение, устанавливающее связь
между областями возможных значений системы сл\в и вероятностями появления
системы в этих областях.
Функцией
распределения системы двух сл\в наз ф-я двух аргументов F(x, y), равная в-ти
совместного выполнения двух неравенств X<x, Y<y.
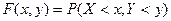
Свойства функции
распределения системы двух сл\в:
1) Если один из аргументов стремится к плюс бесконечности,
то ф-я распр системы стремится к ф-ии распр одной сл\в, соответствующей другому
аргументу.

2) Если оба аргумента стремятся к бесконечности,
то ф-я распр системы стремится к 1.
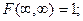
3) При стремлении одного или обоих аргументов к минус
бесконечности ф-я распр стремится к 0.
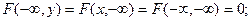
4) Ф-я распр является неубывающей функцией по каждому
аргументу.
5) В-ть попадания случайной точки (X, Y) в произвольный
прямоугольник со сторонами, параллельными координатным осям, вычисляется по
формуле:
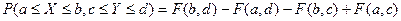
Распределение одной сл\в,
входящей в систему, найденное при условии, что другая сл\в приняла определенное
значение, называется условным законом распределения.
26. Ковариация и коэффициент корреляции (КК) сл\величин. Связь между
некоррелированностью и независимостью сл\величин.
Коэффициентом
корреляции 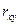 сл\в Х и Y
называется отношение корреляционного момента к произведению средних
квадратических отклонений этих величин
сл\в Х и Y
называется отношение корреляционного момента к произведению средних
квадратических отклонений этих величин
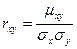 КК является безразмерной величиной. КК
независимых сл\в = нулю.
КК является безразмерной величиной. КК
независимых сл\в = нулю.
Абсолютная величина КК не превышает единицы. 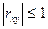 Сл\в называются коррелированными,
если их корреляционный момент отличен от нуля, и некоррелированными, если их корреляционный момент равен нулю. Если случайные величины независимы, то они и
некоррелированы, но из некоррелированности нельзя сделать вывод о их
независимости. Если две величины
зависимы, то они могут быть как коррелированными, так и некоррелированными.
Часто по заданной плотности распределения системы сл\в можно определить
зависимость или независимость этих величин. Наряду с КК степень зависимости сл\в
можно охарактеризовать и другой величиной, которая называется коэффициентом
ковариации. Коэффициент ковариации
определяется формулой:
Сл\в называются коррелированными,
если их корреляционный момент отличен от нуля, и некоррелированными, если их корреляционный момент равен нулю. Если случайные величины независимы, то они и
некоррелированы, но из некоррелированности нельзя сделать вывод о их
независимости. Если две величины
зависимы, то они могут быть как коррелированными, так и некоррелированными.
Часто по заданной плотности распределения системы сл\в можно определить
зависимость или независимость этих величин. Наряду с КК степень зависимости сл\в
можно охарактеризовать и другой величиной, которая называется коэффициентом
ковариации. Коэффициент ковариации
определяется формулой: 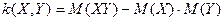
27. Понятие о двумерном нормальном законе распределения. Условные
математические ожидания и дисперсии.
Распределение одной сл\в, входящей в систему, найденное при
условии, что другая сл\в приняла определенное значение, называется условным законом распределения.
Усл закон распр можно задавать как функцией распределения
так и плотностью распределения.
Усл плотность
распределения вычисляется по формулам:
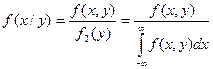 ;
; 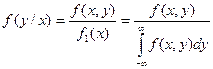 . Усл плотность распр обладает всеми св-ми плотности
распределения одной сл\в.
. Усл плотность распр обладает всеми св-ми плотности
распределения одной сл\в.
Условным м\о
искретной сл\в Y при X = x (х – определенное возможное значение Х)
называется произведение всех возможных значений Y на их условные вероятности. 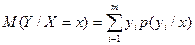
Для непрерывных сл\в: 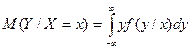 , где f(y/x) – усл
плотность сл\в Y при X=x.
, где f(y/x) – усл
плотность сл\в Y при X=x.
Усл м\о M(Y/x)=f(x) является функцией от х и
называется функцией регрессии Х на Y.
Пример. Найти
условное математическое ожидание составляющей Y при X= x1=1 для дискретной двумерной
сл\в, заданной таблицей:
|
Y
|
X
|
|
x1=1
|
x2=3
|
x3=4
|
x4=8
|
|
y1=3
|
0,15
|
0,06
|
0,25
|
0,04
|
|
y2=6
|
0,30
|
0,10
|
0,03
|
0,07
|
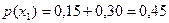 ;
; 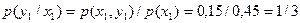
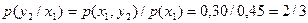
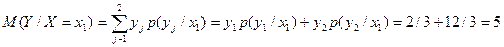
Аналогично определяются усл дисперсия и условные моменты
системы сл\в.
28. Неравенство Маркова (лемма Чебышева) с док-вом для дискретной
сл\величины. Пример.
Теорема. Если сл\в Х принимет только неотриц знач и
имеет мат\о, то для любого положительного числа А верно неравенство: 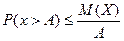 . Доказательство для
дискретной сл\в Х: Расположим значения дискр сл\в Х в порядке возрастания,
из кот часть значений
. Доказательство для
дискретной сл\в Х: Расположим значения дискр сл\в Х в порядке возрастания,
из кот часть значений 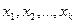 будет не больше
числаА, а др часть
будет не больше
числаА, а др часть 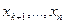 будут больше А, т.е
будут больше А, т.е 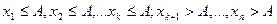
Запишем выражение для м\о M(X): 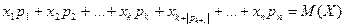 , где
, где 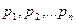
- в-ти т\ч сл\в Х
примет значения 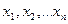 . Отбрасывая первые k неотрицательных слагаемых получим:
. Отбрасывая первые k неотрицательных слагаемых получим: 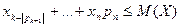 . Заменяя в этом неравенстве значения
. Заменяя в этом неравенстве значения 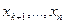 меньшим числом, получим
неравенство:
меньшим числом, получим
неравенство: 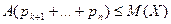 или
или 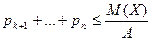 . Сумма в-тей в левой части представляет сумму в-ей событий
. Сумма в-тей в левой части представляет сумму в-ей событий 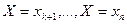 , т.е в-ть соб Х>А. Поэтому
, т.е в-ть соб Х>А. Поэтому 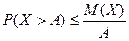 . Т.к события
. Т.к события 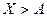 и
и 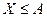 противоположные, то заменяя
противоположные, то заменяя 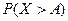 выражением
выражением 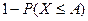 , придём к др форме неравенства Маркова:
, придём к др форме неравенства Маркова: 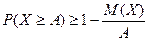 . Неравенство Маркова применимо к любым неотрицательным сл\в.
. Неравенство Маркова применимо к любым неотрицательным сл\в.
29.
Неравенство Чебышева для средней
арифметической сл\в. Теорема Чебышева с док-м и её значение и пример.
Теорема
Чебышева(ср.арифм). Если дисперсии n независимых сл\в 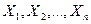 ограничены 1 и той же постоянной, то при неограниченном увеличении
числа n ср арифметическая сл\величин сходится
по в-ти к средней арифм их м\ожиданий
ограничены 1 и той же постоянной, то при неограниченном увеличении
числа n ср арифметическая сл\величин сходится
по в-ти к средней арифм их м\ожиданий 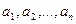 , т.е
, т.е  или
или 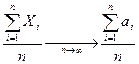 *(над стрелкой Ро-R)
*(над стрелкой Ро-R)
Докажем ф-лу  и выясним смысл
формулировки «сходимость по в-ти». По условию
и выясним смысл
формулировки «сходимость по в-ти». По условию 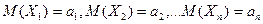 ,
, 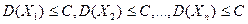 , где С - постоянное число. Получим неравенство Чебышева в
форме (
, где С - постоянное число. Получим неравенство Чебышева в
форме (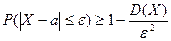 ) для ср арифм
сл\в , те для
) для ср арифм
сл\в , те для 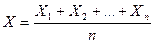 . Найдём м\о M(X) и оценку
дисперсии D(X):
. Найдём м\о M(X) и оценку
дисперсии D(X): 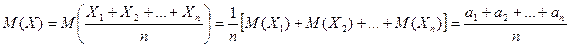 ;
;
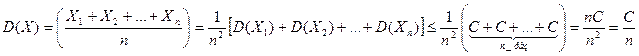 (здесь использованы свойства м\о и дисперсии и т\ч сл\в
(здесь использованы свойства м\о и дисперсии и т\ч сл\в 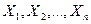 независимы, а след-но, дисперсия их суммы = сумме дисперсий)
независимы, а след-но, дисперсия их суммы = сумме дисперсий)
Запишем неравенство 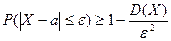 для сл\в
для сл\в 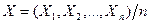 :
:
30. Теорема Чебышева с выводом и его частные случаи для сл\в,
распределённой по биномиальному закону, и для частности события.
Неравенство Чебышева.
Теорема. Для люб сл\в имеющей м\о и
дисперсию, справедливо неравенство Чебышева: 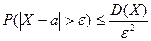 , где
, где 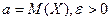 .
.
Применим неравенство Маркова в форме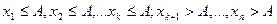 к сл\в
к сл\в 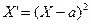 , взяв в кач + числа
, взяв в кач + числа 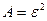 . Получим:
. Получим: 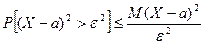 . Т.к неравенство
. Т.к неравенство 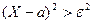 равносильно
неравенству
равносильно
неравенству 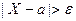 , а
, а 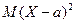 есть дисперсия сл\в Х,
то из неравенства
есть дисперсия сл\в Х,
то из неравенства 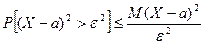 получаем доказываемое
получаем доказываемое 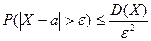 . Учитывая, что события
. Учитывая, что события 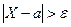 и
и 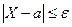 противоположны,
неравенство Чебышева можно записать и в форме:
противоположны,
неравенство Чебышева можно записать и в форме: 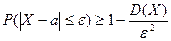 . Неравенство Чебышева применимо для любых сл\в. В форме
. Неравенство Чебышева применимо для любых сл\в. В форме 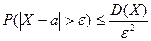 оно устанавливает
верхнюю границу, а в форме
оно устанавливает
верхнюю границу, а в форме 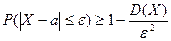 - нижнюю границу в-ти
рассм-го события.
- нижнюю границу в-ти
рассм-го события.
Запишем
неравенство Чебышева в форме 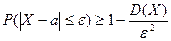 для некоторых сл\в:
для некоторых сл\в:
А) для сл\в Х=m, имеющей биноминальный закон распр с м\о a=M(X)=np и дисперсией D(X)=npq.
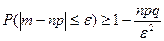 ;
;
Б) для частности m\n события
в n независимых испытаниях, в каждом из
кот оно может произойти с 1 и той же в-тью 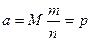 ; и имеющей дисперсию
; и имеющей дисперсию
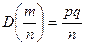 :
: 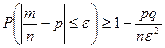 .
.
31. Закон больших чисел. Теорема Бернулли с док-м и её
значение. Пример.
К законам больших
чисел относятся т Чебышева (наиболее общий случай) и т Бернулли (простейший
случай)
Теорема Бернулли Пусть
производится n независимых
испытаний, в каждом из которых в-ть появления события А равно р. Возможно
определить примерно относительную частоту появления события А.
Теорема.
Если в каждом из n
независимых испытаний в-ть р
появления события А постоянно, то
сколь угодно близка к 1 в-ть т\ч отклонение относительной частоты от в-ти р по абсолютной величине будет сколь
угодно малым, если число испытаний р
достаточно велико.
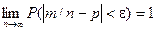 m – число появлений
события А. Из всего сказанного выше
не следует, что с увеличением число испытаний относительная частота неуклонно
стремится к в-ти р, т.е.
m – число появлений
события А. Из всего сказанного выше
не следует, что с увеличением число испытаний относительная частота неуклонно
стремится к в-ти р, т.е.  . В теореме
имеется в виду только в-ть приближения относительной частоты к в-ти
появления события А в каждом
испытании.
. В теореме
имеется в виду только в-ть приближения относительной частоты к в-ти
появления события А в каждом
испытании.
В случае, если вероятности появления события А в каждом опыте различны, то справедлива
следующая теорема, известная как теорема Пуассона. Теорема. Если производится п независимых опытов и вероятность
появления события А в каждом опыте равна рi, то при увеличении п частота
события А сходится по вероятности к среднему арифметическому вероятностей рi.
32. Вариационный ряд, его разновидности. Средняя арифметическая и дисперсия
ряда. Упрощённый способ их расчёта.
33. Генеральная и выборочные совокупности. Принцип образования выборки.
Собственно-случайная выборка с повторным и бесповторным отбором членов. Репрезентативная
выборка. Основная задача выборочного ряда.
34. Понятие об оценке параметров генеральной совокупности. Свойства оценок:
несмещенность, состоятельность, эффективность.
35. Оценка генеральной доли по собственно – случайной выборке. Несмещённость
и состоятельность выборочной доли.
36. Оценка генеральной средней по
собственно – случайной выборке. Несмещённость и состоятельность выборочной
средней.
37. Оценка генеральной дисперсии по собственно – случайной выборке.
Смещённость выборочной дисперсии (без вывода).
38. Понятие об интервальном оценивании. Доверительная вероятность и
доверительный интервал. Предельная ошибка выборки. Ошибки репрезентативности
выборки ( случайные и систематические)
39. Формула доверительной вер-ти при оценке генеральной доли признака.
Средняя квадратическая ошибка повторной и бесповторной выборок и построение
доверительного интервала для генеральной доли признака.
40. Формула доверительной вер-ти при оценке генеральной средней. Средняя
квадратическая ошибка повторной и бесповторной выборок и построение
доверительного интервала для генеральной средней.
41. Определение необходимого объёма повторной и бесповторной выборок при
оценке генеральной средней и доли.
42. Статистическая гипотеза и статистический критерий. Ошибки 1 и 2 ряда.
Уровень значимости и мощности критерия. Принцип практической уверенности.
43. Построение теоретического закона распределения по опытным данным.
Понятие о критериях согласия.
44. Критерий согласия x – Пирсона и схема его
применения.
45. Функциональная, статистическая и корреляционная зависимости. Различия
между ними. Основные задачи теории корреляции.
46. Линейная парная регрессия. Система нормальных уравнений для определения
параметров прямых регрессии. Выборочная ковариация. Формулы для расчета
коэффициентов регрессии.
47. Оценка тесноты связи. Коэффициент корреляции (выборочный), его свойства
и оценка достоверности.