Практическая часть
Имеются
следующие выборочные данные (выборка 25%-ная механическая) о доходах и расходах
бюджетов субъектов РФ за полугодие, млн.руб.
Таблица
1 – Исходные данные
|
Номер
региона
п/п
|
Доходы бюджета
|
Расходы бюджета
|
Номер
региона
п/п
|
Доходы бюджета
|
Расходы бюджета
|
|
1
|
4,2
|
5,4
|
16
|
1,2
|
3,1
|
|
2
|
3,8
|
5,2
|
17
|
3,6
|
4,5
|
|
3
|
6,4
|
8,7
|
18
|
2,2
|
3,8
|
|
4
|
2,1
|
3,2
|
19
|
0,9
|
1,9
|
|
5
|
2,4
|
4,6
|
20
|
2,3
|
3,1
|
|
6
|
2,0
|
3,5
|
21
|
3,5
|
4,6
|
|
7
|
0,7
|
2,0
|
22
|
4,4
|
6,2
|
|
8
|
3,9
|
5,0
|
23
|
4,8
|
7,2
|
|
9
|
8,0
|
7,4
|
24
|
7,5
|
8,0
|
|
10
|
4,2
|
6,0
|
25
|
0,8
|
1,7
|
|
11
|
2,5
|
4,6
|
26
|
3,5
|
4,7
|
|
12
|
3,9
|
4,9
|
27
|
4,1
|
6,5
|
|
13
|
7,6
|
8,6
|
28
|
6,3
|
8,6
|
|
14
|
4,1
|
5,8
|
29
|
5,3
|
6,8
|
|
15
|
0,5
|
1,8
|
30
|
5,2
|
7,1
|
Задание 1
По исходным данным (табл. 1)
необходимо выполнить следующее:
1.
Построить статистический ряд распределения регионов по признаку доходы
бюджета, образовав пять групп с равными интервалами.
2.
Графическим методом и путем расчётов определить
значения моды и медианы полученного ряда распределения.
3.
Рассчитать характеристики ряда распределения: среднюю
арифметическую, среднее квадратическое отклонение, коэффициент вариации.
4.
Вычислить среднюю арифметическую по исходным данным
(табл. 1), сравнить её с аналогичным показателем, рассчитанным в п. 3 для
интервального ряда распределения. Объяснить причину их расхождения.
Сделать выводы по результатам выполнения Задания 1.
Выполнение Задания 1
Целью выполнения данного
Задания является изучение состава и структуры выборочной совокупности регионов
путем построения и анализа статистического ряда распределения регионов по
признаку Доходы бюджетов.
Для построения интервального
вариационного ряда, характеризующего распределение регионов по доходам бюджетов,
необходимо вычислить величину и границы интервалов ряда.
При построении ряда с
равными интервалами величина интервала h определяется по формуле
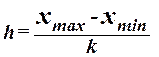 , (1)
, (1)
где 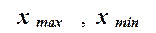 – наибольшее и наименьшее значения признака в
исследуемой совокупности, k- число групп
интервального ряда.
– наибольшее и наименьшее значения признака в
исследуемой совокупности, k- число групп
интервального ряда.
Подставим в данную
формулу исходные данные:
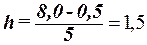 млн. руб.
млн. руб.
При h = 1,5 млн. руб. границы
интервалов ряда распределения имеют следующий вид (табл. 2):
Таблица 2
|
Номер группы
|
Нижняя граница, млн. руб.
|
Верхняя граница, млн. руб.
|
|
1
|
0,5
|
2,0
|
|
2
|
2
|
3,5
|
|
3
|
3,5
|
5,0
|
|
4
|
5
|
6,5
|
|
5
|
6,5
|
8,0
|
Процесс группировки
единиц совокупности по признаку Доходы
бюджета представлен во вспомогательной (разработочной) таблице 3 (графа
4 этой таблицы необходима для построения аналитической группировки в Задании
2).
Таблица 3 – Разработочная таблица для построения интервального ряда
распределения и аналитической группировки
|
Группы регионов по доходам бюджета, млн. руб.
|
Номер региона
|
Доходы бюджета
|
Расходы бюджета
|
|
1
|
2
|
3
|
4
|
|
0,5 - 2,0
|
15
|
0,5
|
1,8
|
|
|
7
|
0,7
|
2
|
|
|
25
|
0,8
|
1,7
|
|
|
19
|
0,9
|
1,9
|
|
|
16
|
1,2
|
3,1
|
|
Всего
|
82
|
4,1
|
10,5
|
|
2,0 - 3,5
|
6
|
2
|
3,5
|
|
|
4
|
2,1
|
3,2
|
|
|
18
|
2,2
|
3,8
|
|
|
20
|
2,3
|
3,1
|
|
|
5
|
2,4
|
4,6
|
|
|
11
|
2,5
|
4,6
|
|
Всего
|
64
|
13,5
|
22,8
|
|
3,5 - 5,0
|
21
|
3,5
|
4,6
|
|
|
26
|
3,5
|
4,7
|
|
|
17
|
3,6
|
4,5
|
|
|
2
|
3,8
|
5,2
|
|
|
8
|
3,9
|
5
|
|
|
12
|
3,9
|
4,9
|
|
|
14
|
4,1
|
5,8
|
|
|
27
|
4,1
|
6,5
|
|
|
1
|
4,2
|
5,4
|
|
|
10
|
4,2
|
6
|
|
|
22
|
4,4
|
6,2
|
|
|
23
|
4,8
|
7,2
|
|
Всего
|
183
|
48
|
66
|
|
5,0 - 6,5
|
30
|
5,2
|
7,1
|
|
|
29
|
5,3
|
6,8
|
|
|
28
|
6,3
|
8,6
|
|
|
3
|
6,4
|
8,7
|
|
Всего
|
90
|
23,2
|
31,2
|
|
6,5 - 8,0
|
24
|
7,5
|
8
|
|
|
13
|
7,6
|
8,6
|
|
|
9
|
8
|
7,4
|
|
Всего
|
46
|
23,1
|
24
|
|
ИТОГО
|
465
|
111,9
|
154,5
|
На основе групповых
итоговых строк «Всего» табл. 3 сформируем итоговую таблицу 4, представляющая
интервальный ряд распределения банков по доходам бюджета.
Таблица 4 – Распределение
регионов по доходам бюджета
|
Номер группы
|
Группы регионов по доходам бюджета, млн. руб.
|
Число регионов в абсолютном выражении
|
Число регионов в относительном выражении
|
Накопленная частота
|
Накопленная частость, %
|
|
1
|
0,5 - 2,0
|
5
|
16,67
|
5
|
16,67
|
|
2
|
2,0 - 3,5
|
6
|
20,00
|
11
|
36,67
|
|
3
|
3,5 - 5,0
|
12
|
40,00
|
23
|
76,67
|
|
4
|
5,0 - 6,5
|
4
|
13,33
|
27
|
90,00
|
|
5
|
6,5 - 8,0
|
3
|
10,00
|
30
|
100,00
|
|
Итого
|
|
30
|
100,00
|
|
|
Вывод. Анализ интервального ряда
распределения изучаемой совокупности регионов показывает, что распределение
регионов по доходам бюджета не является равномерным: преобладают регионы с
доходами бюджета от 3,5 млн. руб. до 5,0 млн. руб. (это 12 регионов, доля
которых составляет 40%); 36,67% регионов имеют доходы бюджета менее 3,5 млн.
руб., а 90% – менее 6,5 млн. руб.
Мода Мо для дискретного ряда – это значение признака, наиболее
часто встречающееся у единиц исследуемой совокупности. В интервальном вариационном
ряду модой приближенно считается центральное значение модального интервала
(имеющего наибольшую частоту). Более точно моду можно определить графическим
методом по гистограмме ряда (рис.1).
Гистограмма распределения
регионов по доходам бюджета
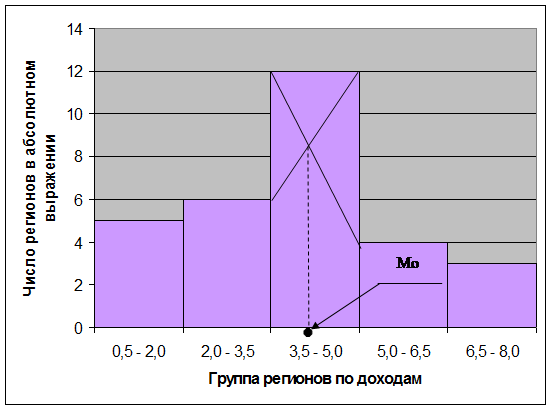
Рис. 1 Определение моды
графическим методом
Конкретное значение моды для интервального ряда
рассчитаем по формуле:
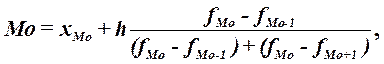 (2)
(2)
где хМo – нижняя
граница модального интервала,
h –величина
модального интервала,
fMo – частота модального интервала,
fMo-1 – частота интервала, предшествующего модальному,
fMo+1 –
частота интервала, следующего за модальным.
Согласно табл. 3
модальным интервалом построенного ряда является интервал 3,5 – 5,0 млн. руб.,
так как его частота максимальна (f = 12).
Расчет моды по формуле
(2):
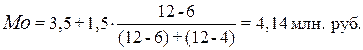
Вывод. Для рассматриваемой совокупности регионов наиболее распространенный доход
бюджета характеризуется средней величиной 4,14 млн. руб.
Медиана Ме – это значение признака, приходящееся на середину
ранжированного ряда. По обе стороны от медианы находится одинаковое количество
единиц совокупности.
Определим медиану
графическим методом по кумулятивной кривой (рис. 2). Кумулята строится по
накопленным частотам.
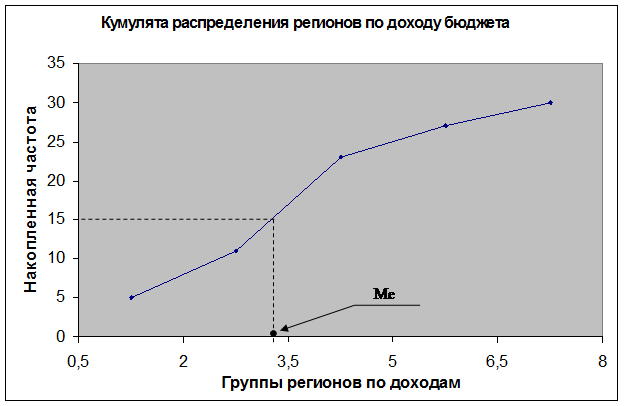
Рис. 2 Определение
медианы графическим методом
Конкретное значение
медианы для интервального ряда рассчитаем по формуле:
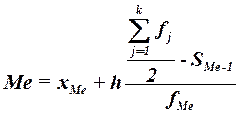 , (3)
, (3)
где
хМе– нижняя граница медианного интервала,
h – величина медианного интервала,
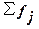 – сумма всех частот,
– сумма всех частот,
fМе – частота медианного интервала,
SMе-1 – кумулятивная (накопленная) частота
интервала, предшествующего медианному.
Найдем медианный
интервал. Таким интервалом будет интервал доходов бюджета регионов (3,5-5,0
млн. руб.), поскольку его накопленная частота равная 23, впервые превышает
величину, равную половине численности единиц (30:2=15).
Расчет значения медианы
по формуле (3):
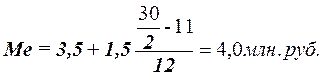
Вывод. В рассматриваемой совокупности
регионов половина регионов имеют в среднем доходы не более 4,0 млн. руб., а
другая половина – не менее 4,0 млн. руб.
Для расчета характеристик
ряда распределения 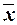 , σ, σ2, Vσ на основе построим вспомогательную
таблицу 5 (
, σ, σ2, Vσ на основе построим вспомогательную
таблицу 5 (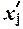 – середина j-го интервала).
– середина j-го интервала).
Таблица 5 – Расчетная
таблица для нахождения характеристик ряда распределения
|
Группы регионов по доходам бюджета, млн. руб.
|
Середина интервала 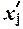
|
Число регионов
fj
|
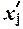 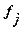
|
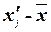
|
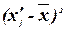
|
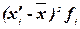
|
|
1
|
 2 2
|
3
|
4
|
5
|
6
|
7
|
|
0,5 - 2,0
|
1,25
|
5
|
6,25
|
-2,7
|
7,29
|
36,45
|
|
2,0 - 3,5
|
2,75
|
6
|
16,5
|
-1,2
|
1,44
|
8,64
|
|
3,5 - 5,0
|
4,25
|
12
|
51
|
0,3
|
0,09
|
1,08
|
|
5,0 - 6,5
|
5,75
|
4
|
23
|
1,8
|
3,24
|
12,96
|
|
6,5 - 8,0
|
7,25
|
3
|
21,75
|
3,3
|
10,89
|
32,67
|
|
Итого
|
|
30
|
118,5
|
|
|
91,8
|
Рассчитаем среднюю
арифметическую взвешенную:
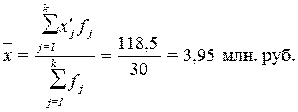 (4)
(4)
Расчет среднего квадратического
отклонения:
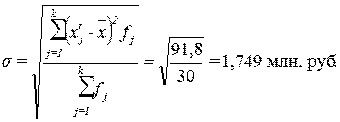 (5)
(5)
Расчет дисперсии:
σ2 =1,7492=3,06
Расчет коэффициента вариации:
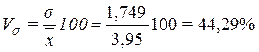 (6)
(6)
Вывод. Значение Vσ = 44,29% превышает 33%,
следовательно, вариация доходов бюджетов в исследуемой совокупности регионов
значительна и совокупность по данному признаку качественно неоднородна. Средняя
величина плохо представляет всю совокупность, является нетипичной, ненадежной.
Для расчета средней
арифметической по исходным данным применяется формула средней арифметической
простой:
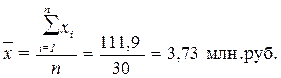 (7)
(7)
Причина расхождения
средних величин, рассчитанных по формулам (7) и (4), заключается в том, что по
формуле (7) средняя определяется по фактическим
значениям исследуемого признака
для всех 30-ти банков, а по формуле (4) средняя
вычисляется для интервального ряда, когда в качестве значений признака берутся
середины интервалов  и, следовательно, значение средней будет менее
точным (за исключением случая равномерного распределения значений признака
внутри каждой группы).
и, следовательно, значение средней будет менее
точным (за исключением случая равномерного распределения значений признака
внутри каждой группы).
Задание 2
По исходным данным табл. 1 с
использованием результатов выполнения Задания 1 необходимо выполнить следующее:
1.
Установить наличие и характер корреляционной связи
между признаками Доходы бюджета и Расходы бюджета, образовав по каждому
признаку пять групп с равными интервалами, используя методы:
а) аналитической группировки;
б) корреляционной таблицы.
2.
Оценить тесноту корреляционной связи, используя
коэффициент детерминации и эмпирическое корреляционное отношение.
Сделать выводы по результатам выполнения Задания 2.
Выполнение
Задания 2
Целью выполнения данного
Задания является выявление наличия корреляционной связи между факторным и
результативным признаками,
установление направления связи и оценка ее тесноты.
По условию Задания 2 факторным
является признак Доходы бюджета (X),
результативным – признак Расходы
бюджета (Y).
1. Аналитическая группировка позволяет изучать взаимосвязь
факторного и результативно признаков.
Основные этапы проведения
аналитической группировки – обоснование и выбор факторного и результативного
признаков, подсчет числа единиц в каждой из образованных групп, определение
объема варьирующих признаков в пределах созданных групп, а также исчисление
средних размеров результативного показателя. Результаты группировки оформляют в
таблице 6.
Таблица 6 – Зависимость
суммы прибыли банков от объема кредитных вложений
|
Номер группы
|
Группы регионов по доходам бюджета, млн. руб. x
|
Число регионов
fj
|
Расходы бюджетов млн. руб.
|
|
Всего
|
В среднем на один банк,
|
|
1
|
2
|
3
|
4
|
5=4:3
|
|
1
|
0,5 - 2,0
|
5
|
10,50
|
2,10
|
|
2
|
2,0 - 3,5
|
6
|
22,80
|
3,80
|
|
3
|
3,5 - 5,0
|
12
|
66,00
|
5,50
|
|
4
|
5,0 - 6,5
|
4
|
31,20
|
7,80
|
|
5
|
6,5 - 8,0
|
3
|
24,00
|
8,00
|
|
Итого
|
|
30
|
154,50
|
5,15
|
Вывод. Анализ данных табл. 6 показывает, что с увеличением доходов
бюджетов от группы к группе систематически возрастает и средние расходы
бюджетов по каждой группе регионов, что свидетельствует о наличии прямой
корреляционной связи между исследуемыми признаками.
2.
Корреляционно-регрессионный
анализ.
Задачи корреляционного
анализа сводятся к измерению тесноты известной связи между варьирующими
признаками, определению причинных связей и оценки факторов, оказывающих
наибольшее влияние на результативный признак.
Задачами регрессионного
анализа является выбор типа модели (формы связи), установление степени влияния
независимых переменных на зависимую и определение расчетных значений зависимой
переменной (функции регрессии).
Для построения
корреляционной таблицы необходимо знать величины и границы интервалов по двум
признакам X и Y. Величина интервала и границы интервалов для
факторного признака Х – Доходы бюджета известны из табл. 6. Для
результативного признака Y – Расходы бюджета величина интервала определяется по
формуле (1) при k = 5, уmax = 8,7 млн. руб., уmin = 1,7 млн. руб.:
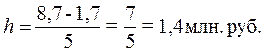
Подсчитывая число
регионов, входящих в каждую группу (частоты групп), получаем интервальный
ряд распределения результативного признака (табл. 7).
Таблица 7 – Распределение
регионов по расходам бюджета
|
Номер группы
|
Группы регионов по расходам бюджета, млн. руб.
y
|
Число регионов
fj
|
|
1
|
1,7 - 3,1
|
4
|
|
2
|
3,1 - 4,5
|
5
|
|
3
|
4,5 - 5,9
|
10
|
|
4
|
5,9 - 7,3
|
6
|
|
5
|
7,3 - 8,7
|
5
|
|
Итого
|
|
30
|
Используя группировки по
факторному и результативному признакам, строим корреляционную таблицу (табл. 8).
Таблица 8 – Корреляционная
таблица зависимости расходов бюджета банков от доходов бюджета
|
Группы регионов по доходам бюджета, млн. руб.
|
Группы регионов по расходам бюджета, млн. руб.
|
|
1,7 - 3,1
|
3,1 - 4,5
|
4,5 - 5,9
|
5,9 - 7,3
|
7,3 - 8,7
|
Итого
|
|
0,5 - 2,0
|
4
|
1
|
|
|
|
5
|
|
2,0 - 3,5
|
|
4
|
2
|
|
|
6
|
|
3,5 - 5,0
|
|
|
8
|
4
|
|
12
|
|
5,0 - 6,5
|
|
|
|
2
|
2
|
4
|
|
6,5 - 8,0
|
|
|
|
|
3
|
3
|
|
Итого
|
4
|
5
|
10
|
6
|
5
|
30
|
Вывод. Анализ данных табл. 8 показывает, что распределение частот групп
произошло вдоль диагонали, идущей из левого верхнего угла в правый нижний угол
таблицы. Это свидетельствует о наличии прямой корреляционной связи между
доходами бюджетов и расходами бюджетов регионов.
Для измерения тесноты
связи между факторным и результативным признаками рассчитывают специальные
показатели – эмпирический коэффициент детерминации 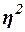 и эмпирическое
корреляционное отношение
и эмпирическое
корреляционное отношение 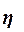 .
.
Эмпирический
коэффициент детерминации 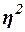 оценивает, насколько
вариация результативного признака Y
объясняется вариацией фактора Х
(остальная часть вариации Y
объясняется вариацией прочих факторов). Показатель
оценивает, насколько
вариация результативного признака Y
объясняется вариацией фактора Х
(остальная часть вариации Y
объясняется вариацией прочих факторов). Показатель 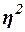 рассчитывается как
доля межгрупповой дисперсии в общей дисперсии по формуле
рассчитывается как
доля межгрупповой дисперсии в общей дисперсии по формуле
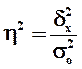 (8)
(8)
где 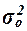 – общая дисперсия
признака Y,
– общая дисперсия
признака Y,
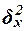 – межгрупповая
(факторная) дисперсия признака Y.
– межгрупповая
(факторная) дисперсия признака Y.
Общая дисперсия
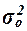 характеризует
вариацию результативного признака, сложившуюся под влиянием всех действующих на
Y факторов
(систематических и случайных). Этот показатель вычисляется по формуле
характеризует
вариацию результативного признака, сложившуюся под влиянием всех действующих на
Y факторов
(систематических и случайных). Этот показатель вычисляется по формуле
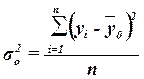 (9)
(9)
где yi – индивидуальные значения
результативного признака;
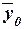 – общая средняя значений
результативного признака;
– общая средняя значений
результативного признака;
n – число единиц совокупности.
Общая
средняя 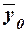 вычисляется как средняя арифметическая простая
по всем единицам совокупности:
вычисляется как средняя арифметическая простая
по всем единицам совокупности:
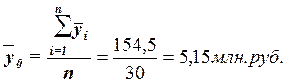 (10)
(10)
Для расчета общей
дисперсии 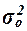 применяется вспомогательная таблица
9.
применяется вспомогательная таблица
9.
|
№ региона п/п
|
Расходы бюджета, млн. руб.
|
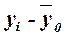
|
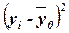
|
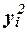
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
5,4
|
0,250
|
0,0625
|
29,160
|
|
2
|
5,2
|
0,050
|
0,0025
|
27,040
|
|
3
|
8,7
|
3,550
|
12,6025
|
75,690
|
|
4
|
3,2
|
-1,950
|
3,8025
|
10,240
|
|
5
|
4,6
|
-0,550
|
0,3025
|
21,160
|
|
6
|
3,5
|
-1,650
|
2,7225
|
12,250
|
|
7
|
2,0
|
-3,150
|
9,9225
|
4,000
|
|
8
|
5,0
|
-0,150
|
0,0225
|
25,000
|
|
9
|
7,4
|
2,250
|
5,0625
|
54,760
|
|
10
|
6,0
|
0,850
|
0,7225
|
36,000
|
|
11
|
4,6
|
-0,550
|
0,3025
|
21,160
|
|
12
|
4,9
|
-0,250
|
0,0625
|
24,010
|
|
13
|
8,6
|
3,450
|
11,9025
|
73,960
|
|
14
|
5,8
|
0,650
|
0,4225
|
33,640
|
|
15
|
1,8
|
-3,350
|
11,2225
|
3,240
|
|
16
|
3,1
|
-2,050
|
4,2025
|
9,610
|
|
17
|
4,5
|
-0,650
|
0,4225
|
20,250
|
|
18
|
3,8
|
-1,350
|
1,8225
|
14,440
|
|
19
|
1,9
|
-3,250
|
10,5625
|
3,610
|
|
20
|
3,1
|
-2,050
|
4,2025
|
9,610
|
|
21
|
4,6
|
-0,550
|
0,3025
|
21,160
|
|
22
|
6,2
|
1,050
|
1,1025
|
38,440
|
|
23
|
7,2
|
2,050
|
4,2025
|
51,840
|
|
24
|
8,0
|
2,850
|
8,1225
|
64,000
|
|
25
|
1,7
|
-3,450
|
11,9025
|
2,890
|
|
26
|
4,7
|
-0,450
|
0,2025
|
22,090
|
|
27
|
6,5
|
1,350
|
1,8225
|
42,250
|
|
28
|
8,6
|
3,450
|
11,9025
|
73,960
|
|
29
|
6,8
|
1,650
|
2,7225
|
46,240
|
|
30
|
7,1
|
1,950
|
3,8025
|
50,410
|
|
Итого
|
154,5
|
0,000
|
126,435
|
922,110
|
Расчет общей
дисперсии по формуле
(9):
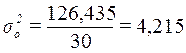
Межгрупповая
дисперсия 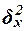 измеряет
систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х
(по которому произведена группировка). Воздействие фактора Х на результативный признак Y
проявляется в отклонении групповых средних
измеряет
систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х
(по которому произведена группировка). Воздействие фактора Х на результативный признак Y
проявляется в отклонении групповых средних 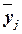 от
общей средней
от
общей средней 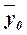 . Показатель
. Показатель 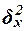 вычисляется по формуле
вычисляется по формуле
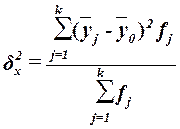 (11)
(11)
где 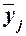 –групповые
средние,
–групповые
средние,
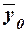 –
общая средняя,
–
общая средняя,
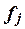 –число единиц в j-ой
группе,
–число единиц в j-ой
группе,
k – число групп.
Для расчета
межгрупповой дисперсии 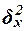 построим вспомогательную таблицу 10.
построим вспомогательную таблицу 10.
Таблица 10 –
Вспомогательная таблица для расчета межгрупповой дисперсии
|
Группы регионов по доходам бюджета, млн. руб.
|
Число регионов 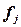
|
Среднее значение  в группе в группе
|

|
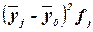
|
|
1
|
2
|
3
|
4
|
5
|
|
0,5 - 2,0
|
5
|
2,10
|
-3,05
|
46,513
|
|
2,0 - 3,5
|
6
|
3,80
|
-1,35
|
10,935
|
|
3,5 - 5,0
|
12
|
5,50
|
0,35
|
1,470
|
|
5,0 - 6,5
|
4
|
7,80
|
2,65
|
28,090
|
|
6,5 - 8,0
|
3
|
8,00
|
2,85
|
24,368
|
|
Итого
|
30
|
|
|
111,375
|
Расчет межгрупповой дисперсии 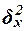 по формуле (11):
по формуле (11):
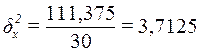
Расчет
эмпирического коэффициента детерминации 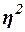 по формуле (8):
по формуле (8):
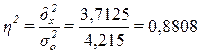 или 88,08%
или 88,08%
Вывод. 88,08% вариации расходов бюджетов
регионов обусловлено вариацией доходов бюджетов регионов, а 11,92% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное
отношение 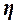 оценивает тесноту связи между факторным и
результативным признаками и вычисляется по формуле
оценивает тесноту связи между факторным и
результативным признаками и вычисляется по формуле
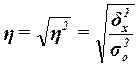 (12)
(12)
Расчет эмпирического
корреляционного отношения 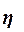 по формуле (12):
по формуле (12):
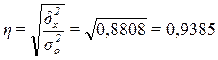 или 93,85%
или 93,85%
Вывод. Согласно шкале Чэддока связь между
доходом бюджета регионов и расходом
бюджета региона является весьма тесной.
Задание 3
По результатам выполнения
задания 1 с вероятностью 0,683 определите:
1. Ошибку выборки среднего дохода
бюджета и границы, в которых он будет находиться в генеральной совокупности.
2. Ошибку выборки доли регионов со
средним доходом бюджета 5 млн. руб. и более и границы, в которых будет
находиться генеральная доля.
Выполнение Задания 3
Целью выполнения данного
Задания является определение для генеральной совокупности регионов границ, в
которых будут находиться величина среднего дохода бюджетов регионов и доля
регионов с доходом бюджета не менее 5 млн. руб.
Значения признаков
единиц, отобранных из генеральной совокупности в выборочную, всегда случайны,
поэтому и статистические характеристики выборки случайны, следовательно, и
ошибки выборки также случайны. Ввиду этого принято вычислять два вида ошибок -
среднюю 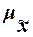 и предельную
и предельную 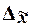 .
.
Для
собственно-случайной и механической выборки с бесповторным способом отбора
средняя ошибка 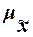 выборочной средней
выборочной средней 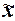 определяется по формуле
определяется по формуле
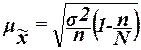 (13)
(13)
где 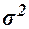 – общая дисперсия выборочных значений
признаков,
– общая дисперсия выборочных значений
признаков,
N – число
единиц в генеральной совокупности,
n – число единиц в выборочной
совокупности.
Предельная
ошибка выборки 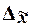 определяет границы, в пределах которых
будет находиться генеральная средняя:
определяет границы, в пределах которых
будет находиться генеральная средняя:
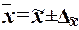 ,
,
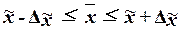 (14)
(14)
где 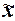 – выборочная средняя,
– выборочная средняя,
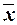 – генеральная средняя.
– генеральная средняя.
Границы задают доверительный
интервал генеральной средней, т.е. случайную область значений, которая с
вероятностью Р гарантированно
содержит значение генеральной средней. Эту вероятность Р называют доверительной
вероятностью или уровнем
надёжности.
В математической
статистике доказано, что предельная ошибка выборки Δ кратна средней ошибке
µ с коэффициентом кратности t
(называемым также коэффициентом доверия), который зависит от значения
доверительной вероятности Р. Для
предельной ошибки выборочной средней 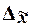 это теоретическое положение
выражается формулой
это теоретическое положение
выражается формулой
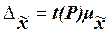 (15)
(15)
Значения t вычислены заранее для различных
доверительных вероятностей Р и протабулированы
По условию
демонстрационного примера выборочная совокупность насчитывает 30 регионов, выборка
25% механическая, следовательно, генеральная совокупность включает 120 регионов.
Выборочная средняя 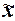 , дисперсия
, дисперсия 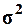 определены в Задании 1 (п. 3).
Значения параметров, необходимых для решения задачи, представлены в табл. 11:
определены в Задании 1 (п. 3).
Значения параметров, необходимых для решения задачи, представлены в табл. 11:
Таблица 16
|
Р
|
t
|
n
|
N
|
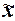
|
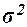
|
|
0,683
|
1,0
|
30
|
120
|
3,95
|
3,06
|
Расчет средней ошибки
выборки по формуле (13):
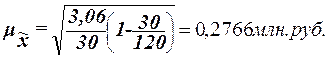
Расчет предельной ошибки
выборки по формуле (15):
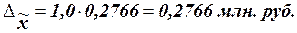
Определение по формуле (14)
доверительного интервала для генеральной средней:
3,95-0,2766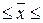 3,95+0,2766,
3,95+0,2766,
3,6734 млн.
руб. 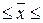 4,2266
млн. руб.
4,2266
млн. руб.
Вывод. На основании проведенного
выборочного обследования регионов с вероятностью 0,683 можно утверждать, что
для генеральной совокупности регионов средний доход бюджета регионов находится
в пределах от 3,673 млн. руб. до 4,227 млн. руб.
Доля
единиц выборочной совокупности, обладающих тем или иным заданным свойством,
выражается формулой
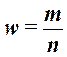 (16)
(16)
где
m – число
единиц совокупности, обладающих заданным свойством;
n – общее число единиц в совокупности.
Для
собственно-случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки 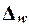 доли единиц, обладающих заданным свойством,
рассчитывается по формуле
доли единиц, обладающих заданным свойством,
рассчитывается по формуле
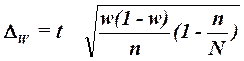 (17)
(17)
где
w – доля
единиц совокупности, обладающих заданным свойством;
(1-w) – доля единиц совокупности, не обладающих заданным свойством,
N – число единиц в генеральной
совокупности,
n– число единиц в выборочной
совокупности.
Предельная
ошибка выборки 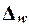 определяет границы, в пределах которых будет
находиться генеральная доля р единиц, обладающих заданным
свойством:
определяет границы, в пределах которых будет
находиться генеральная доля р единиц, обладающих заданным
свойством:
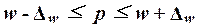 (18)
(18)
По условию Задания 3
исследуемым свойством является равенство или превышение доходов регионов
величины 5 млн. руб.
Число регионов
с заданным свойством определяется из Задания 1:
m=7
Расчет
выборочной доли по формуле (16):
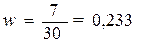
Расчет по формуле (17)
предельной ошибки выборки для доли:
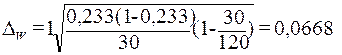
Определение по формуле
(18) доверительного интервала генеральной доли:
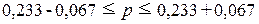
0,166 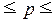 0,300
0,300
или
16,6% 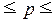 30,0%
30,0%
Вывод. С вероятностью 0,683
можно утверждать, что в генеральной совокупности регионов доля регионов
с доходом бюджета 5 млн. руб. и выше будет находиться в пределах от 16,6% до 30,0%.
Задание 4
Исполнение регионального
бюджета в процентах к валовому региональному продукту (ВРП) характеризуется
следующими данными:
Таблица
17
|
Месяц
|
Налоговые поступления в % к ВРП
|
|
2002 г.
|
2003 г.
|
2004 г.
|
|
Январь
|
2,5
|
2,6
|
2,4
|
|
Февраль
|
2,6
|
2,7
|
2,3
|
|
Март
|
3
|
2,8
|
2,5
|
|
Апрель
|
2,9
|
2,8
|
2,1
|
|
Май
|
2,8
|
2,7
|
2,3
|
|
Июнь
|
2,7
|
2,8
|
2,2
|
|
Июль
|
2,9
|
2,7
|
2,6
|
|
Август
|
2,8
|
2,7
|
2,6
|
|
Сентябрь
|
2,9
|
2,8
|
2,7
|
|
Октябрь
|
3
|
2,9
|
2,8
|
|
Ноябрь
|
3,1
|
3
|
3
|
|
Декабрь
|
3,2
|
2,9
|
3,3
|
ВРП
в 2002 г.
Составил 26 млрд. руб., а в 2003 и 2004 гг. соответственно 29,1 млрд. и 32,2
млрд. руб.
Для анализа сезонных колебаний
налоговых поступлений в регионе:
1. Определите индексы сезонности методом
простой средней.
2. Постройте график сезонной волны.
3. Осуществите прогноз налоговых
поступлений в процентах к ВРП по месяцам 2005 г. при условии, что доля налоговых
поступлений в ВРП региона в 2005
г. составил 70%.
Выполнение Задания 3
Индекс сезонности вычисляется по формуле:
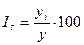 (19)
(19)
где yi – средняя
для каждого месяца;
у – среднемесячный уровень для всего
месяца.
Средний индекс сезонности
для 12 месяцев должен быть равен 100%, тогда сумма индексов должна составлять
1200.
Для расчета
индекса сезонности 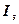 построим таблицу 18.
построим таблицу 18.
Таблица 18 – Индексы
сезонности налоговых поступлений
|
Месяц
|
Налоговые поступления
|
Is
|
|
2002 г.
|
2003 г.
|
2004 г.
|
Среднемесячная
|
|
Январь
|
2,5
|
2,6
|
2,4
|
2,50
|
91,28
|
|
Февраль
|
2,6
|
2,7
|
2,3
|
2,53
|
92,49
|
|
Март
|
3
|
2,8
|
2,5
|
2,77
|
101,01
|
|
Апрель
|
2,9
|
2,8
|
2,1
|
2,60
|
94,93
|
|
Май
|
2,8
|
2,7
|
2,3
|
2,60
|
94,93
|
|
Июнь
|
2,7
|
2,8
|
2,2
|
2,57
|
93,71
|
|
Июль
|
2,9
|
2,7
|
2,6
|
2,73
|
99,80
|
|
Август
|
2,8
|
2,7
|
2,6
|
2,70
|
98,58
|
|
Сентябрь
|
2,9
|
2,8
|
2,7
|
2,80
|
102,23
|
|
Октябрь
|
3
|
2,9
|
2,8
|
2,90
|
105,88
|
|
Ноябрь
|
3,1
|
3
|
3
|
3,03
|
110,75
|
|
Декабрь
|
3,2
|
2,9
|
3,3
|
3,13
|
114,40
|
|
Итого
|
34,4
|
33,4
|
30,8
|
32,87
|
1200,00
|
|
В среднем
|
2,87
|
2,78
|
2,57
|
2,74
|
|
Анализ данных табл.
18 позволяет сделать следующие выводы:
-
налоговые поступления характеризуются мало выраженной сезонностью;
-
налоговые поступления по отдельным месяцам года отклоняются от
среднемесячных на 0,2 – 14,4%;
-
наименьшие налоговые поступления составляют 91,28% в январе, а
наибольшие - в декабре (114,4%)

Рис. 3 Сезонная волна налоговых
поступлений (изменение индексов сезонности в течение года).
Данные расчетов и графика
показывают, что поступление налогов в бюджет имеет сезонный характер с
незначительным их увеличением в первом и четвертом кварталах. Это говорит о
необходимости уменьшения амплитуды колебаний в поступлении налогов в бюджет, с
целью снижения воздействия сезонности на стабильность денежного рынка.
Прогнозирование динамического ряда с сезонными компонентами при
отсутствии в нем тенденции сводится к прогнозированию среднего уровня (y) с
последующей корректировкой его на сезонную компоненту – умножением на
коэффициент сезонности:
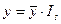 (20)
(20)
Таблица 19 – Прогноз налоговых
поступлений за 2005 г.
в % к ВРП
|
Месяц
|
Налоговые поступления
|
|
2002 г.
|
2003 г.
|
2004 г.
|
2005 г.
|
|
Январь
|
2,5
|
2,6
|
2,4
|
5,32
|
|
Февраль
|
2,6
|
2,7
|
2,3
|
5,40
|
|
Март
|
3,0
|
2,8
|
2,5
|
5,89
|
|
Апрель
|
2,9
|
2,8
|
2,1
|
5,54
|
|
Май
|
2,8
|
2,7
|
2,3
|
5,54
|
|
Июнь
|
2,7
|
2,8
|
2,2
|
5,47
|
|
Июль
|
2,9
|
2,7
|
2,6
|
5,82
|
|
Август
|
2,8
|
2,7
|
2,6
|
5,75
|
|
Сентябрь
|
2,9
|
2,8
|
2,7
|
5,96
|
|
Октябрь
|
3,0
|
2,9
|
2,8
|
6,18
|
|
Ноябрь
|
3,1
|
3,0
|
3,0
|
6,46
|
|
Декабрь
|
3,2
|
2,9
|
3,3
|
6,67
|