Министерство
образования и науки РФ
Федеральное агентство
по образованию
Государственное
образовательное учреждение
Высшего
профессионального образования
Всероссийский заочный
финансово-экономический институт
Филиал в г. Туле
Лабораторная работа
по дисциплине
«Эконометрика»
Выполнил: студент третьего курса
Факультета УС
Специальность
БУА и А
Вечерняя группа
Меркулова Ольга Вячеславовна
05убб 03031
Проверил: Арсеньев Ю.Н.
Тула 2008
Условие задачи
В таблице 1 представлены данные о
деятельности крупнейших компаний США в 1996 г.
Таблица 1.
|
№ п/п
|
Y
|
X1
|
X2
|
X3
|
X4
|
|
1
|
0,9
|
31,3
|
18,9
|
43
|
40,9
|
|
2
|
1,7
|
13,4
|
13,7
|
64,7
|
40,5
|
|
3
|
0,7
|
4,5
|
18,5
|
24
|
38,9
|
|
4
|
1,7
|
10
|
4,8
|
50,2
|
38,5
|
|
5
|
2,6
|
20
|
21,8
|
106
|
37,3
|
|
6
|
1,3
|
15
|
5,8
|
96,6
|
26,5
|
|
7
|
4,1
|
137,1
|
99
|
347
|
37
|
|
8
|
1,6
|
17,9
|
20,1
|
85,6
|
36,8
|
|
9
|
6,9
|
165,4
|
60,6
|
745
|
36,3
|
|
10
|
0,4
|
2
|
1,4
|
4,1
|
35,3
|
|
11
|
1,3
|
6,8
|
8
|
26,8
|
35,3
|
|
12
|
1,9
|
27,1
|
18,9
|
42,7
|
35
|
|
13
|
1,9
|
13,4
|
13,2
|
61,8
|
26,2
|
|
14
|
1,4
|
9,8
|
12,6
|
212
|
33,1
|
|
15
|
0,4
|
19,5
|
12,2
|
105
|
32,7
|
|
16
|
0,8
|
5,8
|
3,2
|
33,5
|
32,1
|
|
17
|
1,8
|
27
|
13
|
142
|
30,5
|
|
18
|
0,9
|
12,4
|
6,9
|
96
|
29,8
|
|
19
|
1,1
|
17,7
|
15
|
140
|
25,4
|
|
20
|
1,9
|
12,7
|
11,9
|
59,3
|
29,3
|
|
21
|
-0,9
|
21,4
|
1,6
|
131
|
29,2
|
|
22
|
1,3
|
13,5
|
8,6
|
70,7
|
29,2
|
|
23
|
2
|
13,4
|
11,5
|
65,4
|
29,1
|
|
24
|
0,6
|
4,2
|
1,9
|
23,1
|
27,9
|
|
25
|
0,7
|
15,5
|
5,8
|
80,8
|
27,2
|
Принятые обозначения:
Y – чистый доход, млдр.
долл.;
X1 – оборот
капитала, млрд. долл;
X2 –
использованный капитал, млрд. долл.;
X3 – численность
служащих, тыс. чел.;
X4 – рыночная
капитализация компании, млрд. долл.
Задание
1. Составьте
матрицу парных коэффициентов корреляции исходных переменных, оцените их
статистическую значимость.
2. Постройте
уравнение регрессии от всех факторов, в линейной форме. Установите, какие
факторы мультиколлинеарны.
3. Оцените
статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу
о значимости параметров регрессионной модели
проверьте с помощью F-критерия;
оцените качество уравнения регрессии с помощью коэффициента детерминации R2.
4. Дайте
сравнительную оценку силы связи факторов с результатом с помощью коэффициентов
эластичности,  и
и  коэффициентов.
коэффициентов.
5. Оцените
точность уравнения через среднюю относительную ошибку аппроксимации.
6. Отберите
информативные факторы в модель по t-критерию для коэффициентов регрессии. Постройте модель только с
информативными факторами и оцените ее параметры.
7. Рассчитайте
прогнозное значение результата, если прогнозное значение факторов составляют
80% от их максимального значения.
8. Рассчитайте
ошибку и доверительный интервал прогноза для уровня значимости 5 или 10% (а=0,5
или а=0,10).
Решение:
Составим
матрицу парных коэффициентов корреляции исходных переменных, используя
инструмент Корреляции (анализ данных EXCEL).
Рис. 1.
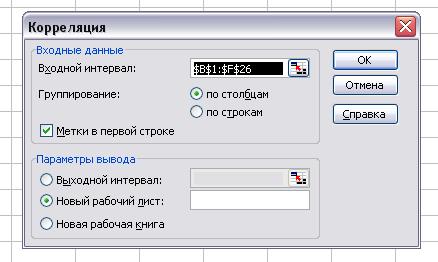
Рис. 2.
Получаем:
.
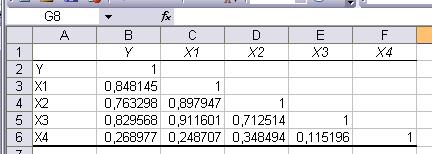
Рис. 3.
Значимость проверим с помощью t-статистики Стьюдента:
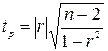 .
.
Табличное значение при уровне
значимости 5% и степенях свободы k=n-2=25-2=23
равно tкр =
2,07.
ryx1 =
0,848, tр=0,848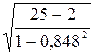 =36,823. Т.к. 36,823>2,07; коэффициент корреляции значим.
=36,823. Т.к. 36,823>2,07; коэффициент корреляции значим.
ryx2 =
0,763, tр=0,763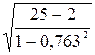 =27,174. Т.к. 27,174>2,07; коэффициент корреляции значим.
=27,174. Т.к. 27,174>2,07; коэффициент корреляции значим.
ryx3 =
0,830, tр=0,830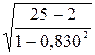 =34,169. Т.к. 34,169>2,07; коэффициент корреляции значим.
=34,169. Т.к. 34,169>2,07; коэффициент корреляции значим.
ryx4 =
0,269, tр=0,269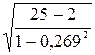 =6,423. Т.к. 6,423>2,07; коэффициент корреляции значим.
=6,423. Т.к. 6,423>2,07; коэффициент корреляции значим.
rx1x2 = 0,898, tр=0,898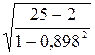 =46,927. Т.к. 46,927>2,07; коэффициент корреляции значим.
=46,927. Т.к. 46,927>2,07; коэффициент корреляции значим.
rx1x3 = 0,912, tр=0,912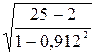 =51,005. Т.к. 51,005>2,07; коэффициент корреляции значим.
=51,005. Т.к. 51,005>2,07; коэффициент корреляции значим.
rx1x4 = 0,249, tр=0,249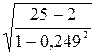 =5,906. Т.к. 5,906>2,07; коэффициент корреляции значим.
=5,906. Т.к. 5,906>2,07; коэффициент корреляции значим.
rx2x3 = 0,713, tр=0,713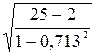 =23,356. Т.к. 23,356>2,07; коэффициент корреляции значим.
=23,356. Т.к. 23,356>2,07; коэффициент корреляции значим.
rx2x4 = 0,348, tр=0,348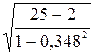 =8,551. Т.к. 8,551>2,07; коэффициент корреляции значим.
=8,551. Т.к. 8,551>2,07; коэффициент корреляции значим.
rx3x4 = 0,115, tр=0,115 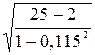 =2,667. Т.к. 2,667>2,07; коэффициент корреляции значим.
=2,667. Т.к. 2,667>2,07; коэффициент корреляции значим.
Анализ матрицы
коэффициентов парной корреляции показывает, что зависимая переменная, имеет
тесную связь (r>0,7)
с Х1 (ryx2=0,763298)
и с Х3 (ryx3=0,829568).
Проверим
наличие мультиколлениарности.
Т.к. rx1x2=0,897947>0,7; rx1x3=0,911601>0,7; rx2x3=0,712514>0,7, то
факторы Х1 и Х2, Х1 и Х3, Х2 и
Х3 тесно связаны между собой, т.е. мультиколлинеарны. Поэтому из
модели надо исключить факторы Х1 и Х2 (оставили Х3 из-за
того, что он наиболее тесно связан сY , чем Х2).
Построим
уравнение множественной регрессии в линейной форме с полным набором
немультиколлинеарных факторов (Х3, Х4) –
y = a0+a3X3+a4X4.
Используем
инструмент Регрессия (анализ данных EXCEL).
Рис. 4.
Рис. 5.
Получаем:
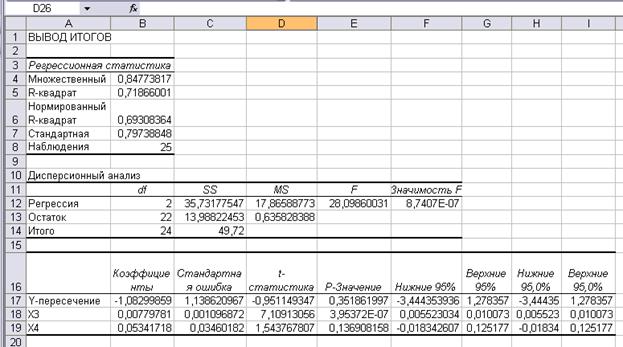
Рис. 6.
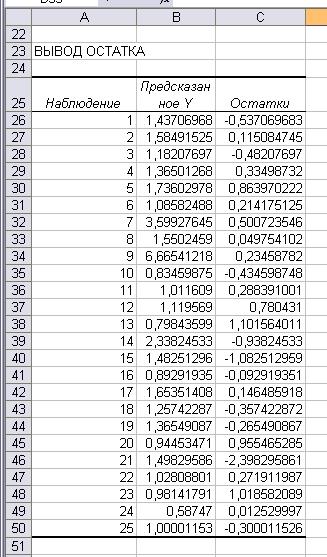
Рис. 7.
Получили
уравнение регрессии от всех немультиколлинеарных факторов (таблица 3.3., второй
столбец):
y=-1.082998589+0.007797808 X3 + 0.053417176 X4
Оценим с
помощью t-критерия
Стьюдента статистическую значимость коэффициентов уравнения множественной
регрессии.
Табличное
значение при 5% уровне значимости и степенях свободы 25-2-1=22 составляет
2,074.
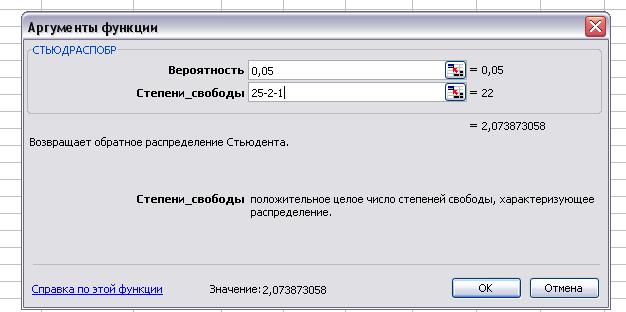
Рис. 8.
Т.к. расчетные
значения: 7,10913056 >2.074$; то коэффициент а3 значим (Х3
значимо воздействует на У). Все остальные коэффициенты незначимы, т.к. tрасч<tтабл.
Проверку
значимости уравнения регрессии произведем на основе вычисления F-критерия Фишера.
Доверительная вероятность p=0.95;
v1=k=2;
v2=n-k-1=25-2-1=22; Fтабл= 3.44;
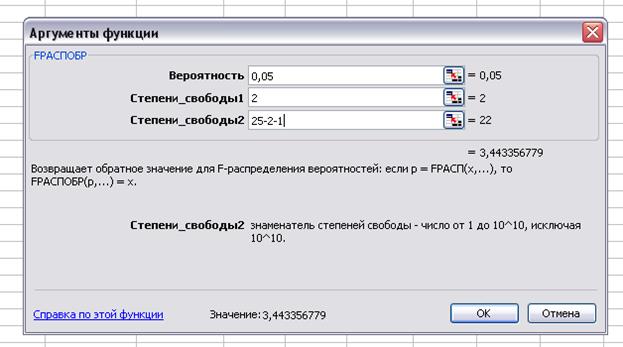
Рис. 9.
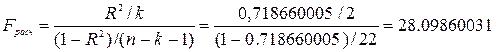 . Поскольку Fрасч>Fтабл, то
уравнение регрессии следует считать адекватным.
. Поскольку Fрасч>Fтабл, то
уравнение регрессии следует считать адекватным.
Значение
коэффициента детерминации R2=0,718660005.
Он показывает долю вариации результативного признака под воздействием изучаемых
факторов. Следовательно, около 71,8% вариации зависимой переменной учтено в
модели обусловлено влиянием факторов.
Коэффициенты эластичности:
Э3=
а3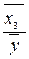 = 0,007797808
= 0,007797808 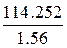 =0,5714 т.е. зависимая переменная у при изменении
фактора х3 на 1% при неизменных остальных факторах в среднем
увеличится на 0,571%.
=0,5714 т.е. зависимая переменная у при изменении
фактора х3 на 1% при неизменных остальных факторах в среднем
увеличится на 0,571%.
Э4=
а4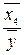 = 0,053417176
= 0,053417176 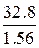 =1,123 т.е. зависимая переменная у при изменении
фактора х4 на 1% при неизменных остальных факторах в среднем
увеличится на 1,123%.
=1,123 т.е. зависимая переменная у при изменении
фактора х4 на 1% при неизменных остальных факторах в среднем
увеличится на 1,123%.
Бета-коэффициенты:
Таблица
2
|
|
y
|
x3
|
x4
|
(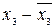 )2 )2
|
(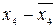 )2 )2
|
(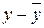 ) )
|
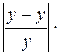 100 100
|
|
|
0,9
|
43
|
40,9
|
5076,847504
|
65,61
|
0,4356
|
59.67
|
|
|
1,7
|
64,7
|
40,5
|
2455,400704
|
59,29
|
0,0196
|
6.77
|
|
|
0,7
|
24
|
38,9
|
8145,423504
|
37,21
|
0,7396
|
68.87
|
|
|
1,7
|
50,2
|
38,5
|
4102,658704
|
32,49
|
0,0196
|
19.71
|
|
|
2,6
|
106
|
37,3
|
68,095504
|
20,25
|
1,0816
|
33.23
|
|
|
1,3
|
96,6
|
26,5
|
311,593104
|
39,69
|
0,0676
|
16.48
|
|
|
4,1
|
347
|
37
|
54171,6315
|
17,64
|
6,4516
|
12.21
|
|
|
1,6
|
85,6
|
36,8
|
820,937104
|
16
|
0,0016
|
3.11
|
|
|
6,9
|
745
|
36,3
|
397843,0395
|
12,25
|
28,5156
|
3.40
|
|
|
0,4
|
4,1
|
35,3
|
12133,4631
|
6,25
|
1,3456
|
108.65
|
|
|
1,3
|
26,8
|
35,3
|
7647,852304
|
6,25
|
0,0676
|
22.18
|
|
|
1,9
|
42,7
|
35
|
5119,688704
|
4,84
|
0,1156
|
41.08
|
|
|
1,9
|
61,8
|
26,2
|
2751,212304
|
43,56
|
0,1156
|
57.98
|
|
|
1,4
|
212
|
33,1
|
9554,671504
|
0,09
|
0,0256
|
67.02
|
|
|
0,4
|
105
|
32,7
|
85,599504
|
0,01
|
1,3456
|
270.63
|
|
|
0,8
|
33,5
|
32,1
|
6520,885504
|
0,49
|
0,5776
|
11.61
|
|
|
1,8
|
142
|
30,5
|
769,951504
|
5,29
|
0,0576
|
8.14
|
|
|
0,9
|
96
|
29,8
|
333,135504
|
9
|
0,4356
|
39.71
|
|
|
1,1
|
140
|
25,4
|
662,959504
|
54,76
|
0,2116
|
21.14
|
|
|
1,9
|
59,3
|
29,3
|
3019,722304
|
12,25
|
0,1156
|
50.29
|
|
|
-0,9
|
131
|
29,2
|
280,495504
|
12,96
|
6,0516
|
266.48
|
|
|
1,3
|
70,7
|
29,2
|
1896,776704
|
12,96
|
0,0676
|
20.92
|
|
|
2
|
65,4
|
29,1
|
2386,517904
|
13,69
|
0,1936
|
50.93
|
|
|
0,6
|
23,1
|
27,9
|
8308,687104
|
24,01
|
0,9216
|
2.09
|
|
|
0,7
|
80,8
|
27,2
|
1119,036304
|
31,36
|
0,7396
|
42.86
|
|
Итого
|
39
|
2856,3
|
820
|
535586,2824
|
538,2
|
49,72
|
1308,14
|
|
Ср. знач.
|
1,56
|
114,252
|
32,8
|
5076,847504
|
65,61
|
0,4356
|
52,33
|
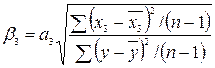 = 0,007797808
= 0,007797808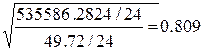 , т.е. при увеличении фактора Х3 на 149,386 тыс чел. У увеличится на
0,809*1,439=1,164 млрд. долл.
, т.е. при увеличении фактора Х3 на 149,386 тыс чел. У увеличится на
0,809*1,439=1,164 млрд. долл.
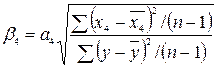 = 0,053417176
= 0,053417176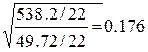 , т.е. при увеличении фактора Х4 на 4,736 млрд.
долл. У увеличится на 0,176*1,439=1,253 млрд. долл.
, т.е. при увеличении фактора Х4 на 4,736 млрд.
долл. У увеличится на 0,176*1,439=1,253 млрд. долл.
Дельта- коэффициенты:
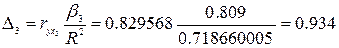 - доля влияния фактора х3 в суммарном влиянии всех
факторов.
- доля влияния фактора х3 в суммарном влиянии всех
факторов.
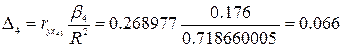 - доля влияния фактора х4 в суммарном влиянии всех
факторов.
- доля влияния фактора х4 в суммарном влиянии всех
факторов.
Средняя относительная ошибка: 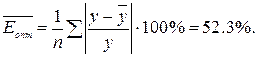 Т.е. в среднем
расчетные значения y отличаются от фактических значений на 52,3%.
Т.е. в среднем
расчетные значения y отличаются от фактических значений на 52,3%.
Построим
уравнение множественной регрессии в линейной форме со значимым фактором (Х3)-
у=а0+а3Х3.
Используем
инструмент регрессии.

Рис. 10
Рис. 11.
Получаем:
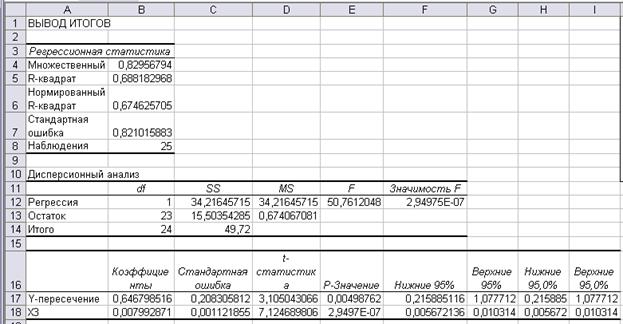
Рис. 12.

Рис. 13.
Получили
уравнение регрессии от значимого фактора Х3:
у=0,646798516+0,007992871*
Х3
Оценим с
помощью t-критерия
Стьюдента статистическую значимость коэффициентов уравнения множественной
регрессии.
Табличное
значение при 5% уровне значимости и степенях свободы 25-1-1=23 составляет
2,069.
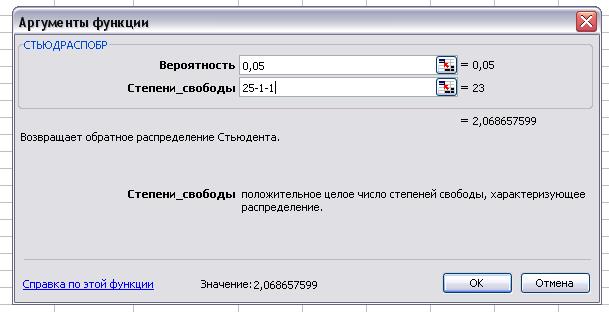
Рис. 14.
Т.к. расчетные
значения: 7,124689806 >2.069; то коэффициент а3 значим (Х3
значимо воздействует на формирование цены квартиры).
3,105043066>2.069; то коэффициент а0
значим.
Проверку
значимости уравнения регрессии произведем на основе вычисления F-критерия Фишера.
Доверительная вероятность p=0.95;
v1=k=1;
v2=n-k-1=25-1-1=23; Fтабл= 4,28;
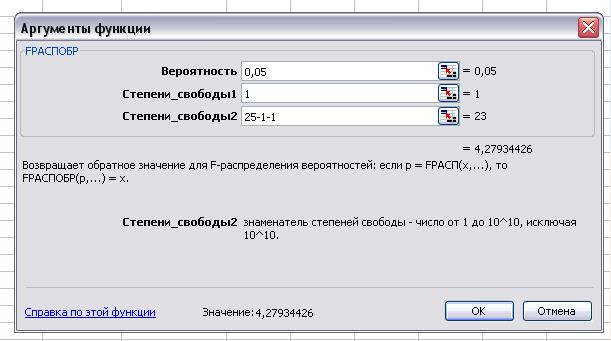
Рис. 15.
 . Поскольку Fрасч>Fтабл, то
уравнение регрессии следует считать адекватным.
. Поскольку Fрасч>Fтабл, то
уравнение регрессии следует считать адекватным.
Значение
коэффициента детерминации R2=
0,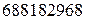 . Он показывает долю вариации результативного признака под
воздействием изучаемых факторов. Следовательно, около 68,8% вариации зависимой
переменной учтено в модели обусловлено влиянием факторов.
. Он показывает долю вариации результативного признака под
воздействием изучаемых факторов. Следовательно, около 68,8% вариации зависимой
переменной учтено в модели обусловлено влиянием факторов.
Проверку
независимости проведем с помощью d-критерия Дарбина-Уотсона.
Таблица.
3.
|
|
y
|
y^
|
e=y-y^
|
et-et-1
|
(et-et-1)2
|
e2
|
|
|
0,9
|
1.44
|
-0.54
|
-
|
|
0.29
|
|
|
1,7
|
1.58
|
0.12
|
0.65
|
0.43
|
0.01
|
|
|
0,7
|
1.18
|
-0.48
|
-0.60
|
0.36
|
0.23
|
|
|
1,7
|
1.37
|
0.33
|
0.82
|
0.67
|
0.11
|
|
|
2,6
|
1.74
|
0.86
|
0.53
|
0.28
|
0.75
|
|
|
1,3
|
1.09
|
0.21
|
-0.65
|
0.42
|
0.05
|
|
|
4,1
|
3.60
|
0.50
|
0.29
|
0.08
|
0.25
|
|
|
1,6
|
1.55
|
0.05
|
-0.45
|
0.20
|
0.00
|
|
|
6,9
|
6.67
|
0.23
|
0.18
|
0.03
|
0.06
|
|
|
0,4
|
0.83
|
-0.43
|
-0.67
|
0.45
|
0.19
|
|
|
1,3
|
1.01
|
0.29
|
0.72
|
0.52
|
0.08
|
|
|
1,9
|
1.12
|
0.78
|
0.49
|
0.24
|
0.61
|
|
|
1,9
|
0.80
|
1.10
|
0.32
|
0.10
|
1.21
|
|
|
1,4
|
2.34
|
-0.94
|
-2.04
|
4.16
|
0.88
|
|
|
0,4
|
1.48
|
-1.08
|
-0.14
|
0.02
|
1.17
|
|
|
0,8
|
0.89
|
-0.09
|
0.99
|
0.98
|
0.01
|
|
|
1,8
|
1.65
|
0.15
|
0.24
|
0.06
|
0.02
|
|
|
0,9
|
1.26
|
-0.36
|
-0.50
|
0.25
|
0.13
|
|
|
1,1
|
1.37
|
-0.27
|
0.09
|
0.01
|
0.07
|
|
|
1,9
|
0.94
|
0.96
|
1.22
|
1.49
|
0.91
|
|
|
-0,9
|
1.50
|
-2.40
|
-3.35
|
11.25
|
5.75
|
|
|
1,3
|
1.03
|
0.27
|
2.67
|
7.13
|
0.07
|
|
|
2
|
0.98
|
1.02
|
0.75
|
0.56
|
1.04
|
|
|
0,6
|
0.59
|
0.01
|
-1.01
|
1.01
|
0.00
|
|
|
0,7
|
1.00
|
-0.30
|
-0.31
|
0.10
|
1.09
|
|
Итого:
|
39
|
39
|
0.00
|
|
30.80
|
13.99
|
d=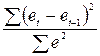 =
=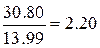 , т.к. 2,20>2, то имеет место отрицательная
автокорреляция.
, т.к. 2,20>2, то имеет место отрицательная
автокорреляция.
d` = 4-2,20=1,8 В качестве
критических табличных уровней при n=25 и 1 объясняющего фактора при уровне значимости в 5% возьмем
величины d1=1.29
и d2=1,45.
Т.к. 1,45<1,8<2, то свойство независимости выполняется.
упрогнозное=0,646798516+0,007992871*745*0,8=5,41
млрд. долл.
Найдем верхнюю
у^прог+ 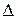 границу прогноза, где
границу прогноза, где
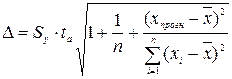 ;
;
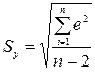 .
.
Получаем: 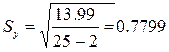 ;
;
ta=0,05; k=25-2= 2.069 и 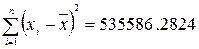 , тогда
, тогда
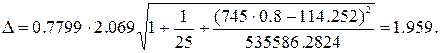
Нижняя
граница: 5,41-1,959=3,451.
Верхняя
граница: 5,41+1,959=7,369.