Всероссийский заочный финансово-экономический институт

Ярославский филиал

Аудиторная работа

по Эконометрике

Вариант 13

Выполнили:

г. Ярославль

2006

Условие задачи:

По данным о потребительских расходах на товар (продукты питания, одежду и обувь, жилье, книги, образование – у) и располагаемых (совокупных) личных доходах (х), с использованием приложения EXCEL:

1.     Построить модель линейной парной регрессии.

2.     Оценить качество полученной модели.

3.     Построить точечный и интервальный прогноз на один шаг.

Исходные данные:

х	3544.8	3576	3668.8	3905.3	4009.3	4135.8	4170.8	4316.3	4393.2
у	497.8	500.9	511.8	531.8	551.1	565.5	583.4	600.9	614.6

Задания по аудиторной работе:

1.           Построить модель линейной парной регрессии:

1.1.   Построить линейную регрессию вида у_х= а + b*x. Дать интерпретацию коэффициента регрессии b.

1.2.   Построить линейную регрессию вида у_t = а₀ + b₀* t, где t – фактор времени t = n;  n – номер наблюдения.   Дать интерпретацию коэффициента регрессии b₀.

1.3.    Определить значения коэффициентов корреляции r_yx и r_yt    и соответственно коэффициентов детерминации R² _yx   и   R² _yt.

1.4.   Сравнить полученные в пунктах 1.1. и 1.2. модели регрессии по значениям коэффициентов детерминации R². Сделать вывод.

2.           Оценить качество регрессионной модели вида у_х = а + b*x, полученной  в пункте 1.1.

2.1.   Оценить статистическую значимость уравнения  линейной парной регрессии по F – критерию Фишера.

2.2.   Оценить статистическую значимость коэффициентов уравнения регрессии a  и  b, вычислив значения:

                -  t – критерия Стьюдента;

                -  доверительных интервалов для коэффициентов   регрессии a  и  b при 5% уровне значимости, α=5%.

2.3. Вычислить среднюю ошибку аппроксимации .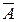

2.4. По показателям адекватности и точности сделать выводы о качестве полученной  модели  и её    пригодности для прогнозирования.

3.  Выполнить прогнозирование на один шаг вперед, используя полученную в п. 1.1. модель вида у_х = а + b*x  .

 3.1. Рассчитать значение точечного прогноза у_пр.

  3.1.1. Рассчитать прогнозное значение фактора х_пр.

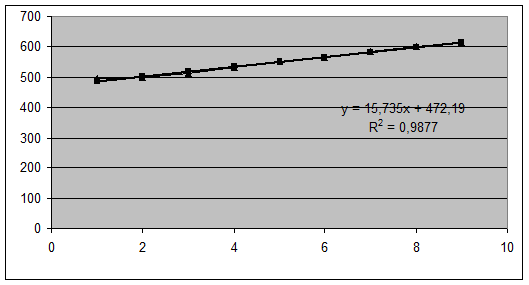
 a) Построить временной ряд х_t по фактическим данным, используя встроенные функции «Мастер диаграмм» и «График».

 б) Аппроксимировать полученный временной ряд  функциями:

          - линейной;

        -  степенной;

      - полиномиальной (второй степени),

используя встроенные функции EXCEL: «Диаграмма», «Добавить линию тренда»,  «Линейная», «Степенная», «Полиномиаль­ная» (второй степени), с выводом вида уравнения регрессия на диаграмме и значения коэффициента детерминации R².

 в) Выбрать по максимальному значению коэффициента детерминации R² функцию, наилучшим образом аппроксимирующую исходные данные х_t, и по ней рассчитать прогнозное значение фактора х_пр=х_t(n+1), где n -  последний номер наблюдений.

 3.1.2. Рассчитать значение точечного прогноза у_пр по уравнению у_х = а + b*x  (см. п. 1.1.), при значении х=х_пр.

3.2. Рассчитать значения интервального прогноза для уровня значимости 5%,   α=5%.

4. На рисунке в координатах Х0У привести:

         - исходные данные (х_i; у_i);

         - график линейной регрессии вида у_х = а + b*x, полученной в  п. 1.1.;

         - значение точечного   прогноза на один шаг вперед и соответствующие значения интервального прогноза.

5. Сделать общий вывод по результатам исследования.

Решение:

1. Построим линейные модели парной регрессии.

1.1. Линейная регрессия вида у_х= а + b*x

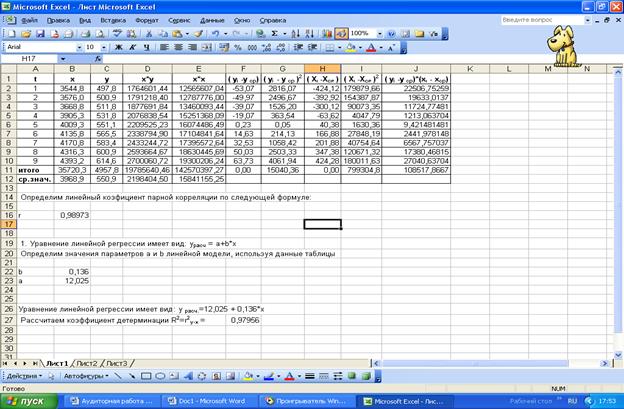
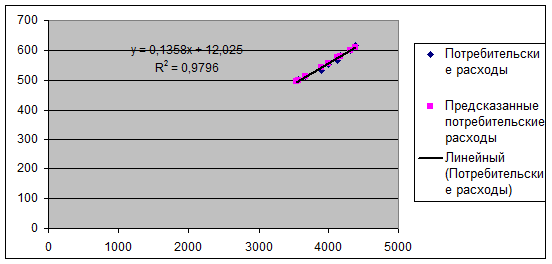
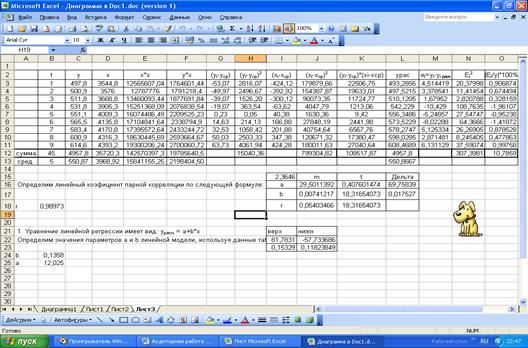
Определим значения параметров a и b линейной модели:

Уравнение линейной регрессии имеет вид:

С увеличением располагаемых личных доходов, потребительские расходы на товары увеличатся в среднем на 13,6.

1.2. Линейная регрессия вида у_t = а₀ + b₀* t

Определим значения параметров a₀ и b₀ линейной модели:

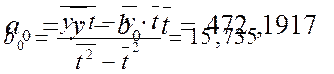Уравнение линейной регрессии имеет вид:

С увеличением времени, потребительские расходы на товары увеличатся в среднем на 1573,5.

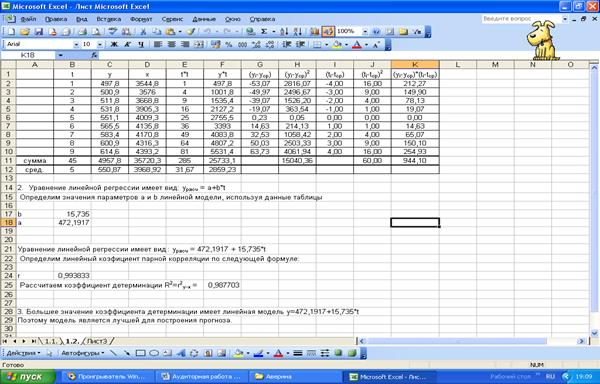
1.3. Определим линейные коэффициенты парной корреляции r_yx и r_yt:

Определим коэффициенты детерминации R² _yx   и   R² _yt    :

R² =r²

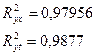
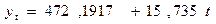1.4. Большее значение коэффициента детерминации имеет линейная модель

Поэтому модель более точная и лучше по качеству для построения прогноза.

2. Оценка качества модели  у_х = а + b*x

2.1. Проверку значимости произведем на основе вычислений F-критерия Фишера.

Т. к. F_рас>F_табл, уравнение регрессии следует признать адекватным.

2.2. Выдвигаем гипотезу H₀ о статистически не значимом отличии показателей от нуля: a=b=r_xy=0.

t_{табл(0,05;7)}=2,3646

Определим случайные ошибки m_a, m_b, m_rxy:

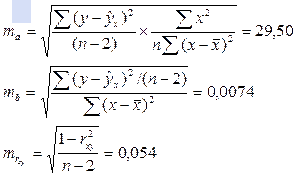
Тогда:

Сравнивая фактические значения t с табличным можно сделать вывод о том, что параметры b и r не случайно отличаются от нуля и являются статистически значимыми,  параметр а статистически незначим (t_a<t_табл).

Рассчитаем доверительный интервал для a и b. Для этого определим предельную ошибку для каждого показателя:

Доверительные интервалы:

 

Анализ верхней и нижней границ доверительных интервалов  приводит к выводу о том, что с вероятностью 0,95 параметр a  принимается нулевым и является статистически незначимым, а параметр b не принимает нулевых значений и не является статистически незначимым.

2.3. Качество модели определяет средняя ошибка аппроксимации:

Ошибка аппроксимации не превышает 5%, значит модель является очень точной.

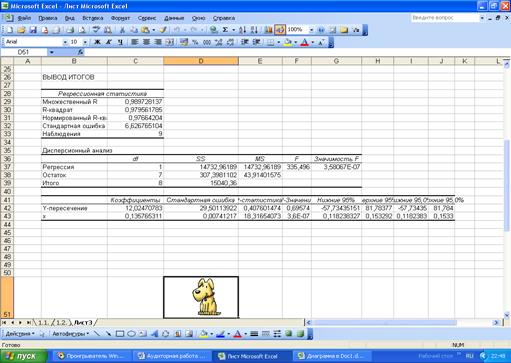
2.4. Модель имеет достаточно большое значение критерия Фишера и коэффициента детерминации. Модель достаточно точная, её можно взять для построения прогноза.

3. Построение прогноза.

3.1. Рассчитаем значение точечного прогноза у_пр.

Строим временной ряд x_t:

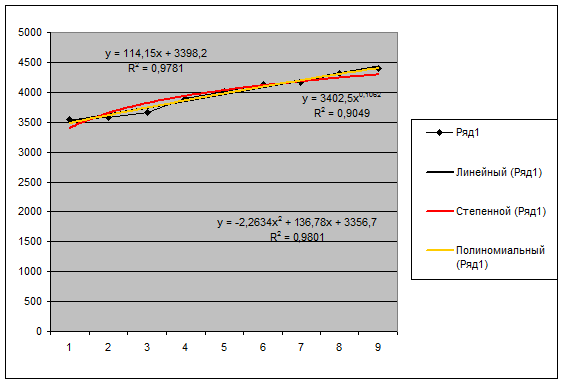
Функция наилучшим образом аппроксимирующая исходные данные  x_t

х_t=-2,2634t²+136,78t+3356,7

х_пр=х_t(10)=-2,2634*10²+136,78*10+3356,7=4498,16

у_пр=12,025+0,136*х_пр=12,025+0,136*4498,16=623,77

3.2. Рассчитаем значения интервального прогноза для уровня значимости 5%,   α=5%.

Ошибка прогноза составит:

t_табл(0,05;7)=2,3646

Х прог	Хпрог - Хсред	(Хпрог - Хсред)2	Упрог	Sу расч	Дельта	Верхняя граница	Нижняя граница
4498,16	529,26	280116,14	623,77	6,6268	18,9367	642,7067	604,8333

Выполненный прогноз оказался надежным, и достаточно точным, так как диапазон верхней и нижней границ доверительного интервала составляет 1,06 раза.