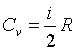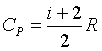Введение

    Еще 200 лет назад законы природы  представлялись как разрозненные правила, выведенные из опыта и почти не связанные между собой. Многие физики пытались  превратить открытые законы, теории,  правила, эффекты и явления  в строгую науку, но сделать это было не легко .Одни считали, что все явления следует объяснять, опираясь на механику, и что все в природе состоит из мельчайших частиц: атомов, монад, корпускул. Другие настаивали на том, что первичным в природе являются жидкости  и что Вселенная  заполнена всепроникающей субстанцией – эфиром. Тепло также считали одной из жидкостей, и теория теплорода была весьма популярной  основой учения о тепле. Истина рождалась в трудной борьбе  идей и мнений.

     История о том, как человек обнаруживает законы природы, как создается величественное здание современного естествознания, -  история поучительная и интересная.

 

 

1.Зарождение и развитие термометрии

    С глубокой древности понятие температуры  в  ощущении человека  связывалось со степенью нагретости тел. Слово температура («лат.temperatura -  смесь, правильное соотношение) принадлежит древнегреческим врачам, которые, смешивая между собой различные лекарства, добивались желаемого результата: согревать или охлаждать тело. Уже тогда в практической деятельности встал вопрос: до какой степени можно согревать или охлаждать? Великий врач Гален (11 в.) предложил все лекарства  классифицировать по степени воздействия на организм человека и назвал эти степени градусами («лаt. gradus -  степень, ступень, шаг). Было четыре главных градуса: градус тепла, градус холода, градус влажности и градус сухости.  Каждый из этих градусов разбивался еще на три – итого была 12-градусная шкала. Таким образом, понятие температура стало определять  величину теплового воздействия на организм в градусах. Однако численную связь между температурой и градусами  древние врачи  установить не могли.

     Новый подход к  изучению тепловых явлений наметился в ХYII веке. Но изучать их было невозможно без точных измерений  температуры тел.

      Первый прибор для измерения температуры сделал Галилео  Галилей (1564-1642) в 1600 году. Он состоял из стеклянного шара, наполненного воздухом, от которого отходила трубка, частично заполненная водой, которая заканчивалась в сосуде, также  наполненном водой. Когда воздух в шаре расширялся или сжимался, уровень воды в трубке изменялся. Этот прибор  измерял довольно неопределенную величину, но все же он позволял сравнивать температуру разных тел  в одно и то же время и в одном и том же месте.

     За термоскопом Галилея последовали многочисленные приборы  флорентийских  академиков. Академик Каспар Энс  в 1636 г. опубликовал книгу «Математический чудотворец», в которой впервые  употребил слово термометр («гр. thermos – теплый + metron – мера) и описал 8-градусную шкалу.

    Действие всех термометров было основано на изменении объема   тел при нагревании. Ими стали измерять давление, влажность и температуру воздуха. Их заполняли уже не водой, а спиртом и наносили деления расплавленной эмалью. Ими  можно было измерять температуру  с точностью до 1⁰.

     Сравнительно хороший термометр сделал изобретатель-самоучка бургомистр Магдебурга  Отто фон Герике (1602-1686). Его прибор состоял из латунного шара, заполненного воздухом, и изогнутой в форме буквы  U трубки со спиртом. Температуру указывал деревянный человечек, который с помощью шнура и блока  был связан с латунной запаянной коробочкой, плававшей в  открытом конце прибора. Для того, чтобы измерять температуру воздуха в каких-то абсолютных единицах, нужно было избрать за начало шкалы какую-то точку. Герике избрал точку, около которой останавливался его человечек при первых заморозках. Это было наивно, но это был первый шаг.

    С  к.XYII в. над созданием температурной шкалы трудятся многие ученые. Понадобилось немало времени, чтобы  придти к мысли о постоянных точках на шкале температур.

    Исаак Ньютон  (1643-1727) опорную точку отсчета – «нуль» помещает в точке замерзания воды. В своей работе «О шкале степеней тепла и холода» он описывает 12-градусную шкалу: 12⁰ отвечали температуре тела здорового человека.

    Нидерландский ученый Христиан Гюйгенс (18629-1695) предложил  избрать в качестве опорной точки  термометра точку кипения воды.

   Парижский академик  Гийом  Амонтан в 1703 г. ввел две постоянные точки отсчета – точку кипения воды и  «абсолютный нуль», при котором «воздух теряет свою упругость». Конечно, здесь Амонтан ошибся (по  современной шкале ~ на 240⁰ ниже нуля), но все же это было уже достижением. В термометрах Амонтана  измерялось не увеличение объема воздуха при нагревании, а изменение его давления, для чего воздух запирался столбиком ртути. Запаяв его, Амонтан исключил зависимость термометра  от давления атмосферы. Его термометр стал физическим инструментом.

    Голландский стеклодув  Даниель Фаренгейт (1686-1736) начинает изготавливать спиртовые, а затем и ртутные термометры, которые согласовывались между собой. Самую низкую температуру он имитировал смесью льда, поваренной соли и нашатыря –«нулевая точка». Вторую «точку замерзания воды» он получал, погружая термометр в смесь льда и воды, и считал её за 32⁰, так как все  расстояние между этими точками делил на 32 части. Свою шкалу он проверял, измеряя температуру человека, и новая точка попадала на 98⁰.Четвертой опорной точкой  он избрал «точку кипения воды», которая попадала на 212⁰. Термометры Фаренгейта прославились своей точностью. Такой шкалой и сегодня иногда пользуются в Англии и США.

    Французский естествоиспытатель  Рене Реомюр (1681 – 1757)  в 1740г. построил свою шкалу на точках замерзания воды – 0⁰ и её кипения – 80⁰. Его  термометры  широко распространились  сначала во Франции, а позже и в России. Их стали вешать в домах и на улицах. Ими широко пользовались вплоть до 30-ых годов  Х1Х века. 

    Шведский астроном и физик Андерс Цельсий (1701-1744) ,тщательно исследовавший термометр  Реомюра, установил, что  точка кипения воды зависит от давления. В итоге появился новый термометр. Точку плавления льда Цельсий принял за 100⁰, а точку кипения воды  при давлении 25 дюймов 3 линии ртутного столба – за 0⁰. Таким образом, вся шкала делилась на 100⁰.

     Шведский ботаник Карл Линней (1707-1778) посчитал более удобным для пользования перевернутую шкалу: 0⁰ -температура плавления льда, 100⁰ - температура кипения воды. Перевернутая  стоградусная шкала Цельсия нашла широкое применение во всем мире.

     Петербургские академики внесли в термометрию свои идеи. Так, академик Ж.Н. Делиль (1688-1768) предложил шкалу, в которой  точка плавления льда принималась за 150⁰, а кипения воды – за 0⁰. Российский  академик  М.В. Ломоносов (1711-1765) применял в своих исследованиях сконструированный им  термометр со шкалой, обратной делилевской.

       Во всех приборах, которые были придуманы  в ХYIII в., измерение температуры сводилось к  измерению длины столбика воды, спирта или ртути. Термометры работали только в ограниченном интервале температур. Перед учеными стояли две главные задачи: во-первых, установить такие опорные точки, которым бы соответствовали  другие выбранные точки, в частности – начало отсчета – и, во-вторых, придумать такое определение  градуса, которое бы не зависело от  конкретного термометра и могло бы быть использовано  для построения шкалы в любом месте и в любое время.

     В 1802 г. французские  физики Джон Дальтон(1766-1844) и Жозеф  Гей-Люссак (1778-1850) сформулировали закон: объём идеального газа  при постоянном давлении меняется линейно с изменением температуры: , где и   - объем газа при температуре t⁰ и 0⁰С соответственно; – температурный коэффициент объемного расширения.

     Газовые термометры  используются как эталонные почти для всех температур, достижимых в лабораториях.  Однако и  газовый термометр был далек от идеала:  реальные газы не всегда  похожи  на идеальный. Перед физиками стояла задача: создать такой термометр, который не зависел бы от  используемого в нем  вещества.

    В ср. Х1Х в. осмыслением понятия температуры и устройством термометра занялся  английский  физик Кельвин (Уильям Томсон) (1824-1907). К этому времени французский военный инженер Сади Карно (1796-1832) теоретически доказал, что  КПД тепловой машины  зависит только от температуры нагревателя и холодильника. Кельвин посмотрел на цикл Карно как на устройство, которое позволяет  измерять отношение  двух температур  Т₁  и Т₂:  . На нем и была построена шкала Кельвина, названная абсолютной шкалой температур. В ней за нулевое значение принят  «абсолютный нуль», а единица температуры принимается в точности равной 1⁰С. Оказалось, что шкала Кельвина  просто сдвинута относительно шкалы  Цельсия.  Чтобы не путать шкалы для абсолютной температуры введена специальная единица  измерения -  кельвин. Величина сдвига  к абсолютному нулю  была рассчитана и составила 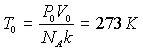. Таким  образом,  Т⁰ К = Т⁰ С +273.   

     После Кельвина вопрос о температуре с теоретической точки зрения стал вполне ясным. Однако нужен был эталонный термометр для практических  измерений. Чтобы измерять абсолютную температуру нужно было выбрать некоторую стандартную систему, находящуюся в стандартном состоянии, и приписать ей некоторое абсолютное значение температуры, т.е. определить исходные точки опоры.

    В 1954 г. по международному соглашению в качестве стандартной системы выбрана вода, а стандартное состояние – равновесие состояния воды, льда и пара. Такой выбор удобен тем, что  существует одно-единственное значение  давления  p = 609 Па  и температуры, при которых три фазы воды могут сосуществовать, находясь в равновесии. Это состояние называется  тройной точкой воды. В этом состоянии абсолютная температура  Т  =  273,16 К = 0,01⁰ С. Теперь численное значение абсолютной температуры  Т   любой системы  можно получить сравнением с температурой  Т_T   в тройной точке.

    Сегодня обсуждается вопрос о замене  тройной точки воды тройной точкой галлия (29,7740⁰ С), которая легче и точнее воспроизводится.

     Шкала с одной опорной точкой называется термодинамической. Ею пользуются в  специальных хорошо оборудованных лабораториях. Для практических целей  и в обычных лабораториях удобнее пользоваться принятой в 1968 г. международной практической температурной шкалой  -  МПТШ 68. В ней Т_K  = 100⁰.              

              Современная наука позволяет измерять температуру с помощью электромагнетизма. Еще в 1821г. немецкий физик Т.И. Зеебек (1770-1831) открыл  первый термоэлектрический эффект, состоящий в следующем: если  температуры Т₁  и Т₂   спаев 1 и 2  двух разнородных металлов, образующих замкнутую цепь, неодинаковы, то в ней будет циркулировать электрический ток. Это явление сегодня  используется для  измерения (особенно дистанционного) температур - термопары.

      Для  измерения температуры, используют также т. н.  белый шум, сопутствующий любому  электромагнитному  явлению. Из-за тепловых  эффектов на ток, несущий полезную информацию, накладываются случайные переменные токи, которые воспринимаются микрофоном и создают шумовой фон. Такой шум можно представить спектром зависимости интенсивности сигнала от частоты. Если этот спектр отвечает хаотическим помехам, то шум называется белым -  он не несет никакой информации, кроме информации о температуре. Выбирая разные явления, можно найти  идеальный (теоретически) метод измерения температуры. С помощью этого метода удалось измерить температуру плавления гелия  по абсолютной шкале с точностью до пяти знаков

      С целью измерения температур  используют и  такое явление, как флуктуация, т. е. временное случайное отклонение от равномерного распределения молекул в газе или жидкости, возникающие в результате теплового движения. Величину флуктуаций тока  вычислил еще в 1927г.  Найквист: .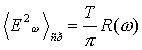

Эта формула также  может служить основой для измерения температуры.

              

Смысл понятия температуры

    Судьба распорядилась так, что,  научившись измерять температуру, физики долгое время не могли разобраться, что же они измеряют, какая разница между температурой и теплом?

     Экспериментальные исследования свойств газов показали, что для любых газов, находящихся в состоянии теплового равновесия, отношение произведения давления  газа на его обьём к числу молекул оказывается одинаковым: 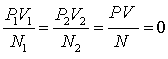. Это позволило  0 принять в качестве естественной меры температуры. Так как 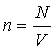   и   (где    – средняя кинетическая энергия поступательного  движения молекул идеального газа), то средняя кинетическая энергия молекул  любых газов, находящихся  в тепловом равновесии, одинакова:  . Отсюда определение температуры: температура -  это характеристика системы, находящейся в состоянии теплового равновесия.   

    Здесь физики столкнулись с новыми проблемами: необходимо было разделить  понятия  «тепло» и «температура». Когда нагревают тело, темпера   тура его повышается. Когда  тепло перетекает от одного тела к другому, температура одного тела падает, а другого повышается. Тепло всегда течет так, чтобы температуры выравнивались, и чтобы система переходила в состояние теплового  равновесия. Когда две системы приходят в состояние теплового равновесия, поток энергии, идущий от более нагретой системы к менее нагретой,  прекращается, т.е. обращается в 0. Каждая система содержит одинаковое количество энергии и имеет одинаковую температуру.

       Английский физик Гемфри Дэви (1778 - 1829) экспериментально установил, что теплота – это форма кинетической энергии.

       Его соотечественник физик Ватерстон   сделал вывод о том, что  температура -  мера кинетической энергии молекул, что придало понятию температуры физический смысл, хотя бы температуре одноатомного идеального газа. Он   также обосновал идею о том, что давление газа на стенки сосуда можно объяснить ударами атомов.

      Количественное определение параметра температуры  теоретически вывел австрийский физик Людвиг Больцман (1844-1906). Он доказал, что у каждой системы одинакова средняя  кинетическая энергия поступательного движения молекулы  - Е. Эта  величина стала впоследствии называться  постоянной Больцмана: k = 1,38  10 Дж / К. Таким образом, температура – мера средней кинетической энергии поступательного движения молекулы  ,  которая может одновременно вращаться, а ее атомы  колебаться относительно центра масс.

        Английский физик Джеймс Максвелл (1831-1879) установил распределение молекул идеального газа по скоростям их теплового движения в макроскопических системах, находящихся в состоянии теплового равновесия. Он же  вывел  окончательную формулу температуры,  которая позволила связать ее с энергией:

        - где p – давление газа,  n – количество молекул в 1 см, m – масса молекулы,  – среднее арифметическое квадратов скоростей молекул. Заменив  (уравнение Клайперона - Менделеева),   (число  Авогардо) и обозначив    (постоянная Больцмана) получим: .

   Таким образом, температуру стали измерять по формуле:  .

    Эта физическая величина  названа абсолютной температурой. 

    Абсолютным нулем температуры  считается  предельная температура, при которой  давление идеального газа  обращается в нуль при фиксированном объеме или  объем идеального газа стремится к нулю при неизменном  давлении: Тmin = 0,  T > 0 (всегда!). 

      Температура – это  физический  макропараметр, одинаковый для всех частей системы тел, находящихся в состоянии теплового равновесия, и не зависящий от числа молекул  в каждой такой части.

     Температура – величина статистическая, понятие  температуры одной или нескольких молекул лишено смысла.

       Температура  - величина не  аддитивная, т.е. температура всего тела не равна сумме температур его частей. 

        Вместе с тем, понятие температуры применимо не только к телам, состоящих из атомов, молекул, ионов, но и к электронному газу, электромагнитному излучению (фотонному газу), атомным ядрам и т.д. 

 

                  Смысл понятий  тепла и теплоемкости

      Античные ученые сопоставляли с теплом и холодом свойства притяжения и отталкивания.

      Смысл этих понятий менялся по мере того, как ученые все лучше и лучше понимали, что же происходит, когда тело нагревается или охлаждается. 

      Настоящая история науки о тепле начинается с  Галилея.  Он был одним  из первых, кто высказал мысль о механической природе тепла, приводя доказательство нагревания твердых тел при трении.

     Философ  Френсис Бэкон (1561-1626), систематизируя данные об источниках тепла, сделал вывод, что теплота есть «расширяющееся движение». Утверждение о том, что тепло является формой движения малых частиц, принадлежит многим ученым ХYII в.: философу Рене Декарту (1596-1650), физику Роберту  Гуку (1635-1703), Исааку Ньютону (1643-1727) и др.  Но эти представления возникали на очень скудной фактической основе.

        Тщательная разработка этой идеи принадлежит русскому ученому  М. В. Ломоносову (1711-1765).  В труде «Размышления о причине теплоты и холода» (1744 г.) он пишет, что теплота – это форма движения  «нечувствительных частиц». Характер этих движений  может быть  поступательным, колебательным и вращательным. Причиной тепла  Ломоносов считает вращательное движение: «частицы горячих тел вращаются быстрее, более холодных  -  медленнее». Однако, современники не пошли по пути  Ломоносова: в теории тепла господствовал теплород.

      Большинство ученых считало тепло жидкостью, перетекающей из одного тела в другое. Жидкость эта была названа теплородом, который считался сродни флогистону -  «огненной материи», выделявшейся из горючих веществ при их горении. Весь ХYIII  век  прошел в борьбе между сторонниками и противниками  теплородной теории тепла. В к. ХYIII в. ошибочную флогистонную теорию сменила кислородная теория горения, но теория теплорода продолжала существование и объяснять  многие явления.

      Но теории и даже эксперименты остаются бесплодными, пока они не  переводятся на язык цифр и формул. Если с понятием температуры было все более-менее ясно, то с понятием теплоты разобраться оказалось труднее.

     У истоков калориметрии  стоял петербургский академик  Г. В. Рихман (1711-1753). Он еще не владел понятием количества теплоты, но логически обосновал совершенно правильную формулу: ,

где  a , b , c  -  массы, а    m , n , o – соответствующие теплоты, т.е. “сумма всех жидких масс, по которой равномерно распределяется теплота отдельных масс относится к сумме всех произведений каждой массы на её теплоту так же, как единица к теплоте смеси”.

       Дело Рихмана продолжили  шведский академик Иоган Вильке(1732-1796) и шотландский химик Джозеф Блэк (1728-1799). Исследуя теплоту смеси воды и снега, Вильке пришел к понятию скрытой теплоты, которая куда-то исчезает. Вскоре Блэк приходит к понятию скрытой теплоты плавления, затем – испарения. В 1777г. французы Антуан Лавуазье(1743-1794) и Пьер Лаплас (1749-1827), построив ледяной калориметр, стали определять  количества тепла, необходимые для нагревания различных тел  до определенной температуры.

      Английский физик Румфорд (Бенджамин Томсон) (1753-1814) не мог понять,  откуда возникает тепло при сверлении металла. Объяснение напрашивалось одно: природа тепла связана с движением, а именно с трением.  И он предположил, что теплота – это некое свойство самого вещества, а не что-то добавляемое к нему.

     Опыты Румфорда, а затем  и Дэви доказывали волновую природу теплоты. Английский ученый Томас Юнг (1773-1829)  утверждал, что теплота по своей природе не отличается от света, только колебания волн несколько медленнее.

       С формированием молекулярно - кинетической теории  понятие тепла  и температуры  получило прочную основу – фундаментальный закон природы, который утверждает, что любая замкнутая система макроскопических тел самопроизвольно переходит в состояние теплового равновесия и остается в таком  состоянии сколь угодно долго.

       Первым строгим результатом  в теории тепла стала теорема                                                                французского инженера Сади Карно(1796-1832).  Он понял  как тепло превращается в работу. Карно доказал только одну теорему, из которой следовала простая формула: . Но за этой формулой оказалась скрыта целая наука.

       В развитии физики есть моменты, когда новая идея изменяет весь дальнейший ход истории. Такую идею  в 1пол. Х1Х в. выдвинул  немецкий врач Роберт Майер (1814- 1878). Используя  соотношение между теплоемкостями газов при постоянном давлении и постоянном объеме, он приходит к выводу, что «опусканию единицы веса с высоты 365 м соответствует нагревание равного веса воды  от 0 до 1⁰». Майер указал совершенно правильный метод определения механического эквивалента тепла: уравнение Майера, устанавливающее связь  между молярными теплоемкостями газа:   Cp = Cv + R , где  R –универсальная газовая постоянная (R= 8,32 Дж / моль К) или между удельными теплоемкостями : Cp = Cv + R / M.

       В  1843 г. английский физик Джеймс  Джоуль (1818-1889) совершил важнейшее открытие в учении о теплоте. С помощью разработанного им прибора (нагревая воду в калориметре вращением колеса с лопастями) он доказал эквивалентность механической и тепловой энергии: «Количество тепла, способное увеличить температуру одного фунта воды на один градус Фаренгейта, равно и может быть превращено в механическую силу, которая в состоянии поднять  838 фунтов на высоту один фут» (1фунт =454г,  1фут =30,5 см). Таким образом, была доказана связь теплоты с энергией и работой.                     

       Долгое время перед учеными стоял вопрос:  каким образом связано количество тепла с температурой?

     Немецкий физик Рудольф Клаузиус (1822-1888)   приходит к выводу, что всякое тело имеет внутреннюю энергию, которую можно увеличивать двумя путями: производя над телом работу или подводя к телу тепло:  . Таким образом,  он  открыл и теоретически доказал, что у температуры есть связанная с ней величина – энтропия (« гр. en – в, внутри  +  thrope – превращение, поворот), увеличение которой, умноженное на температуру, определяет количество тепла, полученного телом. Глубоко вникнув в исследования Карно, Клаузиус пришел к выводу, что в обратимом процессе тепловой машины сохраняется не количество тепла, содержащегося в теле, а совсем другая величина. Эта величина (S), подобно  энергии,  давлению, температуре характеризует состояние газа. Когда к газу подводится небольшая порция тепла  , то  S  возрастает на величину равную .

     После открытия энтропии стало, наконец, ясно, почему было так трудно понять связь между теплом и температурой. Оказалось, что нельзя говорить о количестве тепла, заключенном в теле. Это понятие просто не имеет смысла. Тепло может переходить в работу, создаваться при трении, передаваться от тела к телу – но не сохраняться.  Точный смысл имеет понятие количество тепла, переданного телу или отнятого у тела  (иначе количество внутренней энергии, переданной в процессе теплообмена от одного тела к другому без совершения работы).

       В 1803 г. Блэк  разграничил понятия температуры и количества тепла. Для определения количества тепла он вводит термин «теплоемкость». Экспериментально было доказано, что получая одно и то же количество  тепла , одинаковые по массе , объему, термодинамическому состоянию, но разные по химическому составу тела, нагреваются не одинаково. Величину, характеризующую способность тела изменять свою температуру при сообщении ему определенного количества теплоты, стали называть теплоемкостью  (С). Сравнивали теплоемкости разных тел по формуле: .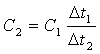

    Отношение изменений температуры тел не меняется, если сообщать телам иное количество теплоты, но по-прежнему одинаковое для обоих тел. Это означало, что теплоемкость не зависит от количества теплоты, сообщаемой  извне телу, а является характеристикой  его тепловых свойств. 

    Теплоемкостью тела (С) стали называть количество теплоты, которое необходимо передать телу (или от тела), чтобы изменить его температуру на один градус:  .

    Удельной теплоемкостью  (с) стали называть количество теплоты, которое необходимо передать однородному телу  массой  1 кг, чтобы нагреть его на 1⁰  C.

     Молярной теплоемкостью ( ) называется  теплоемкость одного моля вещества: , где  М – молярная масса.

     Итак, для каждого  тела теплоемкость имеет свое значение, причем значение это не постоянное, а зависит от условий, в которых происходит изменение температуры тела.

 Значения теплоемкости по видам процесса:

процесс	теплоёмкость
Изотермический
Изохорный
Изобарный

 

   Теплоемкость вещества  зависит от его агрегатного состояния и сильно изменяется при фазовых превращениях. Например, удельная теплоемкость воды  при 20⁰С – 4200 Дж/кгК, льда при 0⁰С - 2100Дж/кгК, а водяного пара при 100 ⁰С - около 1500 Дж/кг К.

 Усиленно развивается теория теплоемкости газов. При обычных температурах нагревание идеального газа приводит к изменению энергии поступательного и вращательного  движения молекул газа.

 

газ			i
одноатомный			3
двухатомный	5
многоатомный	6

 

      Исследования  французских физиков  Пьера  Дюлонга (1785-1838) и Алексиса  Пти (1791-1820) ,  а также  английского ботаника  Роберта  Броуна (1773-1858) , открывшего  «броуновское движение», убедили физиков в том, что теплота – форма кинетической  энергии.   На основе молекулярно-кинетической теории  количеством теплоты (Q ) стали называть энергию, переданную телу в результате теплообмена.

В 1852 г. была введена единица количества теплоты ( количество тепла, необходимое для нагревания 1 г  воды  на 1⁰ С),  позже названная «калорией»(1 кал.=4,184 +- 0,0026 Дж).

       Еще в  1819 г. Дюлонг и Пти собрали достаточно данных, чтобы сделать общий вывод:  удельные теплоемкости химических элементов – не случайные величины, а связанны простым образом с атомными весами элементов. Эмпирически  и  экспериментально они установили закон, согласно которому для всех элементов  в кристаллическом состоянии теплоемкость моля (атомов) вещества не зависит от температуры и приблизительно равна  3 R , где  R – газовая постоянная: .

    Однако дальнейшие измерения  удельных теплоемкостей некоторых веществ (например, углерода в виде алмаза) не согласовывались с их выводами. Этот закон выполняется только при высоких температурах. При низких температурах С_m = С_m (Т) и при , . Классическая теория объяснить это не может.

Итак,  в классической теории теплоемкости кристалл, состоящий из  N атомов, рассматривается как система, состоящая из N  невзаимодействующих гармонических осцилляторов, каждый из которых имеет  3 степени свободы.

       Классический способ измерения теплоемкости: тело, теплоёмкость которого (С_x) хотят измерить, нагревают до определённой температуры t_x и помещают в калориметр с начальной температурой t_0, наполненный водой  или другой жидкостью с известной теплоёмкостью (С_к  и С_ж – теплоёмкости калориметра и жидкости). Измеряя температуру в калориметре после установления теплового равновесия (t), можно вычислить теплоёмкость тела по формуле: 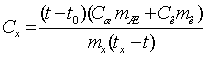, где m_x, m_ж и m_к – массы тела жидкости и калориметра.

Современный способ измерения теплоёмкости: берётся теплоизолированный объем, заполненный исследуемым веществом, в нём размещаются электронагреватель и термопара. Через нагреватель  пропускается электрический ток I длительностью t, который выделит в нём количество тепла Джоуля: dQ=RI²t, и измеряется прирост температуры dT. Теплоёмкость определяется как .

Дальнейшее развитие понятия теплоемкости  имеет место в квантовой механике.

       В 1900 г. немецкий физик-теоретик Макс Планк(1858-1947) высказал предположение, что, возможно, энергия, переносимая излучением, делится на небольшие порции (кванты), величина которых пропорциональна  частоте v  (коэффициент пропорциональности  - постоянная Планка – h).

       В 1907г. Альберт Эйнштейн (1879-1955) применил идею квантов к теории теплоемкости. В квантовой теории теплоемкости Эйнштейна каждый атом (ион), находящийся в узле кристаллической решетки, рассматривается как квантованный  осциллятор. Все осцилляторы колеблются с одинаковой частотой  w. Однако из теории Эйнштейна  следует, что  по экспоненте, а это не согласуется с опытом. Предположение о том, что атомы колеблются независимо, неверно.

       В 1912г. Питер Дебай (1884-1966)  косвенным путем показал, что квантовая теория позволяет объяснить аномальные результаты измерений удельной теплоемкости. Теория  Дебая правильно предсказывала зависимость удельной теплоемкости  от температуры, а ширину участка этой зависимости в шкале температур можно было приписать величине силы взаимодействия атомов твердого тела. В квантовой теории теплоемкости Дебая  кристалл, состоящий из N упруго связанных друг с другом атомов (ионов), рассматривается как связанная система, которая  обладает 3N степенями свободы. Такая система обладает спектром частот колебания.  По закону Дебая при низких температурах  .

В области высоких и низких температур

      Еще столетие назад  ученые считали, что вблизи абсолютного нуля всякое движение прекращается, все замерзает, начинается «мертвая» область. Оказалось, что это не так.

     Явления природы подчиняются своим внутренним масштабам , а не той шкале температур, которую придумали люди. Для каждого явления существуют низкие температуры – такие, при которых энергия  теплового движения меньше или сравнима с энергией, определяющей протекание процесса.  Например, те миллионы градусов, до которых сегодня удается нагревать плазму, это еще очень низкая температура для термоядерного реактора. В нем  энергии нейтронов составляют тысячи электрон-вольт. При еще большей  температуре масштаба 10⁹  - 10¹⁰К  из вакуума могут рождаться  электроны и протоны, а при  10¹³К   - рождаются нуклоны.  В списке планковских единиц есть температура  Т_P – 4*10³¹ K=4*10²⁷ эВ=4*10¹⁸ГэВ.

    Еще столетие назад  ученые считали, что вблизи абсолютного нуля всякое движение прекращается, все замерзает, начинается «мертвая» область. Оказалось, что это не так.

     Явления природы подчиняются своим внутренним масштабам , а не той шкале температур, которую придумали люди. Для каждого явления существуют низкие температуры – такие, при которых энергия  теплового движения меньше или сравнима с энергией, определяющей протекание процесса.  Например, те миллионы градусов, до которых сегодня удается нагревать плазму, это еще очень низкая температура для термоядерного реактора. В нем  энергии нейтронов составляют тысячи электрон-вольт. При еще большей  температуре масштаба 10⁹  - 10¹⁰К  из вакуума могут рождаться  электроны и протоны, а при  10¹³К   - рождаются нуклоны.  В списке планковских единиц есть температура  Т_P – 4*10³¹ K=4*10²⁷ эВ=4*10¹⁸ГэВ.

    Объяснение понятий абсолютной  температуры и абсолютного нуля  дает квантовая механика. Среди энергетических уровней  любой квантовой системы  есть один уровень, который обладает наинизшей энергией. При абсолютном нуле эту энергию просто некому передать. Поэтому нельзя понизить температуру тела до абсолютного нуля, хотя и можно приблизится к нему сколь угодно близко.   

     Сегодня  к сфере низких относят температуры от абсолютного нуля до нескольких кельвинов. Из космоса со всех сторон приходит радиоизлучение, соответствующее температуре 3К (реликтовое излучение, открытое в 1965 г. американцами Пензиасом и  Вильсоном). В природе  нигде нет  места с температурой ниже 3 К. Но в лабораториях можно получить.

     Еще в начале  ХХ в. голландский физик Х. Камерлинг - Оннес (1853 – 1926) при низких температурах получил жидкий гелий, твердый водород, открыл сверхпроводимость ртути, свинца, олова и других металлов.

     Позже советский физик  П. Л. Капица (1894-1984), работая в технике низких температур, открыл сверхтекучесть гелия, понизив его  температуру до ~0,8К.

     Сейчас ученые добрались до 0,001 К. Для получения сверхнизких температур порядка 1.0-1,5мК используется эффект советского физика  И.  Я. Померанчука (1913 - 1966), предсказанный им  в 1950 г., и экспериментально  доказанный в 1957 г. американскими физиками У. М. Фейербенком и Г. К.  Уолтерсом. Эффект состоит в том, что  при температурах ниже 0,3К энтропия жидкого гелия-3 меньше, чем твердого. Поэтому теплота плавления этого изотопа оказывается отрицательной.

                               

Заключение

      Во Вселенной течением всех тепловых процессов управляет энтропия, которая возрастает с возрастанием  Времени, и величина температуры, как и все другие величины, изменяется со временем и координатами.

     Как и все науки, физика пребывает в состоянии непрерывного развития. Постоянно обнаруживаются новые эффекты, открываются связи между разными явлениями природы, формулируются законы.

     Самое удивительное в нашем мире – это то, что он познаваем. Но понять его можно только изучив истоки физической науки. Это, может быть, важнее, чем досконально изучить сегодняшние идеи, которые в конце концов могут и сами измениться.

 

 

Л и т е р а т у р а

Кибец  И. Н., Кибец В.И. Физика. Справочник. -    Харьков: Фолио ;  Ростов н/Д : Феникс, 1997.                             

Кудрявцев П.С. Курс истории физики. Учебн. пособие. - М.: Просвещение, 1974.

Ланге В.Л. Физика и физические явления. – Кишинев: Штиинца, 1985.

Липсон  Г. Великие эксперименты в физике. – М.: «Мир», 1972.

Смородинский Я.А. Температура. Библиотечка «Квант», вып.12. – М.: Наука, 1981.

Эдельман В.С. Вблизи абсолютного нуля. Библиотечка «Квант», вып.26. – М.:  Наука, 1983.

Энциклопедический словарь юного физика. – М.: Педагогика, 1984.