РАЗДЕЛ I. Общая теория статистики.
Тема № 1.
Предмет, задачи, основные категории и понятия теории статистики.
История, пути и направления статистической науки
Термин "статистика" появился в середине 18 века. Означал
"государствоведение". Получил распространение в монастырях.
Постепенно приобрел собирательное значение. С
одной стороны, статистика – это совокупность числовых показателей,
характеризующих общественные явления и процессы (статистика труда, статистика
транспорта). С
другой – под статистикой понимается практическая деятельность по сбору,
обработке, анализу данных по различным направлениям общественной жизни. С третьей
стороны, статистика – это итоги массового учета, опубликованные в различных
сборниках. Наконец,
в естественных науках статистикой называются методы и способы оценки
соответствия данных массового наблюдения математическим формулам. Таким образом, статистика – это общественная наука,
изучающая количественную сторону массовых общественных явлений в неразрывной
связи с их качественной стороной.
Ученые, внесшие вклад в развитие статистики
–
Уильям Петти – основатель статистики. Его заслуга в
том, что он впервые применил числовой метод для анализа закономерностей
общественной жизни. Работа – "Политическая арифметика".
–
Адольф Кетле – бельгийский статистик. Доказал, что даже
кажущиеся случайности общественной жизни обладают внутренней закомерностью и
необходимостью.
–
К.Ф. Герман – русский статистик ("Всеобщая теория
статистики").
–
В.И. Ленин – теория группировок, теория статистического
наблюдения.
–
Целый ряд других ученых.
Предмет
статистики
Статистика изучает количественно определенные качества массовых
социально-экономических явлений. 1 2 3
Существует несколько точек зрения на статистику как на науку:
(1) Статистика
– это универсальная наука, изучающая
массовые явления природы и общества.
(2) Статистика
– это методологическая наука,
разрабатывающая методы исследования для других наук.
(3) Статистика
– это общественная наука.
Явления общественной жизни – это сложное сочетание различных элементов.
–
Общественные явления обладают вполне конкретными
размерами.
–
Общественным явлениям присущи определенные
количественные соотношения, и существуют они независимо от того, изучает ли их
статистика или нет.
Размеры и соотношения количества и качества отдельных явлений статистика
выражает при помощи определенных понятий, статистических показателей. Числовое
значение показателя, относящееся к определенному месту и времени, называют
величиной показателя.
Отрасли
статистики
Общая теория
статистики – это лишь фундамент. В любой своей части она связана с другими науками.
|
Общая теория статистики
|
|
Демографическая
статистика
|
Экономическая статистика
|
Статистика
образования
|
Медицинская
статистика
|
Спортивная
статистика
|
|
Статистика
труда
|
Статистика
заработной платы
|
Статистика
мат.-техн. снабжения
|
Статистика
транспорта
|
Статистика
связи
|
Статистика
финансового кредита
|
|
Высшие финансовые вычисления
|
Статистика денежного обращения
|
Статистика
валютных курсов
|
Прочие
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Статистика также
разрабатывает теорию наблюдения.
Метод
статистики
Метод статистики предполагает
следующую последовательность действий:
–
разработка статистической гипотезы,
–
статистическое наблюдение,
–
сводка и группировка статистических данных,
–
анализ данных,
–
интерпретация данных.
Прохождение каждой стадии связано с использованием специальных методов,
объясняемых содержанием выполняемой работы.
Закон
больших чисел
Массовый характер общественных законов и своеобразие их действий
предопределяет необходимость исследования совокупных данных.
Закон больших чисел порожден особыми свойствами массовых явлений.
Последние в силу своей индивидуальности, с одной стороны, отличаются друг от
друга, а с другой – имеют нечто общее, обусловленное их принадлежностью к
определенному классу, виду. Причем единичные явления в большей степени
подвержены воздействию случайных факторов, ежели их совокупность. Закон
больших чисел в наиболее простой форме гласит, что количественные закономерности
массовых явлений отчетливо проявляются лишь в достаточно большом их числе. Таким образом, сущность его
заключается в том, что в числах, получающихся в результате массового
наблюдения, выступают определенные правильности, которые не могут быть
обнаружены в небольшом числе фактов.
Закон больших чисел выражает диалектику случайного и необходимого. В
результате взаимопогашения случайных отклонений средние величины, исчисленные
для величины одного и того же вида, становятся типичными, отражающими действия
постоянных и существенных фактов в данных условиях места и времени. Тенденции
и закономерности, вскрытые с помощью закона больших чисел, имеют силу лишь как
массовые тенденции, но не как законы для каждого отдельного случая.
Статистическая
закономерность
Статистические закономерности изучают распределение единиц
статистического множества по отдельным признакам под воздействием всей
совокупности факторов. Статистическая
закономерность выступает как объективная закономерность сложного массового
процесса и является формой причинной связи. Она обнаруживается в итоге
массового статистического наблюдения. Этим обуславливается ее связь с законом
больших чисел. Статистическая
закономерность с определенной вероятностью гарантирует устойчивость средних
величин при сохранении постоянного комплекса условий, порождающих данное
явление.
Задачи
статистики
(1) Разработка
системы гипотез, характеризующих развитие, динамику, состояние
социально-экономических явлений.
(2) Организация
статистической деятельности.
(3) Разработка
методологии анализа.
(4) Разработка
системы показателей для управления хозяйством на макро- и микроуровне.
(5) Популяризовать
данные статистического наблюдения.
Организация
государственной статистики в РФ
Принципы:
(1) централизованное
руководство,
(2) единое
организационное строение и методология,
(3) неразрывная
связь с органами государственного управления.
Система государственной статистики имеет иерархическую структуру. Эта
структура имеет федеральный, республиканский, краевой, областной, окружной,
городской и районный уровни.
Госкомстат
имеет управления, отделы, вычислительный центр.
Ряды
распределения
Рядами распределения называются группировки особого вида, при которых по
каждому признаку, группе признаков или классу признаков известны численность
единиц в группе либо удельный вес этой численности в общем итоге. Ряды
распределения могут быть построены или по количественному, или по атрибутивному
признаку. Ряды
распределения, построенные по количественному признаку, называются вариационными рядами. Ряд распределения
может быть построен по непрерывно варьирующему признаку
(когда признак может принимать любые значения в рамках какого-либо интервала) и
по дискретно
варьирующему признаку (принимает строго определенные целочисленные
значения). Непрерывно варьирующий признак изображается
графически при помощи гистограммы. Дискретный же ряд
распределения графически представляется в виде полигона распределения.
Тема № 2. Статистическое
наблюдение.
Понятие
статистического наблюдения
Статистическое наблюдение – это
сбор необходимых данных по явлениям, процессам общественной жизни. Но это не всякий сбор данных, а лишь
планомерный, научно организованный, систематический и направленный на
регистрацию признаков, характерных для исследуемых явлений и процессов. От качества данных, полученных на первом
этапе, зависят конечные результаты исследования.
Формы
статистического наблюдения
Различают две основные формы статистического наблюдения – отчетность и
специально организованное наблюдение.
Отчетность – это такая форма наблюдения, при которой
предприятия, организации представляют в
статистические и вышестоящие органы постоянные сведения, характеризующие
их деятельность. Отчетность предоставляется по заранее определенной программе в
строго определенные сроки и содержит важнейшие показатели, необходимые в
процессе ежедневной работы.
Специально организованное
наблюдение – такое наблюдение, которое организуется со специальной
целью на определенную дату для получения данных, которые в силу различных
причин не собираются статистической отчетност, а также с целью проверки данных
статистической отчетности.
Виды
статистического наблюдения
По времени регистрации фактов статистическое наблюдение может быть
непрерывным, периодическим и единовременным.
Непрерывное (текущее)
наблюдение – ведется систематически (т.е. регистрация фактов производится по
мере их свершения). Пример – ЗАГС.
Периодическое наблюдение
– повторяется через определенные равные промежутки времени. Пример – перепись населения.
Единовременное
наблюдение – производится по мере надобности без соблюдения определенной
периодичности. Пример – оценка и
переоценка основных фондов.
По охвату единиц совокупности выделяют сплошное и несплошное
наблюдение.
Сплошным называется
наблюдение, при котором исследованию подвергаются все единицы изучаемой совокупности.
Несплошным называется
такое наблюдение, при котором исследованию подвергается только часть единиц
изучаемой совокупности, отобранная определенным образом.
Виды
несплошного наблюдения
–
Анкетный способ
Исследуются какие-то
осредненные показатели и
распространяются на всю совокупность.
–
Метод основного массива
Исследуются наиболее
крупные единицы изучаемого явления.
–
Метод направленного долевого отбора
–
Выборочный метод
Его основой является
случайный отбор. Результат гарантируется с определенной вероятностью р.
–
Монографический метод
Подвергаются
тщательному исследованию отдельные единицы совокупности, обычно представители
новых типов, либо самые лучшие (худшие) единицы. Результаты переносятся на всю
совокупность. Позволяет выявить тенденции.
Способы
статистического наблюдения
Основанием для регистрации фактов могут служить либо документы, либо
высказанное мнение, либо хронометражные данные. В связи с этим различают
наблюдение:
–
непосредственное (сами измеряют),
–
документально (из документов),
–
опрос (со слов кого-либо).
В статистике применяются следующие способы сбора информации:
–
корреспондентский (штат добровольных корреспондентов),
–
экспедиционный (устный, специально подготовленные
работники)
–
анкетный (в виде анкет),
–
саморегистрация (заполнение формуляров самими
респондентами),
–
явочный (браки, дети, разводы) и т.д.
Программно-методологические
вопросы статистического наблюдения
Каждое наблюдение проводится с конкретной целью. При его проведении
необходимо установить, что подлежит обследованию. Надо решить следующие
вопросы:
Объект наблюдения –
совокупность предметов, явлений, у которых должны быть собраны сведения. При
определении объекта указываются его основные отличительные черты (признаки).
Всякий объект массовых наблюдений состоит их отдельных единиц, поэтому надо
решить вопрос о том, каков тот элемент совокупности, который послужит единицей
наблюдения.
Единица наблюдения –
это составной элемент объекта, который является носителем признаков, подлежащих
регистрации и основой счета.
Ценз – это определенные
количественные ограничения для объекта наблюдения.
Признак – это
свойство, которое характеризует определенные черты и особенности, присущие единицам
изучаемой совокупности.
Программа наблюдения –
это перечень признаков, подлежащих регистрации. Программа находит отражение в формуляре
наблюдения. Выделяются организационные вопросы: перечень мероприятий,
обеспечивающих правильность наблюдения, а также оргплан, где учитываются
органы наблюдения, время наблюдения, порядок приема и сдачи материала, порядок получения информации.
Период наблюдения –
время, в течение которого должна быть осуществлена регистрация.
Критическая дата наблюдения
– дата, по состоянию на которую сообщаются сведения.
Критический момент –
момент времени, по состоянию на который производится регистрация наблюденных
фактов.
Тема № 3. Сводка и группировка
статистических данных.
Статистическая
сводка
Статистическая сводка – это операция
по обработке собранных данных, которые выражаются в виде показателей,
относящихся к каждой единице объекта статистического наблюдения. В результате
сводки эти данные превращаются в систему статистических таблиц и промежуточных
итогов. По результатам сводки можно выявить наиболее типичные черты и
закономерности изучаемых явлений. Предварительно
составляется программа и план сводки.
В программе определяется подлежащее и сказуемое сводки. Подлежащее составляет вся совокупность
группы или части, на которые разбивается совокупность. Сказуемое – это те показатели, которые характеризуют каждую группу,
часть или всю совокупность в целом.
План сводки – содержит
организационные вопросы.
Статистическая
группировка
Статистическая группировка – это метод исследования массовых
общественных явлений путем выделения и ограничения однородных групп, через
которые раскрываются существенные черты и особенности состояния и развития всей
совокупности.
Основные задачи, которые решаются с помощью группировок:
(1) выделение
социально-экономических типов,
(2) изучение
структуры социально-экономических явлений,
(3) выявление
связи между явлениями.
Важнейшие проблемы:
(1) Определение
группировочного признака (основания группировки).
Группировочный признак – это признак, по
которому происходит определение единиц в группе. Его выбор зависит от цели
группировки и существа данного явления.
(2) Выделение
числа групп.
Число групп определяется с таким
расчетом, чтобы в каждую группу попало достаточно большое число единиц.
(3) Интервалы
Интервалы могут быть равными и неравными.
Последние в свою очередь делятся на равномерно возрастающие и равномерно
убывающие.
Виды
группировок
(1) Типологические группировки
Их задача – выявление социально-экономических типов или однородных в
существенном отношении групп.
|
№ п/п
|
Социально-экономические
типы
|
Мужчины
|
Женщины
|
|
1980
|
1992
|
1980
|
1992
|
|
1.
|
Работники
|
–
|
–
|
–
|
–
|
|
2.
|
Крестьяне
|
–
|
–
|
–
|
–
|
|
3.
|
Служащие
|
–
|
–
|
–
|
–
|
(2) Структурные группировки
Их задача – изучение состава отдельных типических групп при помощи
объединения единиц совокупности, близких друг к другу по величине
группировочного признака.
|
№ п/п
|
Количество посадочных мест
|
Количество столов
|
Число занятых
|
Товарооборот на 1 место
|
|
1.
|
до 25
|
–
|
–
|
–
|
|
2.
|
16 – 50
|
–
|
–
|
–
|
|
3.
|
51 – 70
|
–
|
–
|
–
|
|
4.
|
71 – 100
|
–
|
–
|
–
|
(3) Аналитические группировки
Их задача – выявления влияния одних признаков на другие ( выявить связь
между социально-экономическими явлениями).
|
№ п/п
|
Группы магазинов
по числу рабочих мест
|
Число
магазинов
|
Товарооборот
|
|
на 1 работника
|
на 1 раб. место
|
|
1.
|
до 5
|
100
|
12,0
|
13,0
|
|
2.
|
6 – 10
|
50
|
14,0
|
16,0
|
|
3.
|
11 – 15
|
10
|
15,0
|
17,0
|
|
4.
|
16 – 20
|
4
|
30,0
|
39,0
|
|
5.
|
21 – 25
|
2
|
31,0
|
42,0
|
(4) Комбинационные группировки
В них производится разделение совокупности на группы по двум или более
признакам. При этом группы, образованные по одному признаку, разбиваются на
подгруппы по другому признаку.
Такие группировки дают возможность изучить структуру совокупности по
нескольким признакам одновременно.
|
№ п/п
|
Группы предприятий
по объему основных фондов
|
Оплата труда
в рублях
|
Пол
|
Количество единиц
|
|
1.
|
до 200
|
100 – 120
|
М
|
–
|
|
Ж
|
–
|
|
120 – 140
|
М
|
–
|
|
Ж
|
–
|
|
140 – 160
|
М
|
–
|
|
Ж
|
–
|
|
2.
|
200 – 400
|
100 – 120
|
М
|
–
|
|
Ж
|
–
|
|
120 – 140
|
М
|
–
|
|
Ж
|
–
|
|
140 – 160
|
М
|
–
|
|
Ж
|
–
|
|
3.
|
400 – 600
|
100 – 120
|
М
|
–
|
|
Ж
|
–
|
|
120 – 140
|
М
|
–
|
|
Ж
|
–
|
|
140 – 160
|
М
|
–
|
|
Ж
|
–
|
|
4.
|
600 – 800
|
100 – 120
|
М
|
–
|
|
Ж
|
–
|
|
120 – 140
|
М
|
–
|
|
Ж
|
–
|
|
140 – 160
|
М
|
–
|
|
Ж
|
–
|
Система
группировок
Социально-экономический анализ предполагает использование системы
простых и комбинационных группировок.
Также очень часто прибегают к вторичной группировке – перегруппировка
уже сгруппированных данных. Вторичная группировка может быть проведена методом
простого укрупнения интервала.
Часто также используется процентная перегруппировка.
Пример: Группировка
фермерских хозяйств по наличию скота.
Исходные данные:
|
№ п/п
|
Группы хозяйств
по числу голов
|
% фермерских хозяйств
|
% поголовья
|
% по всему кол-ву скота
|
|
1.
|
без голов
|
26,4
|
2,8
|
9,9
|
|
2.
|
с 1-й головой
|
20,3
|
9,5
|
8,9
|
|
3.
|
с 2-мя головами
|
14,6
|
11,8
|
11,1
|
|
4.
|
с 3-мя –– " ––
|
9,3
|
10,5
|
9,8
|
|
5.
|
с 4-мя –– " ––
|
8,3
|
12,1
|
11,2
|
|
6.
|
с 5-ю –– " ––
|
21,1
|
53,3
|
56,1
|
|
|
Всего:
|
100
|
100
|
100
|
Процентная перегруппировка
|
№ п/п
|
Группы хозяйств
по уровню развития
|
% фермерских хозяйств
|
% поголовья
|
% по всему кол-ву скота
|
|
1.
|
Низкий
|
50
|
14,9
|
21,3
|
|
2.
|
Средний
|
30
|
34,6
|
32,5
|
|
3.
|
Высокий
|
20
|
50,5
|
53,2
|
|
|
Всего:
|
100
|
100
|
100
|
Расчеты:
1. 26,4
+ 20,3 = 46,7
2. 50
– 46,7 = 3,3
3. 3,3
/ 14,6 = 0,226
4. 0,226
* 11,8 = 2,6 0,226
* 11,1 = 2,5
5. 2,8
+ 9,5 + 2,6 = 14,9 9,9
+ 8,9 + 2,5 = 21,3
6. 11,3
+ 9,3 + 8,3 = 28,9
7. 30
– 28,9 = 1,1
8. 1,1
/ 21,1 = 0,052
9. 0,052
* 53,3 = 2,8 0,052
* 56,1 = 2,9
10. (11,8 –
2,6) + 10,5 + 12,1 + 2,8 = 34,6 (11,1
– 2,5) + 9,8 + 11,2 + 2,9 = 32,5
11. 53,3 – 2,8
= 50,5 56,1 – 2,9 = 53,2
Тема № 4. Абсолютные и
относительные велечины.
Абсолютные статистические величины
Абсолютные статистические
величины показывают объем, размеры, уровни различных социально-экономических
явлений и процессов. Они отражают уровни в физических мерах объема, веса и т.п.
В общем, абсолютные статистические величины – это именованные числа. Они всегда
имеют определенную размерность и единицы измерения. Последние определяют
сущность абсолютной величины.
Типы абсолютных величин
(1) Натуральные – такие единицы, которые отражают
величину предметов, вещей в физических мерах (вес, объем, площадь и т.д.).
(2) Денежные (стоимостные) – используются для
характеристики многих экономических показателей в стоимостном выражении.
(3) Трудовые – используются для определения
затрат труда (человеко-час, человеко-день)
(4) Условно-натуральные –единицы, которые
используются для сведения воедино нескольких разновидностей потребительных
стоимостей (т.у.т = 29,3 МДж/кг; мыло 40 % жирности).
Виды абсолютных величин
–
Индивидуальные
– отражают размеры количественных признаков у отдельных единиц изучаемой
совокупности.
–
Общие –
выражают размеры, величину количественных признаков у всей изучаемой совокупности
в целом.
Абсолютные величины отражают
наличие тех или иных ресурсов, это основа материального учета. Они наиболее
объективно отражают развитие экономики.
Абсолютные величины являются
основой для расчета разных относительных статистических показателей.
Относительные
статистические величины
Относительные статистические
величины выражают количественные соотношения между явлениями общественной
жизни, они получаются в результате деления одной абсолютной величины на другую.
Знаменатель (основание
сравнения, база) – это величина, с которой производится сравнение.
Сравниваемая (отчетная,
текущая) величина – это величина, которая сравнивается.
Относительная величина
показывает, во сколько раз сравниваемая величина больше или меньше базисной или
какую долю первая составляет по отношению ко второй. В ряде случае
относительная величина показывает, сколько единиц одной величины приходится на
единицу другой.
Важное свойство – относительная
величина абстрагирует различия абсолютных величин и позволяет сравнивать такие
явления, абсолютные размеры которых непосредственно несопоставимы.
Форма выражения относительных величин
В результате сопоставления
одноименных абсолютных величин получают неименованные относительные
величины. Они могут выражаться в виде долей, кратных соотношений, процентных
соотношений, в виде промилле и т.д.
Результатом сопоставления
разноименных величин являются именованные относительные величины. Их название
образуется сочетанием сравниваемой и базисной абсолютных величин.
Выбор формы зависит от
характера аналитической задачи, которая состоит в том, чтобы с наибольшей ясностью
выразить соотношение.
Виды относительных величин
Все применяемые на практике
относительные статистические величины подразделяются на следующие виды.
Относительная величина динамики
Достигнутый показатель / базисный
показатель.
Относительная величина планового задания
Плановый показатель / базисный
показатель.
Относительная величина выполнения плана
Достигнутый показатель / плановый
показатель.
Относительная величина структуры
Отношение частей и целого.
Относительная величина координации
Соотношение частей целого между
собой.
Относительная величина интенсивности
Характеризует распределение
явления в определенной среде (насыщенность каким-либо явлением). Это всегда
соотношение разноименных величин.
Относительная величина уровня социально-экономического явления
Характеризует размеры производства
различных видов продукции на душу населения.
Относительная величина сравнения
Представляет собой отношение
одноименных величин, относящихся к различным объектам.
Тема № 5. Средние величины в
статистике.
Большое распространение в статистике имеют средние
величины. Средние величины характеризуют качественные показатели коммерческой
деятельности: издержки обращения, прибыль, рентабельность и др.
Средняя - это один из распространенных приемов
обобщений. Правильное понимание сущности
средней определяет ее особую
значимость в условиях рыночной
экономики, когда средняя через единичное и случайное позволяет выявить общее и
необходимое, выявить тенденцию закономерностей экономического развития.
Средняя величина - это обобщающие показатели, в которых
находят выражение действия общих условий, закономерностей изучаемого
явления.
Статистические средние рассчитываются на
основе массовых данных правильно статистически организованного
массового наблюдения (сплошного и выборочного).
Однако статистическая средняя будет
объективна и типична, если она
рассчитывается по массовым данным
для качественно однородной совокупности (массовых явлений). Например,
если рассчитывать среднюю
заработную плату в кооперативах и на госпредприятиях, а результат распространить на всю
совокупность, то средняя фиктивна, так как рассчитана по
неоднородной совокупности, и
такая средняя теряет всякий смысл.
При помощи средней происходит как бы
сглаживание различий в величине признака,
которые возникают по тем или иным причинам у отдельных единиц
наблюдения.
Например, средняя выработка продавца
зависит от многих
причин: квалификации, стажа, возраста, формы обслуживания, здоровья и т.д.
Средняя выработка отражает общее свойство
всей совокупности.
Средняя величина является отражением
значений изучаемого признака, следовательно, измеряется в той же размерности,
что и этот признак.
Каждая средняя величина
характеризует изучаемую совокупность по какому-либо одному
признаку. Чтобы получить
полное и всестороннее представление об изучаемой
совокупности по ряду существенных признаков, в целом необходимо
располагать системой средних величин,
которые могут описать явление с разных сторон.
Существуют различные средние:
*
средняя арифметическая;
*
средняя геометрическая;
*
средняя гармоническая;
*
средняя квадратическая;
*
средняя хронологическая.
Рассмотрим некоторые виды средних, которые
наиболее часто используются в статистике.
Средняя
арифметическая
Средняя арифметическая простая
(невзвешенная) равна сумме отдельных значений признака, деленной на число этих
значений.
Отдельные значения признака называют
вариантами и обозначают через х (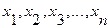 ); число единиц совокупности обозначают через n, среднее
значение признака - через
); число единиц совокупности обозначают через n, среднее
значение признака - через 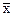 . Следовательно, средняя арифметическая простая равна:
. Следовательно, средняя арифметическая простая равна:
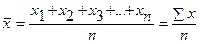
По данным дискретного ряда распределения
видно, что одни и те же значения признака
(варианты) повторяются несколько раз.
Так, варианта х встречается в совокупности 2 раза, а варианта х-16 раз и
т.д.
Число одинаковых значений признака в рядах распределения
называется частотой или весом и обозначается символом n.
Вычислим среднюю заработную плату одного
рабочего 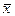 в руб.:
в руб.:
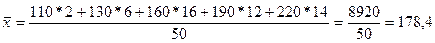
Фонд заработной платы по каждой группе
рабочих равен произведению варианты на частоту,
а сумма этих произведений дает общий фонд заработной платы всех рабочих.
В соответствии с этим, расчеты можно
представить в общем виде:
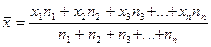
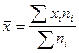
Полученная формула называется средней арифметической взвешенной.
Статистический материал в результате
обработки может быть представлен не только
в виде дискретных рядов распределения,
но и в виде интервальных вариационных рядов с закрытыми или открытыми
интервалами.
Исчисление средней по сгруппированным данным
производится по формуле средней арифметической взвешенной:
В практике экономической статистики иногда
приходится исчислять среднюю по групповым средним или по средним отдельных
частей совокупности (частным средним). В таких случаях за варианты (х)
принимаются групповые или частные средние, на основании которых исчисляется
общая средняя как обычная средняя арифметическая взвешенная.
Основные свойства средней арифметической.
Средняя арифметическая обладает рядом
свойств:
1. От уменьшения или увеличения частот
каждого значения признака х в п раз
величина средней арифметической не изменится.
Если все частоты разделить или умножить на
какое-либо число, то величина средней не изменится.
2. Общий множитель индивидуальных
значений признака может
быть вынесен за знак средней:
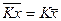
3. Средняя
суммы (разности) двух
или нескольких величин равна сумме (разности) их средних:
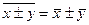
4. Если х = с, где с - постоянная величина,
то  .
.
5. Сумма отклонений значений признака Х от
средней арифметической х равна нулю:
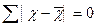
Средняя гармоническая.
Наряду со средней арифметической, в
статистике применяется средняя гармоническая величина, обратная
средней арифметической из
обратных значений признака. Как и средняя арифметическая, она может быть простой
и взвешенной.
Характеристиками вариационных рядов, наряду
со средними, являются мода и медиана.
Мода - это величина признака (варианта), наиболее часто повторяющаяся в
изучаемой совокупности. Для дискретных рядов распределения модой будет значение
варианта с наибольшей частотой.
Для интервальных рядов распределения с
равными интервалами мода определяется по формуле:
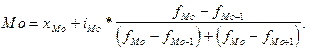
где 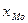 - начальное значение
интервала, содержащего моду;
- начальное значение
интервала, содержащего моду;
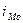 - величина модального
интервала;
- величина модального
интервала;
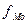 - частота модального
интервала;
- частота модального
интервала;
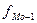 - частота интервала,
предшествующего модальному;
- частота интервала,
предшествующего модальному;
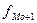 - частота интервала,
следующего за модальным.
- частота интервала,
следующего за модальным.
Медиана - это варианта, расположенная
в середине вариационного ряда. Если ряд распределения дискретный
и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине
упорядоченного ряда (упорядоченный ряд - это расположение единиц совокупности в
возрастающем или убывающем порядке).
Тема № 6. Показатели вариации.
Различие индивидуальных значений признака
внутри изучаемой совокупности в статистике
называется вариацией признака.
Она возникает в результате того, что его индивидуальные значения складываются
под совокупным влиянием разнообразных
факторов, которые по-разному сочетаются
в каждом отдельном случае.
Средняя величина —
это абстрактная, обобщающая характеристика признака изучаемой
совокупности, но она не показывает
строения совокупности, которое весьма
существенно для ее познания. Средняя величина не дает представления о том, как
отдельные значения изучаемого признака группируются вокруг средней, сосредоточены
ли они вблизи или значительно отклоняются от нее. В
некоторых случаях отдельные
значения признака близко примыкают к средней арифметической и мало от
нее отличаются. В таких случаях средняя хорошо представляет всю совокупность.
В других,
наоборот, отдельные значения совокупности далеко отстают от средней, и
средняя плохо представляет всю совокупность.
Колеблемость отдельных значений
характеризуют показатели вариации.
Термин "вариация" произошел от
латинского variatio –“изменение, колеблемость, различие”. Однако не всякие
различия принято называть вариацией. Под вариацией в статистике понимают такие
количественные изменения величины исследуемого признака в пределах однородной
совокупности, которые обусловлены перекрещивающимся влиянием действия различных
факторов. Различают вариацию признака: случайную и систематическую.
Анализ систематической вариации позволяет
оценить степень зависимости изменений в изучаемом признаке от определяющих ее
факторов. Например, изучая силу и характер вариации в выделяемой совокупности,
можно оценить, насколько однородной
является данная совокупность в количественном, а иногда и качественном
отношении, а следовательно, насколько характерной является исчисленная
средняя величина. Степень близости данных отдельных единиц хi к средней
измеряется рядом абсолютных, средних и относительных
показателей.
Для характеристики совокупностей
и исчисленных величин
важно знать, какая вариация изучаемого признака скрывается за средним.
Для характеристики колеблемости признака
используется ряд показателей. Наиболее простой из них - размах вариации.
Размах вариации - это разность между наибольшим (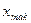 ) и наименьшим (
) и наименьшим (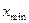 ) значениями вариантов.
) значениями вариантов.
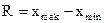
Чтобы дать обобщающую характеристику
распределению отклонений, исчисляют
среднее линейное отклонение d,
которое учитывает различие всех единиц изучаемой совокупности.
Среднее линейное отклонение определяется как
средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений:
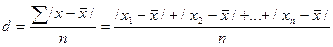 .
.
Порядок расчета среднего линейного отклонения
следующий:
1) по значениям признака исчисляется средняя
арифметическая:
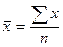 ;
;
2) определяются отклонения каждой варианты 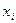 от средней
от средней 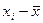 ;
;
3) рассчитывается сумма абсолютных величин
отклонений: 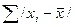 ;
;
4) сумма абсолютных величин отклонений
делится на число значений:
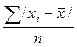 .
.
Если данные наблюдения представлены в виде
дискретного ряда распределения с частотами, среднее линейное отклонение
исчисляется по формуле средней арифметической взвешенной:
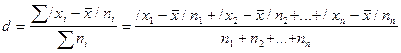
Порядок расчета среднего линейного
отклонения взвешенного следующий:
1) вычисляется средняя арифметическая
взвешенная:
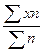 ;
;
2) определяются абсолютные отклонения
вариант от средней /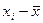 /;
/;
3) полученные отклонения умножаются на
частоты 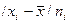 ;
;
4) находится сумма взвешенных отклонений без
учета знака:
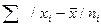 ;
;
5) сумма взвешенных отклонений делится на
сумму частот:
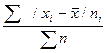 .
.
Основными обобщающими показателями вариации
в статистике являются дисперсии и среднее квадратическое отклонение.
Дисперсия -
это средняя арифметическая квадратов отклонений каждого значения
признака от общей средней. Дисперсия
обычно называется средним квадратом отклонений и обозначается 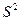 . В зависимости от
исходных данных дисперсия может вычисляться
по средней арифметической простой или взвешенной:
. В зависимости от
исходных данных дисперсия может вычисляться
по средней арифметической простой или взвешенной:
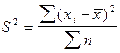 — дисперсия невзвешенная (простая);
— дисперсия невзвешенная (простая);
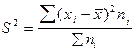 — дисперсия взвешенная.
— дисперсия взвешенная.
Среднее квадратическое отклонение представляет
собой корень квадратный из дисперсии и обозначается S:
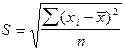 — среднее квадратическое отклонение
невзвешенное;
— среднее квадратическое отклонение
невзвешенное;
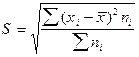 — среднее
квадратическое отклонение взвешенное.
— среднее
квадратическое отклонение взвешенное.
Среднее квадратическое отклонение - это обобщающая характеристика абсолютных
размеров вариации признака в совокупности. Выражается оно в тех же единицах
измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.).
Среднее квадратическое отклонение
является мерилом надежности средней. Чем меньше среднее
квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю
представляемую совокупность.
Вычислению среднего квадратического отклонения предшествует
расчет дисперсии.
Порядок расчета дисперсии взвешенную:
1) определяют среднюю арифметическую взвешенную
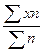 ;
;
2) определяются отклонения вариант от средней 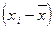 ;
;
3) возводят в квадрат отклонение каждой варианты от средней  ;
;
4) умножают квадраты отклонений на веса (частоты) 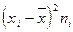 ;
;
5) суммируют полученные произведения
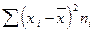 ;
;
6) Полученную сумму делят на сумму весов
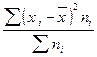 .
.
Свойства дисперсии.
Уменьшение или увеличение весов (частот)
варьирующего признака в определенное число раз дисперсии не изменяет.
Уменьшение или увеличение каждого значения
признака на одну и ту же постоянную величину
А дисперсии не изменяет.
Уменьшение или увеличение каждого значения
признака в какое-то число раз к соответственно уменьшает или увеличивает дисперсию в 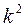 раз, а среднее
квадратическое отклонение - в к раз.
раз, а среднее
квадратическое отклонение - в к раз.
Дисперсия
признака относительно
произвольной величины всегда больше дисперсии относительно средней
арифметической на квадрат разности между средней и произвольной
величиной: 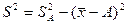 . Если А равна нулю,
то приходим к следующему равенству:
. Если А равна нулю,
то приходим к следующему равенству: 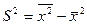 , т.е. дисперсия
признака равна разности между средним квадратом значений признака и
квадратом средней.
, т.е. дисперсия
признака равна разности между средним квадратом значений признака и
квадратом средней.
Каждое свойство при расчете дисперсии может
быть применено самостоятельно или в сочетании с другими.
Порядок расчета дисперсии простой:
1) определяют среднюю арифметическую 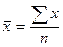 ;
;
2) возводят в квадрат среднюю арифметическую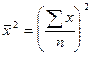 ;
;
3) возводят в квадрат каждую варианту ряда 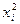 ;
;
4) находим сумму квадратов вариант 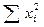 ;
;
5) делят сумму квадратов вариант на их
число, т.е. определяют средний квадрат 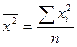 ;
;
6) определяют разность между средним
квадратом признака и квадратом средней 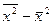 .
.
Порядок расчета дисперсии взвешенной (по формуле 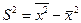 ):
):
1)
определяют
среднюю арифметическую 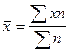 ;
;
2)
возводят в
квадрат полученную среднюю 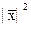 ;
;
3)
возводят в
квадрат каждую варианту ряда 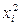 ;
;
4)
умножают
квадраты вариант на частоты 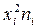 ;
;
5)
суммируют
полученные произведения 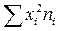 ;
;
6)
делят
полученную сумму на сумму весов и получают средний квадрат признака 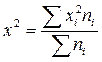 ;
;
7)
определяют
разность между средним значением квадратов и
квадратом средней арифметической, т.е. дисперсию 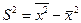 .
.
Для характеристики меры колеблемости
изучаемого признака исчисляются показатели колеблемости в относительных
величинах. Они позволяют сравнивать
характер рассеивания в различных распределениях
(различные единицы наблюдения одного и того же признака в двух
совокупностях, при различных значениях средних,
при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания
осуществляют как отношение абсолютного показателя рассеивания к средней
арифметической, умножаемое на 100%.
1. Коэффициент осцилляции отражает
относительную колеблемость
крайних значений признака вокруг средней.
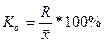 (1)
(1)
2. Относительное линейное отклонение
характеризует долю усредненного значения абсолютных отклонений от средней
величины.
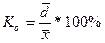 (2)
(2)
3. Коэффициент вариации.
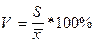 (3)
(3)
Учитывая, что среднеквадратическое
отклонение дает обобщающую характеристику колеблемости всех вариантов
совокупности, коэффициент вариации является
наиболее распространенным показателем колеблемости, используемым для
оценки типичности средних величин. При
этом исходят из того, что если V больше
40 %, то это говорит о большой колеблемости признака в изучаемой совокупности.
Тема № 7. Ряды распределения.
Ряд
распределения или вариационный ряд – упорядоченное распределение единиц
совокупности по возрастающим или по убывающим значениям признака и подсчет
единиц с тем или иным значением признака. Построение рядов распределения
(структурной группировки) является первым этапом изучения вариации и
осуществляется с целью выделения
характерных свойств и закономерностей изучаемой совокупности. В зависимости от
того, какой признак (количественный или качественный) взят за основу
группировки данных, различают типы рядов распределения.
Если за
основу группировки взят качественный признак, то такой ряд распределения
называют атрибутивным (распределение по видам труда, по полу, по профессии, по
религиозному признаку, национальной принадлежности и т.д.).
Если ряд
распределения построен по количественному признаку, то такой ряд называют
вариационным. Построить вариационный ряд - значит упорядочить количественное
распределение единиц совокупности по значениям признака, а затем подсчитать
числа единиц совокупности с этими значениями (построить групповую таблицу).
Выделяют
три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный
ряд.
Ранжированный
ряд - это распределение отдельных единиц совокупности в порядке возрастания или
убывания исследуемого признака.
Другие
формы вариационного ряда - групповые таблицы, составленные по характеру
вариации значений изучаемого признака. По характеру вариации различают
дискретные (прерывные) и непрерывные признаки.
Дискретный
ряд - это такой вариационный ряд, в основу построения которого положены
признаки с прерывным изменением (дискретные признаки). К последним можно
отнести тарифный разряд, количество детей в семье, число работников на
предприятии и т.д. Эти признаки могут принимать только конечное число
определенных значений.
Если
признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость
основных фондов предприятия и т.д., которые в определенных границах могут
принимать любые значения), то для этого признака нужно строить интервальный
вариационный ряд.
Величина
интервала определяется по формуле 
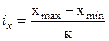 , где
, где
xmax, min - максимальное и минимальное значение
признака, к – число групп.
Частота
(частота повторения) - число повторений отдельного варианта значений признака,
обозначается fi , а сумма частот, равная объему исследуемой
совокупности, обозначается 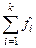 , где к – число вариантов значения признака.
, где к – число вариантов значения признака.
Частоты
ряда f могут заменяться частостями w, выраженными в относительных числах (долях
или процентах). Они представляют собой отношения частот каждого интервала к их
общей сумме, т.е.: 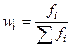 , при этом
, при этом 
Основной
целью анализа вариационных рядов является выявление закономерности
распределения, исключая при этом влияние случайных для данного распределения
факторов. Этого можно достичь, если увеличивать объем исследуемой совокупности
и одновременно уменьшать интервал ряда.
В практике
статистических исследований наиболее часто используются следующие
закономерности распределения: нормальное распределение и распределение
Пуассона.
Нормальное
распределение зависит от двух параметров: средней арифметической и среднего квадратического отклонения. Его
кривая выражается уравнением 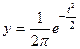
где у -
ордината кривой нормального распределения;
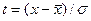 - стандартизованные
отклонения; е и π - математические постоянные; x - варианты вариационного
ряда;
- стандартизованные
отклонения; е и π - математические постоянные; x - варианты вариационного
ряда; 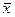 - их средняя
величина;
- их средняя
величина; 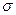 - cреднее квадратическое отклонение.
- cреднее квадратическое отклонение.
Теоретические
частоты при нормальном распределении определяются по формуле: 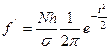 , где N = Sf – сумма всех эмпирических частот вариационного ряда; h – величина интервала в группах.
, где N = Sf – сумма всех эмпирических частот вариационного ряда; h – величина интервала в группах.
При помощи
этой формулы мы получаем теоретическое (вероятностное) распределение, заменяя
им эмпирическое (фактическое) распределение, по характеру они не должны
отличаться друг от друга.
Если
вариационный ряд представляет собой распределение по дискретному признаку, где
при увеличении значений признака х частоты начинают резко уменьшаться, а
средняя арифметическая, в свою очередь, равна или близка по значению к
дисперсии (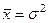 ), такой ряд выравнивается по кривой Пуассона.
), такой ряд выравнивается по кривой Пуассона.
Кривую
Пуассона можно выразить отношением 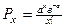 , где Px -
вероятность наступления отдельных значений х;
, где Px -
вероятность наступления отдельных значений х; 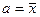 - средняя арифметическая ряда.
- средняя арифметическая ряда.
Теоретические
частоты при распределении Пуассона определяют по формуле: f’ = N Px , где N – общее число
единиц ряда.
Для
расчета обобщающих показателей и для графического изображения вариационных
рядов с неравными интервалами используют плотность распределения, которая
определяется по формулам:
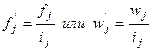 ,
,
где 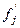 - абсолютная плотность распределения в j-м интервале,
- абсолютная плотность распределения в j-м интервале, 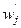 - относительная
плотность распределения в j-м интервале; ij – величина интервала.
- относительная
плотность распределения в j-м интервале; ij – величина интервала.
Объективная
характеристика соответствия теоретических и эмпирических частот может быть
получена при помощи специальных статистических показателей, которые называют
критериями согласия.
Асимметрия распределения
определяется на основе расчета коэффициента асимметрии, котрый является мерой
несимметричности распределения. Если этот коэффициент отчетливо отличается от
0, распределение является асимметричным. Плотность нормального
распределения симметрична
относительно среднего.
Для оценки
близости эмпирических и теоретических частот применяются критерий согласия
Пирсона, критерий согласия Романовского, критерий согласия Колмогорова.
Наиболее
распространенным является критерий согласия К. Пирсона, который можно
представить как сумму отношений квадратов расхождений между f' и f к
теоретическим частотам: 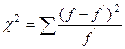
Вычисленное
значение критерия c2расч необходимо сравнить с табличным (критическим)
значением c2табл.
Табличное значение определяется по специальной таблице, оно зависит от принятой
вероятности Р и числа степеней свободы k (при этом k = m - 3, где m - число
групп в ряду распределения для нормального распределения). При расчете критерия
согласия Пирсона должно соблюдаться следующее условие: достаточно большим
должно быть число наблюдений (n ³ 50), при этом если в некоторых интервалах теоретические
частоты меньше 5, то интервалы объединяют для условия больше 5.
Если c2расч
£ c2табл, то расхождения между эмпирическими и теоретическими
частотами распределения могут быть случайными и предположение о близости
эмпирического распределения к нормальному не может быть отвергнуто.
В том
случае, если отсутствуют таблицы для оценки случайности расхождения
теоретических и эмпирических частот, можно использовать критерий согласия В.И.
Романовского (КРом),
который, используя величину c2,
предложил оценивать близость эмпирического распределения кривой нормального
распределения при помощи отношения: 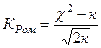 , где m - число групп; k = (m - 3 ) - число степеней свободы
при исчислении частот нормального распределения.
, где m - число групп; k = (m - 3 ) - число степеней свободы
при исчислении частот нормального распределения.
Если
вышеуказанное отношение < 3, то расхождения эмпирических и теоретических
частот можно считать случайными, а эмпирическое распределение - соответствующим
нормальному. Если отношение > 3, то расхождения могут быть достаточно
существенными и гипотезу о нормальном распределении следует отвергнуть.
Критерий
согласия А.Н. Колмогорова используется
при определении максимального расхождения между частотами эмпирического и
теоретического распределения, вычисляется по формуле: 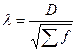 , где D - максимальное значение разности между накопленными
эмпирическими и теоретическими частотами; Sf - сумма эмпирических частот.
, где D - максимальное значение разности между накопленными
эмпирическими и теоретическими частотами; Sf - сумма эмпирических частот.
По
таблицам значений вероятностей l-критерия можно найти величину l, соответствующую вероятности Р. Если величина
вероятности Р значительна по отношению к найденной величине , то можно
предположить, что расхождения между теоретическим и эмпирическим
распределениями несущественны.
Необходимым
условием при использовании критерия согласия Колмогорова является достаточно
большое число наблюдений (не меньше ста).
При анализе
вариационного ряда и его свойств используют графические методы. Интервальный
ряд изображаю столбиковой диаграммой или гистограммой, в которой основания
столбиков, расположенные на оси – абсцисс – это интервалы значений варьирующего
признака, а высоты столбиков – частоты.
Если
имеется дискретный вариационный ряд или используются середины интервалов, то
графическое изображение такого ряда называют полигоном.
Преобразованной
формой вариационного ряда является ряд накопленных частот. Это ряд значений числа
единиц совокупности с меньшими или равными нижней границе соответствующего
интервала значениями признака. Такой ряд называют кумулятивным. Можно построить
кумулятивное распределение «не меньше, чем» – кумулята, и «больше, чем» –
огива.
Тема № 8. Выборочное наблюдение.
Основы выборочного метода
Выборочное наблюдение – одно из
наиболее современных видов статистического наблюдения. Выборочное наблюдение –
это такое наблюдение, при котором обследованию подвергается часть единиц
изучаемой совокупности, отобранных на основе научно разработанных принципов,
обеспечивающих получение достаточного количества достоверных данных, для того
чтобы охарактеризовать всю совокупность в целом.
Средние и относительные
показатели, полученные на основе выборочных данных, должны достаточно полно
воспроизводить или репрезентатировать соответствующие показатели совокупности в
целом.
Логика выборочного наблюдения
(1) определение объекта и целей выборочного
наблюдения;
(2) выбор схема отбора единиц для наблюдения;
(3) расчет объема выборки;
(4) проведение случайного отбора установленного
числа единиц из генеральной совокупности;
(5) наблюдение отобранных единиц по
установленной программе;
(6) расчет выборочных характеристик в
соответствии с программой выборочного наблюдения;
(7) определение ошибки, ее размера;
(8) распространение выборочных данных на
генеральную совокупность;
(9) анализ полученных данных.
Основные преимущества
(1) Выборочное наблюдение можно осуществить по
более широкой программе.
(2) Выборочное наблюдение более дешевое с точки
зрения затрат на его проведение.
(3) Выборочное наблюдение можно организовать
тогда и в тех случаях, когда отчетностью мы воспользоваться не можем.
Основные недостатки
(1) Полученные данные всегда содержат в себе
ошибку, о результатах наблюдения можно судить лишь с определенной степенью достоверности.
Но по сравнению с другими видами наблюдения это достоинство выборочного метода.
(2) Для его проведения требуются
квалифицированные кадры.
Вся совокупность единиц, из
которых производится отбор, называется генеральной. Совокупность единиц
отобранных называется выборочной.
Ошибки выборки
Чтобы оценить степень точности
выборочного наблюдения, необходимо оценить величину ошибок, которые могут
возникнуть в процессе проведения выборочного наблюдения.
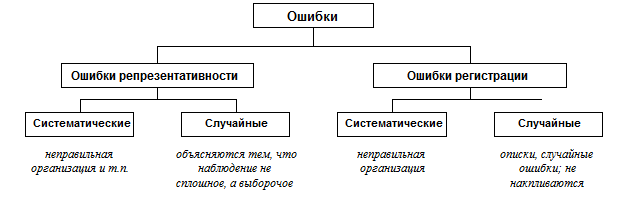 Основное внимание уделяется случайным
ошибкам репрезентативности.
Основное внимание уделяется случайным
ошибкам репрезентативности.
Статистическое
исследование может осуществляться по данным несплошного наблюдения, основная
цель которого состоит в получении характеристик изучаемой совокупности по
обследованной ее части. Одним из наиболее распространенных в статистике методов,
применяющих несплошное наблюдение, является выборочный метод.
Под
выборочным понимается метод статистического исследования, при котором обобщающие
показатели изучаемой совокупности устанавливаются по некоторой ее части на основе
положений случайного отбора. При выборочном методе обследованию подвергается
сравнительно небольшая часть всей изучаемой совокупности (обычно до 5 — 10%,
реже до 15 — 25%). При этом подлежащая изучению статистическая совокупность, из
которой производится отбор части единиц, называется генеральной
совокупностью. Отобранная из генеральной совокупности некоторая часть
единиц, подвергающаяся обследованию, называется выборочной совокупностью
или просто выборкой.
Значение
выборочного метода состоит в том, что
при минимальной численности обследуемых единиц проведение исследования
осуществляется в более короткие сроки и с минимальными затратами труда и
средств. Это повышает оперативность статистической информации, уменьшает ошибки
регистрации.
В
проведении ряда исследований выборочный метод является единственно возможным,
например, при контроле качества продукции (товара), если проверка
сопровождается уничтожением или разложением на составные части обследуемых
образцов (определение сахаристости фруктов, клейковины печеного хлеба, установление
носкости обуви, прочности тканей на разрыв и т.д.).
Проведение
исследования социально — экономических явлений выборочным методом складывается
из ряда последовательных этапов:
1)
обоснование (в соответствии с задачами исследования) целесообразности применения
выборочного метода;
2)
составление программы проведения статистического исследования выборочным методом;
3)
решение организационных вопросов сбора и обработки исходной информации;
4)
установление доли выборки, т.е. части подлежащих обследованию единиц генеральной
совокупности;
5)
обоснование способов формирования выборочной совокупности;
6)
осуществление отбора единиц из генеральной совокупности для их обследования;
7)
фиксация в отобранных единицах (пробах) изучаемых признаков;
8)
статистическая обработка полученной в выборке информации с определением обобщающих
характеристик изучаемых признаков;
9)
определение количественной оценки ошибки выборки;
10)
распространение обобщающих выборочных характеристик на генеральную совокупность.
В
генеральной совокупности доля единиц, обладающих изучаемым признаком, называется
генеральной долей (обозначается р), а средняя величина изучаемого
варьирующего признака — генеральной средней (обозначается 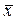 ).
).
В
выборочной совокупности долю изучаемого признака называют выборочной долей, или
частостью (обозначается 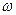 ), а среднюю величину
в выборке — выборочной средней (обозначается
), а среднюю величину
в выборке — выборочной средней (обозначается 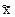 ).
).
Пример.
При
контрольной проверке качества хлебобулочных изделий проведено 5%-ное выборочное
обследование партии нарезных батонов из муки высшего сорта. При этом из 100
отобранных в выборку батонов 90 шт. соответствовали требованиям стандарта.
Средний вес одного батона в выборке составлял 500,5 г при среднем квадратическом
отклонении 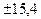 г.
г.
На
основе полученных в выборке данных нужно установить возможные значения доли
стандартных изделий и среднего веса одного изделия во всей партии.
Прежде
всего устанавливаются характеристики выборочной совокупности. Выборочная доля,
или частость, 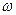 определяется из
отношения единиц, обладающих изучаемым признаком m, к общей численности единиц
выборочной совокупности n:
определяется из
отношения единиц, обладающих изучаемым признаком m, к общей численности единиц
выборочной совокупности n:
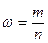
Поскольку
из 100 изделий, попавших в выборку n, 90 ед. оказались стандартными m, то
показатель частости равен: 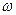 = 90:100=0,9.
= 90:100=0,9.
Средний
вес изделия в выборке х = 500,5 г определен взвешиванием. Но полученные
показатели частости (0,9) и средней величины (500,5 г) характеризуют долю
стандартной продукции и средний вес одного изделия лишь в выборке. Для
 определения соответствующих показателей для всей партии
товара надо установить возможные при этом значения ошибки выборки.
определения соответствующих показателей для всей партии
товара надо установить возможные при этом значения ошибки выборки.
Ошибка
выборки — это объективно возникающее расхождение
между характеристиками выборки и генеральной совокупности. Она зависит от ряда
факторов: степени вариации изучаемого признака, численности выборки, методом
отбора единиц в выборочную совокупность, принятого уровня достоверности
результата исследования.
Определение
ошибки выборочной средней.
При
случайном повторном отборе средняя ошибка выборочной средней рассчитывается
по формуле:
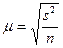 ,
,
 где
где 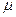 — средняя ошибка
выборочной средней;
— средняя ошибка
выборочной средней;
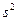 — дисперсия выборочной совокупности;
— дисперсия выборочной совокупности;
n —
численность выборки.
При
бесповторном отборе она рассчитывается по формуле:
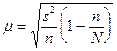 ,
,
где
N — численность генеральной совокупности.
Определение
ошибки выборочной доли.
При
повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:


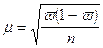 ,
,
где
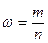 — выборочная доля единиц, обладающих изучаемым признаком;
— выборочная доля единиц, обладающих изучаемым признаком;
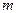 — число единиц,
обладающих изучаемым признаком;
— число единиц,
обладающих изучаемым признаком;
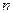 — численность выборки.
— численность выборки.
При
бесповторном способе отбора средняя ошибка выборочной доли определяется по формулам:
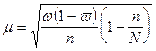
Предельная
ошибка выборки 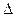 связана со средней ошибкой выборки
связана со средней ошибкой выборки 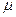 отношением:
отношением:
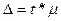 .
.
При
этом t как коэффициент кратности средней ошибки выборки зависит от значения вероятности
Р, с которой гарантируется величина предельной ошибки выборки.
Предельная
ошибка выборки при бесповторном отборе определяется по следующим формулам:
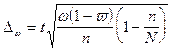 ,
,
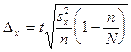 .
.
Предельная
ошибка выборки при повторном отборе определяется по формуле:
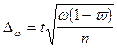 ,
,
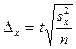 .
.
Малая
выборка.
При
контроле качества товаров в экономических исследованиях эксперимент может проводиться
на основе малой выборки.
Под
малой выборкой понимается несплошное статистическое обследование, при
котором выборочная совокупность образуется из сравнительно небольшого числа
единиц генеральной совокупности. Объем малой выборки обычно не превышает 30
единиц и может доходить до 4 — 5 единиц.
Средняя
ошибка малой выборки 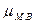 вычисляется по
формуле:
вычисляется по
формуле:
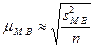 ,
,
где

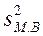 — дисперсия малой
выборки.
— дисперсия малой
выборки.
При
определении дисперсии 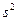 число степеней свободы
равно n-1:
число степеней свободы
равно n-1:
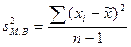 .
.
Предельная
ошибка малой выборки 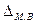 определяется по
формуле
определяется по
формуле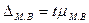
При
этом значение коэффициента доверия t зависит не только от заданной доверительной
вероятности, но и от численности единиц выборки n. Для отдельных значений t и n
доверительная вероятность малой выборки определяется по специальным таблицам
Стьюдента (Табл. 9.1.), в которых даны распределения стандартизированных
отклонений:
 .
.
Поскольку
при проведении малой выборки в качестве доверительной вероятности практически
принимается значение 0,59 или 0,99, то для определения предельной ошибки малой
выборки 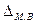 используются следующие
показания распределения Стьюдента:
используются следующие
показания распределения Стьюдента:
|
n
|
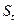
|
|
|
0,95
|
0,99
|
|
4
|
3,183
|
5,841
|
|
5
|
2,777
|
4,604
|
|
6
|
2,571
|
4,032
|
|
7
|
2,447
|
3,707
|
|
8
|
2,364
|
3,500
|
|
9
|
2,307
|
3,356
|
|
10
|
2,263
|
3,250
|
|
15
|
2,119
|
2,921
|
|
20
|
2,078
|
2,832
|
Способы
распространения характеристик выборки на генеральную совокупность.
Выборочный
метод чаще всего применяется для получения характеристик генеральной
совокупности по соответствующим показателям выборки. В зависимости от целей
исследований это осуществляется или прямым пересчётом показателей выборки для
генеральной совокупности, или посредством расчёта поправочных коэффициентов.
Способ
прямого пересчёта. Он состоит в том, что показатели выборочной
доли 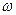 или средней
или средней 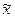 распространяется на
генеральную совокупность с учётом ошибки выборки.
распространяется на
генеральную совокупность с учётом ошибки выборки.
Так,
в торговле определяется количество поступивших в партии товара нестандартных
изделий. Для этого (с учётом принятой степени вероятности) показатели доли
нестандартных изделий в выборке умножаются на численность изделий во всей
партии товара.
Способ
поправочных коэффициентов. Применяется в случаях, когда целью выборочного
метода является уточнение результатов сплошного учета.
В
статистической практике этот способ используется при уточнении данных ежегодных
переписей скота, находящегося у населения. Для этого после обобщения данных
сплошного учета практикуется 10%-ное выборочное обследование с определением так
называемого “процента недоучета”.
Способы отбора единиц из генеральной
совокупности.
В
статистике применяются различные способы формирования выборочных совокупностей,
что обусловливается задачами исследования и зависит от специфики объекта изучения.
Основным
условием проведения выборочного обследования является предупреждение
возникновения систематических ошибок, возникающих вследствие нарушения принципа
равных возможностей попадания в выборку каждой единицы генеральной
совокупности. Предупреждение систематических ошибок достигается в результате
применения научно обоснованных способов формирования выборочной совокупности.
Существуют
следующие способы отбора единиц из генеральной совокупности:
1)
индивидуальный отбор — в выборку отбираются отдельные единицы;
2)
групповой отбор — в выборку попадают качественно однородные группы или серии
изучаемых единиц;
3)
комбинированный отбор — это комбинация индивидуального и группового отбора.
Способы
отбора определяются правилами формирования выборочной совокупности.
Выборка
может быть:
—
собственно-случайная;
—
механическая;
—
типическая;
—
серийная;
—
комбинированная.
Собственно-случайная
выборка состоит в том, что выборочная совокупность
образуется в результате случайного (непреднамеренного) отбора отдельных единиц
из генеральной совокупности. При этом количество отобранных в выборочную
совокупность единиц обычно определяется исходя из принятой доли выборки.
Доля
выборки есть отношение числа единиц выборочной совокупности n к численности
единиц генеральной совокупности N, т.е.
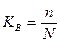 .
.
Так,
при 5%-ной выборке из партии товара в 2 000 ед. численность выборки n
составляет 100 ед. (5*2000:100), а при 20%-ной выборке она составит 400 ед.
(20*2000:100) и т.д.
Механическая
выборка состоит в том, что отбор единиц в
выборочную совокупность производится из генеральной совокупности, разбитой на
равные интервалы (группы). При этом размер интервала в генеральной совокупности
равен обратной величине доли выборки.
Так,
при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке
— каждая 20-я единица (1:0,05) и т.д.
Таким
образом, в соответствии с принятой долей отбора, генеральная совокупность как
бы механически разбивается на равновеликие группы. Из каждой группы в выборку
отбирается лишь одна единица.
Важной
особенностью механической выборки является то, что формирование выборочной
совокупности можно осуществить, не прибегая к составлению списков. На практике
часто используют тот порядок, в котором фактически размещаются единицы
генеральной совокупности. Например, последовательность выхода готовых изделий с
конвейера или поточной линии, порядок размещения единиц партии товара при
хранении, транспортировке, реализации и т.д.
Типическая
выборка. При типической выборке генеральная
совокупность вначале расчленяется на однородные типические группы. Затем из
каждой типической группы собственно-случайной или механической выборкой
производится индивидуальный отбор единиц в выборочную совокупность.
Типическая
выборка обычно применяется при изучении сложных статистических совокупностей.
Например, при выборочном обследовании производительности труда работников
торговли, состоящих из отдельных групп по квалификации.
Важной
особенностью типической выборки является то, что она дает более точные результаты
по сравнению с другими способами отбора единиц в выборочную совокупность.
Для
определения средней ошибки типической выборки используются формулы:
повторный
отбор
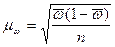 ,
, 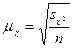
бесповторный
отбор
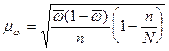 ,
, 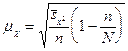
Дисперсия
определяется по следующим формулам:
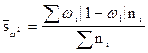 ,
, 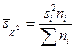
При
одноступенчатой выборке каждая отобранная единица сразу же подвергается
изучению по заданному признаку. Так обстоит дело при собственно-случайной и
серийной выборке.
При
многоступенчатой выборке производят подбор из генеральной совокупности отдельных
групп, а из групп выбираются отдельные единицы. Так производится типическая
выборка с механическим способом отбора единиц в выборочную совокупность.
Комбинированная
выборка может быть двухступенчатой. При этом генеральная совокупность сначала
разбивается на группы. Затем производят отбор групп, а внутри последних
осуществляется отбор отдельных единиц.
Тема № 9. Статистическое изучение
взаимосвязи социально - экономических явлений.
Различают два типа связи между
различными явлениями и их признаками: функциональную или жестко
детерминированную и статистическую или стохастически детерминированную с другой
стороны.
Если с изменением одной из
переменных вторая изменяется строго определенным образом, т.е. значению одной
переменной обязательно соответствует одно или несколько точно заданных значений
другой переменной, связь между ними является функциональной.
При стохастически детерминированной
связи (статистической) с изменением значения одной переменной вторая может в
определенных пределах принимать любые значения с некоторыми вероятностями, но
ее среднее значение или иные статистические (массовые) характеристики
изменяются по определенному закону, т.е. разным значениям одной переменной соответствуют
разные распределения значений другой переменной.
Частным случаем статистической связи
является корреляционная связь.
Корреляционная связь - это связь,
где воздействие отдельных факторов проявляется только как тенденция (в среднем)
при массовом наблюдении фактических данных.
Наиболее простым вариантом
корреляционной зависимости является парная корреляция, т.е. зависимость между
двумя признаками (результативным и факторным или между двумя факторными).
Математически эту зависимость можно выразить как зависимость результативного
показателя у от факторного показателя х. Связи могут быть прямые и обратные. В
первом случае с увеличением признака х увеличивается и признак у, при обратной
связи с увеличением признака х уменьшается признак у.
Методы изучения статистической
связи.
Важнейшей задачей является
определение формы связи с последующим расчетом параметров уравнения, или,
иначе, нахождение уравнения связи (уравнения регрессии).
Могут иметь место различные формы
связи:
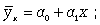
прямолинейная
линейные связи являются основными и
применяются также и при многофакторном анализе.
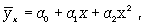 криволинейная в виде:
криволинейная в виде:
параболы второго порядка (или высших
порядков)
параболической связью описывается
взаимосвязь при которой характер связи между факторным и результативным
признаком может измениться на противоположный при прохождении некоторого
оптимального значения.
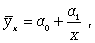
гиперболы
гиперболические зависимости
характерны для связей, в которых результативный признак не может варьироваться
неограниченно, его вариация имеет односторонний предел.
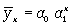
показательной функции
Параметры для всех этих уравнений связи, как
правило, определяют из системы нормальных уравнений, которые должны отвечать
требованию метода наименьших квадратов (МНК):
Другая важнейшая задача - измерение тесноты
зависимости - для всех форм связи может быть решена при помощи вычисления
эмпирического корреляционного отношения:
где -
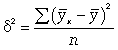
дисперсия в
ряду выравненных значений результативного показателя ; -
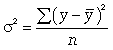
дисперсия в
ряду фактических значений у.
Для определения степени тесноты
парной линейной зависимости служит линейный коэффициент корреляции r, для
расчета которого можно использовать следующие формулы:
Линейный коэффициент корреляции
может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Чем
ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает
направление связи: «+» - прямая зависимость, «-» имеет место при обратной
зависимости.
Общий вид многофакторного уравнения
регрессии имеет вид:
y = a + b1x1 + .. + bkxk
Многофакторная система требует не
одного, а множества показателей тесноты связей. Основой измерения связей
является матрица коэффициентов корреляции. На основе этой матрицы судят о
тесноте связи факторов с результативным признаком и между собой. Не
рекомендуется включать в уравнение регрессии факторы слабо связанные с
результативным признаком, но тесно связанные с другими факторами. Множественный
коэффициент корреляции определяется как отношение части вариации
результативного признака, объясняемой за счет вариации входящих в уравнение
факторов, к общей вариации результативного признака за счет всех факторов. Под
вариацией понимается сумма квадратов отклонений индивидуальных значений от
расчетных по уравнению регрессии (объясненная вариация) или от общей средней
величины признака (общая вариация).
Для случая двух факторов коэффициент
множественной детерминации вычисляется
по формуле из парных коэффициентов корреляции::
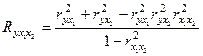
Коэффициент частной детерминации
фактора xm – это доля вариации у, не объясненной ранее
включенными факторами. Если обозначить частный коэффициент детерминации ддя
фактора xm как 
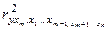 Тогда
Тогда 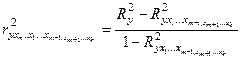
Основные задачи применения
корреляционно-регрессионного анализа.
В соответствии с сущностью
корреляционной связи ее изучение имеет две цели: 1) измерение параметров
уравнения, выражающего связь средних значений зависимой переменной со
значениями независимой переменной; 2) измерение тесноты связи двух (или
большего числа признаков) между собой
Задачи корреляционно-регрессионного
анализа:
1. Задачи выделения важнейших
факторов, влияющих на результативный признак (т.е. вариацию его значений в
совокупности). Эта задача решается на базе мер тесноты связи факторов с
результативным признаком.
2. Задачи оценки хозяйственной
деятельности по эффективности использования факторов производства. Эта задача
решается путем расчета для каждой единицы совокупности тех величин
результативного признака, которые были получены при средней по совокупности эффективности
использования факторов и сравнивания их с фактическими результатами
производства.
3. Задача прогнозирования возможных
значений результативного признака при задаваемых значениях факторных признаков.
Такая задача решается путем подстановки ожидаемых, или планируемых, или
возможных значений факторных признаков в уравнении связи и вычисления ожидаемых
значений результативного признака.
4. Задача подготовки данных,
необходимых в качестве исходных для решения оптимизационных задач.
При решении каждой из названных
задач нужно учитывать особенности и ограничения корреляционно-регрессионного
метода. Всякий раз необходимо специально обосновать возможность причинной
интерпретации уравнения как объясняющего связь между вариацией фактора и
результата. Трудно обеспечить раздельную оценку влияния каждого из факторов.
Непараметрические методы определения
тесноты связи.
В статистической практике могут
встречаться такие случаи, когда качества факторных и результативных признаков
не могут быть выражены численно. Поэтому для измерения тесноты зависимости
необходимо использовать другие показатели. Для этих целей используются так
называемые непараметрические методы.
Наибольшее распространение имеют
ранговые коэффициенты корреляции, в основу которых положен принцип нумерации
значений статистического ряда. При использовании коэффициентов корреляции
рангов коррелируются не сами значения показателей х и у, а только номера их
мест, которые они занимают в каждом ряду значений. В этом случае номер каждой
отдельной единицы будет ее рангом.
Коэффициент корреляции рангов Спирмэна (р)
основан на рассмотрении разности рангов значений результативного и факторного
признаков и может быть рассчитан по формуле
где d = Nx - Ny , т.е. разность
рангов каждой пары значений х и у; n - число наблюдений.
К непараметрическим методам
исследования можно отнести коэффициент ассоциации Кас и коэффициент
контингенции Ккон, которые используются, если, например, необходимо
исследовать тесноту зависимости между качественными признаками, каждый из
которых представлен в виде альтернативных признаков.
Для определения этих коэффициентов
создается расчетная таблица (таблица «четырех полей»), где статистическое
сказуемое схематически представлено в следующем виде:
|
Признаки
|
А(да)
|
А(нет)
|
Итого
|
|
В(да)
|
a
|
b
|
a + b
|
|
В(нет)
|
c
|
d
|
c + d
|
|
Итого
|
a + c
|
b + d
|
n
|
Здесь а, b, c, d - частоты взаимного
сочетания (комбинации) двух альтернативных признаков ; n - общая сумма частот.
Коэффициент ассоциации можно рассчитать по
формуле
Коэффициент контингенции рассчитывается по
формуле
Нужно иметь в виду, что для одних и
тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше
коэффициента ассоциации.
Наконец, следует упомянуть
коэффициент Фехнера, характеризующий элементарную степень тесноты связи,
который целесообразно использовать для установления факта наличия связи, когда
существует небольшой объем исходной информации. Данный коэффициент определяется
по формуле
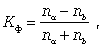
где na
- количество совпадений знаков отклонений индивидуальных величин от их средней
арифметической; nb - соответственно количество несовпадений.
Коэффициент Фехнера может изменяться в пределах -1,0 Кф +1,0.
Целью применения
корреляционно-регрессионного метода является построение такого уравнения
регрессии, которое включает основные факторы, влияющие на вариацию
результативного признака, обладающего высоким (не ниже 0,5) коэффициентом
детерминации и коэффициентами регрессии, интерпретируемыми в соответствие с
теоретическим знанием о природе связей в изучаемой системе.
При использовании корреляционно-регрессионного
метода при анализе социально-экономических явлений необходимо учесть следующие
ограничения.
Интерпретировать корреляционные
показатели строго следует лишь в терминах вариации (различий в пространстве)
отклонений от средней величины. Если задача состоит в изменении связи не между
вариацией двух признаков в совокупности, а меду изменениями признаков объекта
во времени, то корреляционно-регрессионный анализ требует значительных
изменений.
Корреляционно-регрессионный метод
основан на том, что группировка совокупности по одному факторному признаку при
условии, что все другие не связаны с изучаемым, а случайные отклонения и ошибки
взаимопогасились в большой совокупности. Если же фактор связан с другими
факторами, то будет получена не чистая характеристика влияния.
При этом относительная простота и
применение компьютерной техники позволяет достаточно широко и эффективно
применять данных метод на практике.
Параметрический методы определения
тесноты связи состоит в расчете F критерия
Фишера, который рассчитывается по формуле:
F=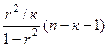
где r2 –
коэффициент корреляции, n – число единиц
в совокупности, к- число степеней свобожы.
Для оценки надежности результатов
уравнения регрессии F сравнивают c Fтабл при заданном уровне вероятности. Если полученное
значение больше табличного, то можно говорить о высокой степени надежности
результатов регрессионного моделирования. Если ниже – то полученные оценки
коэффициентов регрессии статистически незначимы.
Коэффициент конкордации
где n - количество анализируемых объектов, m - количество экспертов, Rij
- ранг j-го объекта, который присвоен
ему i-ым экспертом.
Следует обратить внимание на отличие
значений коэффициента конкордации от коэффициента корреляции, так как он
существует в пределах от 0 до 1. Если мнения экспертов полностью
противоположны, коэффициент конкордации равен нулю (W = 0), а коэффициент корреляции в этом случае будет равен -1.
Тема № 10. Ряды динамики и их
применение в анализе
социально-экономических явлений.
Изменение социально-экономических
явлений во времени изучается статистикой методом построения и анализа
динамических рядов. Ряды динамики - это значения статистических показателей,
которые представлены в определенной хронологической последовательности.
Каждый динамический ряд содержит две
составляющие: 1) показатели периодов времени (годы, кварталы, месяцы, дни или
даты); 2) показатели, характеризующие исследуемый объект за временные периоды
или на соответствующие даты, которые называют уровнями ряда.
Уровни ряда выражаются как
абсолютными, так и средними или относительными величинами. В зависимости от
характера показателей строят динамические ряды абсолютных, относительных и
средних величин. Ряды динамики из относительных и средних величин строят на
основе производных рядов абсолютных величин. Различают интервальные и моментные
ряды динамики.
Динамический интервальный ряд
содержит значения показателей за определенные периоды времени. В интервальном
ряду уровни можно суммировать, получая объем явления за более длительный
период, или так называемые накопленные итоги.
Динамический моментный ряд отражает
значения показателей на определенный момент времени (дату времени). В моментных
рядах исследователя может интересовать только разность явлений, отражающая
изменение уровня ряда между определенными датами, поскольку сумма уровней здесь
не имеет реального содержания. Накопленные итоги здесь не рассчитываются.
Важнейшим условием правильного
построения динамических рядов является сопоставимость уровней рядов,
относящихся к различным периодам. Уровни должны быть представлены в однородных
величинах, должна иметь место одинаковая полнота охвата различных частей
явления.
Для того, чтобы избежать искажения
реальной динамики, в статистическом исследовании проводятся предварительные
расчеты (смыкание рядов динамики), которые предшествуют статистическому анализу
динамических рядов. Под смыканием рядов динамики понимается объединение в один
ряд двух и более рядов, уровни которых рассчитаны по разной методологии или не
соответствуют территориальным границам и т.д. Смыкание рядов динамики может
предполагать также приведение абсолютных уровней рядов динамики к общему
основанию, что нивелирует несопоставимость уровней рядов динамики.
Для характеристики интенсивности
развития во времени используются статистические показатели, получаемые
сравнением уровней между собой, в результате чего получаем систему абсолютных и
относительных показателей динамики: абсолютный прирост, коэффициент роста, темп
роста, темп прироста, абсолютное значение 1% прироста. Для характеристики
интенсивности развития за длительный период рассчитываются средние показатели:
средний уровень ряда, средний абсолютный прирост, средний коэффициент роста,
средний темп роста, средний темп прироста, среднее абсолютное значение 1%
прироста.
Базисные показатели характеризуют
итоговый результат всех изменений в уровнях ряда от периода базисного уровня до
данного (i-го) периода. Рассчитываются как отношение i-го уровня к базисному (начальному).
Цепные показатели характеризуют
интенсивность изменения уровня от одного периода к другому в пределах того
промежутка времени, который исследуется. Рассчитываются как отношение i-го к предшествующему уровню.
Абсолютный прирост выражает
абсолютную скорость изменения ряда динамики и определяется как разность между
данным уровнем и уровнем, принятым за базу сравнения.
Абсолютный прирост (базисный)
где yi - уровень сравниваемого
периода; y0 - уровень базисного периода.
Абсолютный прирост с переменной
базой (цепной), который называют скоростью роста,
где yi - уровень сравниваемого
периода; yi-1 - уровень предшествующего периода.
Коэффициент роста Ki
определяется как отношение данного уровня к предыдущему или базисному,
показывает относительную скорость изменения ряда. Если коэффициент роста
выражается в процентах, то его называют темпом роста.
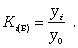
Коэффициент роста базисный
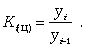
Коэффициент роста цепной
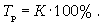 Темп роста
Темп роста
Темп прироста ТП определяется как
отношение абсолютного прироста данного уровня к предыдущему или базисному.
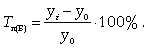
Темп прироста базисный
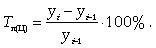
Темп прироста цепной
Темп прироста можно рассчитать и
иным путем: как разность между темпом роста и 100 % или как разность между
коэффициентом роста и 1 (единицей):
1) Тп = Тр -
100%; 2) Тп = Ki - 1.
Абсолютное значение одного процента прироста Ai
. Этот показатель служит косвенной мерой базисного уровня. Представляет собой
одну сотую часть базисного уровня, но одновременно представляет собой и
отношение абсолютного прироста к соответствующему темпу роста. Данный
показатель рассчитывают по формуле
Для характеристики динамики
изучаемого явления за продолжительный период рассчитывают группу средних
показателей динамики. Можно выделить две категории показателей в этой группе:
а) средние уровни ряда; б) средние показатели изменения уровней ряда.
Средние уровни ряда рассчитываются в
зависимости от вида временного ряда.
Для интервального ряда динамики
абсолютных показателей средний уровень ряда рассчитывается по формуле простой
средней арифметической:
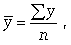
где n - число уровней ряда.
Средний уровень моментного ряда с
равными интервалами рассчитывается по формуле средней хронологической:
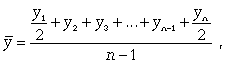
где n - число дат.
Средний уровень моментного ряда с
неравными интервалами рассчитывается по формуле средней арифметической взвешенной,
где в качестве весов берется продолжительность промежутков времени между
временными моментами изменений в уровнях динамического ряда:
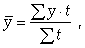
где t -
продолжительность периода (дни, месяцы), в течение которого уровень не
изменялся.
Средний абсолютный прирост (средняя
скорость роста) определяется как средняя арифметическая из показателей скорости
роста за отдельные периоды времени:
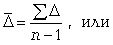
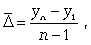
где yn - конечный уровень
ряда; y1 - начальный уровень ряда.
Средний коэффициент роста
рассчитывается по формуле средней геометрической из показателей коэффициентов
роста за отдельные периоды:
 где Кр1 , Кр2 , ..., Кр n-1
- коэффициенты роста по сравнению с предыдущим периодом; n - число
уровней ряда.
где Кр1 , Кр2 , ..., Кр n-1
- коэффициенты роста по сравнению с предыдущим периодом; n - число
уровней ряда.
Средний коэффициент роста можно
определить иначе:
Средний темп роста, %. Это средний
коэффициент роста, который выражается в процентах:
Средний темп прироста , %. Для
расчета данного показателя первоначально определяется средний темп роста,
который затем уменьшается на 100%. Его также можно определить, если уменьшить
средний коэффициент роста на единицу:
Среднее абсолютное значение 1% прироста можно
рассчитать по формуле
В ходе обработки динамического ряда
важнейшей задачей является выявление основной тенденции развития явления
(тренда) и сглаживание случайных колебаний. Для решения этой задачи в
статистике существуют особые способы, которые называют методами выравнивания.
Выделяют три основных способа
обработки динамического ряда: а) укрупнение интервалов динамического ряда и
расчет средних для каждого укрупненного интервала; б) метод скользящей средней;
в) аналитическое выравнивание (выравнивание по аналитическим формулам).
Укрупнение интервалов - наиболее
простой способ. Он заключается в преобразовании первоначальных рядов динамики в
более крупные по продолжительности временных периодов, что позволяет более
четко выявить действие основной тенденции (основных факторов) изменения
уровней. По интервальным рядам итоги исчисляются путем простого суммирования
уровней первоначальных рядов. Для других случаев рассчитывают средние величины
укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по
формулам простой средней арифметической.
Скользящая средняя - это такая
динамическая средняя, которая последовательно рассчитывается при передвижении
на один интервал при заданной продолжительности периода. Если, предположим,
продолжительность периода равна 3, то скользящие средние рассчитываются
следующим образом:
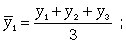
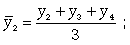
и т.д.
Первую рассчитанную среднюю относят
ко второму периоду, вторую - к третьему, третью - к четвертому и т.д. По
сравнению с фактическим сглаженный ряд становится короче на (m - 1)/2, где m -
число уровней интервала.
Важнейшим способом количественного
выражения общей тенденции изменения уровней динамического ряда является
аналитическое выравнивание ряда динамики, которое позволяет получить описание
плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями,
которые рассчитываются на основе определенной кривой, где уравнение
рассматривается как функция времени. Вид уравнения зависит от конкретного
характера динамики развития. Его можно определить как теоретически, так и
практически. Теоретический анализ основывается на рассчитанных показателях
динамики. Практический анализ - на исследовании линейной диаграммы.
Задачей аналитического выравнивания
является определение не только общей тенденции развития явления, но и некоторых
недостающих значений как внутри периода, так и за его пределами. Способ
определения неизвестных значений внутри динамического ряда называют
интерполяцией. Эти неизвестные значения можно определить: 1) используя
полусумму уровней, расположенных рядом с интерполируемыми; 2) по среднему
абсолютному приросту; 3) по темпу роста. В результате аналитического
выравнивания получают следующую трендовую модель:
где f(t) – уровень, определяемый
тенденцией развития; et – случайное и циклическое отклонение от
тенденции.
Целью аналитического выравнивания
динамического ряда является определение аналитической или графической
зависимости f(t). На практике по имеющемуся временному ряду задают вид и
находят параметры функции f(t), а затем анализируют поведение отклонений от
тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное
объяснение изучаемого процесса.
Чаще всего при выравнивании
используются следующие зависимости:
Линейная зависимость выбирается в тех случаях,
когда в исходном временном ряду наблюдаются более или менее постоянные
абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к
снижению.
Параболическая зависимость
используется, если абсолютные цепные приросты сами по себе обнаруживают
некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных
приростов (разности второго порядка) никакой тенденции развития не проявляют.
Экспоненциальные зависимости
применяются, если в исходном временном ряду наблюдается либо более или менее
постоянный относительный рост (устойчивость цепных темпов роста, темпов
прироста, коэффициентов роста), либо, при отсутствии такого постоянства, –
устойчивость в изменении показателей относительного роста (цепных темпов роста
цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или
темпов роста и т.п.).
Оценка параметров (a0, a1, a2, ...)
осуществляется следующими методами:
1) методом избранных точек,
2) методом наименьших расстояний,
3) методом наименьших квадратов
(МНК).
В большинстве расчетов используют
метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов
отклонений фактических уровней от выравненных:
Для линейной зависимости (f(t)=a0+a1t)
параметр а0 обычно интерпретации не имеет, но иногда его
рассматривают как обобщенный начальный уровень ряда; а1 – сила
связи, т.е. параметр, показывающий, насколько изменится результат при изменении
времени на единицу. Таким образом, а можно представить как постоянный
теоретический абсолютный прирост.
Построив уравнение регрессии, проводят оценку
его надежности. Оценка надежности параметров уравнения проводится на основании
анализа случайной компоненты. Это делается посредством критерия Фишера (F).
Фактический уровень (Fфакт) сравнивается с теоретическим (табличным)
значением:
где k – число параметров функции,
описывающей тенденцию;
n – число уровней ряда;
Fфакт сравнивается с Fтеор
при v1 = (k-1), v2 = (n-k) степенях свободы и уровне значимости a (обычно a =
0,05). Если Fфакт > Fтеор, уравнение регрессии значимо, т.е. построенная
модель адекватна фактической временной тенденции.
Способ определения количественных
значений за пределами ряда называют экстраполяцией. Экстраполирование
используется для прогнозирования тех факторов, которые не только в прошлом и
настоящем обусловливают развитие явления, но и могут оказать влияние на его
развитие в будущем.
Экстраполировать можно по средней
арифметической, по среднему абсолютному приросту, по среднему темпу роста.
При аналитическом выравнивании может иметь место
автокорреляция, под которой понимается зависимость между соседними членами
динамического ряда. Автокорреляцию можно установить с помощью перемещения
уровня на одну дату. Коэффициент автокорреляции вычисляется по формуле
Автокорреляцию в рядах можно
устранить, коррелируя не сами уровни, а так называемые остаточные величины
(разность эмпирических и теоретических уровней). В этом случае корреляцию между
остаточными величинами можно определить по формуле
Анализ рядов динамики предполагает и
исследование сезонной неравномерности (сезонных колебаний), под которыми
понимают устойчивые внутригодовые колебания, причиной которых являются
многочисленные факторы, в том числе и природно-климатические. Сезонные колебания
измеряются с помощью индексов сезонности, которые рассчитываются двумя
способами в зависимости от характера динамического развития.
При относительно неизменном годовом
уровне явления индекс сезонности можно рассчитать как процентное отношение
средней величины из фактических уровней одноименных месяцев к общему среднему
уровню за исследуемый период:
В условиях изменчивости годового
уровня индекс сезонности определяется как процентное отношение средней величины
из фактических уровней одноименных месяцев к средней величине из выровненных
уровней одноименных месяцев:
В простейших случаях для
характеристики взаимосвязи двух или более рядов их приводят к общему основанию,
для чего берут в качестве базисных уровни за один и тот же период и исчисляют
коэффициенты опережения по темпам роста или прироста. Коэффициенты опережения
по темпам роста – это отношение темпов роста (цепных или базисных) одного ряда
к соответствующим по времени темпам роста (также цепным или базисным) другого
ряда. Аналогично находятся и коэффициенты опережения по темпам прироста.
Временной лаг - экономический
показатель, показывающий отставание или опережение одного экономического
явления по сравнению с другим, связанным с ним явлением.
Тема № 11. Индексный метод
анализа. Понятие о индексах.
Сфера их применения и
классификация
Индексами называют сравнительные
относительные величины, которые характеризуют изменение сложных
социально-экономических показателей (показатели, состоящие из несуммируемых
элементов) во времени, в пространстве, по сравнению с планом.
Индекс - это результат сравнения
двух одноименных показателей, при исчислении которого следует различать
числитель индексного отношения (сравниваемый или отчетный уровень) и
знаменатель индексного отношения (базисный уровень, с которым производится
сравнение). Выбор базы зависит от цели исследования. Если изучается динамика,
то за базисную величину может быть взят размер показателя в периоде,
предшествующем отчетному. Если необходимо осуществить территориальное
сравнение, то за базу можно принять данные другой территории. За базу сравнения
могут приниматься плановые показатели, если необходимо использовать индексы как
показатели выполнения плана.
Признак изменение которого
характеризует индекс называется индексируемым.
Признак-вес выполняет функцию веса
по отношению к индексируемому признаку.
При построении индексов решают
следующие вопросы: 1) определение вида индекса и вида показателей с помощью
которых строится индекс; 2) выбор базы (а) данные по той же совокупности и по
тому же признаку за предшествующий период; б) плановое задание; в) данные по
какой-либо другой совокупности, сходной по характеру с изучаемой).
При установлении базы необходимо
соблюдать следующие правила: сопоставимость базисных и отчетных данных;
обеспечить типичность базовых данных.
По степени охвата элементов явления
индексы делят на индивидуальные и общие (сводные).
Индивидуальные индексы (i) - это
индексы, которые характеризуют изменение только одного элемента совокупности.
Общий (сводный) индекс (I) характеризует
изменение по всей совокупности элементов сложного явления. Если индексы
охватывают только часть явления, то их называют групповыми.
В зависимости от способа изучения
общие индексы могут быть построены или как агрегатные (от лат. аggrega -
присоединяю) индексы, или как средние взвешенные индексы (средние из
индивидуальных).
Способ построения агрегатных
индексов заключается в том, что при помощи так называемых соизмерителей можно
выразить итоговые величины сложной совокупности в отчетном и базисном периодах,
а затем первую сопоставить со второй.
Если индексы можно рассчитать на
основе сравнения двух сумм, полученных, например, путем умножения
среднесписочной численности работников в
базисном и отчетном периоде (по каждому j предприятию, структурному подразделению и т.д.) t0j и
t1j и средней
заработной - z0j и
z1j , то
такие индексы называют агрегатными. Таким образом, общие индексы могут быть
рассчитаны не только через осреднение индивидуальных индексов, а и на основе
сравнения двух сумм (агрегатов). Агрегатные индексы считаются основной формой
индексов. Они выполняют две функции: синтетическую и аналитическую.
Первая функция обеспечивается тем,
что в одном индексе обобщаются (синтезируются) непосредственно несоизмеримые
явления, когда мы записываем 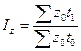 (где z – средняя заработная плата, а t – среднесписочная численность работников), то
благодаря использованию денежного соизмерителя можно агрегировать данные по
различным категориям работников (несопоставимым
по натуральным измерителям).
(где z – средняя заработная плата, а t – среднесписочная численность работников), то
благодаря использованию денежного соизмерителя можно агрегировать данные по
различным категориям работников (несопоставимым
по натуральным измерителям).
Аналитическая функция вытекает из
взаимосвязи индексов, т.к. практически каждый индекс можно рассматривать как
составляющую некой системы индексов, в которой его роль сводится к измерению
одного из факторов общего изменения сложного явления и вклада этого фактора в
соответствующее изменение.
Так, например, индекс цен можно
рассматривать как показатель влияния изменения средней заработной платы на фонд
оплаты труда, что основано на следующей связи признаков: среднесписочная
численность * средняя заработная плата = фонд оплаты труда или tz = w. Системе
признаков соответствует система индексов.
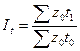 и
и 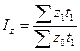
Когда мы указывает индекс
среднесписочной численности работников
или индекс средней заработной платы, мы имеем в виду изменение фонда
оплаты труда за счет изменения среднесписочной численности работников или
средней заработной платы.
При построении агрегатных индексов
пользуются такими понятиями, как индексируемый признак и признак-вес.
Индексируемый признак – это признак, изменение которого характеризует данный
индекс. Например, в It – это t. Значение индексируемого признака изменяется, т.е. отчетное значение сопоставляется с базисным.
Признак-вес выполняет функцию веса
по отношению к индексируемому признаку, его значение в индексе принимается
постоянным, т.к. он не должен искажать оценку изменения индексируемого
признака. Например, в It –
это z.
Если индексы рассматриваются в
системе, то должна обеспечиваться взаимосвязь между ними: It * Iz = Iw
Расчет среднего индекса применяется
при определении общего индекса или общего изменения состояния изучаемого
объекта. Так как расчет среднего индекса как отношения суммы индивидуальных
признаков в текущем и базисном периоде ( 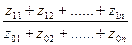 ) или как простой средней из индивидуальных индексов (
) или как простой средней из индивидуальных индексов (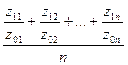 ), т.е. невзвешенных средних
арифметических не учитывает объемов и структуры изучаемого объекта, то
применяют взвешенную среднюю.
), т.е. невзвешенных средних
арифметических не учитывает объемов и структуры изучаемого объекта, то
применяют взвешенную среднюю.
Для расчета среднего индекса может
использоваться другие формы средних величин.
Средняя геометрическая: 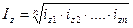
Средняя гармоническая невзвешенная
рассчитывается по формуле:
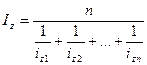
Индексы с постоянными и переменными
весами и метод выявления роли факторов динамики сложных явлений.
При построении агрегатных индексов
веса могут быть закреплены на базисном, отчетном или смешанном уровнях. При
закреплении весов только на базисном или только на отчетном уровне, постоянных
весов, равенство
It * Iz = Iw не выполняется. Например, 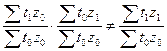
Только когда взаимосвязанные индексы
строятся с весами разных периодов, увязка их в системе выполняется. Например, 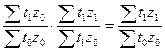 . В приведенном примере индексы первичных признаков стоятся
на весах базисного периода, вторичных – на весах отчетного периода.
Отечественная статистика в своей практике придерживалась именно такого подхода.
Но при таком подходе значение полученных индексов при изменении последовательности
признаков различаются, т.е. если в модели tz = w t и z поменять местами
значения полученных индексов будут иметь расхождения.
. В приведенном примере индексы первичных признаков стоятся
на весах базисного периода, вторичных – на весах отчетного периода.
Отечественная статистика в своей практике придерживалась именно такого подхода.
Но при таком подходе значение полученных индексов при изменении последовательности
признаков различаются, т.е. если в модели tz = w t и z поменять местами
значения полученных индексов будут иметь расхождения.
Различие между индексами с разными
весами можно объяснить при помощи уравнения В.И. Борткевича (1868 – 1931):

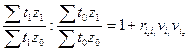 , где
, где 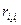 - корреляция между изменением цен и объемом продаж на
отдельные товары,
- корреляция между изменением цен и объемом продаж на
отдельные товары, 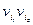 - темпы изменения объемов реализованных товаров и цен
соответственно.
- темпы изменения объемов реализованных товаров и цен
соответственно.
Таким образом, из формулы видно, что
индексы с отчетными и базисными весами будут равны, если выполняется хотя бы
одно из условий: 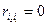 ,
, 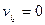 ,
, 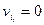 . Чем больше величина сравниваемого периода, тем сильнее проявляется
различие.
. Чем больше величина сравниваемого периода, тем сильнее проявляется
различие.
Однако на практике, как правило,
стремятся получить однозначное решение тем или иным способом. Первый способ
заключается в получении средних оценок изменений, либо путем построения
индексов на средних весах 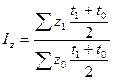
либо через осреднение
равновзвешенных индексов. При этом предпочтение отдается средней
геометрической. 
Второй путь основан на предпочтении
какого-то одного варианта построения взаимосвязанных индексов, применялся в
отечественной практике.
В статистике имеют большое значение
индексы переменного и фиксированного состава, которые используются при анализе
динамики средних показателей.
Индексом переменного состава
называют отношение двух средних уровней.
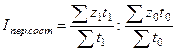
Индекс фиксированного состава есть
средний из индивидуальных индексов. Он рассчитывается как отношение двух
стандартизованных средних, где влияние изменения структурного фактора
устранено, поэтому данный индекс называют еще индексом постоянного состава.
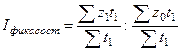
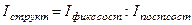
В зависимости от характера и
содержания индексируемых величин различают индексы количественных (объемных)
показателей и индексы качественных показателей.
К индексам количественных (объемных)
показателей относятся такие индексы, как индексы физического объема
производства продукции, затрат на выпуск продукции, стоимости продукции, а
также индексы показателей, размеры которых определяются абсолютными величинами.
Используются различные виды индексов количественных показателей.
Индекс физического объема продукции
(ФОП) отражает изменение выпуска продукции.
Индивидуальный индекс ФОП отражает
изменение выпуска продукции одного вида и определяется по формуле
где q1 и q0 - количество
продукции данного вида в натуральном выражении в текущем и базисном периодах.
Агрегатный индекс ФОП отражает
изменение выпуска всей совокупности продукции, где индексируемой величиной
является количество продукции q, а соизмерителем - цена р:
где q1 и q0 -
количество выработанных единиц отдельных видов продукции соответственно в
отчетном и базисном периодах; p0 - цена единицы продукции
(отдельного вида) в базисном периоде.
При вычислении индекса ФОП в
качестве соизмерителей может выступать также себестоимость продукции или
трудоемкость.
Средние взвешенные индексы ФОП
используются в том случае, если известны индивидуальные индексы объема по
отдельным видам продукции и стоимость отдельных видов продукции (или затраты) в
базисном или отчетном периоде.
Средний взвешенный арифметический
индекс ФОП определяется по формуле
где iq - индивидуальный
индекс по каждому виду продукции; q0 p0 - стоимость продукции каждого вида в
базисном периоде.
Средний взвешенный гармонический
индекс ФОП
где q1 p1 - стоимость
продукции каждого вида в текущем периоде.
Аналогично рассчитывается индекс
затрат на выпуск продукции, который отражает изменение затрат на производство и
может быть как индивидуальным, так и агрегатным.
Между индексами существует также
взаимосвязь и взаимозависимость, как и между самими экономическими явлениями,
что позволяет проводить факторный анализ. Благодаря индексному методу можно
рассматривать все факторы независимо друг от друга, что дает возможность
определить размер абсолютного изменения сложного явления за счет каждого
фактора в отдельности.
Предположим, что результативный
признак зависит от трех факторов и более. В этом случае результативный индекс
примет вид
Изменение результативного индекса за
счет каждого фактора может быть выражено следующим образом:




Для выявления роли каждого фактора в
отдельности индекс сложного показателя разлагают на частные (факторные)
индексы, которые характеризуют роль каждого фактора. При этом используют два
метода: метод обособленного изучения факторов; последовательно-цепной метод.
При первом методе сложный показатель
берется с учетом изменения лишь того фактора, который взят в качестве
исследуемого, все остальные остаются неизменными на уровне базисного периода.
Последовательно-цепной метод
предполагает использование системы взаимосвязанных индексов, которая требует
определенного расположения факторов. Как правило, на первом месте в цепи
располагают качественный фактор. При определении влияния первого фактора все
остальные сохраняются в числителе и знаменателе на уровне базисного периода,
при определении второго факторного индекса первый фактор сохраняется на уровне
базисного периода, а третий и все последующие - на уровне отчетного периода,
при определении третьего факторного индекса первый и второй факторы сохраняются
на уровне базисного периода, четвертый и все остальные - на уровне отчетного
периода и т.д.
Территориальные индексы.
Индексы могут быть использованы не
только как показатели сравнения состояний изучаемого явления во времени, но и в
пространстве, между отдельными территориями. Индексы позволяющие сравнивать
различные территориальные образования между собой носят название
территориальных индексов. При построении территориальных индексов применяются
те же правила, что при сравнении явлении во времени, только в территориальных
индексах в качестве весов используются показатели численности населения, доли в
общих доходах населения от заработной платы и т.д. Кроме того, при сравнении
разных территорий за один период значки «0» и «1» не используются.
Использование индексов при анализе различий между территориями обусловлено
следующим: индексы позволяют сопоставить территории с разным уровнем
социально-экономического развития, с разным уровнем развития производства, с
разной структурой потребительского рынка и доходов и т.д.
Тема № 12. Многомерный
статистический анализ
Дисперсионный анализ.
Целью дисперсионного анализа
является проверка статистической значимости различия между средними (для групп
или переменных). Эта проверка проводится с помощью разбиения суммы квадратов на
компоненты, т.е. с помощью разбиения общей дисперсии (вариации) на части, одна
из которых обусловлена случайной ошибкой (то есть внутригрупповой
изменчивостью), а вторая связана с различием средних значений. Последняя
компонента дисперсии затем используется для анализа статистической значимости
различия между средними значениями. Если это различие значимо, нулевая гипотеза отвергается
и принимается альтернативная гипотеза о существовании различия между средними.
Разбиение суммы квадратов. Для
выборки объема n выборочная дисперсия вычисляется как сумма квадратов
отклонений от выборочного среднего, деленная на n-1 (объем выборки минус единица).
Таким образом, при фиксированном объеме выборки n дисперсия есть функция суммы
квадратов (отклонений). В основе дисперсионного анализа лежит разделение
дисперсии на части или компоненты, т.е. выборка разбивается на две части в
которых вычисляются среднии и сумма квадратов отклонений. Расчет тех же
показателей по выборки в целом дает большее значение дисперсии, что объясняется
расхождение между групповыми средними. Таким образом, дисперсионный анализ
позволяет объяснить внутригрупповую изменчивость, которая при исследовании всей
группы в целом не может быть изменена.
Проверка значимости в дисперсионном
анализе основана на сравнении компоненты дисперсии, обусловленной межгрупповым
и компоненты дисперсии, обусловленной внутригрупповым разбросом (называемой
средним квадратом ошибки). Если верна нулевая гипотеза (равенство средних в
двух популяциях), то можно ожидать сравнительно небольшое различие выборочных
средних из-за чисто случайной изменчивости. Поэтому, при нулевой гипотезе,
внутригрупповая дисперсия будет практически совпадать с общей дисперсией,
подсчитанной без учета групповой принадлежности. Полученные внутригрупповые
дисперсии можно сравнить с помощью F-критерия, проверяющего, действительно ли
отношение дисперсий значимо больше 1.
Преимущества: 1) дисперсионный
анализ существенно более эффективен и, для малых выборок, т.к. более информативен; 2)дисперсионный анализ
позволяет обнаружить эффекты взаимодействия
между факторами и, поэтому, позволяет проверять более сложные гипотезы
Метод главных компонент состоит в
линейном понижении размерности, в котором определяются попарно ортогональные
направления максимальной вариации исходных данных, после чего данные
проектируются на пространство меньшей размерности, порожденное компонентами с
наибольшей вариацией.
Метод главных компонент является
частью факторного анализа, который состоит в том, что две коррелированные
переменные объединены в один фактор. Если пример с двумя переменными
распространить на большее число переменных, то вычисления становятся сложнее,
однако основной принцип представления двух или более зависимых переменных одним
фактором остается в силе.
При сокращении числа переменных
решение о том, когда следует остановить процедуру выделения факторов, главным
образом зависит от точки зрения на то, что считать малой "случайной"
изменчивостью. При повторных итерациях выделяются факторы с все меньшей и
меньшей дисперсией.
Центроидный метод определения
факторов.
Центроидный метод используется при
кластерном анализе. В этом методе расстояние между двумя кластерами
определяется как расстояние между их центрами тяжести при не взвешенном
центроидном методе..
Взвешенный центроидный метод
(медиана) идентичен не взвешенному, за исключением того, что при вычислениях
используются веса для учёта разницы между размерами кластеров (т.е. числами
объектов в них). Поэтому, если имеются (или подозреваются) значительные отличия
в размерах кластеров, этот метод оказывается предпочтительнее предыдущего.
Кластерный анализ.
Термин кластерный анализ в действительности включает в себя набор
различных алгоритмов классификации. Общий вопрос, задаваемый исследователями во
многих областях, состоит в том, как организовать наблюдаемые данные в наглядные
структуры, т.е. определить кластеры схожих объектов. Фактически, кластерный
анализ является не столько обычным статистическим методом, сколько
"набором" различных алгоритмов "распределения объектов по
кластерам". Существует точка зрения, что в отличие от многих других
статистических процедур, методы кластерного анализа используются в большинстве
случаев тогда, когда вы не имеете каких-либо априорных гипотез относительно
классов, но все еще находитесь в описательной стадии исследования. Следует
понимать, что кластерный анализ определяет "наиболее возможно значимое решение".
Алгоритм древовидной кластеризации.
Назначение этого алгоритма состоит в объединении объектов в достаточно большие
кластеры, используя некоторую меру сходства или расстояние между объектами.
Типичным результатом такой кластеризации является иерархическое дерево, которое
представляет собой диаграмму. Диаграмма начинается с каждого объекта в классе
(в левой части диаграммы). Теперь представим себе, что постепенно (очень малыми
шагами) вы "ослабляете" ваш критерий о том, какие объекты являются
уникальными, а какие нет. Другими словами, вы понижаете порог, относящийся к
решению об объединении двух или более объектов в один кластер. В результате, вы
связываете вместе всё большее и большее число объектов и агрегируете
(объединяете) все больше и больше кластеров, состоящих из все сильнее
различающихся элементов. Окончательно, на последнем шаге все объекты
объединяются вместе. На этих диаграммах горизонтальные оси представляют
расстояние объединения (в вертикальных древовидных диаграммах вертикальные оси
представляют расстояние объединения). Так, для каждого узла в графе (там, где
формируется новый кластер) вы можете видеть величину расстояния, для которого
соответствующие элементы связываются в новый единственный кластер. Когда данные
имеют ясную "структуру" в терминах кластеров объектов, сходных между
собой, тогда эта структура, скорее всего, должна быть отражена в иерархическом
дереве различными ветвями. В результате успешного анализа методом объединения
появляется возможность обнаружить кластеры (ветви) и интерпретировать их.
Дискриминантный
анализ используется для принятия решения о том, какие переменные различают
(дискриминируют) две или более возникающие совокупности (группы). Наиболее
общим применением дискриминантного анализа является включение в исследование многих
переменных с целью определения тех из них, которые наилучшим образом разделяют
совокупности между собой. Другими словами, вы хотите построить
"модель", позволяющую лучше всего предсказать, к какой совокупности
будет принадлежать тот или иной образец. В следующем рассуждении термин "в
модели" будет использоваться для того, чтобы обозначать переменные,
используемые в предсказании принадлежности к совокупности; о неиспользуемых для
этого переменных будем говорить, что они "вне модели".
В пошаговом анализе дискриминантных
функций модель дискриминации строится по шагам. Точнее, на каждом шаге
просматриваются все переменные и находится та из них, которая вносит наибольший
вклад в различие между совокупностями. Эта переменная должна быть включена в
модель на данном шаге, и происходит переход к следующему шагу.
Можно также двигаться в обратном
направлении, в этом случае все переменные будут сначала включены в модель, а
затем на каждом шаге будут устраняться переменные, вносящие малый вклад в
предсказания. Тогда в качестве результата успешного анализа можно сохранить
только "важные" переменные в модели, то есть те переменные, чей вклад
в дискриминацию больше остальных.
Эта пошаговая процедура
"руководствуется" соответствующим значением F для включения и
соответствующим значением F для исключения. Значение F статистики для
переменной указывает на ее статистическую значимость при дискриминации между
совокупностями, то есть, она является мерой вклада переменной в предсказание
членства в совокупности.
Для двух групп дискриминантный
анализ может рассматриваться также как процедура множественной регрессии. Если
вы кодируете две группы как 1 и 2, и затем используете эти переменные в
качестве зависимых переменных в множественной регрессии, то получите
результаты, аналогичные тем, которые получили бы с помощью дискриминантного
анализа. В общем, в случае двух совокупностей вы подгоняете линейное уравнение
следующего типа:
Группа = a + b1*x1 + b2*x2 + ... +
bm*xm
где a является константой, и b1...bm
являются коэффициентами регрессии. Интерпретация результатов задачи с двумя
совокупностями тесно следует логике применения множественной регрессии:
переменные с наибольшими регрессионными коэффициентами вносят наибольший вклад
в дискриминацию.
Если имеется более двух групп, то
можно оценить более, чем одну дискриминантную функцию подобно тому, как это
было сделано ранее. Например, когда имеются три совокупности, вы можете
оценить: (1) - функцию для дискриминации между совокупностью 1 и совокупностями
2 и 3, взятыми вместе, и (2) - другую функцию для дискриминации между
совокупностью 2 и совокупности 3. Например, вы можете иметь одну функцию,
дискриминирующую между теми выпускниками средней школы, которые идут в колледж,
против тех, кто этого не делает (но хочет получить работу или пойти в училище),
и вторую функцию для дискриминации между теми выпускниками, которые хотят
получить работу против тех, кто хочет пойти в училище. Коэффициенты b в этих
дискриминирующих функциях могут быть проинтерпретированы тем же способом, что и
ранее.
Каноническая корреляция.
Канонический анализ предназначен для
анализа зависимостей между списками переменными. Если говорить точнее, он
позволяет исследовать зависимость между двумя множествами переменных. При
вычислении канонических корней подсчитывают собственные значения матрицы
корреляций. Эти значения равны доле дисперсии, объясняемой корреляцией между соответствующими
каноническими переменными. При этом полученная доля вычисляется относительно
дисперсии канонических переменных, т.е. взвешенных сумм по двум множествам
переменных; таким образом, собственные значения не показывают абсолютного
значения, объясняемого в соответствующих канонических переменных.
Если извлечь квадратный корень из
полученных собственных значений, получим набор чисел, который можно
проинтерпретировать как коэффициенты корреляции. Поскольку они относятся к
каноническим переменным, их также называют каноническими корреляциями. Как и
собственные значения, корреляции между последовательно выделяемыми на каждом
шаге каноническими переменными, убывают. Однако другие канонические переменные
также могут быть значимо коррелированы, и эти корреляции часто допускают
достаточно осмысленную интерпретацию.
Критерий значимости канонических
корреляций сравнительно несложен. Во-первых, канонические корреляции
оцениваются одна за другой в порядке убывания. Только те корни, которые
оказались статистически значимыми, оставляются для последующего анализа. Хотя на самом деле
вычисления происходят немного иначе. Программа сначала оценивает значимость
всего набора корней, затем значимость набора, остающегося после удаления
первого корня, второго корня, и т.д.
Исследования показали, что
используемый критерий обнаруживает большие канонические корреляции даже при
небольшом размере выборки (например, n = 50). Слабые канонические корреляции
(например, R = .3) требуют больших размеров выборки (n > 200) для обнаружения
в 50% случаев. Отметим, что канонические корреляции небольшого размера обычно
не представляют практической ценности, поскольку им соответствует небольшая
реальная изменчивость исходных данных.
Канонические веса. После определения
числа значимых канонических корней возникает вопрос об интерпретации каждого
(значимого) корня. Напомним, что каждый корень в действительности представляет
две взвешенные суммы, по одной на каждое множество переменных. Одним из
способов толкования "смысла" каждого канонического корня является
рассмотрение весов, сопоставленных каждому множеству переменных. Эти веса также
называются каноническими весами.
При анализе, обычно, пользуются тем,
что чем больше приписанный вес (т.е., абсолютное значение веса), тем больше
вклад соответствующей переменной в значение канонической переменной.
Если вы знакомы с множественной
регрессией, вы можете применить для канонических весов интерпретацию,
использованную для бета - весов в уравнении множественной регрессии.
Канонические веса, в некотором смысле, аналогичны частным корреляциям
переменных, соответствующих каноническому корню. Таким образом, рассмотрение
канонических весов позволяют понять "значение" каждого канонического
корня, т.е. увидеть, как конкретные переменные в каждом множестве влияют на
взвешенную сумму (т.е. каноническую переменную).
Параметрические и непараметрические
методы оценки результатов.
Параметрические методы, основанные
на выборочном распределении определенной статистики. Говоря кратко, если вы
знаете распределение наблюдаемой переменной, то можете предсказать, как в
повторных выборках равного объема будет "вести себя" используемая
статистика - т.е. каким образом она будет распределена.
В практике использование
параметрических методов ограничено из-за объема или размера выборки доступной
для анализа; проблем с точным измерением признаков наблюдаемого объекта
Таким образом, возникает
необходимость в наличие процедур, позволяющих обрабатывать данные "низкого
качества" из выборок малого объема с переменными, про распределение
которых мало что или вообще ничего не известно. Непараметрические методы как
раз и разработаны для тех ситуаций, достаточно часто возникающих на практике,
когда исследователь ничего не знает о параметрах исследуемой популяции (отсюда
и название методов - непараметрические). Говоря более специальным языком,
непараметрические методы не основываются на оценке параметров (таких как
среднее или стандартное отклонение) при описании выборочного распределения
интересующей величины. Поэтому эти методы иногда также называются свободными от
параметров или свободно распределенными.
По существу, для каждого
параметрического критерия имеется, по крайней мере, один непараметрический
аналог. Эти критерии можно отнести к одной из следующих групп:
критерии различия между группами
(независимые выборки);
критерии различия между группами
(зависимые выборки);
критерии зависимости между
переменными.
Различия между независимыми
группами. Обычно, когда имеются две выборки (например, мужчины и женщины),
которые вы хотите сравнить относительно среднего значения некоторой изучаемой
переменной, вы используете t-критерий для независимых. Непараметрическими
альтернативами этому критерию являются: критерий серий Вальда-Вольфовица, U
критерий Манна-Уитни и двухвыборочный критерий Колмогорова-Смирнова. Если вы
имеете несколько групп, то можете использовать дисперсионный анализ. Его
непараметрическими аналогами являются: ранговый дисперсионный анализ
Краскела-Уоллиса и медианный тест.
Различия между зависимыми группами.
Если вы хотите сравнить две переменные, относящиеся к одной и той же выборке
(например, математические успехи студентов в начале и в конце семестра), то
обычно используется t-критерий для зависимых выборок. Альтернативными
непараметрическими тестами являются: критерий знаков и критерий Вилкоксона
парных сравнений. Если рассматриваемые переменные по природе своей
категориальны или являются категоризованными (т.е. представлены в виде частот
попавших в определенные категории), то подходящим будет критерий хи-квадрат
Макнемара. Если рассматривается более двух переменных, относящихся к одной и
той же выборке, то обычно используется дисперсионный анализ (ANOVA) с
повторными измерениями. Альтернативным непараметрическим методом является
ранговый дисперсионный анализ Фридмана или Q критерий Кохрена (последний
применяется, например, если переменная измерена в номинальной шкале). Q
критерий Кохрена используется также для оценки изменений частот (долей).
Зависимости между переменными. Для
того, чтобы оценить зависимость (связь) между двумя переменными, обычно
вычисляют коэффициент корреляции. Непараметрическими аналогами стандартного
коэффициента корреляции Пирсона являются статистики Спирмена R, тау
Кендалла и коэффициент Гамма Если две
рассматриваемые переменные по природе своей категориальны, подходящими
непараметрическими критериями для тестирования зависимости будут: Хи-квадрат,
Фи коэффициент, точный критерий Фишера. Дополнительно доступен критерий
зависимости между несколькими переменными так называемый коэффициент конкордации
Кендалла. Этот тест часто используется для оценки согласованности мнений
независимых экспертов (судей), в частности, баллов, выставленных одному и тому
же субъекту.
Если данные не являются нормально
распределенными, а измерения, в лучшем случае, содержат ранжированную
информацию, то вычисление обычных описательных статистик (например, среднего,
стандартного отклонения) не слишком информативно. Например, в психометрии
хорошо известно, что воспринимаемая интенсивность стимулов (например,
воспринимаемая яркость света) представляет собой логарифмическую функцию
реальной интенсивности (яркости, измеренной в объективных единицах - люксах). В
данном примере, обычная оценка среднего (сумма значений, деленная на число
стимулов) не дает верного представления о среднем значении действительной
интенсивности стимула. (В обсуждаемом примере скорее следует вычислить
геометрическое среднее.) Непараметрическая статистика вычисляет разнообразный
набор мер положения (среднее, медиану, моду и т.д.) и рассеяния (дисперсию, гармоническое
среднее, квартильный размах и т.д.), позволяющий представить более "полную
картину" данных.
РАЗДЕЛ II. Социально
– экономическая статистика.
Тема
№ 1. Система показателей, основные группировки и классификации
в
социально-экономической статистике
Понятие социально-экономическая
статистика имеет два толкования: как область науки и как область практической
деятельности. Социально-экономическая статистика как область науки
разрабатывает систему приемов и методов сбора, обработки и анализа числовой
информации о социальных явлениях и процессах в обществе.
Социально-экономическая статистика как область практической деятельности
направлена на выполнение органами государственной статистики и другими
организациями работы по сбору и обобщению числовых материалов, характеризующих
те или иные социальные процессы.
Социально-экономическая статистика
отличается от других отраслей статистики не только своими особыми предметом и
объектом исследования. Ее своеобразие состоит и в особых каналах получения
исходной информации, и в применении специальных приемов обработки и обобщения
этой информации, и в особых путях практического использования результатов
анализа. Все это подтверждает необходимость выделения социально-экономической
статистики в качестве отдельного направления учетно-статистических работ, а
также как особого направления научных разработок, в рамках которого решаются
теоретико-методологические вопросы социальной статистики.
Социально-экономическая статистика,
как и любая область науки, связана с другими областями знания различными
отношениями. Понимание этих отношений способствует более точному определению
предмета, объекта и методологии социальной статистики. Наиболее тесными
являются связи социально-экономической статистики с другими отраслями статистики,
прежде всего с теорией статистики, разрабатывающей общеметодическую базу для
отраслевых статистик. Единые по своей сущности методические приемы
конкретизируются и модифицируются применительно к задачам и условиям анализа
социальных явлений и процессов. Нередко арсенал методов исследования,
предоставляемых теорией статистики, оказывается недостаточным. В таких случаях
социальная статистика заимствует необходимые методы у других отраслей знания —
социологии, психологии, экономики и др.
Существует полная или частичная
общность объекта исследования социально-экономической статистики с объектами
ряда наук — демографии, социологии, статистики населения, экономики труда,
экономики предприятия, макроэкономики, экономики денежного обращения,
этнографии, медицинской статистики и др. С ними социальная статистика имеет
некоторые точки соприкосновения и в отношении предмета исследования, хотя они
выражены значительно слабее общности объектов исследования. В большей мере
близость наук может проявляться в вопросах определения методологии, методики,
объекта исследования.
Статистический анализ явлений и
процессов, происходящих в социальной и экономической жизни общества,
осуществляется с помощью специфических для статистики методов — методов
обобщающих показателей, дающих числовое измерение количественных и качественных
характеристик объекта, связей между ними, тенденций их изменения. Эти
показатели отражают социальную жизнь общества, выступающую как предмет
исследования социальной статистики.
Сложная и многогранная по своей
природе социальная и экономическая жизнь общества представляет собой систему
отношений разного свойства, разных уровней, разного качества. Будучи системой,
эти отношения взаимосвязаны и взаимообусловлены. Их единство проявляется в
разнообразных формах: во взаимодействии, в соподчиненности, в противоречивости.
Из этого следует, что вычленение отдельных направлений исследования в рамках
социально-экономической статистики не более чем условный прием, облегчающий
познание. Изолированно взятая статистика жилищных условий населения или
статистика бюджетов населения столь же условна. как, например, выделение в
самостоятельную область медицины таких специализаций, как дерматология,
микробиология, онкология и др.
Наиболее результативен такой подход
к определению предмета социально-экономической статистики, при котором
одновременно выделяются для анализа отдельные стороны социальной жизни общества
и принимаются во внимание их единство и взаимосвязь.
К числу наиболее значимых
направлений исследования в социально-экономической статистике относятся:
социальная и демографическая структура населения и ее динамика, уровень жизни
населения, уровень благосостояния, уровень здоровья населения, культура и
образование, моральная статистика, общественное мнение, политическая жизнь.
Применительно к каждой области исследования разрабатывается система
показателей, определяются источники информации и существуют специфические
подходы к использованию статистических материалов в целях регулирования
социально-экономической обстановки в стране и регионах. Вместе с тем все эти
направления дают в конечном счете единую последовательную и интегрированную
информацию о картине социальной жизни, о тенденциях и закономерностях развития
общества.
Определяя в общем виде задачи
социально-экономической статистики, следует выделить те, которые решаются любой
отраслевой статистикой применительно к своему объекту исследования. Такими
задачами для социально-экономической статистики являются: систематический
анализ ситуации в социально-экономической сфере; анализ важнейших тенденций и
закономерностей развития отраслей социальной инфраструктуры: изучение уровня и
условий жизни населения:
- оценка степени дифференциации этих
характеристик; анализ динамики: прогнозирование наиболее вероятного хода
развития на ближайшую и более отдаленную перспективу; исследование факторов,
под влиянием которых сложилась данная ситуация:
- оценка степени соответствия
фактических параметров их нормативным значениям; выяснение соотношения и роли
объективных и субъективных факторов; исследование взаимодействия
социально-экономических процессов с другими составляющими общественного
развития.
Кроме того, существуют особые
задачи, присущие именно социально-экономической статистике. Их специфика
зависит прежде всего от трудностей, возникающих в практике изучения социальных
процессов. К ним относятся следующие.
1. Преодоление автономности
отдельных направлений социально-экономической статистики и обусловленной этим
несопоставимости многих статистических показателей; действительное формирование
единой взаимосвязанной системы социальной статистики. Недоработки в этой
области объясняются не только объективной причиной — резкими различиями в
сущности и формах проявления разных социально-экономических процессов, но и
некоторыми организационными предпосылками. Сбор социальной информации
осуществляется разными подразделениями (секторами, отделами) органов
государственной статистики: статистики цен, бюджетов, статистики труда и т. д.
Социальные показатели оказываются изначально включенными в разные подсистемы
показателей социально-экономической статистики, что накладывает отпечаток на
решение ряда методологических вопросов. Вместе с тем влияет и разный
"возраст" отдельных показателей социальной статистики: одни
показатели используются в практике статистических работ давно и по инерции
сохраняется традиционный подход к решению методических вопросов; другие
показатели возникли недавно и более ориентированы на современные методологии.
2. Достижение соответствия ряда
статистических показателей оценке сущности социально-экономических явлений и
процессов, так как показатели не дают их качественных характеристик.
Учитываются лишь отдельные формальные количественные параметры..
3. Интегрирование исследований на
макро- и микроуровнях, что позволит более глубоко и полно вскрыть первопричины
и механизмы изучаемых процессов. Пока еще социально-экономическая статистика
ориентирована преимущественно на исследование явлений и процессов на
макроуровне, где обнаруживаются конечные результаты процесса. Децентрализация всей
системы управления в стране усиливает актуальность информационного обеспечения
на региональном уровне.
4. Разработка показателей,
построение моделей, оценка гипотез, дифференцирование для наиболее характерных
социально-культурных, социально-этнических, социально-демографических групп
населения. Используемые при этом схемы группировок населения следует
корректировать по мере того, как происходят сдвиги в составе населения.
Действующая система показателей социальной статистики практически нивелирует реально
существующую дифференциацию условий жизнедеятельности различных групп
населения, системы их ценностных ориентации и т. д. Тенденция возрастания
социального расслоения общества усиливает актуальность этого вопроса.
5. Преодоление существующей
несопоставимости показателей социально-экономической статистики и показателей,
представленных в других отраслевых статистиках.
6. Моделирование
социально-экономических связей с целью обнаружения механизмов взаимодействия в
общественной системе. На макроуровне представлен ряд объективно существующих
ограничительных факторов, предопределяющих пределы возможных колебаний
социальных показателей в конкретных условиях (без разрушения системы). Это
важно учитывать при выработке социально-экономических программ.
7. Расширение круга показателей
статистики мнений. Актуальность этой задачи заключается в том, что важнейшей
составляющей социальных процессов выступает психологический фактор.
Субъективные личностные оценки факторов и событий предопределяют реакцию
населения на них, поведение населения в различных сферах жизнедеятельности.
8. Проведение специальных мер,
компенсирующих по возможности такие слабые стороны многих показателей, как:
элементы субъективизма; неточности данных анамнеза (информация о событиях и
фактах прошлых лет, получаемая при опросах населения); неполнота учета фактов,
о которых люди неохотно дают информацию; отсутствие объективных однозначных
критериев и шкал для различного рода оценочных суждений и т. д. Это одно из
важных условий построения полноценной системы показателей социальной
статистики, повышающее ее достоверность и информационную емкость. Смягчить
негативные проявления можно с помощью ряда специальных приемов. Среди них:
совместный анализ информации о фактах и мнениях по одному и тому же вопросу; повторное
обращение в анкетах к тому же вопросу с некоторым изменением оттенков смысла и
редакции; детализация вопроса, т. е. расчленение его на несколько отдельных
вопросов с последующим построением интегрального показателя; контрольные
вопросы, позволяющие выявить недостоверные ответы, и т. д.
Специфика объектов социальной
статистики предопределяет и своеобразие используемых методических приемов.
Многие характеристики не имеют числового выражения. Эти атрибутивные признаки
накладывают свои ограничения на решение методических вопросов.
Поведение населения как потребителя
услуг и участника социально-экономических процессов имеет ту существенную
особенность, что наряду с объективными факторами оно детерминировано
субъективным фактором — сознанием. Индивидуальное, групповое и общественное
сознание вырабатывает особые системы ценностей, социальные нормы, иерархию
приоритетов в сфере потребления. Измерение влияния субъективных факторов
представляет особые трудности, и статистика обращается к методикам, выработанным
социологией и психологией. В связи с большой трудоемкостью таких работ они
выполняются лишь периодически и как выборочные исследования.
В рамках государственной статистики
в нашей стране в порядке текущего учета в основном измеряется объем
предоставляемых населению услуг. Качественные особенности потребления, его
тенденции и факторы не поддаются, как правило, учету на массовом уровне.
Поэтому актуальные и острые социальные проблемы в статистических данных обычно
зафиксированы лишь как симптомы, причины которых не раскрыты.
Систематическое предоставление
информации по названным вопросам региональным и центральным органам власти для
своевременного принятия мер по стабилизации обстановки, предупреждению
возможных кризисов и обострении — актуальная задача статистики.
Для социально-экономической
статистики характерна множественность объектов исследования. Их можно
подразделить на два типа.
Первый и основной тип объектов
составляют потребители услуг, материальных и духовных ценностей, информации.
Они представлены индивидуальными и групповыми объектами. Индивидуальный объект
— человек (население как совокупность индивидов). Это также все население и
отдельные его категории в зависимости от исследуемого социального процесса.
Коллективный объект — группа лиц, совместно осуществляющая потребление,
совместно участвующая в социальном процессе. Такими объектами являются: семья,
трудовой коллектив, садовое товарищество, гаражный кооператив и др.
Второй тип объектов охватывает лиц,
организации, структуры, предоставляющие населению услуги, организующие тот или
иной социальный процесс. Их деятельность определяет объем и качество
предоставленных услуг и ценностей. Производство и потребление услуг, ценностей,
информации составляют две взаимосвязанные стороны процесса. Этим предопределяется
целесообразность их параллельного исследования. Так, жилищная проблема может
быть раскрыта, если информация получена по разным видам объектов: семьям, где
система показателей характеризует жилищные условия и их динамику, и
организациям, формирующим рынок жилья. К ним относятся: строительные
организации, различные жилищные отделы и комиссии в составе местных органов
управления, разнообразные посреднические конторы и фирмы по обмену, купле,
продаже, найму жилья.
В отдельных случаях оба типа объектов
представлены в единстве — когда, например, семьи сами своими силами
осуществляют строительство жилого дома для себя. Однако подобная ситуация носит
эпизодический характер, так как строительство дома — единовременное событие,
потребителем же жилья семья является постоянно, т. е. доминирует один аспект.
Четкое определение объекта
исследования важно потому, что этот вопрос выступает как исходный на стадии
сбора информации, а также на стадии ее обработки — группировки, классификации,
построения системы показателей. Множественность объектов требует особенно
тщательного подхода к исследованию, решению методических вопросов. Но это лишь
одно из проявлений специфики объектов анализа в социальной статистике. Имеются
и другие не менее важные особенности, присущие главным образом социальной
статистике и сравнительно слабо выраженные, например. при изучении чисто
экономических процессов.
Многообразие рыночных и нерыночных,
индивидуальных и коллективно потребляемых услуг, оказываемых населению,
затрудняет обобщение статистической информации о социальной сфере в целом. На
макроуровне Системой национальных счетов (СНС) предусмотрено построение
обобщающих показателей как экономики в целом, так и отдельных секторов.
Выделяют следующие секторы экономики: нефинансовые предприятия; финансовые
учреждения; государственные учреждения; некоммерческие организации,
обслуживающие домашние хозяйства; домашние хозяйства: остальной мир, который
обобщает данные по международному сотрудничеству. Построение СНС по секторам
экономики позволяет не только оценить вклад каждого сектора, но и
проанализировать перераспределение ресурсов и доходов между секторами. По
каждому сектору определяются следующие макропоказатели: валовая добавленная
стоимость; валовой национальный доход; валовой национальный располагаемый
доход; конечное потребление; валовое накопление; национальное сбережение;
чистое кредитование; чистое заимствование.
Рассмотрим состав трех секторов
экономики, оказывающих услуги населению, результат деятельности которых на
стадии использования ВВП обобщает показатель "конечное потребление".
Сектор государственных учреждений
включает организации, финансируемые из федерального бюджета, бюджетов субъектов
РФ, созданные для оказания индивидуальных и коллективно используемых услуг:
центральные, региональные и местные госуч-реждения. государственные
внебюджетные фонды социального обеспечения. Ресурсы сектора формируются за счет
налогов и доходов от государственной собственности.
Сектор некоммерческих организаций
(НКО), обслуживающих домашние хозяйства, представлен юридическими лицами и
социальными организациями, производящими товары и услуги, но не приносящими
прибыли институциональным единицам, их контролирующим.
Среди НКО выделяют: объединения лиц,
предоставляющие льготы своим членам и лицам, обслуживающим их;
благотворительные и филантропические организации; неформальные организации (в
основном в развивающихся странах), занимающиеся оказанием коммунальных услуг.
Сектор домашних хозяйств охватывает
нанимателей, работающих на себя, наемных работников, получателей доходов от
собственности или трансфертов.
Обобщающим показателем деятельности
трех секторов выступает стоимость фактического конечного потребления. Этот
показатель характеризует уровень жизни, так как измеряет стоимость
потребительских товаров и услуг, приобретенных домашними хозяйствами путем
покупки или в качестве трансфертов от единиц государственного и некоммерческого
секторов и использованных для удовлетворения своих потребностей. Вместе с тем
нецелесообразно ограничивать социальный сектор именно данными тремя секторами
экономики. В целях обобщения информации по социальной сфере на региональном
уровне могут быть использованы действующие общероссийские статистические
классификаторы, отражающие состав отраслей и видов деятельности.
Отрасль определяется как
совокупность предприятий или их подразделений, расположенных в одном месте,
занятых одним видом деятельности. Предприятие является институциональной
единицей, способной владеть активами, самостоятельно получать и использовать
доходы, принимать обязательства, заключать договоры. Предприятия, занятые
несколькими видами деятельности, могут подразделяться на заведения, если
имеется возможность получения следующей информации о деятельности каждого
заведения: объеме производства; численности занятых; производимых затратах;
прибыли и др. Для многопрофильных предприятий определяется основной вид
деятельности по наибольшей доле выпуска продукции.
Хозяйственная отрасль ~ совокупность
предприятий и организаций, объединенных общностью функций в процессе
общественного разделения труда. Состав хозяйственных отраслей зафиксирован в
Общероссийском классификаторе отраслей народного хозяйства (ОКОНХ). Чистая
отрасль представляет совокупность заведений. Состав чистых отраслей
зафиксирован в Общероссийском классификаторе видов деятельности, продукции и
услуг (ОКДП).
В соответствии с ОКОНХ социальную
сферу отождествляют с непроизводственной, охватывающей жилищное и коммунальное
хозяйство, непроизводственные виды бытового обслуживания, здравоохранение,
физическую культуру и спорт, социальное обеспечение, образование, культуру и
искусство, науку, финансы, кредит, страхование и пенсионное обеспечение,
управление и общественные объединения. Однако этот перечень ограничен, так как
не включает розничную торговлю и общественное питание, пассажирский транспорт и
связь по обслуживанию населения, т. е. отрасли, оказывающие рыночные услуги
населению. Соединение непроизводственной сферы с отраслями, предоставляющими
рыночные услуги, дает наиболее полное представление о составе сферы по
обслуживанию населения.
Выделение социальной сферы по ОКДП
затруднено в связи с тем, что значительная часть видов деятельности
предоставляет услуги не только населению, но и производственные услуги. При
этом к социальной сфере относятся следующие виды деятельности, оказывающие
рыночные и нерыночные услуги населению: электро-, газо- и водоснабжение;
оптовая и розничная торговля, ремонт автомобилей, бытовых приборов и предметов
личного пользования (в части розничной торговли и ремонтных работ по заказам
населения); гостиницы и рестораны; транспорт, складское хозяйство и связь в
части обслуживания населения; финансовое посредничество в части страхования
населения и пенсионного обеспечения; государственное управление и оборона,
обязательное социальное страхование; образование; здравоохранение и социальные
услуги; предоставление коммунальных, социальных и персональных услуг; ведение
частных домашних хозяйств с наемным обслуживанием. В России возрастает доля
занятых в социальной сфере в общей численности занятых в экономике.
Тема
№ 2. Статистика численности и состава населения. Статистика естественного
движения и миграции населения
Для развития национальной экономики
в целом и для развития ее основных отраслей необходима статистическая
информация о населении. Как статистическая категория население представляет
собой совокупность людей, проживающих на данной территории. Оно непрерывно
изменяется за счет рождения и смертей.
Информация о населении включает его
естественный прирост, его естественное движение, его профессиональный состав,
возрастной состав, численность трудоспособного населения. Единицей наблюдения
или единицей учета в статистике населения может быть как отдельный человек, так
и семья, а также домохозяйство и населенный пункт.
Основным источником информации о
населении является текущий учет (сплошная перепись) населения, который, как
правило, проводится раз в десять лет. Отдельные сведения собираются на основе
выборочной переписи населения. При переписи населения учитываются две категории
населения: наличное население (лица, фактически находящиеся на момент переписи
в данном населенном пункте, включая временно проживающих) и постоянное
население (лица, для которых данный населенный пункт является местом
постоянного проживания, включая временно отсутствующих).
В ходе статистического обследования
населения определяется численность населения на момент проведения переписи.
Сведения о наличном населении очень важны для населенных пунктов, где сильно
влияние сезонного фактора (курортные районы) или для поселков, где используется
рабочая сила вахтовым методом.
По результатам переписи исчисляется
такой показатель, как среднегодовая численность населения, которая представляет
собой среднюю арифметическую из численности на начало и конец календарного периода.
Показатель среднегодовой численности широко используется для расчетов
среднедушевых показателей (потребления, доходов, обеспечения транспортными
коммуникациями, товарами потребления, услугами и т.д.).
Показатели численности населения
предполагают расчет абсолютных и относительных показателей динамики как в целом
по населению, ток и по отдельным группам населения.
В основу отечественной статистики
положено деление населения на городское и сельское.
К городскому населению относятся
жители городских поселений, поселков городского типа, дачных поселков.
Сельское население проживает в
населенных пунктах, которые классифицируются как сельские поселения.
Для характеристики соотношения между
числом граждан, проживающих на данной территории, и ее площадью используется
такой показатель, как плотность населения, который выражается числом лиц,
приходящихся на единицу площади (км2) без учета крупных внутренних
водоемов.
Национальная принадлежность
определяется прежде всего: 1) числом лиц каждой национальности; 2) числом лиц
каждой национальности на 100000 человек населения; 3) долей лиц коренной
национальности в регионе; 4) долей лиц коренной национальности, живущих за
пределами своего региона.
В статистике населения также
выделяют группы по полу и возрасту. В 1998 г. в общей численности населения
мужчины в России составляли 47%, женщины - 53%.
Половая структура населения
складывается под влиянием трех основных факторов: 1) соотношение полов среди
новорожденных (биологическая константа); 2) половые различия в смертности; 3)
половые различия в интенсивности миграции населения.
Возрастной анализ населения,
отражающий процесс воспроизводства населения, широко используется при
разработке экономической и социальной политики. Выделяются: лица моложе
трудоспособного возраста; лица трудоспособного возраста; лица старше
трудоспособного возраста.
Возрастная структура описывается с
помощью группировок и относительных показателей. Чаще всего выделяются
возрастные группы однолетние и пятилетние, но в зависимости от целей анализа
возможны и другие группировки.
Для анализа половозрастной структуры
населения используется один из графических методов, называемый половозрастной
пирамидой.

Чем больше доля численности детей, а
также лиц трудоспособного возраста, тем больше повода говорить о стабильной
структуре данного общества. В противном случае речь может идти об ухудшении
демографической ситуации, а следовательно, и об отсутствии позитивной
перспективы для экономического развития.
Статистика населения включает такие
единицы учета, как семья и домохозяйство. Семья как статистическая единица
определяется как группа лиц, связанных родственными отношениями, проживающих на
одной территории и имеющих общий бюджет.
Брачная структура населения – это
распределение населения по брачному состоянию, обычно в сочетании с полом и
возрастом. Единственным источником информации о брачно-возрастной структуре
населения являются переписи населения.
Распределение населения по брачному
состоянию, или брачно-возрастная структура населения, описывается, так же как и
половозрастная структура, с помощью группировок и относительных показателей.
Каждая половозрастная группа населения подразделяется по категориям брачного
состояния, и определяется удельный вес каждой категории в составе половозрастной
группы. При этом возрастные группы выделяются следующие: до 18 лет, 18 – 19, 20
– 24 года, далее пятилетние возрастные группы до группы 55 – 59 лет, затем
открытый интервал «60 лет и старше».
Для прогнозирования и оценки
состояния экономики страны важен анализ населения по уровню образования, т.к.
преобладание населения с тем или иным уровнем образования обуславливает
размещение производства на данной территории и определяет перспективы его
развития.
Данные переписи населения позволяют
рассчитать простые показатели, характеризующие брачную структуру более
наглядно, чем это можно сделать с помощью процентных долей.
Расчет числа лет, прожитых в браке
одним поколением женщин, условно проживающих от 16 до 50 лет:
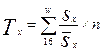 , где
, где  - число лет, прожитых
в браке одной женщиной в среднем из условного поколения;
- число лет, прожитых
в браке одной женщиной в среднем из условного поколения; 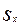 - численность женщин в
возрасте «x», состоящих в браке;
- численность женщин в
возрасте «x», состоящих в браке; 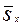 - численность всех
женщин в возрасте «х» лет; n – число лет возрастного интервала.
- численность всех
женщин в возрасте «х» лет; n – число лет возрастного интервала.
Изменение численности населения
между переписями отслеживается с помощью текущего учета населения, который
основывается на статистике естественного и миграционного (механического)
движения населения.
Влияние демографических факторов
определяется из расчета, в котором общий прирост населения подразделяется на
естественный и миграционный.
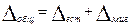
Естественное движение населения -
изменение численности населения за счет рождения и смертей. В статистике широко
используется показатель естественного прироста населения, который определяют
как разность между числом родившихся живыми и числом умерших за определенный
период, имея в виду прежде всего положительный результат (число родившихся
должно превышать численность умерших). Если разница имеет отрицательный
результат, то речь идет о показателе естественной убыли населения.
Воспроизводство населения измеряется
с помощью общего коэффициента рождаемости и общего коэффициента смертности
(рассчитываются на 1000 человек, т.е. в промилле, ‰).
Общий коэффициент рождаемости характеризует
интенсивность деторождения по отношению к населению в целом (всех возрастов) и
вычисляется как отношение числа родившихся живыми в течение года (N) к среднегодовой
численности населения (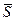 ):
):
Интенсивность смертности населения
измеряется общим коэффициентом смертности, который представляет собой отношение
общего числа умерших в течение года (М) к среднегодовой численности населения:
В статистике населения используется
также коэффициент естественного прироста (убыли), который представляет собой
разность между коэффициентом рождаемости и коэффициентом смертности.
Большое значение для анализа
естественного движения населения имеет расчет возрастных коэффициентов
рождаемости (коэффициентов для отдельных возрастных групп женщин) и суммарного
коэффициента рождаемости, который характеризует среднее число детей, рожденных
женщиной за свою жизнь. В последние годы в России суммарный коэффициент рождаемости
имеет тенденцию к снижению (суммарный коэффициент рождаемости снизился с 2,00 в
1970 г. до 1,24 в 1998 г.).
Важнейшей частью статистической
информации о смертности населения является показатель смертности детей на
первом году жизни. Речь идет о коэффициенте младенческой смертности, который
представляет собой отношение числа умерших в возрасте до одного года (М0)
к числу родившихся живыми:
Обобщающим показателем является
показатель средней продолжительности предстоящей жизни, который может быть
рассчитан для любой возрастной группы населения путем деления суммы предстоящих
человеко-лет, которые предстоит прожить группе лиц от возраста х до предельного
возраста включительно (Tx ), на численность изучаемого поколения,
дожившего до возраста х (Lx ):
Кроме естественного движения большое
влияние на численность населения страны оказывает перемещение населения по
территории страны (миграция населения). Изменение численности населения на
отдельных территориях за счет миграции представляет собой механическое движение
населения.
Миграция населения - это
передвижение людей (мигрантов) через границы тех или иных территорий (страны,
региона, области, района и т.д.), связанное с переменой места жительства
навсегда или на более или менее длительное время. Миграционные потоки являются
важным объектом исследования, поскольку дают сведения о том, как перемещается
население, в каком направлении, что из себя представляет
социально-демографический состав мигрантов.
К основным показателям миграции
относятся следующие:
число прибытий - П;
число выбытий - В;
миграционный прирост - (П - В), если
П > В;
миграционный отток - (П - В), если П
< В.
Выбывшим считается лицо, которое
выехало за пределы данной территории. К прибывшим относятся лица, которые
въехали на данную территорию из-за ее пределов. Число выбывших и прибывших
определяется по показателям регистрационных учетов по месту прибытия и месту
убытия.
Для статистической характеристики
миграционных процессов используют расчетные относительные показатели:
коэффициенты интенсивности (прибытия, выбытия, миграционного оборота),
коэффициент эффективности миграции.
Коэффициент прибытия
Данный коэффициент характеризует
число прибывших на 1000 человек населения в среднем за год.
Коэффициент выбытия
Этот коэффициент характеризует число
выбывших на 1000 человек населения в среднем за год.
Коэффициент интенсивности
миграционного оборота
Данный коэффициент может иметь как
положительное значение (+), так и отрицательное (-) и характеризует в
положительном значении приток, а в отрицательном - отток.
Коэффициент миграционного
(механического) прироста
Коэффициент эффективности миграции
Современные особенности миграции
населения состоят в том, 1) население из регионов со слаборазвитой
экономической инфраструктурой переезжает в регионы с более развитой
инфраструктурой (большие города, г. Москва); 2) миграция населения из «горячих»
точек страны
Исчисление перспективной численности
населения
1. Исчисление численности населения
на основе темпов прироста за предшествующий период.
2. Расчет численности населения на
основе прогнозируемого динамического ряда численности населения: если
существует четкая тенденция, то ее можно продлить на перспективу:
3. Расчет численности населения на
основе таблицы смертности.
Таблица смертности - это система
взаимосвязанных показателей, основанная на вероятность дожития до следующего
года каждой возрастной группы. Показатели дожития требуют большого объема
статистической информации.
Коэффициент дожития 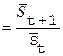
Для каждого поколения рассчитывается
свой коэффициент.
Расчеты численности в этом случае
ведутся отдельно для каждого поколения. Общая численность населения в данном
году равна сумме численности всех поколений, живущих в этом году.
Тема
№ 3. Статистика рынка труда, производительности труда, оплаты труда и затрат на
рабочую силу. Статистика экономически активного населения
ресурсы — это часть населения
страны, которая работает в народном хозяйстве или же способна работать, но по
тем или иным причинам не работает (домохозяйки, учащиеся с отрывом от
производства и др.). Таким образом, трудовые ресурсы включают как занятых, так
и потенциальных работников.
При анализе трудовых ресурсов часто
используется такое понятие как экономически активное население. Под
экономически активным населением (рабочей силой) подразумевается часть
населения, обеспечивающая предложение рабочей силы для производства товаров и
услуг. Численность экономически активного населения измеряется по отношению к
определенному периоду и включает занятых и безработных.
Экономически активное население,
предлагающее свой труд для производства товаров и услуг, включено в Систему
национальных счетов ООН. Численность
экономически активного населения оценивают по данным выборочных обследований
населения по проблемам занятости. В международных стандартах рекомендуется
указывать минимальный возраст, принятый при измерении экономически активного
населения. Он может быть принят на уровне 6 лет (Египет), 10 лет (Бразилия) и
повышаться до 16 лет (США, Швеция). В большинстве стран он составляет 14-15
лет. В некоторых странах предусмотрены два минимальных предела: более низкий -
для получения информации об экономической деятельности и несколько более
высокий - для группировки экономически активного населения: например, в Канаде
- 14и 15лет, Индии - 5 и 15, Венесуэле - 10 и 15, в России - 15 и 16 лет.
Помимо минимального в ряде стран
установлен максимальный возраст- Это означает, что лица старше его исключаются
из расчета численности экономически
активного населения. Например, в Дании, Швеции, Норвегии, Финляндии установлен
верхний предел в 74 года. В России при проведении обследований населения по
проблемам занятости ограничиваются возрастом в 72 года. Вместе с тем при
дальнейшей группировке населения на занятых и безработных, как и в большинстве
стран, максимальный возраст не установлен.
В состав трудовых ресурсов
включаются:
- население в трудоспособном
возрасте (мужчины от 16 до 59 лет и женщины от 16 до 54 лет включительно),
кроме неработающих инвалидов первой и второй групп и неработающих лиц, которые
получают пенсии на льготных условиях;
- фактически работающие подростки от
16 лет и работающие пенсионного возраста (мужчины старше 59 лет и женщины
старше 54 лет).
Население в трудоспособном возрасте
состоит из трудоспособного и нетрудоспособного населения. Численность
трудоспособного населения меньше населения в трудоспособном возрасте.
Показатели численности трудовых
ресурсов. Абсолютный показатель численности трудовых ресурсов — сумма
численности трудоспособного населения в рабочем возрасте и численности
работающих подростков и престарелых. Этот показатель определяется вычитанием из
общей численности населения численности населения в нерабочем возрасте и
нетрудоспособного населения в рабочем возрасте и прибавлением численности работающих
подростков и престарелых. Численность трудовых ресурсов фиксируется на
определенную дату, а поэтому является моментным показателем. Однако такой
показатель для планирования и экономических расчетов малопригоден, поэтому
исчисляются интервальные показатели как средние арифметические (за месяц,
квартал, год) из моментных. Если в исходных данных имеется численность трудовых
ресурсов на начало и конец периода (месяца, квартала, года), то средняя
арифметическая за месяц (квартал, год) определяется как
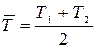
При наличии в исходных данных
показателей численности трудовых ресурсов на равноотстоящие даты на начало
периода (начало месяца, квартала) среднегодовая численность трудовых ресурсов
определяется как средняя хронологическая:
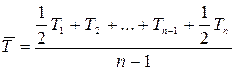
Если моментные показатели трудовых
ресурсов представлены с неравными интервалами на неравноотстоящие даты
(например, через три, четыре, пять месяцев), то среднегодовая численность
трудовых ресурсов определяется как средняя хронологическая взвешенная по
величинам интервалов:
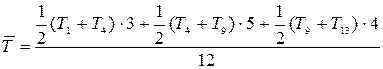
Естественное пополнение трудовых
ресурсов происходит за счет численности лиц, достигших 16 лет, и численности
фактически работающих подростков и пенсионеров. Естественное выбытие
определяется численностью лиц, достигших пенсионного возраста и не оставшихся
работать, численностью лиц в трудоспособном возрасте, перешедших на
инвалидность, и численностью умерших (из числа трудоспособных и работавших
пенсионеров), а также численностью тех пенсионеров, которые перестали принимать
участие в общественном труде.
Разница между естественным
пополнением и выбытием определяет чистый прирост трудовых ресурсов. Он
рассчитывается для страны в целом, так и для отдельной территории в пределах
страны (республики, области, края и т. д.). Однако для отдельных территорий
(регионов) страны характерно и механическое движение трудовых ресурсов
(миграция) — въезд на постоянное жительство и выезд. Разница между числом
въездов и числом выездов определяет механический прирост трудовых ресурсов по
региону. Общий прирост трудовых ресурсов для отдельной территории в пределах
страны равен сумме их естественного и механического приростов.
Абсолютные показатели численности
трудовых ресурсов и их приросты сравниваются с абсолютными показателями
численности населения (всех возрастов, трудоспособного возраста и др.). В
результате рассчитываются относительные показатели на дату или за период
времени:
- доля населения в трудоспособном
возрасте — отношение численности населения в трудоспособном возрасте к
численность населения всех возрастов;
- коэффициент трудоспособности
населения — отношение численности трудоспособного населения в рабочем возрасте
к численности населения всех возрастов;
- коэффициент занятости всего
населения — отношение численности занятого населения независимо от возраста к
численности населения всех возрастов;
- коэффициент трудоспособности
населения в рабочем возрасте — отношение численности трудоспособного населения
в рабочем возрасте к численности населения в трудоспособном возрасте;
- коэффициент занятости
трудоспособного населения — отношение численности занятого трудоспособного
населения к численности трудоспособного населения;
- коэффициент нагрузки
трудоспособного населения — отношение численности населения в нерабочем
возрасте к численности населения в рабочем возрасте;
- коэффициент пенсионной нагрузки
трудоспособного населения — отношение численности населения пенсионного
возраста к численности населения в рабочем возрасте;
- коэффициент замены (возмещения)
трудовых ресурсов — отношение численности населения до трудоспособного возраста
к численности населения в рабочем возрасте;
- коэффициент чистого прироста
трудоспособного населения в рабочем возрасте — отношение чистого
(естественного) прироста трудоспособного населения в рабочем возрасте к
численности трудоспособного населения в рабочем возрасте;
- коэффициент общего (естественного
и механического) прироста трудоспособного населения в рабочем возрасте региона
— отношение общего прироста трудоспособного населения в рабочем возрасте к
численности трудоспособного населения в рабочем возрасте.
Относительные показатели дают
возможность изучить интенсивность абсолютных показателей трудовых ресурсов, а
рассчитанные в динамике — процесс их изменения по годам или иным периодам
времени.
Анализ трудовых ресурсов.
Статистическое изучение трудовых ресурсов основывается на данных текущей
статистики, единовременных обследований по труду и переписей населения.
Одним из основных источников данных
для изучения трудовых ресурсов является статистическая отчетность предприятий.
На предприятиях вычисляют списочную такие показатели как численность
работников, явочную численность, число фактических работающих.
Эти показатели вычисляются на
определенную дату (моментный показатель), за определенный период (средний
показатель).
В списочный состав включаются все
работники, принятые на постоянную, сезонную, временную работу на срок 1 день и
более, со дня зачисления их на работу. В списочном составе работников за каждый
день учитывается как фактически работающие работники, так и отсутствующие по
какой-либо причине.
Под явочным числом понимают число лиц из числа, состоящих в
списке, явившихся на работу.
Под числом фактически работающих
понимаются лица, приступившие к работе из числа явившихся.
Среднесписочная численность
работников вычисляется как отношение суммы всех явок и не явок в чел./днях к
числу календарных дней в периоде.
Среднеявочная численность
рассчитывается как отношение суммы чел/дней всех явок на работу к числу дней
фактической работы предприятия.
Среднесписочная численность
фактически работавших рассчитывается как отношение суммы фактически
отработанных чел/дней к числу дней фактической работы предприятия.
При вычислении среднесписочной
численности нужно иметь в виду, что некоторые категории работников, которые
включаются в списочную численность при вычислен среднесписочной численности
исключаются: женщины, находящиеся в отпуске по беременности и родам; женщины,
находящиеся в отпуске по уходу за ребёнком до 1,5 лет; работники предприятий,
обучающиеся на курсах заочных ВУЗов и техникумов, находящиеся в дополнительном
отпуске без сокращения заработной платы.
Для оценки движения среднесписочного
состава работников вычисляют следующие показатели: выбывшие (распределенные) в
порядке перевода на другое предприятие; выбывшие в связи с переходом на учёбу,
призывом на военную службу, уходом по собственному желанию, за нарушение труд
дисциплины; выбывшие в связи с окончанием срока договора.
Наряду с абсолютным числом выбывших
вычисляют и относит показатели:
Коэффициент оборота по приему =
Число принятых на работу за период / Среднесписочная численность*100
Коэффициент оборота по выбытию =
Число выбывших за период / Среднесписочная численность*100
Коэффициент текучести = Число
уволенных по причинам текучести (по собственному желанию + нарушен труд
дисциплины) / Среднесписочная численность*100
Коэффициент постоянства кадров =
Число лиц, состоящих в списке весь период / Среднесписочная численность или
Списочная численность на конец периода
Коэффициент замещения рабочей силы =
Число принятых на работу / Число уволенных с работы
Если Коэффициент замещения > 1,
то значит на предприятии создаются новые рабочие места, и если К< 1, значит
идёт сокращение раб мест.
Показатели численности и состава
трудовых ресурсов изучаются в различных аспектах: по социально-экономическим
признакам (источники средств существования, социальная принадлежность и др.),
демографическим признакам (пол, возраст, семейное положение, национальность и
др.), профессионально-отраслевым и функциональным группам занятий (профессия,
степень квалификации, отрасль народного хозяйства и др.), уровню
общеобразовательной и специальной подготовки, миграции и др.
Территориальное распределение
трудовых ресурсов определяется особенностями экономических районов, характером
расселения населения. Статистика определяет структуру распределения трудовых
ресурсов региона, степень обеспеченности рабочей силой за счет как внутренних
ресурсов региона, так и рабочей силы из других регионов. Учитывается влияние
сезонности отдельных видов работ и наличия побочных занятий на территориальное
распределение трудовых ресурсов в сельской местности.1
Характер производства во многом
определяет использование персонала и техники в производстве. Но очень важно
учитывать, как в этой системе расходуется такой ресурс, как время.
Статистические наблюдения за использованием рабочего времени также представляют
предмет изучения статистики трудовых ресурсов, который показывает возможности
применения получаемой информации для оптимизации производственных процессов.
Показатели рабочего времени по
данным статистической отчетности и их анализ. Рабочее время — часть
календарного времени, затрачиваемого на производство продукции или выполнение
определенного вида работ. В связи с интенсификацией общественного производства
и повышением его эффективности стоят задачи активного внедрения научной
организации труда, более рационального использования рабочего времени,
сокращения его непроизводительных затрат и потерь за счет организационных, технологических
и социальных мероприятий. Процесс решения этих задач отражают статистические
показатели использования рабочего времени. Исходным служит показатель
календарного фонда времени — число календарных дней месяца, квартала, полугода,
года, приходящихся на одного рабочего или на коллектив рабочих.
Показатель календарного фонда
времени отражает рабочее и внерабочее время. Человеко-дни явок на работу — это
человеко-дни, фактически отработанные, и человеко-дни целодневных простоев.
Человеко-дни неявок на работу — это человеко-дни невыхода на работу по
уважительным и неуважительным причинам. Человеко-дни неявок на работу по
уважительным причинам включают человеко-дни очередных отпусков, праздничных и
выходных дней, отпусков по беременности и родам, неявок по болезни и в связи с
выполнением общественных и общегосударственных обязанностей и других неявок,
разрешенных законом. Человеко-дни неявок по неуважительным причинам — это
человеко-дни невыходов с разрешения администрации и прогулы.
Подробный анализ использования
рабочего времени на предприятиях осуществляется по данным статистической
отчетности (квартальной и годовой), которая составляется по данным первичного
учета, а также по данным фотографий рабочего дня, хронометражных наблюдений и
различных единовременных обследований.
Анализ использования рабочего
времени предполагает расчет следующих показателей:
Календарное время = Сумма
человеко-дней явок на работу + Сумма человеко-дней неявок на работу
Табельный фонд рабочего времени =
Календарная фактическая сумма человеко-дней без праздничных и выходгых
Максимально возможный фонд рабочего
времени = Табельный фонд рабочего времени – сумма человеко-дней очередных
отпусков
Фактический фонд рабочего времени =
Сумма человеко-дней явок – Сумма человеко-дней целодневных простоев.
Коэффициент использования
календарного фонда рабочего времени = Сумма человеко-дней фактически
отработанных / Календарный фонд рабочего времени*100
Коэффициент использования
установленной продолжительности раб дня = Средняя фактическая продолжительность
рабочего дня / Установленная продолжительность рабочего дня*100
Средняя фактическая
продолжительность рабочего дня = Сумма человеко-часов отработанных всего /
Сумма человеко-дней отработанных всего (час)
Коэффициент использования
установленной продолжительности рабочего месяца = средняя фактическая
продолжить рабочего месяца (квартала, полугодия, года) / установленная
продолжительность рабочего месяца (квартала, полугодия, года)*100
Средняя фактическая
продолжительность рабочего месяца = Сумма человеко-дней фактически отработанных
/ Среднесписочная численность
Установленная продолжительность
рабочего месяца = Максимально возможный фонд рабочего времени / Среднесписочная
численность
Среднесписочная численность =
календарный фонд рабочего времени / число календарных дней в периоде
Коэффициент интегрального использования рабочего времени
= Коэффициент использования установленной продолжительности рабочего дня *
Коэффициент использования установленной продолжительности рабочего месяца.
Статистика позволяет отслеживать
качество использования труда на предприятии. Это происходит на основе
соотнесения реального использования элементов труда в производстве с возможным
уровнем их использования. В исследовании этого вопроса процесс труда
разделяется на составные части, которые, будучи проанализированы отдельно,
вновь соединяются в единое целое. Этими вопросами занимается статистика труда.
Условием роста эффективности
предприятия могут являться успехи в производстве. Этого, в свою очередь, можно
добиться через повышение производительности труда, т.е. объема производства на
единицу использованных ресурсов. Рост производительности является средством
роста эффективности использования труда.
Расчет уровня производительности
труда. Производительность труда — это плодотворность трудовой деятельности
работников в сфере материального производства. Важнейшие показатели развития и
совершенствования народного хозяйства — это показатели эффективности
общественного производства. В системе показателей, характеризующих эффективность
общественного производства, ведущий — производительность труда.
Уровень производительности труда
выражается количеством продукции, произведенной в единицу времени: отношением
количества произведенной продукции к живому труду, непосредственно затраченному
на ее производство, или же ко всему воплощенному в ней труду — живому и
овеществленному.
Методы расчета уровня
производительности труда. Уровень производительности труда характеризуется
прямыми и обратными показателями. Прямым показателем служит количество
продукции, выработанной в единицу времени. Если количество продукции обозначить
Q, затраты рабочего времени на весь объем продукции — Т, а уровень
производительности труда— w, то:
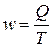
Показателем, обратным уровню
производительности труда, является трудоемкость, т.е. время, затраченное на
производство единицы продукции:
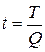
Взаимосвязь трудоемкости и
производительности труда проявляется в соотношениях:
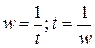
При выпуске однородной продукции
уровень производительности труда исчисляется в натуральных показателях
(например, количество произведенной электроэнергии в единицу времени). Если
продукция одноименная, но разнокачественная, то уровень производительности
труда измеряется в условных натуральных показателях (например, выплавка чугуна
в единицу времени в пересчете на передельный чугун).
Обобщающим показателем уровня
производительности труда является количество продукции (в денежном выражении),
выработанной в единицу времени:
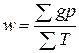 или
или 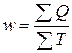
где SQ = Sqp , здесь q — продукция в натуральных измерителях, р — цена единицы
продукции, в которой учтено различие в качестве продукции (при правильном
ценообразовании).
Денежное выражение дает возможность
обобщить разнородную продукцию (различные потребительные стоимости) и
рассчитать уровень производительности труда по различным участкам работы
(бригаде, цеху, предприятию, отрасли, народному хозяйству отдельных регионов и
в целом по стране).
Уровень производительности труда при
выпуске разнородных видов продукции может быть также представлен в трудовом
измерении, т. е. как количество продукции в человеко-часах (чаще всего в
нормативных), выработанной в единицу времени:

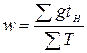
Знаменатель дроби может быть выражен
в человеко-часах, человеко-днях или же среднесписочным числом работающих,
соответственно получаем выработку продукции за человеко-час, человеко-день или
же на одного рабочего или работающего за месяц, квартал, год (за человеко-месяц,
человеко-квартал, человеко-год).
Средняя выработка продукции за 1
человеко-час показывает уровень производительности труда за время чистой работы
(без учета потерь времени в минутах и секундах); выработка за 1 человеко-день
зависит от часовой выработки и степени использования рабочего дня, а выработка
на одного работающего — от дневной выработки и от степени использования
рабочего месяца, квартала, года (количества отработанных дней за данный
период).
Если выработку за 1 человеко-час
умножить на среднюю фактическую продолжительность рабочего дня, то получим
выработку за 1 человеко-день; если выработку за 1 человеко-день умножить на
среднюю фактическую продолжительность рабочего месяца (квартала, года), получим
выработку на одного рабочего за месяц, (квартал, год).
Задачей статистики оплаты труда
являются анализ объема и состава фонда заработной платы, затрат на рабочую
силу, характеристика среднего уровня оплаты труда, анализ динамики заработной
платы в зависимости от других показателей.
В мировой статистической практике в
«заработную» плату включают все виды заработков, которые дополняются премиями,
доплатами, надбавками, компенсационными выплатами и т.д. Следует иметь в виду,
что «заработная плата», с одной стороны, может выступать в виде дохода для наемного
работника, а с другой - это часть издержек производства. Затраты, которые несет
общество или отдельный предприниматель при использовании наемного труда,
включают помимо заработной платы расходы на социальную защиту работников.
Затраты в расчете на одного работника за единицу времени определяются как
стоимость рабочей силы для работодателя, использующего наемный труд.
В ходе статистического анализа
различают фонд заработной платы и выплаты социального характера.
Фонд заработной платы включает
прямые и косвенные выплаты по заработной плате. В прямые выплаты включаются:
начисленные предприятием, учреждением или организацией денежные суммы оплаты
труда за отработанное время (повременные формы, сдельная оплата, тарифные
ставки, оклады); оплата труда в натуральной форме (выражается в стоимостной
форме); выплаты стимулирующего характера - доплаты и надбавки за
профессиональное мастерство, совмещение профессий и т.д.); премии и
вознаграждения (на регулярной или периодической основе); выплаты
компенсирующего характера (оплата за ночное время, за сложные или вредные
условия труда (на полиграфических предприятиях за вредные условия труда идет 4
% -ная надбавка к тарифной ставке), за работу в праздничные и выходные дни, по
районным коэффициентам.
В косвенные выплаты включаются:
выплаты за неотработанное время (отпуска, учебные отпуска, льготная оплата
часов работающих подростков, выплаты за время переподготовки, повышения
квалификации и т.д.); единовременные выплаты (поощрительного характера,
материальная помощь, выплаты по итогам работы за год, за выслугу лет); выплаты
за питание, жилье, топливо отдельным категориям работников на основе
соответствующего законодательcтва.
Данные о фонде заработной платы
необходимы для расчета издержек на рабочую силу, для построения счета
образования доходов в СНС, для анализа экономического роста и уровня жизни, для
построения межотраслевого баланса. ФЗП - это важнейший компонент себестоимости
продукции.
От выплат фонда оплаты труда
отличают выплаты социального характера, которые не включаются в заработную
плату, но являются составным элементом дохода работника. К ним относятся оплаты
социальных льгот (отдых, лечение, проезд, трудоустройство, страховые платежи,
стипендии). Информация о расходах социального характера необходима при определении
сводных расходов на рабочую силу.
Важнейшими статистическими
показателями являются: минимальная заработная плата (устанавливается
законодательством); номинальная заработная плата Zн (денежная сумма
с учетом налогов и других удержаний); реальная заработная плата Zp
(покупательная способность номинальной заработной платы, исчисляемая путем
деления номинальной заработной платы на индекс потребительских цен Iипц
: Zp = Zн : Iипц ); средняя заработная плата.
Среди перечисленных показателей для
аналитических целей особо важен показатель среднего уровня заработной платы.
Различают среднемесячную, среднедневную и среднечасовую заработную плату.
Среднемесячная заработная плата Zмср
рассчитывается как отношение фонда заработной платы Фм ,
начисленного за месяц, к среднесписочной численности работников Чср
:
Среднедневная заработная плата Zдср
рассчитывается как отношение дневного фонда заработной платы Фд к
отработанному времени Тд , учтенному в человеко-днях:
Среднечасовая заработная плата Zчср
рассчитывается как отношение часового фонда заработной платы Фч к отработанным человеко-часам Тч :
Динамика уровней средней заработной платы
анализируется с помощью индексов переменного состава, постоянного состава и
индекса структурных сдвигов.
Индекс переменного состава
заработной платы Iz характеризует изменение среднего уровня
заработной платы в отчетном периоде по сравнению с базисным в зависимости от
изменения средней заработной платы отдельных категорий работников и удельного
веса численности работников с различным уровнем оплаты труда. Для его
исчисления берутся значения фондов начисленной заработной платы отдельных
категорий работников или всего персонала за отчетный и базовый периоды (Ф1
и Ф0 ), среднесписочная численность отдельных категорий работников
или всего персонала в отчетном и базовом периодах (Ч1 и Ч0
) и средняя заработная плата по группам персонала или по предприятиям и
отраслям (Z1 и Z0 ). Индекс рассчитывается следующим
образом:
|
|
 |
Индекс постоянного состава
заработной платы IZ рассчитывается в том случае, если необходимо
отразить только изменение среднего уровня заработной платы в отчетном периоде
по сравнению с базовым без учета структурного фактора (изменения удельного веса
численности работников с различным уровнем заработной платы):
Если необходимо зафиксировать влияние
структурного фактора на изменение среднего уровня заработной платы, то
рассчитывается индекс структурных сдвигов Iстр путем деления индекса
переменного состава заработной платы на индекс постоянного состава заработной
платы:
Используя среднюю заработную плату, можно
рассчитать средний фонд заработной платы как произведение численности
работников и средней заработной платы и затем рассчитать отклонение
фактического фонда заработной платы от базисного фонда с учетом изменения среднего
уровня заработной платы (Z) и количественного состава работников (Ч).
Влияние каждого из двух факторов на
изменение фонда заработной платы определяют следующим образом:
1) влияние изменения численности
работников Ч на прирост или уменьшение фонда заработной платы Ф:
2) влияние изменения среднего уровня
оплаты труда (Z) на прирост или уменьшение фонда заработной платы (Ф):
Тема
№ 4. Статистика национального богатства. Статистика объема и состава
национального богатства
В макроэкономической статистике
категория «национальное богатство» (НБ) используется для оценки уровня
экономического развития страны и характеризует исходную и конечную стадии
процесса общественного воспроизводства. Национальное богатство представляет
собой совокупность накопленных материальных ресурсов (благ), которыми
располагает общество в данный момент времени, создающих необходимые условия
производства товаров, оказания услуг и обеспечения жизни людей.
По источникам происхождения в
составе национального богатства выделяют две основные части: непроизведенные
активы (природные ресурсы) и национальное имущество.
Природные ресурсы (природные
богатства) составляют первую важнейшую группу ресурсов, куда включаются
учтенные и вовлеченные в экономический оборот как невозобновляемые природные
ресурсы (земля, полезные ископаемые), так и возобновляемые природные ресурсы
(вода, воздух, растительные и животные ресурсы).
Вторую важнейшую группу ресурсов
составляет национальное имущество - совокупность накопленных материальных благ,
созданных в ходе трудовой деятельности людей. Сюда относят материальные,
нематериальные, финансовые, нефинансовые активы регионов, отраслей, секторов
экономики, а также юридических и физических лиц. В отдельную группу выделяют
потребительские товары длительного пользования, прямые иностранные инвестиции и
золотой запас. В состав национального имущества включается и личное имущество
граждан.
В методологии системы национальных
счетов (СНС) в основе расчета национального богатства используется понятие
«экономические активы».
Экономические активы - это
находящиеся в собственности объекты, владельцы и пользователи которых могут
извлекать экономические выгоды. Все экономические активы, включаемые в состав
НБ, по рекомендации статистической комиссии ООН подразделяются на две основные
группы: нефинансовые и финансовые активы.
В свою очередь, в группе
нефинансовых активов выделяют произведенные и непроизведенные активы,
материальные и нематериальные активы.
Произведенные активы включают
основные фонды, оборотные фонды, ценности (дорогостоящие товары, стоимость
которых не уменьшается по отношению к общему уровню цен).
Среди непроизведенных активов
выделяют материальные (природные ресурсы) и нематериальные (патенты, авторские
права и пр.).
Финансовые активы представляют собой
средства осуществления финансовых расчетов между институциональными единицами,
связанными финансовыми обязательствами и финансовыми требованиями. Сюда
включают: монетарное золото (резерв покупательной способности); специальные
права заимствования (СПЗ) (международные резервные и платежные средства,
которые используются для безналичных международных расчетов как форма мировых
денег); наличные деньги (валюта) (банкноты и монеты, которые используются для
проведения расчетов и находятся в обращении); депозиты (денежные средства,
размещенные в банках на хранение); ценные бумаги (долговые обязательства, куда
относятся векселя, облигации, депозитные сертификаты, приватизационные чеки,
лотерейные билеты и пр., кроме акций); акции и другие виды акционерного
капитала (свидетельства о внесении определенной доли в уставный капитал, дающие
право на получение дивидендов); ссуды; страховые технические резервы
(формируются страховыми организациями в ходе проведения страховых операций как
обязательные накопительные суммы, выполняющие функцию финансовых гарантий);
дебиторская и кредиторская задолженности (торговые кредиты, авансы в счет
оплаты незавершенных работ и др.).
Классификация финансовых активов
определена Общероссийским классификатором финансовых активов (ОКФА) в 1998 г.
Задачей статистики национального
богатства является аналитическое изучение объема, структуры, динамики и
эффективности использования всего богатства и его составных элементов. Для
решения этой задачи разработана система показателей с обоснованием методологии
их вычисления.
Объем национального богатства
рассчитывается в стоимостном выражении в текущих и сопоставимых ценах на
определенный момент времени. Если объем национального богатства рассчитывается
в текущих ценах, то, следовательно, поставлена задача определения стоимости его
элементов в ценах приобретения в соответствующих периодах. Расчет национального
богатства в постоянных ценах отражает стоимость элементов национального
богатства в ценах того периода, который принят за базовый.
Расчет изменения физического объема
национального богатства или его элементов исчисляется, как правило, в
сопоставимых ценах.
Экономическое и финансовое положение
страны характеризует сводный баланс активов и пассивов, составленный по
экономике в целом.
По методологии СНС объем
национального богатства может быть определен как сумма стоимостей всех
экономических активов (нефинансовых и финансовых) резидентов страны минус их
финансовые обязательства. Баланс активов и пассивов тесно связан со всеми
счетами накопления. Сравнение показателей баланса активов и пассивов начального
и конечного периодов дает возможность определить распределение богатства,
выявить изменения стоимости активов в результате экономических операций, иметь
представление об экономических ресурсах страны, что позволяет дать оценку
размерам внешнего долга страны или оценить ее позицию как кредитора (чистые
требования к «остальному миру»).
Существующая в настоящее время
информационная база национального богатства РФ (основные фонды и материальные
оборотные средства) основывается как на системе статистической и бухгалтерской
отчетности предприятий, фирм, учреждений и организаций, так и на данных
выборочных обследований. Что касается стоимости домашнего имущества,
находящегося в собственности граждан, то она определяется расчетным путем с
использованием данных о товарообороте непродовольственных товаров, данных
бюджетных обследований граждан, а также других специальных обследований.
В отечественной статистике
актуальной проблемой является правильная оценка тех элементов НБ, которые ранее
не оценивались, так как были государственной собственностью и не являлись
объектами купли-продажи (земля и природные ресурсы). Сложность заключается в
том, что для земли и природных ресурсов, не являющихся плодом труда человека,
какие-либо виды оценки, кроме рыночной стоимости, не могут считаться достаточно
обоснованными и использоваться в экономических расчетах. Следовательно,
основным критерием здесь выступает рыночная цена, которая зависит от
совокупности множества факторов (экономическое положение страны; соотношение
спроса и предложения на землю, земельное законодательство; климатические
условия и т.п.).
В системе рыночного хозяйства
применяются следующие виды оценки земли: рыночная стоимость земельного участка;
стоимость строений, ирригационных сооружений, включенных в хозяйство; арендная
цена.
При оценке природных ресурсов -
важного элемента НБ, - учитывая, что природные ресурсы не могут иметь рыночную
стоимость, являясь исключительно собственностью государства, в мировой практике
пока применяют несколько заниженные виды оценки: стоимость разведки и добычи;
действующие в экономике оптовые цены; стоимость концессии.
Статистика основных фондов
Важнейшей частью национального
имущества являются основные фонды, на долю которых приходится более 90%.
К основным фондам относится вся
совокупность произведенных активов или материально-вещественных ценностей
(средств труда), которые многократно (не менее года) в неизменной
натурально-вещественной форме участвуют в процессах производства товаров и
услуг, перенося постепенно (по мере износа) свою стоимость на продукт или
услугу труда.
Порядок отнесения объектов к
основным фондам определяется нормативными актами. В настоящее время состав
основных фондов определяется Общероссийским классификатором основных фондов
(ОКОФ), который был введен в 1996 г. Согласно ОКОФ, в отечественной статистике
принята типовая классификация основных фондов. В их составе выделяют
материальные фонды (производственные и жилые здания, сооружения, машины и
оборудование, транспортные средства, производственный и хозяйственный
инвентарь, рабочий и продуктивный скот, многолетние насаждения, прочие основные
фонды) и стоимостные (капитальные затраты на геологоразведочные, мелиоративные,
ирригационные работы, затраты на программное обеспечение и базы данных ЭВМ,
затраты по обеспечению сферы экономических операций).
При изучении состава основных фондов
используются и группировки по ряду важнейших признаков: отраслевому; по видам
экономической деятельности; по формам собственности; региональному
(территориальному); по принадлежности (собственные и арендованные основные
средства).
В учете основных фондов различают
оценку основных фондов по первоначальной и по восстановительной стоимости.
Полная первоначальная стоимость -
это стоимость основных фондов (объекта) в фактических ценах на момент ввода их
в эксплуатацию. В этой оценке основные фонды поступают на баланс предприятия и
она является базовой для расчета амортизационных отчислений. В зависимости от
источника поступления основных фондов под первоначальной стоимостью понимается
либо сумма фактических затрат, либо договорная оценка стоимости, либо рыночная
стоимость на момент принятия объекта к учету, если он получен безвозмездно.
Остаточная первоначальная стоимость
(первоначальная стоимость за вычетом износа) - это полная первоначальная
стоимость объекта за вычетом суммы износа, что позволяет иметь представление о
фактической стоимости, не перенесенной на произведенный продукт. Поскольку
одинаковые объекты были введены в эксплуатацию в разное время, где действовал
разный уровень цен, то они имеют и разную стоимостную оценку. С целью
правильного определения объема основных фондов и правильной уплаты налога с
каждым новым изменением цен необходимо проводить переоценку основных фондов.
Полная восстановительная стоимость -
это стоимость воспроизводства основных фондов в новом виде (приобретение,
транспортировка, установка аналогичных новых объектов на момент переоценки).
Остаточная восстановительная
стоимость - это полная восстановительная стоимость основных фондов без суммы
износа.
Основные фонды по мере их
эксплуатации подвергаются физическому и моральному износу, который в денежном
выражении в статистике называют амортизацией. От износа амортизация отличается
тем, что она представляет собой процесс переноса стоимости основных фондов на
издержки производства, между тем износ как экономическая категория отражает
лишь процесс старения действующих основных фондов. Тем не менее именно на
основании износа рассчитывается амортизация.
По мере необходимости замены
основных фондов накапливаются денежные средства (амортизационный фонд),
достаточные для обеспечения реновации (полного восстановления) выбывших
основных фондов. Для этих целей служат амортизационные отчисления (включенные в
себестоимость продукции части стоимости действующих основных фондов).
Амортизационные отчисления могут
обеспечить и частичное восстановление основных фондов в ходе капитального
ремонта и модернизации.
Объем ежегодных амортизационных
отчислений А можно рассчитать по формуле
где Sп - полная первоначальная
стоимость основных фондов; Sл - ликвидационная стоимость основных
фондов за вычетом расходов на демонтаж; Т - нормативный срок службы основных
фондов.
Годовая норма амортизации Ан
определяется как отношение объема ежегодных амортизационных отчислений А к
полной первоначальной стоимости основных фондов Sпв :
|
|
 |
В настоящее время предприятия и организации
могут выбрать один из применяемых в настоящее время способов начисления
амортизации: линейный (годовая сумма амортизационных отчислений начисляется
равными долями от полной балансовой стоимости по установленным нормам);
уменьшаемого остатка или ускоренной амортизации (годовая сумма амортизационных
отчислений определяется по остаточной стоимости объекта и норме амортизации);
списания стоимости по сумме лет срока полезного использования (годовая сумма
амортизационных отчислений определяется по полной балансовой стоимости объекта
и коэффициенту как отношению остаточного числа лет до конца срока службы к
сумме лет срока его полезного использования); списания стоимости
пропорционально объему произведенной продукции (годовая сумма амортизационных
отчислений определяется по полной балансовой стоимости объекта и отношению
фактического объема произведенной продукции в текущем периоде к планируемому
выпуску за весь период использования объекта).
Наиболее полное представление об
изменении объема основных фондов за год можно получить на основе балансового
метода.
Балансы основных фондов составляются
в двух видах - по полной первоначальной балансовой стоимости и по остаточной
балансовой стоимости, что может быть выражено в текущих ценах, среднегодовых
ценах и в постоянных ценах базисного периода.
Баланс основных
фондов
по балансовой стоимости, млн. руб.
|
Виды основных
фондов в группировке по разным признакам
|
Наличие на начало
года
|
Поступило в
отчетном году
|
Выбыло в отчетном
году
|
Наличие на конец
года
|
|
Всего
|
В том числе
|
Всего
|
В том числе
|
|
ввод в действие
|
прочие поступления
|
выбытие по ветхости
и износу
|
прочее выбытие
|
|
А
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8 = 1 + 3 + 4 – 6 –
7
|
Баланс основных фондов по полной
балансовой стоимости отражает изменение объема основных фондов без учета их
физического состояния. Взаимосвязь между показателями баланса выражается в
последнем показателе, который есть сумма стоимостей основных фондов на начало
года и стоимостей основных фондов, поступивших в течение отчетного года из
разных источников за вычетом стоимости выбывших основных фондов в течение
отчетного года по всем направлениям выбытия.
В отличие от баланса основных фондов
по полной стоимости, который призван отражать процесс воспроизводства основных
фондов в их физическом объеме, баланс основных фондов по остаточной балансовой
стоимости характеризует изменение реальной стоимости не только по вводу и
выбытию основных фондов, но и с учетом частичного восстановления их стоимости
путем капитального ремонта и амортизации. Схема баланса основных фондов по
остаточной балансовой стоимости.
Баланс основных
фондов
по остаточной стоимости, млн. руб.
|
Виды ОФ в
группировке по разным признакам
|
Наличие ОФ на
начало года
|
В течение года
|
Наличие ОФ на конец
года
|
|
ввод в действие ОФ
|
произведенный
капитальный ремонт
|
выбытие по ветхости
|
амортизация
|
|
А
|
1
|
2
|
3
|
4
|
5
|
6 = 1+2+3–4–5
|
Для характеристики состояния,
движения и использования основных фондов рассчитываются три группы основных
показателей для оценки производственного потенциала предприятия.
Первая группа показателей отражает
состояние основных фондов - коэффициенты годности и износа (по состоянию на
определенную дату).
Коэффициент годности Кгод
рассчитывается как отношение остаточной балансовой стоимости Sобс к
полной балансовой стоимости основных фондов Sпбс :
Коэффициент износа Кизн рассчитывается как
отношение суммы износа И к полной балансовой стоимости основных фондов Sпбс :
Вторая группа показателей отражает движение
(введение или выбытие) основных фондов - коэффициенты обновления и выбытия
основных фондов за год или другой изучаемый период.
Коэффициент обновления Кобн
исчисляется как отношение стоимости введенных в оборот новых основных фондов за
год Р к полной балансовой стоимости на конец года Sпбс к.г.
Коэффициент выбытия Квыб исчисляется
как отношение стоимости выбывших основных средств В в течение года к полной
балансовой стоимости основных фондов на начало года Sпбс н.г. :
Третья группа показателей характеризует
использование основных фондов, к которым относят фондоемкость, фондоотдачу
продукции и фондовооруженность труда основными фондами.
Показатель фондоемкости продукции V
характеризует уровень затрат основных производственных фондов на один рубль
произведенной продукции и исчисляется как отношение среднегодовой стоимости
основных фондов к объему произведенной за год продукции Q:
Показатель фондоотдачи Ф характеризует выпуск
продукции в расчете на один рубль стоимости основных фондов (чем лучше
используются основные фонды, тем выше показатель фондоотдачи). Показатель
рассчитывается как отношение объема произведенной за год продукции Q к
среднегодовой стоимости основных фондов:
Эффективность использования основных фондов
можно определить индексным методом. При этом следует учесть, что объем
продукции и стоимость основных фондов в двух сравниваемых периодах должны
выражаться в сопоставимых ценах (по стоимости в постоянных ценах).
Индекс фондоотдачи Iф рассчитывается
как отношение уровня фондоотдачи в текущем периоде Ф1 к уровню
фондоотдачи в базисном периоде Ф0 :
Показатель фондовооруженности труда
W отражает объем основных фондов, которыми оснащен один работник в процессе
производства продукта труда, и рассчитывается как отношение среднегодовой
стоимости основных производственных фондов к среднесписочной численности
работников или рабочих Т:
Фондоотдача Ф и фондовооруженность труда W
являются факторами роста производительности труда ПТ:
Из данного соотношения видно, что между фондоотдачей,
фондовооруженностью и производительностью труда существует тесная
взаимозависимость. Фондоотдача будет расти, если производительность труда будет
опережать рост фондовооруженности. Но если рост производительности труда ниже,
чем рост фондовооруженности, то фондоотдача падает.
Статистика материальных оборотных
фондов
Помимо основных фондов для успешного
функционирования процесса производства необходимы и материальные оборотные
фонды, которые целиком потребляются в одном производственном цикле, вещественно
входят в продукт и полностью переносят на него свою стоимость.
Материальные оборотные фонды
являются наиболее мобильным и постоянно возобновляемым элементом национального
богатства.
В состав материальных оборотных
фондов включают сырье, основные и вспомогательные материалы, незавершенное
производство в отраслях с длительным циклом (строительные объекты, тяжелая
промышленность, сельское хозяйство, производство кинофильмов и т.д.), готовую
продукцию, товары для перепродажи, государственные материальные резервы
(средства производства и предметы потребления, предназначенные для
использования в чрезвычайных обстоятельствах), производственные запасы
(топливо, горючее, тара, запасные части для ремонта и т.д.). Одна из главных
функций оборотных средств - обеспечение производственного процесса. Поэтому
важнейшей является характеристика наличия материальных оборотных фондов, учет
запасов которых ведется в натуральном и денежном выражении по состоянию на
определенную дату и в среднем за истекший отчетный период.
|
|
 |
В статистическом анализе используется показатель
обеспеченности производственными запасами, который рассчитывается в днях
обеспеченности До как отношение величины фактических производственных запасов
на определенную дату Зф к среднесуточной потребности в данном виде
запасов Зс :
Изменение запасов в течение данного
периода характеризуется показателями их пополнения и выбытия, разница между
которыми отражает или прирост, или сокращение запасов оборотных фондов.
На предприятиях в целях оперативного
управления рассчитывают средний остаток оборотных фондов за данный месяц как
полусумму остатков на начало и конец этого месяца по формуле
Ряд показателей характеризует
процесс использования материальных оборотных средств. К ним относятся:
коэффициент оборачиваемости оборотных фондов, коэффициент закрепления оборотных
фондов, показатель средней продолжительности одного оборота в днях, показатель
суммы средств, высвобождаемых из оборота вследствие ускорения оборачиваемости
оборотных фондов. К этой же группе относятся показатели, характеризующие
материалоемкость продукции, расход важнейших видов материальных ресурсов,
удельный расход конкретного вида сырья или материалов.
Коэффициент оборачиваемости Коб
характеризует скорость оборота оборотных средств (число оборотов стоимости
оборотных средств, равной их среднему остатку за данный период времени) и
представляет собой отношение стоимости реализованной продукции (выручки) Рв к
среднему остатку оборотных фондов за тот
же период (по экономическому содержанию аналогичен коэффициенту фондоотдачи):
Коэффициент закрепления оборотных фондов Кзк
- величина, обратная коэффициенту оборачиваемости (отражает объем материальных
оборотных средств на каждый рубль реализованной продукции). Он исчисляется в
стоимостном выражении (руб.) (по экономическому содержанию аналогичен
коэффициенту фондоемкости):
Показатель средней продолжительности одного
оборота в днях Аоб показывает время (количество дней), в течение
которого совершается один полный оборот материальных оборотных средств (удобен
для сравнения скорости обращения оборотных средств за периоды разной
продолжительности). Он рассчитывается как отношение продолжительности Д
периода, за который определяется показатель (число календарных дней), к
коэффициенту оборачиваемости Коб :
Показатель суммы средств, высвобожденных из
оборота в результате ускорения оборачиваемости материальных оборотных фондов (Свыс
) определяется как разность условного значения среднего остатка оборотных
фондов, которые необходимы для получения фактического объема выручки от
реализации и фактического среднего остатка оборотных фондов:
Эффективность использования оборотных фондов
оценивается показателем материалоемкости продукции (МП), который рассчитывается
как отношение стоимости текущих материальных затрат без амортизации МЗтек
к стоимости произведенной продукции Pп :
Показатели расхода видов материальных ресурсов
используются при расчете металлоемкости, энергоемкости, топливоемкости
(например, ВВП). Данные показатели исчисляются в натуральном выражении в расчете
на единицу продукции (на 1 руб., на 1 тыс. руб. и т.д.).
При характеристике использования
материальных оборотных фондов очень широко используются показатели удельного
расхода конкретного вида материалов, сырья, топлива и других видов оборотных
средств на единицу продукции или услуг (индексы выражаются в процентах).
Показатели уровня удельного расхода определяются как отношение общего их
расхода в натуральном выражении на количество выпущенной продукции или услуг
(также выраженных в натуральном виде).
Инвестиции – долгосрочные вложения
частного или государственного капитала в различные отрасли национальной
(внутренние инвестиции) или зарубежной (заграничные инвестиции) экономики с
целью получения прибыли. В соответствии с законом "Об инвестициях в
РФ" 1991г. под инвестициями понимают денежные средства; целевые банковские
вклады; пай; акции и др. ценные бумаги; технологии; машины и оборудование;
лицензии; кредиты; имущественные права; интеллектуальные ценности, вкладываемые
в предпринимательские и другие виды деятельности с целью получения прибыли
(дохода) и социального эффекта. Такие вложения осуществляются путем
приобретения экономических активов, т.е. экономических объектов, владение или
использование которых приносит и будет приносить в дальнейшем их владельцам
экономическую выгоду. Ориентация на будущие доходы при вложении капитала –
характерная черта, отличающая инвестиции от текущих затрат на производство
товаров и услуг. В связи с этим
инвестиционную деятельность можно также определить как приобретение
экономических активов, способных обеспечить получение доходов в будущем.
В качестве отдачи от инвестиций
принимается разность между доходами в течение срока использования
инвестиционных ресурсов и затратами денежных средств в том же периоде (издержки
производства, налоги и т. д.). Эта разность в итого является либо прибылью либо
убытками.
Инвестиции подразделяются на
реальные, финансовые и интеллектуальные.
Реальные (прямые) инвестиции –
вложение капитала частной фирмой или государством в производство какой-либо
продукции.
Финансовые инвестиции – вложения в
финансовые институты, т.е. вложения в акции, облигации и другие ценные бумаги,
выпущенные частными компаниями или государством, а также в объекты тезаврации,
банковские депозиты.
Интеллектуальные инвестиции –
подготовка специалистов на курсах, передача опыта, лицензий и ноу-хау,
совместные научные разработки и др.
Понятие инвестиционного менеджмента
в условиях переходной экономики, как правило, относится к управлению двумя
видами инвестиций: реальными и финансовыми.
По отношению к совокупности этих
двух видов инвестиций на предприятиях применяют понятие инвестиционного
портфеля, а инвестиции в различные виды активов, связанные единой
инвестиционной политикой, называются портфельными инвестициями.
В развитых странах большую часть
инвестиций составляют финансовые инвестиции.
По этой причине в хозяйственной практике иногда используется более узкое
понятие инвестиций, охватывающее лишь финансовые инвестиции. В частности,
именно такой подход заложен в международных стандартах бухгалтерского учета.
Финансовые инвестиции — вложения в ценные бумаги с целью
последующей игры на изменение курса и (или) получение дивиденда, а также
участия в управлении хозяйствующим субъектом. Портфельные инвестиции не позволяют
инвестору установить эффективный контроль над предприятием и не свидетельствуют
о наличии у инвестора долговременной заинтересованности в развитии предприятия.
Целью портфельных инвестиций
является вложение средств инвесторов в ценные бумаги наиболее прибыльно
работающих предприятий, а также в ценные бумаги, эмитируемые государственными и
местными органами власти с целью получения максимального дохода на вложенные
средства. Портфельные инвестиции
— основной источник средств для финансирования акций, выпускаемых
предприятиями, крупными корпорациями и частными банками.
Финансовые инвестиции ( в российской
хозяйственной практике их называют финансовыми вложениями) подразделяются на
текущие (краткосрочные) и долгосрочные. Согласно международным стандартам бухгалтерского
учета, текущими являются финансовые инвестиции, которые по своей природе
свободно реализуемы и предназначены для владения не более чем на один год.
Долгосрочными инвестициями считаются вложения, осуществленные с намерением получения доходов по ним сроком более одного
года. К ним относятся также вложения в
ценные бумаги, срок погашения (выкупа) которых не установлен, но имеется
намерение получать доходы по ним более одного года.
Реальные инвестиции представляют собой вложения средств с целью
приобретения нефинансовых активов всех видов (произведенных и непроизведенных).
Таким образом, инвестиции в нефинансовые активы состоят из инвестиций в
произведенные и непроизводственные активы. Инвестиции в произведенные активы
включают вложения в основной капитал, в запасы материальных оборотных средств и
в ценности. К инвестициям в непроизведенные активы относятся вложения с целью
приобретения материальных непроизведенных активов (земли; недр с разведанными
залежами полезных ископаемых; некультивируемых биологических ресурсов, таких,
как естественные леса, используемые для лесозаготовок, и т.п.), а также
нематериальных непроизведенных активов (запатентованные экономические объекты и
некоторые другие элементы).
Итак, инвестиции представляют собой
вложения в финансовые либо в нефинансовые активы. Исходя из этого, инвестиции
делят на финансовые вложения и капиталовложения. Кроме того, в отдельный вид
инвестиций выделяют интеллектуальные.
Финансовые инвестиции могут рассматриваться с двух точек зрения:
как стоимость ресурсов,
израсходованных организацией за определенный период на приобретение финансовых
прав – акций, облигаций, долей в уставном капитале других организаций,
банковских вкладов, предоставленных другими организациями займов;
как стоимость активов,
представляющих собой финансовые права,
которыми располагает организация на определенную дату.
В первом случае финансовые инвестиции представляют собой финансовые потоки, которые
характеризуются интервальным показателем и определяются по сумме фактических
затрат инвестора на их приобретение, включая вознаграждение за выполнение
посреднических услуг по покупке ценных бумаг.
Во втором случае
финансовые инвестиции
рассматриваются как накопленная величина, характеризуемая моментным
показателем и определяемая по балансовой
стоимости инвестиции на определенную дату. Балансовая стоимость финансового
актива может отличаться от фактических затрат на его приобретение за счет того,
что в бухгалтерском учете разница между
покупной стоимостью постепенно относится на финансовые результаты
организации. Кроме того, различие возможно за счет того, что имеющиеся у
организации акции, рыночная котировка которых регулярно публикуется, при
составлении годового бухгалтерского баланса отражаются не по стоимости
приобретения, а по рыночной стоимости (если последняя ниже стоимости
приобретения).
В бухгалтерских документах и формах
государственного статистического наблюдения
ведется раздельный учет долгосрочных и краткосрочных финансовых
инвестиций.
Для более полной характеристики
инвестиционного процесса важной является информация о соотношении между
инвестициями, вложенными данной организацией в другие хозяйственные инвестиции,
и инвестициями, вложенными другими
хозяйственными единицами в данную организацию. Накопленная величина первых
представляет собой инвестиционные активы данной организации, накопленная
величина вторых – соответствующие пассивы. Если за определенный период
организация вложила в другие хозяйственные единицы больший объем инвестиций,
чем было вложено в нее за тот же период, то это свидетельствует об увеличении
инвестиционных активов данной организации. В противном случае имеет место
увеличение пассивов.
Таким образом, финансовые инвестиции (их потоки и
накопленные величины) могут быть определены как в валовом, так и в чистом
выражении, т. е. с учетом и без учета принятых финансовых обязательств. Валовые
инвестиции представляют собой финансовые
вложения, осуществляемые данным предприятием в другие хозяйственные единицы.
Чистые инвестиции формируются путем вычитания из валовых инвестиций финансовых
вложений, осуществленных в данное предприятие
другими хозяйственными единицами. Эти выводы справедливы как для
отдельных предприятий и организаций, так и для их территориальных и отраслевых
совокупностей.
Структура финансовых инвестиций,
осуществленных предприятиями и
организациями, изучается с помощью их группировки по видам активов и направлениям
инвестирования. В зависимости от видов активов финансовые инвестиции
подразделяются на вложения в паи и акции других организаций, облигации и другие
долговые обязательства, предоставленные займы, прочие финансовые вложения. В зависимости от направлений инвестирования
финансовые вложения группируются по отраслевой принадлежности объектов, в
которые осуществляется инвестирование.
Темпы изменений финансовых
инвестиций изучаются с использованием показателей динамики.
Инвестиции в нефинансовые активы определяются как сумма инвестиций в
произведенные активы (основной капитал, запасы материальных оборотных средств,
ценности) и инвестиций в непроизведенные активы (землю, недра, нематериальные
непроизведенные активы).
Большую часть всего объема
инвестиций в нефинансовые активы составляют инвестиции в основной капитал. Они
слагаются из инвестиций, вложенных во все виды инвестиционного капитала:
материальный основной капитал –
жилища, другие здания и сооружения, машины и оборудование, культивируемые
активы (племенной, рабочий и продуктивный скот, дающие урожай сады и т. п.)
нематериальный основной капитал –
геолого–разведочные работы, компьютерное программное обеспечение, оригиналы
развлекательных, литературных и художественных произведений.
Инвестиции в основной капитал для
каждой хозяйственной единицы определяются как затраты на приобретение относимых
к основному капиталу активов, их доставку и установку в требуемом месте,
улучшение уже имеющихся активов (капитальный ремонт и модернизацию), а также
затраты на передачу прав собственности на активы, то есть расходы на оплату
услуг юристов, оценщиков, консультантов, вознаграждения агентам по
недвижимости, аукционистам, а также
налоги на продажу активов.
Если приобретаемый инвестором актив
создается в результате выполнения подрядчиком договора подряда, то цена этого
актива обычно определяется на основе сметы. По договорам строительного подряда
в смете учитываются стоимость строительных работ, стоимость оборудования и
работ по его монтажу, а также прочих работ и затрат (проектно – изыскательских
работ, расходов по отводу земельных участков для строительства, затрат,
связанных с компенсацией за снесение строения).
В российской хозяйственной практике
инвестиции в основной капитал (за вычетом затрат на капитальный ремонт зданий, машин и оборудования) часто называют
капитальными вложениями. При проведении статистических наблюдений из общего
объема капитальных вложений обычно выделяется стоимость строительно – монтажных
работ (строительных работ и работ по монтажу оборудования).
Весьма сложной задачей является
определение инвестиций в запасы материальных оборотных средств – сырья и материалов,
незавершенного производства, готовой продукции, товаров для перепродажи. Это
обусловлено тем, что инвестициями оказываются только те вложения в материальные
оборотные средства, которые приводят к увеличению физического объема их
запасов, поскольку именно прирост запасов создает условия для расширения
производства в будущем. Периодически повторяющиеся покупки сырья и материалов
для производства, а также товаров для перепродажи в процессе торговой
деятельности, которые не приводят к расширению масштабов производства или торговли, относятся к сфере текущей
деятельности и не являются инвестициями.
Инвестиции в запасы материальных
оборотных средств определяются как стоимость материальных оборотных
средств, полученных хозяйственной
единицей за некоторый период, за вычетом стоимости средств, выбывших за этот
период. Полученные и выбывшие материальные оборотные средства должны быть
оценены по одним и тем же ценам – средним за указанный период. Аналогичный
результат может быть получен, если из величины запасов материальных оборотных
средств, имеющихся в конце периода, вычесть величину запасов на начало периода
(при условии, что те и другие запасы оценены в средних ценах данного периода).
В развитых странах некоторая часть
инвестиций направляется на приобретение ценностей – драгоценных металлов,
камней, произведений искусства и т. д., которые используются как средства
сохранения во времени стоимости затраченных на их покупку ресурсов. В
российской статистике наблюдение за инвестициями в ценности пока не ведется.
Инвестиции в нематериальные
непроизводственные активы (землю, залежи полезных ископаемых, предназначенные
для лесозаготовок естественные леса) определяются по фактической цене этих
активов без учета затрат на передачу прав собственности на них.
Нематериальные непроизводственные
активы в российской хозяйственной практике включаются в более широкую категорию
«нематериальные активы», которая также охватывает некоторые элементы
нематериальных производственных активов, например программное компьютерное
обеспечение. Инвестиции в нематериальные
активы определяются как сумма затрат инвестора на создание или приобретение
экономических активов, которые представляют собой авторские права на
произведения науки, литературы, искусства, компьютерные программы, права на изобретения,
промышленные образцы, товарные знаки, права на ноу-хау и т. п. В стоимость
нематериальных активов, кроме того, включаются затраты на передачу прав
собственности на землю и недра, а также организационные расходы, связанные с
учреждением юридических лиц.
Таким образом, инвестиции в
нефинансовые активы складываются из инвестиций в произведенные и
непроизведенные активы. Большую часть всего объема инвестиций в нефинансовые
активы составляют инвестиции в основной капитал. Их можно также подразделить по
видам основного капитала на инвестиции в жилища, здания и сооружения, машины и
оборудования, культивируемые активы (материальный основной капитал) и
инвестиции в геолого-разведочные работы и компьютерное программное обеспечение
(не материальный основной капитал).Оцениваются инвестиции в нефинансовые активы
как затраты на приобретение этих активов, их доставку и установку, затраты на
улучшение уже имеющихся активов, а также затраты на передачу прав собственности
на активы. Изменение нефинансовых активов также оценивается показателями
динамики.