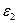ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ И
НАУКЕ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОУ ВПО
Всероссийский Заочный Финансово- Экономический Институт
Факультет:
Финансово-Кредитный
Кафедра: экономико-математических методов и
моделей
Контрольная работа
По предмету: Эконометрика
Вариант 9
Серпухов 2007
Задача 1.
По предприятиям легкой
промышленности региона получена информация, характеризующая зависимость объема
выпуска продукции (Y,
млн руб) от объема капитальных вложений (Х, млн руб).
|
Х
|
У
|
|
26
|
43
|
|
18
|
28
|
|
33
|
51
|
|
42
|
62
|
|
41
|
63
|
|
44
|
67
|
|
15
|
26
|
|
27
|
43
|
|
41
|
61
|
|
19
|
33
|
Требуется:
- Найти параметры уравнения линейной регрессии, дать
экономическую интерпретацию коэффициента регрессии.
- Вычислить остатки;
найти остаточную сумму квадратов; оценить дисперсию остатков
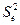; построить график остатков.
- Проверить выполнение предпосылок МНК.
- Осуществить проверку значимости параметров
уравнения регрессии с помощью t-критерия Стьюдента (а =0,05).
- Вычислить коэффициент детерминации, проверить
значимость уравнения с помощью F- критерия Фишера (а = 0,05), найти среднюю относительную
ошибку аппроксимации. Сделать вывод о качестве модели.
- Осуществить прогнозирование среднего значения
показателя Y при
уровне значимости а = 0,1, если прогнозное значение фактора Х составит 80%
от его максимального значения.
- Представить графически: фактические и модельные
значения Y, точки
прогноза.
- Составить уравнения нелинейной регрессии:
- гиперболической;
- степенной;
- показательной.
Привести графики построенных уравнений
регрессии.
- Для указанных
моделей найти коэффициенты детерминации и средние
относительные ошибки аппроксимации. Сравнить модели по этим
характеристикам и сделать вывод.
Решение
Воспользуемся инструментом Регрессия в EXCEL.
Получим следующие данные:
Табл
1
|
ВЫВОД ИТОГОВ
|
|
|
|
|
|
|
Регрессионная статистика
|
|
|
Множественный R
|
0,997256
|
|
|
R-квадрат
|
0,994519
|
|
|
Нормированный R-квадрат
|
0,993737
|
|
|
Стандартная ошибка
|
1,280281
|
|
|
Наблюдения
|
9
|
|
|
|
Табл 2
|
|
|
Дисперсионный анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
2082,082
|
2082,082
|
1270,243
|
3,55E-09
|
|
Остаток
|
7
|
11,47384
|
1,63912
|
|
|
|
Итого
|
8
|
2093,556
|
|
|
|
|
|
|
|
|
|
|
|
Табл 3
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
|
Y-пересечение
|
5,00309
|
1,285545
|
3,891806
|
0,005961
|
1,96326
|
|
26
|
1,389186
|
0,038978
|
35,64048
|
3,55E-09
|
1,297019
|
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
|
8,042919
|
1,96326
|
8,042919
|
|
1,481354
|
1,297019
|
1,481354
|
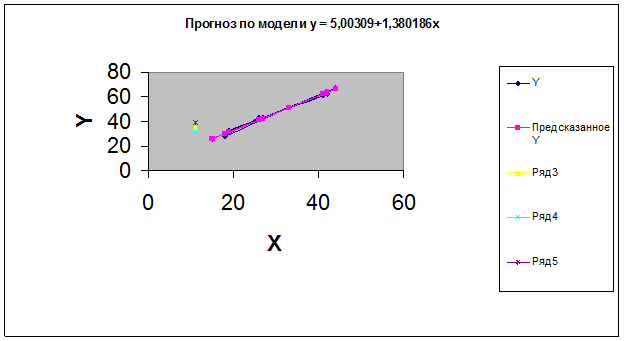
Уравнение линейной регрессии имеет вид: у =а +b*х
Параметры линейного уравнения
возьмем из табл 3 (столбец коэффициенты):
а =5,00309
b =
1,389186
Получим уравнение:
У =5,00309+1,389186*Х
Коэффициент регрессии, исходя из
данных табл 2 равен 1 и больше 0, следовательно переменные х и у положительно
коррелированны. И показывает, что на изменение параметра х на 1 параметр у тоже изменится на 1.
Коэффициент детерминации
показывает долю вариации результативного признака под воздействием изучаемых
факторов. Следовательно, около 99% вариации зависимой переменной учтено в
модели и обусловлено влиянием учтенных факторов.
Коэффициент множественной корреляции R исходя из данных табл 2:
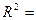0,994519
Он показывает тесноту связи
зависимой переменной Y
от факторной переменной Х:
Вариация результата у
(объема выпуска продукции) на 99,73% объясняется вариацией фактора х
(объемом капиталовложений).
табл 4
|
ВЫВОД ОСТАТКА
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное 43
|
Остатки
|
|
1
|
30,00844
|
-2,00844
|
|
2
|
50,84624
|
0,153759
|
|
3
|
63,34892
|
-1,34892
|
|
4
|
61,95973
|
1,040268
|
|
5
|
66,12729
|
0,872709
|
|
6
|
25,84089
|
0,159114
|
|
7
|
42,51112
|
0,488877
|
|
8
|
61,95973
|
-0,95973
|
|
9
|
31,39763
|
1,602369
|
Рис 1
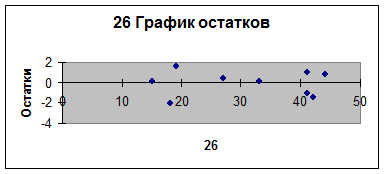
Остаточная сумма квадратов равна 11,47384
Проверка значимости параметров уравнения
регрессии с помощью t-критерия
Стьюдента.
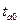= 3,891806
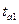= 35,64048
Табличное значение t-критерия при 5%-ном уровне
значимости составляет 2,262157. Так как t расчетное >tтабличного, то коэффициенты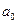 
и 
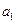существенны (значимы).
Проверка значимости параметров уравнения регрессии с
помощью F-критерия
Фишера.
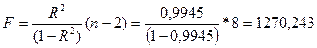
Табличное значение F-критерия составляет 5,59.
Поскольку Fрасчетное > Fтабличного уравнение регрессии следует
признать адекватным.
Стандартная ошибка 1,285545 (исходя из данных табл 3).
В среднем расчетные значения для
степенной модели отличаются от фактических
значений на 1,28 %.
Прогноз.
У =5,00309+1,389186*Х
Х максимальное = 44, прогнозное
значение фактора Х составит 80 % от
Х мах.
Прогнозное значение Х составит
44*0,8 = 35,2
Прогнозное значение У = 5,00309 +
1,289186* 35,2 = 50,38
Ширина доверительного интервала
рассчитывается по формулам:
Коэффициент Стьюдента для m = n – 2 = 9 уровень значимости 0,1 равен 2,08.
Таблица прогнозов (р =90%)
|
Упреждение
|
Нижняя гр-ца
|
Прогноз
|
Верхняя гр-ца
|
|
1
|
32,31
|
35,2
|
38,09
|
Гиперболическая модель
|
|
х
|
у
|
Х
|
уХ
|
Х кв
|
у-у ср
|
(у-у ср)кв
|
у расч
|
|
1
|
26
|
43
|
0,038462
|
1,653846
|
0,001479
|
-4,7
|
22,09
|
46,87758
|
|
2
|
18
|
28
|
0,055556
|
1,555556
|
0,003086
|
-19,7
|
388,09
|
30,6165
|
|
3
|
33
|
51
|
0,030303
|
1,545455
|
0,000918
|
3,3
|
10,89
|
54,63855
|
|
4
|
42
|
62
|
0,02381
|
1,47619
|
0,000567
|
14,3
|
204,49
|
60,81564
|
|
5
|
41
|
63
|
0,02439
|
1,536585
|
0,000595
|
15,3
|
234,09
|
60,26322
|
|
6
|
44
|
67
|
0,022727
|
1,522727
|
0,000517
|
19,3
|
372,49
|
61,84516
|
|
7
|
15
|
26
|
0,066667
|
1,733333
|
0,004444
|
-21,7
|
470,89
|
20,0468
|
|
8
|
27
|
43
|
0,037037
|
1,592593
|
0,001372
|
-4,7
|
22,09
|
48,23267
|
|
9
|
41
|
61
|
0,02439
|
1,487805
|
0,000595
|
13,3
|
176,89
|
60,26322
|
|
10
|
19
|
33
|
0,052632
|
1,736842
|
0,00277
|
-14,7
|
216,09
|
33,398
|
|
сумма
|
306
|
477
|
0,375973
|
15,84093
|
0,016343
|
|
2118,1
|
476,9973
|
|
ср. знач.
|
30,6
|
47,7
|
0,037597
|
1,584093
|
0,001634
|
|
|
|
|
Е
|
Е кв
|
|Ei/y|*100%
|
|
-3,87758
|
15,0356
|
-0,09018
|
|
-2,6165
|
6,846072
|
-0,09345
|
|
-3,63855
|
13,23901
|
-0,07134
|
|
1,184357
|
1,402702
|
0,019103
|
|
2,73678
|
7,489967
|
0,043441
|
|
5,154841
|
26,57238
|
0,076938
|
|
5,9532
|
35,44059
|
0,228969
|
|
-5,23267
|
27,3808
|
-0,12169
|
|
0,73678
|
0,542845
|
0,012078
|
|
-0,398
|
0,158404
|
-0,01206
|
|
0,00267
|
134,1084
|
-0,00819
|
|
|
|
-0,00082
|
Уравнение гиперболической
функции имеет вид: ŷ = a +
b/x
Произведем линеаризацию модели
путем замены Х = 1/х
Тогда уравнение примет вид:
ŷ = a + bХ- линейное уравнение регрессии.
Значение параметров а
и b линейной модели определим по формулам:
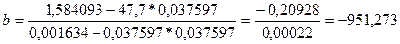
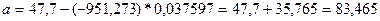
Получим следующее уравнение
гиперболический модели:
У=83,465 – 951,273/х
Определим индекс корреляции:
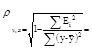
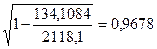
Индекс детерминации:
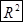= 0,9678*0,9678=0,9366
Вариация результата Y (объема выпуска продукции)
на 93,66% объясняется вариацией фактора Х (объема капитальных вложений).
Рассчитаем F-критерий Фишера:
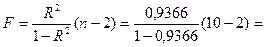118,18
F табл = 5,59
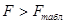F > F табл для для = 0,05; k1
= m = 1, k2 = n - m = 7
Уравнение регрессии в
вероятностью 0,95 в целом статистически значимое, т. к.
Средняя относительная ошибка:
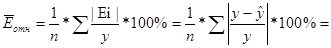1. 0,82%
В среднем расчетные
значения у для гиперболической модели отличается от фактической на 0,82%
Гиперболическая модель
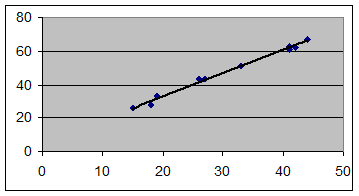
Степенная модель
|
|
факт (у)
|
lg (y)
|
факт (х)1
|
lg (x)
|
YX
|
X в кв.
|
у расч
|
|
1
|
43
|
1,633468
|
26
|
1,414973
|
2,311314
|
2,00215
|
41,60273
|
|
2
|
28
|
1,447158
|
18
|
1,255273
|
1,816578
|
1,575709
|
30,1179
|
|
3
|
51
|
1,70757
|
33
|
1,518514
|
2,592969
|
2,305885
|
51,29585
|
|
4
|
62
|
1,792392
|
42
|
1,623249
|
2,909499
|
2,634938
|
63,40043
|
|
5
|
63
|
1,799341
|
41
|
1,612784
|
2,901947
|
2,601072
|
62,07237
|
|
6
|
67
|
1,826075
|
44
|
1,643453
|
3,001068
|
2,700937
|
66,04515
|
|
7
|
26
|
1,414973
|
15
|
1,176091
|
1,664138
|
1,383191
|
25,66043
|
|
8
|
43
|
1,633468
|
27
|
1,431364
|
2,338088
|
2,048802
|
43,00518
|
|
9
|
61
|
1,78533
|
41
|
1,612784
|
2,879351
|
2,601072
|
62,07237
|
|
10
|
33
|
1,518514
|
19
|
1,278754
|
1,941805
|
1,635211
|
31,58296
|
|
сумма
|
477
|
16,55829
|
306
|
14,56724
|
24,35676
|
21,48897
|
476,8554
|
|
ср. знач.
|
47,7
|
1,655829
|
30,6
|
1,456724
|
2,435676
|
2,148897
|
47,68554
|
|
Е
|
Е в кв
|
у-у ср
|
(у -у ср) кв
|
(у-у расч)/у
|
|Ei/y|*100%
|
|
1,397271
|
1,952367
|
1,397271
|
1,952367
|
0,032495
|
0,032495
|
|
-2,1179
|
4,485483
|
-2,1179
|
4,485483
|
-0,07564
|
-0,07564
|
|
-0,29585
|
0,087527
|
-0,29585
|
0,087527
|
-0,0058
|
-0,0058
|
|
-1,40043
|
1,961216
|
-1,40043
|
1,961216
|
-0,02259
|
-0,02259
|
|
0,927627
|
0,860492
|
0,927627
|
0,860492
|
0,014724
|
0,014724
|
|
0,954854
|
0,911745
|
0,954854
|
0,911745
|
0,014252
|
0,014252
|
|
0,339572
|
0,115309
|
0,339572
|
0,115309
|
0,01306
|
0,01306
|
|
-0,00518
|
2,69E-05
|
-0,00518
|
2,69E-05
|
-0,00012
|
-0,00012
|
|
-1,07237
|
1,149984
|
-1,07237
|
1,149984
|
-0,01758
|
-0,01758
|
|
1,417044
|
2,008015
|
1,417044
|
2,008015
|
0,042941
|
0,042941
|
|
0,144632
|
13,53216
|
0,144632
|
13,53216
|
-0,00426
|
-0,00426
|
|
|
|
|
|
|
-0,00043
|
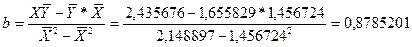
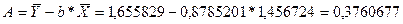
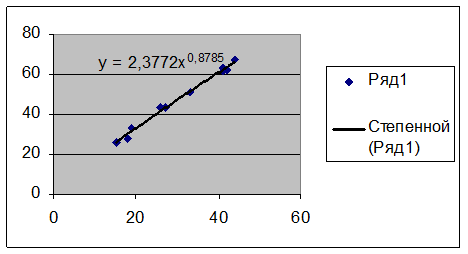
Уравнение будет иметь вид:
Y = 0,3760677 + 0,8785201*X
Перейдем к исходным переменным х
и у, выполнив потенцирование данного уравнения:
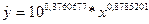
Получим уравнение степенной
модели регрессии:
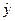= 2,377211 *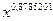
Степенная
модель
Определим индекс корреляции:
Связь между показателем у и
фактором х сильная.
= 
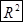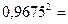0,936
Вариация результата Y (объема выпуска продукции)
на 93,6% объясняется вариацией фактора Х (объема капитальных вложений).
Рассчитаем F-критерий Фишера:
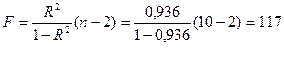
F табл = 5,59
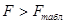F > F табл для для = 0,05; k1
= m = 1, k2 = n - m = 7
Уравнение регрессии в
вероятностью 0,95 в целом статистически значимое, т. к.
Средняя относительная ошибка:
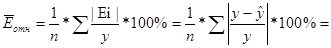
1/10*0,00426*100 =0 ,0426
В среднем расчетные значения для
степенной модели отличаются от фактических
значений на 4,26%
Показательная модель
|
y
|
Y
|
x
|
Yx
|
x2
|
Y-Yср
|
(Y-Yср)кв
|
|
43
|
1,6335
|
26
|
42,47
|
676
|
0,0
|
0,00
|
|
28
|
1,4472
|
18
|
26,05
|
324
|
-0,2
|
0,04
|
|
51
|
1,7076
|
33
|
56,35
|
1089
|
0,1
|
0,00
|
|
62
|
1,7924
|
42
|
75,28
|
1764
|
0,1
|
0,02
|
|
63
|
1,7993
|
41
|
73,77
|
1681
|
0,1
|
0,02
|
|
67
|
1,8261
|
44
|
80,35
|
1936
|
0,2
|
0,03
|
|
26
|
1,4150
|
15
|
21,22
|
225
|
-0,2
|
0,06
|
|
43
|
1,6335
|
27
|
44,10
|
729
|
0,0
|
0,00
|
|
61
|
1,7853
|
41
|
73,20
|
1681
|
0,1
|
0,02
|
|
33
|
1,5185
|
19
|
28,85
|
361
|
-0,1
|
0,02
|
|
477
|
16,5583
|
306
|
521,65
|
10466
|
0,0
|
0,21
|
|
47,7
|
1,655828928
|
30,6
|
52,16480816
|
1046,6
|
|
|
|
х-х ср
|
(х-х ср)кв
|
ŷ
|
у-у расч
|
(у-у расч)кв
|
|Ei/y|*100%
|
|
-4,6
|
21,16
|
39,2234
|
3,776605
|
14,26274
|
2,312016
|
|
-12,6
|
158,76
|
30,54328
|
-2,54328
|
6,468279
|
-1,75743
|
|
2,4
|
5,76
|
48,8198
|
2,1802
|
4,753274
|
1,276785
|
|
11,4
|
129,96
|
64,68509
|
-2,68509
|
7,209698
|
-1,49805
|
|
10,4
|
108,16
|
62,69393
|
0,306071
|
0,09368
|
0,170102
|
|
13,4
|
179,56
|
68,85913
|
-1,85913
|
3,456374
|
-1,0181
|
|
-15,6
|
243,36
|
27,80863
|
-1,80863
|
3,271151
|
-1,27821
|
|
-3,6
|
12,96
|
40,46913
|
2,53087
|
6,405302
|
1,549384
|
|
10,4
|
108,16
|
62,69393
|
-1,69393
|
2,869395
|
-0,9488
|
|
-11,6
|
134,56
|
31,51334
|
1,486664
|
2,210171
|
0,979026
|
|
|
1102,4
|
477,309652
|
-0,30965
|
51,00006
|
-0,21328
|
|
|
|
47,7309652
|
|
|
|
|
Уравнение показательной кривой
имеет вид: ŷ = a * bx
|
|
Для построения этой модели
необходимо произвести линеаризацию переменных. Для этого произведем
логарифмирование обеих частей уравнения: lg ŷ = lg a + x lg b
|
|
Обозначим Y = lg ŷ; A = lg a; B = lg b
|
|
Тогда уравнение примет вид: Y
= A + Bx - линейное уравнение регрессии.
|
|
Значение параметров А и B
линейной модели определим по формулам:
|
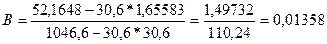
А=1,65583 + 0,01358*30,6 =1,24025
Уравнение будет иметь вид:
Y =1,24025 – 0,01358*х
Перейдем к исходным переменным
х и у, выполнив потенцирование данного
уравнения:
=
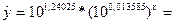
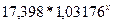
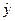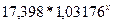
Определим индекс корреляции:
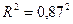=0,76
Вариация результата Y (объема выпуска продукции)
на 76% объясняется вариацией фактора Х (объема капитальных вложений).
Рассчитаем F-критерий Фишера:
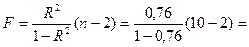25,33
F табл = 5,59
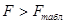F > F табл для для = 0,05; k1
= m = 1, k2 = n - m = 7
Уравнение регрессии в вероятностью
0,95 в целом статистически значимое, т. к.
Средняя относительная ошибка:
1
2,4%
В среднем
расчетные значения у для степенной модели отличается от фактической на 2,4%
Показательная модель
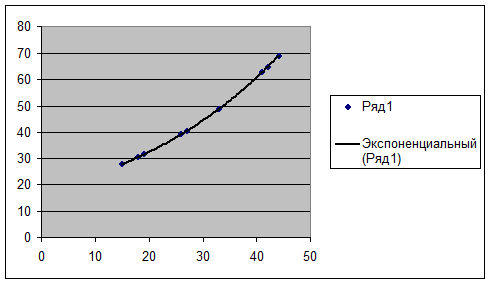
Построим сводную таблицу:
|
Модель
|
Коэффициент детерминации
|
F-критерий Фишера
|
Индекс корреляции
|
Средняя относительная ошибка
|
|
Степенная
|
0,936
|
117
|
0,9675
|
0,00043
|
|
Показательная
|
0,76
|
25,33
|
0,87
|
0,21328
|
|
Гиперболическая
|
0,93366
|
118,18
|
0,9678
|
0,00082
|
Все модели за исключением показательной
имеют примерно одинаковые характеристики, но наибольшее значение F-критерия Фишера и большее
значение коэффициента детерминации имеет гиперболическая модель. Ее можно взять
в качестве лучшей для построения прогноза.
Задача 2а и 2б
Даны по две СФМ, которые заданы в виде матриц коэффициентов модели.
Необходимо записать системы одновременных уравнений и проверить обе
системы на идентифицируемость.
Задача 2а
|
|
|
|
|
|
|
|
|
|
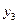
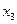
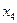
1
|
- 1
|
|
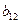
0
|
|
|
|
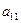
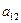
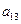
0
|
|
2
|
0
|
-1
|
|
|
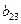
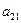
0
|
|
|
|
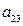
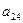
3
|
0
|
|
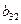
-1
|
|
|
|
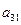
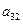
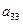
0
|
= - + + + +
= - + + + +
= - + + +
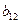
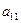
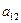
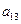
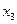
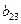
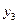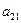
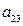
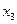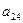
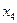
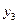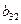
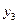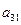
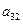
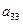
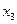
Модель имеет три эндогенные (, , 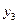) и четыре экзогенные
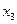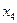(, , , ) переменные. Проверим каждое уравнение системы на
необходимое (Н) и достаточное (Д) условия идентификации.
Необходимое условие – выполнение счетного правила:
Д +1 = Н – уравнение
идентифицируемо;
Д + 1 < Н – уравнение
неидентифицируемо;
Д + 1 >Н – уравнение сверхидентифицируемо,
Где Н число эндогенных переменных в уравнении,
Д – число, предопределенных переменных, отсутствующих в уравнении, но
присутствующих в системе.
Достаточное условие -
определитель матрицы, составленной из коэффициентов при переменных,
отсутствующем уравнении, не равен нулю, и ранг этой матрицы не менее числа
эндогенных переменных системы без единицы.
1 уравнение:
Н: эндогенных переменных 2 (, ),
Отсутствующих экзогенных 1 ().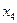
2 = 1 + 1 , следовательно,
уравнение точно идентифицируемо.
Д: в первом уравнении отсутствуют
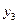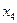(, ), построим матрицу коэффициентов при них в других уравнениях
системы.
построим матрицу коэффициентов
при них в других уравнениях системы.
А = 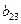*0 – (-1)*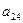 
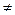0,
Ранг матрицы = 2, следовательно,
дополнительное условие идентификации выполнено.
Следовательно, первое уравнение
идентифицируемо.
2 уравнение:
Н: эндогенных переменных 2 (, ),
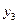Отсутствующих экзогенных 1 ().
2 = 1 + 1 , следовательно,
уравнение точно идентифицируемо.
Д: в первом уравнении
отсутствуют (, ), построим матрицу
коэффициентов при них в других уравнениях системы.
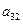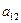
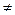А = - - 0*0,
Ранг матрицы = 2, следовательно,
дополнительное условие идентификации выполнено.
Следовательно, второе уравнение
идентифицируемо.
3 уравнение:
Н: эндогенных переменных 2 (,),
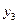Отсутствующих экзогенных 1 ().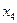
2 = 1 + 1 , следовательно,
уравнение точно идентифицируемо.
Д: в первом уравнении
отсутствуют (, 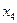), построим матрицу коэффициентов при них в других уравнениях
системы.
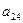А = - - 0*0 0,
Ранг матрицы = 2, следовательно,
выполняется условие идентификации выполнено.
Следовательно, третье уравнение идентифицируемо
Исследуемая система точно идентифицируема.
Задача 2б
|
|
|
|
|
|
|
|
|
|
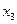
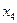
1
|
- 1
|
|
|
|
|
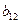
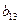
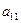
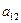
0
|
0
|
|
2
|
|
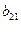
-1
|
|
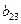
0
|
0
|
|
|
|
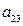
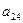
3
|
|
|
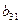
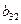
-1
|
0
|
0
|
|
|
= - + + + +
= - + + +
= + - + +
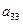
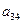
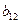
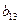
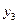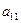
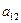
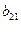
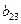
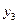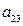
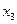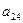
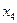
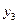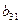
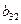
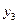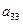
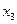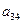
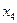
1 уравнение :
Н: эндогенных переменных 3 (, ),
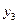Отсутствующих экзогенных 2 (, ).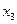
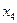3 = 2 + 1 , следовательно,
уравнение точно идентифицируемо.
Д: в первом уравнении
отсутствуют (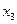, 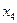), построим матрицу коэффициентов при них в других уравнениях
системы.
А = * - * 
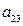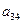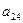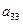
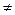0,
Ранг матрицы = 2, следовательно,
выполняется условие идентификации выполнено.
Следовательно, первое уравнение
идентифицируемо.
2 уравнение:
Н: эндогенных переменных 3 (, ),
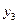Отсутствующих экзогенных 2 (,).
3 = 2 + 1 , следовательно,
уравнение точно идентифицируемо.
Д: в первом уравнении отсутствуют
и построим матрицу
коэффициентов при них в других уравнениях системы.
А = 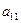*0-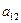*0 = 0,
Ранг матрицы = 2, следовательно,
дополнительное условие идентификации не выполнено.
Следовательно, второе уравнение не идентифицируемо.
3 уравнение:
Н: эндогенных переменных 3 (, ),
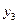Отсутствующих экзогенных 2 (,).
3 = 2 + 1 , следовательно,
уравнение точно идентифицируемо.
Д: в первом уравнении отсутствуют
и построим матрицу
коэффициентов при них в других уравнениях системы.
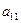А = *0-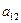*0 = 0,
Ранг матрицы = 2, следовательно,
выполняется условие идентификации не
выполнено.
Следовательно, третье уравнение
не идентифицируемо.
Исследуемая система не идентифицируема.
Задача 2в
По данным таблицы, используя метод
наименьших квадратов. Построить структурную форму модели вида:
= 
+ + +
,
= 
+
+ 
+
.
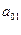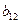
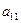
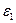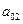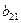
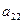
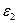Табл 1
|
|
у1
|
у2
|
х1
|
х2
|
|
1
|
25,1
|
21,8
|
8
|
7
|
|
2
|
41,7
|
33,8
|
10
|
14
|
|
3
|
12,5
|
12,5
|
7
|
1
|
|
4
|
25,9
|
23,4
|
7
|
8
|
|
5
|
41,7
|
36
|
5
|
17
|
|
6
|
9,4
|
11,4
|
2
|
2
|
Решение
Структурную модель преобразуем в
приведенную форму модели:
= 
+ 
+ 
;
= 
+ 
+ 
,
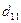
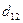
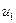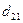
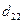
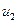Где 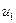и 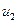- случайные ошибки.
Для каждого уравнения приведенной формы
при расчете коэффициентов d
модно применить МНК.
Для упрощения расчетов можно работать с
отклонениями от средних уровней у = у –
у ср, х = х – х ср. Преобразованные таким образом данные табл 1 сведены в табл
2. Здесь же показаны промежуточные расчеты, необходимые для определения
коэффициентов d.
Табл 2
|
|
у1
|
у2
|
х1
|
х2
|
у1*х1
|
х1
в кв
|
х1*х2
|
у1*х2
|
|
1
|
-0,95
|
-1,35
|
1,5
|
-1,17
|
-1,425
|
2,25
|
-1,755
|
1,1115
|
|
2
|
15,65
|
10,65
|
3,5
|
5,83
|
54,775
|
12,25
|
20,405
|
91,2395
|
|
3
|
-13,55
|
-10,65
|
0,5
|
-7,16
|
-6,775
|
0,25
|
-3,58
|
97,018
|
|
4
|
-0,15
|
0,25
|
0,5
|
-0,17
|
-0,075
|
0,25
|
-0,085
|
0,0255
|
|
5
|
15,65
|
12,85
|
-1,5
|
8,84
|
-23,475
|
2,25
|
-13,26
|
138,346
|
|
6
|
-16,65
|
-11,75
|
-4,5
|
-6,17
|
74,925
|
20,25
|
27,765
|
102,7305
|
|
сумма
|
0
|
0
|
0
|
0
|
97,95
|
37,5
|
29,49
|
430,471
|
|
у2*х1
|
у2*х2
|
х2
в кв
|
|
-2,025
|
1,5795
|
1,3689
|
|
37,275
|
62,0895
|
33,9889
|
|
-5,325
|
76,254
|
51,2656
|
|
0,125
|
-0,0425
|
0,0289
|
|
-19,275
|
113,594
|
78,1456
|
|
52,875
|
72,4975
|
38,0689
|
|
63,65
|
325,972
|
202,8668
|
Для нахождения коэффициентов d первого приведенного уравнения можно использовать следующую
систему нормальных уравнений:
;
.
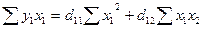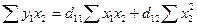Подставляя рассчитанные в табл 2 значения сумм, получим:
97,5 = 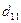*37,5 + 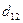*29,49,
430,471 = 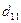*29,49 + 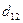*202,8668.
Решение этих уравнений дает
значения 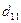= 4,16 и 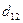= - 1,9685.
Первое уравнение приведенной
формы модели примет вид:
= 4,16 - 1,9685 +
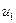
Для нахождения коэффициентов d второго приведенного уравнения можно использовать следующую
систему нормальных уравнений:
;
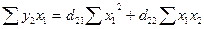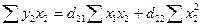
Подставляя рассчитанные в табл 2 значения сумм, получим:
63,65 = 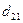*37,5 + 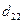*29,49,
325,972 = 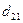*29,49 + 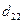*202,8668.
Решение этих уравнений дает
значения 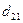= 0,489 и 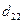= 1,536.
Второе уравнение приведенной
формы модели примет вид:
= 0,489 + 1,536 +
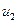
Для перехода от приведенной формы к структурной форме модели найдем из второго уравнения
приведенной модели:
= (-0,489)/1,536.
Подставим это выражение в первое уравнение приведенной модели,
найдем структурное уравнение:
= 4,16- 1,9685(-0,489)/1,536 = 4,786 - 1,28.
Получим: 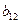= -1,28; 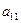= 4,786.
Найдем из первого уравнения
приведенной формы модели:
= ( + 1,9665)/4,16.
Подставим это выражение во второе уравнение приведенной модели,
найдем структурное уравнение:
= 0,489( + 1,9665)/4,16 + 1,536 = 0,115 + 1,763.
Получим: 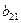= 0,115, 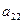= 1,763
Сводные члены структурной формы
находим из уравнений:
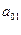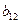
= ср - ср - 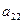ср = 26,05 – (- 1,28)*23,15 – 4,786*6,5 = 26,05 + 29,632 –
31,109 = 24,573
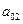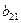
= ср - ср - 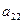ср = 23,15 – 0,115*26,05 -1,763 *8,17 = 23,15 – 2,996 –
14,404 = 5,75
Окончательный вид структурной модели:
= + +
+
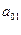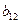
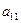
= 24,573 – 1,28 + 4,786+
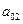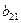
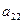
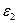= + + + = 5,75 + 0,115 +1,763 +