Сравнительный анализ моделей Штакельберга и Бертрана

Содержание

Введение.......................................................................................................... 3

Глава 1. Теория поведения фирм на олигополистическом рынке однородной продукции...................................................................................................... 4

1.1. Особенности олигополистического рынка. Взаимодействие фирм. Выбор модели поведения...................................................................................................................................................... 4

1.2. Модель Штакельберга - лидерство по объему производства..................................... 5

1.3. Модель Бертрана - ценовой лидер................................................................................. 10

1.4. Практическая значимость моделей............................................................................. 16

Глава 2. Сравнительный анализ моделей............................................... 19

2.1. Количественная оценка спроса на продукцию фирм. Отраслевой спрос.............. 19

2.3. Сравнение моделей........................................................................................................... 24

Заключение.................................................................................................. 26

Список использованной литературы....................................................... 28

Введение

Олигополистическая модель рынка является одной из самых интересных и сложных. Таких фирм в отрасли должно быть немного. Товары, которые производятся олигополиями могут быть как однородными так и дифференцированными. Немногочисленность фирм связана с существованием барьеров входа в отрасль. Поведение фирм очень взаимозависимо. Поэтому классифицировать модели олигополии приходится по ряду признаков и различным критериям: отсутствию или наличию сговора; виду стратегической переменной; повторяемости взаимодействия; отсутствию или наличию дифференциации продукта и т.д.

Цель работы: провести сравнительный анализ моделей Штакельберга и Бертрана.

Данная цель решается с помощью раскрытия следующих основных задач:

-   выявить особенности олигополистического рынка. Взаимодействие фирм. Выбор модели поведения;

-   раскрыть модель Штакельберга - лидерство по объему производства;

-   описать модель Бертрана - ценовой лидер;

-   обозначить практическую значимость моделей;

-   провести сравнение моделей.

Глава 1. Теория поведения фирм на олигополистическом рынке однородной продукции

1.1. Особенности олигополистического рынка. Взаимодействие фирм. Выбор модели поведения

Олигополия – это рыночная структура, при которой в реализации какого-либо товара доминируют несколько (примерно от трех до пяти) продавцов, а появление новых продавцов затруднено или невозможно. Господство относительно малого числа фирм на рынке – главный признак олигополии.

Основная причина существования олигополистической структуры – значительный эффект масштаба, т.е. эффективность требует, чтобы производственная мощность фирмы занимала большую долю совокупного рынка. Следовательно, доступ к такому производству затруднен, поскольку для организации крупного предприятия необходимы большие инвестиции. Это является основным барьером для вступления в олигополистическую отрасль. Другими барьерами могут быть, например, патент или лицензия на какую-либо технологию или владение территорией, на которой находится сырьевое месторождение.

Для олигополии характерно три признака:

1) В отрасли присутствует две или несколько фирм (обычно до 10) так, что отрасль не является чисто монополизированной.

2) Кривая спроса каждой фирмы имеет падающий характер, поэтому в отрасли не действуют правила совершенной конкуренции.

3) В отрасли функционирует по крайней мере одна крупная фирма, любое действие которой вызывает ответную реакцию конкурентов, поэтому нельзя считать, что в отрасли наблюдается монополистическая конкуренция.

На олигопольном рынке продукция может быть и не быть дифференцированной.

Для олигополии характерно ограничение доступа на рынок других фирм. Среди можно назвать следующие причины этого:

1) эффект масштаба может сделать не выгодным существование многих фирм на рынке.

2) лицензирование и патенты затрудняют доступ на рынок.

3) контроль над редкими источниками сырья.

В отличие от рынка с совершенной конкуренцией каждая из фирм олигополистов при формировании своей экономической политики вынуждена принимать во внимание реакцию со стороны конкурентов. При олигополии цены меняются не столь часто как при совершенной конкуренции, обычно через какие-нибудь промежутки времени и на значительную величину.

1.2. Модель Штакельберга - лидерство по объему производства

Модель асимметричной дуополии, предложенная Г. фон Штакельбергом в 1934 г., представляет развитие моделей количественной дуополии Курно и Чемберлина. Асимметрия дуополии Штакельберга заключается в том, что дуополисты могут придерживаться разных типов поведения ≈ стремиться быть лидером или оставаться последователем. Последователь Штакельберга придерживается предположений Курно, он следует своей кривой реагирования и принимает решения о прибылемаксимизирующем выпуске, полагая выпуск соперника заданным. Лидер Штакельберга, напротив, не столь наивен, как обыкновенный дуополист Курно, Он настолько изощрен в понимании рыночной ситуации, что не только знает кривую реагирования соперника, но и инкорпорирует ее в свою функцию прибыли, так что последняя принимает вид

p_i = f(q_i, R_j(q_i).                                                                                   (1)

А затем он максимизирует свою прибыль, действуя подобно монополисту.

Ясно, что в случае дуополии возможны четыре комбинации двух типов поведения.

1. Дуополист 1 ≈ лидер, дуополист 2 ≈ последователь.

2. Дуополист 2 ≈ лидер, дуополист 1 ≈∙ последователь.

3. Оба дуополиста ведут себя как последователи.

4. Оба дуополиста ведут себя как лидеры.

В случаях 1 и 2 поведение дуополистов совместимо, один ведет себя как лидер, другой ≈ как последователь. Здесь не возникает конфликта и исход их взаимодействия стабилен. Случай 3 по сути представляет ситуацию дуополии Курно, оба дуополиста руководствуются своими кривыми реагирования, и исход их взаимодействия стабилен. Нередко поэтому говорят, что модель Курно ≈ это частный случай модели Штакельберга.

А вот в последнем случае, когда оба дуополиста стремятся стать лидерами, каждый из них предполагает, что соперник будет вести себя в соответствии со своей кривой реагирования, т.е. как монополист Курно, тогда как на деле ни один из них не придерживается такого типа поведения. Исходом подобного взаимодействия становится неравновесие Штакельберга, ведущее к развязыванию ценовой войны. Она будет продолжаться до тех пор, пока один из дуополистов не откажется от своих притязаний на лидерство либо дуополисты вступят в сговор. Сам Штакельберг считал именно случай 4 наиболее обычным исходом дуополии.

Рассмотрим возможные исходы подробнее.

Последователь Штакельберга, а затем при определенном количественном решении соперника, представляющегося последователю лидером, приспосабливает свой выпуск к прибылемаксимизирующему уровню. Лидер понимает, что его соперник ведет себя как последователь, и при данной его функции реагирования определяет свой прибылемаксимизирующий выпуск. Поэтому в случае 4 каждый дуополист определяет максимум своей прибыли исходя из предположения, что он является лидером, а соперник ≈ последователем. Если в результате прибыль лидера окажется выше прибыли последователя, дуополист выберет положение лидера, независимо от того, что решит соперник. В противном случае он выберет положение последователя.

Исходя из аналитической версии модели Курно, представим функцию прибыли лидера (1) для дуополиста 1, подставив в уравнение его прибыли (функцию реагирования дуополиста 2. Тогда функция примет вид

p₁ = aq₁ - bq₁² - bq₁[(a - c)/2b - q_i/2] - cq₁,                                         (2)

что после преобразований и перестановок дает

p₁ = ((a - c)/2)q₁ - (b/2)q₁².                                                                 (3)

Приравнивая производную (3) по q1 нулю, имеем

dp₁/dq₁ = (a - c)/2 - bq₁ = 0,

откуда

q^l₁ = (a - c)/2b. (4)

Это и есть оптимальный выпуск лидера Штакельберга. Он обеспечивает максимум его прибыли, поскольку условие второго порядка также выполняется b > 0 по предположению). В силу симметричности ситуации, возникающей в случае 4, прибылемаксимизирующий выпуск дуополиста 2, тоже претендующего на роль лидера, также составит

q^l₂ = (a - c)/2b.                                                                                   (4*)

(Верхний индекс I в (4) и (4*) означает прибылемаксимизирующий выпуск лидера).

Определим теперь прибылемаксимизирующий выпуск последователя Штакельберга:

q^f₁ = [(a - c)/2b] √ [1/2 (a - c)/2b] = (a - c)/4b/i<>,                                       (5)

q^f₂ = [(a - c)/2b] √ [1/2 (a - c)/2b] = (a - c)/4b/i<>.                                       (5*)

(Верхний индекс /"в (5) и (5*) означает прибылемаксимизирующий выпуск последователя).

Таким образом, прибылемаксимизирующий выпуск последователя, qfi, вдвое ниже прибылемаксимизирующего выпуска лидера, qli (i = 1, 2). Сравнив (4), (4*), (5) и (5*), заметим, что прибылемаксимизирующий выпуск лидера Штакельберга тот же, что и у дуополиста Курно, а последователя вдвое меньше, чем у последнего.

В случаях 1 и 2, когда один дуополист, неважно какой именно, ведет себя как лидер, а другой как последователь, их общий выпуск будет равен сумме либо (4) и (5*), либо (4*) и (5), т. е.

Q = (a - c)/2b + (a - c)/4b = 3(a - c)/4b.                                           (6)

Подставив (7) в функцию рыночного спроса, найдем равновесную цену олигополии Штакельберга в ситуациях 1, 2. Она будет равна

P = a - b ∙ 3(a - c)/4b = (a + 3c)/4.                                                     (7)

(6) и (7) ≈ параметры равновесия Штакельберга.

Для того чтобы от равновесия перейти к неравновесию Штакельберга (от случаев 1 и 2 к случаю 4), определим сначала прибыли лидера и последователя. Это, между прочим, поможет нам понять стремление олигополистов Штакельберга именно к неравновесию. Подставим сначала значение ql1 из (4) в (4). Прибыль лидера, если им окажется дуополист 1, составит

p^l₁ = [(a - c)/2][(a - c)/2b] √ (b/2) [(a - c)²/4b²] = [(a - c)²/4b] √ [(a - c)²/8b] = (a - c)²/8b.                                                                                                           (8)

Симметрично прибыль дуополиста 2, если тот окажется лидером, будет

p^l₁ = (a - c)²/8b.                                                                                  (8*)

Определим теперь прибыль последователя, подставив значения qf и ql. Если им окажется дуополист 1, то

p^f₁ = a(a - c)/4b - b[(a - c)/4b]² - b[(a - c)/4b][(a - c)/2b] - c(a - c)/4b = [(a - c)²/4b] √ [a(a - c)²/16b] √ [a(a - c)²/8b],

откуда после упрощений и перестановок получим

p^f₁ = (a - c)²/16b.                                                                               (9)

Симметрично прибыль дуополиста 2, если он окажется последователем, будет

p^f₂ = (a - c)²/16b.                                                                               (9*)

Сопоставив теперь (9) с (8), а (9*) с (8*), мы заметим, что прибыль лидера вдвое превышает прибыль последователя, будь то дуополист 1 или 2. Поэтому-то и тот и другой предпочтут оказаться лидерами. Но тогда их прибыли окажутся не максимальными, а, напротив, минимальными. Действительно, подставив значения прибылемаксимизирующих выпусков обоих стремящихся стать лидерами дуополистов, т. е. (1) и (1*), в уравнение линейной функции спроса, получим

P = a - b[(a - c)/2b + (a - c)/2b]. (10)

Это равенство цены предельным (и средним) затратам (р = с = МС = АС) означает, что прибыль дуополистов равна нулю, а это несовместимо со стабильным исходом. Таким образом, ситуация, разрешающаяся стабильным решением в модели Курно, обращается в неравновесие Штакельберга при некотором изменении предположений о поведении дуополистов. Ниже приведены основные параметры равновесия Штакельберга:

Выпуск	Прибыль	Рыночная цена
Лидера	последователя	отрасли	лидера	последователя
(a - c)/2b	(a - c)/4b	3(a - c)/4b	(a - c)2/8b	(a - c)2/16b	(a + c)/4

 

1.3. Модель Бертрана - ценовой лидер

Традиционно экономисты принимают не цену, а количество (величину выпуска) в качестве управляемой (или стратегической) переменной предприятия. Действительно, при совершенной конкуренции, когда предприятия являются ценополучателями, величина выпуска, как мы видим, есть единственная переменная, управляемая самим предприятием. Напротив, при несовершенной конкуренции предприятие, как мы помним, может выбрать в качестве стратегической переменной либо выпуск, либо цену (но не то и другое одновременно). Модели Курно и Чемберлина базируются на традиционном подходе, полагающем выпуски дуополистов управляемыми переменными. Модель Курно (как более раннюю) неоднократно критиковали в этой связи, подчеркивая, что именно цена, а не выпуск является стратегической переменной. Едва ли не первым с такой критикой и предложением принять в качестве стратегической переменной цену выступил в 1883г. французский математик Ж. Бертран,

Дуополисты Бертрана во всем подобны дуополистам Курно, отлично лишь их поведение. Дуополисты Бертрана исходят из предположения о независимости цен, устанавливаемых друг другом, от их собственных ценовых решений. Иначе говоря, не выпуск соперника, а назначенная им цена является для дуополиста параметром, константой. Для того чтобы лучше понять отличие модели Бертрана от модели Курно, представим ее также в терминах изопрофит и кривых реагирования.

В связи с изменением управляемой переменной (с выпуска на цену) и изопрофиты, и кривые реагирования строятся в двухмерном пространстве цен, а не выпусков. Изменяется и их экономический смысл. Изопрофита, или кривая равной прибыли, дуополиста 1 ≈ это множество точек в пространстве цен (P₁, P₂), соответствующих комбинациям цен P₁ и P₂, обеспечивающим этому дуополисту одну и ту же сумму прибыли. Соответственно изопрофита дуополиста 2 ≈ это множество точек в том же пространстве цен, соответствующих комбинациям (соотношениям) цен З₁ и P₂ , обеспечивающим одну и ту же прибыль дуополисту 2. Семейства таких кривых равной прибыли, или изопрофит дуополистов 1 (p¹₁, p²₁, p³₁, p⁴₁) и 2 (p¹₂, p²₂, p³₂, p⁴₂). Изопрофиты дуополиста 1 выпуклы к оси его цены (P₁), а дуополиста 2 к оси его цены (P₂).

Такая конфигурация изопрофит означает, что дуополист 1 должен будет снизить цену до определенного уровня, например с P'₁ до P''₁, чтобы сохранить свою прибыль неизменной (остаться на изопрофите p²₁) в случае снижения дуополистом 2 своей цены с P'₂ до P''₂. Однако, если и после этого дуополист 2 продолжит снижать свою цену, дуополист 1 не сможет сохранить свою прибыль неизменной. Очевидно, что при сколь-либо более низкой, чем P''₂, цене дуополиста 2 дуополист 1 должен будет перейти на более низкую, чем p²₁, изопрофиту, а это означает, что величина его прибыли уменьшится. Чем ближе к оси цены лежит изопрофита соответствующего дуополиста, тем более низкий уровень равной прибыли она отображает.

Таким образом, при любом изменении цены дуополиста 2 существует единственная цена дуополиста 1, максимизирующая его прибыль. Эта прибылемаксимизирующая цена определяется самой низкой точкой наиболее высоко лежащей изопрофиты дуополиста 1. Такие точки (e₁ ≈ q₄ ) по мере перехода к более высоким изопрофитам смещаются вправо. Это значит, что, увеличивая свою прибыль, дуополист 1 делает это за счет привлечения покупателей дуополиста 2, повышающего свою цену, даже если при этом дуополист 1 тоже увеличивает цену. Соединив наиболее низко лежащие точки всех последовательно расположенных изопрофит, мы получим кривую реагирования дуополиста 1 на изменения цен дуополистом 2 ≈ R₁(P₂). Абсциссы точек этой кривой представляют собой прибылемаксимизирующие цены дуополиста 1 при заданных ординатами этих точек ценах дуополиста 2. Соответственно линия R₂(P₁) представляет кривую реагирования дуополиста 2 на множестве его изопрофит (p¹₂, p²₂, p³₂, p⁴₂)

Теперь, зная кривые реагирования дуополистов Бертрана, мы можем определить равновесие Бертрана как иной (по сравнению с равновесием Курно) частный случай равновесия Нэша, когда стратегия каждого предприятия заключается не в выборе им своего объема выпуска, как в случае равновесия Курно, а в выборе им уровня цены, по которой он намерен реализовать свой выпуск. Графически равновесие Бертрана ≈ Нэша, как и равновесие Курно ≈ Нэша, определяется пересечением кривых реагирования обоих дуополистов, но не в пространстве выпусков (как в модели Курно), а в пространстве цен.

Равновесие Бертрана ≈ Нэша представлено точкой В ≈ N. Обратите внимание на то, что обе кривые реагирования Бертрана в отличие от кривых реагирования Курно восходящие. Это значит, что цены дуополистов Бертрана имеют выраженную тенденцию к сближению в противоположность выпускам дуополистов Курно.

Равновесие Бертрана достигается, если предположения дуополистов о ценовом поведении друг друга сбываются. Если дуополист 1 полагает, что его соперник установит цену P¹₂, он в целях максимизации прибыли выберет, согласно своей кривой реагирования, цену P¹₁. Но в таком случае дуополист 2 может на самом деле установить на свою продукцию цену P²₂, исходя из своей кривой реагирования. Если предположить (как мы это делали при рассмотрении равновесия Курно), что кривая реагирования дуополиста 1 круче, чем соответствующая кривая дуополиста 2, то тогда этот итеративный процесс приведет дуополистов к равновесию Бертрана ≈ Нэша (т. е. в точку В ≈ N), где их кривые реагирования пересекутся. Маршрут их конвергенции в точку В≈N окажется подобен маршруту конвергенции выпусков дуополистов Курно, показанному стрелками. Поскольку продукция обоих дуополистов однородна, каждый из них предпочтет в состоянии равновесия один и тот же уровень ее цены. В противном случае дуополист, назначивший более низкую цену, захватит весь рынок. Поэтому равновесие Бертрана≈Нэша характеризуется единой ценой, принадлежащей в двухмерном пространстве цен лучу, исходящему из начала координат под углом 45╟.

Кроме того, в состоянии равновесия Бертрана≈Нэша равновесная цена окажется равной предельным затратам каждого из дуополистов. В противном случае дуополисты, руководствуясь каждый стремлением овладеть всем рынком, будут снижать свои цены, а это их стремление может быть парализовано, лишь когда они уравняют свои цены не только между собой, но и с предельными затратами. Естественно, что в этом случае общая отраслевая прибыль окажется нулевой. Таким образом, несмотря на исключительную немногочисленность продавцов (в дуополии их лишь двое), модель Бертрана предсказывает, по сути дела, совершенно конкурентное равновесие отрасли, имеющей строение дуополии.

Пусть, как и в модели Курно, рыночный спрос представлен линейной функцией Р = а - bQ, где Q = q₁ + q₂. Тогда обратная функция спроса будет

Q = q₁ + q₂ = (a/b) √ (1/b)P (11.53)

Если при данной цене дуополиста 1, P₁ > МС, дуополист 2 устанавливает цену З₂ > МС, остаточный спрос дуополиста 1 будет зависеть от соотношения цен P₁ и P₂. А именно при P₁ > P₂, q₁ = 0 все покупатели, привлеченные более низкой ценой, перейдут к дуополисту 2. Напротив, при P₁ < P₂ весь рыночный спрос окажется захваченным дуополистом 1. Наконец, в случае равенства цен обоих дуополистов, P₁ = P₂, рыночный спрос окажется поделенным между ними поровну и составит (а/b - 1/b P)0,5 для каждого.

Функция спроса дуополиста 1 отображена имеющей разрыв (АВ) кривой спроса DP₂ABD'. Если дуополист 2 установит цену P₂, то спрос на продукцию дуополиста 1 окажется нулевым, что соответствует вертикальному сегменту (DP₂) его кривой спроса. При P₁ = P₂ рынок будет поделен поровну (сегмент P₂А будет принадлежать дуополисту 1, а сегмент АВ дуополисту 2). Наконец, если дуополист 1 ответит на P₂ снижением своей цены ниже этого уровня, он захватит весь рынок (сегмент BD'). Каждое из предприятий-дуополистов может оставаться рентабельным, понемногу снижая цену с целью увеличения своей доли рыночного спроса до тех пор, пока не будет достигнуто равенство

P₁ = P₂ = MC

которое и характеризует состояние равновесия Бертрана≈ Нэша.

Таким образом, в отличие от модели Курно, предсказывающей достижение совершенно конкурентного результата лишь по мере увеличения числа олигополистов, а именно когда п/(п + 1) приближается к единице, модель Бертрана предрекает совершенно конкурентный результат сразу же при переходе от монополии одного продавца к дуополии. Причина этого кардинального различия выводов в том, что каждый дуополист Курно сталкивается с нисходящей остаточной кривой спроса, тогда как дуополист Бертрана ≈ с кривой спроса совершенно эластичной по цене соперника, так что снижение цены оказывается прибыльным, пока она остается выше предельных затрат. В табл. 1 приведены равновесные выпуски и цены, предсказываемые моделями Курно и Бертрана, а также моделями монополии и совершенной конкуренции.

Таблица 1

Равновесные объемы выпуска и цены в моделях Курно и Бертрана при совершенной конкуренции и монополии

Модель	Цена	Выпуск отрасли
Монополии Курно (n = 2) Курно (n/(n + 1) ® 1) Бертрана (n = 2) Совершенной конкуренции	(a + c)/2 a/3 + 2c/3 ® c c c	(a - c)/2b 4/3 (a - c)/2b ® (a - c)/b (a - c)/b (a - c)/b

После изучения моделей Курно и Бертрана, предсказывающих при п = 2 существенно разные исходы, у вас возникнет естественный вопрос, чья модель "лучше", "правильнее", словом, какую из них следует использовать при анализе олигополии. Прежде чем попытаться ответить на него, подумаем вот над чем. Мало того, что дуополисты Курно и Бертрана "наивны" и не способны корректировать свое поведение под влиянием опыта или, как часто говорят, не способны к "научению делом" (англ, learning by duing), они наделены еще одним, удобным для построения модели, но очень нереалистичным, свойством ≈ их производственные мощности буквально "безразмерны" и способны сжиматься и расширяться, как резиновые. Ведь дуополисты могут, не неся никаких дополнительных затрат, свободно варьировать объем своего выпуска от нуля до величины, равной всему рыночного спросу. При этом их предельные и средние затраты остаются неизменными, какая-либо экономичность или неэкономичность от масштаба отсутствует.

1.4. Практическая значимость моделей

Интересным приложением является модель олигополии Штакельберга, где фирмы принимают решение не одновременно, а по очереди. Фирма, делающая первых ход (лидер), может предсказать наилучший ответ второй фирмы (ведомого). Равновесие по Штакельбергу можно трактовать как равновесие по Нэшу, если считать, что стратегией лидера является выпуск, а стратегией второй фирмы – ответ на выпуск первой фирмы. Поэтому неудивительно, что равновесие по Штакельбергу отличается от равновесия по Курно.

Оптовый спотовый рынок электроэнергии Англии и Уэльса, получивший название Тhe Pool, работал по следующему принципу. За сутки до торгов все генерирующие компании подавали заявки на продажу электроэнергии для каждого торгового периода. Заявка содержала количество и цену предлагаемой электроэнергии. Торговый период длился 30 минут, таким образом сутки состояли из 48 торговых периодов.

Системный оператор, получив заявки, анализировал их и составлял график подключения генераторов к сети по возрастанию стоимости предлагаемой электроэнергии: первым подключается тот генератор, который предложил самую низкую цену, затем следующий, запрашиваемая цена которого была самой низкой из оставшихся заявок, и т.д. до тех пор, пока объем предлагаемой электроэнергии не превысит прогнозируемый спрос. График предложения электроэнергии строился для каждого торгового периода. Цена электроэнергии для каждого периода (спотовая цена или так называемая Pool Purchasing Price (PPP)) определялась заявкой последнего подключенного генератора и была единой для всех генераторов, включенных в график. Потребители, покупающие электроэнергию на оптовом рынке, уплачивали PPP плюс некоторую надбавку.

Идеология, лежащая в основе The Pool, основана на модели конкуренции по Бертрану. Предполагалось, что генераторы будут конкурировать друг с другом за потребителей и для расширения сбыта будут "подрезать" цену на рынке. В равновесии каждый генератор будет предлагать электроэнергию по цене, равной своим предельным издержкам. В результате цена на электроэнергию на оптовом рынке будет полностью отражать затраты на ее производство, а если данная цена слишком высока (в генерации оказываются задействованы неэффективные генераторы с высокими издержками), это будет служить инвесторам сигналом о выгодности вложений в отрасль. Кроме того, относительно высокая цена электроэнергии, определяемая издержками неэффективных генераторов, гарантирует прибыль для эффективных производителей.

Таким образом, эффективность Тhe Pool была обусловлена теоретическими рассуждениями. Однако реальная жизнь опровергла все теоретические схемы. Прежде всего, в основе теоретической модели конкуренции по Бертрану лежит предположение о том, что продавцов много, доля каждого из них на рынке незначительна и действия их не могут повлиять на общую ситуацию. Реальная расстановка сил на британском рынке электроэнергии в начале 90-х годов значительно отличалась от предположений теории. После либерализации было образовано всего 3 генерирующие компании: Nuclear Electricity (NE), объединившая все АЭС, а также National Power (NP) и PowerGen (PG), состоявшие из тепловых электростанций. При этом генерация электроэнергии между компаниями была распределена неравномерно, почти три четверти производства приходилось на NP и PG.

Механизм ценообразования на рынке Тhe Pool в действительности означал, что последний генератор, заявка которого устанавливает цену на всем рынке, действует в таких условиях как эффективный монополист (максимизирует свою прибыль на остаточном спросе). Небольшое количество генерирующих компаний, а также тот факт, что АЭС имеют ограничения в маневре мощностью (атомные станции не могут быстро изменить мощность, их основная цель – обеспечение базовой нагрузки в сети), привели к тому, что на оптовом рынке электроэнергии Англии и Уэльса в начале 90-х годов сложилась дуополия.

Глава 2. Сравнительный анализ моделей

2.1. Количественная оценка спроса на продукцию фирм. Отраслевой спрос

Рассмотрим теперь модели олигополии, ориентированные на цену как стратегическую переменную. В них фирмы устанавливают цену и реализуют по ней определенный рыночным спросом объем выпуска.

В модели Штакельберга олигополисты выбирают две линии поведения: лидера и последователя.

Последователь будет реагировать на действия лидера, приспосабливая свой выпуск в соответствии с выпуском лидера. В свою очередь последователь предполагает, что на его действия не реагируют.

Лидер придерживается противоположной точки зрения, его выбор ведет к изменению ожиданий последователя, и это он учитывает при принятии своих решений.

Алгоритм в решении задач похож на вариант модели Курно, но необходимо учитывать разделение функций лидера и последователя. (Но для решения задач по модели Штакельберга необходимо в начале посчитать модель Курно).

Рассмотрим модель в которой 1-производитель Лидер, а 2-последователь

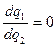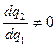Следовательно, , где и является по сути первым уравнением реакции в модели Курно, а , где и является вторым уравнением реакции в модели Курно

Предположим, что отраслевой спрос представлен формулой 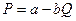, где Q – общий выпуск двух фирм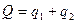

Подставив, получим: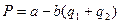

Функции затрат – прямые пропорциональности от выпуска каждой из фирм: 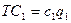, а 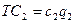, для удобства предположим что

Прибыль Лидера будет равна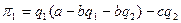

Прибыль Последователя будет равна: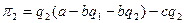

отсюда можно вывести уравнение реакции для Лидера и фирмы Последователя.

Так как уравнения реакции в модели Курно:

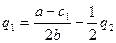
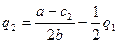
то в соответствии с условиями модели ,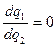

а .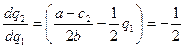

Следовательно, условия максимизации прибыли примут вид:

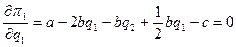
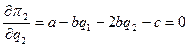
Уравнения реакции Лидера и Последователя будут иметь следующий вид:

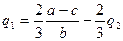 Лидер

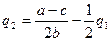 Последователь

Решив систему из уравнений реакции Лидера и Последователя получим равновесные выпуски для них.

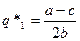 Лидер

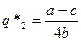 Последователь

Мы видим, выпуск лидера в два раза превышает выпуск последователя. Теперь можно определить, как это отразится на прибыли дуополистов.

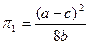
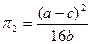
Поэтому мы можем прийти к выводу, что фирме выгодно выбирать стратегию лидера.

Французский математик Жозеф Бертран (1883 г.) в качестве альтернативы дуополии Курно предложил свою модель дуополии.

Он исходил из тех же предпосылок, которые сделал Курно (отсутствие сговора, однократность взаимодействия, однородность продукта, наличие неизменных и равных предельных издержек у фирм, закрытый вход).

Но в качестве стратегической переменной выступает цена, а не объем выпуска. Причем цену определяет каждый из дуополистов Бертрана, считая выбор соперника неизменным.

Пусть в отрасли действуют всего 2 фирмы, производится однородный продукт с одинаковыми и неизменными предельными издержками.

Предположим для простоты, что функция спроса - линейна: Q = q1 + q2 = a / b – 1 / bP). В этом случае спрос на продукцию каждой из фирм зависит от цен на товар. Если цена, назначенная фирмой 1, превысит цену, назначенную фирмой 2, то никто не захочет покупать продукцию у фирмы 1.

 

Рис. 1. Кривая спроса дуополиста Бертрана

Если эта цена снизится до Р2, то поскольку выпускается одинаковая продукция, покупатели обоих фирм смогут удовлетворить за счет продукции каждой из фирм половину своего спроса.

Если же Р1 хотя бы незначительно снизится по сравнению с Р2, покупатели полностью переключатся на продукт фирмы 1 (при этом предполагается, что каждая фирма имеет такие производственные мощности, которые в состоянии обеспечить рыночный спрос в полном объеме).

Таким образом, кривая спроса на продукцию фирмы 1 состоит из трех отрезков (рис. 1):

d1(Р1, Р2) = 0, если Р1 > Р2 (отрезок аР2 )

d1(Р1, Р2) = D(p1)/2, если Р1 = Р2 (т. А )

d1(Р1, Р2) = D(p1), если Р1 < Р2 (отрезок Bb ).

Также будет выглядеть и функция спроса для фирмы 2.

Каждой фирме выгодно назначить цену чуть-чуть ниже конкурента. Тогда фирма, снизившая цену первой, сможет захватить весь рынок, поскольку продукция однородная, а потребители ведут себя рационально и выбирают при прочих равных тот товар, который дешевле. Предполагая (в соответствии с допущениями модели), что объявленные соперником цены неизменны, эта фирма фактически становится монополистом, захватывает весь рынок.

Но фирма-конкурент, оставшись без покупателей, вынуждена будет тоже снизить цену, причем несколько сильнее, чем это сделала первая фирма. Тогда все покупатели перейдут ко второй фирме. Теперь первая фирма, столкнувшись с проблемой реализации продукции, снизит цену еще больше и т.д. Таким образом, модель Бертрана является моделью "ценовой войны" в дуополии. Равновесие будет достигнуто лишь при снижении рыночной цены до уровня, ниже которого ее опускать уже нецелесообразно, т.е. до уровня предельных издержек. Поскольку МС=соnst, то МС=АС (предельные издержки равны средним).

Итак, в модели Бертрана результатом ценовой войны (при соблюдении всех вышеназванных предпосылок) становится объем производства, который производился бы и в условиях рынка совершенной конкуренции.

В качестве стратегических переменных Бертран рассматривал цены.[1] Анализ дуополии Бертрана допускает выпуск однородного продукта. На таком рынке существуют барьеры входа, препятствующие конкуренции со стороны других фирм и отсутствие соглашений между ними. Целью же каждой фирмы является максимизация прибыли. При этом цены устанавливаются одновременно, а каждый участник не может прогнозировать реакцию конкурента на свой выбор уровня цены. Средние издержки в модели постоянные и равны между собой в долгосрочном периоде.

Тогда механизм, моделируемый Бертраном, можно упрощенно представить следующим образом. Пусть фирма А назначает свою цену первой. Но как только она назначила цену, эта цена становится базовой для принятия решения фирмой В. Если фирма В назначит цену выше значения, установленного фирмой А, она не сможет продать свою продукцию. Если  фирма В назначит цену на уровне фирмы А или чуть-чуть ниже, то  она имеет шанс  успешных продаж.

Подобную стратегию может осуществить и фирма А. В результате на рынке сложится ситуация, получавшая название  ценовой конкуренции. Это означает, что взаимодействие двух крупных фирм с  равными предельными издержками оказывается нестабильным и приводит к ценовой войне, истощающей силы обеих участников.

На практике же при ценовой войне цены не опускается до уровня издержек, поскольку конкурируют фирмы, обладающие рыночной властью. Этот результат получил название парадокс Бертрана. Если бы этого парадокса не было, то постепенно все рынки монополистической конкуренции постепенно превращались бы в совершенные рынки. Но этого на практике нет.

2.3. Сравнение моделей.

Модель Бертрана в отличие от моделей Курно и Штакельберга предполагают наличие ценового взаимодействия фирм на олигополистическом рынке. Таким образом конкуренция заключается в том, что каждая фирма устанавливает свою цену.

Условия модели Бертрана:

1) На рынке действуют две фирмы

2) Продукт производится однородный

3) Целью каждой фирмы является максимизация прибыли

4) Отсутствуют соглашения фирм друг с другом

5) Фирмы назначают цены одновременно так, что каждая не может прогнозировать реакцию конкурента на сделанный ею самой выбор.

Таким образом объем продаж в модели Бертрана является функцией от цены.

Две фирмы выбирают цены p₁ и p₂. Затраты фирм носят пропорциональный характер:

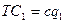
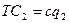
Существует три варианта определения выпуска первого конкурента в зависимости от ценовой стратегии:

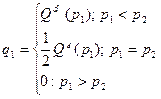
Равновесие по Нэшу (Отсутствие стимулов к изменению своего выбора если остальные игроки (конкуренты) придерживаются принятого решения) возникает когда p₁ = p₂ = c в других случаях ситуация неравновесна.

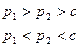
Олигополия ведет себя на при совершенной конкуренции, но базируется это на совершенно других допущениях. «Ценовая война» приводит к истощению ресурсов обеих фирм и к нулевой прибыли. В реальной жизни этого не происходит и этому есть множество причин. Например сговор при котором олигополия выступает как монополия и имеет монопольную прибыль.

Заключение

В ходе проведения теоретического и методологического исследования были сделаны следующие выводы.

Для олигополистической фирмы характерны следующие черты:

*                высокий уровень концентрации капитала и производства;

*               способность влиять на объемы производства и уровень цен в отрасли.

Отношения между олигополистическими фирмами характеризуются как взаимозависимость. Фирмы, знающие, что их действия затронут конкурентов в отрасли, принимают решения только после того, как они выяснят характер реакции соперников. Олигополистические фирмы используют в основном методы неценовой конкуренции. Существуют доказательства, что во многих олигополистических отраслях цены оставались стабильными в течение длительного периода времени. В отличие от других рыночных структур не существует универсальной теории олигополии. Вместо этого теория олигополии состоит из довольно значительного количества различных моделей, каждая из которых описывает специальный случай, который имеет место только при определенных обстоятельствах.

Особенности российских олигополистических структур состоят в том, что олигополии охватывают все основные отрасли производства. Сложившиеся олигополистические структуры на рынке товаров и услуг практически делают невозможным свободный выход на рынок и поддержание добросовестной конкуренции между предприятиями в материальном производстве подавляющая часть предприятий жестко привязаны друг к другу и практически не имеет возможности выбирать поставщиков сырья, комплектующих изделий, оборудования и других средств производства. В такой ситуации складываются идеальные условия для произвольного роста цен по всей технологической цепочке. 

Модель Бертрана – модель олигополии, в которой фирмы конкурируют, выбирая цены и оставляя рынку определить количество продукции, которое они смогут продать по этим ценам.

Модель Штакельберга – модель олигополиии, в которой фирмы движутся последовательно и при первый, начавший движение, считается рыночным лидером.

Список использованной литературы

1.     Авдашева С.Б., Розанова Н.М., Теория организации отраслевых рынков. М., 1998., Гл. 8. С. 208-216.

2.     Вехи экономической мысли/Под общ. ред. А. Г. Слуцкого. – СПб.: Экономическая школа, 2003. – Т. 5:Теория отраслевых рынков, 2003. – 668 с.

3.     Вурос А.Д., Розанова Н.М. Экономика отраслевых рынков. М.: ТЕИС, 2000, Гл. 6. С. 114-152.

4.     Вэриан Х.Р. Микроэкономика. Промежуточный уровень. Современный подход: Учеб. для вузов /Под ред. Н.Л. Фроловой. – М.: Изд. об-ние "ЮНИТИ", 1997. – 767 с.

5.     Гальперин В. М. Микроэкономика:Учеб. для вузов по экон. специальностям и направле- ниям: В 2 т./В. М. Гальперин, С. М. Игнатьев, В. И. Моргунов; Общ. р ед. В. М. Гальперина; Ин-т "Отк- рытое о- во".-СПб.:Экономическая школа, 2004-.-(Библиотека экономи ческой школы;Вып. 22). Т. 2,2004.-500 с.

6.     Джуха В.М. Микроэкономика: Учеб. пособие. – М.; Рос- тов н/Д: МарТ, 2004. – 254 c.

7.     Долан Э.Д., Линдсей Д.Е. Микроэкономика/Под общ. ред. Б.С. Лисовика, В.В. Лукашевича. – СПб.: Литера плюс, 1997. – 446 с.

8.     Иохин В.Я. Экономическая теория: введение в рынок и микроэкономический анализ: Учеб.. – М.: ИНФРА-М, 1997. –510 с.

9.     Кабраль Луис М.Б. Организация отраслевых рынков: вводный курс. – М.: Новое знание, 2003. – 357 с.

10.            Максимова В.Ф. Микроэкономика: Учебник. – М., 1996. – 327 с.:

11.            Микроэкономика: Теория и российская практика: Учеб. для вузов /Под ред. А.Т. Грязновой, А.Ю. Юданова. – М.: КноРус, 2002. – 541 с.

12.            Нуреев Р.М. Основы экономической теории. Микроэкономика: Теория. Задачи. Вопросы. Тесты: Учебник. – М.:Высш. шк., 1996. – 446 с.:

13.            Петров А.М. Микроэкономика: Учеб. для вузов. –  Челябинск: Рекпол, 2000. – 205 с.

14.            Пиндайк Р.С., Рубинфельд Д.Л. Микроэкономика=Microeconomics. – М.: Дело, 2000. – 807 с.

15.            Тироль Ж. Рынки и рыночная власть СПб., 1996. С. 355-358.

16.            Франк Р.Х. Микроэкономика и поведение: Учеб. для вузов. – М.: Инфра-М, 2000. – 694 с.

17.            Ховард К. и др. Экономическая теория. Теория свободного рынка: Учеб. для вузов. – М.: Банки и биржи: ЮНИТИ, 1997. – 278 с.

18.            Хэй Д., Моррис Д. Теория организации промышленности. СПб., 1999. Т.2. Гл. 16. С. 433-456.

19.            Чемберлин Э. Теория монополистической конкуренции. Реориентация теории стоимости/ Под ред. О.Я. Ольсевича. – М.: Экономика, 1996. – 349 с.

20.            Шерер Ф.М., Росс Д. Структура отраслевых рынков. М., 1997.

21.            Шестакова К.Д. Микроэкономика: Учеб. пособие. – М.: Издательство РИОР, 2005. – 126 с.

---

[1] Bertrand J.  Theoric mathematique de la richesse sociale. - Journal des Savants, September 1883, p. 499 - 508.