Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Всероссийский заочный финансово-экономический институт

Филиал в г. Барнауле

Факультет                                                                     Региональная кафедра

«Финансово-кредитный»                                           математики и информатики

 

                                                     

Контрольная работа

Вариант № 8

Барнаул 2007 г

Задача 1

  По предприятиям легкой промышленности региона получена информация, характеризующая зависимость обмена выпуска продукции (Y, млн. руб.) от объема капиталовложений (X, млн. руб.).

Наблюдение	Объем выпуска продукции, Y	Объем капиталовложения, X
10	13	3
4	19	7
8	15	7
3	22	10
5	21	12
7	20	14
1	26	17
9	30	20
6	26	21
2	27	22

 Т р е б у е т с я :

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 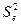; построить график остатков.

3. Проверить выполнение предпосылок МНК.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α = 0,05).

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α = 0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α = 0,1, если прогнозное значение фактора X составит 80% от его максимального значения.

7. Представить графически: фактические и модельные значения Y, точки прогноза.

8. Составить уравнения нелинейной регрессии:

- гиперболической;

- степенной;

- показательной.

Привести графики построенных уравнений регрессии.

9. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

Решение

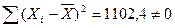  1). Отсортируем значение фактора Х по возрастанию. Коэффициенты а и в существуют, если . В нашем примере . Значения коэффициентов а и в можно увидеть из итогов программы «регрессия» (a =11,78; в=0,76).

Строим линейную регрессионную модель вида: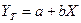  

 

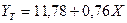
Вывод: при увеличении объема капиталовложений на 1 млн. руб., объем выпуска продукции увеличится в среднем  на 0,76млн. руб.

 2). Остатки вычисляются автоматически в программе «регрессия».

Остатки
-1,064014282
1,892884468
-2,107115532
2,610558531
0,089007906
-2,432542719
1,285131344
3,002805407
-1,757969906
-1,518745218

Остаточная сумма квадратов (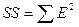) так же есть в программе «регрессия» в графе «SS». Дисперсию остатков можно рассчитать (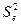= SS/n = 3,796).

SS

226,9392757

37,96072431

264,9

3). Предпосылки МНК (условия Гаусса – Маркова)

 - свойство случайности величины Е;

 - мат. Ожидание случайного члена равно 0, а дисперсия постоянна;

 - случайные члены для любых 2 наблюдений некоррелированы;

 - распределение случайного члена является нормальным.

1) Первое условие проверяется с помощью критерия поворотных точек (Р), затем рассчитаем критическое значение (Ркрит = 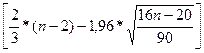). Число поворотных точек вычислим с помощью функции если (категория логические). Р = 6, след. Ркрит = 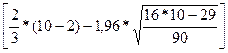= 2.

Так как Р > Ркрит, след. компонента случайна, т.е. свойство случайности остатков выполняется.

2) М(Ei) выполняется автоматически. Находим с помощью функции СРЗНАЧ среднее значение остатков. Оно равно 0.

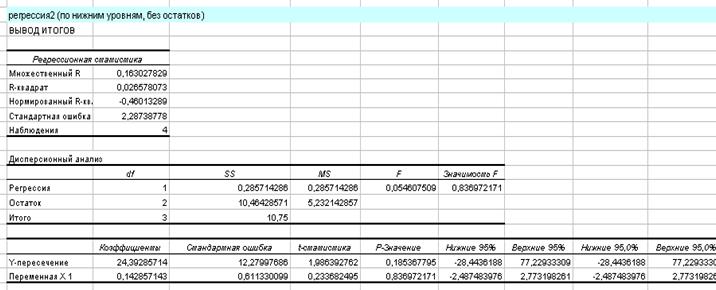
Условие D(Ei) = 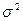выполняется в 2 этапа:

а) отсутствие гетероскедастичности

б) проверяется с помошью теста Голдфельда – Квандта:

 - упорядочим все 10 наблюдений по возрастанию переменной Х;

 - выберем 4 первых и 4 последних наблюдений m. Строим по ним отдельные (вспомогательные) регрессии

SS1=	9,292929293
SS2=	10,46428571

- рассчитываем статистику F =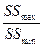

SSmax/SSmin=

1,126048137

 - по таблице критических точек распределения Фишера находим

Fкрит (α; k1; k2). K1 = k2 = m – p – 1

F kp=

=FРАСПОБР(0,05;2;2)

 Fкрит = 19. Т.к. F < Fкрит, то гипотеза об отсутствии гетероскедастичности принимается, т.е. модель можно считать гомоскедастичной, след. Условие D(Ei) = 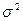выполняется.

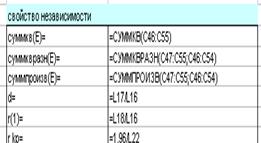
3) Проверим на наличие автокорреляции с помощью критерия Дарбина – Уотсона.

суммкв(Е)=	37,96072431
суммквразн(Е)=	99,20984854
суммпроизв(Е)=	-13,36355668

                    

свойство независимости
суммкв(Е)=	37,96072431
суммквразн(Е)=	99,20984854
суммпроизв(Е)=	-13,36355668
d=	2,613486712
r(1)=	-0,352036399
r kp=	0,619806421

    

     

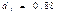
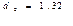  (из таблицы). d=2.61 попадает в зону Но это свидетельствует об отсутствии автокорреляции в остатках.

Так как r(1) < r kp, след. Гипотеза об отсутствии автокорреляции принимается, и свойство независимости остатков выполняется.

4) Последнее условие проверяется с помощью R/S – критерия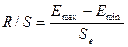

Se находится из программы «регрессия» в графе «стандартная ошибка».

                                                                    

нормальное распределение
Emax=	3,002805407
Emin=	-2,432542719
S(E)=	2,178322873
R/S=	2,495198574

нормальное распределение
Emax=	=МАКС(C46:C55)
Emin=	=МИН(C46:C55)
S(E)=	2,17832287279183
R/S=	=(L24-L25)/L26

  

 

По таблице критических значений R/S при n= 10, α= 0,05 R/S = 2,495 попадает в интервал между к1 и к2, след. Распределение случайного члена является нормальным.

Вывод: все пункты проверки предпосылок МНК выполняются.

 4) Для проверки значимости коэффициента корреляции с помощью t- критерия Стьюдента используем 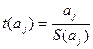. Из итогов программы «регрессия»  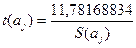, t(a) = 7,2854489,   t(b) = 6,915643232 , 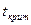  = 2,306004133

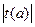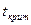>, т.е. коэффициент  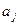 является значимым его необходимо оставить.

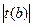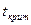>, т.е. коэффициент  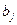является значимым, его необходимо оставить.

5). Из итогов программы «регрессия» 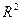=0,8567 r =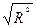=0,93. Так как индекс детерминации равен 0,93, следует, что связь между объемом выпуска продукции (Y) и объемом капиталовложений (X) тесная.

 Оценим значимость уравнения по критерию Фишера.

 Из итогов программы «регрессия» найдем F-статистику(47,826). 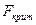 (0,05; 1; 8) = 5,32 (по таблице F- критерия Фишера). 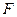>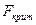, след. Уравнение является значимым. Объем выпущенной продукции на 46,8% зависит от объема капиталовложений и на 53,2% от неучтенных. 

  Так как 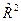= 0,838785146 (из программы регрессия), то модель является довольно хорошей.

 Для расчета средней ошибки аппроксимации необходимо провести дополнительные расчеты. С помощью функции ABS рассчитаем относительную погрешность. Затем по формуле находим среднюю ошибку аппроксимации.

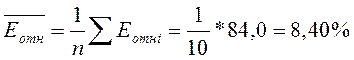
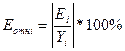  = 8,,40, 

 5% <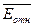<15% след. Модель удовлетворительная.

Модель является адекватной и  качественной, т.к. почти все пункты проверки выполняются.

6).

прогнозирование
Х*=	17,6
Y*=	25,17
Хср=	13,3
квадроткл(X)=	392,1
S(Yт*)=	0,835625601
	0,383609616
размах=	3,141629735
нижн.гр.=	22,030
верх.гр.=	28,313

  

Находим прогнозное значение величины Х*, оно равно 17,6. Находим прогнозное значение величины Y* = a + bX* = 25,17. Рассчитаем стандартную ошибку прогнозирования  .

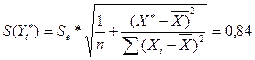Хср=	13,3
квадроткл(X)=	392,1

Вычисляем размах доверительного интервала U(Yt*)=S(Yt*)*tкрит,

Tкрит =( α; n-p-1)=(0,1;8)=1,86   

размах=

2,70

Определяем границы доверительного интервала Uнижн = Yt*- U(Yt*)

Uверх = Yt*+ U(Yt*)

нижн.гр.=	22,476
верх.гр.=	27,867

7).

                   

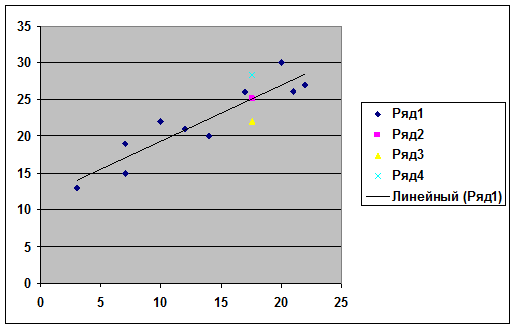
   8). Гиперболическая модель 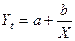. Введем новую переменную 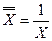, тогда 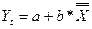. Рассчитываем столбец значения 1/Х, Yt, E, Eотн. С помощью программы «регрессия» находим а и в.

  

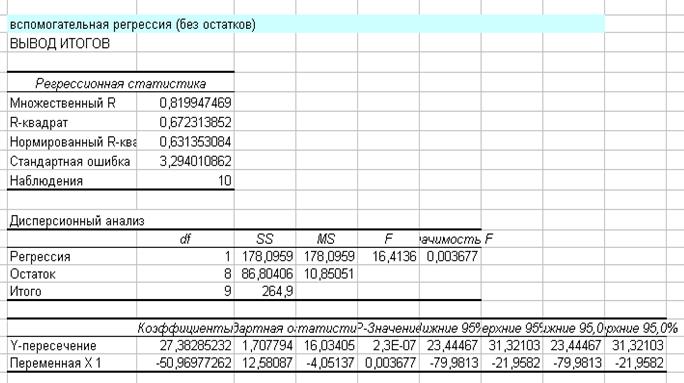
а=27,38; в=-50,97. Чтобы рассчитать Yt, будем последовательно подставлять в модель 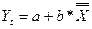 значения 1/Х. Е = Y- Yt, Eотн рассчитаем с помощью функции ABS. Eотн = ABS (Y/E).

X	Y	1/Х	Yт	Е	Е отн
3	13	0,33	10,39	2,61	20,05%
7	19	0,14	20,10	-1,10	5,80%
7	15	0,14	20,10	-5,10	34,01%
10	22	0,10	22,29	-0,29	1,30%
12	21	0,08	23,14	-2,14	10,17%
14	20	0,07	23,74	-3,74	18,71%
17	26	0,06	24,38	1,62	6,21%
20	30	0,05	24,83	5,17	17,22%
21	26	0,05	24,96	1,04	4,02%
22	27	0,05	25,07	1,93	7,16%

 

Рассчитаем сумму квадратов Е с помощью функции СУММКВ (категория математические), она равна 86,80. Еср. Отн рассчитаем с помощью функции СРЗНАЧ, она равна Еотн = 12,47%.

Для расчета  R-квадрата нужно найти квадратное отклонение У(с помощью функции КВАДРОТКЛ):

Квадроткл(У)=264,90

R-квадрат = 1- (суммкв (Е) / квадроткл (Y)) = 0,67.

         

                   

суммкв(Е)=	86,80
R-квадрат=	0,67
Е ср.отн.=	12,47%

суммкв(Е)=	=СУММКВ(E56:E65)
R-квадрат=	=1-(I56/F3)
Е ср.отн.=	=СРЗНАЧ(F56:F65)

 

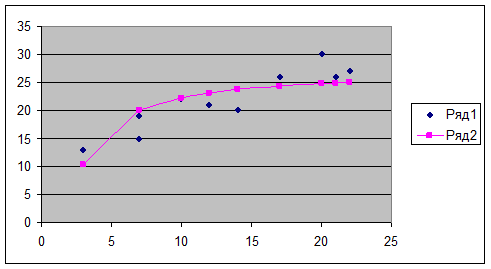
Степенная модель 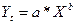, 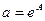. Эта модель является стандартной. Она имеется в программе Excel. Строим по исходным данным точечный график и добавляем степенную линию тренда. На вкладке «параметры» ставим флажок «показывать уравнение на графике».

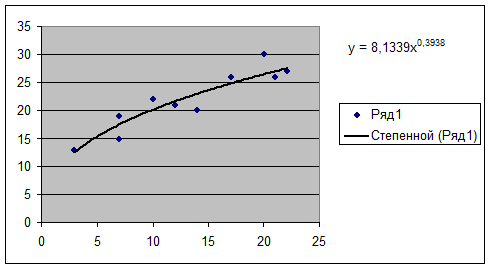
Далее аналогично гиперболической модели.

 

X	Y	Yт	Е	Е отн
3	13	12,54	0,46	3,56%
7	19	17,50	1,50	7,88%
7	15	17,50	-2,50	16,68%
10	22	20,14	1,86	8,45%
12	21	21,64	-0,64	3,05%
14	20	23,00	-3,00	14,98%
17	26	24,82	1,18	4,53%
20	30	26,46	3,54	11,79%
21	26	26,98	-0,98	3,76%
22	27	27,48	-0,48	1,76%

суммкв(Е)=	36,63
R-квадрат=	0,86
Е ср.отн.=	7,64%

 

 Показательная модель 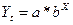 . Эта модель также является стандартной и имеется в программе Excel.

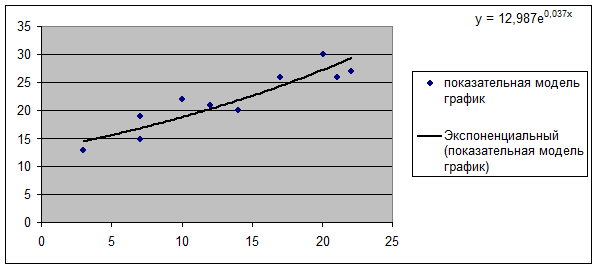
Для расчета Yt необходимо вычислить значение величины b с помощью функции EXP. B= 1,04.

X	Y	Yт	Е	Е отн
3	13	14,61	-1,61	12,37%
7	19	17,09	1,91	10,05%
7	15	17,09	-2,09	13,93%
10	22	19,22	2,78	12,62%
12	21	20,79	0,21	0,99%
14	20	22,49	-2,49	12,45%
17	26	25,30	0,70	2,70%
20	30	28,46	1,54	5,15%
21	26	29,59	-3,59	13,82%
22	27	30,78	-3,78	13,99%

	b=	1,04
суммкв(Е)=	54,62
R-квадрат=	0,79
Е ср.отн.=	9,81%

9).

сводная таблица характеристик качества
модель	R-квадрат	Е ср.отн.
степенная	0,86	7,64%
показательная	0,79	9,81%
гиперболическая	0,67	12,46%

Для выбора наилучшей моделей выделим наименьшую Eотн. и наибольший R-квадрат. По этим характеристикам наилучшая степенная модель.

Задача 2а и 2б

  Для варианта даны по две СФМ, которые заданы в виде матриц коэффициентов модели. Необходимо записать системы одновременных уравнений и проверить обе системы на идентифицируемость.

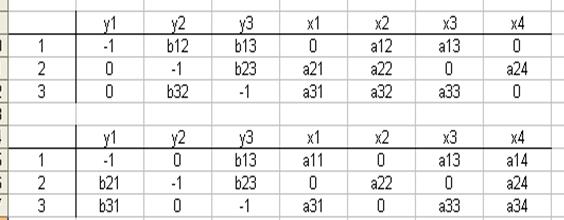
Решение задачи 2а. В данной СФМ три экзогенных (Х1, Х2, Х3) и три эндогенных (Y1, Y2,Y3) переменных. Составим системы одновременных уравнений:

                                               

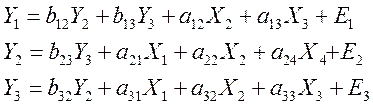
Проверка необходимого условия (счетное правило): 1 ур-е: N=3, K=2. N=2+1, 3=3, след. Уравнение идентифицируемое. 2 ур-е: N=2, K=1. N=1+1, 2=2, след. Уравнение идентифицируемое. 3 ур-е: N=2, K=1. N=1+1, 2=2, след. Уравнение идентифицируемое. Вывод: система идентифицируема.

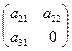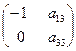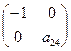Проверка достаточного условия: 1 ур-е:    , ∆ ≠ 0, след. Уравнение идентифицируемое. 2 ур-е: , ∆ ≠ 0, след. Уравнение идентифицируемое. 3 ур-е: , ∆ ≠ 0, след. Уравнение идентифицируемое. Вывод: система идентифицируема.  Таким образом, оба условия выполняются, значит, система, действительно,  идентифицируема.

Решение задачи 2б 

                      

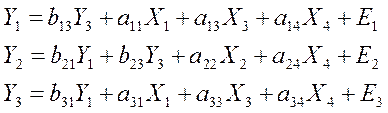
Проверка необходимого условия (счетное правило): 1 ур-е: N=2, K=1. N=1+1, 2=2, след. Уравнение идентифицируемое. 2 ур-е: N=3, K=2. N=2+1, 3=3, след. Уравнение идентифицируемое. 3 ур-е: N=2, K=1. N=1+1, 2=2, след. Уравнение идентифицируемое. Вывод: система идентифицируема.

Проверка достаточного условия: 1 ур-е: 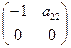, ∆ = 0, след. Уравнение неидентифицируемое. Вывод: система неидентифицируема.

Задача 2в

  По данным таблицы, используя КМНК, построить структурную форму модели вида:

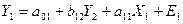
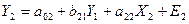
	y1	y2	x1	x2
1	51,3	39,4	3	10
2	112,4	77,9	10	13
3	67,5	45,2	5	3
4	51,4	37,7	3	7
5	99,3	66,1	9	6
6	57,1	39,6	4	1

 

Решение задачи 2в

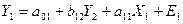
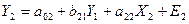
Проверим систему на идентифицируемость.

Счетное правило: 1 ур-е: N=2, K=1. N=1+1, 2=2, след. Уравнение идентифицируемое. 2 ур-е: N=2, K=1. N=1+1, 2=2, след. Уравнение идентифицируемое.

Достаточное условие:

                                 

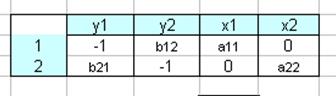
1 ур-е: (), ∆ ≠ 0, след. Уравнение идентифицируемое.

2 ур-е: (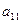), ∆ ≠ 0, след. Уравнение идентифицируемое.

Вывод: система идентифицируема.   

Перейдем к системе приведенных уравнений:

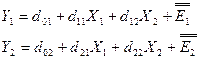
С помощью программы регрессия найдем коэффициенты 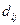.Для первого уравнения :

	Коэффициенты
Y-пересечение	23,57198618
Переменная X 1	8,327599309
Переменная X 2	0,36074266

                                   Y1 = 23,57+8,33X1+0,36X2+E1

Для второго уравнения:

	Коэффициенты
Y-пересечение	18,02039724
Переменная X 1	5,021519862
Переменная X 2	0,676148532

                                       Y2 = 18,02+5,02X1+0,68X2+E2

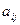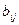Для нахождения и используем метод Гаусса. В первом уравнении исключим Х2 с помощью второго уравнения. Помножим второе уравнение на    -0,36, а первое на 0,68и сложим их. Получившееся делим на 0,68.

вычисление структурных коэффициентов (метод Гаусса)
матрица коэффициентов приведенных уравнений
уравнение	своб.к-т	Y1	Y2	X1	X2
1-ое	23,57	-1	0	8,33	0,36
2-ое	18,02	0	-1	5,02	0,68
исключение Х2
уравнение	своб.к-т	Y1	Y2	X1	X2
1-ое	9,54	-0,68	0,36	3,86	0
нормировка: b11=-1
уравнение	своб.к-т	Y1	Y2	X1	X2
1-ое	14,03	-1	0,53	5,68	0

Y1 = 14,03+0,53Y 2+5,68X1+E1

Во втором уравнении исключим Х1 с помощью первого уравнения. Помножим второе уравнение на 8,33, а первое на -5,02 и сложим их. Получившееся делим на 8,33.

вычисление структурных коэффициентов (метод Гаусса)
матрица коэффициентов приведенных уравнений
уравнение	своб.к-т	Y1	Y2	X1	X2
1-ое	23,57	-1	0	8,33	0,36
2-ое	18,02	0	-1	5,02	0,68
исключение Х2
уравнение	своб.к-т	Y1	Y2	X1	X2
1-ое	31,79	5,02	-8,33	0	3,86
нормировка: b11=-1
уравнение	своб.к-т	Y1	Y2	X1	X2
1-ое	3,82	0,60	-1	0	0,46

Y2 = 3,82+0,60Y 1+0,46X2+E2