Оглавление
Задание
1____________________________________________________ 3
Задание 2____________________________________________________ 5
Задание 3____________________________________________________ 7
Задание 4____________________________________________________ 9
Задание 5___________________________________________________ 12
Задание 1
1. Определите, на какой диаграмме показаны временные данные, а на какой
пространственные (рис. 2, 3).
Рис.
2. Структура использования денежных доходов за 2001 г.
(диаграмма
для сравнения)
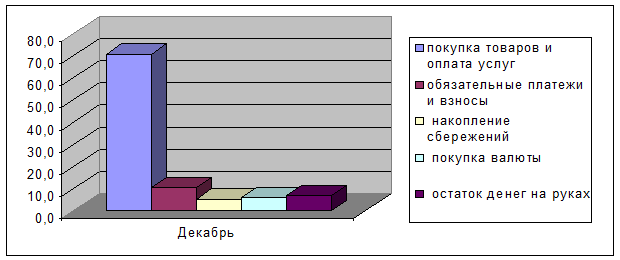
Рис. 3. Структура использования денежных доходов за
2001 г.
(диаграмма для сравнения)
2. Дайте определение регрессии.
3. Определите виды регрессий:
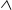 у = 12,5 –
1,44х1 + 5х2 – 2,27х3 + е,
у = 12,5 –
1,44х1 + 5х2 – 2,27х3 + е,
y =
1/(11+10,45х1–9,44х2+3,33 х3–1,37х4+е),
– гипербола
y = e45,54+100x+е. – экспоненциальная
4. Покажите, где здесь результирующая и объясняющие
переменные. Что обозначает е в
уравнениях регрессии?
Решение:
1. На рисунке 2 показаны временные данные, а на рисунке 3 –
пространственные.
2. Регрессия – зависимость среднего значения
какой-либо величины от некоторой другой величины или от нескольких величин
3. 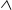 у = 12,5 – 1,44х1 + 5х2
– 2,27х3 + е, – множественная линейная регрессия.
у = 12,5 – 1,44х1 + 5х2
– 2,27х3 + е, – множественная линейная регрессия.
y =
1/(11+10,45х1–9,44х2+3,33 х3–1,37х4+е),
– гипербола
y = e45,54+100x+е. – экспоненциальная
4. у = 12,5
– 1,44х1 + 5х2 – 2,27х3 + е
у – результирующая,
х1, х2, х3 – объясняющие
переменные,
е – ошибка регрессии.
y =
1/(11+10,45х1–9,44х2+3,33 х3–1,37х4+е),
у – результирующая,
х1, х2, х3 , х4–
объясняющие переменные,
е – ошибка регрессии.
y = e45,54+100x+е.
у – результирующая,
х – объясняющие переменные,
е – ошибка регрессии.
Задание 2
1. Дайте определение парной регрессии.
2. По Российской Федерации за 2001 год известны значения
двух признаков (см. табл. 2).
Таблица 2
|
Месяц
|
Расходы на
покупку продовольственных товаров
в общих
расходах, %, (у)
|
Средний денежный
доход
на душу
населения, руб., (x)
|
|
Январь
|
69
|
1964,7
|
|
Февраль
|
65,6
|
2292,0
|
|
Март
|
60,7
|
2545,8
|
|
Апрель
|
…
|
…
|
|
Май
|
…
|
…
|
|
Июнь
|
…
|
…
|
|
Июль
|
…
|
…
|
|
Август
|
…
|
…
|
|
Сентябрь
|
…
|
…
|
|
Октябрь
|
53,3
|
3042,8
|
|
Ноябрь
|
50,9
|
3107,2
|
|
Декабрь
|
47,5
|
4024,7
|
Для оценки зависимости у
от х построена парная линейная регрессионная модель с помощью метода наименьших
квадратов:
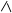 у
= а + bх + е, где а =
у
= а + bх + е, где а = 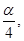 b =
b =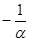 .
.
Парный коэффициент корреляции rxy=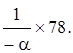
 Средняя
ошибка аппроксимации А =
Средняя
ошибка аппроксимации А = 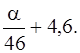
Известно, что Fтабл = 4,96, а Fфакт = 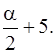
Определите коэффициент детерминации. Оцените линейную модель
через среднюю ошибку аппроксимации и F-критерий Фишера.
Решение:
2. Число 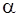 = 184. Тогда найдем
коэффициенты парной линейной регрессионной модели а =46 и b = -0,005.
Получим уравнение регрессии
= 184. Тогда найдем
коэффициенты парной линейной регрессионной модели а =46 и b = -0,005.
Получим уравнение регрессии
у = 46 – 0,005х + е.
Значит, с увеличением среднего
денежного дохода на 1 руб. доля расходов на покупку продовольственных товаров
снижается в среднем на 0,005 %.
Линейный коэффициент
парной корреляции rxy
= – 0,424 (связь умеренная, обратная).
Найдем
коэффициент детерминации, rxy2 = 0,180. Вариация результата на 18,0 %
объясняется вариацией фактора х.
Средняя ошибка
аппроксимации А = 60, что говорит о высокой ошибке аппроксимации (недопустимые
пределы). В среднем расчетные значения отклоняются от фактических на 60 %.
Проверяем F-критерий Фишера. Для этого сравним Fтабл и Fфакт. Fтабл < Fфакт (4,96 <
97), значит Н0 – гипотеза о случайной природе оцениваемых характеристик
отклоняется и признается их статистическая значимость и надежность с
вероятностью 0,95.
Вывод. Линейная
парная модель плохо описывает изучаемую закономерность.
Задание 3
В табл. 3 приведены данные, формирующие цену на строящиеся
квартиры в двух различных районах.
Таблица 3
|
Район, a/б
|
Жилая площадь, м2
|
Площадь кухни, м2
|
Этаж, средние/крайние
|
Дом, кирпич./панел.
|
Срок сдачи, через сколько мес.
|
Стоимость квартиры, тыс. дол.
|
|
1
|
17,5
|
8
|
1
|
1
|
6
|
17,7
|
|
1
|
20
|
8,2
|
1
|
2
|
1
|
31,2
|
|
2
|
23,5
|
11,5
|
2
|
2
|
9
|
13,6
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
|
1
|
77
|
17
|
2
|
1
|
1
|
56,6
|
|
2
|
150,5
|
30
|
2
|
2
|
2
|
139,2
|
|
2
|
167
|
31
|
2
|
1
|
5
|
141,5
|
Имеется шесть факторов, которые могут оказывать влияние на
цену строящегося жилья:
район, где расположена строящаяся квартира (а или б);
жилая площадь квартиры;
площадь кухни;
этаж (средний или крайний);
тип дома (панельный или кирпичный);
срок сдачи квартиры (через сколько месяцев).
Определите минимальный объем выборки Nmin. Для оценки зависимости
у от х построена линейная множественная регрессионная модель с помощью метода
наименьших квадратов
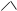 у = а0 + а1х1
+ а2х2 + а3х3 + а4х4
+ а5х5 + а6х6 + е,
у = а0 + а1х1
+ а2х2 + а3х3 + а4х4
+ а5х5 + а6х6 + е,
где а0 = 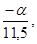 а1 =
а1 = 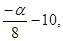 а2 =
а2 = 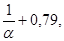 а3 =
а3 = 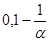 , а4 =
, а4 = 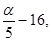 а5 =
а5 =
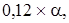 а6 =
а6 = 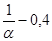 .
.
Какие фиктивные переменные были использованы в модели?
Дайте экономическую интерпретацию полученной модели.
Решение:
Образец решения рассмотрим на конкретном примере. Найдем
минимальный объем выборки nmin.
Число факторов, включаемых в модель,
m = 6, а число
свободных членов в уравнении n = 1.
Nmin
= 5(6 + 1) = 35.
Число α = 184. Тогда
найдем коэффициенты линейной множественной регрессионной модели: а0
= – -16,00, а1 = –
33,00, а2 = 0,80, а3 = 0,99, а4 = 20,80 а5 = 22,08, а6 = – 0,39.
Получили уравнение регрессии
 у
= –16,00 – 33,00х1 + 0,80х2 + 0,99х3 + 20,80х4
+ 22,08х5 – 0,39х6 + е.
у
= –16,00 – 33,00х1 + 0,80х2 + 0,99х3 + 20,80х4
+ 22,08х5 – 0,39х6 + е.
Экономическая интерпретация полученной модели: квартиры в
районе a стоят на 33,00 % дешевле,
чем в районе b. При увеличении жилой площади на 1
% стоимость квартиры возрастает на 0,80 %. При увеличении площади кухни на 1 %
стоимость квартиры увеличивается на 0,99 %. Квартиры на средних этажах стоят на
20,80 % дороже, чем на крайних. Квартиры в кирпичных домах стоят на 22,08 %
дороже, чем в панельных. При увеличении срока сдачи дома на 1 % стоимость
квартиры уменьшается на 0,39 %.
Фиктивные переменные – район, этаж, дом.
Задание 4
Постройте модель сезонных колебаний дохода торгового
предприятия, используя первую гармонику ряда Фурье по данным, приведенным в
табл. 5, изобразите графически.
Таблица 5
|
Месяц
|
Доход, тыс. руб.
|
|
Январь
|
58,33+112×(1/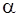 ) )
|
|
Февраль
|
52+112×(1/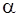 ) )
|
|
Март
|
43,67+112×(1/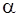 ) )
|
|
Апрель
|
41,02+112×(1/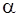 ) )
|
|
Май
|
42,77+112×(1/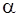 ) )
|
|
Июнь
|
50,01+112×(1/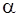 ) )
|
|
Июль
|
56,6+112×(1/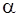 ) )
|
|
Август
|
64,74+112×(1/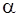 ) )
|
|
Сентябрь
|
71,04+112×(1/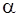 ) )
|
|
Октябрь
|
73,54+112×(1/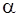 ) )
|
|
Ноябрь
|
72,16+112×(1/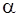 ) )
|
|
Декабрь
|
66,3+112×(1/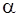 ) )
|
Воспользуйтесь вспомогательной табл. 6.
Таблица 6
|
t
|
cos t
|
sin t
|
|
0
|
1,00
|
0,00
|
|
0,523599
|
0,87
|
0,50
|
|
1,047198
|
0,50
|
0,87
|
|
1,570796
|
0,00
|
1,00
|
|
2,094395
|
-0,50
|
0,87
|
|
2,617994
|
-0,87
|
0,50
|
|
3,141593
|
-1,00
|
0,00
|
|
3,665191
|
-0,87
|
-0,50
|
|
4,18879
|
-0,50
|
-0,87
|
|
4,712389
|
0,00
|
-1,00
|
|
5,235988
|
0,50
|
-0,87
|
|
5,759587
|
0,87
|
-0,50
|
Решение:
Число 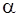 =184. Тогда исходная таблица будет выглядеть следующим
образом:
=184. Тогда исходная таблица будет выглядеть следующим
образом:
Таблица 7
|
Месяц
|
Периоды, t
|
Доход, тыс. руб.
|
|
Январь
|
0
|
58,939
|
|
Февраль
|
0,5236
|
52,609
|
|
Март
|
1,0471
|
44,279
|
|
Апрель
|
1,5707
|
41,629
|
|
Май
|
2,0943
|
43,379
|
|
Июнь
|
2,618
|
50,619
|
|
Июль
|
3,1416
|
57,209
|
|
Август
|
3,6652
|
65,349
|
|
Сентябрь
|
4,1888
|
71,649
|
|
Октябрь
|
4,7124
|
74,149
|
|
Ноябрь
|
5,236
|
72,769
|
|
Декабрь
|
5,7596
|
66,909
|
Если мы рассматриваем год как цикл, то n=12. Параметры уравнения могут быть
найдены по формулам:
Получили а0 = 58,290. Найдем промежуточные
значения
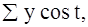
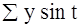 (табл. 8).
(табл. 8).
Таблица 8
|
Месяц
|
Периоды, t
|
Доход, тыс. руб.
|
y×cos t
|
y×sin t
|
|
Январь
|
0
|
58,939
|
58,9387
|
0
|
|
Февраль
|
0,5236
|
52,609
|
45,56043
|
26,3044
|
|
Март
|
1,0471
|
44,279
|
22,14309
|
38,34432
|
|
Апрель
|
1,5707
|
41,629
|
0,00401
|
41,6287
|
|
Май
|
2,0943
|
43,379
|
-21,6858
|
37,56911
|
|
Июнь
|
2,618
|
50,619
|
-43,8372
|
25,30908
|
|
Июль
|
3,1416
|
57,209
|
-57,2087
|
-0,00042
|
|
Август
|
3,6652
|
65,349
|
-56,5934
|
-32,6748
|
|
Сентябрь
|
4,1888
|
71,649
|
-35,8237
|
-62,0499
|
|
Октябрь
|
4,7124
|
74,149
|
0,000817
|
-74,1487
|
|
Ноябрь
|
5,236
|
72,769
|
36,38512
|
-63,0191
|
|
Декабрь
|
5,7596
|
66,909
|
57,94508
|
-33,4536
|
Σycost=5,83
Σysint=-96,19
Найдем коэффициенты: а1= 0,97,
b1
=–16,03.
Получили yt
= 58,186 + 0,97×cos t –
16,03×sin t.
Подставим фактические значения t
в полученную первую гармонику ряда Фурье.
Таблица 9
|
Месяц
|
Периоды, t
|
yt
|
|
Январь
|
0
|
59,156
|
|
Февраль
|
0,5236
|
51,015
|
|
Март
|
1,0471
|
44,725
|
|
Апрель
|
1,5707
|
42,156
|
|
Май
|
2,0943
|
43,755
|
|
Июнь
|
2,618
|
49,327
|
|
Июль
|
3,1416
|
57,216
|
|
Август
|
3,6652
|
65,357
|
|
Сентябрь
|
4,1888
|
71,647
|
|
Октябрь
|
4,7124
|
74,216
|
|
Ноябрь
|
5,236
|
72,617
|
|
Декабрь
|
5,7596
|
67,045
|
Строим график исходных данных и первой гармоники ряда Фурье (рис. 3).
Рис. 3. Первая
гармоника ряда Фурье
Задание 5
В торгово-розничную сеть поступило 3 вида взаимозаменяемой
продукции разных производителей: А1, А2, А3. Предположим, что покупатели
приобретают продукцию только одного из них. Пусть в среднем они стремятся
поменять её не более одного раза в год, и вероятности таких изменений
постоянны.
Результаты маркетинговых исследований покупательского спроса
на продукцию дали следующее процентное соотношение:
Х1 % покупателей продукции А1 переходит на продукцию А2,
Х2 % покупателей продукции А2 – на продукцию А3,
Х3 % покупателей продукции А3 – на продукцию А1,
где Х1 = 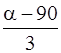 , Х2 =
, Х2 = 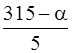 , Х3 =
, Х3 = 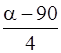 .
.
Требуется:
1. Построить граф состояний.
2. Составить матрицу переходных вероятностей для средних
годовых изменений.
3. Предположить, что общее число покупателей постоянно, и
определить, какая доля из их числа будет покупать продукцию А1, А2 и А3 через 2
года.
4. Определить какая продукция будет пользоваться наибольшим спросом.
Решение:
Число 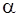 =184. Тогда Х1 = 31,33; Х2 = 26,2; Х3 = 23,5.
=184. Тогда Х1 = 31,33; Х2 = 26,2; Х3 = 23,5.
Построим граф состояний:
Составим матрицу переходных вероятностей:
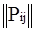 =
= 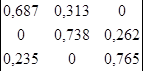 .
.
Зададим вектор начальных вероятностей:
P(0)
= 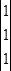 ,
,
т.е. P1(0)
= 1, P2(0) =
1 и P3(0) =
1.
Определим вероятности состояния Pi(k) после первого шага (после первого
года):
P1(1)
= P1(0)×P11 + P2(0)×P21 + P3(0)×P31 = 0,922;
P2(1)
= P1(0)×P12 + P2(0)×P22 + P3(0)×P32 = 1,051;
P3(1)
= P1(0)×P13 + P2(0)×P23 + P3(0)×P33 = 1,027.
Определим вероятности состояний после второго шага (после
второго года):
P1(2) = P1(1)×P11
+ P2(1)×P21
+ P3(1)×P31
= 0,874
P2(2) = P1(1)×P12
+ P2(1)×P22
+ P3(1)×P32
= 1,065;
P3(2) = P1(1)×P13
+ P2(1)×P23
+ P3(1)×P33
= 1,055.
Вывод. Через 2
года 87,4 % покупателей будут приобретать продукцию А1, число покупателей
продукции А2 увеличится в 1,065 раза, число покупателей продукции А3 увеличится
в 1,055 раза.
Продукция А2 будет пользоваться наибольшим спросом.