Министерство образования Российской Федерации
Всероссийский заочный финансово-экономический институт
Филиал г.Барнаула
Аудиторная работа
по ЭММ и ПМ
Вариант 4
|
|
|
Выполнила студентка
3 курса
Проверил Кайгародова М.А.
|
Г.Барнаул – 2005г.
Задача 1.
Управляющему
банка были представлены 4 проекта, претендующие на получение кредита в банке.
Доступная наличность банка, потребности проектов и прибыль по ним приведены в
таблице (тыс долл).
|
Проект
|
Период 1
|
Период 2
|
Период 3
|
Период 4
|
Прибыль
|
|
А
|
8
|
8
|
10
|
10
|
12
|
|
В
|
7
|
9
|
9
|
11
|
18
|
|
С
|
5
|
7
|
9
|
11
|
16
|
|
Д
|
9
|
8
|
7
|
6
|
17,5
|
|
Ресурс банка
|
22
|
25
|
38
|
30
|
|
При оценке этих предложений следует принять во внимание потребность
проектов в наличности и массу доступной наличности для соответствующих
периодов.
Какие проекты следует финансировать и какое количество наличности необходимо
в течение каждого периода, чтобы максимизировать прибыль?
Задача 2.
Менеджер транспортного отдела составляет план перевозок продукции фирмы
в стандартных контейнерах на следующий месяц. Цены перевозок одного контейнера,
величины заказов и запасы на складах даны в таблице.
|
Склады
|
|
|
|
|
Клиенты
|
|
|
|
|
Ресурсы
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
|
1
|
3
|
17
|
7
|
17
|
9
|
14
|
9
|
1
|
48
|
14
|
4
|
|
2
|
3
|
6
|
6
|
8
|
17
|
12
|
16
|
5
|
5
|
13
|
11
|
|
3
|
9
|
5
|
6
|
16
|
8
|
10
|
11
|
8
|
8
|
18
|
17
|
|
4
|
12
|
16
|
6
|
16
|
14
|
3
|
5
|
14
|
11
|
17
|
20
|
|
Заказ
|
2
|
2
|
5
|
4
|
5
|
4
|
4
|
1
|
2
|
3
|
|
Заказы в сумме превышают запас на складах. Найдите план перевозок,
минимизирующий транспортные издержки.
Задача 1.
1.
Составим ЭММ.
Обозначим через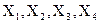 
финансирование проекта.
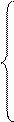
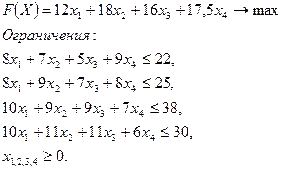
2. Решим данную задачу с помощью пакета Excel, который содержит программу (надстройку) Поиск решения, позволяющий реализовать
модели линейной, нелинейной и дискретной оптимизации.
3.
Введем исходные
данные
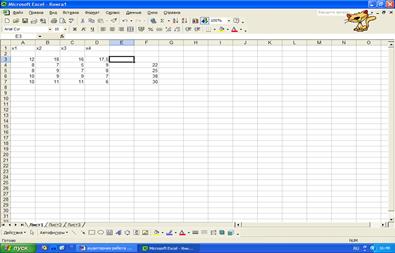
4. Введем зависимость для целевой функции:
·
Поместим курсор в
ячейку Е3;
·
В строке Меню указатель мыши на имя Вставка, появляется диалоговое окно, в
котором выбираем Функция;
·
На экране
появляется Мастер функций – шаг 1 из 2;
·
Выбираем в Категории – Математические;
·
Помещаем курсор в
окно «Выберете функции» и выбираем СУММПРОИЗВ, затем нажимаем на ОК,
появляется диалоговое окно «Аргументы функции» (СУММПРОИЗВ);
·
В строке «Массив 1» вводим $А$2:$D$2;
·
В строке «Массив
2» вводим А3:D3, нажимаем курсором на ОК и на экране
в ячейки Е4 введена функция.
5. Вводим зависимость для ограничений. Для этого
необходимо скопировать содержимое ячейки Е3 в ячейки Е4-Е7.
6.
Запустим
команду Сервис – Поиск решения.
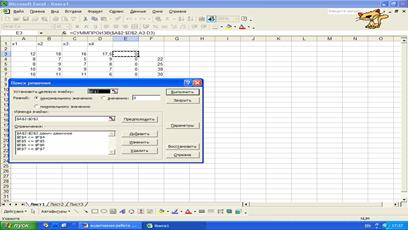
7.
в диалоговом
окне Поиск решения:
·
назначим ячейку
для целевой функции $Е$3 и введем тип целевой функции – максимум;
·
введем изменяемые
ячейки $A$2:$D$2;
·
введем
ограничения: поместим указатель мыши на кнопку Добавить, появится диалоговое окно, в которое вводятся ограничения:
$A$2:$D$2=двоичная
·
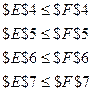
введем параметры
для решения задачи: Неотрицательное значение
·
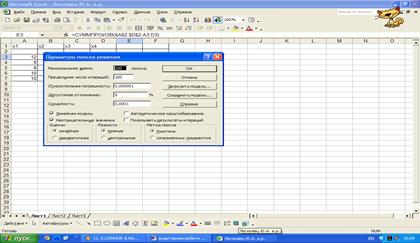
поместим
указатель мыши на кнопку Выполнить и
получим решение данной задачи.
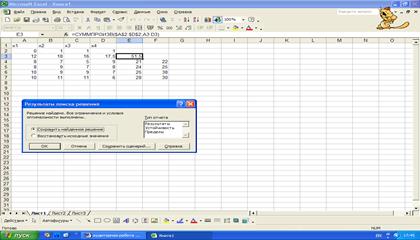
Вывод: Оптимальный план показывает, что следует
финансировать В,С и Д проект. Количество наличности ресурсов необходимо в
течение каждого периода составляет: в 1-ый период – 21, во 2-ой период – 24, в
3-ий период – 25 и в 4-ый период – 28.
Задача 2.
1.
Составим ЭММ. В
качестве управляющих параметров возьмем цену и ограничения на выпуск продукции.
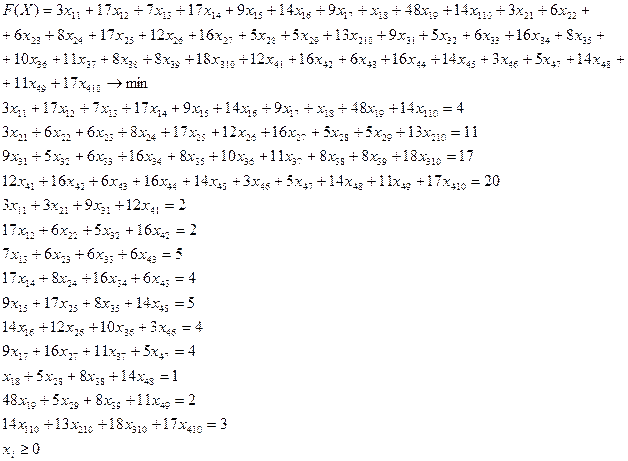
2.
Создадим матрицу
перевозок, для этого необходимо выполнить резервирование изменяемых ячеек: в
блок ячеек В2:L5 вводится «1».
3.
Выполним
суммирование по столбцам и строкам в матрице перевозок.
4.
Введем исходные
данные в блок ячеек В10:L13.
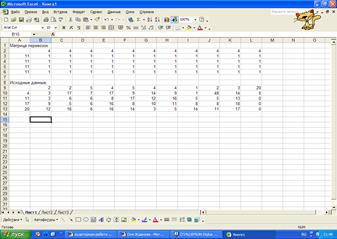
5.
Назначим целевую
функцию:
·
Поместим курсор в
ячейку В15;
·
В строке Меню указатель мыши на имя Вставка, появляется диалоговое окно, в
котором выбираем Функция;
·
На экране
появляется Мастер функций – шаг 1 из 2;
·
Выбираем в Категории – Математические;
·
Помещаем курсор в
окно «Выберете функции» и выбираем СУММПРОИЗВ, затем нажимаем на ОК,
появляется диалоговое окно «Аргументы функции» (СУММПРОИЗВ);
·
В строке «Массив 1» вводим В2:L6;
·
В строке «Массив 2» вводим B10:L13, нажимаем
курсором на ОК и на экране в ячейки B15
введена функция.
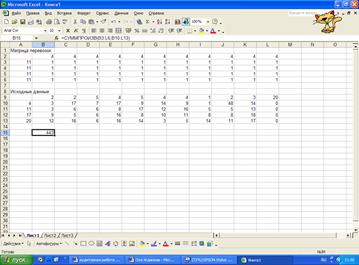
6.
Введем
зависимости из математической модели.
7.
Запустим команду Меню – Сервис – Поиск решения.
8.
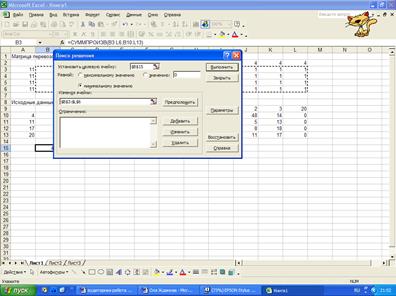
В Диалоговом окне
Поиск решения:
·
Введем целевую
ячейку $B$15;
·
Установим
направление изменения целевой функции - минимум;
·
Введем изменяемые
ячейки $B$3:$L$6;
·
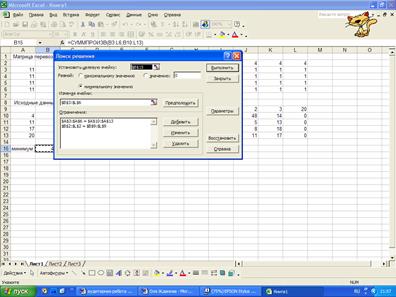
Введем
ограничения: поместим указатель мыши на кнопку Добавить, появится диалоговое окно, в которое вводятся ограничения:
$A$3:$A$6=$A$10:$A$13
$B$2:$L$2=$B$9:$L$9
·
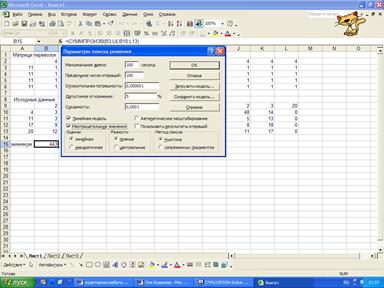
Введем параметры
для решения задачи: Линейное и неотрицательное значение;
·
Поместим
указатель мыши на кнопку Выполнить.
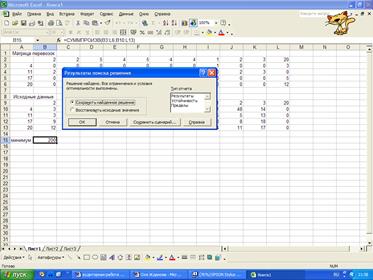
Вывод: Оптимальный план показывает, что перевозка
продукции происходит с минимальными затратами, равные 200 у.е., которые будут
обеспечены при следующем плане перевозок:
·
С 1 склада
перевозить продукцию будут: 8 фирма в объеме 1 у.е. и 11 фирма в объеме 3 у.е.;
·
Со 2 склада
перевозить продукцию будут: 1 фирма в объеме 2 у.е., 4 фирма в объеме 4 у.е., 9
фирма в объеме 2 у.е. и 10 фирма в объеме 3 у.е.;
·
С 3 склада
перевозить продукцию будут: 2 фирма в объеме 2 у.е., 3 фирма в объеме 5 у.е., 5
фирма в объеме 5 у.е. и 11 фирма в объеме 5 у.е.
·
С 4 склада
перевозить продукцию будут: 6 фирма в объеме 4 у.е., 7 фирма в объеме 4 у.е. и
11 фирма в объеме 12 у.е.