Вариант 20

Фирма по производству мебели может выпускать письменные полки з типов: одноярусные, двухъярусные, угловые. Соответствующие нормы затрат, запасы сырья и стоимость готовых изделий приведены в следующей таблице.

Необходимые ресурсы	Нормы затрат	Наличие
Одноярусная полка	Двухъярусная полка	Полка угловая
Плиты ДСП, м2	0,6	1	1,2	500
Плиты ламинированные, м2	0,4	0,7	0,6	400
Время на производство, ч	6	10	8	4000
Стоимость одного изделия, руб.	850	1490	1200

Составить план выпуска продукции, максимизирующий стоимость продукции.

Экономико-математическая модель

Обозначим через Х1, Х2, Х3 объемы производства соответствующего вида продукции.

Целевая функция – это математическая запись критерия оптимальности, т.е выражение которое необходимо максимизировать f(x)=850Х1+1490Х2+1200Х3.

Ограничения по ресурсам:

0,6Х1+Х2+1,2Х3 <=500

0,4Х1+0,7Х2+0,6Х3 <=400

6Х1+10Х2+8Х3 <=4000

Решение.

1) Создать форму для ввода условий задачи. Создайте текстовую форму – таблицу для ввода условий задачи (рис. 1.1)

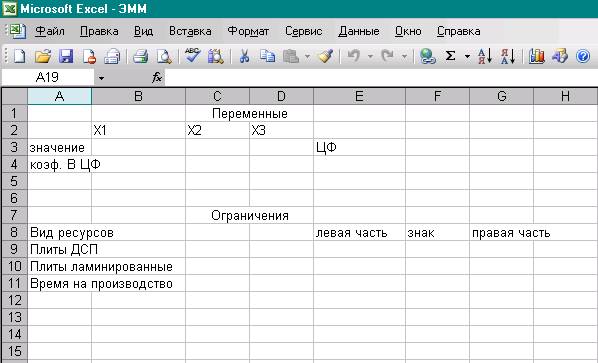
Рис. 1.1

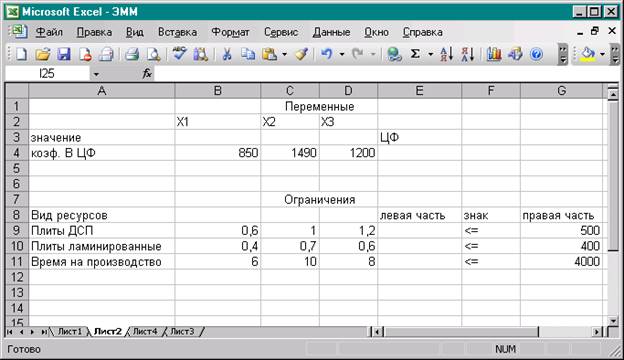
Рис. 1.2

2)Указатель адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки). Обозначить через Х1, Х2, Х3 количество полок каждого типа. В нашей задаче оптимальные значения компонент вектора Х=(Х1, Х2, Х3) будут помещены в ячейках B3:D3, оптимальное значение целевой функции – в ячейке F4.

3)Ввести исходные данные задачи в созданную форму – таблицу, представленную на рис. 1.2

4) Ввести зависимость для целевой функции:

·        Курсор в ячейку Е4.

·        Курсор на кнопку «Мастер функций», расположенную на панели инструментов.

·        На экране появляется диалоговое окно Мастер функций шаг 1 из 2 (рис. 1.3.)

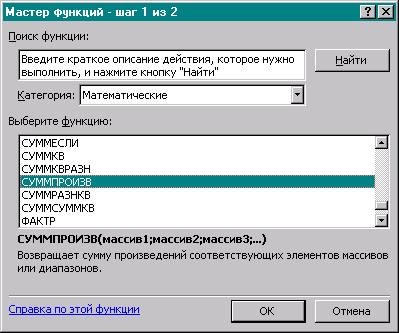
Рис. 1.3

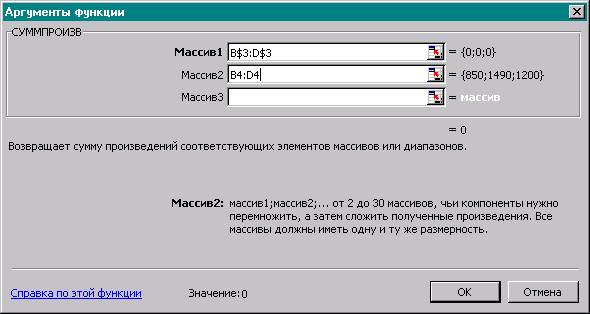
Рис 1.4

Курсор в окно «Категория» на категорию математические;

·        Курсор в окно Функции на СУММПРОИЗВ;

·        На экране появляется диалоговое окно СУММПРОИЗВ (рис. 1.4)

·        В строку «Массив 1» ввести В$3:D$3;

·        В строку «Массив 2» ввести В4:D4;

·        Кнопка «ОК». На экране: в ячейку Е4 введена функция (рис.1.4)

5)Ввести зависимости для ограничений:

·        Курсор в ячейку Е4;

·        На панели инструментов Копировать в буфер

·        Курсор в ячейку Е9

·        На панели инструментов кнопка Вставить из буфера

·        Курсор в ячейку Е10

·        На панели инструментов кнопка Вставить из буфера

·        Курсор в ячейку Е11

·        На панели инструментов кнопка Вставить из буфера

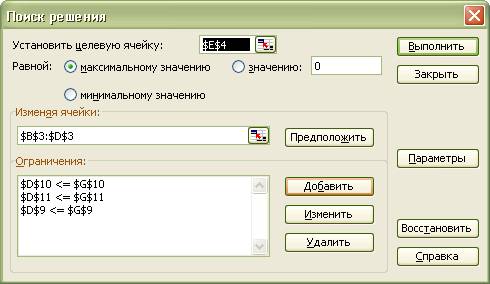
В строке Меню указатель мыши на имя Сервис, Поиск Решения. Появляется диалоговое окно Поиск решения (рис. 1.6).

Рис. 1.5

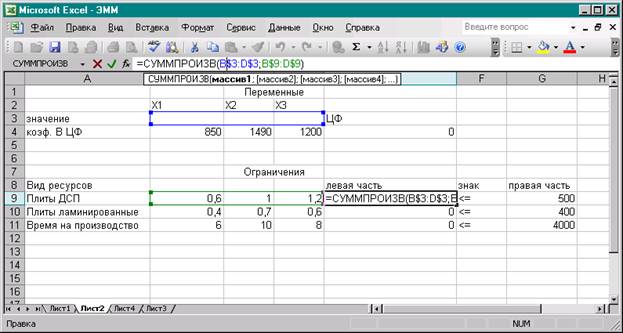
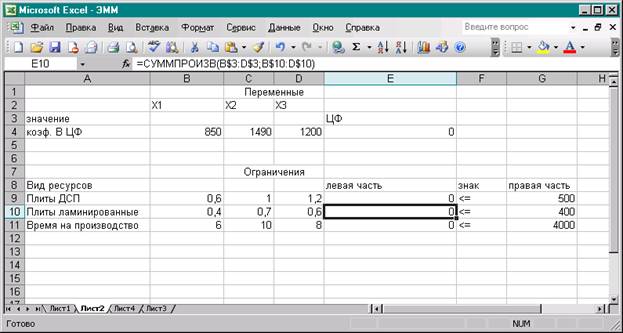
Рис 1.6

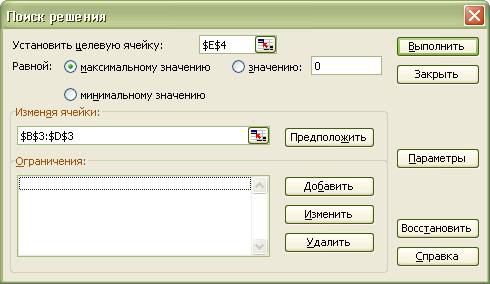
6) Назначить целевую функцию (установить целевую ячейку):

·        Курсор в строку Установить целевую ячейку;

·        Введите адрес ячейки $E$4;

·        Введите направление целевой функции – Максимальному значению

·        Курсор в строку Изменяя ячейки;

·        Введите адреса искомых переменных B$3:D$3

7)Ввести ограничения:

·        Указатель мышки на кнопку Добавить. Появляется диалоговое окно Добавление ограничений (рис. 1.7)

·        В строке Ссылка на ячейку введите адрес $E$9

·        Введите знак ограничения <=

·        В строке ограничения введите адрес $G$9

·        Указатель мыши на кнопку Добавить. На экране вновь диалоговое окно Добавление ограничения (рис. 1.7)

·        Введите остальные ограничения задачи, по вышеописанному алгоритму

·        После введения последнего ограничения кнопка ОК.

Рис 1.7.

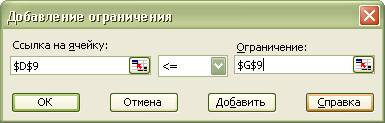
На экране появляется диалоговое Окно Поиск решений с введенными условиями (рис. 1.8.)

Рис. 1.8

8) Ввести параметры для решения ЗЛП:

·        в диалоговом окне указатель мыши на кнопку Параметры. На экране появляется диалоговое окно Параметры поиска решения (рис. 1.9)

Рис 1.9

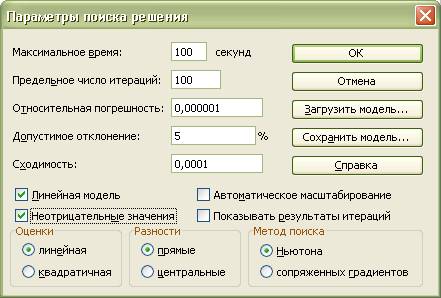
·        установите флажки в окнах Линейная модель (это обеспечит применение симплекс-метода) и Неотрицательные значения;

·        указатель мыши на ОК. На экране диалоговое окно Поиск решения

·        указатель мыши выполнить.

 Через непродолжительное время появится диалоговое окно Результаты поиска решения и исходная таблица с заполненными ячейками В3:D3 и ячейка E4 с максимальным значением целевой функции (рис. 1.10).

Рис. 1.10

Рис. 1.11

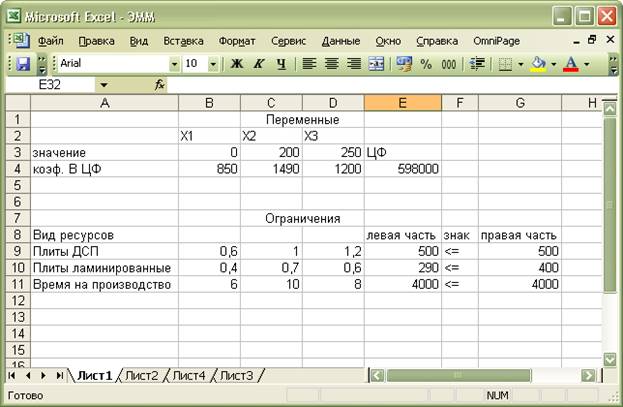
Полученное решение (рис.1.11) означает, что максимальный доход 598 000 руб.фирма может получить при выпуске и реализации 200 двухъярусных полок и 250 угловых полок.

2.Транспортная задача

Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ  может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам  работ. Имеются экономические оценки транспортных затрат (в у.е.) на перевозку 1 тонны песку с карьеров на ремонтные участки.

Требуется:

1.Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.

2.Определить, что произойдет с оптимальным планом, если изменятся условия перевозок: а)появится запрет на перевозки от первого  карьера до второго участка работ; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами.

                                    2.2.Матрица планирования

Карьер	Участок работ	Предложение
В1	В2	В3	В4	В5
А1	5	3	4	6	4	40
А2	3	4	10	5	7	20
А3	4	6	9	3	4	100
Потребности	25	10	20	30	15

 

Экономико-математическая модель.

В данном случае предложение и потребности совпадают ,т.е. мы имеем дело с закрытой моделью транспортной задачи.

Решение

1).

1.Выполним резервирование изменяемых ячеек: в блок В3:F6 вводим «1».

2.Введем  условие реализации мощностей поставщиков, т.е.

                                               ,

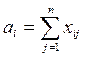где 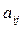 - мощность i поставщика;

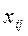- объем поставки груза от i –го поставщика к  j -му потребителю;

n – количество потребителей.

Для этого:

- курсов в ячейку А3,

- щелкнуть знак « »,

-выделить ячейки B3:F3,

- нажать ENTER.

Аналогичные действия для ячеек А4,А5.

3.Введем условие удовлетворения запросов потребителей, т.е.

                                              ,

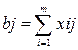где b – мощность j-го потребителя;

m –количество поставщиков.

Для этого:

- курсор в В6;

-щелкнуть знак« »,

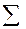-выделить ячейки B3:F6,

- нажать ENTER.

Аналогичные действия для ячеек С6-F6.

4.В таблицу «Исходные данные» введем исходные данные.

5.Назначение целевой функции.

- курсор в ячейку В13,

- курсор на кнопку «Мастер функций»;

- курсор в окно «Категория» на категорию «Математические»;

- курсор в окно Функции на СУММПРОИЗВ,

- в строку «Массив 1» ввести B$10:F$12;

- в строку «Массив 2» ввести В$3:F$5;

- «ОК».

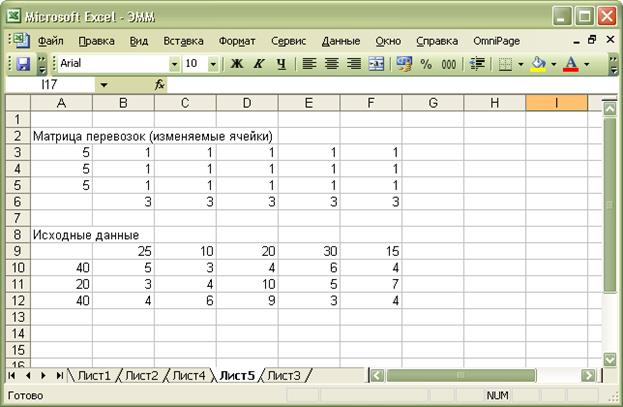
Меню – Сервис – Поиск решения. Появляется окно Поиск решения.

6.Назначить целевую функцию:

-курсор в строку «Установить целевую ячейку»;

-ввести адрес ячейки В13;

-поставить точку у «Минимальному значению»;

-курсор в строку «Изменяя ячейки»;

-ввести адреса ячеек B$3:F$6.

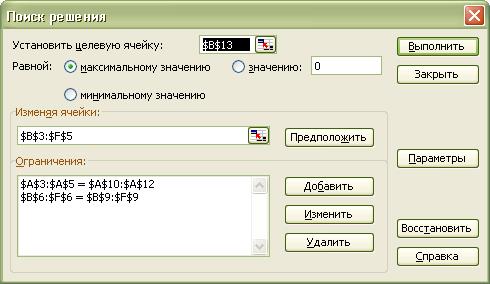
7.Ввести ограничения.

-«Добавить»;

-«Ссылка на ячейку»,введем адрес $А$3:$А$5;

-введем знак ограничений  «=»;

- в строке «Ограничения» введем $А$10:$А$12,

- «ОК».

-«Добавить»;

- «Ссылка на ячейку», введем адрес $В$6:$F$6;

-знак ограничений «=» ;

- в строке «Ограничения» введем $В$9:$F$9.

- «ОК».

7.Введем параметры для решения ЗЛП.

-в диалоговом окне указатель мыши на кнопку «Параметры».

-установить флажки в окнах Линейная модель и Неотрицательные значения. «ОК»

- «Выполнить»,  «ОК».

Результат решения:

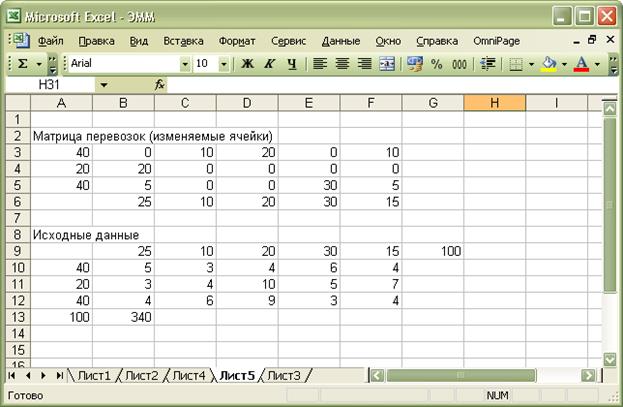
Вывод: для обеспечения минимальных совокупных транспортных издержек необходимо:

- перевезти от первого карьера до второго участка работ 10т песка, до второго - 20т, до пятого  10т песка;

 

- от второго карьера  до первого участка работ необходимо перевезти 20т песка;

- от третьего карьера до первого участка – 5т. песка., до четвертого – 30т., до пятого – 5т.

2.

Изменим исходные данные:

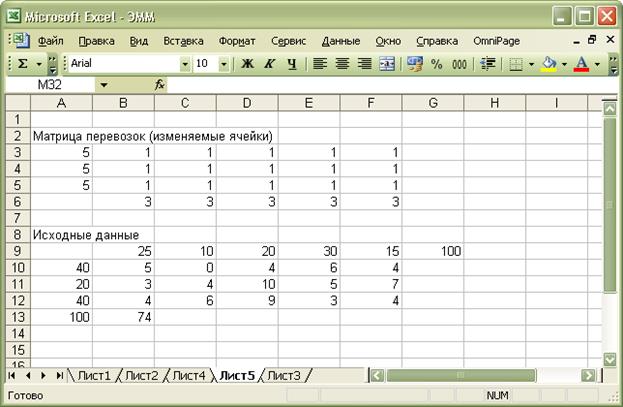
Выполним  расчеты, аналогичные расчетам первой части задачи. В результате получим:

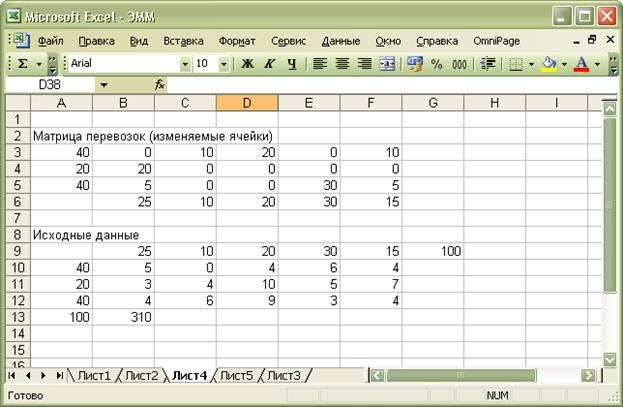
Вывод: оптимальный план существенно уменьшится: с 340 т снизится до 310т.