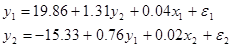Задача 1

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (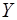, млн. руб.) от объема капиталовложений (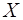, млн. руб.)

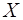
	36	28	43	52	51	54	25	37	51	29
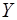
	85	60	99	117	118	125	56	86	115	68

Требуется:

1.     Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2.     Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 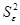; построить график остатков.

3.     Проверить выполнение предпосылок МНК.

4.     Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента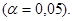

5.     Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью 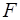- критерия Фишера 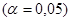, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

6.     Осуществить прогнозирование среднего значения показателя 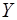 при уровне значимости  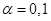,  если прогнозное значения фактора Х составит 80% от его максимального значения.

7.     Представить графически: фактические и модельные значения 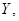 точки прогноза.

8.     Составить уравнения нелинейной регрессии:

·        гиперболической;

·        степенной;

·        показательной.

Привести графики построенных уравнений регрессии.

9.     Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод. 

Решение:

    1)  Сначала, для удобства решения, отсортируем все x и y в порядке возрастания (табл.1)

x	25	28	29	36	37	43	51	51	52	54
y	56	60	68	85	86	99	115	118	117	125

Табл.1.

     Для расчёта параметров уравнения линейной регрессии, воспользуемся инструментом анализа данных Регрессия. Для этого в главном меню выбираем Сервис/Анализ данных/ Регрессия. Заполняем диалоговое окно ввода данных и параметров вывода (рис.2)

Рис.2. Диалоговое окно ввода параметров инструмента Регрессия.

Результаты регрессионного анализа для данных представлены на рис.3.

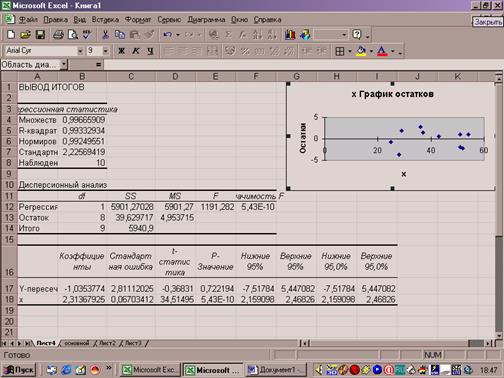
Рис.3.Результаты применения инструмента Регрессия

     Таким образом, получено уравнение регрессии y=-1+2.32x

Экономическая интерпретация коэффициента регрессии заключается в том, что если объёмы капиталовложений возрастут на 1 млн., то объём выпуска продукции возрастёт на 2,32 млн.руб.

2) Вычислим остатки, найдём остаточную сумму квадратов (рис.4) и построим график остатков (рис.5)

№ п/п	x	y	ypi	ei	ei2
1	25	56	56,807	-0,807	0,651
2	28	60	63,748	-3,748	14,045
3	29	68	66,061	1,939	3,758
4	36	85	82,257	2,743	7,524
5	37	86	84,571	1,429	2,043
6	43	99	98,453	0,547	0,299
7	51	115	116,962	-1,962	3,850
8	51	118	116,962	1,038	1,077
9	52	117	119,276	-2,276	5,180
10	54	125	123,903	1,097	1,203

Рис.4.

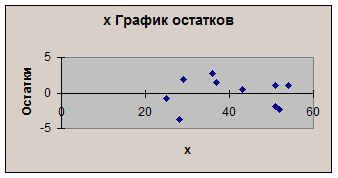
Рис.5.

     По графику остатков можно сказать о гомоскедастичности остаточной компоненты, подтверждать эти данные будем аналитическим исследованием.

3) Проверим выполнение предпосылок МНК, то есть остаточная компонента должна удовлетворять четырём требованиям:

1) Математическое ожидание остаточной компоненты равно нулю

    М(е)=0

2) Последовательные уровни должны быть некоррелируемы

     r(e_i;е_i+1)=0

3) Дисперсия остатков должна быть гомоскедастичной

     D(e)=0

      4) Ряд значений остаточной компоненты должен соответствовать                 нормальному закону распределения.

     Математическое ожидание остаточной компоненты равно нулю, так как 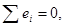 значит первое требование выполнено. Независимость последовательных уровней остаточной компоненты проверяется с помощью критерия Дарбина-Уотсона. Для этого вычисляется d_расч.

d_расч=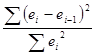, произведем необходимые расчёты (рис.6)

    

№ п/п	x	y	ypi	ei	ei^2	еi-ei-1	(еi-ei-1)2
1	25	56	56,807	-0,807	0,651
2	28	60	63,748	-3,748	14,045	-2,941	8,650
3	29	68	66,061	1,939	3,758	5,686	32,334
4	36	85	82,257	2,743	7,524	0,804	0,647
5	37	86	84,571	1,429	2,043	-1,314	1,726
6	43	99	98,453	0,547	0,299	-0,882	0,778
7	51	115	116,962	-1,962	3,850	-2,509	6,297
8	51	118	116,962	1,038	1,077	3,000	9,000
9	52	117	119,276	-2,276	5,180	-3,314	10,980
10	54	125	123,903	1,097	1,203	3,373	11,375
Итого:					39,630		81,787

Рис.6.

d_расч=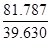=2,064     d_расч>2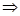переходим к d    d_расч=4-d_расч=4-2,064=1,936

1,936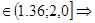последовательные уровни остаточной компоненты независимы, значит второе требование выполнено.

 

        Для применения МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора х_j остатки e_i  имеют одинаковую дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность. Чтобы проверить это мы исключим из рассмотрения с центральных наблюдений; при этом (п-с):2>p, где р – число оцениваемых параметров. Разделим совокупность из (п-с) наблюдений на две группы (соответственно с малыми и с большими значениями фактора х) и определим по каждой из групп уравнение регрессии. Определим остаточную сумму квадратов для первой (S₁) и второй (S₂) групп и найдем их отношения: F_расч=S₁:S₂. При выполнении гипотезы о гомоскедастичности отношение F_расч будет удовлетворять F-критерию со степенями свободы ((п-с-2р):2) для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.

     В нашем случае п=10, с=2, р=2, выделим 2 центральных наблюдения из всей совокупности и рассчитаем уравнение регрессии для каждой из двух оставшихся групп с помощью инструмента Регрессия, а их остатки запишем в соответствующую графу. (рис.7)

№ п/п	x	y	ypi	ei	ei^2	Еi
1	25	56	56,807	-0,807	0,651	0,969
2	28	60	63,748	-3,748	14,045	-3,177
3	29	68	66,061	1,939	3,758	2,108
4	36	85	82,257	2,743	7,524	0,100
5	37	86	84,571	1,429	2,043
6	43	99	98,453	0,547	0,299
7	51	115	116,962	-1,962	3,850	-0,917
8	51	118	116,962	1,038	1,077	2,083
9	52	117	119,276	-2,276	5,180	-1,750
10	54	125	123,903	1,097	1,203	0,583
Итого:					39,630

Рис.7

     Возведём в квадрат остаточные компоненты каждой группы и подсчитаем сумму каждой из них (рис.8)

№ п/п	x	y	ypi	ei	ei^2	Еi	Ei^2
1	25	56	56,807	-0,807	0,651	0,969	0,939
2	28	60	63,748	-3,748	14,045	-3,177	10,093
3	29	68	66,061	1,939	3,758	2,108	4,442
4	36	85	82,257	2,743	7,524	0,100	0,010
5	37	86	84,571	1,429	2,043		15,485
6	43	99	98,453	0,547	0,299
7	51	115	116,962	-1,962	3,850	-0,917	0,840
8	51	118	116,962	1,038	1,077	2,083	4,340
9	52	117	119,276	-2,276	5,180	-1,750	3,062
10	54	125	123,903	1,097	1,203	0,583	0,340
Итого:					39,630		8,583

Рис.8

     Затем большую сумму поделим на меньшую, таким образом найдём F_расч

F_расч=15,485/8,583=1,804.  F_табл находим на уровне значимости 0,05 со степенями свободы ((п-с-2р):2). Таким образом F_крит=F_0.05;2;2=19,00

F_расч<F_крит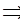> остатки гомоскедастичны, это значит что третье требование выполнено.

    

     Чтобы проверить соответствие ряда значений остаточной компоненты нормальному закону распределения, нужно подсчитать R/S_расч.

R/S_расч=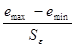,  где S_e=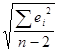

S_e=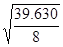= 2.23  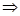R/S_расч=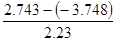=2,91

Так как R/S_расч 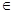(2,7;3,7), то остаточная компонента распределена по нормальному закону и значит четвёртое требование выполнено.

Все предпосылки МНК выполнены.

4) Чтобы осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента, нужно сравнить t_расч и t_крит. Значение t_крит зависит от принятого уровня значимости (в данном случае a=0,05) и от числа степеней свободы (п-р-1), где п-число единиц совокупности,  р-число факторов.

     В нашем случае t_{расч a0}=-0.37, а t_крит=t_0.05;7=2,3646, так как t_расч<t_крит, то коэффициент a₀ является статистически незначимым,  t_{расч а1}=34,515>t_крит, поэтому коэффициент а₁ является статистически значимым, надёжным, на него можно опираться в анализе и прогнозе.

5) Чтобы вычислить коэффициент детерминации воспользуемся формулой: 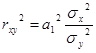. Для этого произведём необходимые расчёты (рис.9)

№ п/п	x	y
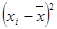
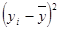
1	25	56	243,36	1361,61
2	28	60	158,76	1082,41
3	29	68	134,56	620,01
4	36	85	21,16	62,41
5	37	86	12,96	47,61
6	43	99	5,76	37,21
7	51	115	108,16	488,41
8	51	118	108,16	630,01
9	52	117	129,96	580,81
10	54	125	179,56	1030,41
Итого:	406	929	1102,4	5940,9
среднее	40,6	92,9	-	-
s	11,067	25,692	-	-
s2	122,48	660,08	-	-

Рис.9

s_x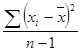²=  s_y²=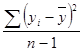

Исходя из этого найдём коэффициент детерминации: 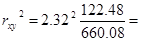0,99

Это означает, что 99% вариации объёма выпуска продукции (у) объясняется вариацией фактора х – объёмом капиталовложений.

     Проверка значимости уравнения регрессии с помощью F-критерия Фишера состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического F_крит значений F-критерия Фишера. F_факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

F_факт=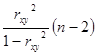, где п- число единиц совокупности.

F_крит – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a.

 F_факт =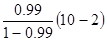=792

F_крит=F_0,05;1;8=5,32 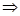 F_факт>F_крит

     Следовательно, гипотеза Н₀ о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надёжность. Значит уравнение значимо и может быть перенесено для прогнозирования на любой объект генеральной совокупности.

     Найдём величину средней ошибки аппроксимации :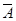

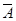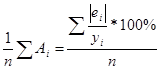=  Произведём необходимые расчёты (рис.10)

№ п/п	x	y	ei	Аi
1	25	56	-0,807	1,440
2	28	60	-3,748	6,246
3	29	68	1,939	2,851
4	36	85	2,743	3,227
5	37	86	1,429	1,662
6	43	99	0,547	0,553
7	51	115	-1,962	1,706
8	51	118	1,038	0,879
9	52	117	-2,276	1,945
10	54	125	1,097	0,877
Итого:	406	929	0	21,387

Рис.10

Следовательно, 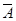=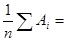21,387:10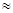2,1%

Качество построенной модели оценивается как хорошее, так как 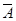 не превышает 8 – 10%.  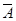<5%, поэтому модель точна и по ней можно прогнозировать с достаточно высокой вероятностью.

6) Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Точечный прогноз получается подстановкой в модель прогнозного значения фактора х.

y_np=a₀+a₁x_np

x_пр=х_max*0.8 

x_пр=54*0,8=43,2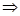  

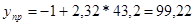
Для получения интервального прогноза найдём ширину доверительного интервала.

U_пр=S_e*t_кр*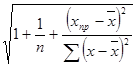, где S_e=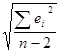,  t_кр=t_табл=t_0.1;n-2

Произведём необходимые расчёты (рис.11)

№ п/п	x	y
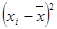
1	25	56	243,36
2	28	60	158,76
3	29	68	134,56
4	36	85	21,16
5	37	86	12,96
6	43	99	5,76
7	51	115	108,16
8	51	118	108,16
9	52	117	129,96
10	54	125	179,56
Итого:	406	929	1102,4
среднее	40,6	92,9

Рис.11

t_кр= t_табл=t_0.1;8 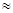1,85

S_e=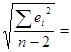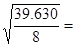2.23; 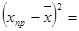   (43,2-40,6)²=6,76

U_пр=2,23*1,85*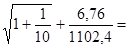4,3

Следовательно, интервальный прогноз будет выглядеть:

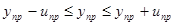
94,92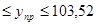

7) Представим графически: фактические и модельные значения  у, точки прогноза (рис.12)

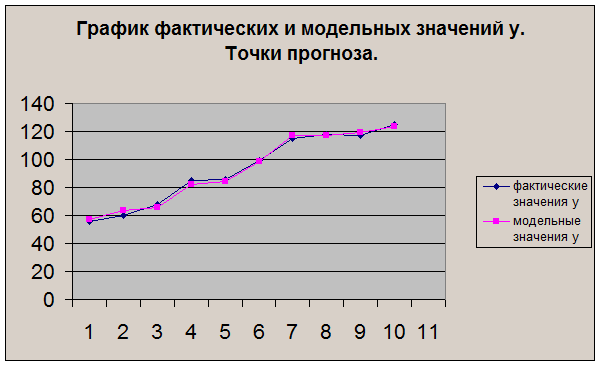
Рис.12

8) Уравнение гиперболической модели у=а+b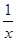 линеаризуется при замене: z=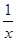. Тогда у=a+bz. Для расчётов используем данные в табл.13

№ п/п	x	y	z	yz
1	25	56	0,0400	2,24
2	28	60	0,0357	2,1429
3	29	68	0,0345	2,3448
4	36	85	0,0278	2,3611
5	37	86	0,0270	2,3243
6	43	99	0,0233	2,3023
7	51	115	0,0196	2,2549
8	51	118	0,0196	2,3137
9	52	117	0,0192	2,25
10	54	125	0,0185	2,3148
Итого:	406	929	0,2652	22,84889
среднее	40,6	92,9	0,026522	2,284889
s2	122,48	660,08	0,0000616

Табл.13

Значения параметров регрессии а и b составили:

b=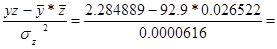-2907.6

a=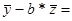92.9-(-2907.6)*0.026522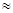170

Получено уравнение: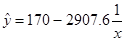

График построенной модели представлен на рис.14

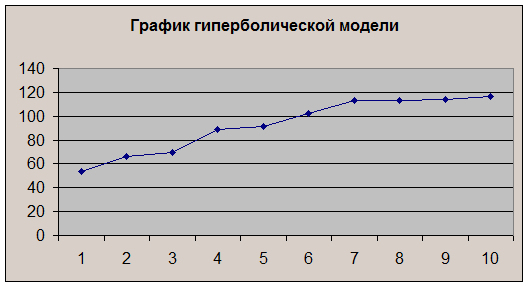
Рис.14

     Построению степенной модели y=ax^b предшествует процедура линеаризации переменных. В данном примере линеаризация производится путём логарифмирования обеих частей уравнения:

lg y=lg a+b*lg x

Y=С+b*X,  где Y=lg y, X=lg x, С=lg a

Для расчётов используем данные таблицы 15

№ п/п	x	y	Y	X	YX	(Xi-Xcp)^2
1	25	56	1,7482	1,3979	2,4439	0,0380
2	28	60	1,7782	1,4472	2,5733	0,0212
3	29	68	1,8325	1,4624	2,6799	0,0170
4	36	85	1,9294	1,5563	3,0028	0,0013
5	37	86	1,9345	1,5682	3,0337	0,0006
6	43	99	1,9956	1,6335	3,2598	0,0016
7	51	115	2,0607	1,7076	3,5188	0,0131
8	51	118	2,0719	1,7076	3,5379	0,0131
9	52	117	2,0682	1,7160	3,5490	0,0152
10	54	125	2,0969	1,7324	3,6327	0,0195
Итого:	406	929	19,5161	15,9290	31,2316	0,1408
среднее			1,9516	1,5929	3,1232
s2				0,0156

Табл.15

Рассчитаем С и b:

b==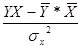

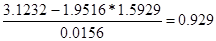
С=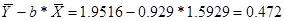

Получим линейное уравнение: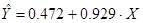

Выполнив его потенцирование, получим: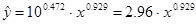  

График построенной модели представлен на рис.16

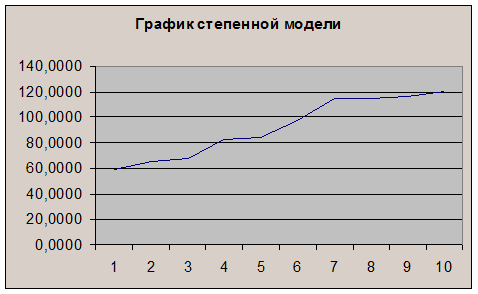
Рис.16

     Построению уравнения показательной кривой y=ab^x также предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:

lg y=lg a+x*lg b   Y=A+Bx, где Y=lg y, B=lgb, А=lg a

В таблицу данных запишем новый столбец Y_i, введём в него функцию, возвращающую десятичный логарифм числа. Для этого выделим столбец Y_i, на панели инструментов выбираем кнопку Вставка функции, в окне Категория выбираем математические , в окне Функция – log10. (рис.17)

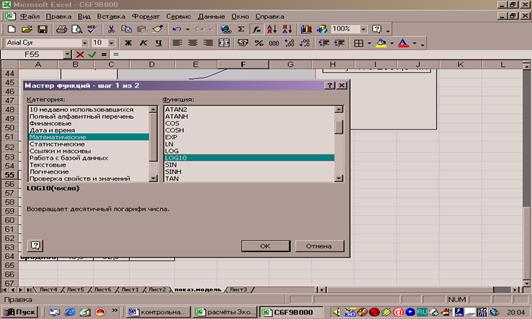Рис.17

Заполняя аргументы функции в графе число выделить столбец у_i.

Далее воспользуемся инструментом анализа данных Регрессия. Для этого в главном меню надо последовательно выбрать Сервис/Анализ данных/Регрессия, щёлкнуть ОК. Заполнить диалоговое окно ввода данных и параметров вывода. Входной интервал У – выделить столбец Y_i, входной интервал Х – выделить столбец х_i , установить соответствующие флажки в диалоговом окне. (рис.18)

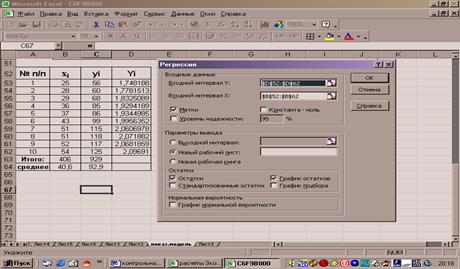
рис.18

     Результаты регрессионного анализа: А=1,5, В=0,01 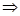 получим линейное уравнение: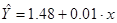

Произведём потенцирование полученного уравнения и запишем его в обычной форме: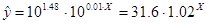

График построенной модели представлен на рис.19

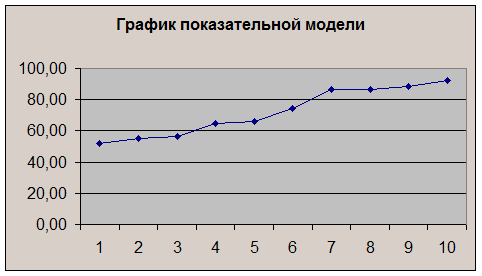
Рис.19

9) Найдём коэффициент детерминации для гиперболической модели 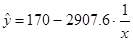, по формуле: R²=1-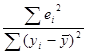. Для расчётов используем данные табл.20

№ п/п	x	y	yпр	ei	ei^2	(yi-ycp)^2
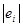
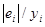
1	25	56	53,7	2,3	5,29	1361,61	2,3	0,0411
2	28	60	66,2	-6,2	38,44	1082,41	6,2	0,1033
3	29	68	69,7	-1,7	2,89	620,01	1,7	0,025
4	36	85	89,2	-4,2	17,64	62,41	4,2	0,0494
5	37	86	91,4	-5,4	29,16	47,61	5,4	0,0628
6	43	99	102,4	-3,4	11,56	37,21	3,4	0,0343
7	51	115	113	2	4	488,41	2	0,0174
8	51	118	113	5	25	630,01	5	0,0424
9	52	117	114,1	2,9	8,41	580,81	2,9	0,0248
10	54	125	116,2	8,8	77,44	1030,41	8,8	0,0704
Итого:	406	929			219,83	5940,9		0,4709
среднее	40,6	92,9

Табл.20

Коэффициент детерминации будет равен: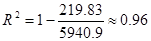

Это значит, что 96%изменений у происходит под влиянием х, если модель гиперболическая. Рассчитаем среднюю относительную ошибку аппроксимации для этой модели, по формуле: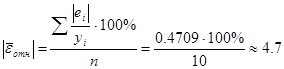

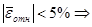 модель адекватна и точна.

Вычислим коэффициент детерминации для степенной модели , для расчётов используем данные таблицы 21.

№ п/п	x	y	yпр	ei	ei^2	(yi-ycp)^2
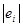
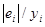
1	25	56	58,88	-2,88	8,30	1361,61	2,88	0,0514
2	28	60	65,42	-5,42	29,36	1082,41	5,42	0,0903
3	29	68	67,59	0,41	0,17	620,01	0,41	0,006
4	36	85	82,62	2,38	5,65	62,41	2,38	0,028
5	37	86	84,75	1,25	1,56	47,61	1,25	0,0145
6	43	99	97,45	1,55	2,40	37,21	1,55	0,0157
7	51	115	114,19	0,81	0,66	488,41	0,81	0,007
8	51	118	114,19	3,81	14,52	630,01	3,81	0,0323
9	52	117	116,27	0,73	0,54	580,81	0,73	0,0062
10	54	125	120,42	4,58	21,01	1030,41	4,58	0,0366
Итого:	406	929			84,17	5940,9		0,2882
среднее	40,6	92,9

Табл.21

Коэффициент детерминации будет равен: R²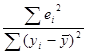=1-=1-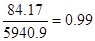

Это значит, что 99% изменений у происходит под влиянием х.

Найдём среднюю относительную ошибку аппроксимации для этой модели:

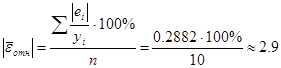
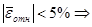 модель адекватна и точна.

Рассчитаем коэффициент детерминации для показательной модели 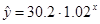, для этого используем данные таблицы 22.

№ п/п	x	y	yпр	ei	ei^2	(yi-ycp)^2
1	25	56	51,84	4,16	17,28	1361,61	4,16	0,0743
2	28	60	55,02	4,98	24,84	1082,41	4,98	0,083
3	29	68	56,12	11,88	141,21	620,01	11,88	0,1747
4	36	85	64,46	20,54	421,87	62,41	20,54	0,2416
5	37	86	65,75	20,25	410,08	47,61	20,25	0,2355
6	43	99	74,04	24,96	622,76	37,21	24,96	0,2521
7	51	115	86,76	28,24	797,77	488,41	28,24	0,2456
8	51	118	86,76	31,24	976,23	630,01	31,24	0,2647
9	52	117	88,49	28,51	812,80	580,81	28,51	0,2437
10	54	125	92,07	32,93	1084,69	1030,41	32,93	0,2634
Итого:	406	929			5309,53	5940,9		2,0787
среднее	40,6	92,9

Табл.22

Таким образом, коэффициент детерминации будет равен: R²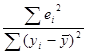=1-=1-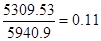 

Это значит, что 11% изменений у происходит под влиянием х, если модель показательная.

Вычислим среднюю относительную ошибку аппроксимации для данной модели: 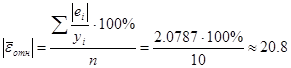 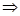 модель неадекватна и не точна.

     Сравнивая модели по коэффициенту детерминации, который показывает тесноту связи между факторами, и средней относительной ошибке аппроксимации, которая определяет точность модели, можно сказать что степенная модель лучше всех описывает взаимосвязь (ее коэффициент детерминации ближе всех к 1 и самая маленькая величина средней относительной ошибки аппроксимации), гиперболическая чуть хуже и очень плохо описывает изучаемую взаимосвязь показательная модель.

Задача 2

      По данным таблицы для своего варианта, используя косвенный метод наименьших квадратов, построить структурную форму модели вида 

y₁= a₀₁  + b₁₂ y₂ +  a₁₁ x₁ + e₁                                                                                                   

y₂= a₀₂  + b₂₁ y₁ + a₂₂ x₂ + e₂

n	y1	y2	x1	x2
1	61,3	31,3	9	7
2	88,2	52,2	9	20
3	38	14,1	4	2
4	48,4	21,7	2	9
5	57	27,6	7	7
6	59,7	30,3	3	13

Решение:

     Для построения модели мы располагаем информацией, представленной в таблице:

n	y1	y2	x1	x2
1	61,3	31,3	9	7
2	88,2	52,2	9	20
3	38	14,1	4	2
4	48,4	21,7	2	9
5	57	27,6	7	7
6	59,7	30,3	3	13
Сумма:	352,6	177,2	34	58
ср.знач:	58,77	29,53	5,67	9,67

     Пусть структурная форма модели (СФМ), исходя из  матрицы парных коэффициентов корреляции есть:

       

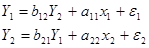
Преобразуем СФМ в приведённую форму:

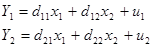      u₁ и u₂ – случайные ошибки

Для каждого уравнения приведённой формы при расчёте коэффициентов d можно применить МНК. Для упрощения расчётов можно работать с отклонениями от средних уровней Y=y-y_cp и X=x-x_cp (y_cp и x_cp – средние

значения). Преобразованные таким образом данные сведены в таблицу 23.

N	Y1	Y2	X1	X2
1	2,53	1,77	3,33	-2,67
2	29,43	22,67	3,33	10,33
3	-20,77	-15,43	-1,67	-7,67
4	-10,37	-7,83	-3,67	-0,67
5	-1,77	-1,93	1,33	-2,67
6	0,93	0,77	-2,67	3,33

Табл.23

     Для нахождения коэффициентов d₁₁ и d₁₂ первого уравнения приведенной формы, решаем следующую систему уравнений:

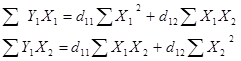
     Необходимые расчёты приведены в таблице 24.

n	Y1	Y2	X1	X2	Y1X1	Y1X2	X1^2	X2^2	X1X2
1	2,53	1,77	3,33	-2,67	8,44	-6,76	11,11	7,11	-8,89
2	29,43	22,67	3,33	10,33	98,11	304,14	11,11	106,78	34,44
3	-20,77	-15,43	-1,67	-7,67	34,61	159,21	2,78	58,78	12,78
4	-10,37	-7,83	-3,67	-0,67	38,01	6,91	13,44	0,44	2,44
5	-1,77	-1,93	1,33	-2,67	-2,36	4,71	1,78	7,11	-3,56
6	0,93	0,77	-2,67	3,33	-2,49	3,11	7,11	11,11	-8,89
Сумма:					174,33	471,33	47,33	191,33	28,33

Табл.24

Подставляя рассчитанные в таблице 24 значения, получим:

174,33=47,33d₁₁+28,33d₁₂

471,33=28,33d₁₁+191,33d₁₂

Решение этих уравнений даёт значения d₁₁=2.4  и d₁₂=2.1. Первое уравнение приведённой формы модели примет вид:

y₁=2.4x₁+2.1x₂

    

     Для нахождения коэффициентов d₂₁ и d₂₂  второго уравнения приведённой формы можно использовать следующую систему нормальных уравнений:

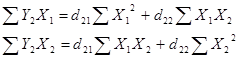
Необходимые расчёты приведены в таблице 25.

n	Y1	Y2	X1	X2	X1^2	X2^2	X1X2	Y2X1	Y2X2
1	2,53	1,77	3,33	-2,67	11,11	7,11	-8,89	5,89	-4,71
2	29,43	22,67	3,33	10,33	11,11	106,78	34,44	75,56	234,22
3	-20,77	-15,43	-1,67	-7,67	2,78	58,78	12,78	25,72	118,32
4	-10,37	-7,83	-3,67	-0,67	13,44	0,44	2,44	28,72	5,22
5	-1,77	-1,93	1,33	-2,67	1,78	7,11	-3,56	-2,58	5,16
6	0,93	0,77	-2,67	3,33	7,11	11,11	-8,89	-2,04	2,56
Сумма:					47,33	191,33	28,33	131,27	360,77

Табл.25

Подставляя рассчитанные значения, получим:

131,27=47,33d₂₁+28,33d₂₂

360,77=28,33d₂₁+191,33d₂₂

Решение этих уравнений даёт значения d₂₁=1.8 и d₂₂=1.6. Второе уравнение приведённой формы модели примет вид:

y₂=1.8x₁+1.6x₂

     Для перехода от приведённой формы к структурной форме, выразим x₂ из второго уравнения приведённой формы и подставим это выражение в первое уравнение приведённой формы. Таким образом будет получено первое уравнение структурной модели.

1,6х₂=у₂-1,8х₁ 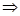  х₂=0,625у₂-1,125х₁

у₁=2,4х₁+2,1(0,625у₂-1,125х₁)

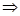
у₁=1,31у₂+0,04х₁ – первое уравнение СФМ

   Из первого уравнения приведённой формы выразим х₁

2,4х₁=у₁-2,1х₂ 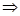   х₁=0,42у₁-0,88х₂

Во второе уравнение приведённой формы подставляем х₁

у₂=1,8(0,42у₁-0,88х₂)+1,6х₂

у₂=0,76у₁+0,02х₂ – второе уравнение СФМ

     Для нахождения свободных членов этих уравнений, то есть для перехода к исходным координатам, воспользуемся уравнениями:

а₀₁=у_1ср-b₁₂ y_{2 cp}-a₁₁ x_{1 cp}= 58.77-1.31*29.53-0.04*5.67=19.86

a₀₂=y_{2 cp}-b₂₁y_{1 cp}-a₂₂ x_{2 cp}= 29.53-0.76*58.77-0.02*9.67=-15.33

Окончательный вид структурной модели: