Задача 4

Дисконтировать 150 у.д.е. на 5 месяцев при простой учетной ставке          d = 0,06 в год. Найти годовую процентную ставку.

Решение

Согласно формуле

P = A (1 - dt),

где  А – накопленная стоимость – по условиям задачи 150 у.д.е.;

Р – начальная стоимость;

d – учетная ставка – по условиям задачи 0,06;

t – период времени – по условиям задачи – 5 месяцев, т.е. 5/12 года.

P = 150 * (1 – 0,06*5/12) = 146,25 у.д.е.

Годовая процентная ставка связана с учетной формулой   i = d / (1 - d).

То есть годовая процентная ставка i = 0,06 / (1 – 0,06) = 0,0638 или 6,38%.

Задача 11

Дано х = 4, y = 4, z = 3.

Вексель с номинальной стоимостью 100*х + 400 у.д.е. (800 у.д.е.) с процентной ставкой (0,1*у + 12)% (12,4%) годовых сроком на z + 70 дней (73 дня) продается через 40 – z дней (37 дней) после подписания векселя банку с учетной ставкой (10 – 0,1*y) % (9,6%) годовых. Найти норму прибыли продавца и банка, если х – номер варианта, y – пятая цифра, z – четвертая цифра зачетной книжки.

Решение

Найдем фактическую стоимость векселя по формуле А = P (1 + it)

А = 800 * (1 + 0,124*73/365) = 819,84.

Чтобы найти цену продажи необходимо дисконтировать фактическую стоимость А по формуле:

P₁ = A (1 - dt) = 819,84 * (1 – 0,096*36/365) = 812,08.

Норма прибыли находится по формуле

a = (С-С_о)*100/(С_о*t),

где С_о – начальная сумма, С – накопленная сумма, t – время накопления.

Тогда норма прибыли продавца

a_п = (Р₁ – 800) / (800*37/365) = (812,08 - 800) / (800*37/365) = 0,149 – 14,9%.

Норма прибыли банка

a_б = (А – Р ₁) / (Р₁*36/365) = (819,84–812,08) / (812,08*36/365) = 0,0969 – 9,69%.

 

Задача 15

Даны две номинальные процентные ставки 11,5% в год сроком на 7 дней и 11,375% сроком на 14 дней. Найти накопление 1 000 000 у.д.е. за два последовательных недельных срока и на один двухнедельный срок.

Решение

По формуле А = Р (1 + h*i_h (t)) находим накопление капитала:

А) за первый недельный срок А₁ = 1000000*(1+0,115*7/365) = 1002205,5

Б) за второй недельный срок А₂ = 1002205,5*(1+0,115*7/365) = 1004415,8

В) за двухнедельный срок А₃ = 1004415,8*(1+0,11375*14/365) = 1008798,08.

То есть общее накопление капитала за два последовательных недельных срока и на один двухнедельный срок равно А₃ = 1008798,08

Задача 25

Сумма 350 у.д.е. инвестируется при силе процента d = at в год. Накопленная стоимость за 4 года начиная с момента t = 2 равна 500 у.д.е. Найти а.

Решение

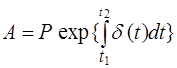
Согласно формуле

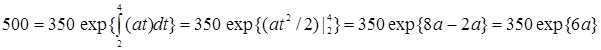
Логарифмируя полученное равенство получим

ln1,429 = 6a, a = 0,357/6 = 0,0595

То есть d = 0,0595*а.

Задача 35

Найти текущую стоимость на момент t = 0 четырех ежегодных выплат в размере 1000 у.д.е., если первая выплата производится в момент t = 2. Сила процента определяется формулой Студли с параметрами р = 0,17; r = 0,6;           s = 0,06.

Решение

Текущую стоимость потока на момент t = 0 определим из выражения

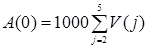
В случае формулы Студли величина V(t) находится из равенства

Подставив исходные данные получим

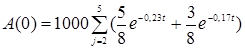
В результате расчетов получим:

V(2) = 0,6615; V(3) = 0,5387; V(4) = 0,439; V(5) = 0,3582

A(0) = 1000 * (0,6615 + 0,5387 + 0,439 + 0,3582) = 1997,4.

Задача 45

Задана сделка в виде дискретного потока наличности

Сtj	-5	-3	6	9
tj	1	2	4	6

где С_tj – доходы или расходы, выраженные условных денежных единицах, соответственно t_j – моменты времени, в которые происходят поступления или выплаты денег. Требуется: а) составить уравнение стоимости; б) определить, имеет ли сделка доходность и вычислить с точностью до одного процента.

Решение

          a) Уравнение стоимости имеет вид

Подставляя исходные данные, получим:

          Упростим данное выражение, умножив обе его части на множитель (1+i)⁶, получим уравнение стоимости:

б) Для того, чтобы определить имеет ли сделка доходность не решая уравнение необходимо определить соответствует ли она двум правилам:

1)     А₁ ¹0, А_n ¹ 0.

2)     После исключения нулевых значений последовательность             А₁, А₂, … А_n имеет ровно одну перемену знака.

При соблюдении этих правил уравнение стоимости имеет ровно один положительный корень.

А₁ = -5; А₂ = -5 – 3 = -8; А₃ = -8 + 6 = -2; А₄ = -2 + 9 = 7.

Таким образом, последовательность {А_i} = {-5; -8; -2; 7} имеет одну перемену знака (вначале идут отрицательные члены, затем положительный), причем А₁ ¹0, А₄ ¹ 0. Сделка имеет доходность.

Найдем ее. Воспользуемся методом бисекции или деления отрезка пополам. Введем функцию:

Решение уравнения будем искать при i > 0. Находим сначала интервал, на концах которого функция f(i) принимает значения противоположных знаков. Тогда, корень i₀ находится внутри найденного интервала. Такой интервал находится подбором.

f(0) = -5-3+6+9 = 7 > 0; f(0,5) = -2,7 < 0.

Следовательно, в качестве исходного интервала можно взять (0; 0,5). Найдем середину этого интервала i₁ = 0,25 и вычислим f(0,25) = -1,1. Теперь из двух интервалов (0; 0,25) и (0,25; 0,5) выберем тот, на концах которого функция f принимает значения различных знаков. Это интервал (0; 0,25). Повторяя этот процесс выберем середину i₂ = 0,125 и найдем f(0,125) = 1,37 >0.

Аналогично новый интервал будет (0,125; 0,25). Его середина i₃ = 0,188, а f(0,188) = -0,111<0.

Следующий интервал (0,125; 0,188): середина i₄ =0,156, f(0,156)=0,555 > 0.

Следующий интервал (0,156; 0,188): середина i₅ =0,172, f(0,172)=0,205 > 0.

Следующий интервал (0,172; 0,188). Длина данного интервала 0,016. Поэтому, если в качестве приближенного значения i₀ взять середину интервала, то погрешность будет меньше половины, то есть меньше 0,008 и, следовательно, меньше заданного 1%.

Итак, i₀ = (0,172+0,188)/2 = 0,18. Доходность сделки равна 18%.