СОДЕРЖАНИЕ
Задача
1. 2
Задача
2. 3
Задача
3. 4
Задача
4. 5
Задача
5. 7
СПИСОК
ЛИТЕРАТУРЫ.. 9
ВАРИАНТ
2
Задача 1
За отчетный квартал потребление топлива на производственные нужды по
предприятию следующее: уголь – 1200 т, газ – 380 тыс. м3, нефть –
210 т. Определить, какую долю в общем объеме потребленного топлива занимает
уголь, если коэффициенты пересчета в условное топливо следующие: уголь – 0,9 т;
газ – 1,2 тыс. м3, нефть – 1,3 т.
Решение
Условное топливо – энергетический эквивалент различных видов горючих
ископаемых, выражаемый в тоннах условного топлива и допускающий возможность их
сопоставления и сложения.
Пересчитаем потребление топлива на производственные нужды по предприятию в
условное топливо:
─ уголь: 1200*0,9 = 1080 т усл. топлива
─ газ: 380*1,2 = 456 т усл. топлива
─ нефть: 210*1,3 = 273 т усл. топлива
Общий объем потребленного топлива в условных единицах составит:
1080+456+273 = 1809 т усл. топлива
Долю (удельный вес) составных частей целого в их общем итоге
характеризуют показатели структуры и обычно выражаются в виде коэффициентов
(доли единиц) или процентах.
Потребление угля в общем объеме потребленного топлива составило:
1080/1809 = 0,597, или 59,7 %
Задача 2
Имеются данные о себестоимости транспортной работы по автотранспортным
предприятиям объединения.
|
№ предприятия,
входящего в объединение
|
Август
|
Сентябрь
|
|
Транспортная
работа, тыс. т-км
|
Себестоимость 10
т-км, руб.
|
Общая сумма затрат
на транспортную работу, тыс. руб.
|
Себестоимость 10
т-км, руб.
|
|
1
2
3
|
20800
8500
30000
|
0,512
0,540
0,497
|
10784,7
4609,6
14526,2
|
0,521
0,536
0,481
|
Определить, на сколько процентов изменилась средняя себестоимость 10 т-км
по объединению в сентябре по сравнению с августом.
Решение
Необходимо найти среднюю себестоимость 10 т-км по объединению в августе и
сентябре.
Вид и форма средней выбирается исходя из экономического содержания
исчисленного показателя. В условии
задачи имеются данные об объеме транспортной работы и себестоимости 10
т-км, то исходя из экономического содержания показателя для определения средней
себестоимости 10 т-км по объединению за август, применяется средняя арифметическая
взвешенная:
,
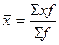(1)
где х – себестоимость 10 т-км,
f – транспортная работа.
Средняя себестоимость 10 т-км по объединению за август составит:
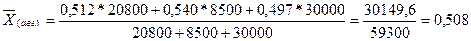руб.
Так как по условию задачи отсутствуют данные о частоте появления
признака, но имеется информация об общем значении признака (общей сумме затрат на
транспортную работу), то для расчета средней себестоимости 10 т-км по
объединению за сентябрь применяем формулу средней гармонической взвешенной:
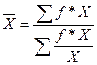(2)
Средняя себестоимость 10 т-км по объединению за сентябрь составит:
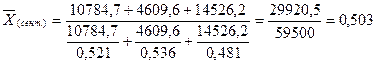руб.
Чтобы определить, на сколько процентов изменилась средняя себестоимость
10 т-км по объединению в сентябре по сравнению с августом, нужно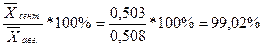 
Таким образом, в сентябре по сравнению с августом средняя себестоимость
10 т-км по объединению снизилась на 0,98%.
Задача 3
С целью определения средних затрат времени при поездках на работу
населением города планируется выборочное наблюдение на основе случайного
повторного отбора. Сколько людей должно обследовано, чтобы с вероятностью 0,954
ошибка выборочной средней не превышала 1 мин. при среднем квадратическом
отклонении 15 мин?
Решение
Численность случайной повторной выборки определяется по следующей
формуле:
,
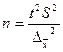(3)
где t – гарантийный коэффициент, при вероятности
0,954 t = 2;
S – среднее квадратическое отклонение признака в
выборочной совокупности; S = 15 мин.;
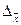– ошибка выборочной средней; 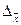= 1 мин.
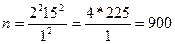людей
Таким образом, с целью определения средних затрат времени при поездках на
работу населением города должно быть обследовано 900 людей.
Задача 4
Динамика объема реализации услуг коммунальных предприятий города в
процентах к 1993 г. составила: 1994 г. – 108,0; 1995 г. – 110,5; 1996 г. –
125,0; 1997 г. – 153,2.
Определить: а) коэффициенты роста для 1996 и 1997 гг. по сравнению с 1995
г.; б) среднегодовой темп прироста за период 1993 – 1997 гг.
Решение
а) Темп (коэффициент) роста (Тр) – это соотношение
последующего уровня ряда к предыдущему (цепные темпы роста) или постоянному,
принятому за базу сравнения (базисные темпы роста):
Цепные коэффициенты (темпы) роста
рассчитываются по формуле:
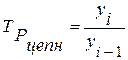(4)
Базисные коэффициенты (темпы) роста
рассчитываются по формуле:
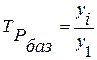, (5)
По условию задачи известны следующие
данные:
Тр1994/1993 = 108,0 %; Кр1994/1993
= 1,08
Тр1995/1993 = 110,5 %; Кр1995/1993
= 1,105
Тр1996/1993 = 125,0 %; Кр1996/1993
= 1,25
Тр1997/1993 = 153,20 %; Кр1997/1993
= 1,532
Между показателями динамики,
вычисленными с постоянной и переменной
базой, существует определенная связь. Может быть осуществлен переход от коэффициентов
роста с постоянной базой к коэффициентам роста с переменной базой и
наоборот.
Если известны коэффициенты роста с
постоянной базой, то частные от последовательного деления этих коэффициентов
равны соответствующим коэффициентам роста с переменной базой:
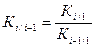(6)
Определим коэффициенты роста для 1996 и 1997
гг. по сравнению с 1995 г.:
Кр1996/1995 =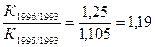 
Кр1997/1995 =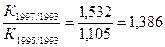 
б) Средний темп прироста показывает, на сколько процентов изменился
уровень ряда в среднем за данный период. Средний темп прироста выражается в
коэффициентах или процентах.
Среднегодовой темп прироста определяется по формуле:
,
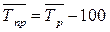(7)
где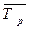 
– среднегодовой темп роста.
Среднегодовой темп роста определяется по формуле:
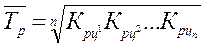, (8)
где Крц1, Крц2,
Крцn–
цепные коэффициенты роста.
Определим среднегодовой темп роста за период 1993 – 1997 гг.:
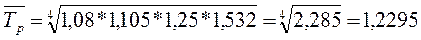, или 122,95 %
Тогда среднегодовой темп прироста за период 1993 – 1997 гг.составит:
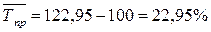
Задача 5
Известны следующие данные по промышленному предприятию за два года:
|
Вид продукции
|
Произведено, тыс.
шт.
|
Среднесписочное
число рабочих, чел.
|
Оптовая цена 1996
г., тыс. руб.
|
|
1996
|
1997
|
1996
|
1997
|
|
1
2
|
18,5
24,2
|
19,3
23,9
|
46
43
|
50
45
|
75
54
|
Определите: а) индекс физического объема продукции; б) индекс
производительности труда; в) индекс затрат труда.
Решение
а) Индекс физического объема продукции определяется по формуле:
,
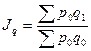(9)
где q0,
q1 – объем
выпуска продукции соответственно базисного и отчетного периодов;
р0 – оптовая
цена продукции базисного года (1996
г.).
Индекс физического объема продукции составит:
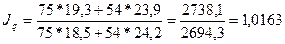
Объем выпуска двух видов продукции
в среднем увеличился в 1997 году на 1,63 % по сравнению с 1996 годом.
б) Индекс производительности труда одного рабочего определяется по
формуле:
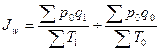, (10)
где Т0, Т1 –
затраты труда, единица измерения – среднесписочная численность рабочих.
Индекс производительности труда на
одного рабочего составит:
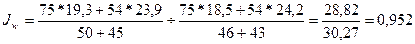
Производительность труда одного рабочего по двум видам продукции в
среднем снизилась в 1997 году на 4,8 % по
сравнению с 1996 годом.
в) Индекс затрат труда определяется по формуле:
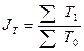(11)
Индекс затрат труда составит:
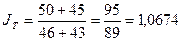
Затраты труда (численность рабочих) по двум видам продукции в среднем
увеличились в 1997 году на 6,74% по сравнению с 1996 годом.
СПИСОК ЛИТЕРАТУРЫ
1. Гусаров В.М. Теория статистики. – М.: ЮНИТИ, 1998. – 448 с.
2. Давыдова Л. А. Теория статистики в вопросах и ответах: Учебное
пособие. – М.: Издательство ТК Велби, 2005. – 160 с.
3. Елисеева И.И., Юзбашев М.М. Общая теория статистики. – М.: Финансы и
статистика, 1998. – 368 с.
4. Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. –
М.: ИНФРА-М. 2002. – 416 с.
5. Теория статистики / Под редакцией Шмойловой Р. А. – М.: Финансы и статистика,
2002. – 576 с.