ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Филиал в г.Уфа
Лабораторная работа
По дисциплине: «Эконометрика»
Вариант темы № 6
«Анализ деятельности предприятий одной отрасли РФ-2»
Уфа, 2008 г.
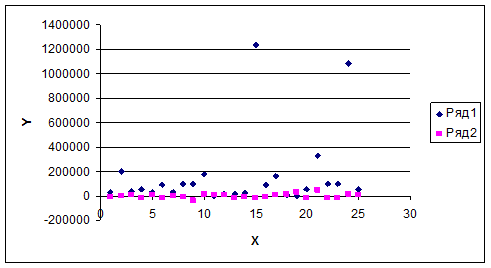
1.6 По данным, представленным в табл. 2.6 (n=25), изучается зависимость объема выпуска продукции Y (млн.руб) от следующих факторов (переменных):
Х1-численность промышленно-производственного персонала, чел.;
Х2-среднегодовая стоимость основных фондов,млн.руб.;
Х3-износ основных фондов,%
Х4-электровооруженность, кВт*ч;
Х5-техническая вооруженность одного рабочего, млн.руб.;
Х6-выработка товарной продукции на одного работающего, руб; Таблица 2.6
|
№ наблюдения |
Y |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
|
1 |
32900 |
864 |
16144 |
39,5 |
4,9 |
3,2 |
36354 |
|
2 |
203456 |
8212 |
336472 |
46,4 |
60,5 |
20,4 |
23486 |
|
3 |
41138 |
1866 |
39208 |
43,7 |
24,9 |
9,5 |
20866 |
|
4 |
57342 |
1147 |
63273 |
35,7 |
50,4 |
34,7 |
47318 |
|
5 |
27294 |
1514 |
31271 |
41,8 |
5,1 |
17,9 |
17230 |
|
6 |
94552 |
4970 |
86129 |
49,8 |
35,9 |
12,1 |
19025 |
|
7 |
28507 |
1561 |
48461 |
44,1 |
48,1 |
18,9 |
18262 |
|
8 |
97788 |
4197 |
138657 |
48,1 |
69,5 |
12,2 |
23360 |
|
9 |
101734 |
6696 |
127570 |
47,6 |
31,9 |
8,1 |
15223 |
|
10 |
175322 |
5237 |
208900 |
58,6 |
139,4 |
29,7 |
32920 |
|
11 |
2894 |
547 |
6922 |
70,4 |
16,9 |
5,3 |
5291 |
|
12 |
16649 |
710 |
8228 |
37,5 |
17,8 |
5,6 |
23125 |
|
13 |
19216 |
940 |
18894 |
62 |
27,6 |
12,3 |
20848 |
|
14 |
23684 |
3528 |
27486 |
34,4 |
13,9 |
3,2 |
6713 |
|
15 |
1237132 |
52412 |
1974472 |
35,4 |
37,3 |
19 |
22581 |
|
16 |
88569 |
4409 |
162229 |
40,8 |
55,3 |
19,3 |
20522 |
|
17 |
162216 |
6139 |
128731 |
48,1 |
35,1 |
12,4 |
26396 |
|
18 |
10201 |
802 |
6714 |
43,4 |
14,9 |
3,1 |
13064 |
|
19 |
3190 |
442 |
478 |
43,2 |
0,2 |
0,6 |
6847 |
|
20 |
55410 |
2797 |
60209 |
57,1 |
37,2 |
13,1 |
20335 |
|
21 |
332448 |
10280 |
540780 |
51,5 |
74,45 |
21,5 |
32339 |
|
22 |
97070 |
4560 |
108549 |
53,6 |
32,5 |
13,2 |
20675 |
|
23 |
98010 |
3801 |
169995 |
60,4 |
75,9 |
27,2 |
26756 |
|
24 |
1087322 |
46142 |
972349 |
50 |
27,5 |
10,8 |
23176 |
|
25 |
55004 |
2535 |
163695 |
25,5 |
65,5 |
19,9 |
21698 |
Задание:
1. Построить матрицу парных коэффициентов корреляции. Установить, какие факторы мультиколлинеарны.
2. Построить уравнение множественной регрессии в линейной форме с полным набором факторов.
3. Оценить статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.
4. Используя пошаговую множественную регрессию (метод исключения или метод включения), построить модель регрессии за счет значимых факторов. Оценить качество уравнения регрессии с помощью коэффициента детерминации.
5. Рассчитать прогнозные значения результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
Решение:
1) Построим матрицу парных коэффициентов корреляции с использованием инструмента Корреляция.
Для проведения корреляционного анализа выполним следующие действия:
1. EXCEL => команда Сервис => Анализ данных.
2. В диалоговом окне Анализ данных выберем инструмент Корреляция. Таблица 1
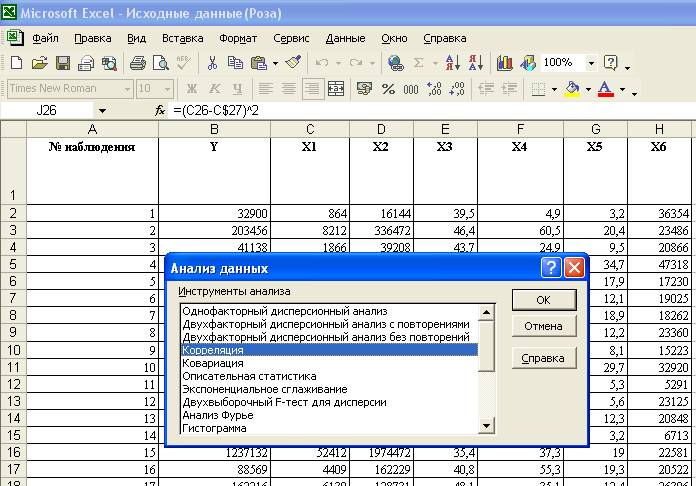
3. В диалоговом окне Корреляция в поле Входной интервал необходимо ввести диапазон ячеек, содержащих исходные данные.
4. Выберем параметры вывода =>ОК. Таблица 2
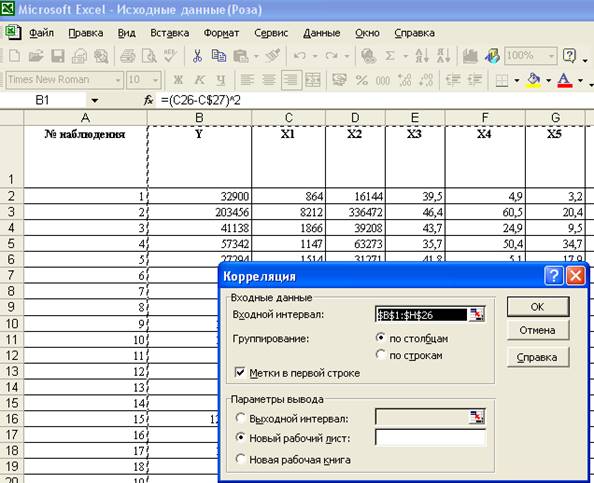
Таблица 3
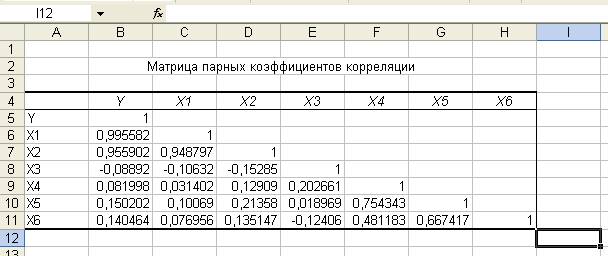
Таблица 3.1
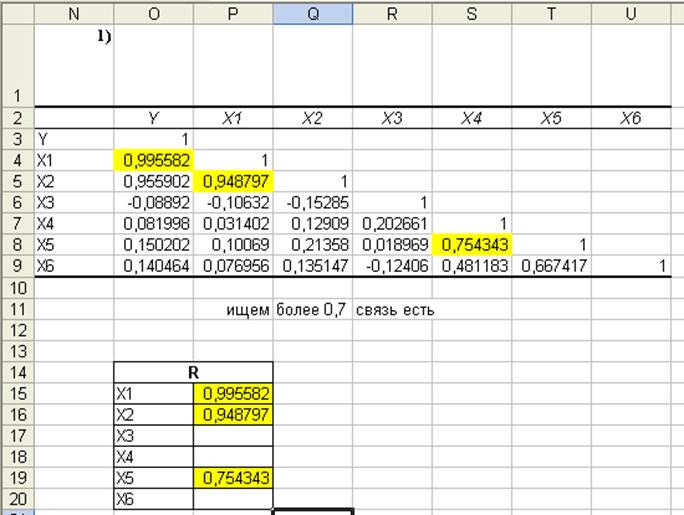
Так как Rx1x2 = 0,949>0,7 , то x1 и x2 факторы коллинеарные.
Так как Rx4x5 = 0,754>0,7 , то x4 и x5 факторы коллинеарные.
2) Построим уравнение множественной регрессии в линейной форме с полным набором факторов.
Для проведения регрессионного анализа выполним следующие действия:
1. EXCEL => команда Сервис => Анализ данных.
2. В диалоговом окне Анализ данных выберем инструмент Регрессия
3. В диалоговом окне Регрессия в поле Входной интервал Y вводим адрес одного диапазона ячеек, который представляет зависимую переменную. В поле Входной интервал X вводим адреса диапазонов, которые содержат значения независимых переменных.
4. Выберем параметры вывода =>ОК.
Таблица 4
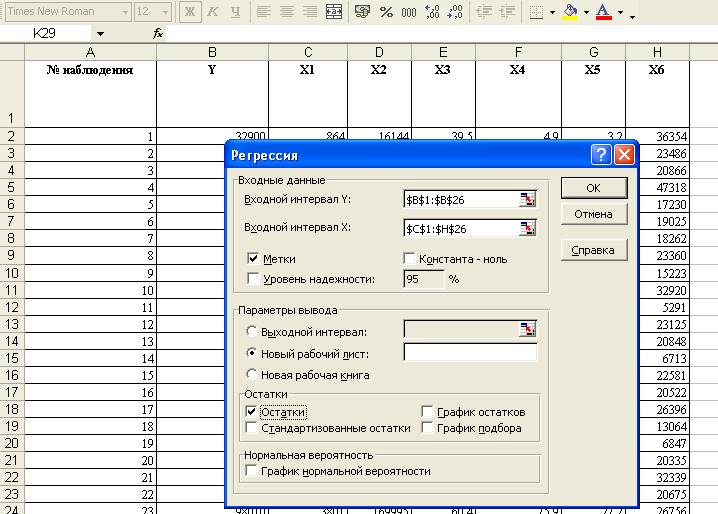
Таблица 5
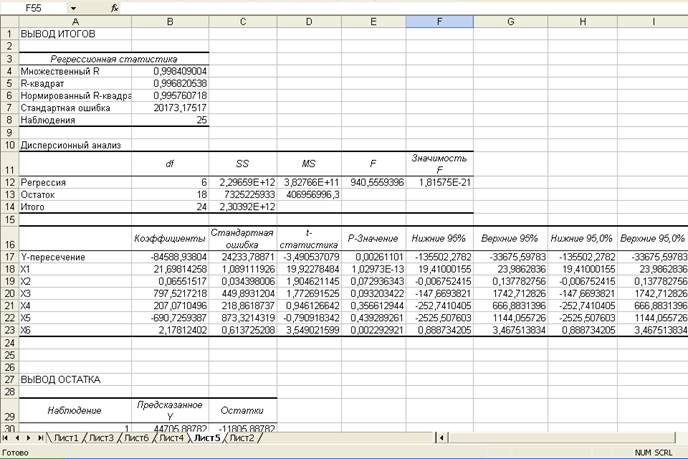
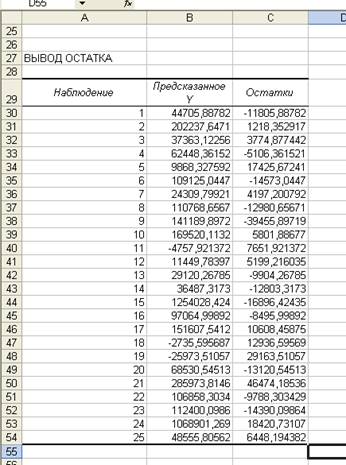
Регрессионный анализ
Во втором столбце таблицы 5 содержатся коэффициенты уравнения регрессии а0, а2, а3 а4. В третьем столбце содержатся стандартные ошибки коэффициентов уравнения регрессии, а в четвертом – t – статистика, используемая для проверки значимости коэффициентов уравнения регрессии. Уравнение регрессии зависимости у от х можно записать в следующем виде:
y=-84588,938+21,698X1+0,065X2+797,522X3+207,071X4-690,726X5+2,178X6
3) Оценим статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента:
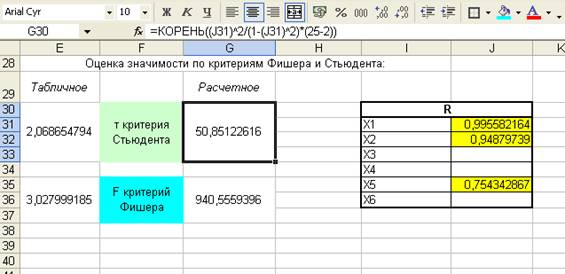
Табличное значение t-критерия Стьюдента находим с помощью функции СТЬЮДРАСПОБР:
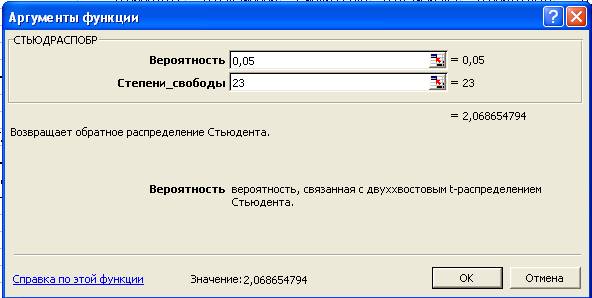
Расчетное
значение t-критерия Стьюдента находим по формуле: ![]()
Оценим значимость факторов с помощью Т–критерия Стьюдента, для этого, определим его табличное значение при уровне значимости 0,05.
Df =n-k-1=
Сравним расчетные значения с табличным по модулю: если t-расч.>t -табл., то фактор считается статистически значимым, и наоборот.
Табличное значение F-критерия Фишера находим с помощью функции FРАСПОБР:
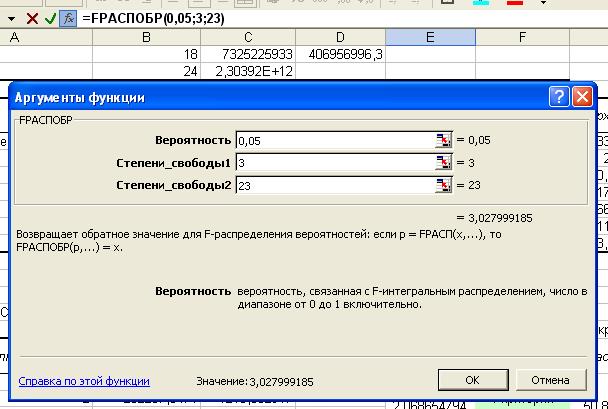
Расчетное значение берем из дисперсионного анализа:
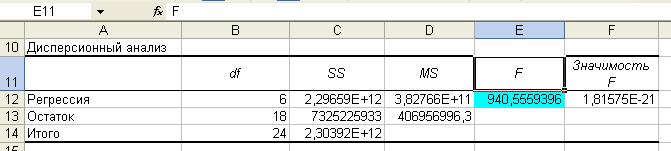
Так как Fрасч. > Fтабл. (940,5 > 3,03), то уравнение регрессии можно признать статистически значимым (адекватным).
4) Используя пошаговую множественную регрессию (метод исключения), строим модель регрессии за счет значимых факторов.
Для значимых факторов проводим регрессионный анализ.
Действие первое. Х5 исключаем, т.к. он не значим (-690,726<t-табл.=2,068655).
Проводим регрессионный анализ:
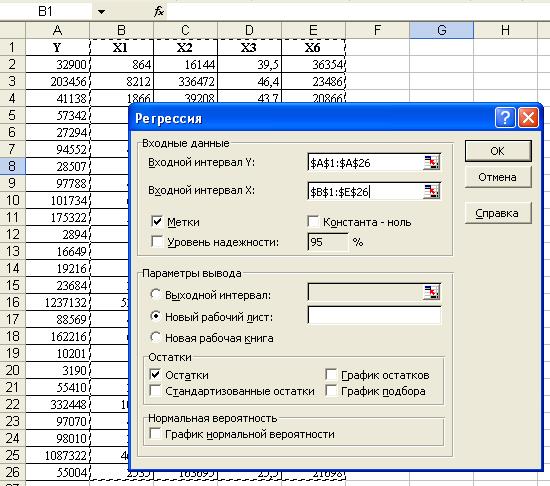
В диалоговом окне Регрессия в поле Входной интервал Y вводим адрес одного диапазона ячеек, который представляет зависимую переменную. В поле Входной интервал X вводим адреса диапазонов, которые содержат значения независимых переменных.
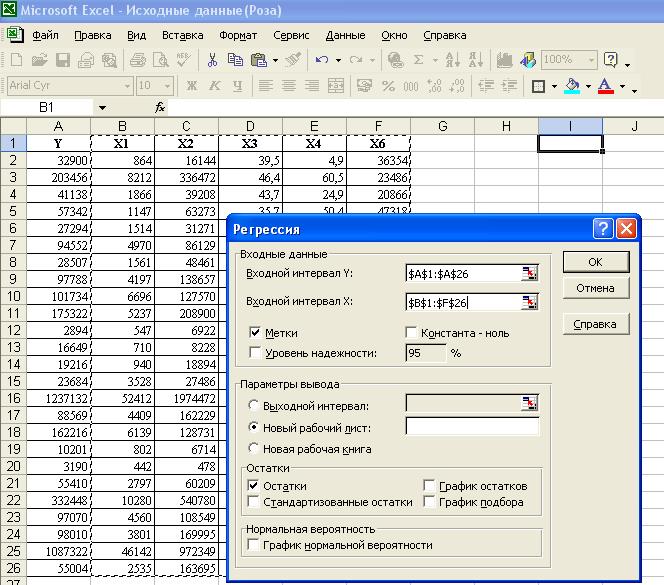
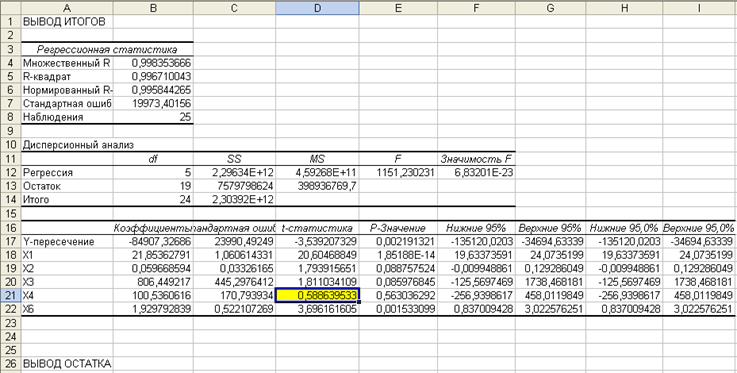
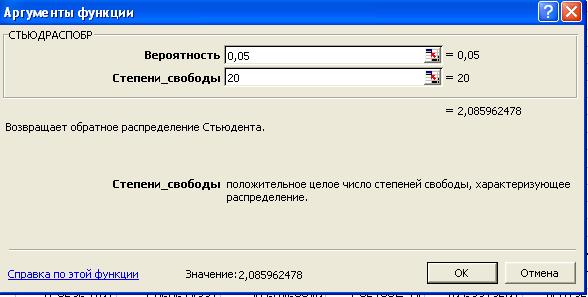
Сравниваем значения t-статистики с t-критерием Стьюдента (х4=0,58864<2.0859625),
Действие второе. Исключаем незначимый фактор Х4 и снова проводим регрессионный анализ:
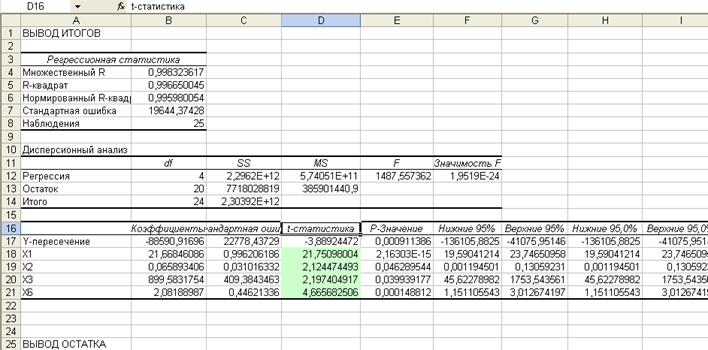
Сравниваем значения t-статистики с t-критерием Стьюдента (2,085965), все факторы значимы.
Уравнение регрессии за счет значимых факторов будет иметь вид:
y=-88590,917+21,668X1+0,066X2+899,583X3+2,082X6
Коэффициент детерминации равен 0,99665, близок к 1 , модель можно считать качественной.
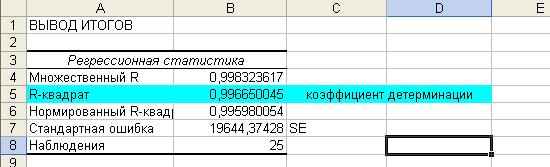
5) Рассчитаем прогнозные значения результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
Находим транспонированную матрицу:
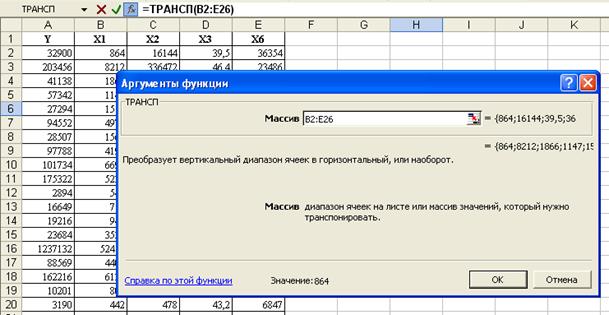
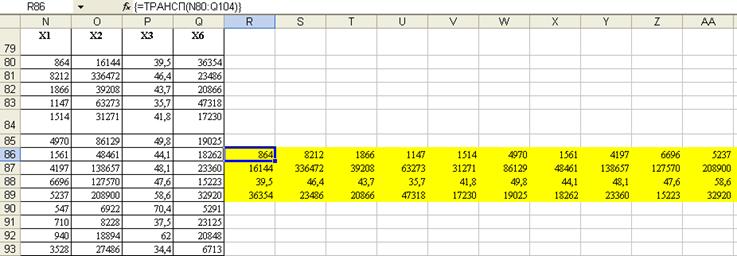
Находим (ХтХ):
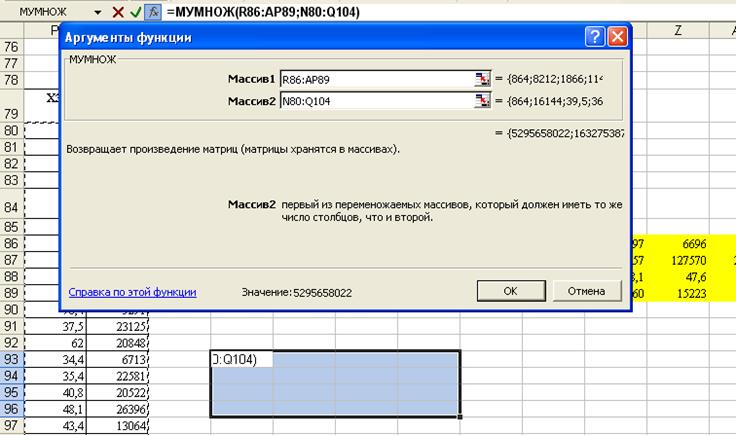
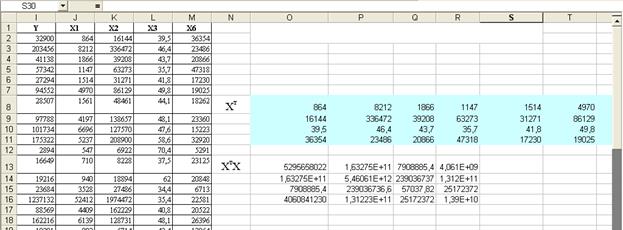
Находим обратную матрицу:
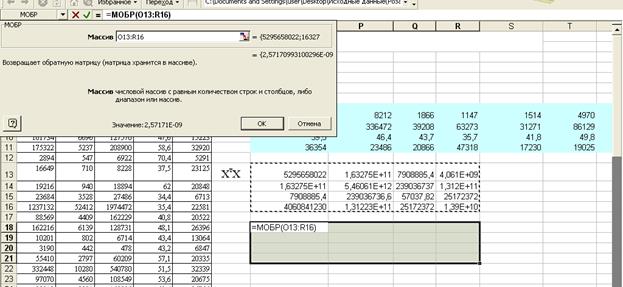
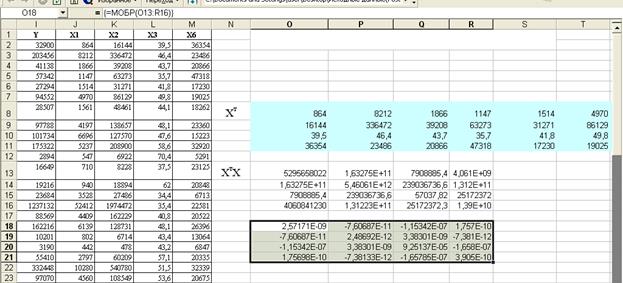
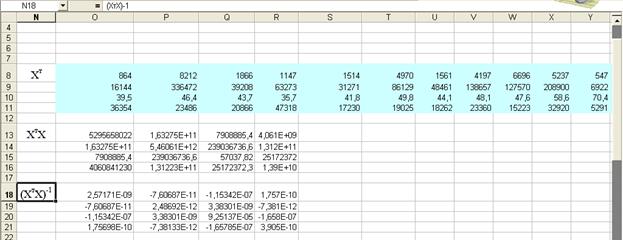
Находим прогнозные значения результата, если прогнозные значения факторов составляют 80% от их максимальных значений: Хпрогн = Хmax*0.8
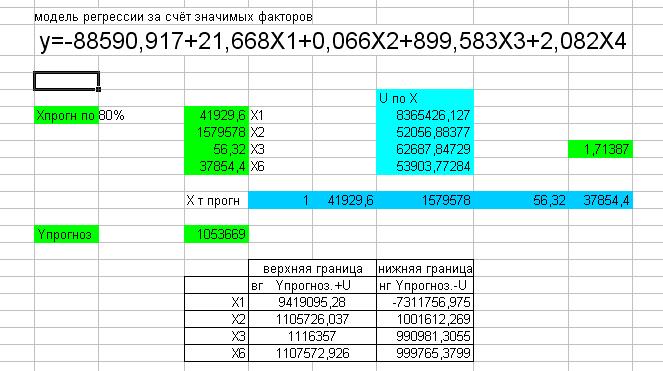
Yр(N+l) = y=
-88590,917+21,668*41929,6+0,066*1579578+899,583*56,32+2,082*37854,4=1053669,1
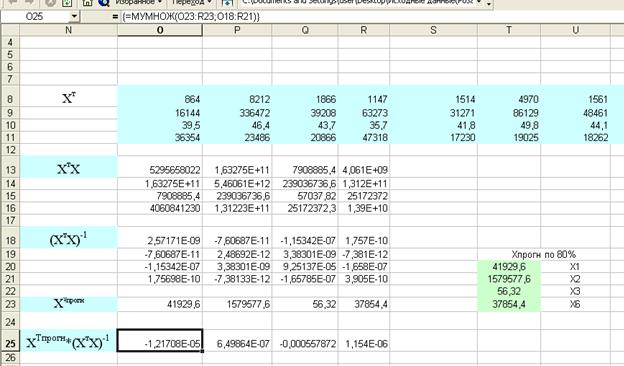
Затем используя
формулу: U(1)=setкp![]() , находим доверительный
интервал:
, находим доверительный
интервал:
1. разбив формулу на несколько частей сначала найдем:
ХТпрогн*(ХтХ)-1 * Хпрогн(по 80%)
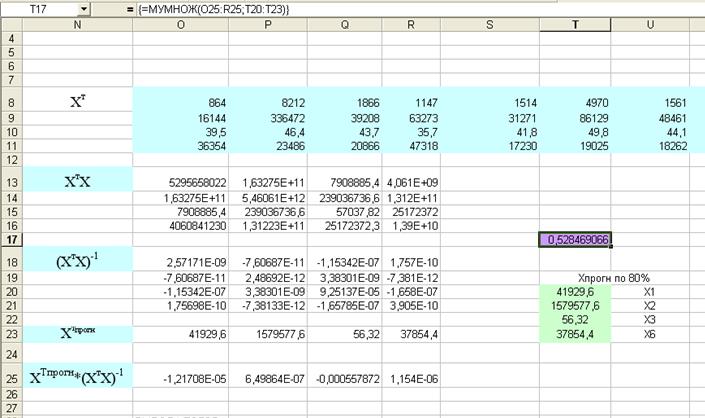
Ответ: 0,528469066
2. затем находим: ![]()
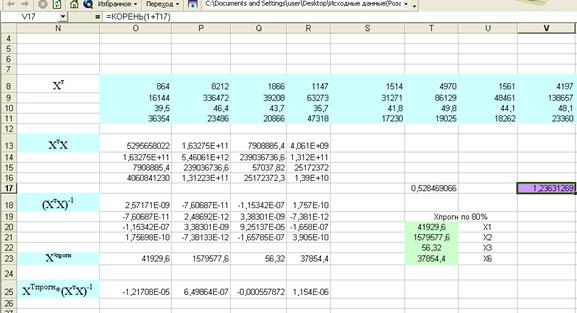
Ответ: 1,23631269
3.
находим: tкp![]()
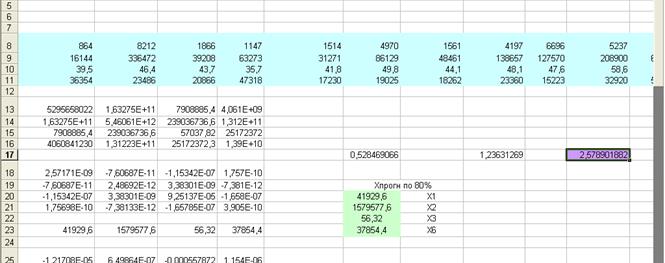
Ответ: 2,578901882
4. Находим: setкp![]()
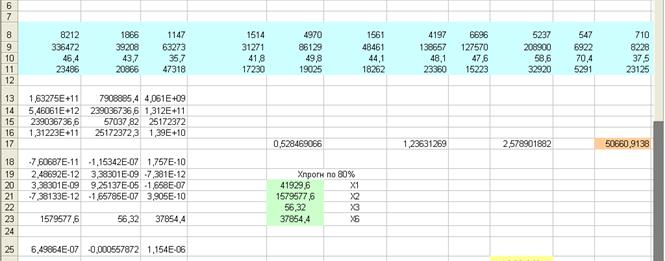
Ответ: 50660,9138
Yр(N+l) = y=
-88590,917+21,668*41929,6+0,066*1579578+899,583*56,32+2,082*37854,4=1053669,1
Доверительный интервал прогноза будет иметь следующие границы:
Верхняя граница прогноза: Yр(N+l)+ U(1)= 1053669,1+50660,9138=1104330,014
Нижняя граница прогноза: Yр(N+l) - U(1)= 1053669,1-50660,9138=1003008,186
|
Упреждение |
Прогноз |
Нижняя граница |
Верхняя граница |
|
1 |
1053669,1 |
1003008,186 |
1104330,014 |