Министерство образования РФ
Всероссийский заочный финансово-экономический институт
Кафедра статистики
Курсовая работа
по дисциплине «Статистика»
на тему
«Статистические методы изучения цен и инфляции»
Исполнитель:
__________________
Специальность:
___________________
Группа: ___________________
№ зачетной книжки:
___________________
Руководитель:
___________________
Барнаул 2008 ГодВведение
Статистика
цен входит составной частью в социально-экономическую статистику, она изучает
всю систему цен, действующую в сфере экономических отношений.
Цена
является важнейшим стоимостным измерителем. Цену как объект изучения статистики
цен следует рассматривать с позиций макро- и микроэкономики. С позиций
макроэкономики на цену воздействуют отраслевые пропорции, системы
распределения национального дохода, налогообложения и кредитования, порядок
формирования затрат и т.д. С микроэкономических позиций цена рассматривается
как механизм, функционирующий на уровне конкретного предприятия, фирмы, с
помощью которого можно обеспечить прибыль.
Объектом
данной курсовой работы является статистика цен и инфляции. Ее предмет – методы
статистического изучения цен и инфляции .
Цель
исследования – рассмотреть статистические методы изучения цен и инфляции.
Задачи:
-
Изучить имеющийся монографический и
учебный материал по данной проблеме;
-
Дать характеристику понятиям «цены» и
«инфляция»;
-
Проанализировать статистические методы
изучения цен и инфляции;
-
Сделать
необходимые для решения экономической задачи расчеты;
-
По данным расчетного задания построить
различные графики и таблицы;
-
Провести статистическое исследование с
применением компьютерной техники и методов, освоенных при выполнении расчетной
задачи.
Оглавление
Введение…………………………………………….....……………......…..…..3
Теоретическая часть…...…………………………...……………………....5
1. Статистика цен и
инфляции...........................................…………………....5
1.1. Понятие статистики цен............ ………………….....................………...5
1.2. Понятие инфляции…………......................................................................7
2. Статистические методы изучения цен
и инфляции………....….…….….11
2.1. Метод статистической
сводки.................................................................11
2.2. Метод группировки…………………………………………....…..…...12
2.3. Индексный метод..……………………………………………..….……15
2.4. Графический
метод..................................................................................19
3. Вывод по
методам.........................................................................................20
Расчетная часть..............................................................................................22
Аналитическая
часть:
Анализ динамики цен на говядину......................................................................33
Заключение.........................................................................................................38
Список
литературы............................................................................................39
Теоретическая часть. Доработка
Определение сводных индексов по формуле с рекурсивной системой
расчета идентично расчетам по агрегатной форме с постоянными весами. Например,
если стоимостной объем брать за декабрь предыдущего года, то в нем
можно выделять цену и количество q0, имея
временной ряд базисных индексов, можно получить временной
ряд цепных индексов.
При этом в программном обеспечении расчетов
сводных индексов цен в основном используется не абсолютная величина стоимостных объемов товарных групп, а их удельный вес. Пример
расчета с условными данными приведен в табл.1.
•
Таблица
11 [6, 123]
Динамика
потребительских цен по группам товаров
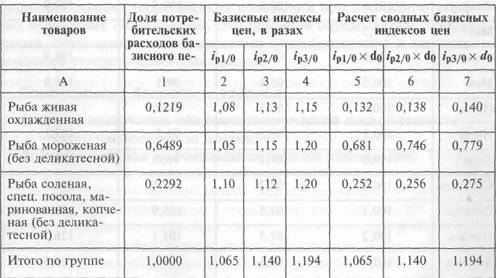
Сводные индексы цен текущего месяца к предыдущему (цепные) определяются
делением каждого текущего индекса на предыдущий базисный
индекс. В приведенном примере цепные индексы цен равны:
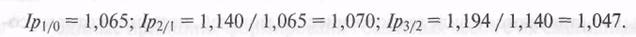
Суммарные стоимостные или удельные веса,
используемые в расчетах сводных индексов в производственном и потребительском
секторах, в отечественной статистике ежегодно обновляются,
поскольку на данном этапе для российской экономики характерны
существенные структурные изменения в производстве и
потреблении товаров.
Месячные индексы цен, рассчитанные к
декабрю предыдущего года, используются при определении
месячных, квартальных, полугодовых и годовых.
3. Вывод по методам
К числу особенностей
статистического анализа данных о ценах и инфляции следует отнести метод
массового наблюдения, научной обоснованности качественного содержания группировок
и его результатов, вычисление и анализ обобщенных и обобщающих показателей цен
и инфляции. Что касается конкретных методов экономической, промышленной или
статистики культуры, населения, национального богатства и т.п., то здесь могут
быть свои специфические методы сбора, группировки и анализа соответствующих
совокупностей (суммы фактов). В экономической статистике, например, широко
применяется балансовый метод как наиболее распространенный метод взаимной
увязки отдельных показателей в единой системе экономических связей в
общественном производстве. К методам применяемых в экономической статистике
также относятся составление группировок, исчисление относительных показателей
(процентное соотношение), сравнения, исчисление различных видов средних величин,
индексов и т.п. Метод связующих звеньев состоит в том, что два объемных, т.е.
количественных показателя сопоставляются на основе существующего между ними
отношения. Кроме названных методов широкое распространение получили
математико-статистические методы исследования, которые расширяются по мере
движения масштабов применения ЭВМ и создания автоматизированных систем.
Самым надёжным и
доступным методом измерения
инфляционных процессов считается индексный метод.
В связи с применением индексного метода
возникают методологические проблемы:
§ способ расчета индексов;
§ методика статистики цен для
построения и корректировки
индексов;
§ отбор базовых показателей за период,
охваченный анализом;
§ пересчёт выделяемых
показателей из фактических в
постоянные цены, используя соответствующий индекс цен.
Расчетная
часть
Имеются следующие выборочные данные по
торговым точкам города (выборка 15%-ная механическая):
|
№
п/п
|
Цена за единицу товара, руб.
|
Количество
проданного
товара,
тыс.шт.
|
№
п/п
|
Цена за единицу товара, руб.
|
Количество
проданного
товара,
тыс.шт.
|
|
1
|
25
|
31
|
16
|
28
|
21
|
|
2
|
28
|
24
|
17
|
21
|
28
|
|
3
|
16
|
45
|
18
|
18
|
38
|
|
4
|
24
|
26
|
19
|
27
|
20
|
|
5
|
32
|
28
|
20
|
26
|
22
|
|
6
|
20
|
33
|
21
|
25
|
38
|
|
7
|
22
|
44
|
22
|
17
|
35
|
|
8
|
26
|
29
|
23
|
19
|
28
|
|
9
|
23
|
25
|
24
|
20
|
39
|
|
10
|
16
|
48
|
25
|
22
|
26
|
|
11
|
23
|
31
|
26
|
26
|
33
|
|
12
|
28
|
27
|
27
|
18
|
43
|
|
13
|
17
|
23
|
28
|
21
|
22
|
|
14
|
19
|
44
|
29
|
24
|
26
|
|
15
|
25
|
29
|
30
|
27
|
26
|
Задание 1
По
исходным данным:
1.
Постройте
статистический ряд распределения организаций (предприятий) по признаку - цена
товара, образовав четыре группы с равными интервалами.
2.
Рассчитайте
характеристики интервального ряда распределения: среднюю арифметическую,
среднее квадратическое отклонение, коэффициент вариации, моду и медиану.
Сделайте
выводы по результатам выполнения задания.
Решение
1. Для
того, чтобы произвести группировку необходимо вычислить величину
группировочного интервала по формуле: 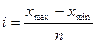 , где хmax
и xmin максимальное
и минимальное значения цены товара, n -
число образуемых групп.
, где хmax
и xmin максимальное
и минимальное значения цены товара, n -
число образуемых групп.
Величина
группировочного интервала будет равна: 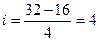 руб.
руб.
Образуем
группы, которые отличаются друг от друга по цене товара на данную величину (4
руб.):
Первая
группа будет иметь размеры: 16+4=20 руб.
Вторая
группа будет иметь размеры: 20+4=24 руб.
Третья
группа будет иметь размеры: 24+4=28 руб.
Четвертая
группа будет иметь размеры: 28+4=32 руб.
Группировку
данных по торговым точкам произведем в рабочей таблице 2.2.
Таблица 2.2.
Рабочая таблица с группировкой
|
Группы
|
Группы по цене товара,
руб.
|
№ п/п
|
Цена за единицу товара,
руб.
|
|
I
|
16-20
|
3
|
16
|
|
|
|
6
|
20
|
|
|
|
10
|
16
|
|
|
|
13
|
17
|
|
|
|
14
|
19
|
|
|
|
18
|
18
|
|
|
|
22
|
17
|
|
|
|
23
|
19
|
|
|
|
24
|
20
|
|
|
|
27
|
18
|
|
|
Итого
|
10
|
|
|
II
|
20-24
|
4
|
24
|
|
|
|
7
|
22
|
|
|
|
9
|
23
|
|
|
|
11
|
23
|
|
|
|
17
|
21
|
|
|
|
25
|
22
|
|
|
|
28
|
21
|
|
|
|
29
|
24
|
|
|
Итого
|
8
|
|
|
III
|
24-28
|
1
|
25
|
|
|
|
2
|
28
|
|
|
|
8
|
26
|
|
|
|
12
|
28
|
|
|
|
15
|
25
|
|
|
|
16
|
28
|
|
|
|
19
|
27
|
|
|
|
20
|
26
|
|
|
|
21
|
25
|
|
|
|
26
|
26
|
|
|
|
30
|
27
|
|
|
Итого
|
11
|
|
|
IV
|
28-32
|
5
|
32
|
|
|
Итого
|
1
|
|
В
результате группировки получим ряд распределения, представленный в таблице 2.3.
Таблица 2.3.
Ряд распределения данных по торговым
точкам города по цене товара
|
Группы
|
Группы по цене товара, руб.
|
№ п/п
|
|
I
|
16-20
|
10
|
|
II
|
20-24
|
8
|
|
III
|
24-28
|
11
|
|
IV
|
28-32
|
1
|
2.
Рассчитаем характеристики интервального ряда распределения: среднюю
арифметическую, среднее квадратическое отклонение, коэффициент вариации, моду и
медиану.
Среднюю
арифметическую рассчитаем по формуле: 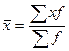
Расчет
характеристик ряда распределения представим в таблице 2.4.
Таблица 2.4.
Расчет характеристик ряда
распределения
|
Группы
|
Группы по цене товара, руб.
|
Число, f
|
xi
|
xf
|
x-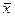 =x-22,4 =x-22,4
|
(x-x)2f
|
fнак
|
|
I
|
16-20
|
10
|
18
|
180
|
-4,4
|
193,6
|
10
|
|
II
|
20-24
|
8
|
22
|
176
|
-0,4
|
1,28
|
18
|
|
III
|
24-28
|
11
|
26
|
286
|
3,6
|
142,56
|
29
|
|
IV
|
28-32
|
1
|
30
|
30
|
7,6
|
57,76
|
30
|
|
|
|
30
|
|
672
|
|
395,2
|
|
Определим
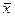 по формуле:
по формуле: 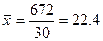 руб.
руб.
Определим
дисперсию по формуле: 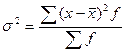 .
.
Получим:
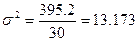 .
.
Определим
среднее квадратическое отклонение: 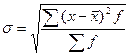 .
.
Получим:
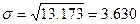 руб.
руб.
Определим
коэффициент вариации по формуле: 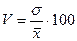 .
.
Получим:
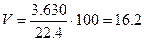 %
%
Вывод: так как V<33%,
то совокупность считается однородной.
Определим
моду по формуле: 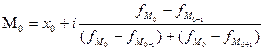
Получим:
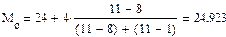 руб.
руб.
Вывод: в изучаемой совокупности наиболее часто встречаются данные по торговым
точкам по цене товара 24,923 руб.
Определим медиану по формуле: 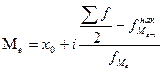
Получим: 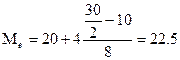 руб.
руб.
Вывод: в изучаемой совокупности 50% торговых точек города имеют цену за
единицу товара менее 22,5 руб., а 50% - более 22,5 руб.
В результате расчетов получили, что средняя арифметическая
равна 22,4 руб., среднее квадратическое отклонение равно 3,630 руб.,
коэффициент вариации равен 16,2%, совокупность считается однородной, т.к.
коэффициент вариации больше 33%, мода равна 24,923 руб., что показывает, что в
изучаемой совокупности наиболее часто встречаются данные по торговым точкам с
ценой товара 24,923 руб., медиана равна 22,5 руб., что показывает, что в
изучаемой совокупности 50% торговых точек города имеют цену за единицу товара
менее 22,5 руб., а 50% - более 22,5 руб.
Задание 2
По исходным данным:
1.
Установите
наличие и характер связи между признаками – цена товара и количество
проданного товара методом аналитической группировки, образовав четыре
группы с равными интервалами по факторному признаку.
2.
измерьте
тесноту корреляционной связи между названными признаками с использованием
коэффициентов детерминации и эмпирического корреляционного отношения.
Сделайте выводы по результатам выполнения задания.
Решение
От цены товара зависит количество проданного товара,
следовательно фактор цены товара должен быть взят в основу группировки.
1. Для
того, чтобы произвести группировку необходимо вычислить величину
группировочного интервала по формуле: 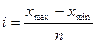 , где хmax
и xmin максимальное
и минимальное значения цены товара, n
- число образуемых групп.
, где хmax
и xmin максимальное
и минимальное значения цены товара, n
- число образуемых групп.
Величина
группировочного интервала будет равна:
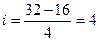 руб.
руб.
Образуем
группы, которые отличаются друг от друга по цене товара на данную величину (4
руб.):
Первая
группа будет иметь размеры: 16+4=20 руб.
Вторая
группа будет иметь размеры: 20+4=24 руб.
Третья
группа будет иметь размеры: 24+4=28 руб.
Четвертая
группа будет иметь размеры: 28+4=32 руб.
Аналитическую
группировку произведем в таблице 2.5.
Таблица 2.2.
Аналитическая группировка по
факторному признаку
|
Группы
|
Группы по цене товара, руб.
|
№ п/п
|
Цена за
единицу
товара, руб.
|
Количество проданного товара, тыс.шт.
|
|
1
|
2
|
3
|
4
|
5
|
|
I
|
16-20
|
3
|
16
|
45
|
|
|
|
6
|
20
|
33
|
|
|
|
10
|
16
|
48
|
|
|
|
13
|
17
|
23
|
|
|
|
14
|
19
|
44
|
|
|
|
18
|
18
|
38
|
|
|
|
22
|
17
|
35
|
|
|
|
23
|
19
|
28
|
|
|
|
24
|
20
|
39
|
|
|
|
27
|
18
|
43
|
|
|
Итого
|
10
|
180
|
376
|
|
1
|
2
|
3
|
4
|
5
|
|
II
|
20-24
|
4
|
24
|
26
|
|
|
|
7
|
22
|
44
|
|
|
|
9
|
23
|
25
|
|
|
|
11
|
23
|
31
|
|
|
|
17
|
21
|
28
|
|
|
|
25
|
22
|
26
|
|
|
|
28
|
21
|
22
|
|
|
|
29
|
24
|
26
|
|
|
Итого
|
8
|
180
|
228
|
|
III
|
24-28
|
1
|
25
|
31
|
|
|
|
2
|
28
|
24
|
|
|
|
8
|
26
|
29
|
|
|
|
12
|
28
|
27
|
|
|
|
15
|
25
|
29
|
|
|
|
16
|
28
|
21
|
|
|
|
19
|
27
|
20
|
|
|
|
20
|
26
|
22
|
|
|
|
21
|
25
|
38
|
|
|
|
26
|
26
|
33
|
|
|
|
30
|
27
|
26
|
|
|
Итого
|
11
|
291
|
300
|
|
IV
|
28-32
|
5
|
32
|
28
|
|
|
Итого
|
1
|
32
|
28
|
|
|
Итого
|
|
683
|
932
|
Результаты
аналитической группировки представим в сводной таблице 2.6.
Таблица 2.6.
Сводная аналитическая таблица
|
Группы
|
Группы по
цене товара,
руб.
|
№
п/п
|
Цена за единицу товара, руб.
|
Количество
проданного товара, тыс.шт.
|
|
всего по
группе
|
на 1 п/п
|
всего по
группе
|
на 1
п/п
|
|
I
|
16-20
|
10
|
180
|
18
|
376
|
37,6
|
|
II
|
20-24
|
8
|
180
|
22,5
|
228
|
28,5
|
|
III
|
24-28
|
11
|
291
|
26,455
|
300
|
27,273
|
|
IV
|
28-32
|
1
|
32
|
32
|
28
|
28
|
|
Итого
|
|
30
|
683
|
22,767
|
932
|
31,067
|
31.067=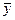
Сравнивая
графы 5 и 7 сводной аналитической таблицы, видим, что с увеличением цены за
единицу товара уменьшается количество проданного товара, значит, между этими
показателями имеется обратная зависимость.
2.
Запишем формулу для расчета коэффициента детерминации: 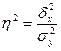
Запишем
формулу для расчета межгрупповой дисперсии: 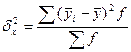
Расчет
межгрупповой дисперсии произведем в рабочей таблице 2.7.
Таблица 2.7.
Расчет межгрупповой дисперсии
|
Группы
|
Количество
проданного товара, тыс.шт.
|
№ п/п
|
yi-y=yi-31.067
|
(yi-y)2f
|
|
I
|
37,6
|
10
|
6,533
|
426,801
|
|
II
|
28,5
|
8
|
-2,567
|
52,716
|
|
III
|
27,273
|
11
|
-3,794
|
158,339
|
|
IV
|
28
|
1
|
-3,067
|
9,406
|
|
Итого
|
|
|
|
647,262
|
Межгрупповая
дисперсия будет равна: 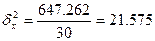
Найдем
общую дисперсию по формуле: 
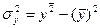
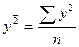
Расчет
среднего значения квадрата представим в таблице 2.8.
Таблица 2.8.
Расчет среднего значения квадрата
|
№ п/п
|
Количество проданного товара, тыс.шт.
|
y2
|
|
1
|
2
|
3
|
|
1
|
31
|
961
|
|
2
|
24
|
576
|
|
3
|
45
|
2025
|
|
4
|
26
|
676
|
|
5
|
28
|
784
|
|
6
|
33
|
1089
|
|
7
|
44
|
1936
|
|
8
|
29
|
841
|
|
9
|
25
|
625
|
|
10
|
48
|
2304
|
|
11
|
31
|
961
|
|
12
|
27
|
729
|
|
13
|
23
|
529
|
|
14
|
44
|
1936
|
|
1
|
2
|
3
|
|
15
|
29
|
841
|
|
16
|
21
|
441
|
|
17
|
28
|
784
|
|
18
|
38
|
1444
|
|
1
|
2
|
3
|
|
19
|
20
|
400
|
|
20
|
22
|
484
|
|
21
|
38
|
1444
|
|
22
|
35
|
1225
|
|
23
|
28
|
784
|
|
24
|
39
|
1521
|
|
25
|
26
|
676
|
|
26
|
33
|
1089
|
|
27
|
43
|
1849
|
|
28
|
22
|
484
|
|
29
|
26
|
676
|
|
30
|
26
|
676
|
|
Итого
|
|
30790
|
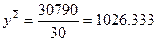
Определим
общую дисперсию: 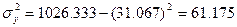 .
.
Определим
коэффициент детерминации: 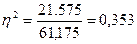 или 35,3%.
или 35,3%.
Вывод: вариация количества товара 35,3%
обусловлена вариацией цены товара.
Определим
эмпирическое корреляционное отношение по формуле: 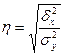 .
.
Получим:
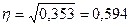 .
.
Вывод: т.к. эмпирическое корреляционное
отношение меньше 0,7, то можно сделать вывод, что связь между ценой товара и
количеством проданного товара слабая.
Задание 3
По результатам выполнения задания 1 с вероятностью 0,954
определите:
1.
Ошибку
выборки средней цены товара и границы, в которых будет находиться средняя цена
товара в генеральной совокупности.
2.
Ошибку
выборки доли магазинов со средней ценой товара до 20 руб. и границы, в которых
будет находиться генеральная доля.
Решение
По результатам
выполнения задания 1 получили следующий ряд распределения:
|
Группы
|
Группы по цене товара, руб.
|
№ п/п
|
|
|
|
I
|
16-20
|
10
|
|
|
II
|
20-24
|
8
|
|
|
III
|
24-28
|
11
|
|
|
IV
|
28-32
|
1
|
|
В задании 1 были рассчитаны характеристики ряда
распределения:
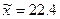 руб.
руб.
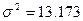
Среднюю
ошибку определим по формуле: 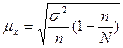
N=200.
Получим:
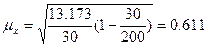 руб.
руб.
Предельную
ошибку рассчитаем по формуле: 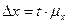
Получим:
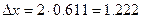 руб.
руб.
Найдем
приделы средней генеральной совокупности:
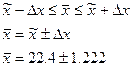
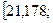
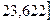
Вывод: с вероятностью 0,954 можно
утверждать, что предельная ошибка выборки составит 1,222 руб., средняя цена
товара в генеральной совокупности будет находится в пределах от 21,178 руб. до
23.622 руб.
2.
Определим ошибку выборки доли магазинов со средней ценой товара до 20 руб.,
границы в которых будет находиться генеральная совокупность.
1) m –
число магазинов со средней ценой товара до 20 руб.
m=8
2)
найдем долю магазинов со средней ценой товара до 20 руб.:
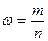
Получим:
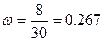 или 26,7%
или 26,7%
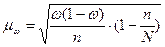
Получим:
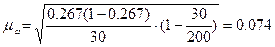 или 7,4%
или 7,4%
Предельную
ошибку рассчитаем по формуле: 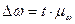
Получим:
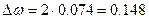 или 14,8%
или 14,8%
Пределы
рассчитаем по формуле:
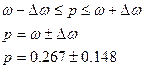
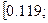
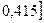 или в процентах
или в процентах 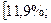
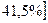
Вывод: с вероятностью 0,954 можно
утверждать, что доля магазинов со средней ценой товара до 20 руб. будет
находится в пределах от 11,9% до 41,5%.
Задание 4
Имеются
следующие данные о продаже товара А на рынках города:
|
Рынок
|
Базисный период
|
Отчетный период
|
|
Цена,
руб./кг
|
Объем
продаж, т
|
Цена,
руб./кг
|
Объем
продаж, т
|
|
I
|
31,9
|
32
|
36,8
|
35
|
|
II
|
34,8
|
24
|
36,5
|
36
|
|
III
|
28,3
|
61
|
33,3
|
36
|
Определите:
1.
Общие
индексы цен переменного, постоянного состава, структурных сдвигов.
2.
Абсолютное
изменение средней цены под влиянием отдельных факторов.
Сделайте
выводы.
Решение
|
Рынок
|
Базисный период
|
Отчетный период
|
p0q0
|
p0q1
|
p1q1
|
|
Цена, руб./кг
p0
|
Объем продаж, т
q0
|
Цена, руб./кг
p1
|
Объем продаж, т
q1
|
|
I
|
31,9
|
32
|
36,8
|
35
|
1020,8
|
1116,5
|
1288
|
|
II
|
34,8
|
24
|
36,5
|
36
|
835,2
|
1252,8
|
1314
|
|
III
|
28,3
|
61
|
33,3
|
36
|
1726,3
|
1018,8
|
1198,8
|
|
Итого
|
|
117
|
|
107
|
3582,3
|
3388,1
|
3800,8
|
1. Найдем индекс цен переменного состава по формуле:
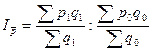
Получим: 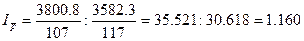
Вывод: средняя цена на трех рынках в
отчетном периоде по сравнению с базисным увеличилась на 16%, что обусловлено
увеличением цены на каждом рынке и изменением структуры продаж.
Найдем индекс цен постоянного состава
по формуле: 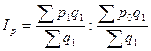
Получим: 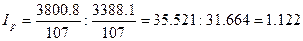
Вывод: средняя цена на трех рынках увеличилась на 12,2%, что обусловлено
только изменением цены на каждом рынке.
Найдем индекс цен структурных сдвигов по формуле: 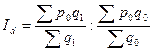
Получим: 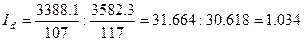
Вывод: изменение в структуре продаж на трех рынках привело к увеличению
средней цены на 3,4%.
Покажем взаимосвязь между индексами: 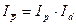
Получим: 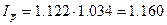 - равенство верно.
- равенство верно.
2.
Найдем
абсолютный прирост средней цены за счет изменения:
a)
Цены
на каждом рынке: 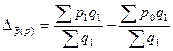
Получим: 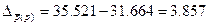 руб.
руб.
b)
Структуры продаж: 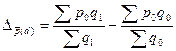
Получим:
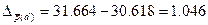 руб.
руб.
c)
двух факторов: 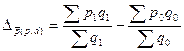

Получим: 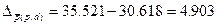 руб.
руб.
Проверим
взаимосвязь абсолютных приростов: 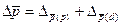
Получим:
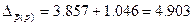 руб.
руб.
Вывод: индекс цен переменного состава
равен 1,160 – означает, что средняя цена на трех рынках в отчетном периоде по
сравнению с базисным увеличилась на 16%, что обусловлено увеличением цены на
каждом рынке и изменением структуры продаж. Индекс цен постоянного состава
равен 1,122 – означает, что средняя цена на трех рынках увеличилась на 12,2%,
что обусловлено только изменением цены на каждом рынке. Индекс цен структурных
сдвигов равен 1,034 – означает, что
изменение в структуре продаж на трех рынках привело к увеличению средней цены
на 3,4%. Абсолютный прирост средней цены за счет изменения цены на каждом рынке
составил 3,857 руб., за счет изменения структуры продаж – 1,046 руб., за счет
изменения двух факторов одновременно – 4,903 руб.
Аналитическая часть
3.1. Постановка задачи
Средние
цены на товары (услуги) складываются под влиянием многообразных ассортиментных,
а также территориальных сдвигов, сезонных колебаний и т.д. уровень средних цен
по РФ рассчитывается как среднеарифметическая величина из уровней цен по
регионам, взвешенных на удельный вес численности населения регионов в общей
численности населения России.
По
данным Российского статистического ежегодника 2006 за несколько лет,
представленным в таблице 3.1, проведем анализ динамики цен на говядину, для
чего рассчитаем следующие показатели:
·
абсолютный
прирост;
·
темп
роста;
·
темп прироста;
·
абсолютное
значение 1% прироста;
·
средний
за период уровень ряда, абсолютный прирост, темпы роста и прироста.
Таблица 3.1.
Средние потребительские цены на говядину
(на конец года; рублей за кг)
|
Год
|
Средняя потребительская цена на говядину
|
|
2000
|
15,62
|
|
2001
|
14,88
|
|
2002
|
19,47
|
|
2003
|
18,34
|
|
2004
|
19,69
|
|
2005
|
19,63
|
Методика решения задачи
Расчет
показателей анализа ряда динамики осуществим по формулам, представленным в
таблице 3.2.
Таблица 3.2.
Формулы расчетных показателей
|
Показатель
|
Базисный
|
Цепной
|
Средний
|
|
Абсолютный прирост
|
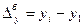 (1) (1)
|
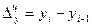 (2) (2)
|
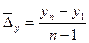 (3) (3)
|
|
Темп
роста
|
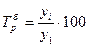 (4) (4)
|
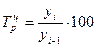 (5) (5)
|
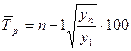 (6) (6)
|
|
Темп
прироста
|
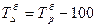 (7) (7)
|
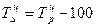 (8) (8)
|
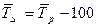 (9) (9)
|
Средний
уровень в интервальном ряду динамики вычисляется по формуле: 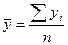 (10).
(10).
Для определения абсолютной величины, стоящей за каждым
процентом прироста средней потребительской цены, рассчитывают показатель
абсолютного значения 1% прироста: 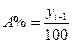 (11).
(11).
Числовые обозначения:
у1 – уровень первого периода; уi – уровень сравниваемого периода; уi-1 – уровень предыдущего периода; уn – уровень последнего периода; n – число уровней динамики.
Технология выполнения компьютерных
расчетов
Расчеты показателей анализа динамики средних потребительских
цен на сахар-песок выполнены с применением пакета прикладных программ обработки
электронных таблиц MS Excel в среде Windows.
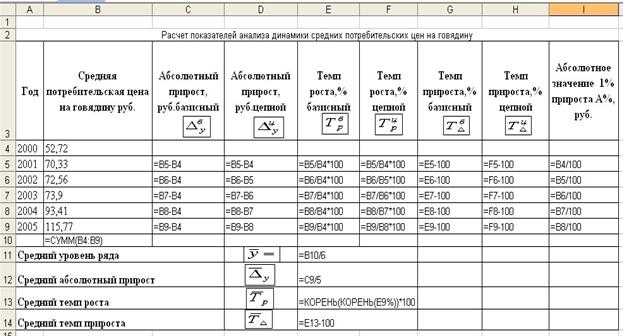
Расположение на рабочем листе Excel исходных данных (таблица
3.1.) и расчетных формул (1-11) представлено в таблице 3.3.
Таблица 3.3.
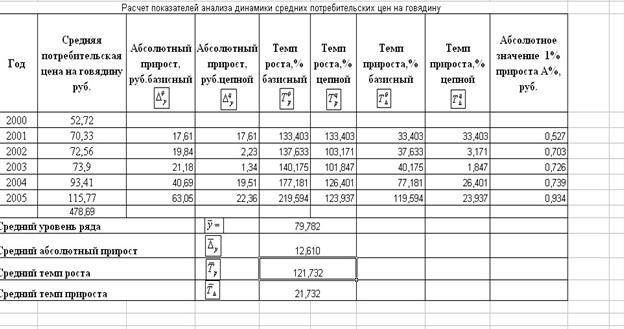
Результаты расчетов приведены в таблице 3.4.
Таблица 3.4.
На рисунке 1 представлено графическое изображение динамики
средних потребительских цен на говядину за 2000-2005 гг.
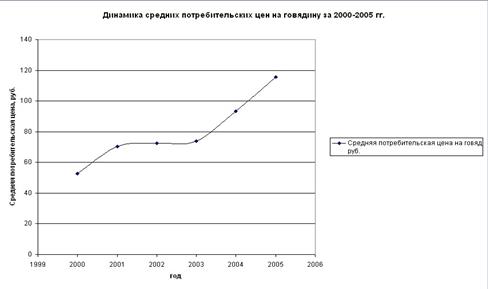
Рисунок 1. Диаграмма динамики
средних потребительских цен на говядину за 2000-2005 гг.
Анализ результатов статистических
компьютерных расчетов
Результаты проведенных расчетов позволяют сделать следующие
выводы.
Средняя потребительская цена за 6 лет выросла на 63,05 руб.
Наблюдается положительная динамика в течении всего периода.
Она носит скачкообразный характер, о чем говорят цепные абсолютные приросты и
цепные темпы роста и прироста. Это же подтверждает и графическое изображение
динамики средних потребительских цен на говядину (рисунок 1).
В течение анализируемого периода средний показатель средней
потребительской цены на говядину составил 79,782 руб., в среднем за год она увеличилась
на 12,61 руб. или 21,7% (Тр=121,7).
Ускоренный рост средних потребительских цен на говядину можно
увидеть и по увеличивающемуся абсолютному значению 1% прироста.
ЗАКЛЮЧЕНИЕ
Цена -
многофункциональное экономическое
явление, ведущая рыночная категория, процессы
их образования и изменения представляют
собой предмет статистического исследования.
Статистика цен -
самостоятельный блок, входящий как
составная часть в статистику рынка и соответственно в
социально-экономическую статистику. Поэтому в органах государственной
статистики сформирована самостоятельная
служба статистики цен. Для
измерения инфляции наиболее важным является статистика цен, точнее их индексов. В настоящее время инфляция - один из самых опасных
процессов, негативно воздействующих на финансы, денежную и
экономическую систему в
целом; инфляция означает
не только снижение покупательной
способности денег, она
подрывает возможности хозяйственного регулирования, сводит
на нет усилия
по проведению структурных
преобразований, восстановлению нарушенных пропорций. Поэтому во всесторонней и объективной информации
о ценах и инфляции в глубоком анализе
закономерностей и тенденций их
изменения заинтересовано все
общество, а не только властные структуры и маркетинговые службы.
Для
снижения вероятности роста инфляции, необходимой для достижения стабильности в
экономике, нужен контроль за количеством денег, находящихся в обращении,
которые в свою очередь зависят от величины валового внутреннего продукта (ВВП)
и интенсивности движения денежной массы. ВВП России в августе 2007 года вырос
на 6,4% по сравнению с августом 2006 года. Об этом на пресс-конференции сообщил
директор сводного департамента макроэкономического прогнозирования
Минэкономразвития РФ Андрей Клепач. За январь-август 2007 года ВВП России вырос
по сравнению с аналогичным периодом 2006 года на 7,7%, заявил А. Клепач. По его
словам, повышение прогноза по росту ВВП связано в основном с высокими ценами на
нефть.
В
расчетной части курсовой работы решены конкретные задачи из варианта № 19. По
результатам выполнения задания №1 сделаны выводы: средняя арифметическая равна
22,4 руб., среднее квадратическое отклонение равно 3,630 руб., коэффициент
вариации равен 16,2%, совокупность считается однородной, т.к. коэффициент
вариации больше 33%, мода равна 24,923 руб., что показывает, что в изучаемой
совокупности наиболее часто встречаются данные по торговым точкам с ценой
товара 24,923 руб., медиана равна 22,9 руб., что показывает, что в изучаемой
совокупности 50% торговых точек города имеют цену за единицу товара менее 22,9
руб., а 50% - более 22,9 руб. В задании №2 выявлено, что связь между ценой
товара и количеством проданного товара слабая. В задании №3 с вероятностью
0,954 определено, что доля магазинов со средней ценой товара до 20 руб. будет
находится в пределах от 17,9% до 48,7%. В задании №4 определено, что индекс цен
переменного состава равен 1,160 – означает, что средняя цена на трех рынках в
отчетном периоде по сравнению с базисным увеличилась на 16%, что обусловлено
увеличением цены на каждом рынке и изменением структуры продаж. Индекс цен
постоянного состава равен 1,122 – означает, что средняя цена на трех рынках
увеличилась на 12,2%, что обусловлено только изменением цены на каждом рынке.
Индекс цен структурных сдвигов равен
1,034 – означает, что изменение в структуре продаж на трех рынках привело к
увеличению средней цены на 3,4%. Абсолютный прирост средней цены за счет
изменения цены на каждом рынке составил 3,857 руб., за счет изменения структуры
продаж – 1,046 руб., за счет изменения двух факторов одновременно – 4,903 руб.
В аналитической части исследована динамика средних
потребительских цен на говядину за 2000-2005 гг. в качестве статистического
материала для проведения исследования использованы данные, опубликованные в
Российском статистическом ежегоднике. Расчеты в аналитической части работы
выполнены с применением средств компьютерной техники при помощи пакета
прикладных программ MS Excel. По результатам анализа расчетных показателей установили,
что в течение анализируемого периода средний показатель средней потребительской
цены на говядину составил 79,782 руб., в среднем за год она увеличилась на
12,61 руб.