Всероссийский заочный финансово – экономический институт
|
|
|
Факультет: Финансово – кредитный
Кафедра: Экономико-маиематических
методов и моделей
Специальность: Финансы и кредит
|
|
Контрольная работа
По дисциплине
«Эконометрика»
Выполнил:
Студент III курса Арасланова А.Н.
Проверил:
Преподаватель Хусаинова З.Ф.
Уфа
2007
ПОСТРОЕНИЕ ЛИНЕЙНОЙ ПАРНОЙ РЕГРЕССИИ
Вариант 4
X
|
36
|
28
|
43
|
52
|
51
|
54
|
25
|
37
|
51
|
29
|
|
Y
|
104
|
77
|
117
|
137
|
143
|
144
|
82
|
101
|
132
|
77
|
По предприятиям легкой промышленности региона получена
информация, характеризующая зависимость объема выпуска продукции (У, млн.руб.)
от объема капиталовложений (Х, млн.руб.)
Требуется:
1.
Найти параметры уравнения линейной регрессии, дать
экономическую интерпретацию коэффициента регрессии.
2.
Вычислить остатки: найти остаточную сумму квадратов;
оценить дисперсию остатков Se2;
построить график остатков.
3.
Проверить выполнение предпосылок МНК.
4.
Осуществить проверку значимости параметров уравнения
регрессии с помощью t –
критерия Стьюдента при α = 0,05.
5.
Вычислить коэффициент детерминации, проверить
значимость уравнения регрессии с помощью F – критерия Фишера при α = 0,05, и найти среднюю
относительную ошибку апроксимации. Сделать вывод о качестве модели.
6.
Осуществить прогнозирование среднего значения
показателя У при уровне значимости α = 0,1, если прогнозное значение
фактора Х составит 80% от его максимального значения.
7.
Представить график фактических и модельных показателей
линейной модели.
8.
Составить уравнение нелинейной регрессии:
a.
Гиперболической
b.
Степенной
c.
Показательной
Привести
графики построенных уравнений регрессии.
9. Для указанных моделей найти
коэффициенты детерминации, коэффициенты эластичности и средние относительные
ошибки апроксимации. Сравнить модели по этим характеристикам и сделать вывод.
РЕШЕНИЕ:
Составим
вспомогательную таблицу 1 и 2:
Таблица 1
|
|
х
|
у
|
ху
|
х2
|
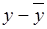
|
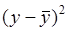
|
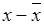
|
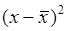
|
|
1
|
36
|
104
|
3744
|
1296
|
-7,4
|
54,76
|
-4,6
|
21,16
|
|
2
|
28
|
77
|
2156
|
784
|
-34,4
|
1183,36
|
-12,6
|
158,76
|
|
3
|
43
|
117
|
5031
|
1849
|
5,6
|
31,36
|
2,4
|
5,76
|
|
4
|
52
|
137
|
7124
|
2704
|
25,6
|
655,36
|
11,4
|
129,96
|
|
5
|
51
|
143
|
7293
|
2601
|
31,6
|
998,56
|
10,4
|
108,16
|
|
6
|
54
|
144
|
7776
|
2916
|
32,6
|
1062,76
|
13,4
|
179,56
|
|
7
|
25
|
82
|
2050
|
625
|
-29,4
|
864,36
|
-15,6
|
243,36
|
|
8
|
37
|
101
|
3737
|
1369
|
-10,4
|
108,16
|
-3,6
|
12,96
|
|
9
|
51
|
132
|
6732
|
2601
|
20,6
|
424,36
|
10,4
|
108,16
|
|
10
|
29
|
77
|
2233
|
841
|
-34,4
|
1183,36
|
-11,6
|
134,56
|
|
сумма
|
406
|
1114
|
47876
|
17586
|
0
|
6566,4
|
0
|
1102,4
|
|
Ср.зн.
|
40,6
|
111,4
|
4787,6
|
1758,6
|
-
|
656,64
|
-
|
110,24
|
Таблица 2
|
|
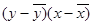
|
|
1
|
34,04
|
|
2
|
433,44
|
|
3
|
13,44
|
|
4
|
291,84
|
|
5
|
328,64
|
|
6
|
436,84
|
|
7
|
458,64
|
|
8
|
37,44
|
|
9
|
214,24
|
|
10
|
399,04
|
|
сумма
|
2647,6
|
|
Ср.зн.
|
264,76
|
Здесь 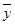 ,
, 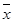 - средние значения
- средние значения
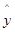 - расчетные значения
- расчетные значения
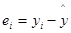 -погрешность (остаток, невязка).
-погрешность (остаток, невязка).
1. Найдем параметры уравнения линейной
регрессии 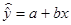
Значения параметров a и b определим, используя данные таблицы
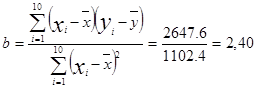
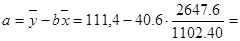 13,892
13,892
Уравнение линейной регрессии принимает вид
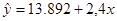
С увеличением объема капиталовложений на
1млн. руб. объем выпускаемой продукции увеличиться в среднем на 2400 тыс. руб.
Это свидетельствует об эффективности работы предприятия.
Зная значения 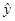 уравнения регрессии
составим дополнительную таблицу3
уравнения регрессии
составим дополнительную таблицу3
Таблица 3
|
|
х
|
у
|

|
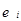
|
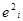
|
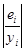 х100% х100%
|
Точки поворота
|
|
1
|
36
|
104
|
100,35232
|
3,64768
|
13,30557
|
3,50738
|
-
|
|
2
|
28
|
77
|
81,138897
|
-4,13897
|
17,13107
|
5,37529
|
1
|
|
3
|
43
|
117
|
117,16401
|
-0,16401
|
0,02690
|
0,14018
|
1
|
|
4
|
52
|
137
|
138,77903
|
-1,77903
|
3,16495
|
1,29856
|
1
|
|
5
|
51
|
143
|
136,37736
|
6,62264
|
43,85936
|
4,63122
|
1
|
|
6
|
54
|
144
|
143,58237
|
0,41763
|
0,17441
|
0,29002
|
1
|
|
7
|
25
|
82
|
73,93396
|
8,06604
|
65,06100
|
9,83663
|
1
|
|
8
|
37
|
101
|
102,75399
|
-1,75399
|
3,07648
|
1,73662
|
0
|
|
9
|
51
|
132
|
136,37736
|
-4,37736
|
19,16128
|
3,31618
|
0
|
|
10
|
29
|
77
|
83,54064
|
-6,54064
|
42,77997
|
8,49434
|
-
|
|
сумма
|
406
|
1114
|
1114,00001
|
-0,00001
|
207,74
|
38,62642
|
6
|
|
Ср.зн.
|
40,6
|
111,4
|
111,00
|
-
|
20,774
|
3,862642
|
-
|
2.
Дисперсия
остатков
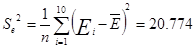
Проверка гипотезы о М (Еi)=0:
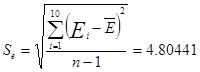
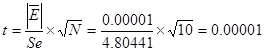
tтабл(a=0.05, n=N-1=9)=2,25
t< tтабл => гипотеза о М (Еi)=0 принимается.
Число точек поворота р=6
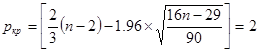
ркр<р => свойства случайности ряда остатков выполнено.
Построим график остатков
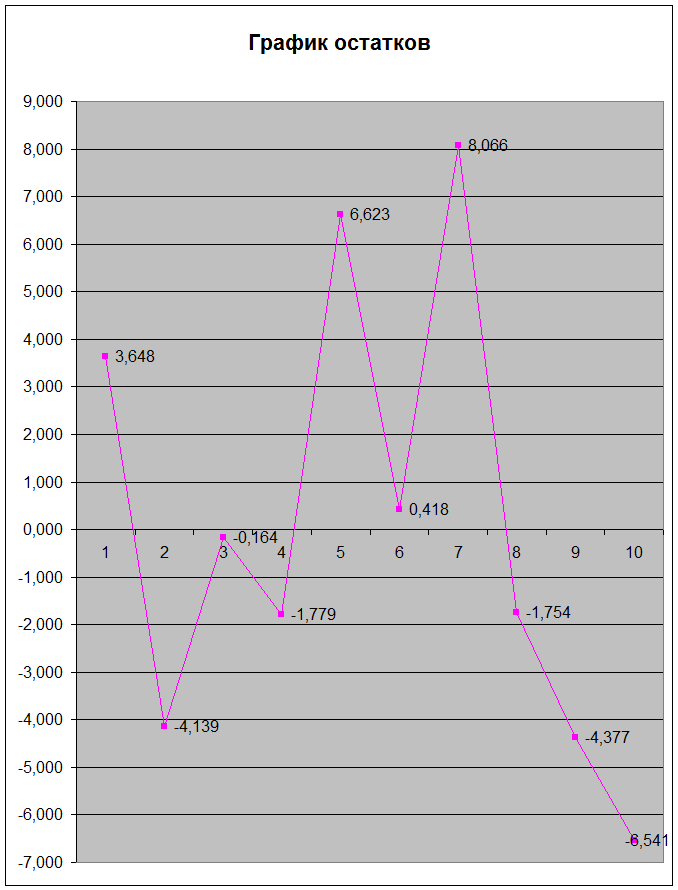
3. Проверить выполнение предпосылок МНК.
Метод наименьших квадратов позволяет
получить такие оценки параметров, при которых сумма квадратов отклонений
фактических значений результативного у от теоретических 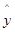 минимальна, т.е.
минимальна, т.е. 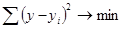
В данном случае остаточная сумма квадратов
составляет 781,76; откуда среднеквадратическое отклонение равно 27,96; что
является достаточно малым отклонением.
4. Оценим значимость параметров регрессии
Анализ статистической значимости параметров модели проверяем по t-критерию Стьюдента при уровне значимости
α=0,05 (Таблица 4)
В качестве меры точности применяют
несмещенную оценку дисперсии остаточной компоненты, которая представляет собой
отношение суммы квадратов уровней остаточной компоненты к величине 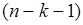 , где k – количество факторов включенных в модель. Квадратный корень из
величины
, где k – количество факторов включенных в модель. Квадратный корень из
величины 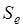 называется стандартной
ошибкой оценки:
называется стандартной
ошибкой оценки:
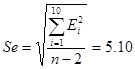
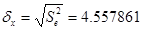
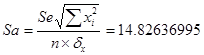
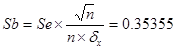
Таблица 4
Анализ значимости параметров регрессии
|
Фактическое значение
t-критерия Стьюдента
|
Табличное значение
t-критерия
Стьюдента
|
Вывод о значимости параметра
|
|
Критерий
коэффициента b: 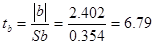
|
Для α=0,05 и df = n – 2 = 8
значение tтабл=2,31
|
Значим, т.к. 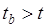
|
|
Критерий
коэффициента a: 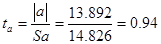
|
Не значим, т.к. 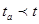
|
Анализ верхней и
нижней границ доверительных интервалов приводит к выводу о том, что с
вероятность ρ = 1 – α = 0,95 параметры b, находясь в указанных границах, не
принимает нулевого значения, т.е. не является статистически незначимыми и
существенно отличен от нуля.
4.1
R/S – критерий
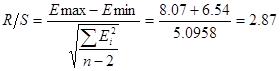
2,87 Є (2,67-3,57), =>свойство нормальности распределения
выполняется.
5. Долю дисперсии, объясняемую регрессией, в общей дисперсии
результативного признака у
характеризует коэффициент детерминации 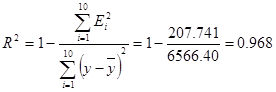 -означает, что
вариация y на 96,8%
объясняется фактором х. Доля неучтенных факторов составляет 3,2%.
-означает, что
вариация y на 96,8%
объясняется фактором х. Доля неучтенных факторов составляет 3,2%.
Расчет F-критерия Фишера – оценивает значимость уравнения регрессии и
состоит в проверке гипотезы Н0: 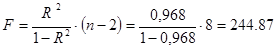
где n –
число единиц совокупности
F > Fтабл
=5,32 для α=0,05,
Поэтому уравнение регрессии
с вероятностью 0,95 в целом статистически значимое и Н0 – гипотеза о
случайной природе оцениваемых характеристик отклоняется и признается их
статистическая значимость и надежность.
Средняя относительная ошибка:

Качество построенной модели оценивается
как хорошее, т.к. средняя относительная ошибка не превышает 8-10%
Расчет коэффициента эластичности:
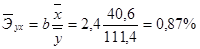
Следовательно, при
изменении фактора х на 1% от своего среднего значения, то себестоимость
единицы продукции возрастет на 0,87%
6. Осуществим
прогнозирование среднего значения показателя Y при уровне значимости a=0,1, если прогнозное
значение фактора X
составит 80% от его максимального значения.
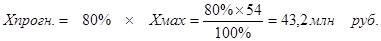
Подставим
Хпрогн. в нашу модель и расчитаем Y(Xпрогн)
Y(X)=13,892+2,402 х 43,2 = 117,66
млн руб.
Ошибка прогноза:
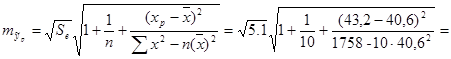 =2,25*1,05=2,37
=2,25*1,05=2,37
Предельная ошибка прогноза, которая в 99% случаев не будет
превышена (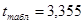 )
)
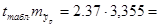 7,95135
7,95135
Доверительный интервал прогноза
43,2-7,95135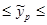 43,2+7,95135
43,2+7,95135
35,24865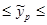 51,15135
51,15135
Вывод:
Выполненный прогноз оказался точным ρ = 1 – α = 0,99, т.к. диапазон
верхней и нижней границ доверительного интервала Dγ составляет 1,45
раза и не превышает порогового значения точности.
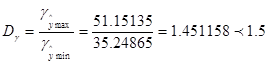
7. Представим график линейной модели и
результатов прогноза.
8.
а) Определим параметры гиперболической модели: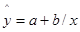
Для этого введем Х=1/х и составим таблицы
5 и 6
Таблица 5
|
|
х
|
у
|
X=1/x
|
yX
|
Х2
|
|
1
|
36
|
104
|
0,2778
|
2,88789
|
0,0077
|
|
2
|
28
|
77
|
0,3571
|
2,75000
|
0,00128
|
|
3
|
43
|
117
|
0,02326
|
2,72093
|
0,00054
|
|
4
|
52
|
137
|
0,01923
|
2,63462
|
0,00037
|
|
5
|
51
|
143
|
0,01961
|
2,80392
|
0,00038
|
|
6
|
54
|
144
|
0,01852
|
2,6667
|
0,00034
|
|
7
|
25
|
82
|
0,04000
|
3,28000
|
0,00160
|
|
8
|
37
|
101
|
0,02703
|
2,72973
|
0,00073
|
|
9
|
51
|
132
|
0,01961
|
2,58824
|
0,0038
|
|
10
|
29
|
77
|
0,3448
|
2,65517
|
0,00119
|
|
сумма
|
406
|
1114
|
0,26522
|
27,71816
|
0,00759
|
|
среднее
|
40,6
|
111,4
|
0,02652
|
2,7182
|
0,00076
|
Таблица 6
|
|

|
Еi
|
Е2i
|
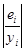 х100% х100%
|
|
1
|
107,27158
|
-3,27158
|
10,70324
|
3,14575
|
|
2
|
81,17996
|
-4,17996
|
17,47207
|
5,42852
|
|
3
|
122,13773
|
-5,13773
|
26,39627
|
4,39122
|
|
4
|
13537024
|
1,62276
|
2,65612
|
1,18961
|
|
5
|
134,13059
|
8,86941
|
78,6643
|
6,20238
|
|
6
|
137,71179
|
6,28821
|
39,54159
|
4,36684
|
|
7
|
67,09049
|
14,90951
|
222,29349
|
18,18233
|
|
8
|
109,73970
|
-8,73970
|
76,38236
|
1,61408
|
|
9
|
134,13059
|
-2,13059
|
4,53941
|
1,61408
|
|
10
|
85,22644
|
-8,22644
|
67,67432
|
10,68329
|
|
сумма
|
1113,98911
|
0,01089
|
546,32530
|
63,85756
|
|
среднее
|
111,39891
|
0,0011
|
54,6325
|
6,38576
|
Найдем коэффициенты a и b.

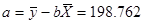
Тогда уравнение гиперболической модели
будет: 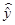 = 198,762-3293,898/х
= 198,762-3293,898/х
Построим график гиперболической модели:
б) Определим параметры степенной
модели: 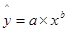
Составим вспомогательные таблицы 7 и 8
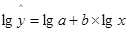
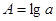
Таблица 7
|
|
х
|
у
|
Y=ln(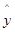 ) )
|
X=lg(x)
|
YX
|
X2
|
|
1
|
36
|
104
|
2,0903
|
1,55630
|
3,1394
|
2,42208
|
|
2
|
28
|
77
|
1,88649
|
1,44746
|
2,73005
|
2,09427
|
|
3
|
43
|
117
|
2,06819
|
1,63347
|
3,37832
|
2,66822
|
|
4
|
52
|
137
|
2,13672
|
1,71600
|
3,66662
|
2,94467
|
|
5
|
51
|
143
|
2,15534
|
1,70757
|
3,68039
|
2,91580
|
|
6
|
54
|
144
|
2,15836
|
1,73239
|
3,73913
|
3,00119
|
|
7
|
25
|
82
|
1,91381
|
1,39794
|
2,67540
|
1,95424
|
|
8
|
37
|
101
|
2,00432
|
1,56820
|
3,14318
|
2,45926
|
|
9
|
51
|
132
|
2,12057
|
1,70757
|
3,62103
|
2,91580
|
|
10
|
29
|
77
|
1,88649
|
1,46240
|
2,75880
|
2,13861
|
|
сумма
|
406
|
1114
|
20,34733
|
15,92901
|
32,53203
|
25,51411
|
|
среднее
|
40,6
|
111,4
|
2,034733
|
1,592901
|
3,253203
|
2,551411
|
Таблица 8
|
|

|
Еi
|
E2i
|
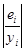 х100% х100%
|
|
1
|
100,77225
|
3,22775
|
10,41837
|
3,10361
|
|
2
|
81,23127
|
-4,23127
|
17,90365
|
5,49516
|
|
3
|
117,36251
|
-0,36251
|
0,13141
|
0,30984
|
|
4
|
138,14111
|
-1,14111
|
1,30313
|
0,83293
|
|
5
|
135,85933
|
7,14067
|
50,98917
|
4,99348
|
|
6
|
142,68611
|
1,31389
|
1,72631
|
0,91242
|
|
7
|
73,70665
|
8,29331
|
68,77833
|
10,11380
|
|
8
|
103,16857
|
-2,16857
|
4,70270
|
2,14710
|
|
9
|
135,85933
|
-3,85933
|
14,89443
|
2,92373
|
|
10
|
83,71344
|
-6,71344
|
45,07028
|
8,71875
|
|
сумма
|
1112,50061
|
1,49939
|
215,91743
|
39,55082
|
|
среднее
|
111,2501
|
0,14994
|
21,591743
|
3,955082
|
Найдем коэффициенты a и b.
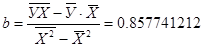
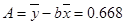
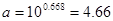
Тогда уравнение степенной модели принимает
вид: 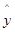 =4,66*х0,86
=4,66*х0,86
Построим график степенной
модели:
в) Определим уравнение показательной
модели: 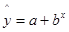
Составим вспомогательные таблицы 9 и 10
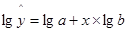
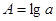
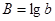
Таблица 9
|
|
х
|
у
|
х2
|
Y=lg(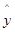 ) )
|
xY
|
|
1
|
36
|
104
|
1296
|
2,01703
|
72,61320
|
|
2
|
28
|
77
|
784
|
1,88649
|
52,82174
|
|
3
|
43
|
117
|
1849
|
2,06819
|
88,93199
|
|
4
|
52
|
137
|
2704
|
2,13672
|
111,10947
|
|
5
|
51
|
143
|
2601
|
2,15534
|
109,92214
|
|
6
|
54
|
144
|
2916
|
2,15836
|
116,55157
|
|
7
|
25
|
82
|
625
|
1,91381
|
47,84535
|
|
8
|
37
|
101
|
1369
|
2,00432
|
74,15989
|
|
9
|
51
|
132
|
2601
|
2,12057
|
108,14927
|
|
10
|
29
|
77
|
841
|
1,88649
|
54,70823
|
|
сумма
|
406
|
1114
|
175586
|
20,34733
|
836,81285
|
|
среднее
|
40,6
|
111,4
|
17558,6
|
2,034733
|
86,681285
|
Таблица 10
|
|

|
Еi
|
E2i
|
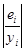 х100% х100%
|
|
1
|
97,73227
|
6,26773
|
39,28444
|
6,02667
|
|
2
|
81,71609
|
-4,71609
|
22,24150
|
6,12479
|
|
3
|
114,30155
|
2,69845
|
7,28163
|
2,30637
|
|
4
|
139,79732
|
-2,79732
|
7,82500
|
2,04184
|
|
5
|
136,70442
|
6,24558
|
39,63433
|
4,40250
|
|
6
|
146,19464
|
-2,19464
|
4,81644
|
1,52406
|
|
7
|
76,41149
|
5,55851
|
31,23144
|
6,81526
|
|
8
|
99,94349
|
1,05656
|
1,11632
|
1,04610
|
|
9
|
136,70442
|
-4,70442
|
22,13157
|
3,56395
|
|
10
|
83,56490
|
-6,56490
|
43,09791
|
8,52584
|
|
сумма
|
1113,07054
|
0,92946
|
218,66059
|
42,37738
|
|
среднее
|
111,307054
|
0,092946
|
21,866059
|
4,237738
|
Найдем коэффициенты
a и b.
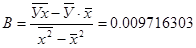
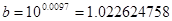
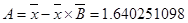
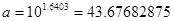
Тогда
уравнение степенной модели будет: 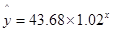
График показательной
модели.

9. а) Оценка качества гиперболической модели:
Рассчитаем коэффициент детерминации: 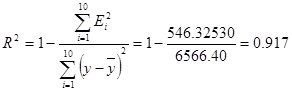 -означает, что
вариация y на 91,7%
объясняется фактором х. Доля неучтенных факторов составляет 8,3%.
-означает, что
вариация y на 91,7%
объясняется фактором х. Доля неучтенных факторов составляет 8,3%.
Расчет F-критерия Фишера :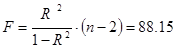
где n –
число единиц совокупности
F > Fтабл
=5,32 для α=0,05,
Поэтому уравнение регрессии
с вероятностью 0,95 в целом статистически значимое и Н0 – гипотеза о
случайной природе оцениваемых характеристик отклоняется и признается их
статистическая значимость и надежность.
Средняя относительная ошибка:
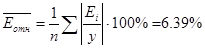
Качество построенной модели оценивается
как плохое, т.к. средняя относительная ошибка превышает 8-10%
б)Оценка
качества степенной модели:
Рассчитаем коэффициент детерминации: 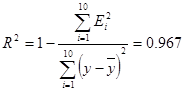 -означает, что
вариация y на 96,7%
объясняется фактором х. Доля неучтенных факторов составляет 3,3%.
-означает, что
вариация y на 96,7%
объясняется фактором х. Доля неучтенных факторов составляет 3,3%.
Расчет F-критерия Фишера :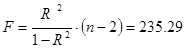
где n –
число единиц совокупности
F > Fтабл
=5,32 для α=0,05,
Поэтому уравнение регрессии
с вероятностью 0,95 в целом статистически значимое и Н0 – гипотеза о
случайной природе оцениваемых характеристик отклоняется и признается их
статистическая значимость и надежность.
Средняя относительная ошибка:
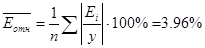
Качество построенной модели оценивается
как хорошее, т.к. средняя относительная ошибка не превышает 8-10%
в) Оценка
качества показательной модели:
Рассчитаем коэффициент детерминации: 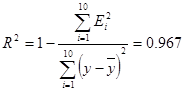 -означает, что
вариация y на 96,7%
объясняется фактором х. Доля неучтенных факторов составляет 3,3%.
-означает, что
вариация y на 96,7%
объясняется фактором х. Доля неучтенных факторов составляет 3,3%.
Расчет F-критерия Фишера :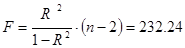
где n –
число единиц совокупности
F > Fтабл
=5,32 для α=0,05,
Поэтому уравнение регрессии
с вероятностью 0,95 в целом статистически значимое и Н0 – гипотеза о
случайной природе оцениваемых характеристик отклоняется и признается их
статистическая значимость и надежность.
Средняя относительная ошибка:
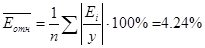
Качество построенной модели оценивается
как хорошее, т.к. средняя относительная ошибка не превышает 8-10%
Построим сводную таблицу 11:
Таблица 11
|
 Параметры Параметры
Модель
|
R2
|
F-критерий Фишера
|
Коэффициент корреляции
|
|
|
Линейная
|
0,968
|
344,87
|
0,984
|
3,86%
|
|
Степенная
|
0,967
|
235,29
|
0,983
|
3,96%
|
|
Показательная
|
0,967
|
232,24
|
0,983
|
4,24%
|
|
Гиперболическая
|
0,917
|
88,15
|
0,958
|
6,39%
|
Вывод:
Из сводной таблицы видно, что лучшей моделью является линейная Y(X)=13,892+2,402X, т.к. именно в этой модели
максимальные значения коэффициента детерминации, значение F-критерия
Фишера и минимальная погрешность.
Следовательно, первоначальные значения наилучшим образом описываются линейной
моделью.
Литература:
1. Методические указания ВЗФЭИ
2. Елисеева И.И. Практикум по
эконометрике – М.: Финансы и статистика, 2001 – 189с.
3. Елисеева И.И. Учебник по эконометрике
– М.: Финансы и статистика, 2003 – 342с.
4. Нименья И.Н. Статистика. Конспект
лекций - М.: Эксмо, 2007. - 175 с.
5. Кремер Н.Ш., Путко Б.А.
Эконометрика/Учебник для вузов – М.:Юнити-Дана, 2007. – 311 с.
________ А.Н. Арасланова
«___»_____________2008г.