Содержание
Задача
№1....................................................................................... 2
Задача
№2..................................................................................... 16
Литература.................................................................................... 21
Задача
1. Эконометрическое моделирование
стоимости квартир
в Московской области
Строительная фирма занимается реализацией квартир в строящихся
домах городов Подольск и Люберцы Московской области. Для выработки
управленческих решений компании необходимо осуществить эконометрическое
моделирование стоимости квартир на основании исходных данных, представленных в
таблице.
|
№
|
Цена
квартиры тыс.долл.
|
Город
области (1-Подольск, 0-Люберцы)
|
Число
комнат в квартире
|
Общая
площадь квартиры, кв.м.
|
|
|
Y
|
X1
|
X2
|
X3
|
|
41
|
38,0
|
1
|
1
|
41,9
|
|
42
|
62,2
|
1
|
2
|
69,0
|
|
43
|
125,0
|
0
|
3
|
67,0
|
|
44
|
61,1
|
1
|
2
|
58,1
|
|
45
|
67,0
|
0
|
1
|
32,0
|
|
46
|
93,0
|
0
|
2
|
57,2
|
|
47
|
118,0
|
1
|
3
|
107,0
|
|
48
|
132,0
|
0
|
3
|
81,0
|
|
49
|
92,5
|
0
|
3
|
89,9
|
|
50
|
105,0
|
1
|
4
|
75,0
|
|
51
|
42,0
|
1
|
1
|
36,0
|
|
52
|
125,0
|
1
|
3
|
72,9
|
|
53
|
170,0
|
0
|
4
|
90,0
|
|
54
|
38,0
|
0
|
1
|
29,0
|
|
55
|
130,5
|
0
|
4
|
108,0
|
|
56
|
85,0
|
0
|
2
|
60,0
|
|
57
|
98,0
|
0
|
4
|
80,0
|
|
58
|
128,0
|
0
|
4
|
104,0
|
|
59
|
85,0
|
0
|
3
|
85,0
|
|
60
|
160,0
|
1
|
3
|
70,0
|
|
61
|
60,0
|
0
|
1
|
60,0
|
|
62
|
41,0
|
1
|
1
|
35,0
|
|
63
|
90,0
|
1
|
4
|
75,0
|
|
64
|
83,0
|
0
|
4
|
69,5
|
|
65
|
45,0
|
0
|
1
|
32,8
|
|
66
|
39,0
|
0
|
1
|
32,0
|
|
67
|
86,9
|
0
|
3
|
97,0
|
|
68
|
40,0
|
0
|
1
|
32,8
|
|
69
|
80,0
|
0
|
2
|
71,3
|
|
70
|
227,0
|
0
|
4
|
147,0
|
|
71
|
235,0
|
0
|
4
|
150,0
|
|
72
|
40,0
|
1
|
1
|
34,0
|
|
73
|
67,0
|
1
|
1
|
47,0
|
|
74
|
123,0
|
1
|
4
|
81,0
|
|
75
|
100,0
|
0
|
3
|
57,0
|
|
76
|
105,0
|
1
|
3
|
80,0
|
|
77
|
70,3
|
1
|
2
|
58,1
|
|
78
|
82,0
|
1
|
3
|
81,1
|
|
79
|
280,0
|
1
|
4
|
155,0
|
|
80
|
200,0
|
1
|
4
|
108,4
|
По условию задачи требуется:
1. Рассчитать матрицу парных коэффициентов
корреляции; оценить статистическую значимость коэффициентов корреляции.
Для расчета указанных коэффициентов используем Excel/сервис/анализ данных/КОРРЕЛЯЦИЯ:
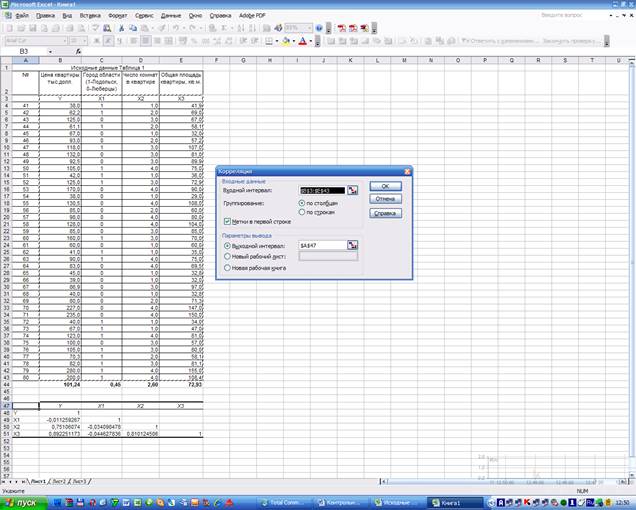
Получим матрицу коэффициентов парной корреляции между
всеми имеющимися переменными:
|
|
Y
|
X1
|
X2
|
X3
|
|
Y
|
1
|
|
|
|
|
X1
|
-0,011259267
|
1
|
|
|
|
X2
|
0,75106074
|
-0,034098478
|
1
|
|
|
X3
|
0,892251173
|
-0,044627836
|
0,810124506
|
1
|
Проанализируем коэффициенты корреляции
между результирующим признаком Y и каждым из
факторов Xj:
r(Y,X1)=-0,01<0 – значит, между переменными Y и X1 наблюдается обратная корреляционная зависимость,
значит цена квартиры выше для г. Люберцы.
|r(Y,X1)|=0,01<0,4 – это зависимость слабая.
r(Y,X2)=0,75>0 –
следовательно, между переменными Y и X2
наблюдается прямая корреляционная зависимость: чем выше число комнат, тем выше цена
квартиры.
r(Y,X2)=0,75>0,7 – следовательно, зависимость является тесной.
r(Y,X3)=0,89>0 – следовательно, между переменными Y и X3 наблюдается прямая корреляционная зависимость: чем
больше общая площадь квартиры, тем выше стоимость квартиры.
r(Y,X3)=0,89>0,7 – следовательно, зависимость является тесной.
Для проверки значимости найденных коэффициентов
корреляции используем критерий
Стьюдента.
Для каждого коэффициента корреляции r(Y, Xj)
вычислим t-статистику по формуле:
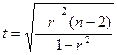
где,  n - количество исходных данных; r –
проверяемый коэффициент.
n - количество исходных данных; r –
проверяемый коэффициент.
Результаты расчетов занесем в
корреляционную таблицу.
|
|
Y
|
X1
|
X2
|
X3
|
t-статистики
|
|
Y
|
1
|
|
|
|
|
|
X1
|
-0,011259267
|
1
|
|
|
0,069411185
|
|
X2
|
0,75106074
|
-0,034098478
|
1
|
|
7,012446419
|
|
X3
|
0,892251173
|
-0,044627836
|
0,810124506
|
1
|
12,18100887
|
Определим критическое значение tкр,
для чего используем Еxcel/вставка/функция/
СТЬЮДРАСПОБР: при этом принимаем уровень значимости α = 5% = 0,05; число
степеней свободы k=n-2=40-2=38.
Получим значение tкр=2,02.

Сопоставим фактические значения tr
с критическим tкр и сделаем выводы в соответствии со схемой:


 не
знач. 2,02 знач.
не
знач. 2,02 знач.
 0 tкр t
0 tкр t
t(r(Y,X1))=0,07<tкр=2,02 – следовательно коэффициент корреляции r(Y,X1) не
является значимым, его отличие от нуля незакономерно. На основании выборочных
данных есть основание утверждать, что зависимость между ценой квартиры Y и городом области X1
недостоверна.
t(r(Y,X2))=7,01>tкр=2,02 – следовательно, коэффициент корреляции r(Y,X2) является
значимым. На уровне значимости 5%
выборочные данные позволяют сделать вывод о наличии линейной корреляционной
связи между признаками Y и X2,
зависимость цены квартиры Y от числа
комнат в квартире X2 является достоверной.
t(r(Y,X3))=12,18>tкр=2,02 – следовательно, коэффициент корреляции r(Y,X3) является
значимым. На уровне значимости 5%
выборочные данные позволяют сделать вывод о наличии линейной
корреляционной связи между признаками Y и X3,
зависимость цены квартиры Y от общей
площади квартиры X3 является достоверной.
Таким образом, тесные и значимые зависимости
наблюдается между ценой квартиры Y и числом
комнат в квартире X2, и ценой
квартиры Y и общей площадью квартиры X3.
Зависимость между ценой квартиры Y и городом области X1 не
является значимой, т.е. достоверной.
2.
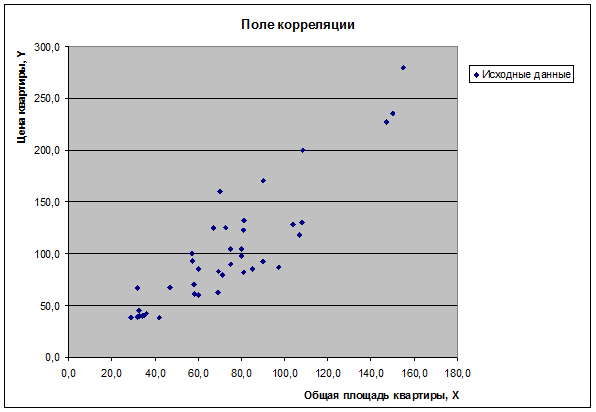
Построить поле корреляции результативного признака и наиболее тесно связанного
с ним фактора.
Для построения поля корреляции используем Мастер
диаграмм (точечная) – покажем исходные данные Y и значения наиболее информативного фактора X3,
т.к. t(r(Y,X3))=12,18> t(r(Y,X2))=7,01.
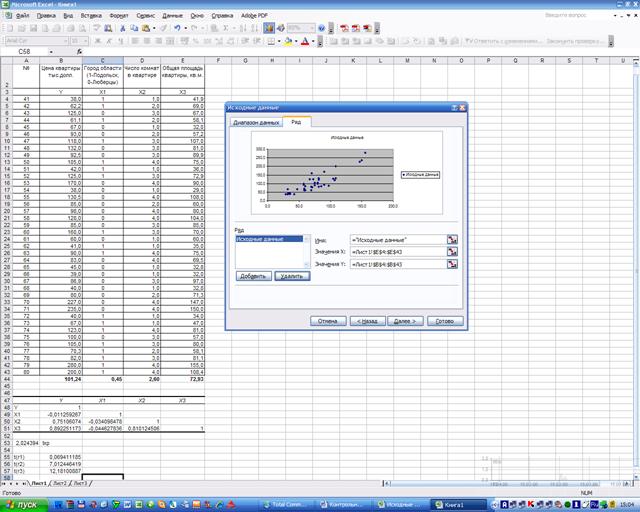
В результате получим
диаграмму «Поле корреляции»:
3. Рассчитать параметры линейных парных
регрессий для всех факторов X.
Для построения парной линейной модели Yr = a + b·X1 используем программу РЕГРЕССИЯ (Сервис/Анализ
данных). В качестве «входного интервала X» покажем значение фактора X3:
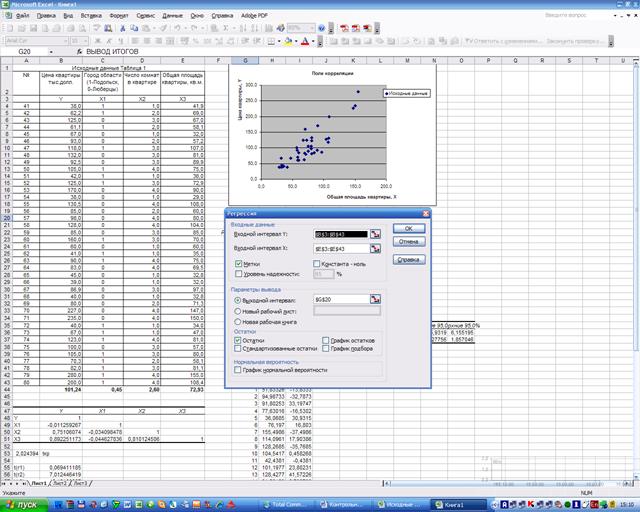
Результаты вычисления
представлены в таблицах:
ВЫВОД ИТОГОВ
|
Регрессионная статистика
|
|
Множественный
R
|
0,892251173
|
|
R-квадрат
|
0,796112156
|
|
Нормированный
R-квадрат
|
0,790746687
|
|
Стандартная
ошибка
|
26,20741042
|
|
Наблюдения
|
40
|
|
Дисперсионный анализ
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
101909,5
|
101909,5
|
148,377
|
1,08E-14
|
|
Остаток
|
38
|
26099,48
|
686,8284
|
|
|
|
Итого
|
39
|
128009
|
|
|
|
|
|
Коэффи-циенты
|
Стандартная ошибка
|
t-ста-тистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
|
Y-пересечение
|
-14,88832959
|
10,39497
|
-1,43226
|
0,160244
|
-35,9319
|
6,155195
|
|
X3
|
1,592400817
|
0,130728
|
12,18101
|
1,08E-14
|
1,327756
|
1,857046
|
ВЫВОД ОСТАТКА
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
Стандартные
остатки
|
|
1
|
51,83326465
|
-13,8333
|
-0,534738041
|
|
2
|
94,98732679
|
-32,7873
|
-1,267425394
|
|
3
|
91,80252516
|
33,19747
|
1,283280059
|
|
4
|
77,63015789
|
-16,5302
|
-0,638989022
|
|
5
|
36,06849656
|
30,9315
|
1,195686772
|
|
6
|
76,19699715
|
16,803
|
0,649536104
|
|
7
|
155,4985578
|
-37,4986
|
-1,449542525
|
|
8
|
114,0961366
|
17,90386
|
0,692090919
|
|
9
|
128,2685039
|
-35,7685
|
-1,382665638
|
|
10
|
104,5417317
|
0,458268
|
0,017714798
|
|
11
|
42,43809983
|
-0,4381
|
-0,016935167
|
|
12
|
101,19769
|
23,80231
|
0,920101
|
|
13
|
128,427744
|
41,57226
|
1,607015215
|
|
14
|
31,29129411
|
6,708706
|
0,259331426
|
|
15
|
157,0909587
|
-26,591
|
-1,027898873
|
|
16
|
80,65571944
|
4,344281
|
0,167932309
|
|
17
|
112,5037358
|
-14,5037
|
-0,560655742
|
|
18
|
150,7213554
|
-22,7214
|
-0,878315668
|
|
19
|
120,4657399
|
-35,4657
|
-1,370962007
|
|
20
|
96,57972761
|
63,42027
|
2,451571129
|
|
21
|
80,65571944
|
-20,6557
|
-0,798466539
|
|
22
|
40,84569901
|
0,154301
|
0,005964652
|
|
23
|
104,5417317
|
-14,5417
|
-0,562124511
|
|
24
|
95,7835272
|
-12,7835
|
-0,494159439
|
|
25
|
37,34241721
|
7,657583
|
0,296011167
|
|
26
|
36,06849656
|
2,931503
|
0,113320062
|
|
27
|
139,5745497
|
-52,6745
|
-2,036184966
|
|
28
|
37,34241721
|
2,657583
|
0,102731398
|
|
29
|
98,64984867
|
-18,6498
|
-0,720927691
|
|
30
|
219,1945905
|
7,805409
|
0,301725549
|
|
31
|
223,971793
|
11,02821
|
0,426305863
|
|
32
|
39,2532982
|
0,746702
|
0,028864471
|
|
33
|
59,95450882
|
7,045491
|
0,272350183
|
|
34
|
114,0961366
|
8,903863
|
0,344187334
|
|
35
|
75,87851699
|
24,12148
|
0,932438936
|
|
36
|
112,5037358
|
-7,50374
|
-0,290064065
|
|
37
|
77,63015789
|
-7,33016
|
-0,283354246
|
|
38
|
114,2553767
|
-32,2554
|
-1,246862355
|
|
39
|
231,9337971
|
48,0662
|
1,858044927
|
|
40
|
157,727919
|
42,27208
|
1,634067617
|
Коэффициенты модели
содержатся в таблице итогов РЕГРЕССИИ (столбец Коэффициенты).
Таким образом, модель (3) построена, ее уравнение
имеет вид:
YТ = -14,9 + 1,6·X3
Коэффициент регрессии b = 1,6 – следовательно, при увеличении общей площади квартиры
(X3) на 1
кв.м. стоимость квартиры (Y) увеличится в
среднем на 1,6 тыс. долларов.
Свободный член а = - 14,9 в данном уравнении не имеет реального смысла.
Для построения модели, отражающей
зависимости цены квартиры Y от города
области X1,
проведем аналогичные расчеты (используем программу РЕГРЕССИЯ):
|
|
Коэффициенты
|
|
Y-пересечение
|
101,8136
|
|
X1
|
-1,2803
|
Таким образом, модель (1) построена, ее уравнение
имеет вид:
YТ = 101,81 - 1,28·X1
Коэффициент регрессии b = -1,28 – следовательно, цена квартиры в Люберцах в среднем на
1,28 тыс. долл. выше чем в Подольске.
Свободный член а = 101,81 в данном уравнении не имеет
реального смысла.
Для построения модели зависимости цены квартиры Y от числа комнат в квартире X2,
проведем аналогичные расчеты:
|
|
Коэффициенты
|
|
Y-пересечение
|
7,539299
|
|
X2
|
36,03777
|
Таким образом, модель (2) построена, ее уравнение
имеет вид:
YТ = 7,54 + 36,04·X2
Коэффициент регрессии b = 5,99 –
следовательно, при увеличении числа комнат в квартире (X2) на одну, стоимость квартиры (Y) увеличится в среднем на 36,04 тыс. долларов.
Свободный член а = 7,54 в данном уравнении не имеет реального смысла.
4.
Оценить качество каждой модели через коэффициент детерминации, среднюю ошибку
аппроксимации и F – критерий
Фишера. Выбрать лучшую модель.
Для
удобства все результаты будем заносить в сводную таблицу.
Коэффициенты
детерминации R2 определены для каждой модели программой РЕГРЕССИЯ
(таблицы «Регрессионная статистика») и составляют:
|
Модель
|
R-квадрат
|
Ēотн
|
F
|
|
YТ = -14,9 + 1,6·X3
(3)
|
0,796112
|
|
|
|
YТ = 101,81 + 1,28·X1
(1)
|
0,000127
|
|
|
|
YТ = 7,54 + 36,04·X2
(2)
|
0,564092
|
|
|
Таким образом, вариация цены квартиры Y на 79,61% объясняется (по модели (3)) вариацией
размера общей площади квартиры X3; на 0,01% (по модели (1)) вариацией городом области
квартиры X1 и на 56,41% (по модели (2)) вариацией количества
комнат в квартире X2.
Для вычисления средней
относительной ошибки аппроксимации рассмотрим остатки модели Ei=Yi–Yn, содержащиеся в столбце Остатки итогов программы
РЕГРЕССИЯ (таблица «Вывод остатка»). Дополним таблицу столбцом относительных
погрешностей, которые вычислим по формуле:
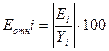 - с помощью функции ABS, и определим, по вычисленному столбцу относительных погрешностей, среднее
значение Ēотн (функция СРЗНАЧ) для каждой модели.
- с помощью функции ABS, и определим, по вычисленному столбцу относительных погрешностей, среднее
значение Ēотн (функция СРЗНАЧ) для каждой модели.
Данные расчетов для модели (3)
приведены в таблице:
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
Стандартные остатки
|
Eотн i
|
|
1
|
51,83326465
|
-13,83326465
|
-0,534738041
|
36,40333
|
|
2
|
94,98732679
|
-32,78732679
|
-1,267425394
|
52,71274
|
|
3
|
91,80252516
|
33,19747484
|
1,283280059
|
26,55798
|
|
4
|
77,63015789
|
-16,53015789
|
-0,638989022
|
27,05427
|
|
5
|
36,06849656
|
30,93150344
|
1,195686772
|
46,16642
|
|
6
|
76,19699715
|
16,80300285
|
0,649536104
|
18,06774
|
|
7
|
155,4985578
|
-37,49855784
|
-1,449542525
|
31,77844
|
|
8
|
114,0961366
|
17,9038634
|
0,692090919
|
13,56353
|
|
9
|
128,2685039
|
-35,76850387
|
-1,382665638
|
38,66865
|
|
10
|
104,5417317
|
0,458268305
|
0,017714798
|
0,436446
|
|
11
|
42,43809983
|
-0,438099829
|
-0,016935167
|
1,043095
|
|
12
|
101,19769
|
23,80231002
|
0,920101
|
19,04185
|
|
13
|
128,427744
|
41,57225605
|
1,607015215
|
24,45427
|
|
14
|
31,29129411
|
6,70870589
|
0,259331426
|
17,65449
|
|
15
|
157,0909587
|
-26,59095866
|
-1,027898873
|
20,37621
|
|
16
|
80,65571944
|
4,344280561
|
0,167932309
|
5,110918
|
|
17
|
112,5037358
|
-14,50373578
|
-0,560655742
|
14,79973
|
|
18
|
150,7213554
|
-22,72135539
|
-0,878315668
|
17,75106
|
|
19
|
120,4657399
|
-35,46573987
|
-1,370962007
|
41,7244
|
|
20
|
96,57972761
|
63,42027239
|
2,451571129
|
39,63767
|
|
21
|
80,65571944
|
-20,65571944
|
-0,798466539
|
34,4262
|
|
22
|
40,84569901
|
0,154300988
|
0,005964652
|
0,376344
|
|
23
|
104,5417317
|
-14,5417317
|
-0,562124511
|
16,15748
|
|
24
|
95,7835272
|
-12,7835272
|
-0,494159439
|
15,40184
|
|
25
|
37,34241721
|
7,657582785
|
0,296011167
|
17,01685
|
|
26
|
36,06849656
|
2,931503439
|
0,113320062
|
7,516675
|
|
27
|
139,5745497
|
-52,67454967
|
-2,036184966
|
60,61513
|
|
28
|
37,34241721
|
2,657582785
|
0,102731398
|
6,643957
|
|
29
|
98,64984867
|
-18,64984867
|
-0,720927691
|
23,31231
|
|
30
|
219,1945905
|
7,805409474
|
0,301725549
|
3,438506
|
|
31
|
223,971793
|
11,02820702
|
0,426305863
|
4,692854
|
|
32
|
39,2532982
|
0,746701805
|
0,028864471
|
1,866755
|
|
33
|
59,95450882
|
7,045491183
|
0,272350183
|
10,51566
|
|
34
|
114,0961366
|
8,903863402
|
0,344187334
|
7,238913
|
|
35
|
75,87851699
|
24,12148301
|
0,932438936
|
24,12148
|
|
36
|
112,5037358
|
-7,503735781
|
-0,290064065
|
7,146415
|
|
37
|
77,63015789
|
-7,330157887
|
-0,283354246
|
10,42697
|
|
38
|
114,2553767
|
-32,25537668
|
-1,246862355
|
39,33583
|
|
39
|
231,9337971
|
48,06620294
|
1,858044927
|
17,1665
|
|
40
|
157,727919
|
42,27208101
|
1,634067617
|
21,13604
|
|
|
|
|
|
20,5389
|
Для модели (3) Ēотн= 20,24%.
Расчет и получение данных для
моделей (2) и (3) выполняются аналогично.
Для модели (1) Ēотн= 54,13%,  для модели (2)
Ēотн= 23,45%.
для модели (2)
Ēотн= 23,45%.
Результаты внесем в сводную
таблицу:
|
Модель
|
R-квадрат
|
Ēотн
|
F
|
|
YТ = -14,9 + 1,6·X3 (3)
|
0,796112
|
20,24%
|
|
|
YТ = 101,81 + 1,28·X1
(1)
|
0,000127
|
54,13%
|
|
|
YТ = 7,54 + 36,04·X2
(2)
|
0,564092
|
23,45%
|
|
Оценим точность построенных
моделей в соответствии со схемой:
точная удовлетв.
неудовлетв.
0 5% 15% Ēотн
Ēотн 1 = 20,24% > 15%
Ēотн 2 = 54,13% > 15%
Ēотн 3 = 23,45% > 15%
Все
значения Ēотн>15%
– следовательно, точность всех трех построенных моделей неудовлетворительная.
Проверим значимость полученных уравнений
с помощью F – критерия
Фишера. F –
статистики определены программой РЕГРЕССИЯ (таблица «Дисперсионный анализ») и
составляют:
|
Модель
|
R-квадрат
|
Ēотн
|
F
|
|
YТ = -14,9 + 1,6·X3 (3)
|
0,796112
|
20,24%
|
148,377
|
|
YТ = 101,81 + 1,28·X1
(1)
|
0,000127
|
54,13%
|
0,00482
|
|
YТ = 7,54 + 36,04·X2
(2)
|
0,564092
|
23,45%
|
49,1744
|
Критическое
значение Fкр = 4,08 найдено для уровня значимости α = 5% и чисел
степеней свободы k1 = 1, k2 = 40 (функция РАСПОБР).
Оценим значимость полученных
уравнений моделей в соответствии со схемой:


 не
знач. 4,08 знач.
не
знач. 4,08 знач.
 0 Fкр t
0 Fкр t
Сравнение показывает:
F3=148,38>Fкр=4,08 – следовательно, уравнение модели (1) является значимым, зависимая
переменная Y достаточно хорошо описывается
включенной в модель факторной переменной X3.
F1=0,005<Fкр=4,08 – следовательно, уравнения модели (2) не является значимым, его
использование нецелесообразно.
F2=49,17>Fкр=4,08 – следовательно, уравнение модели (3) является значимым, зависимая
переменная Y достаточно хорошо описывается
включенной в модель факторной переменной X2.
Вывод: на основании
оценки качества моделей по коэффициенту детерминации, средней ошибке аппроксимации и критерию Фишера,
наилучшей является модель (3)
зависимости цены квартиры Y от размера общей
площади квартиры X3.
Однако результаты
оценки модели по средней ошибке аппроксимации показывают, что точность модели
(1) неудовлетворительная, следовательно, использовать эту модель для прогнозирования в реальных
условиях нецелесообразно. Необходимо построить более точную модель.
5. С использованием лучшей модели осуществить
прогнозирование среднего значения показателя Y при уровне значимости α=0,1, если прогнозное
значение фактора X составит 80%
от его максимального значения. Представить графически фактические и модельные
значения Y, результаты
прогнозирования.
Согласно условию задачи, прогнозное значение факторной
переменной X3 составит 80% от X3max
– x*=124,0 кв.м.
Рассчитаем по уравнению (3) прогнозное значение
показателя Y:
Y*Т = -14,9 + 1,6·124,0= -14,9+ 198,4 =
182,569 тыс.
долл.
Таким образом, при использовании в прогнозировании
лучшей модели, прогнозная цена квартиры общей площадью 124,0 кв.м. составит 182,569
тыс. долларов.
Зададим достоверную вероятность p = 1-α и построим доверительный прогнозный интервал
для среднего значения Y.
Для этого нужно рассчитать стандартную ошибку
прогнозирования для среднего значения результирующего признака
S(Y*r) = SE ·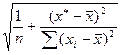
Предварительно
подготовим:
- стандартную
ошибку модели SE = 26,207 (таблица «Регрессионная статистика»
итогов РЕГРЕССИИ).
- по столбцу исходных
данных Xi найдем среднее значение
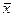 = 72,93 (функция СРЗНАЧ) и определим ∑(хi –
= 72,93 (функция СРЗНАЧ) и определим ∑(хi – 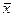 )² = 40189,26 (функция КВАДРОТКЛ).
)² = 40189,26 (функция КВАДРОТКЛ).
- tкр(10%, 40) = 1,68 (функция СТЬЮДРАСПОБР).
Следовательно, стандартная
ошибка прогнозирования для среднего значения составляет
S(Y*T) = 26,207 ·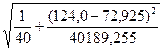 = 7,859
= 7,859
Размах
доверительного интервала для среднего значения
U(Y*T) = tкр· S(Y*T) = 1,68 · 7,859
= 13,202
Границами
прогнозного интервала будут
Uнижн = Y*T - U(Y*T) = 182,569 – 13,202 = 169,367
Uверх. = Y*T + U(Y*T) = 182,569 + 13,202 = 195,771
Таким образом, с надежностью 90% можно утверждать, что
ожидаемая средняя цена квартиры жилой площадью 124,0 кв.м. будет находится в
пределах от 169,367 тыс. долларов до 195,771 тыс. долларов.
Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные (поле
корреляции).


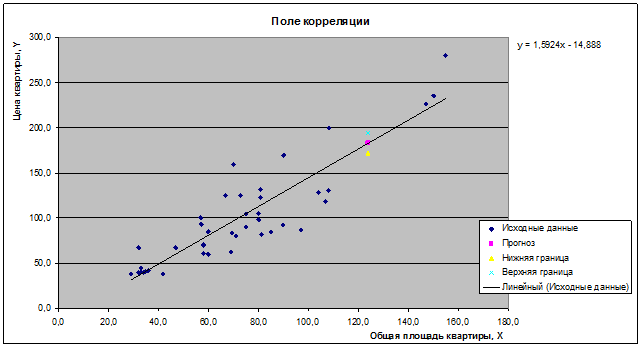
6.
Используя пошаговую множественную регрессию (метод исключения или метод
включения), построим модель формирования цены квартиры за счет значимых
факторов. Дать экономическую интерпретацию коэффициентов модели регрессии.
В нашей задаче фактор X1 (город
области) не является значимым, а фактор X2 (число
комнат в квартире) является значимыми, однако в познавательных целях, методом
включения построим двухфакторные модели, сохраняя в них наиболее информативный
фактор – X3(общая площадь квартиры).
В качестве «входного интервала X» укажем значения факторов X2 и X3, с
помощью программы РЕГРЕССИЯ получим:
|
|
Коэффициенты
|
|
Y-пересечение
|
-16,47476878
|
|
X2
|
3,940559372
|
|
X3
|
1,473662179
|
Таким образом, модель (4) зависимости цены квартиры Y от общей площади квартиры X3 и количества
комнат в квартире X2 построена, ее уравнение имеет вид:
YТ = -16,47 + 3,94·X2
+ 1,47·X3
Используем
в качестве «входного интервала X» значения
факторов X1 и X3, с помощью программы РЕГРЕССИЯ получим:
|
|
Коэффициенты
|
|
Y-пересечение
|
-16,5189
|
|
X1
|
3,254065
|
|
X3
|
1,59468
|
Таким образом модель (5) зависимости цены квартиры Y от общей площади квартиры X3 и города
области X1
построена, ее уравнение имеет вид:
YТ = -16,52 + 3,25·X1
+ 1,59·X3
Построим
множественную модель регрессии, учитывая все факторы X1, X2, X3.
|
|
Коэффициенты
|
|
Y-пересечение
|
-18,0924
|
|
X1
|
3,23487
|
|
X2
|
3,932395
|
|
X3
|
1,476174
|
Таким
образом, трехфакторная модель (6) зависимости цены квартиры Y от общей площади квартиры X3, количества
комнат в квартире X2 и города области X1
построена, ее уравнение имеет вид:
YТ = -18,09 + 3,23·X1
+ 3,93·X2 + 1,48·X3
Выберем лучшую из построенных
множественных моделей.
Для сравнения моделей с различным количеством учтенных
в них факторов используем нормированные коэффициенты детерминации, которые
содержатся в строке «нормированый R-квадрат»
итогов программы РЕГРЕССИЯ. Чем больше величина нормированного коэффициента
детерминации, тем лучше модель.
|
Модель
|
Нормированный
R-квадрат
|
|
YТ = -16,47 + 3,94·X2 + 1,47·X3 (4)
|
0,787535
|
|
YТ = -16,52 + 3,25·X1
+ 1,59·X3 (5)
|
0,785953
|
|
YТ = -18,09 + 3,23·X1 + 3,93·X2
+ 1,48·X3 (6)
|
0,782508
|
Анализ коэффициентов детерминации показывает, что все
три модели практически равнозначны, но лучшей
из них является модель (4),
показывающая зависимость цены квартиры Y от общей площади квартиры X3 и количества
комнат в квартире X2.
Коэффициент
регрессии b3=1,47, следовательно, при увеличении общей площади квартиры
X3 на 1
кв.м. при неизменном значении количества комнат в квартире X2, цена
квартиры увеличится в среднем на 1,47 тыс. долларов.
Коэффициент
регрессии b2=3,94, следовательно, при изменении количества комнат в квартире X2 в
сторону увеличения на одну, при неизменной общей площади квартиры X3, цена
квартиры увеличится в среднем на 3,94 тыс. долларов.
Свободный
коэффициент не имеет экономического смысла.
7.
Оценить качество построенной модели. Выяснить, улучшилось ли качество модели по
сравнению с однофакторной моделью? Дать
оценку влияния значимых факторов на результат с помощью коэффициентов
эластичности, β- и Δ- коэффициентов.
Для оценки качества выбранной модели (4) используем
коэффициент детерминации
R-квадрат,
среднюю относительную ошибку аппроксимации и F-критерий
Фишера.
Коэффициент детерминации R-квадрат
выпишем из итогов РЕГРЕССИИ (таблица «Регрессионная статистика» для модели
(4)).
R² = 0,7984 = 79,84%, следовательно вариация (изменения) цены квартиры Y на 79,84% объясняется по данному уравнению вариацией общей
площади квартиры X3 и количества комнат в квартире X2.
Используем исходные данные yi и найденные программой РЕГРЕССИЯ остатки Ei
(таблица «Вывод остатка» для модели (4)). Рассчитаем относительные погрешности
и найдем среднее значение Ēотн = 21,11%.
Сравнение показывает, что 21,11%>15%. Следовательно, точность
модели неудовлетворительная.
С помощью F – критерия
Фишера проверим значимость модели в
целом. Для этого выпишем из итогов РЕГРЕССИИ (таблица «Дисперсионный анализ» для модели (4))
F=73,28. Определим критическое значение Fкр (5%,2,37) = 3,25 (Функция FРАСПОБР).
Сравним найденные величины:
F=73,28>Fкр=3,25 – следовательно, уравнение модели в целом является значимым, зависимая переменная Y достаточно хорошо описывается включенными в модель
факторными переменными X2 и X3 .
Дополнительно с помощью t-критерия Стьюдента проверим значимость отдельных коэффициентов модели.
t-статистики
для коэффициентов уравнения регрессии приведены
в итогах программы РЕГРЕССИЯ. Для выбранной модели (4) получим следующие
значения:
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
|
Y-пересечение
|
-16,47476878
|
10,75309349
|
-1,532095745
|
0,134005
|
|
X2
|
3,940559372
|
6,040960563
|
0,652306753
|
0,518236
|
|
X3
|
1,473662179
|
0,224692418
|
6,558575451
|
1,11E-07
|
Критическое
значение tкр = 2,026 найдено для
уровня значимости α=5% и числа
степеней свободы k = 40 – 2 - 1 = 37 (Приложение 1
или функция СТЬЮДРАСПОБР).
Схема проверки:


 не
знач. 2,03 знач.
не
знач. 2,03 знач.
 0 tкр t
0 tкр t
Для
свободного коэффициента а= -16,47
определена статистика t(а) = -1,53.
│t(а)│=0,77<tкр=2,03, следовательно, свободный коэффициент а не является значимым,
его можно исключить из модели.
Для коэффициента регрессии b2 = 3,94 определена статистика t(b2) = 0,65.
│t(b2)│= 0,65<tкр=2,03, следовательно, свободный коэффициент b2 не является значимым, его можно исключить из модели.
Для коэффициента регрессии b3 = 1,47 определена статистика t(b3) = 6,56.
│t(b3)│=6,56>tкр=2,03, следовательно, коэффициент регрессии b3 является значимым, следовательно фактор
общей площади квартиры нужно сохранить в модели.
Выводы о значимости коэффициентов модели сделаны на
уровне значимости α = 5%.
Рассматривая
столбец «Р-значение», отметим, что свободный коэффициент a можно считать значимым на уровне 0,13 = 13%;
коэффициент регрессии b2 – на уровне 0,52 = 52%; коэффициент регрессии b3
– на уровне 0,000000111 = 0, 00001%.
При добавлении в уравнение новых факторных переменных
автоматически увеличивается коэффициент детерминации R² и уменьшается средняя ошибка
аппроксимации, при этом не всегда
улучшается качество модели. Поэтому для сравнения качества парной модели (3) и
выбранной множественной модели (4) используем нормированные коэффициенты детерминации.
|
Модель
|
Нормированный R-
квадрат
|
|
YТ = -14,9 + 1,6·X3 (3)
|
0,790747
|
|
YТ = -16,47 + 3,94·X2
+ 1,47·X3 (4)
|
0,787535
|
Таким образом, при добавлении в уравнение регрессии
фактора количества комнат в квартире (X2) качество
модели ухудшилось, что говорит не в пользу сохранения фактора X2 в
модели.
Средние коэффициенты
эластичности в случае линейной модели определяются формулами:
Эj = bj· 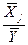 , j = 1,2,…,
, j = 1,2,…,
где 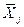 ,
, 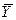 – выборочные средние
признаков Xj и Y; bj –
коэффициенты регрессии.
– выборочные средние
признаков Xj и Y; bj –
коэффициенты регрессии.
Подготовим 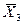 =72,93;
=72,93; 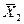 =2,6;
=2,6; 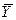 =101,24
=101,24
Э3 = 3,94· 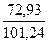 = 2,838; Э2
= 1,47·
= 2,838; Э2
= 1,47· 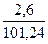 = 0,378
= 0,378
Следовательно, при увеличении общей площади квартиры X3 на 1% и
неизменном значении количества комнат в квартире X2
стоимость квартиры увеличивается в среднем на 2,838%.
Изменение количества комнат в квартире в % выражать не
имеет логического смысла.
Бета-коэффициенты определяются формулами βj = bj· 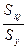 , j = 1,2,…,
, j = 1,2,…,
где Sxj , Sy - выборочные средние квадратичные (стандартные)
отклонения признаков Xj и Y.
bj – коэффициенты регрессии.
Подготовим Sx3 = 32,101;
Sx2 = 1,194;
Sy =
57,291 (функция СТАНДАРТОТКЛОН).
Рассчитаем: β3 = 0,8237, β2 = 0,0821.
Таким образом, при увеличении только фактора X3 на одно
свое стандартное отклонение результат Y
увеличивается в среднем на 0,8237 своего стандартного отклонения Sу, при увеличении только фактора X2 на его
одно стандартное отклонение результат
Y увеличивается в среднем на 0,0821 своего стандартного
отклонения Sу.
Дельта – коэффициенты определяются формулами ∆j = βj· 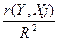 , j = 1,2,…,
, j = 1,2,…,
где r(Y, Xj) – соответствующие выборочные коэффициенты парной
корреляции.
Коэффициенты парной корреляции r(Y, X3) = 0,892;
r(Y, X2) = 0,751
найдены с помощью программы КОРРЕЛЯЦИЯ (п.1 данной задачи), коэффициент
детерминации
R2=0,798
определен из рассматриваемой двухфакторной модели программой РЕГРЕССИЯ.
Вычислим дельта –
коэффициенты:
∆3 = 0,823·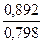 = 0,9205
= 0,9205
∆2 = 0,082·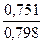 = 0,0772
= 0,0772
Значит, по уравнению полученной линейной
двухфакторной модели изменение результирующего фактора Y (цены квартиры) на 92,05% объясняется воздействием
фактора X3 (общей площади квартиры) и на 7,72% влиянием фактора X2 (количество
комнат в квартире).
 Задача 2.
Исследование динамики экономического показателя на основе
Задача 2.
Исследование динамики экономического показателя на основе
анализа одномерного временного ряда.
В течении девяти последовательных недель фиксировался
спрос Y(t) (млн. руб.)
на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого
показателя приведен ниже.
|
№ наблюдения
|
Спрос на кредитные ресурсы Y
в млн. руб.
|
|
1
|
8
|
|
2
|
13
|
|
3
|
15
|
|
4
|
19
|
|
5
|
25
|
|
6
|
27
|
|
7
|
33
|
|
8
|
35
|
|
9
|
40
|
Требуется:
- Проверить наличие аномальных наблюдений.
Используем метод Ирвина, основанный на определении
λt –
статистики.
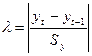 ,
,
где Sy – выборочное
среднеквадратичное (стандартное) отклонение признака Y.
Подготовим Sy = 10,9
(функция СТАНДОТКЛОН) и рассчитаем λt – статистики.
|
№ наблюдения
|
Спрос на кредитные
ресурсы Y
в млн. руб.
|
λt
|
|
1
|
8
|
|
|
2
|
13
|
0,45861696
|
|
3
|
15
|
0,183446784
|
|
4
|
19
|
0,366893568
|
|
5
|
25
|
0,550340352
|
|
6
|
27
|
0,183446784
|
|
7
|
33
|
0,550340352
|
|
8
|
35
|
0,183446784
|
|
9
|
40
|
0,45861696
|
Табличные
значения λкр
определим при n=9 и уровне значимости α =
5% – λкр=1,5.
Схема проверки:
не аном. 1,5 аном.

0 λкр λ
Все
величины статистики λi<λкр=1,5
– поэтому все наблюдения Yi
признаются не аномальным и не требуют замены.
2.
Построить линейную модель временного ряда
Yt=a+b·t, параметры которой
оценить МНК.
С помощью
программы «РЕГРЕССИЯ» найдем
|
|
Коэффициенты
|
|
Y-пересечение
|
4,055555556
|
|
t
|
3,966666667
|
Таким образом, a = 4,056; b = 3,967.
Модель построена, ее уравнение имеет вид Yt = 4,056 + 3,967·t
Коэффициент
регрессии b = 3,967
показывает, что с каждой последующей неделей спрос на кредитные ресурсы финансовой
компании увеличивается в среднем на 3,967 млн. рублей.
3.
Оценить адекватность построенной модели, используя свойства независимости остаточной компоненты, случайности и
соответствия нормальному закону распределения.
Проверка
перечисленных свойств состоит в исследовании Ряда остатков et, который содержится в таблице «Вывод остатка» итогов РЕГРЕССИИ.
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
1
|
8,022222222
|
-0,022222222
|
|
2
|
11,98888889
|
1,011111111
|
|
3
|
15,95555556
|
-0,955555556
|
|
4
|
19,92222222
|
-0,922222222
|
|
5
|
23,88888889
|
1,111111111
|
|
6
|
27,85555556
|
-0,855555556
|
|
7
|
31,82222222
|
1,177777778
|
|
8
|
35,78888889
|
-0,788888889
|
|
9
|
39,75555556
|
0,244444444
|
Для проверки свойства независимости
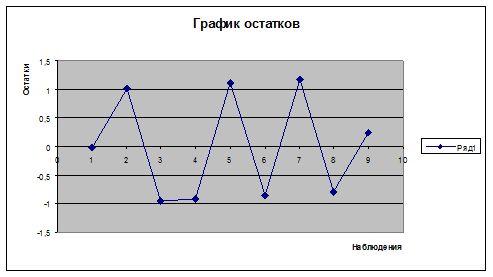
остаточной компоненты используем критерий Дарбина-Уотсона. Согласно
этому критерию вычислим по формуле статистику:
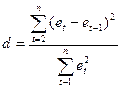
Подготовим
для вычислений:
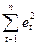 = 6,82;
= 6,82; 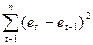 = 22,01
= 22,01
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
(ei -e(i-1))х2
|
|
1
|
8,022222222
|
-0,022222222
|
|
|
2
|
11,98888889
|
1,011111111
|
1,067777778
|
|
3
|
15,95555556
|
-0,955555556
|
3,867777778
|
|
4
|
19,92222222
|
-0,922222222
|
0,001111111
|
|
5
|
23,88888889
|
1,111111111
|
4,134444444
|
|
6
|
27,85555556
|
-0,855555556
|
3,867777778
|
|
7
|
31,82222222
|
1,177777778
|
4,134444444
|
|
8
|
35,78888889
|
-0,788888889
|
3,867777778
|
|
9
|
39,75555556
|
0,244444444
|
1,067777778
|
|
|
|
6,822222222
|
22,00888889
|
Таким
образом, 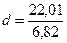 = 3,23
= 3,23
По таблице d–статистики
Дарбина–Уотсона определим критические
уровни:
нижний
d1 = 0,82; верхний d2 = 1,32.
Сравним полученную фактическую величину d с критическими уровнями d1 и d2 и сделаем вывод согласно схеме:




 не вып. доп. пров. вып. вспом
d´ = 4 – d
не вып. доп. пров. вып. вспом
d´ = 4 – d
0
0,82 1,32 2
4
d = 3,23 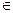 (2;4) – следовательно,
используем d´= 4 – 3,23 = 0,77.
(2;4) – следовательно,
используем d´= 4 – 3,23 = 0,77.
d´= 0,77 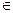 (0;0,82) –
следовательно свойство независимости
остатков построенной модели не выполняется.
(0;0,82) –
следовательно свойство независимости
остатков построенной модели не выполняется.
Для проверки свойства случайности остаточной
компоненты используем критерий поворотных точек (пиков), основой которого
является определение количества поворотных точек для ряда остатков.
С помощью Мастера
диаграмм построим график остатков ei.
Поворотными считаются точки максимумов и
минимумов на этом графике – в нашей задаче: вторая, третья, пятая, шестая,
седьмая, восьмая. Их количество p = 6.
По
формуле 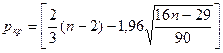 , при n = 9 вычислим
критическое значение
, при n = 9 вычислим
критическое значение
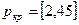 = 2.
= 2.
Сравним значения p и pкр и сделаем вывод согласно схеме:

 не
вып. вып.
не
вып. вып.
0 ркр =
2 р
р=6>ркр=
2 – следовательно, свойство случайности для ряда остатков выполняется.
Для проверки соответствия ряда остатков нормальному
закону распределения используем R/S критерий.
В соответствии с этим критерием вычислим
по формуле статистику
R/S = 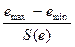 .
.
Подготовим
для вычислений:
emax = 1,178 – максимальный уровень ряда остатков.
emin = - 0,956 – минимальный уровень ряда остатков.
S(е) = 0,987 – стандартная ошибка модели (таблица «Регрессионная статистика» вывода итогов
РЕГРЕССИИ).
Получим R/S = 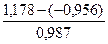 = 2,161
= 2,161
По таблице критических границ отношений R/S определим
критический интервал.
При
n = 9 и уровне значимости α = 5% можно
использовать интервал (2,67;3,69).
Сопоставим фактическую величину R/S с критическим
интервалом и сделаем вывод согласно схеме:
не
вып. вып. не
вып.
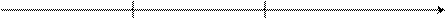
(2,67 -критич. интервал – 3,69) R/S
2,161  (2,67;3,69) –
следовательно, для построенной модели свойство
нормального распределения остаточной
компоненты не выполняется.
(2,67;3,69) –
следовательно, для построенной модели свойство
нормального распределения остаточной
компоненты не выполняется.
Вывод:
Проведенная
проверка показывает, что для построенной модели не выполняется условия
нормального распределения остаточной компоненты.
Таким
образом, данная трендовая модель не является адекватной реальному ряду
наблюдений, и ее нельзя использовать для построения прогнозных оценок.
4.
Оценить точность модели на основе использования средней относительной
ошибки аппроксимации.
Используем исходные данные yi (сглаженный ряд) и найденные программой РЕГРЕССИЯ
остатки ei (таблица «Вывод
остатка»).
По
формуле 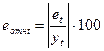 рассчитаем столбец относительных погрешностей и найдем
среднее значение
рассчитаем столбец относительных погрешностей и найдем
среднее значение 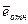 = 3,703 = 3,7%
= 3,703 = 3,7%
Сравним
значение 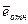 и сделаем вывод в
соответствии со схемой:
и сделаем вывод в
соответствии со схемой:
высок. удовл. неуд.
0 5% 15% eотн
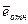 = 3,7% < 5% -
следовательно, точность модели высокая.
= 3,7% < 5% -
следовательно, точность модели высокая.
5.
Осуществить прогноз спроса на следующие две недели (прогнозный интервал
рассчитать при доверительной
вероятности р = 70%).
Следующие две недели соответствуют периодам упреждения
k1 = 1 и k2 = 2, при
этом
t*1 = n + k1 = 10 и t*2
= n + k2 = 11
Согласно уравнению модели получим точечные прогнозные
оценки:
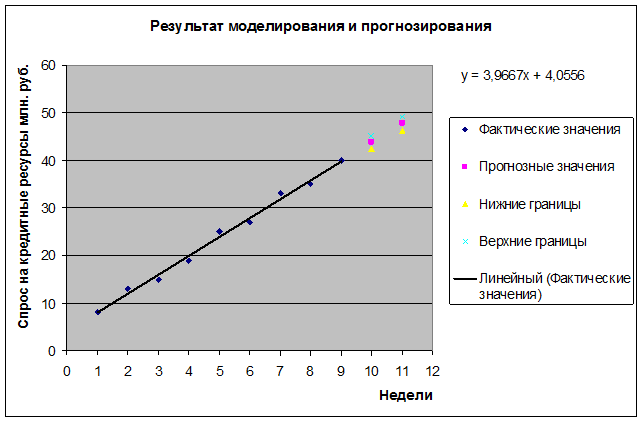
y*10 = 4,056+3,967·10 = 43,7222
y*11 = 4,056+3,967·11 = 47,6889
Таким образом, ожидаемы
спрос на кредитные ресурсы в следующие две недели будет составлять около 43,7222
млн. рублей и 47,6889 млн. рублей соответственно.
Для оценки точности прогнозирования рассчитаем границы
прогнозного интервала для индивидуальных значений результирующего признака
(доверительная вероятность 70%)
Подготовим:
tкр = 1,12 (функция СТЬЮДРАСПОБР при α=30%, k =9-2=7);
S(e) = 0,987
(строка «стандартная ошибка» итогов
РЕГРЕССИИ);
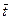 = 5 (функция СРЗНАЧ);
= 5 (функция СРЗНАЧ);
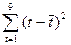 =60 (функция
КВАДРОТКЛ);
=60 (функция
КВАДРОТКЛ);
Вычислим размах прогнозного интервала для
индивидуальных значений, используя формулу:
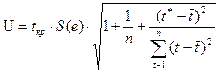
При t*1 = 10 получим U10 = 1,3656 и определим границы доверительного интервала:
Uниж 10 = y´10
- U10 =
43,7222 – 1,3656 = 42,3566
Uверх 10 = y´10
+ U
10 =
43,7222 + 1,3656 = 45,0878
При t*2 = 11 получим U11 = 1,4453 и определим границы доверительного интервала:
Uниж 11 = y´11
- U
11
= 47,6889 – 1,4453 = 46,2436
Uверх 11 = y´11
+ U
11
= 47,6889 + 1,4453 = 49,1342
Вывод: Таким
образом, с надежностью 70% можно утверждать, что спрос на кредитные ресурсы в
следующие две недели будет составлять от 42,3566 млн. рублей до 45,0878 млн.
рублей в первую прогнозируемую неделю и от 46,2436 млн. рублей до 49,1342 млн.
рублей во вторую прогнозируемую неделю.
6.
Представить графически фактические значения показателя, результаты
моделирования и прогнозирования.
Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные.
Затем с помощью опции Добавить линию тренда… построим линию модели. Покажем на графике
результаты прогнозирования. Для чего в опции Исходные данные добавим ряды.
Литература
1. Эконометрика: Учебник/ Под
редакцией И.И. Елисеевой.
М.; Финансы и статистика, 2004 г.
2. Эконометрика: Методические
указания по выполнению
контрольной работы.
3. Эконометрика: Задания для
выполнения контрольной работы.
4. Эконометрика: Методические
указания по решению задач и
выполнению контрольной работы (для
студентов 2-го высшего
образования).