Тема преступности никогда не теряет своей актуальности. Особенно в последнее время, вследствие неблагоприятной социально-экономической ситуацией в России и в частности в городе Новосибирске. Количество преступлений увеличивается, в связи с этим в данной работе проводится статистическое исследование динамики количества преступлений (нанесения тяжких телесных повреждений) в г. Новосибирске в период с 1985 по 2002 гг.

Статистические данные динамики количества преступлений (нанесения тяжких телесных повреждений) в г. Новосибирске в период с 1985 по 2002 гг. приведены в табл. 1

Таблица 1

Динамика количества преступлений (нанесения тяжких телесных повреждений) в г. Новосибирске[1]

Динамику увеличения количества преступлений представим на рис. 1.

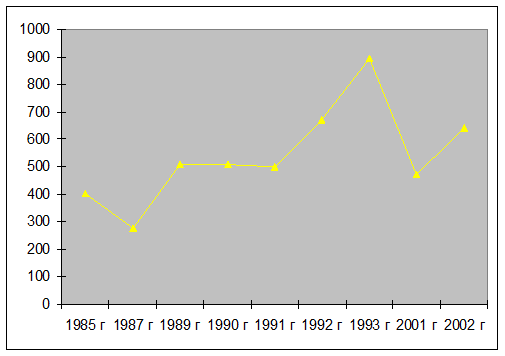
Рисунок 1. Динамика изменения количества преступлений за рассматриваемый период

График динамики преступлений за рассматриваемый период имеет «переломы» в 1987 г  и в 2001 году (снижение). Как видно из рис. 1, с 1985 по 1993 год наблюдается тенденция увеличения количества преступлений, причем пик преступлений приходится 1993 год, с 1993 года по 2001 год – наблюдается тенденция снижения количества преступлений, а с 2001- увеличения.

Зная общее количество преступлений, совершенных в Новосибирске, можно рассчитать долю тяжких телесных повреждений в общем числе (табл. 2).

Таблица 2

Доля тяжких телесных повреждений в общем числе

Продолжение табл. 2

Полученные данные представим на графике (рис. 2).

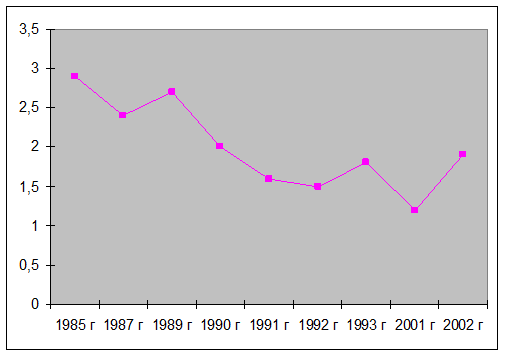
Рисунок 2

Как видно из рис. 2, доля тяжких телесных повреждений в общем числе преступлений с рассматриваемый период времени снизилась. График имеет три «перелома» (увеличения): в 1989, 1993 и 2002 году.

Рассчитаем среднюю хронологическую тяжких телесных повреждений:

y_cp=∑y_i/n=4869/9 = 541

Рассчитаем приросты преступлений по формулам:

Абсолютные приросты цепные и базисные:

∆_цепной=y_i - y_i-1;    ∆_базисн=y_i – y₀

Темпы роста цепные и базисные:

Т_цепной =100*y_i / y_i-1 ;    Т_базисн=100*y_i / y₀

Темпы прироста цепные и базисные:

∆Т_цепной =100*∆_цепной / y_i-1 = Т_цепной - 100;

∆Т_базисн=100*∆_базисн / y₀= Т_базисн - 100

Абсолютное содержание 1% прироста:

А=∆_цепной /∆Т_цепной= y_i-1/100

Расчет приведем в табл. 3

Предполагаем, что между динамикой преступлений и годом имеется линейная зависимость:

Y = a + bt

Для нахождения коэффициентов а и b необходимо составить систему уравнений:

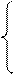
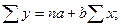
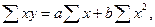 где n – численность совокупности (в данном случае n =9).

Выражая из данной системы коэффициенты, можно получить:

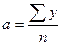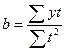, , в данном случае

а = 4869/9 = 541 тыс. ед.

b = 2488/60= 41,47 тыс. ед.

Уравнение тренда: y = 541+ 41,47t.

Выбираем модель изменения уровня – аналитическое выравнивание. Расчет приведен в таблице. Выровненные значения показаны на графике.

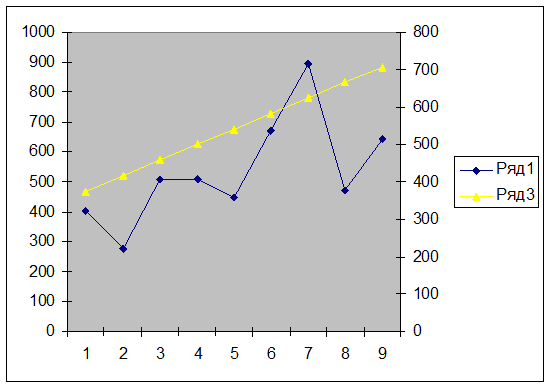
Рисунок.3. Выровненные значения количества преступлений

Средний абсолютный прирост:

∆y_ср=∑∆_цепные/(n-1)=913,334 /8 = 14,16

Таким образом, проведя данное исследование, можно сделать следующие выводы.

1. В целом наблюдается тенденция увеличения количества преступлений (нанесения тяжких телесных повреждений) в г. Новосибирске в рассматриваемый период с 1985 по 2002 г., однако в 1987 г  и в 2001 году наблюдаются «переломы» (снижение) количества преступлений.

2. В динамика доли тяжких телесных повреждений в общем количестве преступлений наблюдается снижений, однако в 1989 и 1993 гг. также наблюдаются «переломы» - увеличение преступлений.

3. Неблагоприятным является тот факт, что с 2002 года можно отметить увеличение количества рассматриваемых преступлений.

4. Средняя хронологическая тяжких телесных повреждений равна 541 тыс.

5. Средний абсолютный прирост за рассматриваемый период равен 14,16 тыс.

Задача 2

Используя данные Новосибирского государственного комитета по статистике и своего варианта, определить

1. Показатели дифференциации: средневзвешенное значение среднедушевого дохода, модального и медианного дохода, децильных значений среднедушевого дохода, коэффициента дифференциации

2. Сделать вывод

Таблица 1

Распределение домохозяйств по размеру среднедушевого денежного дохода за 2000г.

Решение:

Среднее значение среднедушевого денежного дохода:

58800/28 = 2100 руб.

Модальный размер среднедушевого дохода равен:

М_о=x₀+h*( m₂- m₁)/( ( m₂- m₁)+( m₂- m₃))

 Модальный интервал (750,1-900), т.к. m_max=8

    М_о =750,1+150*(8,0-7,6)/((8,0-7,6)+(8,0+7,7))= 753,83

. Медианный среднедушевой доход:

М_е= x₀+h*(1/2*∑m_i-Sдо М_е)/m_{мед.инт}

 ∑m_i/2=100/2=50 -  середина ряда.

М_е= 750,1+150 *(0,5* 100 -75)/8 = 281,35 тыс. руб.

Децильный коэффициент дифференциации равен:

Кd = d₉ / d₁

d₁ = x1+h*(0,1*∑m_i-Sдо М_е)/m_{мед.инт} =  75+ 150*(0,1*100-75)/8 = 196,875

d₉ = x9+h*(0,9 *∑m_i-Sдо М_е)/m_{мед.инт} =  4125 + 150*(0,9 *100-75)/8 = 8343,75

Кd = d₉ / d₁  = 8343,75/196,875 = 42,38

Полученные значения:

- моды (753,83 руб.),

- медианы (281,35  руб.),

-  среднего значения (2100 руб.) среднедушевого денежного дохода в 1 квартале 1995 г. показывают  неравномерный  характер  распределения  среднедушевых  денежных  доходов  в данной совокупности.

- Минимальные доходы 10 %-в самого богатого населения превышают максимальные доходы 10 %-в наименее обеспеченного населения в 42,38 раз

Модальный размер среднедушевого дохода равен:

М_о=x₀+h*( m₂- m₁)/( ( m₂- m₁)+( m₂- m₃))

 Модальный интервал (300,1-450,0), т.к. m_max=13,7

    М_о =300,1+150*(13,7-10,2)/((13,7-10,2)+(13,7+12,6))=  317,71

. Медианный среднедушевой доход:

М_е= x₀+h*(1/2*∑m_i-Sдо М_е)/m_{мед.инт}

 ∑m_i/2=100/2=50 -  середина ряда.

М_е= 300,1+150 *(0,5* 100 -375)/8 = 302. руб.

Децильный коэффициент дифференциации равен:

Кd = d₉ / d₁

d₁ = x1+h*(0,1*∑m_i-Sдо М_е)/m_{мед.инт} =  150+ 150*(0,1*2,5)/8 = 154,68

d₉ = x9+h*(0,9 *∑m_i-Sдо М_е)/m_{мед.инт} =  4050 + 150*(0,9 *100)/8 = 5737,5

Кd = d₉ / d₁  = 5737,5/154,68= 37,09

Полученные значения:

- моды (317,71 руб.),

- медианы (302  руб.),

-  среднего значения (2100 руб.) среднедушевого денежного дохода в 1 квартале 1995 г. показывают  неравномерный  характер  распределения  среднедушевых  денежных  доходов  в данной совокупности.

- Минимальные доходы 10 %-в самого богатого населения превышают максимальные доходы 10 %-в наименее обеспеченного населения в 37,09 раз

Задача 2

На основе следующих данных «Российского статистического ежегодника, 1999 г.» таблицы № 1 рассчитать по данным своего варианта 1) размах вариации рассматриваемой пенсии; ) коэффициент вариации пенсии - простой и взвешенный, 3) полученные результаты проанализировать и сделать вывод.

Таблица № 1

Расчетная таблица

R = 1405,92-8,91 = 1397,01

Коэффициенты вариации:

Vпростой =103130,27/5/332,4 *100 = 66,05%

Vвзвешенный =1450056,38/5/332,4 *100 = 872,47%

Полученные коэффициенты больше 30 %, совокупность размеров пенсий является неоднородной

Расчетная таблица

R = 205,47-11,47= 194

Коэффициенты вариации:

Vпростой =239406,85/5/200,4*100 = 238,92%

Vвзвешенный =37552,5/5/200,4*100 = 37,47%

Полученные коэффициенты больше 30 %, совокупность размеров пенсий является неоднородной

Литература

1.                Гришин А.Ф. Статистика: Учеб. Пособие. – М.: Финансы и статистика, 2003. – 240с

2.                 Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник.-М.:ИНФРА – М., 1996.- 416 с.

3.                Ефремова М.Р. «Общая теория статистики»; М.: «Инфра-М», 1996

4.                Сборник задач по теории статистики: Учебное пособие/Под ред. проф. В.В.Глинского и к.э.н. Л.К.Серга. – М.: ИНФРА-М; 2002.-257 с.

5.                Экономическая статистика (под. ред. Ю.Н. Иванова) М.:ИНФРА-М, 1998

[1] http://strateg.novo-sibirsk.ru/2004/invest/target/t04.htm