Задание 1. Укажите, какие пары понятий
представляют собой отношение:
А –
подчинения (первое понятие родовое);
В –
подчинения (первое понятие видовое);
С –
пересечения;
D – соподчинения;
E – противоречия.
1) а – турист, побывавший в Париже; б –
турист, побывавший во Франции;
2) а – турист, не бывавший в Париже; б – турист, не бывавший во Франции;
3) а – человек, не имеющий права
принимать участие в выборах органов государственной
власти РФ; б – студент, не принимавший
участия в выборах органов государственной власти;
4) а – медведь, участвовавший в
цирковых представлениях; б – медведь, не участвовавший в цирковых
представлениях [Медведь];
5) а – человек, не имеющий права
принимать участие в выборах органов государственной
власти РФ; б – студент УрГЮА, не являющийся гражданином РФ;
6) а – автобус; б – водитель автобуса;
7) а – человек, не имеющий права
принимать участие в выборах органов государственной
власти РФ; б – студент вуза, получающий
впервые образование этой ступени;
8) а – студент, соблюдающий правила
проведения экзамена; б – студент, пользующийся шпаргалками во время
экзамена.
Решение
Находятся в отношении А – подчинения (первое понятие родовое):
2), т.к. турист, который не был в Париже, мог тем не
менее побывать во Франции, например, в Марселе;
5), т.к. студенты УрГЮА,
не являющиеся гражданами РФ входят в число людей, не имеющих права принимать участие в выборах органов государственной
власти РФ.
Находятся в отношении В – подчинения (первое понятие видовое):
1), т.к. Париж – это часть Франции.
Находятся в отношении С –
пересечения:
3), т.к. некоторые студенты (не граждане РФ и моложе 18
лет) не имеют права
принимать участие в выборах органов государственной
власти РФ и наоборот, некоторые люди, не
имеющие права принимать участие в выборах органов государственной власти
РФ, могут оказаться студентами;
7), т.к. некоторые люди, не имеющие права принимать участие в выборах
органов государственной власти РФ, могут оказаться студентами вуза, получающий впервые образование этой ступени
и наоборот.
Находятся в отношении D – соподчинения:
6), т.к. автобус и водитель автобуса вместе составляют автобус как пассажирский
транспорт, перевозящий людей.
Находятся в отношении E – противоречия:
4), т.к. медведь не может одновременно участвовать и не участвовать в цирковых
представлениях.
8), т.к. студент, соблюдающий правила проведения экзамена не пользуется шпаргалками во время экзамена и
наоборот.
Задание 2.
Найдите круги Эйлера, соответствующие перечню понятий:
студент, студент первого курса, студент очной формы обучения, совершеннолетний
гражданин РФ.
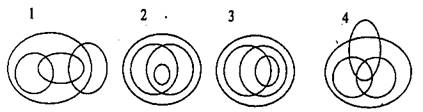
Решение
Перечню понятий: студент, студент первого курса, студент очной формы обучения,
совершеннолетний гражданин РФ соответствуют
круги Эйлера «4».
Задание 3. Установите, какие перечни
понятий соответствуют кругам Эйлера
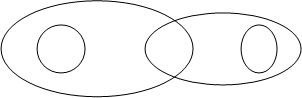
1) писатель; американец; автор детективных романов;
американец, живший в XX в.;
2) медведь; обитатель зоопарка;
медведь, живущий на воле, страус из Лондонского зоопарка;
3) учащийся; студент; учащийся
вуза; учащийся государственного учебного заведения;
4) норма; запрещающая норма;
обязывающая норма; норма уголовного права;
5) депутат Государственной думы
РФ; председатель Государственной думы РФ; депутат представительного органа
государственной власти; писатель.
Решение
Данным кругам
Эйлера соответствует перечень понятий 1).
Задание 4*. Перечислите определения, нарушающие
правила:
А –
соразмерности;
В –
ясности;
С –
недопустимости круга в определении.
1) Консерватор – человек, не имеющий
либеральных убеждений.
2) Римское право – краеугольный
камень всех последующих кодификаций и теорий гражданского права.
3) Кикимора – существо женского пола.
4) Охра – минеральная краска желтого
или красного цвета.
5) Самоучитель – учебник для обучения
чему-либо.
Решение.
Определения,
нарушающие правила А – соразмерности:
1),
т.к. человек, не имеющий
либеральных убеждений, не обязательно является консервативным, можно просто не
иметь твердых убеждений;
4), т.к. правая часть определения
шире чем левая (охра является краской желтого цвета).
Определения,
нарушающие правила В – ясности:
3), т.к. понятие кикиморы не
определено.
Определения, нарушающие правила С – недопустимости круга в определении:
5), т.к. левая и правая части
определения определяются друг через друга.
Задание 5*. Перечислите, какие деления понятий
нарушают правила:
А –
соразмерности;
В –
проведения деления по одному основанию;
С –
взаимоисключения членов деления.
1) Студенты первого курса делятся на
добросовестно дежуривших в столовой и уклонившихся от дежурства.
2) Вузы делятся на институты и
университеты.
3) Студенты делятся на успешно
сдавших сессионные зачеты и подлежащих отчислению.
4) Федеральное собрание состоит из
двух палат – Совета Федерации и Государственной думы.
5) Государственная власть в
Российской Федерации делится на законодательную и исполнительную.
Решение.
Деления
понятий, нарушающие правила А – соразмерности:
2), т.к. имеются еще академии;
5), т.к. имеется еще судебная власть.
Деления понятий, нарушающие правила В
– проведения деления по одному основанию:
1), т.к. уклонение от дежурства
подменяет признак недобросовестного дежурства.
Деления понятий, нарушающие правила С – взаимоисключения членов деления:
3), т.к. студенты могут подлежать
отчислению не только за неуспеваемость, но и друние причины, например, неоплату
за обучение.
Задание 6.
Пусть А – Арнольд проголосовал за законопроект; В –
Билл проголосовал за законопроект; C – Саймон
проголосовал за законопроект. Формализуйте приведенные ниже
суждения. Для получившихся формул постройте таблицы истинности и укажите:
А –
какие из них соответствуют приведенной ниже таблице;
В – какие являются тавтологиями
(логическими законами).
|
A
|
B
|
C
|
Результат
|
|
И
|
И
|
И
|
Л
|
|
И
|
И
|
Л
|
Л
|
|
И
|
Л
|
И
|
И
|
|
И
|
Л
|
Л
|
И
|
|
Л
|
И
|
И
|
И
|
|
Л
|
И
|
Л
|
И
|
|
Л
|
Л
|
И
|
И
|
|
Л
|
Л
|
Л
|
И
|
1. По крайней мере, Саймон или Билл
проголосовали за законопроект.
Если Арнольд не голосовал «за», то без сомнения также не голосовал «за» и Саймон.
Следовательно, если Билл
проголосовал «за», то точно не голосовал «за» Арнольд.
2. Если Арнольд проголосовал «за», то
Саймон точно не голосовал «за».
А если Арнольд не проголосовал «за», то Билл тоже не голосовал «за». Следовательно, если Билл проголосовал «за», то точно не
голосовал «за» Арнольд.
3. Если Саймон и Арнольд проголосовали
«за», то Билл уж точно не
голосовал «за». А если «за» голосует Арнольд, то обязательно «за» голосует и Саймон.
Следовательно, если Билл
проголосовал «за», то точно не голосовал «за» Арнольд.
4. Саймон голосует «за» тогда и только тогда, когда «за»
голосует Арнольд. Однако Арнольд не голосует
«за», если и только если «за»
голосует Билл. Следовательно, если Билл
проголосовал «за», то точно не голосовал «за» Арнольд.
Решение
Формализуем
приведенные суждения:
1. 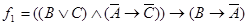 .
.
Построим таблицы истинности для первого суждения:
|
A
|
B
|
C
|
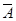
|
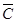
|
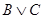
|
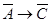
|
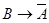
|
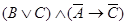
|
f1
|
|
И
|
И
|
И
|
Л
|
Л
|
И
|
И
|
Л
|
И
|
Л
|
|
И
|
И
|
Л
|
Л
|
И
|
И
|
И
|
Л
|
И
|
Л
|
|
И
|
Л
|
И
|
Л
|
Л
|
И
|
И
|
И
|
И
|
И
|
|
И
|
Л
|
Л
|
Л
|
И
|
Л
|
И
|
И
|
Л
|
И
|
|
Л
|
И
|
И
|
И
|
Л
|
И
|
Л
|
И
|
Л
|
И
|
|
Л
|
И
|
Л
|
И
|
И
|
И
|
И
|
И
|
И
|
И
|
|
Л
|
Л
|
И
|
И
|
Л
|
И
|
Л
|
И
|
Л
|
И
|
|
Л
|
Л
|
Л
|
И
|
И
|
Л
|
И
|
И
|
Л
|
И
|
2. 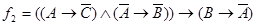 .
.
Построим таблицы истинности для второого суждения:
|
A
|
B
|
C
|
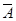
|
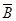
|
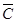
|
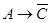
|
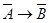
|
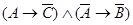
|
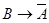
|
f2
|
|
И
|
И
|
И
|
Л
|
Л
|
Л
|
Л
|
И
|
Л
|
Л
|
И
|
|
И
|
И
|
Л
|
Л
|
Л
|
И
|
И
|
И
|
И
|
Л
|
Л
|
|
И
|
Л
|
И
|
Л
|
И
|
Л
|
Л
|
И
|
Л
|
И
|
И
|
|
И
|
Л
|
Л
|
Л
|
И
|
И
|
И
|
И
|
И
|
И
|
И
|
|
Л
|
И
|
И
|
И
|
Л
|
Л
|
И
|
Л
|
Л
|
И
|
И
|
|
Л
|
И
|
Л
|
И
|
Л
|
И
|
И
|
Л
|
Л
|
И
|
И
|
|
Л
|
Л
|
И
|
И
|
И
|
Л
|
И
|
И
|
И
|
И
|
И
|
|
Л
|
Л
|
Л
|
И
|
И
|
И
|
И
|
И
|
И
|
И
|
И
|
3. 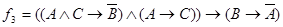 .
.
Построим таблицы истинности для третьего суждения:
|
A
|
B
|
C
|
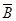
|
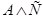
|
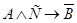
|
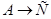
|
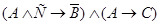
|
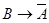
|
f3
|
|
И
|
И
|
И
|
Л
|
И
|
Л
|
И
|
Л
|
Л
|
И
|
|
И
|
И
|
Л
|
Л
|
Л
|
И
|
Л
|
Л
|
Л
|
И
|
|
И
|
Л
|
И
|
И
|
И
|
И
|
И
|
И
|
И
|
И
|
|
И
|
Л
|
Л
|
И
|
Л
|
И
|
Л
|
Л
|
И
|
И
|
|
Л
|
И
|
И
|
Л
|
Л
|
И
|
И
|
И
|
И
|
И
|
|
Л
|
И
|
Л
|
Л
|
Л
|
И
|
И
|
И
|
И
|
И
|
|
Л
|
Л
|
И
|
И
|
Л
|
И
|
И
|
И
|
И
|
И
|
|
Л
|
Л
|
Л
|
И
|
Л
|
И
|
И
|
И
|
И
|
И
|
4. 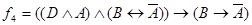 .
.
Построим таблицы истинности для четвертого суждения:
|
A
|
B
|
C
|
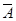
|
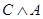
|
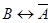
|
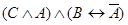
|
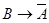
|
f4
|
|
И
|
И
|
И
|
Л
|
И
|
Л
|
Л
|
Л
|
И
|
|
И
|
И
|
Л
|
Л
|
Л
|
Л
|
Л
|
Л
|
И
|
|
И
|
Л
|
И
|
Л
|
И
|
И
|
И
|
И
|
И
|
|
И
|
Л
|
Л
|
Л
|
Л
|
И
|
Л
|
И
|
И
|
|
Л
|
И
|
И
|
И
|
Л
|
И
|
Л
|
И
|
И
|
|
Л
|
И
|
Л
|
И
|
Л
|
И
|
Л
|
И
|
И
|
|
Л
|
Л
|
И
|
И
|
Л
|
Л
|
Л
|
И
|
И
|
|
Л
|
Л
|
Л
|
И
|
Л
|
И
|
Л
|
И
|
И
|
Из таблицы истинности для
получившихся формул следует, что:
-
суждение
1 соответствуют приведенной таблице;
-
суждения
3 и 4 являются тавтологиями (логическими законами).
Задание 7.
Укажите пары суждений, находящиеся в отношении: А
– противоречия; В – подчинения.
1. Любая книга полезна. – Некоторые книги
полезны.
2. Все студенты представили контрольную работу вовремя. – Ни один студент
не представил контрольную работу вовремя.
3. Любой юрист должен уметь рассуждать. – Некоторые юристы
не должны уметь рассуждать.
4. Любая книга полезна. – Неверно, что
любая книга полезна.
5. Все владельцы нового автомобиля
счастливы. – Некоторые владельцы нового автомобиля
счастливы.
Решение.
Для
противоречия характерна строгая несовместимость: при истинности любого из
суждений другое всегда будет ложным. Следовательно, пары суждений, находящиеся в отношении А – противоречия: 2, 3, 4.
Для подчинения
характерно то, что если одно суждение истинно, то и другое будет истинным, но
не наоборот. Следовательно, пары
суждений, находящиеся в отношении В – подчинения: 1, 5.
Задание 8.
Укажите, какие из приведенных ниже непосредственных умозаключений, являются:
А –
правильным превращением;
В – правильным обращением;
C – правильным противопоставлением
предикату.
1. Все ядовитые
вещества опасны для жизни, следовательно, все опасные для жизни вещества являются ядовитыми.
2. Некоторые грибы ядовиты,
следовательно, некоторые грибы не ядовиты.
3. Все, кто хорошо изучил теорию, решат эту задачу.
Следовательно, некоторые из тех, кто решит эту задачу, хорошо изучили теорию.
4. Некоторые организаторы беспорядков были задержаны, следовательно, некоторые из задержанных были организаторами беспорядков.
5. Некоторые организаторы беспорядков были задержаны, следовательно, некоторые из тех, кого не задержали, были организаторами беспорядков.
Решение.
Превращение
суждения состоит в установлении отношения субъекта к понятию, противоречащему
предикату исходного суждения. Преобразование одного суждения в другое,
противоположное по качеству с предикатом, противоречащим предикату исходного
суждения, называется превращением.
Преобразование
суждения, в результате которого субъект исходного суждения становится
предикатом, а предикат – субъектом заключения, называется обращением.
Преобразование
суждения, в результате которого субъектом становится понятие, противоречащее
предикату, а предикатом – субъект исходного суждения, называется
противопоставлением предикату.
Из приведенных непосредственных
умозаключений, являются А
– правильным превращением:
2 (схема превращения суждения I).
Из приведенных непосредственных
умозаключений, являются В
– правильным обращением: 3 (схема обращения суждения A); 4 (схема обращения суждения I).
Из приведенных непосредственных
умозаключений, являются C – правильным противопоставлением предикату: 5 (схема противопоставления
предикату суждения O).
Задание 9. Установите, в каких
силлогизмах термин «политик» является: А – средним термином; В – меньшим термином.
1. Все политики – лицемеры, значит, некоторые люди не лицемеры, так как они не политики.
2. Некоторые люди – политики, значит, некоторые люди – лицемеры, так как есть лицемеры,
являющиеся политиками.
3. М. не лицемер, значит, он не политик, так как все политики – лицемеры.
4. Некоторые политики не лицемеры, так
как К. – политик, но не лицемер.
Решение.
Меньшим
термином силлогизма называется понятие, которое в заключении является
субъектом.
Большим термином
силлогизма называется понятие, которое в заключении является предикатом.
Средним
термином силлогизма называется понятие, входящее в обе посылки и отсутствующее
в заключении.
Термин «политик» является средним термином в
силлогизмах: 1, 2.
Термин «политик» является меньшим термином в
силлогизмах: 3.
Задание 10. Укажите, в каких
силлогизмах нарушены правила:
А – средний термин должен быть распределен хотя бы в одной из
посылок;
В – хотя бы одна из посылок должна быть общим суждением (для разных
вариантов разные правила);
C – все правила соблюдаются.
1. Ни один политик не выражает интересов всего населения, часть населения живет на севере,
значит, ни один политик не выражает интересов населения, живущего на севере.
2. Всякая кража наказуема, значит, действия Р. ненаказуемы,
так как эти действия не
являются кражей.
3. Некоторые
необычные истории не сказки, значит некоторые необычные истории не выдуманы,
так как все сказки выдуманы.
4. Некоторые
расчетливые люди – банкиры, но все расчетливые люди внимательны, значит
некоторые банкиры внимательны.
5. Курение
вредно, значит, невежество не вредно, так как невежество не курение.
Решение.
Термин
считается распределенным, если он взят в полном объеме. Нарушено правило А – средний термин должен быть распределен хотя бы в одной из
посылок в силлогизмах: 1, 5.
Нарушено
правило В – хотя бы одна из посылок должна быть общим суждением в силлогизмах: 3.
C – все правила соблюдаются в
силлогизмах: 4.
Задание 11. Установите, какие
умозаключения являются:
А – правильными
дилеммами;
В – правильными условно-категорическими.
1. Если книга не является библиографической редкостью, ее нельзя продать за
большие деньги. Книгу господина Н. удалось продать за большие деньги, следовательно, она является
библиографической
редкостью.
2. Умозаключения бывают сложными или простыми. Данное умозаключение не простое, значит, оно
сложное.
3. Если на выборах
победит А., то понизится курс ценных бумаг,
а если победит В., то снизятся налоги. Однако на выборах может победить только один из двух (А. или В.),
следовательно, или понизится курс
ценных бумаг, или снизятся налоги.
4. Если К. виновен, то П. дал ложные показания, а если П.
дал ложные показания, то
он будет наказан, значит, если К. виновен, то П. будет наказан.
5. Если приговор вынесен при строгом
соблюдении процессуальных
норм, то он признается законным. Приговор по делу Р. вынесен с нарушением процессуальных
норм, следовательно, он незаконен.
6. Если В. победит, то Г. займет второе место, а если В. не
победит, то Г. займет третье место. Но В. может или победить, или проиграть,
значит, Г. займет второе или третье место.
Решение.
Умозаключение, в котором одна предпосылка условное
суждение, а другая – разделительное суждение, содержащее две альтернативы,
называется дилеммой. Дилеммами являются следующие умозаключения: 3, 6.
Условно-категорическим
называется умозаключение, в котором одна из посылок – условное, а другая
посылка и заключение – категорические суждения. Условно-категорическими
являются следующие умозаключения: 1, 2, 4, 5.
Задание 12. Законспектируйте
тему «Индуктивные умозаключения»
(см., например: Кириллов В. Я, СтарченкоА. А. Логика. М, 2000. С.
162-182, или воспользуйтесь любым другим учебником по логике, содержащим данный раздел).
Решение.
Индуктивным называется
умозаключение, в форме которого протекает эмпирическое
обобщение, когда на основе повторяемости
признака у явлений определенного класса заключают
о его принадлежности всем явлениям этого класса.
В истории физики, например, опытным путем было установлено,
что железные стержни хорошо проводят электричество. Такое же свойство было
обнаружено у медных стержней и у серебра. Учитывая принадлежность указанных проводников к металлам, было сделано индуктивное обобщение, что всем металлам
свойственна электропроводность.
Посылками индуктивного умозаключения выступают суждения,
в которых фиксируется полученная опытным путем информация об устойчивой
повторяемости признака Р у ряда
явлений -
S1, S2, ..., Sn, принадлежащих одному и тому же классу К. Схема
умозаключения в простой и
символической записи имеет следующий вид:

Основная
функция индуктивных выводов в процессе познания
– генерализация, т. е. получение
общих суждений. По своему содержанию и познавательному значению эти обобщения могут носить различный характер
– от простейших обобщений
каждодневной практики до эмпирических обобщений в науке или универсальных
суждений, выражающих всеобщие законы науки.
Индуктивные
умозаключения представляют собой логические процедуры, в форме которых
обобщаются результаты опытных исследований.
В зависимости от полноты и
законченности эмпирического
исследования различают два вида индуктивных умозаключений: полную индукцию
и неполную индукцию.
Полная
индукция.
Полная
индукция – это умозаключение, в
котором на основе повторяемости
признака у каждого из явлений определенного
класса заключают о принадлежности этого признака всему классу явлений.
Такого рода индуктивные умозаключения применяются лишь в тех случаях, когда исследователь имеет
дело с замкнутыми классами, число элементов в которых является конечным и легко обозримым (например,
число (планет Солнечной системы, виды треугольников и т.п.).
Схема
умозаключения полной индукции в простой и
символической записи имеет следующий вид:

Содержательно-фактическая полнота
эмпирического исследования предопределяет
демонстративный характер выводов
в умозаключениях
полной индукции. Если посылки индуктивного
умозаключения истинны и если они фиксируют информацию о всех элементах класса, то
заключение с
необходимостью также будет истинным.
Демонстративность полной индукции
позволяет использовать этот вид
умозаключения в доказательном рассуждении. Так, в геометрии теорема о сумме внутренних углов треугольника доказывается отдельно для трех видов треугольников – остроугольных, прямоугольных, тупоугольных. Учитывая, что в каждом из них сумма
углов равна 180°
и все они составляют замкнутое
(исчерпывающее) множество, на этой основе
строят индуктивное обобщение: во всяком треугольнике сумма его
внутренних углов равна 180°.
Применение
полной индукции в рассуждениях ограничено
практически перечисляемыми множествами явлений. Если невозможно охватить весь класс интересующих исследователя предметов
или явлений, то эмпирическое обобщение
строится в форме неполной индукции.
Неполная
индукция.
Неполная
индукция – это умозаключение, в
котором на основе повторяемости
признака у некоторых явлений определенного
класса заключают о принадлежности этого
признака всему классу явлений.
Схема неполной индукции в простой и символической записи имеет следующий вид:

Неполнота индуктивного обобщения выражается в
том, что исследуют не все, а лишь некоторые элементы класса – от S1
до Sn. Если у каждого из них обнаруживают повторяющийся
признак Р, то заключают о его принадлежности
всему классу явлений. Логический переход в
неполной индукции от некоторых ко всем элементам класса не является
произвольным. Он оправдывается эмпирическими
основаниями – подтверждаемой тысячелетней практикой зависимостью между
всеобщим характером конкретных признаков и устойчивой их повторяемостью в опыте для определенного рода явлений.
Для умозаключений неполной индукции характерно ослабленное
логическое следование – истинные посылки обеспечивают получение не
достоверного, а лишь проблематичного
заключения.
Проблематичность обобщений в выводах неполной индукции отражает неполноту или незаконченность
самого эмпирического исследования.
Существенное влияние на характер логического следования
в выводах неполной индукции оказывает способ отбора
исходного эмпирического материала, который проявляется в методичности или
систематичности формирования посылок индуктивного умозаключения. По способу отбора различают два вида неполной
индукции: индукцию путем
перечисления (энумеративную), получившую название популярной индукции, и индукцию путем исключения (элиминативную), которую называют научной индукцией.
Популярная
индукция.
Популярной
индукцией называют обобщение, в
котором путем перечисления
устанавливают повторяемость признака
у некоторых явлений класса, на основе чего проблематично заключают о его принадлежности всему классу явлений.
В процессе многовековой деятельности люди сталкиваются с устойчивой повторяемостью определенных явлений. На этой основе возникают обобщения,
которые используются для объяснения наступивших и предсказания будущих событий и явлений. Логический механизм большинства таких обобщений – популярная индукция. Ее иногда называют индукцией через
простое перечисление при отсутствии противоречащего случая. Если среди исследованных встречается хотя бы один
противоречащий случай, индуктивное обобщение
считается несостоятельным.
Популярная индукция определяет первые
шаги и в развитии научных
знаний. Любая наука начинает с эмпирического исследования – наблюдения над соответствующими объектами с целью их описания, классификации,
выявления устойчивых свойств, отношений и зависимостей. Первые обобщения в науке обязаны простейшим индуктивным умозаключениям путем простого перечисления повторяющихся признаков.
Умозаключения популярной индукции строятся на
основе повторяемости признаков при отсутствии противоречащего случая. Полученные обобщения всегда имеют
проблематичный характер, степень их обоснованности
варьируется от маловероятных до весьма правдоподобных. Вероятность индуктивных заключений определяется, во-первых, разнообразием отбора
наблюдаемых случаев, во-вторых,
количеством наблюдаемых однотипных
случаев. При соблюдении этих требований индуктивные обобщения часто выполняют важную эвристическую функцию выдвижения плодотворных догадок и предположений. Вместе с тем такие обобщения не
могут выступать в качестве оснований
строго доказательных рассуждений.
Методы
научной индукции.
Научной
индукцией называют умозаключение,
в посылках которого наряду с повторяемостью признака у некоторых явлений класса содержится также информация о зависимости этого признака
от определенных свойств
явления.
Если в популярном индуктивном
обобщении вывод опирается
на повторяемость признака, то научная индукция не ограничивается такой простой
констатацией, а систематически исследует само явление, которое рассматривается
как сложное, состоящее из ряда относительно самостоятельных
компонентов или обстоятельств.
Каждое из них
методично анализируется для выявления связи с повторяющимся признаком. Методы
анализа научной индукции являются обобщением практики научных наблюдений и экспериментальных исследований. Теоретической основой этих методов выступают основные свойства
причинной связи как важнейшей формы объективной зависимости между явлениями.
Причинной (каузальной)
называется такая объективная связь между двумя явлениями,
когда одно из них – причина – вызывает другое – действие. Для причинной связи
характерны следующие свойства: всеобщность связи; последовательность во времени; необходимый характер связи; однозначная зависимость между причиной и действием.
Данные свойства причинной зависимости выполняют
роль познавательных принципов, рационально направляющих
эмпирическое исследование и формирующих особые методы научной индукции,
которые применяются при исследовании
причинных, функциональных и других видов условной зависимости между
явлениями. Их применение связано с определенным огрублением реальных взаимосвязей между явлениями, которое выражается в следующих допущениях:
-
предшествующее явление рассматривается как сложное, состоящее из
простых обстоятельств – А, В, С, D и т. д.;
-
каждое из обстоятельств считается относительно
самостоятельным и не вступает во
взаимодействия с другими;
-
выделенные
обстоятельства рассматриваются как полный их перечень
и предполагается, что исследователь не упустил других обстоятельств.
Указанные допущения в соединении с основными свойствами причинной связи составляют логическую основу выводов научной индукции,
определяя специфику логического
следования при применении методов установления причинных связей.
Основные
методы рассуждений при применении методов
научной индукции.
1. Метод сходства. Применение этого метода
связано с анализом нескольких случаев,
когда после каждого из них появляется
определенное действие, причина которого неизвестна. Заметно отличаясь
друг от друга, каждый случай имеет при этом
некоторое сходное обстоятельство.
Метод сходства
называют методом нахождения сходного в различном, ибо сравниваемые случаи
нередко заметно отличаются друг от друга. В этих условиях требуются определенные навыки наблюдения и анализа, чтобы выделить среди множества различных
обстоятельств нечто повторяющееся и сходное.
2. Метод различия. По методу различия сравниваются два случая, в одном из которых
исследуемое явление наступает, а в другом не наступает; при этом второй
случай отличается от первого лишь одним
обстоятельством, а все другие являются сходными.
Метод различия называют методом нахождения
различного в сходном, ибо сравниваемые случаи
совпадают друг с другом по многим свойствам. Здесь также требуются определенные навыки наблюдения и анализа, чтобы выделить нередко малозаметное
различие между двумя внешне
одинаковыми явлениями.
Применяется метод различия как в процессе
наблюдения над явлениями в естественных условиях, так и в условиях лабораторного или производственного эксперимента.
3. Соединенный метод сходства и различия. Этот
метод представляет собой комбинацию первых
двух методов, когда путем анализа множества случаев обнаруживают как сходное в различном, так и различное в сходном.
4. Метод сопутствующих изменений. Метод
применяется при анализе случаев, в которых
видоизменение одного из обстоятельств сопровождается видоизменением исследуемого действия.
Предыдущие
индуктивные методы основывались на повторяемости
либо отсутствии определенного обстоятельства. Однако не все причинно связанные явления
допускают нейтрализацию или замену отдельных их факторов. Например, исследуя влияние трения
на скорость движения
тела, невозможно в принципе исключить само трение.
Точно так же, определяя влияние Луны на величину морских приливов, мы не можем изменить массу Луны.
5. Метод
остатков. Применение метода связано с установлением причины,
вызывающей определенную часть сложного
действия, при условии, что причины, вызывающие другие части этого
действия, уже выявлены.
Статистические
обобщения.
Особым видом умозаключений неполной индукции являются статистические
обобщения, связанные с анализом массовых событий. К ним относятся, например,
массовые транспортные перевозки пассажиров и грузов, рождаемость и смертность людей, распространение
заболеваний, транспортные происшествия, динамика преступлений и многие другие.
Статистическое
обобщение – это умозаключение неполной индукции, в котором установленная в посылках
количественная информация о частоте
определенного признака в исследуемой группе (образце) переносится в заключении на все множество явлений этого рода. В отличие от индукции, через
перечисление при отсутствии противоречащего случая в посылках
статистического умозаключения
фиксируется следующая информация:
-
общее число
составляющих группу или образец случаев;
-
число случаев, в
которых присутствует интересующий исследователя признак;
-
частота появления интересующего признака.
Тщательность статистического описания исследуемого
образца и логически корректный перенос частоты признака на популяцию обеспечивают высокую вероятность и тем самым
практическую эффективность статистических
обобщений в различных областях науки, культуры и производства.