Задача 1. Вариант 5
Эконометрическое моделирование стоимости квартир в Московской области
Даны следующие
исходные данные:
|
Y-цена
квартиры, тыс. руб.
|
X3
(общая площадь квартиры)
|
X5
(этаж квартиры)
|
X6(площадь
кухни)
|
|
115
|
70,4
|
9
|
7
|
|
85
|
82,8
|
5
|
10
|
|
69
|
64,5
|
6
|
10
|
|
57
|
55,1
|
1
|
9
|
|
184,6
|
83,9
|
1
|
9
|
|
56
|
32,2
|
2
|
7
|
|
85
|
65
|
12
|
8,3
|
|
265
|
169,5
|
10
|
16,5
|
|
60,65
|
74
|
11
|
12,1
|
|
130
|
87
|
6
|
6
|
|
46
|
44
|
2
|
10
|
|
115
|
60
|
2
|
7
|
|
70,96
|
65,7
|
5
|
12,5
|
|
39,5
|
42
|
7
|
11
|
|
78,9
|
49,3
|
14
|
13,6
|
|
60
|
64,5
|
11
|
12
|
|
100
|
93,8
|
1
|
9
|
|
51
|
64
|
6
|
12
|
|
157
|
98
|
2
|
11
|
|
123,5
|
107,5
|
12
|
12,3
|
|
55,2
|
48
|
9
|
12
|
|
95,5
|
80
|
6
|
12,5
|
|
57,6
|
63,9
|
5
|
11,4
|
|
64,5
|
58,1
|
10
|
10,6
|
|
92
|
83
|
9
|
6,5
|
|
100
|
73,4
|
2
|
7
|
|
81
|
45,5
|
3
|
6,3
|
|
65
|
32
|
5
|
6,6
|
|
110
|
65,2
|
10
|
9,6
|
|
42,1
|
40,3
|
13
|
10,8
|
|
135
|
72
|
12
|
10
|
|
39,6
|
36
|
5
|
8,6
|
|
57
|
61,6
|
8
|
10
|
|
80
|
35,5
|
4
|
8,5
|
|
61
|
58,1
|
10
|
10,6
|
|
69,6
|
83
|
4
|
12
|
|
250
|
152
|
15
|
13,3
|
|
64,5
|
64,5
|
12
|
8,6
|
|
125
|
54
|
8
|
9
|
|
152,3
|
89
|
7
|
13
|
1.
Рассчитайте матрицу
парных коэффициентов корреляции; оцените статистическую значимость коэффициентов
корреляции.
2.
Постройте поле
корреляции результативного признака и наиболее тесно связанного с ним фактора.
3.
Рассчитайте
параметры линейной парной регрессии для
каждого фактора Х..
4.
Оцените качество
каждой модели через коэффициент детерминации, среднюю ошибку аппроксимации и
F-критерий Фишера. Выберите лучшую модель.
5.
Для выбранной модели
осуществите прогнозирование среднего значения показателя 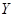 при уровне значимости
при уровне значимости 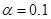 , если прогнозное значения
фактора
, если прогнозное значения
фактора 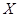 составит 80% от его максимального
значения. Представьте графически: фактические и модельные значения, точки прогноза.
составит 80% от его максимального
значения. Представьте графически: фактические и модельные значения, точки прогноза.
6.
Используя пошаговую
множественную регрессию (метод исключения или метод включения), постройте
модель формирования цены квартиры за счёт значимых факторов. Дайте
экономическую интерпретацию коэффициентов модели регрессии.
7.
Оцените качество
построенной модели. Улучшилось ли качество модели по сравнению с однофакторной
моделью? Дайте оценку влияния значимых факторов на результат с помощью
коэффициентов эластичности, b - и D - коэффициентов.
Решение:
При
решении данной задачи расчеты и построение графиков и диаграмм будем вести с
использованием настройки Excel Анализ данных.
1. Рассчитаем матрицу парных коэффициентов корреляции и оценим
статистическую значимость
коэффициентов корреляции.
Чтобы рассчитать матрицу парных коэффициентов корреляции скопируем
таблицу с исходными данными в Excel. Далее воспользуемся инструментом
Корреляция, входящим в настойку Анализ данных.
В диалоговом окне Корреляция в поле
Входной интервал вводим диапазон ячеек, содержащих исходные данные. Так
как мы выделили и заголовки столбцов, то устанавливаем флажок Метки в первой
строке.
Получили следующие результаты:
Таблица 1.1. Матрица парных
коэффициентов корреляции:
|
|
Y-цена
квартиры, тыс. руб.
|
X3
(общая площадь квартиры)
|
X5
(этаж квартиры)
|
X6(площадь
кухни)
|
|
Y-цена
квартиры, тыс. руб.
|
1
|
|
|
|
|
X3 (общая
площадь квартиры)
|
0,845551302
|
1
|
|
|
|
X5 (этаж
квартиры)
|
0,146382617
|
0,228859567
|
1
|
|
|
X6(площадь
кухни)
|
0,277274009
|
0,485159132
|
0,413008439
|
1
|
Анализ матрицы коэффициентов парной корреляции показывает, что
зависимая переменная Y, т.е. цена квартиры имеет более тесную связь с Х3 (общая
площадь квартиры). Коэффициент корреляции равен 0,845.Это означает, что на 84,5
зависимая переменная Y (цена квартиры) зависит от показателя Х4 общая площадь
квартиры. Также зависимая переменная Y (цена квартиры) имеет среднюю связь с Х6
(площадь кухни) и слабую связь с Х5
(этаж квартиры).
Статистическая значимость коэффициентов корреляции определим с
помощью t-критерия Стьюдента. Табличное значение сравниваем с расчетными
значениями.
Для
каждого коэффициента r(Y, Xj) вычислим t-статистику по формуле t = 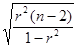 и занесем результаты расчетов в корреляционную
таблицу:
и занесем результаты расчетов в корреляционную
таблицу:
|
|
Y-цена
квартиры, тыс. руб.
|
X3
(общая площадь квартиры)
|
X5
(этаж квартиры)
|
X6(площадь
кухни)
|
Критерий
Стьюдента
|
|
Y-цена
квартиры, тыс. руб.
|
1
|
|
|
|
|
|
X3 (общая
площадь квартиры)
|
0,845551302
|
1
|
|
|
9,762849051
|
|
X5 (этаж
квартиры)
|
0,146382617
|
0,228859567
|
1
|
|
0,912189112
|
|
X6(площадь
кухни)
|
0,277274009
|
0,485159132
|
0,413008439
|
1
|
1,77898418
|
Вычислим табличное значение с помощью функции СТЬЮДРАСПОБР.
tтабл.= 2,024 при доверительной вероятности равной 0,95 и степенью
свободы (n-2)
Статистическим значимым является фактор Х3.
2. Построим поле
корреляции результативного признака (стоимости квартиры) и наиболее тесно
связанного с ним фактора (жилой площади
квартиры).
Для этого воспользуемся инструментом
построения точечной диаграммы программы Excel.
В
результате получаем поле корреляции цены квартиры,
тыс. долл. и жилой площади квартиры, кв.м. (рисунок 1.1.)
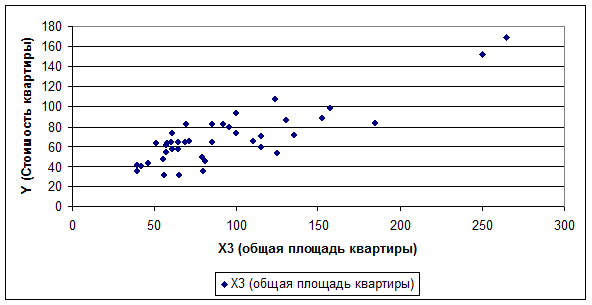
Рисунок
1.1.
3. Рассчитаем параметры линейной парной регрессии для каждого фактора Х.
Для расчета параметров линейной парной регрессии воспользуемся
инструментом Регрессия, входящим в настойку Анализ данных.
В диалоговом окне Регрессия в
поле Входной интервал Y вводим адрес диапазона ячеек, которые представляет зависимую переменную, т.е.
стоимость квартир. В поле Входной интервал Х вводим адрес диапазона, который
содержит значения независимых переменных. Выполним поочередно вычисления
параметры парной регрессии для каждого фактора.
Для Х3 получили следующие данные,
представленные в таблице 1.2:
Таблица 1.2
|
Регрессионная
статистика
|
|
|
|
|
Множественный R
|
0,845551
|
|
|
|
|
R-квадрат
|
0,714957
|
|
|
|
|
Нормированный
R-квадрат
|
0,707456
|
|
|
|
|
Стандартная
ошибка
|
27,85076
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
|
Регрессия
|
1
|
73931,14
|
73931,14
|
95,31322
|
|
Остаток
|
38
|
29475,27
|
775,6651
|
|
|
Итого
|
39
|
103406,4
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
|
Y-пересечение
|
-13,1088
|
11,7886
|
-1,11199
|
0,273128
|
|
X3 (общая
площадь квартиры)
|
1,542594
|
0,158007
|
9,762849
|
6,62E-12
|
Уравнение регрессии
зависимости цены квартиры от общей площади квартиры имеет вид:
Y3=-13,109+1,542*X3
Для Х5 получили
следующие данные, представленные в таблице
1.3:
Таблица 1.3
|
Регрессионная
статистика
|
|
|
|
|
Множественный R
|
0,146383
|
|
|
|
|
R-квадрат
|
0,021428
|
|
|
|
|
Нормированный
R-квадрат
|
-0,00432
|
|
|
|
|
Стандартная
ошибка
|
51,6034
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
|
Регрессия
|
1
|
2215,779
|
2215,779
|
0,832089
|
|
Остаток
|
38
|
101190,6
|
2662,911
|
|
|
Итого
|
39
|
103406,4
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
|
Y-пересечение
|
80,34288
|
16,71508
|
4,806612
|
2,42E-05
|
|
X5 (этаж
квартиры)
|
1,88757
|
2,069274
|
0,912189
|
0,36742
|
Уравнение регрессии
зависимости цены квартиры от этажа квартиры имеет вид:
Y5=80,343+1,888*X5
Для Х6 получили
следующие данные, представленные в таблице
1.4:
Таблица 1.4
|
Регрессионная
статистика
|
|
|
|
|
Множественный R
|
0,277274
|
|
|
|
|
R-квадрат
|
0,076881
|
|
|
|
|
Нормированный
R-квадрат
|
0,052588
|
|
|
|
|
Стандартная
ошибка
|
50,11997
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
|
Регрессия
|
1
|
7949,975
|
7949,975
|
3,164785
|
|
Остаток
|
38
|
95456,44
|
2512,011
|
|
|
Итого
|
39
|
103406,4
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
|
Y-пересечение
|
33,37295
|
34,79737
|
0,959065
|
0,343589
|
|
X6(площадь
кухни)
|
5,994758
|
3,369765
|
1,778984
|
0,083243
|
Уравнение регрессии
зависимости цены квартиры от площади кухни имеет вид:
Y6=33,373+5,993*X6
4. Оценим качество каждой модели через коэффициент детерминации,
среднюю ошибку аппроксимации и F-критерий Фишера. Установим, какая модель
является лучшей.
Коэффициент
детерминации, среднюю ошибку аппроксимации мы получили в результате расчетов,
проведенных в пункте 3.
А)
Коэффициент детерминации определяет,
какая доля вариации признака У учтена в модели и обусловлена влиянием не него фактора Х. Чем
больше значение коэффициента детерминации, тем теснее связь между признаками в
построенной математической модели
Из
таблиц 1.2, 1.3, 1.4 видно, что наибольшее значение коэффициента детерминации
имеет фактор X3 (0,715).
Исходя
из данного критерия наиболее адекватной является модель уравнения регрессии
зависимости цены квартиры от общей площади квартиры (Х3)
Б)
Средняя ошибка аппроксимации:
Для
вычисления средней относительной ошибки аппроксимации рассмотрим остатки модели
Еi = Yi – YТi, содержащиеся в столбце Остатки
итогов программы РЕГРЕССИЯ (таблица «вывод остатка»). Дополним таблицу столбцом
относительных погрешностей, которые вычислим по формуле Еотн.i = 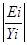
 100
с помощью функции ABS.
100
с помощью функции ABS.
Выполнение
расчетов для модели (3):
|
Наблюдение
|
Предсказанное
Y-цена квартиры, тыс. руб.
|
Остатки
|
Относительный
остаток
|
|
1
|
95,48979294
|
19,51021
|
0,204317199
|
|
2
|
114,6179543
|
-29,618
|
0,258405888
|
|
3
|
86,38849036
|
-17,3885
|
0,201282489
|
|
4
|
71,88810998
|
-14,8881
|
0,207101146
|
|
5
|
116,3148073
|
68,28519
|
0,587072225
|
|
6
|
36,56271523
|
19,43728
|
0,531614916
|
|
7
|
87,15978719
|
-2,15979
|
0,024779629
|
|
8
|
248,3608244
|
16,63918
|
0,066995975
|
|
9
|
101,0431301
|
-40,3931
|
0,399761271
|
|
10
|
121,0968476
|
8,903152
|
0,073520926
|
|
11
|
54,76532038
|
-8,76532
|
0,160052389
|
|
12
|
79,4468189
|
35,55318
|
0,447509184
|
|
13
|
88,23960275
|
-17,2796
|
0,195825935
|
|
14
|
51,68013307
|
-12,1801
|
0,235683083
|
|
15
|
62,94106677
|
15,95893
|
0,253553587
|
|
16
|
86,38849036
|
-26,3885
|
0,305463034
|
|
17
|
131,5864845
|
-31,5865
|
0,240043532
|
|
18
|
85,61719353
|
-34,6172
|
0,404325254
|
|
19
|
138,0653779
|
18,93462
|
0,137142435
|
|
20
|
152,7200176
|
-29,22
|
0,191330633
|
|
21
|
60,93569501
|
-5,7357
|
0,094127014
|
|
22
|
110,298692
|
-14,7987
|
0,134169243
|
|
23
|
85,46293416
|
-27,8629
|
0,326023608
|
|
24
|
76,51589095
|
-12,0159
|
0,157037849
|
|
25
|
114,926473
|
-22,9265
|
0,199488181
|
|
26
|
100,1175739
|
-0,11757
|
0,001174358
|
|
27
|
57,07921087
|
23,92079
|
0,419080586
|
|
28
|
36,25419649
|
28,7458
|
0,792895893
|
|
29
|
87,46830592
|
22,53169
|
0,257598382
|
|
30
|
49,05772385
|
-6,95772
|
0,141827286
|
|
31
|
97,95794279
|
37,04206
|
0,378142457
|
|
32
|
42,42457112
|
-2,82457
|
0,066578661
|
|
33
|
81,91496875
|
-24,915
|
0,304156482
|
|
34
|
41,65327429
|
38,34673
|
0,920617319
|
|
35
|
76,51589095
|
-15,5159
|
0,202779981
|
|
36
|
114,926473
|
-45,3265
|
0,394395406
|
|
37
|
221,3654354
|
28,63456
|
0,129354271
|
|
38
|
86,38849036
|
-21,8885
|
0,253372761
|
|
39
|
70,19125696
|
54,80874
|
0,780848576
|
|
40
|
124,182035
|
28,11797
|
0,226425385
|
|
Среднее
значение
|
28,26%
|
|
|
|
|
|
По
столбцу относительных погрешностей найдем среднее значение 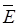 отн
=
28,26% (с помощью функции СРЗНАЧ).
отн
=
28,26% (с помощью функции СРЗНАЧ).
Выполнение
расчетов для модели (5):
|
Наблюдение
|
Предсказанное
Y-цена квартиры, тыс. руб.
|
Остатки
|
Относительный
остаток
|
|
1
|
97,33101061
|
17,66899
|
0,181535045
|
|
2
|
89,78073243
|
-4,78073
|
0,05324898
|
|
3
|
91,66830198
|
-22,6683
|
0,247286156
|
|
4
|
82,23045425
|
-25,2305
|
0,306826157
|
|
5
|
82,23045425
|
102,3695
|
1,244910376
|
|
6
|
84,1180238
|
-28,118
|
0,334268716
|
|
7
|
102,9937192
|
-17,9937
|
0,174706957
|
|
8
|
99,21858016
|
165,7814
|
1,670870714
|
|
9
|
101,1061497
|
-40,4561
|
0,4001354
|
|
10
|
91,66830198
|
38,3317
|
0,418156519
|
|
11
|
84,1180238
|
-38,118
|
0,453149302
|
|
12
|
84,1180238
|
30,88198
|
0,367126744
|
|
13
|
89,78073243
|
-18,8207
|
0,209629972
|
|
14
|
93,55587152
|
-54,0559
|
0,5777924
|
|
15
|
106,7688583
|
-27,8689
|
0,261020477
|
|
16
|
101,1061497
|
-41,1061
|
0,406564287
|
|
17
|
82,23045425
|
17,76955
|
0,216094462
|
|
18
|
91,66830198
|
-40,6683
|
0,443646289
|
|
19
|
84,1180238
|
72,88198
|
0,866425207
|
|
20
|
102,9937192
|
20,50628
|
0,199102245
|
|
21
|
97,33101061
|
-42,131
|
0,432863178
|
|
22
|
91,66830198
|
3,831698
|
0,041799596
|
|
23
|
89,78073243
|
-32,1807
|
0,358436956
|
|
24
|
99,21858016
|
-34,7186
|
0,349920147
|
|
25
|
97,33101061
|
-5,33101
|
0,054771964
|
|
26
|
84,1180238
|
15,88198
|
0,188805864
|
|
27
|
86,00559334
|
-5,00559
|
0,058200788
|
|
28
|
89,78073243
|
-24,7807
|
0,276013926
|
|
29
|
99,21858016
|
10,78142
|
0,108663315
|
|
30
|
104,8812888
|
-62,7813
|
0,598593796
|
|
31
|
102,9937192
|
32,00628
|
0,310759539
|
|
32
|
89,78073243
|
-50,1807
|
0,558925407
|
|
33
|
95,44344107
|
-38,4434
|
0,402787668
|
|
34
|
87,89316289
|
-7,89316
|
0,08980406
|
|
35
|
99,21858016
|
-38,2186
|
0,385195798
|
|
36
|
87,89316289
|
-18,2932
|
0,208129532
|
|
37
|
108,6564279
|
141,3436
|
1,300830286
|
|
38
|
102,9937192
|
-38,4937
|
0,37374822
|
|
39
|
95,44344107
|
29,55656
|
0,309676166
|
|
40
|
93,55587152
|
58,74413
|
0,627904241
|
|
Среднее
значение
|
40,17%
|
|
|
|
|
|
По
столбцу относительных погрешностей найдем среднее значение 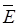 отн
=
40,17% (с помощью функции СРЗНАЧ).
отн
=
40,17% (с помощью функции СРЗНАЧ).
Выполнение
расчетов для модели (6):
|
Наблюдение
|
Предсказанное
Y-цена квартиры, тыс. руб.
|
Остатки
|
Относительный
остаток
|
|
1
|
75,33626321
|
39,66374
|
0,526489304
|
|
2
|
93,32053829
|
-8,32054
|
0,089160848
|
|
3
|
93,32053829
|
-24,3205
|
0,260612923
|
|
4
|
87,32577993
|
-30,3258
|
0,34727179
|
|
5
|
87,32577993
|
97,27422
|
1,11392329
|
|
6
|
75,33626321
|
-19,3363
|
0,256666078
|
|
7
|
83,12944908
|
1,870551
|
0,022501664
|
|
8
|
132,2864676
|
132,7135
|
1,003228333
|
|
9
|
105,9095308
|
-45,2595
|
0,427341435
|
|
10
|
69,34150484
|
60,6585
|
0,874779042
|
|
11
|
93,32053829
|
-47,3205
|
0,507075282
|
|
12
|
75,33626321
|
39,66374
|
0,526489304
|
|
13
|
108,3074342
|
-37,3474
|
0,344827984
|
|
14
|
99,31529665
|
-59,8153
|
0,602276776
|
|
15
|
114,9016684
|
-36,0017
|
0,313325898
|
|
16
|
105,310055
|
-45,3101
|
0,430253835
|
|
17
|
87,32577993
|
12,67422
|
0,14513721
|
|
18
|
105,310055
|
-54,3101
|
0,51571576
|
|
19
|
99,31529665
|
57,6847
|
0,580823955
|
|
20
|
107,1084825
|
16,39152
|
0,153036595
|
|
21
|
105,310055
|
-50,1101
|
0,475833528
|
|
22
|
108,3074342
|
-12,8074
|
0,11825074
|
|
23
|
101,7132
|
-44,1132
|
0,43370182
|
|
24
|
96,91739331
|
-32,4174
|
0,334484783
|
|
25
|
72,33888402
|
19,66112
|
0,271791807
|
|
26
|
75,33626321
|
24,66374
|
0,327382004
|
|
27
|
71,13993235
|
9,860068
|
0,138601026
|
|
28
|
72,93835986
|
-7,93836
|
0,108836556
|
|
29
|
90,92263495
|
19,07737
|
0,209819756
|
|
30
|
98,11634498
|
-56,0163
|
0,570917567
|
|
31
|
93,32053829
|
41,67946
|
0,446626889
|
|
32
|
84,92787658
|
-45,3279
|
0,533722005
|
|
33
|
93,32053829
|
-36,3205
|
0,38920198
|
|
34
|
84,32840075
|
-4,3284
|
0,051327912
|
|
35
|
96,91739331
|
-35,9174
|
0,370598012
|
|
36
|
105,310055
|
-35,7101
|
0,339094448
|
|
37
|
113,1032409
|
136,8968
|
1,210369907
|
|
38
|
84,92787658
|
-20,4279
|
0,240532054
|
|
39
|
87,32577993
|
37,67422
|
0,431421513
|
|
40
|
111,3048134
|
40,99519
|
0,368314589
|
|
Среднее
значение
|
41,03%
|
|
|
|
|
|
По
столбцу относительных погрешностей найдем среднее значение 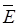 отн
=
41,03% (с помощью функции СРЗНАЧ).
отн
=
41,03% (с помощью функции СРЗНАЧ).
В) Для проверки значимости модели регрессии
используется F-тест. Для этого выполняется сравнение 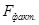 и
критического (табличного)
и
критического (табличного)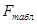 значений
F-критерия Фишера.
значений
F-критерия Фишера.
Расчетные значения приведены в таблицах 1.2,
1.3, 1.4 (обозначены буквой F).
Разнесем
результаты в сводную таблицу:
|
Модель
|
R-квадрат
|
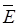 отн отн
|
F
|
|
X3
|
0,715
|
28,26%
|
95,313
|
|
X5
|
0,021
|
40,17%
|
0,832
|
|
X6
|
0,077
|
41,03%
|
3,165
|
Оценим
точность построенных моделей в соответствии со схемой:
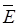 отн1
=
28,26% > 15%,
отн1
=
28,26% > 15%, 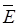 отн2
=
40,17% > 15%,
отн2
=
40,17% > 15%, 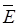 отн3
=
41,03% > 15%. Точность всех трех моделей неудовлетворительная. Ближе к 15%
отн3
=
41,03% > 15%. Точность всех трех моделей неудовлетворительная. Ближе к 15% 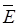 отн
модели (Х3).
отн
модели (Х3).
Проверим
значимость полученных уравнений с помощью F – критерия Фишера.
F
– статистики определены программой РЕГРЕССИЯ (таблицы «Дисперсионный анализ») и
представлены в последнем столбце сводной таблицы.
С
помощью функции FРАСПОБР найдем значение Fкр = 4,10 для уровня
значимости α = 5%, и чисел степеней
свободы k1 = 1, k2 = 38.
Схема
проверки:
F
= 95,313 > Fкр = 4,10, следовательно уравнение модели (X3)
является значимой и ее использование целесообразно.
F
= 0,832 < Fкр = 4,10, следовательно уравнение модели (X5) не
является значимой и ее использование нецелесообразно.
F
= 3,165 < Fкр = 4,10, следовательно уравнение модели (X6) не
является значимой и ее использование нецелесообразно.
Зависимая
переменная Y достаточно хорошо описывается включенной в модель (Х3) факторной
переменной Х3.
Вывод:
на
основании оценки качества моделей по коэффициенту детерминации, средней ошибке
аппроксимации и критерию Фишера наилучшей является модель (Х3) зависимости цены
квартиры от ее общей площади. Однако эту модель нецелесообразно использовать
для прогнозирования в реальных условиях, поскольку ее точность
неудовлетворительная, и дальнейшие расчеты проведем в учебных целях.
5. Для выбранной модели зависимости цены квартиры от общей площади
квартиры осуществим
прогнозирование среднего значения показателя 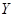 при уровне значимости
при уровне значимости 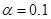 , если прогнозное значения
фактора
, если прогнозное значения
фактора 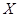 составит 80% от его
максимального значения.
составит 80% от его
максимального значения.
Рассчитаем прогнозное значение Х, по условию оно составит 80% от
максимального значения.
Рассчитаем Хmax в Excel с помощью функции МАКС.
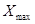 = 169,5кв.м
= 169,5кв.м
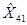 =0,8
*169,5 = 135,6 кв.м
=0,8
*169,5 = 135,6 кв.м
Для
получения прогнозных оценок зависимой переменной подставим полученное значение
независимой переменной в линейное уравнение:
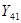 =
-13,109+1,543*135,6
= 196,07 тыс.долл.
=
-13,109+1,543*135,6
= 196,07 тыс.долл.
Определим доверительный интервал прогноза, который будет иметь
следующие границы:
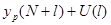
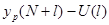
Для вычисления доверительного интервала для прогнозного значения
рассчитываем величину отклонения от линии регрессии. Для модели парной
регрессии величина отклонения рассчитывается:
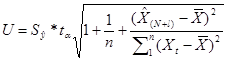
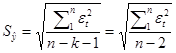 , т.е.
значение стандартной ошибки из таблицы 1.2.
, т.е.
значение стандартной ошибки из таблицы 1.2.
(Так
как число степеней свободы равно единице, то знаменатель будет равен n-2).
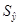 =
27,851
=
27,851
Для расчета коэффициента 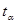 воспользуемся функцией
Excel СТЬЮДРАСПОБР, вероятность возьмем равную 0,1, число степеней свободы 38.
воспользуемся функцией
Excel СТЬЮДРАСПОБР, вероятность возьмем равную 0,1, число степеней свободы 38.
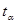 = 1,686
= 1,686
По
столбцу данных Х3 найдем среднее значение 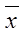 =
42,04 (функция СРЗНАЧ) и определим
=
42,04 (функция СРЗНАЧ) и определим 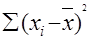 = 31068,79 (функция КВАДРОТКЛ);
= 31068,79 (функция КВАДРОТКЛ);
U=50,72
Определим верхнюю и нижнюю границы интервала.
U+=196,50+50,72= 246,79
U-=196,50-50,72= 145,34
Таким образом, прогнозное значение 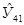 = 196,07 тыс.долл., будет находиться между нижней
границей, равной 145,34 тыс.долл. и верхней
границей, равной 246,79 тыс.долл.
= 196,07 тыс.долл., будет находиться между нижней
границей, равной 145,34 тыс.долл. и верхней
границей, равной 246,79 тыс.долл.
Фактические и модельные значения, точки прогноза представлены
графически на рисунке 1.2.
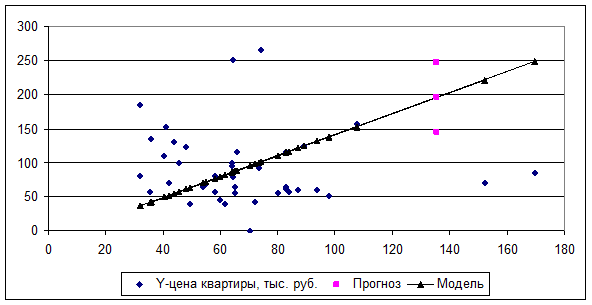
Рисунок 1.2.
6.
Используя пошаговую множественную регрессию (метод исключения), построим модель
формирования цены квартиры за счёт значимых факторов.
Для построения множественной регрессии воспользуемся функцией
Регрессия программы Excel, включив в нее все факторы. В результате получаем
результативные таблицы, из которых нам необходим t-критерий Стьюдента.
Таблица 1.5
|
Регрессионная
статистика
|
|
|
Множественный R
|
0,859133222
|
|
|
|
|
R-квадрат
|
0,738109894
|
|
|
|
|
Нормированный
R-квадрат
|
0,716285718
|
|
|
|
|
Стандартная
ошибка
|
27,42723504
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
|
Регрессия
|
3
|
76325,3
|
25441,77
|
33,82075
|
|
Остаток
|
36
|
27081,12
|
752,2532
|
|
|
Итого
|
39
|
103406,4
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
|
Y-пересечение
|
14,03808781
|
19,14992
|
0,733062
|
0,468267
|
|
X3 (общая
площадь квартиры)
|
1,696055642
|
0,178063
|
9,525005
|
2,24E-11
|
|
X5 (этаж
квартиры)
|
0,083714215
|
1,208402
|
0,069277
|
0,945153
|
|
X6(площадь
кухни)
|
-3,814797999
|
2,255565
|
-1,69128
|
0,099424
|
|
|
|
|
|
|
Получаем модель
вида:
Y=14,038+1,696*X3+0,084*X5-3,815*X6
Поскольку 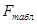 <
< 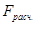 (4,10 < 33,821), уравнение регрессии
следует признать адекватным.
(4,10 < 33,821), уравнение регрессии
следует признать адекватным.
Выберем наименьшее по модулю значение t-критерия Стьюдента, оно
равно 0,069, сравниваем его с табличным значением, которые рассчитываем в
Excel, уровень значимости берем равным 0,10, число степеней свободы
n-m-1=40-4=36: 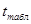 =1,688.
=1,688.
Поскольку
0,069 < 1,688 модель следует признать не адекватной.
Поскольку
фактор X5 статистически не значим, то построим модель с учетом только факторов
Х3 и Х6.
Таблица 1.6
|
Регрессионная
статистика
|
|
|
|
|
Множественный R
|
0,859112903
|
|
|
|
|
R-квадрат
|
0,73807498
|
|
|
|
|
Нормированный
R-квадрат
|
0,723916871
|
|
|
|
|
Стандартная
ошибка
|
27,05586127
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
|
Регрессия
|
2
|
76321,68
|
38160,84242
|
52,1309
|
|
Остаток
|
37
|
27084,73
|
732,0196288
|
|
|
Итого
|
39
|
103406,4
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
|
Y-пересечение
|
14,04035138
|
18,8906
|
0,743245502
|
0,462027
|
|
X6(площадь
кухни)
|
-3,759364352
|
2,080306
|
-1,807121155
|
0,07888
|
|
X3 (общая
площадь квартиры)
|
1,696496871
|
0,17554
|
9,664443592
|
1,15E-11
|
Получаем модель
вида:
Y=14,040+1,696*X3-3,759*X6
Поскольку 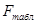 <
< 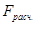 (4,10 < 52,131), уравнение регрессии
следует признать адекватным.
(4,10 < 52,131), уравнение регрессии
следует признать адекватным.
Выберем наименьшее по модулю значение t-критерия Стьюдента, оно
равно 1,807, сравниваем его с табличным значением, которые рассчитываем в
Excel, уровень значимости берем равным 0,10, число степеней свободы
n-m-1=40-4=36: 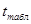 =1,688.
=1,688.
Поскольку
1,807 > 1,688 модель следует признать адекватной.
Коэффициент
парной корреляции независимых переменных X3 (общая площадь квартиры) и X6 (площадь кухни) меньше
0,8 (см. табл. 1.1.) в исходных данных отсутствует мультиколлинеарность.
7. Оцените качество построенной
модели.
Для
оценки качества выбранной множественной модели YТ = 14,040+1,696*X3-3,759*X6 аналогично п.4 данной
задачи используем коэффициент детерминации R-квадрат, среднюю относительную
ошибку аппроксимации и F – критерий Фишера.
Коэффициент
детерминации R-квадрат выпишем из итогов РЕГРЕССИИ (таблица «Регрессионная
статистика» для модели).
R2
= 0,738, следовательно, вариация цены квартиры Y на 73,8% объясняется по
данному уравнению вариацией общей площади квартиры Х3 и площади
кухни Х6.
Используем
исходные данные Yi и найденные программой РЕГРЕССИЯ остатки Еi
(таблица «Вывод остатка» для модели). Рассчитаем относительные погрешности и
найдем среднее значение 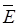 отн.
отн.
|
Наблюдение
|
Предсказанное
Y-цена квартиры, тыс. руб.
|
Остатки
|
Относительный
остаток
|
|
1
|
107,1581806
|
7,841819
|
0,073179848
|
|
2
|
116,9166488
|
-31,9166
|
0,272986346
|
|
3
|
85,87075602
|
-16,8708
|
0,196466839
|
|
4
|
73,68304979
|
-16,683
|
0,226416385
|
|
5
|
122,5421597
|
62,05784
|
0,506420325
|
|
6
|
42,35200015
|
13,648
|
0,322251601
|
|
7
|
93,10992385
|
-8,10992
|
0,087100531
|
|
8
|
239,5670592
|
25,43294
|
0,106162095
|
|
9
|
94,09281115
|
-33,4428
|
0,355423658
|
|
10
|
139,079393
|
-9,07939
|
0,065282087
|
|
11
|
51,09257017
|
-5,09257
|
0,0996734
|
|
12
|
89,51461316
|
25,48539
|
0,28470644
|
|
13
|
78,50814138
|
-7,54814
|
0,096144696
|
|
14
|
43,94021208
|
-4,44021
|
0,101051221
|
|
15
|
46,55029192
|
32,34971
|
0,694941036
|
|
16
|
78,35202732
|
-18,352
|
0,234225303
|
|
17
|
139,3374787
|
-39,3375
|
0,282318003
|
|
18
|
77,50377888
|
-26,5038
|
0,341967569
|
|
19
|
138,9440368
|
18,05596
|
0,129951336
|
|
20
|
150,1735835
|
-26,6736
|
0,177618346
|
|
21
|
50,35982895
|
4,840171
|
0,096111745
|
|
22
|
102,7680466
|
-7,26805
|
0,070722826
|
|
23
|
79,5897478
|
-21,9897
|
0,276288698
|
|
24
|
72,75755744
|
-8,25756
|
0,113494154
|
|
25
|
130,4137234
|
-38,4137
|
0,294552769
|
|
26
|
112,2476712
|
-12,2477
|
0,10911292
|
|
27
|
67,54696358
|
13,45304
|
0,199165672
|
|
28
|
43,51644652
|
21,48355
|
0,493688139
|
|
29
|
88,56204957
|
21,43795
|
0,242067009
|
|
30
|
41,80804027
|
0,29196
|
0,006983339
|
|
31
|
98,59448255
|
36,40552
|
0,369244977
|
|
32
|
42,7837053
|
-3,18371
|
0,074413968
|
|
33
|
80,9509151
|
-23,9509
|
0,295869603
|
|
34
|
42,3113933
|
37,68861
|
0,890743693
|
|
35
|
72,75755744
|
-11,7576
|
0,161599122
|
|
36
|
109,7372194
|
-40,1372
|
0,365757576
|
|
37
|
221,9083298
|
28,09167
|
0,126591328
|
|
38
|
91,13386611
|
-26,6339
|
0,292249931
|
|
39
|
71,81690323
|
53,1831
|
0,740537316
|
|
40
|
116,1568363
|
36,14316
|
0,3111583
|
|
|
|
|
25,46%
|
По
столбцу относительных погрешностей найдем среднее значение 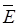 отн
=
25,46% (с помощью функции СРЗНАЧ).
отн
=
25,46% (с помощью функции СРЗНАЧ).
Сравнение
показывает, что 22,69% > 15%. Следовательно, точность модели
неудовлетворительная.
С
помощью F – критерия Фишера проверим значимость модели в целом. Для этого
выпишем из итогов РЕГРЕССИИ (таблица «дисперсионный анализ» для модели ) F =
52,131.
С
помощью функции FРАСПОБР найдем значение Fкр = 3,25 для уровня
значимости α = 5%, и чисел степеней
свободы k1 = 2, k2 = 37.
F
= 61,01 > Fкр = 3,25, следовательно, уравнение модели является
значимым, его использование целесообразно, зависимая переменная Y достаточно
хорошо описывается включенными в модель факторными переменными Х3 и
Х6.
Дополнительно
с помощью t – критерия Стьюдента проверим значимость отдельных коэффициентов
модели.
t
– статистики для коэффициентов уравнения регрессии приведены в итогах программы
РЕГРЕССИЯ. Для выбранной модели получены следующие значения (табл. 1.6).
Критическое
значение tкр найдено для уровня значимости α = 5% и числа
степеней свободы k = 40 – 2 – 1 = 37. tкр = 2,03 (функция
СТЬЮДРАСПОБР).
Для
свободного коэффициента a= 14,04 определена статистика t(a) = 0,74.
|t(a)|
= 0,74 < tкр = 2,03, следовательно, свободный коэффициент a не
является значимым, его можно исключить из модели.
Для
коэффициента регрессии b1 = -3,76 определена статистика
t(b1)= -1,81.
|t(b1)|
= 1,81 < tкр = 2,03, следовательно, коэффициента регрессии b1
не является значимым, его и фактор можно исключить из модели.
Для
коэффициента регрессии b2=1,696 определена статистика t(b2)=
9,66.
|t(b2)|
= 9,66 > tкр = 2,03, следовательно, коэффициента регрессии b2
является значимым, его и фактор общей площади квартиры нужно сохранить в
модели.
Выводы
о значимости коэффициентов модели сделаны на уровне значимости α = 5%.
Рассматривая столбец «P-значение», отметим, что свободный коэффициент a можно
считать значимым на уровне 0,46 = 46%; коэффициент регрессии b1 – на
уровне 0,08 = 8%;, а коэффициент регрессии b2 – на уровне 1,15E-11 =
0,0000000000115 = 0,0000000001%.
При
добавлении в уравнение новых факторных переменных автоматически увеличивается
коэффициент детерминации R2 и уменьшается средняя ошибка
аппроксимации, хотя при этом не всегда улучшается качество модели. Поэтому для
сравнения качества однофакторной и выбранной множественной модели используем
нормированные коэффициенты детерминации.
|
Модель
|
Нормированный R-квадрат
|
|
Y3=-13,109+1,542*X3
|
0,707456
|
|
Y=14,040+1,696*X3-3,759*X6
|
0,723916
|
Таким
образом, при добавлении в уравнение регрессии фактора Х6 качество
модели улучшилось, что говорит в пользу сохранения фактора Х6 в
модели.
Средние
коэффициенты эластичности в случае линейной модели определяются формулами Эj = bj * 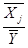 .
.
С
помощью функции СРЗНАЧ найдем: 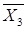 =
69,208,
=
69,208, 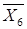 =
10,055,
=
10,055, 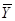 =
93,65. Тогда Э3 = 1,25, Э6
= -0,40 .
=
93,65. Тогда Э3 = 1,25, Э6
= -0,40 .
Следовательно,
при изменении общей площади на 1% цена квартиры увеличится в среднем на 1,25%.
Увеличение
площади кухни на 1% приводит к уменьшению цены квартиры в среднем на 0,40%.
Бета-коэффициенты
определяются формулами βj = bj * 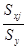 .
.
С
помощью функции СТАНДОТКЛОН найдем SX3 = 28,224; SX6 =
2,382; SY = 51,492. Тогда
β3=
0,930 β6=
-0,174
Таким
образом, при увеличении только фактора Х3 на одно свое стандартное
отклонение результат Y увеличивается в среднем на 0,93 своего стандартного
отклонения SY, а при
увеличении только фактора Х6 на одно его стандартное отклонение –
уменьшается на 0,174 SY.
Дельта-коэффициенты
определяются формулами Δj = βj * 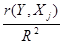 .
.
Коэффициенты
парной корреляции r(Y, X3) = 0,846, и r(Y, X6) = 0,277 найдены с помощью
программы КОРРЕЛЯЦИЯ. Коэффициент детерминации R2 = 0,738 определен
для рассматриваемой двухфакторной модели программой РЕГРЕССИЯ.
Вычислим
дельта-коэффициенты:
Δ3
= 1,065; Δ6 =-0,065.
Поскольку
Δ6 < 0, то факторная переменная Х6 выбрана
неудачно и ее нужно исключить из модели.
Значит,
по уравнению полученной линейной двухфакторной модели изменение результирующего
фактора Y (цены квартиры) на 100% объясняется воздействием фактора Х3
(общей площадью квартиры).
Список литературы
1.
Эконометрика: Учебник/под ред.
И.И.Елисеевой. – М.: Финансы и статистика,2002.
2.
Практикум по эконометрике: Учебное
пособие/ И.И.Елисеева, С.В. Курышева, Н.М. Горденко и др..; под ред.
И.И.Елисеевой.- М.: Финансы и статистика, 2001.