Курский государственный университет
В.И.Гуров, Г.Н.Яценко
ПРАКТИКУМ
ПО ТЕОРИИ
СТАТИСТИКИ

Курск 2005
Курский государственный университет
В.И.Гуров, Г.Н.Яценко
Практикум по теории статистики
Рекомендован
учебно-методическим
советом факультета экономики и менеджмента
Курского
государственного университета
в
качестве учебного пособия для студентов экономических специальностей
Курск 2005
ББК 60.6Я 73
Гуров В.И.,
Яценко Г.Н. Практикум по теории статистики. – Курск: Курск. гос. ун-т, 2005. –
136 с.
В «Практикуме
по теории статистики» содержатся решения типовых задач и задачи для
самостоятельного решения по важнейшим темам: «Сводка и группировка
статистических данных», «Средние величины»,
«Показатели вариации», «Выборочное наблюдение», «Ряды динамики»,
«Индексы», «Корреляционный анализ». Их
решение поможет в усвоении учебного материала.
Издание
предназначено для студентов экономических факультетов, позволит усвоить курс
теории статистики.
Рецензент: А.С. Паранян – д-р экон. наук. профессор, зав.
кафедрой анализа и
аудита Курской
государственной сельскохозяйственной академии
имени проф. И.И.Иванова
© Гуров В.И., Яценко Г.Н., 2005
© Курский госуниверситет, 2005
Содержание
Введение. 5
Тема
1. Сводка и группировка статистических данных. 6
Тема
2. Средние величины. 16
Тема
3. Показатели вариации. 27
Тема
4. Выборочное наблюдение. 44
Тема
5. Ряды динамики. 53
Тема
6. Индексы.. 83
Тема
7. Статистические методы изучения взаимосвязей социально-экономических явлений. 97
7.1.
Виды и формы связей. Понятие о статистической связи. 97
7.2.
Основные статистические методы изучения взаимосвязей. 99
7.3.
Корреляционно-регрессионный метод
анализа. Уравнение регрессии как форма аналитического выражения статистической
связи. 104
7.4.
Однофакторные (парные) модели регрессии. 106
7.5.
Показатели тесноты связи альтернативных признаков. 118
Приложение
1. 129
Приложение
2. 130
Приложение
3. 131
Приложение
4. 131
Приложение5. 132
Приложение
6. 133
Приложение
7. 134
Приложение
8. 135
Введение
В современных
условиях предъявляются повышенные требования к уровню подготовки экономистов
любой специальности.
Работа
экономиста постоянно связана с использованием и анализом статистических данных,
которые необходимы для оценки состояния социально-экономических процессов любой
сферы деятельности на всех уровнях хозяйствования и управления.
Чтобы
всесторонне анализировать происходящие в стране процессы, необходимо овладеть
статистической методологией и, прежде всего, основами теории статистики – науки,
разрабатывающей понятия и категории статистики, методы отбора, обработки,
обобщения и анализа массовых общественных явлений, структурных различий, методы
изучения динамики и анализа
закономерностей развития, моделирования и прогнозирования конкретных
социально-экономических процессов.
Знание
статистики значительно повышает профессиональный уровень экономиста, его
компетентность и, следовательно, качество аналитической работы.
Усвоение курса
общей теории статистики невозможно без самостоятельного решения задач по
расчету статистических показателей,
составлению таблиц, графиков и т.д. Практикум по теории статистики поможет
студентам в практических самостоятельных занятиях и при выполнении письменных
контрольных заданий, курсовых работ.
«Практикум»
состоит из семи тем, соответствующих темам курса теории статистики. В каждой теме приводится
разбор одной или нескольких типовых
задач, а также предлагаются задачи для самостоятельного решения. Приведенные в
задачах данные – условные.
Тема 1. Сводка и группировка статистических данных
Практические
занятия по теме предусматривают решение
следующих типов задач:
1. Построение
рядов распределения по количественному признаку.
2. Построение
группировки.
3. Проведение
вторичной группировки.
Решение типовых задач
№1. Для двадцати рабочих зарегистрированы
следующие индивидуальные значения (варианты) изучаемого признака – тарифные
разряды:
|
Табельный номер рабочего
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
Тарифный разряд
рабочего (X)
|
4
|
3
|
5
|
4
|
4
|
3
|
5
|
4
|
6
|

3
|
6
|
4
|
5
|
3
|
6
|
3
|
5
|
4
|
5
|
4
|
Построить ряд
распределения рабочих по тарифному разряду.
Решение: Тарифный разряд – дискретный
признак. Располагая значения признака первичного ряда в возрастающем порядке,
получаем ранжированный ряд:
|
Табельный номер рабочего
|
2
|
6
|
10
|
14
|
16
|
1
|
4
|
5
|
8
|
12
|
18
|
20
|
3
|
7
|
19
|
13
|
17
|
15
|
9
|
11
|
|
Тарифный разряд
рабочего (X)
|
3
|
3
|
3
|
3
|
3
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
5
|
5
|
5
|
5
|
5
|
6
|
6
|
6
|
Рассматривая
этот ранжированный ряд, видим, что некоторые значения признака повторяются.
Цифры, показывающие количество повторений отдельных вариант, называются
численностями (частотами) и обозначаются буквой f. Сумма частот (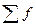 ) равна объему изучаемой совокупности (n).
) равна объему изучаемой совокупности (n).
Таблица 1.1
Ряд
распределения рабочих по тарифному разряду
|
Тарифный разряд (Х)
|
Число рабочих с
данным тарифным разрядом
|
|
В абсолютном
выражении (f)
|
В долях к итогу ( ) )
|
В процентах к итогу
(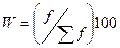 ) )
|
|
А
|
1
|
2
|
3
|
|
3
|
5
|
0,25
|
25
|
Продолжение
таблицы 1.1
|
А
|
1
|
2
|
3
|
|
4
5
6
|
7
5
3
|
0,35
0,25
0,15
|
35
25
15
|
|
Итого:
|
20
|
1,0
|
100
|
 Оформляя результаты подсчета численностей (частот) в таблицу 1.1, получаем дискретный
вариационный ряд, характеризующий распределение изучаемого признака.
Оформляя результаты подсчета численностей (частот) в таблицу 1.1, получаем дискретный
вариационный ряд, характеризующий распределение изучаемого признака.
Основными
элементами вариационного ряда являются
варианты (х) и соответствующие им
частоты (f).
Частоты ряда,
выраженные в относительных числах (долях) и рассчитанные путем деления каждой
частоты на их общую сумму, называются частостями и обозначаются W. Их можно определять и в процентах.
№2. Имеются данные о стаже работы на
предприятии по 15 рабочим одной бригады. Первичный ряд величины стажа работы на
данном предприятии отдельных рабочих выглядит
следующим образом (в годах):
2,2; 1,4; 8,4; 2,4; 4,3; 11,4; 3,2; 4,8; 7,1; 6,2; 5,3;
5,8; 4,4; 5,6; 3,8.
Построить ряд
распределения рабочих по стажу работы.
Решение: Стаж работы – непрерывно
варьирующий признак. Определяем величину интервала группировочного признака:
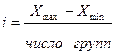 ,
,
где - Xmin и Xmax наименьшее и
наибольшее значения признака в совокупности.
Количество
групп (интервалов) в ряду при достаточном числе наблюдений (n>200-300) рекомендуется брать от 10 до 20; при предполагаемом нормальном
распределении часто берут количество групп равным 12. По способу Стерджесса
размер интервала устанавливается в зависимости от величины размаха вариации и
численности единиц в изучаемой совокупности (n) по формуле:
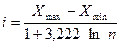 .
.
В нашем
примере количество групп примерно равно 5 (точнее 4,907)
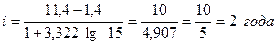 .
.
Существуют
следующие правила записи величины
интервала группировки. Если величина интервала
(i) имеет:
- один знак до
запятой, например 0,77; 2,571; 3,82, то число округляется до десятых 0,8; 2,6;
3,8;
- две значащие
цифры до запятой, например, 16, 891, то величина интервала округляется до
целого числа (до 16);
- трехзначное,
четырехзначное и так далее число, то эту величину следует округлять до
ближайшего числа кратного 100 или 50. Например, 657 следует округлять до 700,
420 – до 450 и т.д.
Нижнюю границу
первого интервала принимают равной минимальному значению признака, верхняя
граница первого интервала соответствует значению (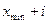 ).
).
Для
последующих групп границы определяются аналогично, т.е. последовательно
прибавляется величина интервала.
Следовательно,
в нашем примере интервалы рабочих по стажу работы будут следующими:
1,4 –
3,4; 3,4 – 5,4; 5,4 – 7,4;
7,4 – 9,4; 9,4 – 11,4.
Подсчитаем
теперь число рабочих в каждой группе. Единицы с величиной признака, равной
нижней границе интервала, в группу включаются, а равные верхней границе - не включаются, за исключением последнего
интервала. Результаты представим в таблице 1.2, которую дополним частостями и накопленными частотами.
Накопленные частоты
(F) показывают, сколько единиц совокупности имеют значение
признака не больше данного значения. Определяются последовательным прибавлением
к частоте в первом интервале последующих частот ряда.
Таблица 1.2
Ряд распределения
рабочих по стажу работы
|
Группы рабочих по
стажу, г.
|
Число рабочих,
чел., f
|
Число рабочих, в %
к итогу, W%
|
Накопленные частоты,
F
|
|
1.4 – 3,4
3,4 – 5,4
5,4 – 7,4
7,4 – 9,4
9,4 – 11,4
|
4
5
4
1
1
|
26,7
33,4
26,7
6,6
6.6
|
4
9
13
14
15
|
|
Итого
|
15
|
100,0
|
|
№3. В отчетном периоде работа 30-ти
предприятий отрасли характеризуется данными, представленными в табл.1.3.
Таблица 1.3
|
№ п/п
|
Основные производственные
фонды, млн. руб.
|
Фактический выпуск продукции,
млн. руб.
|
№
п/п
|
Основные производственные
фонды, млн. руб.
|
Фактический выпуск продукции, млн.
руб.
|
|
A
|
1
|
2
|
A
|
1
|
2
|
|
1
2
3
4
5
6
7
8
9
|
1,2
2,4
3,5
4,9
3,8
6,5
1,6
2,0
4,7
|
3,7
2,9
5,6
5,4
2,8
9,8
1,8
2,5
4,5
|
17
18
19
20
21
22
23
24
25
|
3,3
3,1
7,1
3,1
3,5
3,1
5,6
2,9
2,9
|
1,3
3,4
9,0
2,5
4,6
3,6
8,2
3,9
3,9
|
Продолжение
таблицы 1.3
|
A
|
1
|
2
|
A
|
1
|
2
|
|
10
11
12
13
14
15
16
|
1,7
3,2
7,2
2,0
2,5
3,9
5,3
|
2,3
3,2
8,6
1,5
3,2
4,3
5,4
|
26
27
28
29
30
|
3,5
4,8
1,6
1,8
4,2
|
4,5
6,1
1,9
2,2
5,6
|
|
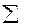
|
106,9
|
129,2
|
С целью
выявления зависимости между стоимостью
основных производственных фондов и выпуском продукции проделайте следующую работу:
1) произведите
аналитическую группировку предприятий по размеру основных производственных
фондов, образовав четыре группы с равными интервалами. По каждой группе
предприятий подсчитайте: 1) число предприятий; 2) стоимость основных
производственных фондов – всего и в
среднем на одно предприятие; 3) стоимость выпуска продукции – всего и в среднем
на одно предприятие. Результаты оформите в таблице. Сделайте краткие выводы;
2) произведите
комбинационную группировку по двум признакам: по стоимости основных
производственных фондов и выпуску продукции. Результаты оформите в виде
комбинационной и корреляционной таблиц. Сделайте краткие выводы.
Решение: 1. Группировки, которые
применяются для исследования взаимосвязи
между явлениями, называются аналитическими. Чтобы исследовать взаимосвязь между
признаками с помощью метода аналитических группировок, необходимо произвести
группировку единиц совокупности по факторному признаку и по каждой группе
исчислить среднее значение результативного признака, вариация которого от
группы к группе под влиянием группировочного признака будет указывать на
наличие или отсутствие взаимосвязи.
Для этого
необходимо, прежде всего, определить, какой признак является факторным и какой
результативным. Из экономической теории известно, что факторным признаком
является среднегодовая стоимость основных фондов, а зависящим результативным
признаком будет служить объем выпуска продукции. Следовательно, группировочным
признаком будет служить среднегодовая
стоимость основных производственных фондов. Для образования групп предприятий
по стоимости основных производственных фондов определим величину интервала
группировки по формуле:
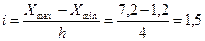 млн. руб.
млн. руб.
Определим
группы: 1,2 – 2,7; 2,7 – 4,2; 4,2 – 5,7; 5,7 – 7,2.
Для подсчета
числа предприятий в каждой из образованных групп, определения объемов
варьирующих признаков в пределах созданных групп построим рабочую таблицу 1.4.
Таблица
1.4
Распределение
предприятий по среднегодовой стоимости основных фондов
|
Группы п/п
|
Группы предприятий по стоимости
основных производственных фондов, млн. руб.
|
Номер и число предприятий
|
Основные производственные
фонды, млн. руб.
|
Выпуск продукции, млн. руб.
|
|
A
|
Б
|
1
|
2
|
3
|
|
I
|
1,2- 2,7
|
1
2
7
8
10
13
14
28
29
|
1,2
2,4
1,6
2,0
1,7
2,0
2,5
1,6
1,8
|
3,7
2,9
1,8
2,5
2,3
1,5
3,2
1,9
2,2
|
|
|
Итого
|
9
|
16,8
|
22,0
|
|
II
|
2,7 – 4,2
|
5
11
15
17
18
20
21
22
24
25
26
|
2,8
3,2
3,9
3,3
3,1
3,1
3,5
3,1
2,9
2,9
3,5
|
2,8
3,2
4,3
1,3
3,4
2,5
4,6
3,6
3,9
3,9
4,5
|
|
|
Итого
|
11
|
35,3
|
38,0
|
|
III
|
4,2 – 5,7
|
3
4
9
16
23
27
30
|
4,5
4,9
4,7
5,3
5,6
4,8
4,2
|
5,6
5,4
4,5
6,4
8,2
6,1
5,6
|
|
|
Итого
|
7
|
34,0
|
41,8
|
|
IV
|
5,7 – 7,2
|
6
12
19
|
6,5
7,2
7,1
|
9,8
8,6
9,0
|
|
|
Итого
|
3
|
20,8
|
27,4
|
|
|
Всего
|
30
|
106,9
|
129,2
|
Полученные в
рабочей таблице показатели по группам
занесем в соответствующие строки и графы сводной групповой таблицы 1.5.
Таблица
1.5
Зависимость
выпуска продукции от среднегодовой стоимости основных производственных фондов
|
Группы п/п
|
Группы предприятий по стоимости
основных производственных фондов, млн. руб.
|
Число предпри-ятий
|
Стоимость основных производственных фондов, млн. руб.
|
Выпуск продукции, млн. руб.
|
|
Всего
|
В среднем на одно предприятие
|
Всего
|
В среднем на одно предприятие
|
|
А
|
Б
|
1
|
2
|
3
|
4
|
5
|
|
I
II
III
IV
|
1,2 – 2,7
2,7 – 4,2
4,2 – 5,7
5,7 – 7,2
|
9
11
7
3
|
16,8
35,3
34,0
20,8
|
1,86
3,21
4,85
6,93
|
22,0
38,9
41,8
27,4
|
2,44
3,45
5,97
9,13
|
|
|
Итого
|
30
|
106,9
|
3,56
|
129,2
|
4,31
|
Данные
группировки показывают, что наиболее крупные предприятия имеют лучшие
производственные показатели. Сравнение основных производственных фондов по
стоимости и среднему выпуску продукции
на одно предприятие (гр.3 и 5 табл. 1.5) по группам показывает, что с ростом
стоимости основных производственных фондов увеличивается выпуск продукции в
среднем на одно предприятие. Следовательно, между данными признаками существует
прямая корреляционная зависимость.
II. Чтобы произвести
группировку предприятий по двум признакам, необходимо каждую из образованных
групп по размеру стоимости основных производственных фондов разбить на подгруппы
по выпуску продукции и дать их характеристику. Представим полученные показатели
в комбинационной таблице 1.6.
Таблица
1.6
Группировка
предприятий по стоимости основных производственных
фондов
и выпуску продукции
|
Группы п/п
|
Группы предприятий
|
Число пред-приятий
|
Основные производственные
фонды, млн. руб.
|
Выпуск продукции, млн. руб.
|
|
|
По стоимости основных
производственных фондов, млн. руб.
|
По выпуску продукции, млн. руб.
|
|
|
Всего
|
В среднем на одно предприятие
|
Всего
|
В среднем на одно предприятие
|
|
|
A
|
Б
|
В
|
1
|
2
|
3
|
4
|
5
|
|
|
I
|
1.2 – 2,7
|
1,3 – 3,0
3,0 – 5,0
Свыше 5,0
|
7
2
-
|
13,1
3,7
-
|
1,87
1,85
-
|
15,1
6,9
-
|
2,15
3,45
-
|
|
|
|
Итого
|
|
9
|
16,8
|
1,86
|
22,0
|
2,44
|
|
|
II
|
2,7 – 4,2
|
1,3 – 3,0
3,0 – 5,0
Свыше 5,0
|
3
8
-
|
9,2
26,1
-
|
3,06
3,26
-
|
6,6
31,4
-
|
2.2
3,92
-
|
|
|
|
Итого
|
|
11
|
35,3
|
3,20
|
38,0
|
3,45
|
|
Продолжение
таблицы 1.6
|
A
|
Б
|
В
|
1
|
2
|
3
|
4
|
5
|
|
III
|
4,2 – 5,7
|
1,3 – 3,0
3,0 – 5,0
Свыше 5,0
|
-
1
6
|
-
4,7
29,3
|
-
4,7
4,9
|
-
4,5
37,3
|
-
4,5
6,21
|
|
|
Итого
|
|
7
|
34,0
|
4,85
|
41,8
|
5,97
|
|
IV
|
5.7 – 7,2
|
1,3 – 3,0
3,0 – 5,0
Свыше 5,0
|
-
-
3
|
-
-
20,8
|
-
-
6,93
|
-
-
27,4
|
-
-
9,13
|
|
|
Итого по подгруппам
|
1,3 – 3,0
3,0 – 5,0
Свыше 5,0
|
10
11
9
|
22,3
34,5
50.1
|
2,23
3,13
5,57
|
21,7
42,8
64,7
|
2,17
3,89
7,18
|
|
|
Всего
|
|
30
|
106,9
|
3,56
|
129,2
|
6,31
|
Данные
комбинационной таблицы показывают, что выпуск продукции находится в прямой зависимости от стоимости
основных производственных фондов. Эту зависимость можно выявить также с помощью
корреляционной таблицы 1.7.
Корреляционная
таблица – это специальная комбинационная таблица, в которой представлена
группировка по двум взаимосвязанным признакам: факторному и результативному. Концентрация частот около
диагоналей матрицы данных
свидетельствует о наличии и направлении корреляционной связи между признаками.
Таблица
1.7
Распределение
предприятий по стоимости основных
производственных
фондов и выпуску продукции
|
Стоимость основных
производственных фондов, млн. руб.
|
Выпуск продукции, млн. руб.
|
|
1,3-
-3,0
|
3,0-
-4,7
|
4,7-
-6,4
|
6,4-
-8,1
|
8,1-
-9,8
|
Итого
|
|
А
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1,2 – 2,7
2,7 – 4,2
4,2 – 5,7
5,7 – 7,2
|
7
3
-
-
|
2
8
1
-
|
-
-
4
-
|
-
-
1
-
|
-
-
1
3
|
9
11
7
3
|
|
Итого
|
10
|
11
|
4
|
1
|
4
|
30
|
Как видно из
таблицы 1.7, распределение числа предприятий произошло вдоль диагонали,
проведенной из левого верхнего угла в правый нижний угол таблицы, т.е.
увеличение признака «стоимость основных
производственных фондов» сопровождается увеличением признака «выпуск
продукции». Характер концентрации частот по этой диагонали корреляционной таблицы свидетельствует о
наличии прямой тесной корреляционной связи между изучаемыми признаками.
№ 4. Имеются данные о группировке
предприятий по стоимости основных производственных фондов по двум отраслям
промышленности, представленные в таблице 1.8
Для сравнения
структуры предприятий по стоимости основных производственных фондов произведите
перегруппировку предприятий первой
отрасли, взяв за основу распределение предприятий второй отрасли. Сведите
полученные данные в таблицу и сделайте выводы.
Таблица
1.8
|
I отрасль
|
II отрасль
|
|
Группы предприятий по стоимости
основных производственных фондов, млн. руб.
|
Уд. вес предприятий,
%
|
Группы предприятий по стоимости
основных производственных фондов, млн. руб.
|
Уд. вес
предприятий, %
|
|
До 10
10 – 12
12 – 15
15 – 20
20 - 30
|
10
10
20
30
22
8
|
До 10
10 – 15
15 – 25
25 – 30
Свыше 30
|
5
20
40
25
10
|
|
Итого:
|
100
|
Итого
|
100
|
Решение: В первой отрасли надо
произвести вторичную группировку, образовав такое же число групп и с теми же
интервалами, что и во второй отрасли, для чего произведем следующие расчеты и
построим таблицу 1.9.
Таблица
1.9
Вторичная
группировка предприятий двух отраслей по среднегодовой стоимости основных средств
|
Группы предприятий по стоимости
основных производственных фондов, млн. руб.
|
Удельный вес предприятий, %
|
|
I отрасль
|
II отрасль
|
|
До 10
10 – 15
15 – 25
25 – 30
Свыше 30
|
10
10+20 = 30
30 + 11* = 41
11
8
|
5
20
40
25
10
|
|
|
100
|
100
|
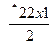 = 11.
= 11.
В результате
перегруппировки получены сопоставимые
данные по двум отраслям, которые позволяют сделать вывод о том, что во II отрасли больше предприятий, технически оснащенных (с большим объемом
среднегодовой стоимости), чем в I
отрасли. Удельный вес предприятий со среднегодовой стоимостью основных фондов,
большей 25 млн. руб., во II
отрасли 35%, а в I
отрасли 19%.
Задачи
№1.1 Имеются следующие данные о
месячной заработной плате рабочих бригады (тыс. руб.):
3,5; 4,0; 4,5; 5,0; 6,0; 1,5; 3,0; 3,5; 4,0;
3,0; 4,5; 4,0; 3,0;
6,5; 5,5; 7,5; 6,5; 7,0.
Постройте ряд
распределения рабочих по размеру заработной платы, образовав четыре группы с
равными интервалами. Постройте график ряда распределения.
№1.2 Имеются данные о дневной выручке денег от
продажи товаров в торговых киосках
города, тыс. руб.:
44; 46; 48; 55; 54; 58; 60; 50; 49; 55;
51.
Постройте ряд
распределения торговых киосков по объему дневной выручки, образовав четыре
группы с равными интервалами. Изобразите ряд графически с помощью гистограммы и
полигона частот.
№1.3 Имеются данные о выработке продукции рабочими
бригады за смену, шт.:
7,
8,
8, 9, 10, 12, 3,
6,
7,
8,
6, 9, 8, 6,
13, 11, 9, 11, 15, 13, 14.
Постройте ряд
распределения рабочих по выработке продукции с равными интервалами. Изобразите
ряд графически. Сделайте выводы.
№1.4 Имеются
следующие данные о стаже рабочих бригады:
2; 4; 5; 5; 6; 7; 7; 8; 8; 10; 11; 4; 3; 3; 4; 4; 5; 9; 3;6.
1.
Постройте ряд распределения рабочих по стажу работы с
равными интервалами, образовав три группы рабочих.
2.
Определите средний стаж рабочих бригады по данным ряда
распределения и по первичным данным. Какая средняя точнее?
3.
Представьте ряд распределения графически.
№1.5 Имеются следующие данные о
количестве произведенной продукции рабочими цеха за смену (в штуках):
10; 14; 22; 12; 15; 11; 16; 14; 19; 23; 13; 18; 17; 16; 19; 19; 15; 25; 21; 22; 16.
1.
Построить ряд распределения рабочих по количеству
произведенной продукции, образовав три группы с равными интервалами.
2.
По данным ряда распределения определите среднюю выработку
продукции (количество произведенной продукции) на одного рабочего.
№1.6 За отчетный год имеются следующие
данные по предприятиям отрасли промышленности:
|
№ п/п
|
Производство продукции, тыс.т.
|
Общая сумма затрат на
производство продукции, тыс. руб.
|
№
п/п
|
Производство продукции, тыс.т.
|
Общая сумма затрат на
производство продукции, тыс. руб.
|
|
A
|
1
|
2
|
A
|
1
|
2
|
|
1
2
3
4
5
6
7
8
9
10
11
12
|
11,2
9,6
1,7
2,1
5,1
4,6
3,1
6,1
7,4
5,5
2,0
4,2
|
880
790
160
190
510
400
280
510
610
470
180
400
|
13
14
15
16
17
18
19
20
21
22
23
24
25
|
9,8
11,5
12,0
3,6
2,6
5,9
7,8
9,5
4,8
9,0
7,9
7,0
3,7
|
780
860
900
320
240
510
650
780
430
720
580
700
330
|
Для выявления
связи между размером выпуска продукции и себестоимостью единицы продукции
произведите группировку предприятий по
объему производства продукции, образовав пять групп предприятий с равными интервалами.
По каждой
группе и в целом по всем предприятиям подсчитайте:
1)
число предприятий;
2)
объем выпущенной
продукции – всего и в среднем на одно
предприятие;
3)
сумму затрат –
всего и в среднем на единицу продукции.
Результаты представьте в таблице.
Укажите подлежащее, сказуемое и вид таблицы. Дайте анализ показателей таблицы,
сделайте выводы.
№1.7 Имеются следующие данные о
распределении предприятий по стоимости произведенной продукции:
|
Группы предприятий
по стоимости произведенной продукции, млн. руб.
|
Число предприятий
|
|
1 – 3
3 – 5
5 – 10
10 – 30
30 - 50
|
4
14
24
42
16
|
Произведите
вторичную группировку предприятий по
стоимости произведенной продукции, образовав следующие группы: 1 – 5; 5
- 10; 10 – 20; 20 – 30; 30-40; свыше 40.
№ 1.8 Разработайте и постройте макет статистической
таблицы, в которой была бы отражена зависимость потребления населением
отдельных товаров от формирующих его факторов.
№1.9
Постройте макет таблицы,
укажите подлежащее, сказуемое и вид таблицы: 1) для изучения распределения
предприятий по размеру выпуска продукции; 2) для характеристики распределения
работающих по размеру заработной платы; 3) для характеристики распределения
предприятий по проценту выполнения плана; 4) для характеристики распределения
населения по возрасту.
№ 1.10
Для изучения распределения
предприятий по мощности постройте макет таблицы, в подлежащем которой должны
быть группы предприятий по размеру основных фондов, а в сказуемом – число
предприятий и их удельный вес в процентах к итогу, размер основных фондов, выпуск продукции – всего и на один рубль
основных фондов, размер прибыли. Укажите вид таблицы.
№ 1.11 Для изучения степени механизации труда
спроектируйте макет таблицы, в подлежащем которой должны быть группы
предприятий по проценту механизации труда, а в сказуемом – число предприятий и
их удельный вес в процентах к итогу; число рабочих, размер валовой продукции –
всего и в среднем на одного рабочего. Укажите вид таблицы.
№ 1.12 Имеются следующие данные о стаже работы и средней месячной заработной плате рабочих –
сдельщиков:
|
№ рабочего
|
Стаж, лет
|
Месячная зарплата,
руб.
|
№ рабочего
|
Стаж, лет
|
Месячная зарплата,
руб.
|
|
1
2
3
4
5
6
7
8
9
10
|
1,0
6,5
9,2
4,5
6,0
2,5
2,7
16,0
14,0
11,0
|
2500
3400
3600
2900
2850
2620
2600
3200
3800
4000
|
11
12
13
14
15
16
17
18
19
20
|
12,0
10,5
9,0
5,0
10,2
5,0
5,4
7,5
8,0
8.5
|
4200
3900
3100
2820
3960
2900
3100
3400
3000
3900
|
Для выявления
зависимости между стажем работы и месячной заработной платой сгруппируйте
рабочих-сдельщиков по стажу, образовав, пять групп рабочих с равными
интервалами.
По каждой группе и в целом по совокупности рабочих
подсчитайте: 1) число рабочих; 2) средний стаж работы; 3) среднемесячную
заработную плату.
Результаты
представьте в таблице. Дайте анализ показателей таблицы и сделайте краткие
выводы.
Тема 2.
Средние величины
Практические занятия
предусматривают решение следующих типов задач:
1)
исчисление средней арифметической простой по
индивидуальным данным;
2)
исчисление средней арифметической взвешенной в
дискретном ряде распределения;
3)
исчисление средней арифметической взвешенной в
интервальном ряде распределения с закрытыми и открытыми интервалами;
4)
расчет средней
арифметической из групповых средних;
5)
расчет средней гармонической;
6)
расчет моды;
7)
расчет медианы.
Решение типовых задач
№1. Имеются следующие данные о
производстве рабочими продукции А за смену:
|
Номер рабочего
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Выпущено
изделий за смену, шт.
|
16
|
17
|
18
|
17
|
16
|
17
|
18
|
20
|
21
|
18
|
Определить
среднюю выработку продукции рабочими данной группы.
Решение:
В данном
случае расчет следует производить по формуле простой средней арифметической:
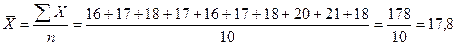 .
.
Простая
средняя арифметическая применяется, когда данные первичны, т.е. данные не
сгруппированы, представлены индивидуально в виде их перечня в любом порядке или
ранжированного ряда.
№2 Имеются данные о заработной плате работников:
|
Месячная заработная
плата (х), тыс. руб.
|
Число рабочих, f
|
Xf
|
|
5,5
6,5
8,0
9,5
11,0
|
2
4
8
20
16
|
11
26
64
190
176
|
|
Итого:
|
50
|
467
|
Определить
среднюю заработную плату работников.
Решение: Основой расчета является
экономическое содержание показателя:
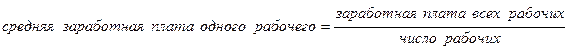
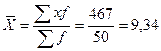 тыс. руб.
тыс. руб.
Частотами
(весами) могут быть относительные величины, взятые в процентах или
коэффициентах. Метод расчета средней и конечный результат от этого не
изменяется.
Представим данные о численности рабочих в условии
приведенной выше типовой задачи в относительных величинах:
|
Месячная заработная
плата (х), тыс. руб.
|
Число рабочих в %
к итогу
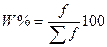
|
Доля рабочих в
коэффициентах
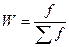
|
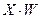
|
|
5,5
6,5
8,0
9,5
11,0
|
4
8
16
40
32
|
0,04
0.08
0,16
0,40
0,32
|
2,20
5.20
12,80
38,00
35,20
|
|
Итого:
|
100,0
|
1,00
|
93,40
|
Средняя
заработная плата рабочего, взвешенная по процентным соотношениям, будет равна
средней, полученной при решении типовой задачи 2:
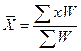 ;
;
 тыс. руб.
тыс. руб.
Если весами
являются частоты, выраженные в коэффициентах, то вычисления упрощаются; так как
сумма коэффициентов всегда равна единице, то расчет средней сводится к
определению суммы произведений вариант на частоты (в данном случае
коэффициенты):
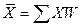 .
.
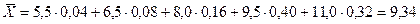 тыс. руб.
тыс. руб.
№3
Имеются следующие данные:
|
Группы рабочих по
количеству произведенной продукции за смену, шт.
|
Число рабочих, f
|
Середина интервала,
х
|
xf
|
|
6 – 10
10 – 14
14 – 18
18 – 22
22 - 26
|
10
30
40
15
5
|
8
12
16
20
24
|
80
360
640
300
120
|
|
Итого:
|
100,0
|
|
1500
|
Определите
среднюю выработку продукции одним рабочим за смену.
Решение: исчисление средней по
сгруппированным данным производится по формуле средней арифметической взвешенной:

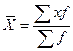 .
.
Чтобы
применить эту формулу необходимо варианты признака выразить одним числом
(дискретным). За такое дискретное число принимается средняя арифметическая
простая из верхнего и нижнего значения интервала. Так, для первой группы
дискретная величина Х
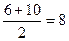 .
.
Дальнейший
расчет производится обычным методом
определения средней арифметической взвешенной:
 шт.
шт.
Итак, все
рабочие произвели 1500 шт. изделий за смену, а каждый в среднем произвел 15 шт.
В данном ряду
варианты осредняемого признака представлены в виде закрытых интервалов.
Преобразуем рассмотренный ряд в ряд с открытыми интервалами.
|
Группы рабочих по
количеству произведенной продукции за смену, шт.
|
Число рабочих, f
|
|
1
|
2
|
|
1
|
2
|
|
до 10
10 – 14
14 – 18
18 – 22
свыше 20
|
10
30
40
15
5
|
|
Итого:
|
100
|
В таких рядах
условно величина интервала первой группы принимается равной величине интервала
последующей, а величина интервала последней группы – величине интервала предыдущей.
Дальнейший расчет аналогичен изложенному выше.
№4. Выработка продукции за смену на предприятии
характеризуется следующими данными:
|
Бригада, №
|
Дневная выработка
продукции, шт.(x)
|
Число рабочих, чел. (f)
|
|
I
II
III
|
40
60
70
|
8
11
16
|
Определить среднедневную
выработку продукции рабочих цеха.
Решение: Основой расчета является экономическое
содержание показателя:
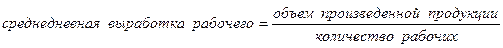
Расчет
производим по средней арифметической взвешенной:
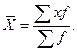
В
этой задаче варианты (дневная выработка продукции) являются не индивидуальными,
а средними по бригаде величинами. Весами выступает число рабочих в бригаде.
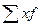 - объем произведенной продукции на предприятии.
- объем произведенной продукции на предприятии.
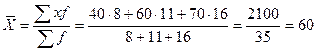 шт.
шт.
№5 Определить средний процент
выполнения плана прибыли акционерным обществом (АО)
|
Предприятия
АО
|
Плановая
прибыль за 1 год, млн. руб.
(f)
|
Выполнение
плана прибыли, %. (х)
|
|
1
2
3
4
|
2000
920
1200
280
|
102
80
95
85
|
|
Итого:
|
4400
|
|
Требуется
определить средний процент выполнения плана прибыли АО.
Решение: Основой расчета является
экономическое содержание показателя:
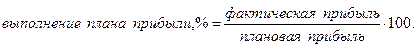
В
этой задаче варианты (процент выполнения плана прибыли) являются не
индивидуальными, а средними по
предприятию. Веса представлены плановой прибылью. При вычислении
среднего процента выполнения плана прибыли следует использовать формулу средней
взвешенной арифметической величины:
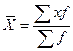 ,
,
где
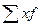 - фактическая прибыль,
получаемая путем умножения вариант (процент выполнения плана прибыли) на веса
(плановая прибыль).
- фактическая прибыль,
получаемая путем умножения вариант (процент выполнения плана прибыли) на веса
(плановая прибыль).
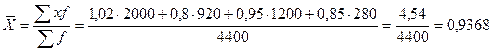 или 93,68%.
или 93,68%.
Произведя
вычисления, варианты (х) лучше брать в коэффициентах. Это позволяет получить
фактический объем прибыли в абсолютных значениях (млн. руб.) как в целом, так и
по каждому предприятию АО, что дает возможность сравнивать фактическую прибыль
с плановой, находить абсолютные приросты прибыли, производить сравнения.
Наряду
со средней арифметической в статистике применяется средняя гармоническая
величина, обратная средней арифметической из обратных значений признака. Как и
средняя арифметическая, она может быть простой и взвешенной.
№ 6.
Издержки производства и себестоимость единицы продукции А по трем акционерным
обществам (АО) характеризуются следующими данными:
|
Предприятия
(АО)
|
Издержки
производства, млн. руб.
(М)
|
Себестоимость
единицы продукции, тыс. руб. (Х)
|
|
1
2
3
|
2000
4800
1100
|
40
30
25
|
|
Итого:
|
7900
|
|
Определить
среднюю себестоимость изделия А по трем АО:
Решение: Основой расчета является
экономическое содержание показателя:
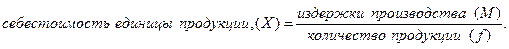
В
условии задачи даны себестоимость единицы продукции (Х) и издержки производства
(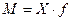 ), поэтому исходя из экономического содержания показателя
надо применять среднюю гармоническую взвешенную:
), поэтому исходя из экономического содержания показателя
надо применять среднюю гармоническую взвешенную:
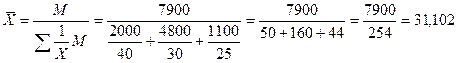 тыс. руб.
тыс. руб.
№ 7. Имеются данные о распределении
рабочих по затратам времени на обработку одной детали:
Таблица 2.1
|
Затраты
времени на одну деталь, мин.
|
Число
рабочих, чел. (f)
|
|
А
|
1
|
|
4
– 5
5
– 6
6
– 7
7
– 8
8
– 9
9
– 10
10
- 11
|
8
18
23
30
12
6
3
|
|
Итого:
|
100
|
Определить
обобщающие характеристики:
1)
средние затраты времени на обработку одной детали;
2)
моду;
3)
медиану.
Решение:
1.
В интервальном ряду распределения с равными интервалами среднее значение
признака определяется по формуле средней арифметической взвешенной
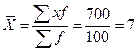 мин.
мин.
Таблица 2.2
Рабочая таблица
|
Затраты
времени на одну деталь, мин.
|
Число
рабочих, чел. (f)
|
X
|
Хf
|
Накопленные
частоты, (F)
|
|
1
|
2
|
3
|
4
|
5
|
|
4
– 5
5
– 6
6
– 7
7
– 8
8
– 9
9
– 10
10
- 11
|
8
18
23
30
12
6
3
|
4,5
5,5
6,5
7,5
8,5
9,5
10,5
|
36,0
99,0
149,5
225,0
102,0
57,0
31,5
|
8
26
49
79
91
97
100
|
|
Итого:
|
100
|
|
700,0
|
|
2.
Значение признака, наиболее часто встречающееся в совокупности, называется
модой. Для интервальных вариационных рядов распределения мода рассчитывается по формуле
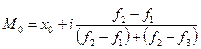 ,
,
где х0
– нижняя граница модального интервала;
i - величина интервала группировки;
f1
- частота интервала, предшествующему
модальному;
f2 - частота
модального интервала;
f3- частота
интервала следующего за модальным.
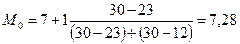 мин.
мин.
3.
Медианой называется значение признака у
единицы, стоящей в середине ранжированного ряда. Медиана делит ряд на две
равные части. Для интервального вариационного ряда медиана определяется по
формуле:
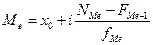 ,
,
где
х0 – нижняя граница
медианного интервала;
i – величина интервала
группировки;
NМе – номер медианы (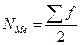 );
);
FМе-1 –
накопленная частота интервала предшествующего медианному;
fМе – частота медианного интервала.

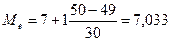 мин.
мин.
Таким
образом, одна половина рабочих затрачивает на обработку детали до 7,033 мин.,
другая свыше 7,033 мин.
В
симметричных совокупностях три обобщающие характеристики равны между собой 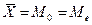 . Для общественно-экономических явлений характерны
асимметричные распределения. В них замечается определенная тенденция удлиняться
в какую – либо сторону (левую или
правую) от точки наибольшей плотности. Различают два типа асимметрии:
правостороннюю, где
. Для общественно-экономических явлений характерны
асимметричные распределения. В них замечается определенная тенденция удлиняться
в какую – либо сторону (левую или
правую) от точки наибольшей плотности. Различают два типа асимметрии:
правостороннюю, где 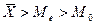 и левостороннюю, где
и левостороннюю, где 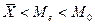 .
.
Наличие скошенности в рядах однородных
совокупностей служит косвенным указанием на то, что исследуемый процесс
проходит активную стадию развития. При исследовании вариации признаков, относительно которых
имеется заинтересованность в их увеличении (выполнение норм,
производительность труда, выпуск
продукции и т.д.), правосторонняя асимметрия свидетельствует о прогрессивном
развитии, о том, что оно идет в сторону
увеличения показателя, а левосторонняя асимметрия указывает на наличие большого
количества отстающих участков. При исследовании вариации признаков,
относительно которых имеется заинтересованность в их уменьшении (себестоимость,
трудоемкость и т.д.), правосторонняя
асимметрия свидетельствует о недостаточном развитии изучаемого процесса,
левосторонняя – об успешном его развитии.
В
нашем примере исчисленные обобщающие характеристики показывают левостороннюю
асимметрию в распределении рабочих по затратам рабочего времени на изготовление одной детали (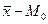 = 7–7,28 = -0,28 < 0).
Эти данные говорят о прогрессивности развития явления. Увеличение доли рабочих
с меньшими затратами времени на одну деталь, в конечном счете, приводит к
эффективности использования рабочего времени.
= 7–7,28 = -0,28 < 0).
Эти данные говорят о прогрессивности развития явления. Увеличение доли рабочих
с меньшими затратами времени на одну деталь, в конечном счете, приводит к
эффективности использования рабочего времени.
Задачи
№2.1 Имеются данные о распределении рабочих
двух акционерных обществ по тарифным разрядам (см. таблицу 2.3).
Определите
средний тарифный разряд рабочего:
1)
по АО №1;
2)
по АО №2.
Сравните
полученные результаты
3) по двум АО вместе
Таблица 2.3
|
Тарифный
разряд
|
Число
рабочих в АО
|
|
№1
|
№2
|
|
1
|
2
|
3
|
|
I
II
III
IV
V
VI
|
4
10
16
30
28
12
|
2
8
17
30
25
18
|
|
Итого:
|
100
|
100
|
№2.2 Имеются данные о расходе сырья на единицу
продукции:
|
Расход сырья на единицу, г
|
Обследовано
изделий, шт.
|
|
36 – 40
40 – 44
44 – 48
48 – 52
52 и
выше
|
5
28
52
12
3
|
|
Итого:
|
100
|
Определите
средний расход сырья на одно изделие.
№2.3 Имеются данные о распределении
вкладов населения в филиалах сберегательного банка двух районов:
|
Размер
вклада, руб.
|
Число
вкладчиков, в % к итогу
|
|
1
район
|
2
район
|
|
До
800
800 –
1100
1100
– 1400
1400
– 1700
1700
– 2000
Свыше
2000
|
12
28
35
13
9
3
|
6
10
29
41
12
2
|
|
Итого:
|
100
|
100
|
Определите
средний размер вклада в филиалах сберегательного банка первого и второго
районов. Сравните полученные результаты и объясните, почему средний размер
вклада в филиалах 2 района оказался выше, чем в филиалах 1 района.
№2.4 Имеются следующие данные:
|
Объекты
кредитования
|
Среднегодовые
остатки задолженности по кредиту, млн. руб.
|
Ставка
процентов, %
|
|
Базисный
период
|
Отчетный
период
|
|
Первый
Второй
Третий
|
10
4
15
|
12
5
10
|
18
20
15
|
Определите
среднюю ставку процентов по краткосрочным ссудам в базисном и отчетном
периодах.
№ 2.5 Имеются данные о получении прибыли акционерными обществами района за отчетный год:
|
АО
|
Получено
прибыли за отчетный год, тыс. руб.
|
Выполнение
плана прибыли, %
|
|
1
2
3
|
612
288
306
|
105
90
93
|
Определить:
1) средний процент выполнения плана прибыли АО; 2) сколько недополучено прибыли
АО района.
№2.6
Имеются данные о производстве и себестоимости продукции «А» по двум
предприятиям:
|
Предприятие
№
|
Базисный
год
|
Отчетный
год
|
|
Себестоимость
единицы, руб.
|
Производство,
тыс. шт.
|
Себестоимость
единицы, руб.
|
Производство,
тыс.шт.
|
|
1
2
|
14,0
22,0
|
60
40
|
13,0
21,6
|
40
60
|
Определить
среднюю себестоимость продукции в базисном и отчетном годах. Объясните, почему
при более низкой себестоимости по каждому предприятию в отчетном году средняя
себестоимость оказалась выше, чем в базисном году.
№2.7 Имеются следующие данные о заработной плате
рабочих двух цехов за два месяца:
|
№
цеха
|
Сентябрь
|
Октябрь
|
|
Средняя
зарплата, руб.
|
Численность
рабочих, чел.
|
Средняя
зарплата, руб.
|
Фонд
зарплаты, тыс. руб.
|
|
1
2
|
3000
3400
|
500
300
|
3210
3260
|
1508,7
1010,6
|
Вычислите
среднюю заработную плату рабочих по двум цехам завода: а) за сентябрь; б) за
октябрь. Сравните полученные результаты. Укажите виды средних.
№2.8 Имеются данные по предприятиям за отчетный
год:
|
Заводы
|
I квартал
|
II квартал
|
|
План
выпуска продукции млн. руб.
|
%
выполнения плана
|
Фактический
выпуск, млн. руб.
|
%
выполнения плана
|
|
1
2
|
240
300
|
100
110
|
162
345
|
108
115
|
Определите
средний процент выполнения плана выпуска продукции за I и II кварталы. Сделайте выводы.
№ 2.9 Бригада токарей была занята
обточкой одинаковых деталей в течение 8 – часового рабочего дня. Первый токарь
затрачивал на одну деталь 10 мин., второй – 15 мин., третий – 12 мин.,
четвертый – 14 мин., пятый – 16 мин.
Определите
среднее время, необходимое для изготовления одной детали.
№2.10 По двум предприятиям,
вырабатывающим продукцию «А», имеются следующие данные:
|
Номер
завода
|
Базисный
год
|
Отчетный
год
|
|
Затраты
времени на единицу продукции, мин.
|
Изготовлено
продукции, тыс. шт.
|
Затраты
времени на единицу продукции, мин.
|
Затраты
времени на всю продукцию, мин.
|
|
1
2
|
20
30
|
15
22
|
20
15
|
30 000
50
000
|
Вычислите
средние затраты времени на одну деталь в целом по двум предприятиям за базисный
и отчетный годы. Какие виды и формы средних величин Вы применили, почему?
№2.11 Стоимость стратегически важных
товаров, задержанных и не пропущенных таможенной службой при вывозе из России в
январе 2005 г., характеризуется следующими данными:
|
Страны
|
Стоимость
задержанных товаров, млн. руб.
|
В
% от общей стоимости вывозимых товаров
|
|
Латвия
Эстония
Беларусь
|
1900
700
800
|
20
7
8
|
Вычислить
общий средний процент задержанных таможенной службой товаров по совокупности
стран.
№ 2.12 Заработная плата бригады строителей по
отдельным профессиям за месяц характеризуется следующими данными:
|
Маляры
|
Штукатуры
|
Кровельщики
|
|
Зарплата,
руб.
|
Число
рабочих, чел.
|
Зарплата,
руб.
|
Число
рабочих, чел.
|
Зарплата,
руб.
|
Число
рабочих, чел.
|
|
5200
5400
5600
|
1
1
1
|
5300
5600
5800
|
3
3
3
|
5500
5700
5900
|
3
7
4
|
|
Итого:
|
3
|
-
|
9
|
-
|
14
|
Определить
среднюю заработную плату рабочих по каждой профессии и в целом по бригаде.
№2.13 Определить средний процент брака
в составе всей произведенной продукции по следующим данным:
|
Изделия
|
%
брака
|
Стоимость
брака, тыс. руб.
|
|
1
2
3
|
1,5
2,0
0,8
|
900
1200
600
|
№2.14 В трех партиях выпущенных цехом деталей оказалось
забракованными:
|
Партия
|
Количество
забракованных деталей
|
%
забракованных деталей от общего числа деталей в партии
|
|
1
2
3
|
46
63
72
|
2,7
2,1
1.9
|
Вычислить
средний процент брака во всех трех партиях вместе.
№2.15 Распределение рабочих предприятия
по степени выполнения норм выработки за 1 квартал характеризуется следующими
показателями:
|
Группы
рабочих по выполнению норм выработки, (%)
|
Число
рабочих
|
|
апрель
|
май
|
июнь
|
|
До
90
90-
100
100
– 110
110
– 120
120
– 130
130
– 140
140
- 150
|
5
7
28
21
18
15
6
|
2
3
26
32
24
10
3
|
-
2
14
36
28
12
8
|
|
Итого:
|
100
|
100
|
100
|
Определите
моду и медиану, и средний процент выполнения норм выработки по каждому
ряду распределения. Сделайте выводы.
Тема 3. Показатели вариации
Практические
занятия по теме предусматривают решение следующих типов задач:
1.
Определение показателей вариации (размаха
вариации 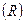 , среднего линейного отклонения
, среднего линейного отклонения 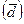 , среднего квадратичного отклонения
, среднего квадратичного отклонения 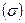 , дисперсии
, дисперсии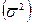 , коэффициента вариации
, коэффициента вариации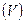 ).
).
2.
Расчет групповой, межгрупповой и общей дисперсий по правилу сложения дисперсий, коэффициента детерминации
и эмпирического корреляционного отношения.
Решение типовых
задач
№1. Имеются следующие данные о
производительности труда рабочих в двух бригадах:
Таблица №3.1
|
Табельный
номер рабочего
|
Произведено
продукции за смену, шт. (х)
|
|
I бригада
|
II бригада
|
|
1
2
3
4
5
|
4
6
24
30
36
|
16
18
20
22
24
|
|
Итого:
|
100
|
100
|
Определить: 1) размах вариации 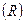 , 2) среднее линейное отклонение
, 2) среднее линейное отклонение 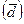 ,
,
3)
среднее квадратичное отклонение 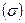 , 4) коэффициент вариации
, 4) коэффициент вариации 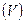 .
.
Решение:
1.
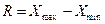 , где
, где 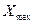 - максимальное
значение признака,
- максимальное
значение признака, 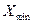 - минимальное значение признака. Для нашего примера размах вариации
производительности труда для первой бригады составляет:
- минимальное значение признака. Для нашего примера размах вариации
производительности труда для первой бригады составляет: 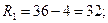 для второй бригады:
для второй бригады: 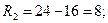
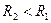 . Этот показатель прост в вычислении и указывает на общие
размеры вариации, но он не дает представления о степени колеблемости внутри
совокупности, так как вычисляется на основе только двух крайних значений
признака совокупности.
. Этот показатель прост в вычислении и указывает на общие
размеры вариации, но он не дает представления о степени колеблемости внутри
совокупности, так как вычисляется на основе только двух крайних значений
признака совокупности.
2.
Для первичного ряда среднее линейное отклонение есть средняя арифметическая из
абсолютных отклонений отдельных значений признака от общей средней:
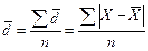 .
.
Порядок
расчета среднего линейного отклонения следующий:
а)
по значениям признака исчисляется средняя арифметическая: 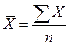 ;
;
б)
определяются отклонения каждой варианты Х от средней: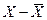 ;
;
в)
рассчитывается сумма абсолютных величин отклонений: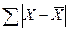 ;
;
г)
сумма абсолютных величин отклонений делится на число значений:
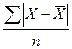 .
.
В
нашем примере средняя производительность труда рабочих первой бригады-
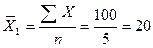 шт.,
шт.,
-
второй бригады
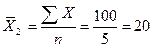 шт.
шт.
Таблица 3.2
|
Табельный
номер рабочего
|
1
бригада
|
2 бригада
|
|
Х
|
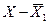
|
|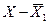 | |
|
(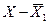 )2 )2
|
X
|
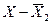
|
|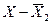 | |
|
(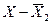 )2 )2
|
|
1
2
3
4
5
|
4
6
24
30
36
|
-16
-14
+4
+10
+16
|
16
14
4
10
16
|
256
196
16
100
256
|
16
18
20
22
24
|
-4
-2
0
+2
+4
|
4
2
0
2
4
|
16
4
0
4
16
|
|
Итого
|
100
|
0
|
60
|
824
|
100
|
0
|
12
|
40
|
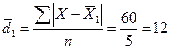 шт.,
шт., 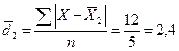 шт.,
шт.,
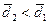 .
.
Считается,
что среднее линейное отклонение дает необъективную оценку вариации, как правило,
занижает ее.
3.
Корень квадратный из дисперсии называется средним квадратическим отклонением
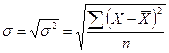 .
.
Для
первой бригады:
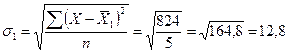 шт.
шт.
Для
второй бригады:
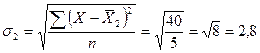 шт.
шт.
Среднеквадратическое
отклонение является наиболее
распространенным показателем степени вариации.
4.
Коэффициент вариации – относительный показатель колеблемости, равный
процентному отношению среднего квадратического отклонения к средней
арифметической:
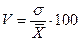 .
.
Для
первой бригады:
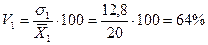
Для
второй бригады:
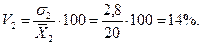
Анализ
полученных данных говорит о том, что производительность труда работников первой
бригады отличается от средней производительности труда (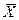 = 20шт.) в среднем на 12,8 шт., или на 64%, а второй бригады
– в среднем на 2,8 шт., или на 14%. Величины показателей вариации
свидетельствуют о том, что совокупность
рабочих второй бригады по уровню производительности труда однороднее
совокупности рабочих первой бригады. Значение коэффициента вариации рабочих первой бригады превышает 40%,
следовательно, вариация производительности труда рабочих велика, найденная
средняя производительность труда плохо представляет всю совокупность рабочих,
не является ее типичной, надежной характеристикой, а саму совокупность нет
оснований считать однородной по производительности труда. Значение коэффициента
вариации у рабочих второй бригады не превышает 40 %. Это говорит об
относительно невысокой колеблемости признака, о типичности, надежности средней
производительности труда, об
однородности рабочих второй бригады по производительности труда.
= 20шт.) в среднем на 12,8 шт., или на 64%, а второй бригады
– в среднем на 2,8 шт., или на 14%. Величины показателей вариации
свидетельствуют о том, что совокупность
рабочих второй бригады по уровню производительности труда однороднее
совокупности рабочих первой бригады. Значение коэффициента вариации рабочих первой бригады превышает 40%,
следовательно, вариация производительности труда рабочих велика, найденная
средняя производительность труда плохо представляет всю совокупность рабочих,
не является ее типичной, надежной характеристикой, а саму совокупность нет
оснований считать однородной по производительности труда. Значение коэффициента
вариации у рабочих второй бригады не превышает 40 %. Это говорит об
относительно невысокой колеблемости признака, о типичности, надежности средней
производительности труда, об
однородности рабочих второй бригады по производительности труда.
№2. При изучении норм расхода сырья
получили следующее распределение изделий по весу:
|
Вес
изделий, г.
|
Число изделий, шт.
|
|
До
20
20
– 22
22
– 24
24
– 26
Свыше
26
|
10
20
50
15
5
|
|
Итого
|
100
|
Вычислите:
1)
среднее линейное отклонение;
2)
среднее квадратическое отклонение;
3)
коэффициент вариации.
Решение:
1.
В вариационном ряду среднее линейное отклонение
определяется по формуле:
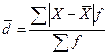 , где
, где 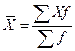 .
.
Расчет
этой величины удобно осуществлять в таблице.
|
Вес
изделий, г.
|
Число
изделий, (f)
|
Х
|
Хf
|
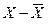
|
|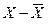 |f |f
|
(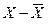 )2 )2
|
(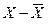 )2f )2f
|
|
До 20
20 – 22
22 – 24
24 – 26
Свыше
26
|
10
20
50
15
5
|
19
21
23
25
27
|
190
420
1150
375
135
|
-3,7
-1,7
0,3
2,3
4,3
|
37,0
34.0
1,5
34,5
21,5
|
13,69
2,89
0,09
5,29
18,49
|
136,90
57,80
4,500
79,35
92,45
|
|
Итого
|
100
|
|
2270
|
|
128
|
|
371,00
|
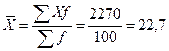 г.
г. 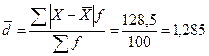 г.
г.
Следовательно,
вес изделий отклоняется от среднеарифметического веса в среднем на 1, 285 г.
2.
Среднее квадратическое отклонение
вариационного интервального ряда определяется по формуле:
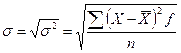 .
.
Предоставив необходимые расчеты в таблице,
подсчитаем:

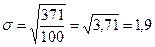 г.
г.
3. Коэффициент вариации:
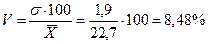
Так
как V<40% , то средний
вес изделий, равный 22,7 г., является типичной величиной в данной однородной совокупности,
и вес изделий от среднего веса в среднем отклоняется на 1,9 или на 8,48%.
№ 3.
Имеется статистическая информация о фондоотдаче тридцати организаций, руб.:
1,05; 0,96; 1,12; 1,19; 1,08; 1,98; 1,3; 1,16; 1,065; 1,0; 1,1; 1,23; 1,13;
1,03; 0,9; 1,06; 1,15; 1,07; 1,17; 0,94; 1,02; 1,06; 1,18; 0,99; 1,1; 1,28; 1,09; 1,25; 1,04; 1,12.
1.
Постройте статистический ряд распределения организаций
по фондоотдаче, образовав пять групп с равными интервалами.
2.
Постройте графики полученного ряда распределения.
Графически определите значения моды и медианы.
3.
Рассчитайте характеристики ряда распределения: среднюю
арифметическую, моду и медиану, квадратическое
отклонение, коэффициент вариации.
4.
Вычислите среднюю арифметическую по исходным данным,
сравните ее с аналогичным показателем, рассчитанным в п. 3. Объясните причину их расхождения.
Решение:
Необходимо
построить ряд распределения организаций по признаку «фондоотдача», образовав
пять групп с равными интервалами. Величину интервала группировки организаций по
фондоотдаче определяем по формуле:
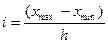
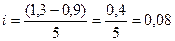 руб.
руб.
Таким
образом, интервалы получились: 0,9 – 0,98; 0,98 – 1,06; 1,06 – 1,14; 1,14 –
1,22; 1,22 – 1,3.
Подсчитаем
частоты, частости и накопленные частоты и представим результаты в таблице 3.3:
Таблица 3.3
Ряд распределения организаций по фондоотдаче
|
Группы
организаций по фондоотдаче, руб.
|
Число
организаций,
f
|
Число
организаций в % к итогу
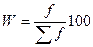
|
Накопленные
частоты, F
|
Х
|
|
А
|
1
|
2
|
3
|
4
|
|
0,9 – 0,98
0,98 – 1,06
1,06 – 1,14
1,14 – 1,22
1,22 – 1,3
|
3
7
11
5
4
|
10
23,333
36,667
26,667
13,333
|
3
10
21
26
30
|
0,94
1,02
1,1
1,18
1,26
|
|
|
30
|
100
|
|
|
2.
Ряды распределения могут быть изображены графически. Основные графики
следующие:
-
полигон частот ряда распределения организаций по фондоотдаче (рис. 3. 1);
- гистограмма ряда распределения организаций по
фондоотдаче (рис.3.2);
-
кумулята распределения организаций по фондоотдаче (рис. 3.3).
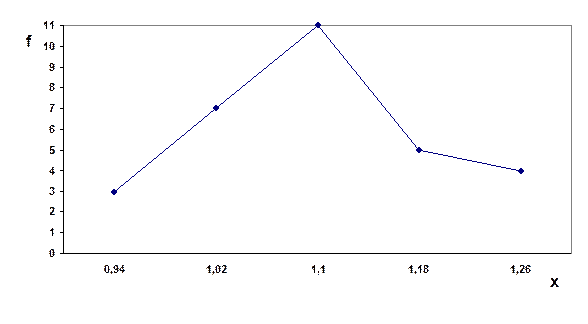
Рис.3.1
Полигон частот ряда распределения организаций по фондоотдаче

1.092 
0.9 0,98 1,06
1,14 1,22
1,3
Рис.3.
2 Гистограмма ряда распределения
организаций по фондоотдаче
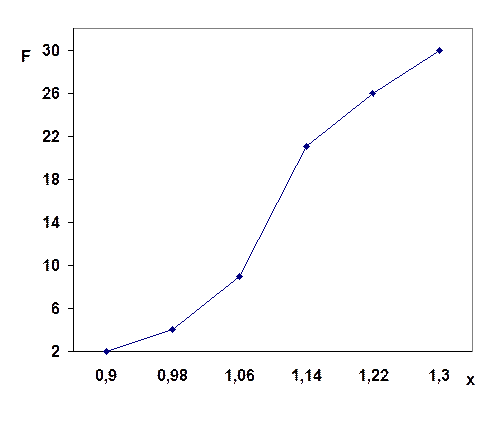

 15
15
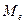
1,096
Рис. 3.3 Кумулята ряда распределения организаций по
фондоотдаче
Анализ
ряда и графиков показывает, что распределение организаций по фондоотдаче
не является равномерным, чем больше
фондоотдача организаций отличается от средней фондоотдачи, тем реже такие
организации встречаются.
3.
Чтобы найти моду, первоначально определим модальный интервал данного ряда. Из
таблицы 3.3 видно, что наибольшая
частота соответствует интервалу, где значение варианты лежит в пределах от 1,06
до 1,14. Это и есть модальный интервал. Для расчета определенного значения модальной
величины признака, заключенного в этом интервале, применяют такую формулу:

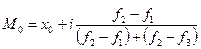 .
.
где
х0 – нижняя граница
модального интервала, в нашем случае 1,06;
i - величина интервала группировки, в нашем примере 0,08;
f1
- частота интервала, предшествующему
модальному (7);
f2 - частота
модального интервала (11);
f3 - частота
интервала следующего за модальным (5).
Подставляя
числовые значения из нашего задания в эту формулу, получим:
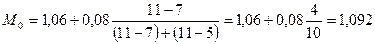 руб.
руб.
Исчислим
теперь медиану. Для нахождения медианы в интервальном вариационном ряде
определим сначала интервал, в котором она находится (медианный интервал).
Половина
суммы частот у нас равна 15. Следовательно, согласно табл. 3.3 медианным
интервалом у нас будет интервал со
значением фондоотдачи от 1,06 до 1,14.
Формула
для исчисления медианы в вариационном
интервальном ряде будет иметь такой вид:
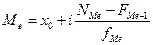 ,
,
где
х0 – нижняя граница
медианного интервала;
NМе – номер медианы;
FМе-1 – накопленная частота интервала,
предшествующего медианному;
fМе – частота
медианного интервала.
Подставляя
в эту формулу значения, получим:

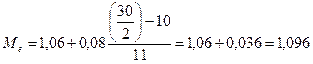 руб.
руб.
Средняя
арифметическая для ряда распределения определяется по формуле средней
арифметической взвешенной (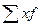 см. табл. 3.4, гр.3):
см. табл. 3.4, гр.3):
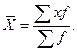
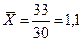 руб.
руб.
Следовательно,
средняя арифметическая равна 1,1; мода-1,092 и медиана- 1,096. Соотношение этих
трех величин указывает на направление и степень асимметрии распределения. Так как значение средней
арифметической больше значения медианы и моды, то есть 1,1 >1,096>1,092,
то это правосторонняя асимметрия (положительная). Правосторонняя асимметрия
свидетельствует о прогрессивном развитии отрасли, о том, что оно идет в сторону
увеличения эффективности использования основных производственных фондов (увеличения
фондоотдачи) организаций.
Чтобы
вычислить среднее квадратическое отклонение, нужно определить дисперсию
признака. Формула этого показателя такая:
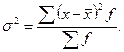
Корень
квадратный из дисперсии и будет средним
квадратическим отклонением:
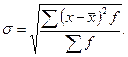
Проделаем
в таблице 3.4 необходимые расчеты для нахождения дисперсии, среднего
квадратического отклонения и коэффициента вариации.
Таблица 3.4
Вычисление дисперсии, среднего квадратического отклонения
и коэффициента вариации
|
Группы
организаций по фондоотдаче, руб.
|
Число
организаций, f
|
X
|
Xf
|
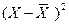
|
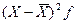
|
|
А
|
1
|
2
|
3
|
4
|
5
|
|
0,9 – 0,98
0,98 – 1,06
1,06-1,14
1,14 – 1,22
1,22 – 1.3
|
3
7
11
6
4
|
0,94
1,02
1,1
1,18
1,26
|
2,82
7,14
12,1
5,9
5,04
|
0,026
0,006
0
0,006
0,026
|
0,078
0,042
0
0,036
0,104
|
|
Итого:
|
30
|
|
33
|
0,064
|
0,26
|
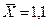 руб.
руб.

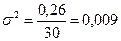
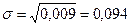
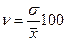
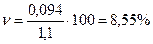
Анализ полученных данных говорит о том, что
фондоотдача организаций отличается от средней фондоотдачи на 0,94 руб., или на
8,55%. Значение коэффициента вариации v не превышает 40 %.
Отсюда следует, что вариация фондоотдачи
не высокая и средняя фондоотдача,
рассчитанная по средней арифметической взвешенной, является типичной, надежной
величиной, свидетельствующей об однородности совокупности.
4.
Вычислим среднюю арифметическую по исходным данным и сравним ее с аналогичным показателем, рассчитанным по
таблице 3.4. Средняя арифметическая 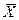 для первичных данных
вычисляется по формуле простой средней арифметической:
для первичных данных
вычисляется по формуле простой средней арифметической:
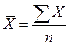 ,
, 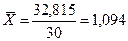 руб.
руб.
Данный
результат, полученный на основе средней арифметической простой, отличается от
средней арифметической взвешенной. Это объясняется тем, что в расчете на основе
ряда распределения мы уже не располагаем исходными индивидуальными данными, а
вынуждены ограничиваться сведениями о величине середины интервала.
№ 4. Имеются данные о
производительности труда рабочих:
|
Табельный
номер рабочего
|
Произведено
продукции за смену, шт. (х)
|
|
В
дневную смену
|
В
ночную смену
|
|
1
2
3
4
5
|
10
16
14
8
12
|
10
12
8
8
12
|
Определите:
1)
частные дисперсии;
2)
среднюю из частных дисперсий;
3)
межгрупповую дисперсию;
4)
общую дисперсию (по правилу сложения дисперсий и обычным способом);
5)
эмпирическое корреляционное отношение.
Сделайте
выводы.
Решение:
Это
первичные данные.
1.
Для расчета групповых дисперсий воспользуемся формулой:

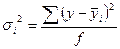 , где
, где 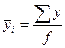 .
.
Расчет дисперсий по группам представим в таблице 3.5:
Таблица 3.5
|
Табельный
номер рабочего
|
В
дневную смену
|
В
ночную смену
|
|
Произведено продукции,
шт.
(у)
|
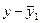
|
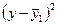
|
Произведено продукции, шт. (у)
|
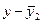
|
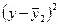
|
|
1
2
3
4
5
|
10
16
14
8
12
|
-2
-4
+2
-4
0
|
4
16
4
16
0
|
10
12
8
8
12
|
0
+2
-2
-2
+2
|
0
4
4
4
4
|
|
|
60
|
|
40
|
50
|
|
16
|
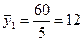 шт.
шт. 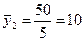 шт.
шт.
Подставив
полученные значения в формулу, получим:
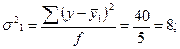
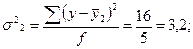
2.
Средняя из групповых дисперсий равна:
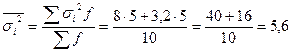 .
.
3.
Для определения межгрупповой дисперсии предварительно следует подсчитать общую
среднюю как среднюю взвешенную из групповых средних:
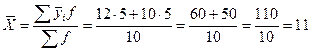 шт.
шт.
Затем
рассчитаем межгрупповую дисперсию:
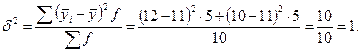
4.
Общую дисперсию исчислим по правилу сложения дисперсий:
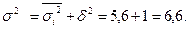
Проверим
полученный результат, исчислив общую дисперсию обычным способом:
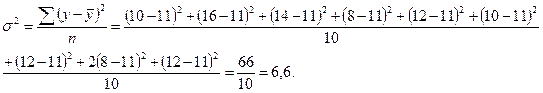
4)
Коэффициент детерминации равен:
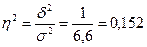 или 15,2 %.
или 15,2 %.
Эмпирическое
корреляционное отношение составит:
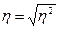 ;
; 
Коэффициент
детерминации показывает, какая доля всей вариации признака обусловлена
фактором, положенным в основу группировки. Коэффициент детерминации 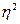 = 15,2%, следовательно, фактор времени работы (ночное или
дневное) на 15,2 % обуславливает вариацию производительности труда рабочих.
Эмпирическое корреляционное отношение показывает тесноту связи между группировочным и
результативным признаками. Корреляционное отношение изменяется от 0 до 1.
= 15,2%, следовательно, фактор времени работы (ночное или
дневное) на 15,2 % обуславливает вариацию производительности труда рабочих.
Эмпирическое корреляционное отношение показывает тесноту связи между группировочным и
результативным признаками. Корреляционное отношение изменяется от 0 до 1.
Если
связь отсутствует, то корреляционное отношение равно нулю. В этом случае
дисперсия групповых средних 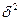 будет равна нулю, т.е.
все групповые средние будут равны между собой, межгрупповой вариации не будет.
Значит, группировочный признак никак не
влияет на образование общей вариации.
будет равна нулю, т.е.
все групповые средние будут равны между собой, межгрупповой вариации не будет.
Значит, группировочный признак никак не
влияет на образование общей вариации.
Если
связь функциональная, то корреляционное отношение будет равно единице. В этом
случае дисперсия групповых средних равна общей
дисперсии (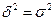 ), т е. внутригрупповой вариации не будет. Это означает, что
группировочный признак целиком определяет вариацию изучаемого признака. Чем
больше значение
), т е. внутригрупповой вариации не будет. Это означает, что
группировочный признак целиком определяет вариацию изучаемого признака. Чем
больше значение  приближается к
единице, тем полнее, ближе к функциональной зависимости корреляционная связь
между признаками.
приближается к
единице, тем полнее, ближе к функциональной зависимости корреляционная связь
между признаками.
Для
качественной оценки тесноты связи на основе показателя  можно воспользоваться
следующей таблицей (шкалой Чеддока):
можно воспользоваться
следующей таблицей (шкалой Чеддока):
|
Величина
|
0,1 –
0,3
|
0,3 –
0,5
|
0,5 –
0,7
|
0,7 –
0,9
|
0,9 –
0,99
|
|
Сила
связи
|
слабая
|
умеренная
|
заметная
|
тесная
|
Весьма
тесная
|
Убедившись с помощью группировки и  , что связь достаточно тесная, можно перейти к
корелляционно-регрессионному анализу.
, что связь достаточно тесная, можно перейти к
корелляционно-регрессионному анализу.
В
нашем примере 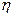 =0,389, что говорит об умеренной связи между временем работы
рабочих (ночное или дневное) и их производительностью труда.
=0,389, что говорит об умеренной связи между временем работы
рабочих (ночное или дневное) и их производительностью труда.
№4
По исходным данным таблицы 3.6
Таблица 3.6
Статистическая
информация о фондоотдаче тридцати организаций
|
№
организации
|
Выпуск
продукции
|
Фондоотдача
|
|
А
|
1
|
2
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
36,45
23,4
46,540
59,752
41,415
26,86
79.2
54,720
40,424
30,21
42,418
64,575
56,612
35,42
14,4
36,936
53,392
41,0
55,680
18,2
31,8
39,204
57,128
28,44
43,344
70.720
41,832
69,345
35,903
50,22
|
1,05
0,96
1,12
1,19
1,08
0,98
1,3
1,16
1,065
1
1,1
1,23
1,13
1,03
0,9
1,06
1,15
1,07
1,17
0,94
1,02
1,06
1,18
0,99
1,1
1,28
1,09
1,25
1,04
1,12
|
|
Итого
|
1320,540
|
32,815
|
|
|
|
|
|
1)
установите
наличие и характер связи между признаками – выпуском продукции и
эффективностью использования основных производственных фондов (фондоотдачей), образовав, пять групп с
равными интервалами по обоим признакам, методом аналитической группировки;
2)
измерьте тесноту корреляционной связи между названными
признаками с помощью использования коэффициента детерминации и эмпирического
корреляционного отношения. Сделайте выводы.
Решение:
1.
Связь между признаками «выпуск продукции» и «фондоотдача» изучается с помощью
аналитической группировки. Поскольку аналитическая группировка предполагает
разделение совокупности на группы по факторному признаку, его необходимо
определить. В нашем примере факторным
признаком является фондоотдача, т.к. от нее зависит выпуск продукции.
Определяем величину интервала группировки по факторному признаку по формуле:
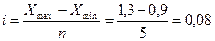 руб.
руб.
Группы
будут: 0,9 – 0,98; 0,98 – 1,06; 1,06 – 1,14;
1,14 – 1,22; 1,22 – 1,3.
Чтобы
дополнить эти данные средними по группам значениями выпуска продукции,
необходимо построить рабочую таблицу 3.7:
Таблица 3.7
Распределение организаций по фондоотдаче
|
Группы
организаций по фондоотдаче, руб.
|
Номер и
число организаций
|
Выпуск
продукции, млн. руб.
|
|
А
|
1
|
2
|
|
0,9 – 0,98
|
2
15
20
|
23,4
14,4
18,2
|
|
Итого
|
3
|
56
|
|
0,98 – 1,06
|
1
6
10
14
21
24
29
|
36,45
26,86
30,21
35,42
31,80
28,44
35,903
|
|
Итого
|
7
|
225,083
|
|
1,06 – 1,14
|
3
5
9
11
13
16
18
22
25
27
30
|
46,54
41,415
40,424
42,418
51,612
41
36,936
39,204
43,344
41,832
50,220
|
|
Итого
|
11
|
474,945
|
|
1,14 – 1,22
|
4
8
17
19
23
|
59,752
54,720
53,392
55,680
57,128
|
|
Итого
|
5
|
280,672
|
|
1,22 – 1,3
|
7
12
26
28
|
79,200
64,575
70,720
69,435
|
|
Итого
|
4
|
283,840
|
|
Всего
|
30
|
1320,54
|
|
|
|
|
На
основании таблицы 3.7 построим итоговую таблицу 3.8 аналитической группировки.
Таблица 3.8
Зависимость выпуска продукции организаций от
фондоотдачи
|
Группы
организаций по фондоотдаче, руб.
|
Число
организаций, 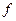
|
Выпуск
продукции, млн. руб.
|
|
Всего 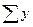
|
В
среднем на одну организацию,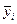
|
|
А
|
1
|
2
|
3
|
|
0,9 – 0,98
0,98 – 1,06
1,06 – 1,14
1,14 – 1,22
1,22 – 1,3
|
3
7
11
5
4
|
56
225,083
474,945
280,672
283,84
|
18,666
32,154
43,177
56,134
70,960
|
|
Итого
|
30
|
1320,54
|
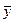 =44,018 =44,018
|
Групповые
средние результативного признака определяются по формуле простой средней
арифметической:
 .
.
Общая
средняя результативного признака по
совокупности в целом может быть определена двумя способами:
1)
по первичным данным по формуле простой средней арифметической:
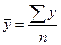 ,
,
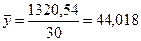 ;
;
2)
по вторичным данным, по формуле взвешенной средней арифметической:
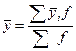 ,
,
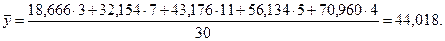
Анализ
таблицы 3.8 (графы А и 3) показывает, что с ростом фондоотдачи от группы к группе
возрастает и выпуск продукции в среднем на одну организацию. Отсюда следует,
что между фондоотдачей и выпуском продукции в среднем на одну организацию
существует прямая корреляционная взаимосвязь.
2.
Коэффициент детерминации равен 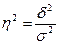
Если
учесть, что величина межгрупповой дисперсии характеризует влияние только
факторного признака, а величина общей дисперсии характеризует влияние всех
признаков, влияющих на результативную величину, то частное от деления
межгрупповой дисперсии на общую дисперсию укажет на силу влияния факторного
признака на результативный.
Эмпирическое
корреляционное отношение определяется по формуле:
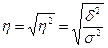
Все
расчеты проделаем в таблице 3.9.
Таблица
3.9
Рабочая
таблица для определения межгрупповой дисперсии 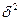
|
Группы
организаций по фондоотдаче, руб.
|
Число
организаций, 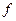
|
Выпуск
продукции в среднем на 1 организацию, млн. руб. 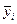
|
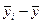
|
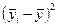
|
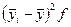
|
|
А
|
1
|
2
|
3
|
4
|
5
|
|
0,9 – 0,98
0,98 – 1,06
1,06 – 1,14
1,14 – 1,22
1,22 – 1,3
|
3
7
11
5
4
|
18,667
32,155
43,177
56,134
70,96
|
-25,351
-11,863
-0,841
12,116
26,942
|
642,67
140,737
0,708
146,807
725,872
|
1928,069
985,162
7,783
734,037
2903,487
|
|
Итого
|
30
|
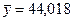
|
-
|
-
|
6558,538
|
Межгрупповая
дисперсия выпуска продукции равна:
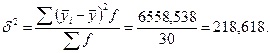
Рассчитаем
теперь общую дисперсию уровней выпуска продукции по индивидуальным данным 30
организаций. Для этого составим таблицу 3.10.
Опираясь
на данные таблицы 3.10, рассчитаем общую дисперсию:
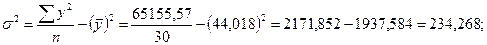
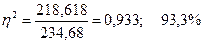 ;
; 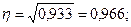
100
– 93,3 = 6,8 %.
Таблица
3.10
Рабочая
таблица для расчета общей дисперсии 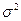
|
y
|
y2
|
|
1
|
2
|
|
36,45
23,4
46,54
59,752
41,415
26,860
79,2
54,72
40,424
30,210
42,418
64,575
51,612
|
1328,60
547,56
2165,97
3570,3
1715,2
721,46
6272,64
2994,28
1634,1
912,64
1899,29
4169,93
2663,8
|
Продолжение
таблицы 3.10
|
35,42
14,4
36,936
53,392
41
55,68
18,2
31,8
39,204
57,128
28,44
43,344
70,72
41,832
69,345
35,903
50,022
|
1254,58
207,36
1364,27
2850,71
1681
3100,26
331,24
1011,24
1536,95
3263,61
808,83
1878,7
5001,32
1749,92
4808,73
1289,03
2522,05
|
|
Итого:
|
65155,57
|
Выводы: Величина коэффициента детерминации
говорит о том, что вариация выпуска продукции на 93,3 % зависит от вариации
фондоотдачи организаций и на 6,8 % от вариации прочих признаков. Эмпирическое
корреляционное отношение, равное 0,966, свидетельствует о весьма тесной связи
между фондоотдачей и выпуском продукции.
Задачи
№3.1 В результате обследования работы
станков в механических цехах завода получены следующие данные:
|
Цех
|
Отработано
станко-часов
|
|
Токарными
станками
|
Заточными
станками
|
|
1
2
3
4
5
|
2100
1900
2300
2500
1700
|
800
100
1200
600
700
|
Определите:
среднее линейное отклонение, среднее квадратическое отклонение, коэффициент
вариации времени работы: 1) токарных станков; 2) заточных станков.
№3.2 Имеются следующие данные о
количестве произведенной рабочими цеха за смену продукции (в штуках):
10 14 12
15 11 16
14 19 23
13 19 16
19 15 25
21 22
1.
Постройте ряд распределения рабочих по количеству произведенной продукции,
образовав три группы с равными интервалами. Изобразите ряд графически.
2.
По данным ряда распределения определите: а) среднюю выработку продукции
(количество произведенной продукции на одного рабочего); б) коэффициент
вариации выработки продукции.
№3.3 Имеются следующие данные о распределении
рабочих по стажу:
|
Группы
рабочих по стажу
|
До
5
|
5
– 10
|
10
- 15
|
15
- 20
|
20
- 25
|
Свыше
25
|
|
Число
рабочих
|
20
|
30
|
20
|
10
|
12
|
8
|
Вычислите:
1. Средний стаж рабочих и среднее квадратическое отклонение.
2.
Коэффициент вариации.
Поясните
полученные результаты.
№ 3.4 Доля бракованной продукции
по пяти
цехам завода составила:
|
Цех
|
1
|
2
|
3
|
4
|
5
|
|
Бракованная
продукция, %
|
0,5
|
0,25
|
1,0
|
1,2
|
0,8
|
По
каждому цеху определить дисперсию и среднее квадратическое отклонение доли
бракованной продукции.
№3.5 Имеются следующие данные, полученные в
результате группировки.
|
Группы
предприятий по стоимости основных производственных фондов, млн. руб.
|
Число
предприятий
|
Валовая
продукция на одно предприятие, млн. руб.
|
|
1
– 2
2
– 3
3
– 4
4
- 5
|
2
10
5
3
|
1,7
2.4
3,7
4,7
|
|
|
20
|
3,0
|
Общая
дисперсия результативного признака равна 1,4. Определите эмпирическое корреляционное отношение.
№3.6 Имеются следующие данные,
полученные в результате обследования рабочих цеха.
|
Группы
рабочих
|
Число
рабочих
|
Средняя
выработка, шт.
|
Среднее
квадратическое отклонение, шт.
|
|
Квалифицированные
Малоквалифицированные
|
70
30
|
100
50
|
1
2
|
Определите:
общую, межгрупповую и среднюю их групповых дисперсий, коэффициент детерминации,
эмпирическое корреляционное отношение. Сделайте выводы.
Тема 4. Выборочное наблюдение
Практические
занятия по данной теме предусматривают решение следующих типов задач:
1.
Определение ошибки выборочной средней и доли при случайном, механическом,
типическом и серийном отборах.
2.
Определение необходимой численности выборки при изучении средней и доли для случайного, механического, типического
и серийного отборов.
Решение типовых
задач
№1. Для изучения расхода сырья на
единицу продукции проведена двухпроцентная случайная выборка, в результате
которой получены следующие обобщенные
данные:
|
Расход
сырья на единицу, г.
|
Обследовано
изделий, шт. (f)
|
|
18
– 20
20
– 22
22
– 24
24
– 26
26
и выше
|
5
28
52
12
3
|
Определить:
1)
средний расход сырья на одно изделие;
2)
дисперсию и среднее квадратическое отклонений;
3)
коэффициент вариации;
4)
с вероятностью 0,954: предельную ошибку выборочной
средней и возможные пределы расхода сырья для всей партии изделий;
5)
возможные пределы удельного веса изделий с расходом
сырья от 20 до 24 г.
Решение:
Все
необходимые расчеты представим в таблице 4.1.
Таблица 4.1.
|
Расход
сырья на ед.г.
|
Число
изделий, шт., 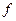
|
Середина
интервала, (Х)
|
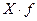
|
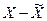
|
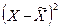
|
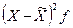
|
|
А
|
1
|
2
|
3
|
4
|
5
|
6
|
|
18-20
20 – 22
22 – 24
24 – 26
Свыше
26
|
5
28
52
12
3
|
19
21
23
25
27
|
95
588
1196
300
81
|
-3,6
-1,6
0,4
2,4
4,4
|
12,96
2,56
0,16
5,76
19,36
|
64,8
71,68
8,32
69,12
58,08
|
|
Итого
|
100
|
|
|
|
|
272,0
|
Средний
расход сырья на одно изделие в выборке равен:
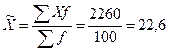 г.
г.
Вычислим
дисперсию и среднее квадратическое отклонение.
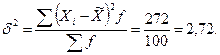
Среднее квадратическое
отклонение равно корню квадратному из дисперсии
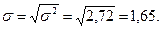
Коэффициент
вариации:
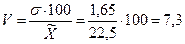 %.
%.
Предельная
ошибка выборочной средней:
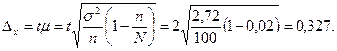
Следовательно,
границы генеральной средней будут находиться в пределах
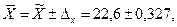 или
или 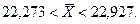
С вероятностью
0,954 можно утверждать, что расход сырья на единицу продукции всей партии может изменяться от 22,273 до 22,927
г.
Ошибка
выборочной доли определяется по формуле:
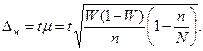
Сначала определим
выборочную долю (частость):
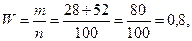 или 80 %
или 80 %
Выборка
показала, что расход сырья от 20 до 24 граммов на единицу продукции приходится
на 80% изделий. Определим предельную ошибку доли:
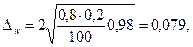 или 7.9 %
или 7.9 %
С учетом
ошибки генеральная доля ожидается в границах:
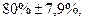 или
или 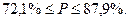
Следовательно,
с вероятностью 0,954 можно утверждать, что во всей партии продукции удельный
вес изделий с расходом сырья от 20 до 24 граммов ожидается в пределах не менее
72,1 % и не более 87,9 %.
На практике
применяют не только случайный отбор или механический, но и другие виды. Особое
значение придается типической выборке, т.е. такой, когда генеральная совокупность
разбивается на группы по изучаемому
признаку, а затем из каждой группы
производится отбор единиц, как правило пропорционально объему единиц в группах.
Типическая выборка обеспечивает
наибольшую репрезентативность.
Для типической
выборки предельная ошибка
репрезентативности определяется по формуле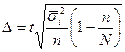 ,
,
где 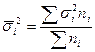 - средняя дисперсия из
групповых дисперсий.
- средняя дисперсия из
групповых дисперсий.
№2. По материалам выборочного
обследования 625 семей области получены следующие данные:
Таблица
4.2
|
Семья
|
Обследовано семей,
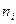
|
Доля расходов на
платные услуги, %
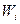
|
Доля расходов на
платные услуги, в коэффициентах
|
Дисперсия доли,
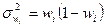
|
|
1
|
2
|
3
|
4
|
5
|
|
Городских поселений
Сельской местности
|
500
125
|
37,0
24,0
|
0,37
0,24
|
0,2331
0,1824
|
|
|
n=625
|
-
|
-
|
-
|
Выборка 2%-ная
проведена по методу типического пропорционального отбора. В группах применялся
механических отбор семей.
С вероятностью
0,954 определить пределы доли расходов на платные услуги жителями области.
Решение:
Доля расходов
на платные услуги жителями области находится в
пределах:
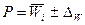 .
.
Следовательно,
для решения необходимо предварительно определить среднюю долю расходов по 2
группам населения, а затем ее ошибку.
Средняя доля
равна:
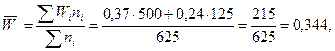 или 34,4 %.
или 34,4 %.
Для расчета
ошибки выборки типического отбора надо вычислить среднюю из групповых
дисперсий. В графе 5 таблицы 4.2 показан
расчет групповых дисперсий доли. Вычислим среднюю из них:
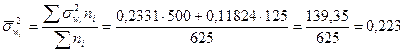 .
.
Теперь
вычислим предельную ошибку типической выборки:
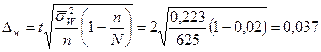 , 3,7%;
, 3,7%;
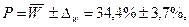 или
или 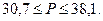
Таким образом,
можно с вероятностью 0,954 утверждать, что доля расходов населения области на платные услуги ожидается в
пределах не менее 30,7 % и не более 38,1 %.
Аналогично
вычисляется ошибка типической выборки для выборочной средней (для варьирующего
признака).
№3. В механическом цехе завода в десяти бригадах
работает 100 рабочих. В целях изучения квалификации рабочих была произведена
20% - ная серийная бесповторная выборка, в которую вошли 2 бригады. Получено
следующее распределение обследованных рабочих по разрядам:
|
Рабочие
|
Разряды рабочих
в бригаде 1
|
Разряды рабочих
в бригаде 2
|
Рабочие
|
Разряды рабочих
в бригаде 1
|
Разряды рабочих
в бригаде 2
|
|
1
2
3
4
5
|
2
4
5
2
5
|
3
6
1
5
3
|
6
7
8
9
10
|
6
5
8
4
5
|
4
2
1
3
2
|
Необходимо
определить с вероятностью 0,997 пределы, в
которых находится средний разряд рабочих механического цеха.
Решение.
Определим выборочные средние по бригадам и
общую среднюю:
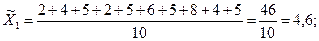
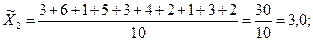
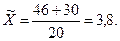
Определим
межсерийную дисперсию:
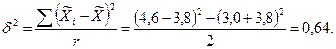
Рассчитаем
среднюю ошибку выборки:
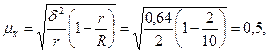
где R-число серий в генеральной совокупности;
r-число отобранных серий.
Вычислим
предельную ошибку выборки с вероятностью 0,997
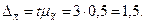
С вероятностью 0,997 можно утверждать, что
средний разряд рабочих механического цеха находится в пределах 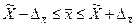 ,
, 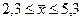 .
.
№4. 200
ящиков деталей упакованы по 40 штук в каждом. Для проверки качества деталей был
проведен сплошной контроль деталей в 20 ящиках (выборка бесповторная). В
результате контроля установлено, что доля бракованных деталей составляет 15 %.
Межсерийная дисперсия равна 49. С вероятностью 0,997 определить пределы, в
которых находится доля бракованной продукции в партии ящиков.
Решение:
Определим
среднюю ошибку выборки для доли:
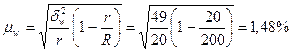
Предельная
ошибка выборки для доли с вероятностью 0,997 равна:

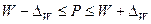
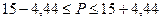
С вероятностью
0,997 можно утверждать, что доля бракованных деталей в партии может изменяться
от 10,56 до 19,44 %.
Задачи
4.1 В результате случайного
выборочного обследования 100 торговых киосков города получены следующие сводные
данные о дневной выручке частного бизнеса:
|
Выручка от продажи
товара, тыс. руб.
|
Число торговых
киосков
|
|
До 100
100 – 120
120 – 140
140 – 160
160 – 180
180 – 200
200 и выше
|
10
12
22
26
18
7
5
|
|
|
100
|
Определить:
1)
среднедневную выручку от продаж товаров;
2)
среднее квадратическое отклонение и коэффициент
вариации;
3)
с вероятностью 0,954 ожидаемую выручку от продажи
товаров частных торговых киосков города.
№4.2 Для
изучения качества продукции из партии
деталей в 1000 штук отобрано в механическом порядке 100 деталей. Средний
диаметр обследованных деталей оказался равным 300 мм., а среднее квадратическое отклонение – 10 мм. Определите с вероятностью 0,997 пределы, в
которых ожидается средний диаметр деталей во всей партии.
№ 4.3
На электроламповом заводе в порядке случайной выборки проверено 1600
ламп, из которых 48 оказались бракованными. Средняя продолжительность горения
ламп равнялась 900 часам при среднеквадратическом отклонении, равном 50 часам.
С вероятностью
0,954 определите:
1) пределы, в
которых находится процент бракованных ламп;
2) пределы, в
которых находится средняя продолжительность горения ламп.
№4.4 В цехе 1000 человек. С целью
определения затрат времени рабочими на изготовление одной детали необходимо
провести выборочное обследование рабочих
методом механического отбора. Предварительным обследованием установлено,
что среднее квадратическое отклонение затрат рабочего времени на изготовление
одной детали составило 5 мин.
Определите,
какое число рабочих необходимо отобрать, чтобы с вероятностью 0,954 ошибка
выборки не превышала 1 минуты.
№4.5 В городе 40 000 семей методом
случайного бесповторного отбора было обследовано 3000 семей. В результате
обследования было установлено, что 1000 семей являются владельцами акций.
С вероятностью
0,997 определите пределы, в которых будет находитЬся доля семей, имеющих акции
в городе.
№4.6 В целях изучения норм расходования
сырья на единицу продукции проведена 2–процентная механическая выборка партии
изделий, в результате чего получены
следующие данные:
|
Все изделия, г.
|
Число изделий, шт.
|
|
До 200
200 – 205
205 – 210
210 – 215
свыше 215
|
4
10
60
20
6
|
|
Итого
|
100
|
По данным обследования
определите:
1) средний вес
изделия: дисперсию и среднее квадратическое отклонение; коэффициент вариации;
2) с
вероятностью 0,954 возможные пределы: а) среднего веса изделия во всей партии
изделий; б) удельного веса изделий с расходом сырья на единицу продукции от 205
до 210 г.
№ 4.7 Из партии 4000 деталей отобрано
1000 деталей. Среди отобранных деталей 2% оказались бракованными. С какой
вероятностью можно утверждать, что вся партия содержит не более 2,5 % брака.
№4.8 Из партии готовой продукции
методом случайного отбора отобрано 250 изделий, из которых 5 оказались
бракованными.
Определите с
вероятностью 0,954 возможные пределы процента брака во всей партии.
№4.9 Средний вес изделия в выборочной
совокупности, состоящей из 100 единиц, оказался 5 кг. при среднем
квадратическом отклонении 0,5 кг. С какой вероятностью можно утверждать, что
вес изделия во всей партии не превысит
5,1 кг.
№4.10 Сколько деталей нужно отобрать из
1000 штук для определения одного из ее параметров, чтобы с вероятностью 0,954 можно было бы утверждать, что ошибка выборки не превысит 1,0 мм. Среднее
квадратическое отклонение признака-6 мм.
№4.11 Сколько деталей надо отобрать из 10000 штук
для определения ее веса, чтобы с
вероятностью 0,96 можно было утверждать,
что ошибка выборки не превысит 0,5 г. По пробным испытаниям дисперсия веса
детали установлена - 4.
№ 4.12 Для изучения трудовой деятельности лиц
пенсионного возраста в районе проведена 2%-ная типичная выборка с механическим
отбором в каждой группе. В результате обследования получены следующие сводные
данные:
|
Социальные группы
|
Обследовано
пенсионеров, чел.
|
Доля работающих
пенсионеров (%)
|
|
Рабочие
Служащие
|
600
400
|
20
30
|
|
|
1000
|
|
С вероятностью
0,954 определите границы (пределы), в которых находится доля работающих
пенсионеров в районе.
№4.13 Для изучения производительности
труда рабочих проведено 10-ти процентное выборочное обследование по методу
типического пропорционального отбора, в результате которого получены следующие
данные:
|
Группы рабочих по разряду
|
Число отобранных
рабочих
|
Среднее время
обработки одного изделия
|
Среднее
квадратическое отклонение, мин.
|
|
II
IV
|
30
70
|
7
5
|
2
1
|
|
|
100
|
|
|
Определите с
вероятностью 0,954, в каких пределах находится среднее время обработки одного
изделия рабочими завода данных разрядов.
№ 4.14 Для установления среднего срока
службы деталей из совокупности,
включающей 1000 штук кассет с деталями, методом механического отбора проверено
10 штук кассет. Результаты проверки показали,
что средний срок службы деталей в отобранных кассетах составил (месяцев):
7; 8,2;
8,6; 7,8; 5,8;
8,8; 7,2; 6,1; 6,0. Средний срок
службы деталей в выборке – 7,6 месяца.
С вероятностью
0,997 определите пределы, в которых находится средний срок службы деталей во всей совокупности.
№4.15 Из механического цеха завода на
склад готовой продукции поступило 500 ящиков деталей по 50 штук в каждом. Для
установления доли бракованных деталей методом механического отбора было
проверено 10 ящиков. Результаты проверки показали, что доля бракованных деталей
составляет 10 %. Дисперсия серийной выборки равна 25.
С вероятностью
0,954 определите долю бракованных деталей по всей партии деталей, поступивших
на склад готовой продукции.
№4.16 В механическом цехе завода А имеется 10
бригад по 20 рабочих в каждой бригаде. Для установления квалификации рабочих
цеха проектируется серийная выборка.
Какое количество бригад необходимо отобрать,
чтобы с вероятностью 0,954 ошибка
выборки не превышала 1,0, если на основе предыдущих обследований известно, что
дисперсия серийной выборки равна 0,9?
№ 4.17
Для изучения стажа работников
акционерного общества проведена 1%ая
механическая выборка, результаты которой предоставлены ниже:
|
Стаж, лет
|
Выборочная
численность работников, человек
|
|
До 3
3 – 5
5 – 7
7 – 9
Свыше 9
|
7
24
35
30
4
|
|
|
100
|
Определите с
вероятностью 0,954:
1)
предельную ошибку выборочной средней;
2)
возможные пределы, в которых находится средний
стаж работников АО.
№4.18 Для установления среднего размера
кредита было проведено выборочное обследование (выборка типическая, 5%-ная, с
пропорциональным отбором внутри типических групп).
В результате
выборки получены следующие данные:
|
Типы банков
|
Число банков
|
Средний размер
кредита, млн. руб.
|
Среднее
квадратическое отклонение, млн. руб.
|
|
I
I I
|
2
8
|
20
10
|
3
2
|
С вероятностью 0,954 определите средний размер кредита в генеральной
совокупности.
№ 4.19 Для определения среднего размера
вклада в сбербанке было проведено выборочное исследование (выборка 10%-ная
механическая). В результате выборки установлено, что средний размер вклада
составил 3 тыс. руб. при среднем квадратическом отклонении 2 тыс. руб.
С вероятностью
0,954 определите границы, в которых будет находится средний размер вклада в
сбербанке.
№4.20 В сберегательных банках города
методом случайной повторной выборки было отобрано 1400 счетов вкладчиков.
Средний размер остатков вклада по этим счетам составил 3,8 тыс. руб. при
коэффициенте вариации 32 %.
Какова
вероятность того, что ошибка репрезентативности при определении среднего
размера остатков вклада не превысит 0,05 тыс. руб.?
№4.21 Сколько фирм необходимо проверить налоговой инспекции
района, чтобы ошибка доли фирм, несвоевременно уплачивающих налоги, не превысила 5 %? По данным
предыдущей проверки доля таких фирм составила 32 %. Доверительную вероятность
принять равной: а) 0,954; б) 0,997.
№4.22 Для определения среднего размера
кредита в коммерческом банке проведена 2-процентная пропорциональная типическая
выборка счетов с механически отбором в группах заемщиков. В результате
обследования получены следующие данные:
|
Заемщики
|
Число счетов
|
Средний размер
кредита, тыс. руб.
|
Среднее
квадратическое отклонение, тыс. руб.
|
|
Юридические лица
Физические лица
|
60
40
|
110
32
|
18
10
|
Определите с
вероятностью 0,997 возможные границы среднего размера кредита банка.
№4.23 Для характеристики уровня жизни
населения района, проведена 5%-ная пропорциональная типическая выборка с
механическим отбором семей. В результате которой получены следующие показатели:
|
Население
|
Обследовано,
человек
|
Удельный вес
населения с доходами ниже прожиточного минимума, %
|
|
Городских поселений
Сельской местности
|
500
150
|
28
19
|
С вероятностью 0,954 определите
границы, в которых находится доля населения с доходами ниже прожиточного минимума
по району.
Тема
5. Ряды динамики
Практические
занятия по данной теме предусматривают решение следующих типов задач:
1.
Приведение рядов динамики к сопоставимому виду.
2.
Определение среднего уровня ряда динамики.
3.
Определение показателей изменения уровней ряда
динамики.
4.
Определение в рядах динамики общей тенденции развития.
5.
Определение в рядах внутригодовой динамики индексов
сезонности.
Решение типовых задач
№1. Имеются следующие данные о валовом сборе овощей в
районе, тыс. ц.
|
Годы
|
1999
|
2000
|
2001
|
2002
|
2003
|
2004
|
|
В старых границах
В новых границах
|
832,0
-
|
864
|
900
1260
|
-
1000
|
-
980
|
-
700
|
Приведите ряды
динамики к сопоставимому виду (сомкните ряд). Укажите вид полученного ряда
динамики. Изобразите его графически.
Решение:
Для приведения ряда динамики к сопоставимому
виду определим для 2001 года коэффициент соотношения уровней двух рядов:
1260:
900= 1,4.
Умножая на этот коэффициент уровни динамики в старых
границах, получаем их сопоставимыми с уровнями в новых границах.
В 1999
г……………………………. 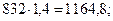
В 2000
г……………………………..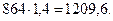
Теперь
представим полученные данные о валовом сборе овощей в виде ряда
динамики:
|
1999
|
2000
|
2001
|
2002
|
2003
|
2004
|
|
1164,8
|
1209,6
|
1260
|
1000
|
980
|
700
|
Получим полный
интервальный ряд динамики, который графически можно изобразить в виде
столбиковой (рис 5.1.) или линейной диаграммы (статистическая кривая, рис. 5.2).

Рис.5.1 Валовой сбор овощей в 1999 – 2004 годах , тыс. ц.
Столбиковая
диаграмма для графического изображения уровней ряда динамики удобна тем, что
расстояние столбиков (прямоугольников) друг от друга не зависит от
величины интервалов времени.
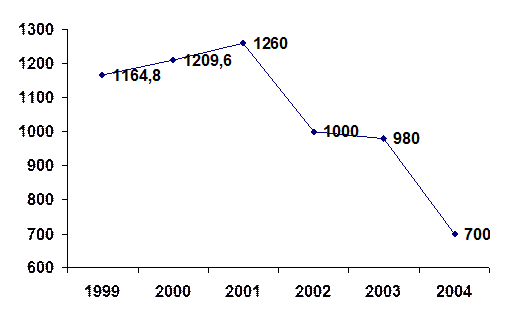
Рис. 5.2.
Динамика валового сбора овощей в 1999 – 2004 годах (тыс. ц.)
Чаще всего для
наглядного изображения динамики применяют линейные графики, особенно когда речь
идет о наглядном изображении данных, характеризующих итоги какого-либо процесса
за определенные периоды времени. Преимущество
линейных графиков состоит в том, что динамика изображается в виде сплошной
линии, характеризующей непрерывность процесса. Следует иметь в виду, что для графического изображения каких-либо
явлений, данные которых охватывают различные периоды времени, интервалы между
периодами времени (длина отрезков) при нанесении шкалы на оси абсцисс должны быть пропорциональны величинам
продолжительности периодов.
При построении
графиков большое значение имеет выбор соотношения между размерами оси абсцисс
(горизонтальной оси) и ординат
(вертикальной оси). При этом следует
руководствоваться так называемым правилом «золотого сечения». По этому правилу
чертеж должен быть расположен в прямоугольнике, в котором длина вертикальной оси (высота графика) должна
относиться к длине всей горизонтальной оси (т.е. к ширине графика) приблизительно как
5:8.
Например, если
общая длина горизонтальной оси равна 16 см., то общая длина вертикальной оси
должна составить 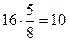 см.
см.
Принято
считать, что наиболее оптимальным для зрительного восприятия является график,
выполненный на поле прямоугольной формы с соотношением сторон от 1:1.3 до
1:1,5. Иногда используется и поле графика с равными сторонами, т.е. имеющее
форму квадрата.
При анализе
рядов динамики широко применяется
графический метод. Это объясняется тем, что табличное представление ряда
динамики и описательные характеристики чаще всего не позволяют понять характер
процесса, а по графику можно сделать определенные выводы, которые потом могут
быть проверены с помощью расчетов. Графический анализ обычно задает направление
дальнейшего анализа ряда динамики. В EXCEL для анализа рядов динамики
(временных рядов) можно использовать средство
Мастер диаграмм.
№2. Имеются данные о различной
реализации хлебобулочных изделий в торговой сети города по кварталам, т:
|
I
|
II
|
II
|
IV
|
|
4680
|
3640
|
2760
|
4048
|
Приведите
уровни ряда к сопоставимому виду.
Решение:
Для приведения
этого ряда динамики к сопоставимому виду определим размер среднедневной
реализации с учетом числа дней торговли
по кварталам, т:
|
I
|
II
|
II
|
IV
|
|
4680:90=52
|
3640:91=40
|
2760:92=30
|
4048:92=44
|
Получен ряд
динамики сопоставимых уровней различной реализации хлебобулочных изделий в
торговой сети города по кварталам (среднедневная
реализация), т:
№3. Динамика продукции (в сопоставимых ценах) характеризуется
следующими данными по АО (тыс. руб.):
|
2000
|
2001
|
2002
|
2003
|
2004
|
|
10200
|
10650
|
11100
|
11325
|
11800
|
Определить среднегодовое
производство продукции за период 2000-2004 годы.
Решение:
Для интервального ряда динамики
средний уровень исчисляется по формуле простой средней арифметической:
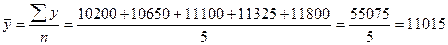 тыс. руб. т.е. в
течение периода с 2000 по 2004 годы АО в среднем ежегодно производило продукции
на 11015 тыс. руб.
тыс. руб. т.е. в
течение периода с 2000 по 2004 годы АО в среднем ежегодно производило продукции
на 11015 тыс. руб.
№4.
Имеются данные об остатках сырья и материалов на складе предприятия (тыс. руб.):
|
На 1.1
|
На 1.2
|
На 1.3
|
На 1.4
|
|
200,0
|
227,5
|
232,5
|
230,0
|
Требуется
определить среднемесячный остаток сырья и материалов на складе предприятий за
1-й квартал.
Решение:
Для полного
моментного ряда динамики средний уровень исчисляется по формуле простой средней хронологической:
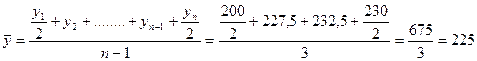 тыс. руб.
тыс. руб.
№5. Имеются данные о товарных
запасах розничного торгового предприятия
(тыс. руб.):
|
На 1.1. 2004 г.
|
На 1.5. 2004 г.
|
На 1.8. 2004 г.
|
На 1.1. 2005 г.
|
|
61,1
|
57,5
|
51,3
|
74,7
|
Требуется
исчислить среднегодовой товарный запас розничного торгового предприятия за 2004
год.
Решение:
Имеем неполный
моментный ряд. Средний уровень такого ряда исчисляют по формуле средней
хронологической взвешенной.
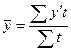 , где
, где
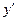 - средние уровни
интервала между датами;
- средние уровни
интервала между датами;
t – величина интервала времени
(число месяцев или дней между моментами времени).
Чтобы
воспользоваться этой формулой, нужно превратить моментный ряд в интервальный:
|
|
у
|
Длина периода,
месяцев
|
Средний уровень
товарных запасов в интервалах между датами (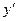 ) )
|
|
1,1
1,5
1,8
1,11
|
61,1
57,5
51,3
74,7
|
-
4
3
5
|
-
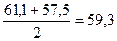
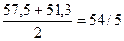
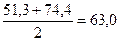
|
Средний уровень товарных запасов за год
составит:

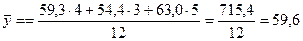 тыс. руб.
тыс. руб.
№6. За январь месяц произошли следующие
изменения в списочном составе работников предприятия, чел.:
|
Состояло по списку
на 1.1
Выбыло с 5.1
Зачислено с 12.1
Зачислено с 26.1
|
842
4
5
2
|
Необходимо
определить среднюю дневную списочную численность работников предприятия за
январь.
Решение:
Запишем данные
в виде ряда:
|
|
Число работников,
чел. (у)
|
|
1.1
5.1
12.1
26.1
|
842
838
843
845
|
Это неполный
моментный ряд динамики. Для определения среднего уровня такого ряда динамики используют среднюю
арифметическую взвешенную:
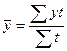 , где
, где
у – уровни,
сохраняющиеся без изменения в течение промежутков времени t;
t – продолжительность каждого
календарного периода с постоянной численность работающих.
Для расчета
средней численности работников определим продолжительность t каждого календарного периода с
постоянной численностью работающих и общее число человеко-дней.
|
|
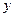
|
Длина периода,
месяцев, t
|
Число человекo-дней , yt
|
|
1.1
5.1
12.1
26.1
|
842
838
843
845
|
4
7
14
6
|
3368
5866
11802
5070
|
|
|
|
31
|
26106
|
Среднедневная
списочная численность работников в январе:
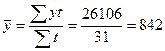 чел.
чел.
№7.
Имеются данные о выпуске продукции «А» по месяцам отчетного года.
|
Месяц
|
Январь
|
Февраль
|
Март
|
Апрель
|
Май
|
Июнь
|
|
Выпуск продукции,
тыс. шт.
|
40,2
|
38,8
|
37,1
|
34,4
|
34,4
|
31,0
|
Необходимо
рассчитать аналитические показатели ряда
динамики.
Решение:
Простейшими
показателями, которые используются при измерении скорости изменения уровней
ряда динамики, являются абсолютный прирост (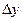 ), темп роста (
), темп роста (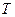 ), темп прироста (
), темп прироста (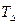 ), а также абсолютное
значение одного процента прироста (А) , пункты роста.
), а также абсолютное
значение одного процента прироста (А) , пункты роста.
В зависимости
от задачи исследования абсолютные приросты, темы проста и темпы прироста в
моментных и интервальных рядах с равностоящими уровнями (полных) могут быть
исчислены с переменной базой сравнения (в этом случае их называют цепными) и с постоянной базой
сравнения (в этом случае их называют базисными).
Абсолютный прирост (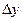 ) характеризует абсолютную скорость роста, показывает, на
сколько единиц увеличился (или
уменьшился) уровень данного периода или
момента времени по сравнению с предыдущим (или базисным) уровнем.
) характеризует абсолютную скорость роста, показывает, на
сколько единиц увеличился (или
уменьшился) уровень данного периода или
момента времени по сравнению с предыдущим (или базисным) уровнем.
Абсолютный
прирост может быть положительным,
отрицательным и равным нулю.
Цепной абсолютный
прирост-это разность между последующим уровнем ряда и предыдущим уровнем.
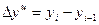 . Подсчитываем в гр. 2 табл. 5.1.
. Подсчитываем в гр. 2 табл. 5.1.
Базисный
абсолютный прирост – это разность между последующим уровнем и базисным.
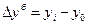 . Подсчитываем в гр. 3
табл.5.1.
. Подсчитываем в гр. 3
табл.5.1.
Знак «-» свидетельствует о снижении выпуска
продукции. Из полученных значений видно,
что по месяцам периода происходило
систематическое возрастание абсолютного снижения выпуска продукции,
причем базисные и цепные показатели
абсолютной убыли показывают, что в снижении выпуска продукции имело место
замедление в мае месяце.
Между цепными
и базисными абсолютными приростами существует взаимосвязь.
Каждый
базисный абсолютный прирост равен сумме
цепных абсолютных приростов и каждый цепной абсолютный прирост равен разности
соответствующих базисных абсолютных
приростов.
Интенсивность изменения уровней оценивается отношением
уровней. Относительными показателями динамики, характеризующими интенсивность
изменения уровней являются темпы роста и
прироста. Выражаются темпы роста в коэффициентах или процентах.
Цепной темп
роста исчисляют отношением последующего уровня у предыдущему:
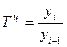 (расчет см. гр.4.
табл.5.1).
(расчет см. гр.4.
табл.5.1).
Базисный –
отношением каждого последующего уровня к базисному уровню
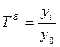 (расчет см. гр.5.
табл.5.1).
(расчет см. гр.5.
табл.5.1).
Темпы роста – только положительные числа.
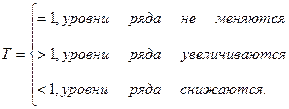
Темпы роста
(Т) (снижения) показывают, во сколько раз уровень данного периода или
момента времени больше предыдущего или базисного уровня (если Т>1) или какую
часть предыдущего или базисного уровня составляет уровень данного периода или
момента времени (если Т<1).
Между цепными
и базисными темпами роста имеется взаимосвязь:
- каждый
базисный темп роста равен произведению соответствующий цепных темпов роста;
- каждый
цепной темп роста равен отношению последующего базисного к предыдущему.
Темп прироста
(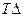 ) (сокращения)
показывает, на сколько процентов уровень данного периода или момента времени
больше (или меньше) предыдущего или базисного уровня.
) (сокращения)
показывает, на сколько процентов уровень данного периода или момента времени
больше (или меньше) предыдущего или базисного уровня.
Цепной темп
прироста (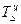 ) определяется двумя способами:
) определяется двумя способами:
1) отношением
цепного абсолютного прироста к предыдущему уровню
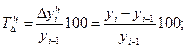
2) 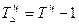 или
или 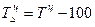 (расчет см. гр.6. табл.5.1.)
(расчет см. гр.6. табл.5.1.)
Базисный темп
прироста (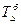 ) определяется двумя способами:
) определяется двумя способами:
1)
отношением базисного абсолютного прироста к базисному
уровню:
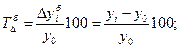
2) 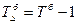
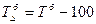 (расчет см. гр. 7
табл.5.1.)
(расчет см. гр. 7
табл.5.1.)
Темп прироста
может быть положительным, отрицательным и равным нулю.
Между 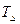 взаимосвязи не
существует, их нельзя суммировать и перемножать.
взаимосвязи не
существует, их нельзя суммировать и перемножать.
Пункты роста (Пр) ( их иногда называют темпами наращивания)
определяются двумя способами:
1)
делением цепных абсолютных приростов на базисный
уровень
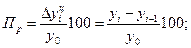
2) разностью
между базисными темпами роста:
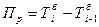 (расчет см. гр.8.
табл.5.1.)
(расчет см. гр.8.
табл.5.1.)
В отличие от
темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста
можно суммировать, в результате получая базисный темп прироста соответствующего
периода. Например, сумма пунктов роста равна – 22,9 (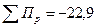 ), соответствует темпу
прироста выпуска продукции в июне по сравнению с январем.
), соответствует темпу
прироста выпуска продукции в июне по сравнению с январем.
Таблица 5.1
|
Годы
|
Выпуск продукции, тыс. шт.
|
Абсолютные приросты, тыс. шт.
|
Темпы роста (снижения), в
коэффициентах
|
Темпы прироста (сокращения)
|
Пункты роста, %
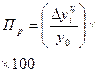
или
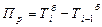
|
Абсолютное значение 1%
прироста, тыс. руб.
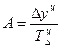
или
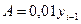
|
|
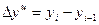
|
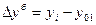
|
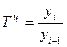
|
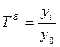
|
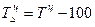
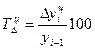
|
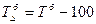
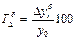
|
|
А
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Январь
|
40,2
|
-
|
-
|
-
|
1,000
|
-
|
-
|
-
|
-
|
|
Февраль
|
38,8
|
37,1 - 40,2 = - 1,4
|
37,1 - 40,2 = - 1,4
|
38,8/40,2=
=0,965
|
38,8/40,2=
=0,965
|
96,5-100=3,5
|
96,5-100=3,5
|
96,5-100=3,5
|

|
|
Март
|
37,1
|
37,1-38,8 = - 1,7
|
37,1-40,2=-3,1
|
37,1/38,8=
=0956
|
37,1/40,2=
=0,923
|
95,6-100=-7,7
|
95,6-100=-7,7
|
92,3-96,5=-4,2
|
0,388
|
|
Апрель
|
34,4
|
-2,7
|
- 5,8
|
0,927
|
0,856
|
-7,3
|
-14,4
|
85,6-92,3=-6,7
|
0,371
|
|
Май
|
34,4
|
0
|
- 5,8
|
1,000
|
0,856
|
0
|
-14,4
|
0
|
0,344
|
|
Июнь
|
31,0
|
-3,4
|
-9,2
|
0,901
|
0,771
|
-9,9
|
-22,9
|
-8,5
|
0,344
|
|
|
|
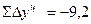
|
-
|
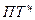 =0,771 =0,771
|
-
|
-
|
|
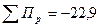
|
|
Абсолютное значение (содержание одного процента прироста (А):
можно подсчитать двумя способами:
1)
отношением цепного абсолютного прироста к цепному темпу
прироста
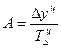 ;
;
2)
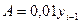 (расчет см. гр.
9 табл.5.1.)
(расчет см. гр.
9 табл.5.1.)
В полном
интервальном ряду динамики средний
уровень определяется по формуле простой средней арифметической:
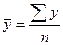 .
.
Средний
месячный выпуск продукции «А» за период с января по июнь месяц составлял:
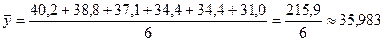 тыс.шт.
тыс.шт.
Средний абсолютный прирост (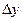 ) характеризует среднюю абсолютную скорость роста (или
снижения) уровня, вычисляется двумя способами:
) характеризует среднюю абсолютную скорость роста (или
снижения) уровня, вычисляется двумя способами:
1)
как простая средняя арифметическая из цепных абсолютных
приростов
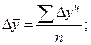
2)
как отношение базисного абсолютного прироста к числу
периодов
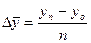 .
.
Средний
абсолютный прирост показывает, на сколько единиц увеличивался или уменьшался по сравнению с
предыдущим уровень в среднем за единицу времени (в среднем ежемесячно, ежегодно
и т.д.).
1. 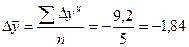 тыс. шт.
тыс. шт.
2. 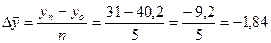 тыс.шт.
тыс.шт.
В течение
периода с января по июнь выпуск
продукции «А» в среднем ежемесячно снижался на 1,84 тыс. шт.
Средний
абсолютный прирост можно использовать для экстраполяции и интерполяции. Под
экстраполяцией понимают нахождение уровней за пределами ряда. Экстраполяция, проводимая в будущее,
называется перспективной, или
прогнозированием, а в прошлое-ретроспективной.
При
прогнозировании уровней явления на базе ряда динамики с постоянными абсолютными
приростами (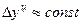 ) применяется формула:
) применяется формула:
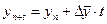 , где
, где
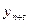 - прогнозируемый
уровень; n+t – номер этого уровня (года);
- прогнозируемый
уровень; n+t – номер этого уровня (года);
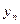 - конечный уровень
базисного ряда динамики за который рассчитан
- конечный уровень
базисного ряда динамики за который рассчитан 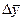 ;
;
t - срок прогноза;
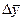 - средний абсолютный
прирост.
- средний абсолютный
прирост.
Чем короче срок
экстраполяции, тем более точные и надежные результаты дает прогноз.
При
интерполяции применяется формула:
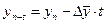 .
.
Средний темп роста (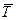 ) показывает, во сколько раз увеличивался (или снижался)
уровень по сравнению с предыдущим в среднем за единицу времени (в среднем
ежегодно, ежемесячно и т.п.).
) показывает, во сколько раз увеличивался (или снижался)
уровень по сравнению с предыдущим в среднем за единицу времени (в среднем
ежегодно, ежемесячно и т.п.).
Определяется
по формуле средней геометрической двумя способами:
|
В полном ряду динамики
|
В неполном ряду динамики
|
|
1. 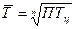
|
1. 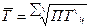 , где , где 
|
|
2.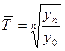
|
2. 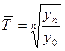
|
В примере 7:
1. 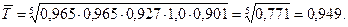
2.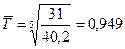 , следовательно, в течение периода с января по июнь выпуск
продукции «А» ежемесячно составлял 0,949 от предыдущего.
, следовательно, в течение периода с января по июнь выпуск
продукции «А» ежемесячно составлял 0,949 от предыдущего.
Средний темп
прироста (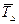 ) ( снижения),
выраженный в процентах, показывает, на сколько процентов увеличивался (или
уменьшался) уровень по сравнению с предыдущим в среднем за единицу времени ( в
среднем ежегодно, ежемесячно).
) ( снижения),
выраженный в процентах, показывает, на сколько процентов увеличивался (или
уменьшался) уровень по сравнению с предыдущим в среднем за единицу времени ( в
среднем ежегодно, ежемесячно).
Средний темп
прироста характеризует среднюю интенсивность изменения, т.е. среднюю
относительную скорость изменения уровня. Определяется по формулам:
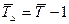 или
или 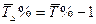 .
.
В примере 7:
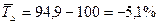 , следовательно, выпуск продукции «А» в течение периода с
января по июнь в среднем ежемесячно снижался на 5,1 %.
, следовательно, выпуск продукции «А» в течение периода с
января по июнь в среднем ежемесячно снижался на 5,1 %.
Прогнозирование
уровня явления на базе ряда динамики со стабильными темпами роста (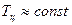 ) осуществляется по формуле:
) осуществляется по формуле:
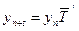 .
.
Среднее абсолютное значение одного процента
прироста за период определяется по формуле простой средней арифметической
из абсолютных значений одного процента прироста.
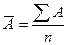 .
.
В примере 7:
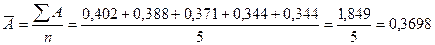 шт.
шт.
Коэффициент опережения. При
характеристике процесса опережения различных явлений можно сопоставлять только
относительные показатели динамики, исчисленные за один и тот же период. Поэтому
ряды динамики, уровни которых непосредственно несопоставимы, приводят сначала к
одному основанию, т.е. выражают в виде базисных темпов роста, а затем на основе
темпов роста вычисляют коэффициенты относительного опережения по формуле
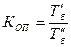 ,
,
где 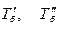 - базисные темпы роста первого и второго рядов
соответственно.
- базисные темпы роста первого и второго рядов
соответственно.
№8. Имеются относительные показатели
естественного движения населения района в расчете на 1000 чел. населения.
|
Год
|
Коэффициенты
рождаемости, %
|
Коэффициенты
смертности, %
|
|
1
|
2
|
3
|
|
2000
2001
2002
2003
2004
|
12
10,5
11,4
10,2
9,6
|
14
15
17
18
18,5
|
Определить
коэффициенты опережения.
Решение: Уровни этих рядов динамики
непосредственно несопоставимы из – за
возрастной структуры населения, которая различна в разные годы. В данном случае
несопоставимость устраняют приведением рядов
динамики к одному основанию, то есть расчетом базисных темпов роста.
Расчет
базисных темпов роста осуществляется в табл. 5.2. гр. 3,4.
Таблица
5.2
|
Годы
|
Коэффициент
рождаемости,   %0 %0
|
Коэффициент
смертности, %0
|
Базисные темпы
роста, %
|

|
|
коэффициента
рождаемости
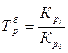
|
коэффициента
смертности,
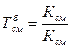
|
|
А
|
1
|
2
|
3
|
4
|
5
|
|
2000
|
12,0
|
14
|
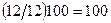
|
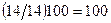
|
-
|
|
2001
|
10,5
|
15
|
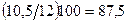
|
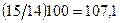
|
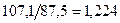
|
|
2002
|
11,4
|
17
|
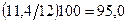
|
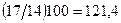
|
1б
|
|
2003
|
10,2
|
18
|
85,0
|
128,6
|
1,513
|
|
2004
|
9,6
|
18,5
|
80,0
|
132,1
|
1,651
|
Коэффициент
опережения по формуле  рассчитан в таблице 5.2,
гр.5.
рассчитан в таблице 5.2,
гр.5.
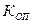 показывает, во сколько
раз быстрее растет уровень одного ряда динамики по сравнению с уровнем другого
ряда динамики. Так, для 2004 года коэффициент опережения равен:
показывает, во сколько
раз быстрее растет уровень одного ряда динамики по сравнению с уровнем другого
ряда динамики. Так, для 2004 года коэффициент опережения равен:
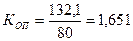
Следовательно,
смертность в районе в 2004 году росла в 1, 651 раза быстрее, чем рождаемость.
Если за период
2000 – 2004 годы среднегодовой темп
снижения рождаемости составлял 0,946, а
среднегодовой темп роста смертности - 1,072, то коэффициент опережения можно определить
следующим образом
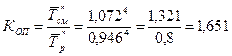
Следовательно,
за период 2000 – 2004 смертность в
районе росла в1.651 раза быстрее, чем рождаемость.
№9. Численность населения региона возросла за
период с 1.1. 2003 по 1.01.2005 на 5,3%, при этом удельный вес мужского
населения за этот период увеличился с 41,9 до 45,4 %.
Определить
показатели динамики численности мужского и женского населения региона.
Решение:
Исходим из
следующих соотношений:
численность общая удельный
женского =
численность Х вес
населения населения женщин
численность общая удельный
мужского =
численность Х вес
населения населения мужчин
Изменения
численности населения характеризуется темпами роста (Т). По условию задачи темп роста общей численности населения за
рассматриваемый период составил:
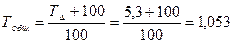
Темп роста
удельного веса мужского населения:
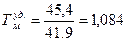
Аналогично
определяем темп роста удельного веса женского населения:
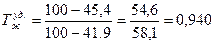
На основе
приведенных соотношений получим:
1) 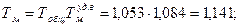
2) 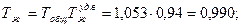
где 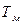 ,
, 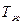 - соответственно темп
роста численности мужчин и женщин.
- соответственно темп
роста численности мужчин и женщин.
Следовательно,
численность мужского населения региона возросла за указанный период на 14,1%, а
женского снизилась на 1 %.
№10 Имеются данные о выпуске продукции предприятия по месяцам:
|
Месяц
|
Выпуск продукции,
тыс. руб.
|
Месяц
|
Выпуск продукции,
тыс. руб.
|
|
Январь
Февраль
Март
Апрель
Май
июнь
|
23
19
22
25
24
27
|
Июль
Август
Сентябрь
Октябрь
Ноябрь
декабрь
|
28
24
26
29
30
26
|
Требуется
выявить основную тенденцию выпуска продукции с помощью скользящей средней.
Решение:
Если колебания
ряда не имеют волнообразного характера, то для вычисления скользящей средней
следует брать в «укрупненный» интервал нечетное количество уровней ряда (три,
пять, и т.д.). Скользящие средние для укрупненного интервала, охватывающего три
уровня, определяются по следующим формулам:
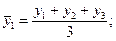
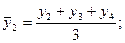 и т.д.
и т.д.
Результаты
расчета трехмесячных скользящих средних представим в таблице 5.3 гр.3:
Таблица
5.3
|
Месяц
|
Выпуск продукции,
тыс. руб. (у)
|
Скользящая
трехмесячная сумма выпуска продукции
|
Трехмесячная
скользящая средняя
|
|
А
|
1
|
2
|
3
|
|
Январь
|
23 (у1)
|
-
|
-
|
|
Февраль
|
19 (у2)
|
64(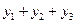 ) )
|
21,3(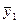 ) )
|
|
Март
|
22 (у3)
|
66(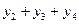 ) )
|
22,0(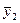 ) )
|
|
Апрель
|
25 (у4)
|
71(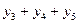 ) )
|
23,7(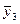 ) )
|
|
Май
|
24 (у5)
|
76……………….
|
25,3……..
|
|
Июнь
|
27 (у6)
|
79………….………
|
26,3……..
|
|
Июль
|
28 (у7)
|
79…………………
|
26,3……..
|
|
Август
|
24 (у8)
|
79………………….
|
26,3……..
|
|
Сентябрь
|
27 (у9)
|
80………………….
|
26,7……..
|
|
Октябрь
|
29 (у10)
|
83………………….
|
27,7……..
|
|
Ноябрь
|
30 (у11)
|
85(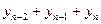 ) )
|
28,3(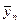 ) )
|
|
Декабрь
|
26(у12)
|
-
|
-
|
В гр.1 таблицы
5.3 нет четкой тенденции роста производства продукции. Наряду с ростом имеется
в отдельные месяцы и снижение производства продукции. Сглаженные значения (табл.5.3
гр.3) отчетливо отражают основную тенденцию – систематическое увеличение
выпуска продукции на предприятии в течении года.
№11 Имеются данные о выпуске продукции
предприятием:
|
Месяцы
|
январь
|
февраль
|
март
|
апрель
|
май
|
июнь
|
июль
|
август
|
сентябрь
|
|
Объем продукции, тыс. руб.
|
63,5
|
69,8
|
64,7
|
70,8
|
77,5
|
82,4
|
86,1
|
83,3
|
85,9
|
Требуется выявить основную тенденцию выпуска продукции
за январь – сентябрь методом аналитического выравнивания ряда динамики по
уравнению прямой и построить график. Рассчитать интервальный прогноз выпуска
продукции на октябрь месяц с вероятностью 0,95.
Решение:
Уравнение
прямой линии выражается формулой:
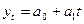 .
.
Для определения величины параметров 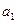 и
и 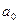 используются
нормальные уравнения способа наименьших квадратов, которые в данном случае принимают следующий вид:
используются
нормальные уравнения способа наименьших квадратов, которые в данном случае принимают следующий вид:
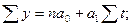
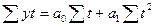 ,
,
где у - величины уровней эмпирического
(фактического ) ряда динамики;
n -
количество уровней эмпирического
ряда динамики;
t – временные показатели
(месяцы, кварталы, годы).
Так как
количество уровней в выравниваемом ряде динамики – нечетное, то для упрощения
расчетов временные показатели (t)
обозначим следующим образом:
|
Месяцы
|
январь
|
февраль
|
март
|
апрель
|
май
|
июнь
|
июль
|
август
|
сентябрь
|
|
t
|
-4
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
4
|
В этом случае 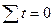 и система нормальных
уравнений принимает следующий вид:
и система нормальных
уравнений принимает следующий вид:
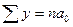
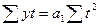 .
.
Значения
параметров уравнения прямой определяются по формулам:
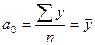 ,
,  .
.
Таблица
5.4.
|
+Месяцы
|
Выпуск продукции,
тыс. шт. (у)
|
Условные обозначения
дат (t)
|
t2
|
yt
|
Выравненный ряд
динамики выпуска продукции
yt
|
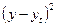
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Cентябрь
|
63,5
69,8
64,7
70,8
77,5
82,4
86,1
83,3
85,9
|
-4
-3
-2
-1
0
1
2
3
4
|
16
9
4
1
0
1
4
9
16
|
-254,0
-209,4
-129,4
-70,8
0
+82,4
+172,4
+149,9
+343,6
|
64,368
67,276
70,184
73,002
76,000
78,908
81,816
84,724
87,632
|
0,753
6,371
30,074
5,722
2,250
9,560
18,530
2,028
3,000
|
|
Итого
n=9
|
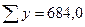
|
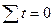
|
60
|
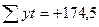
|
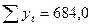
|
78,111
|
Рассчитаем
величины параметров:
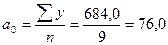
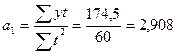
По исчисленным
параметрам составляем уравнение прямой выравненного ряда динамики:
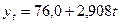
Полученное
уравнение показывает, что выпуск продукции предприятия за исследуемый период
увеличивался в среднем на 2,908 тыс. руб. в месяц. Таким образом, величина
параметра а1 уравнения прямой характеризует среднюю величину
абсолютного прироста выравненного ряда динамики.
На основании
этого уравнения определим величины уровней выравненного ряда динамики, а
именно:
для января 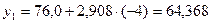 тыс. шт.;
тыс. шт.;
для февраля 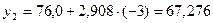 тыс.шт.;
тыс.шт.;
для сентября 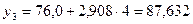 тыс.шт.
тыс.шт.
Для проверки
правильности рассчитанных величин уровней выравненного ряда динамики
используются следующие сопоставления.
Сумма значений
эмпирического ряда 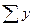 должна совпадать с
суммой исчисленных значений выравненного ряда
должна совпадать с
суммой исчисленных значений выравненного ряда 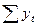 , т.е.
, т.е. 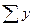 =
=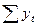 .
.
В нашем
примере 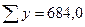 тыс. шт.;
тыс. шт.; 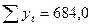 тыс. шт.
тыс. шт.
Кроме того,
любой уровень выравненного ряда 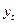 можно получить путем
прибавления величины параметра а1
к исчисленному значению предшествующего
уровня выравненного ряда.
можно получить путем
прибавления величины параметра а1
к исчисленному значению предшествующего
уровня выравненного ряда.
Так, в нашем
примере:
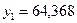 тыс. шт.
тыс. шт.
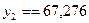 тыс.шт.
тыс.шт.
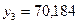 тыс.шт. и т.д. см. гр.6 Табл. 5.4.
тыс.шт. и т.д. см. гр.6 Табл. 5.4.
 Построим
график 5.3:
Построим
график 5.3:

Выравненный по
прямой ряд
 динамики
динамики
Фактический ряд динамики



Рис.5.3. Выравнивание ряда динамики по прямой
Уравнение
тренда можно использовать для интерполяции (чтобы найти недостающие члены ряда)
и для экстраполяции (для прогноза – для предсказания дальнейшего развития).
Для прогнозирования возможного выпуска продукции
в октябре месяце в уравнение тренда
подставим t=5, получим:
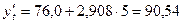 тыс. шт.
тыс. шт.
Это точечный
прогноз. На практике результат экстраполяции прогнозируемых уровней обычно выполняется
интервальными оценками. Для определения границ интервалов используется формула:
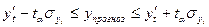 ,
,
где 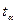 - коэффициент доверия
по распределению Стьюдента;
- коэффициент доверия
по распределению Стьюдента;
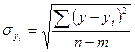 - остаточное среднее
квадратическое отклонение тренда,
скорректированное по числу степенной свободы (n-m);
- остаточное среднее
квадратическое отклонение тренда,
скорректированное по числу степенной свободы (n-m);
n – число уровней
фактического ряда динамики;
m – число параметров
адекватной модели тренда.
В нашем
примере число степеней свободы составляет 7 (n-m=9-2=7).
При уровне значимости 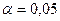 коэффициент
доверия
коэффициент
доверия 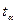 по таблице Стьюдента
(Приложение 5) равен 2,365. При
по таблице Стьюдента
(Приложение 5) равен 2,365. При 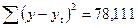 (см. гр. 7 табл.5.4).
(см. гр. 7 табл.5.4).
Значение
остаточного среднего квадратического отклонения 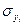 составит:
составит:
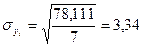 .
.
Значения вероятностных
границ интервала равны:
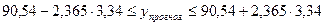
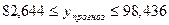 .
.
Следовательно,
с вероятностью 0,95 можно утверждать, что выпуск продукции в октябре может быть
не меньше 82,644 тыс.шт. и не больше 98,436 тыс.шт.
№12.
Реализация картофеля на рынках города за три года характеризуется
следующими данными:
|
Годы
|
Месяцы
|
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII
|
XI
|
X
|
XII
|
XII
|
|
I
II
III
|
70
71
63
|
71
85
60
|
82
84
59
|
190
308
261
|
280
383
348
|
472
443
483
|
295
261
305
|
108
84
129
|
605
630
670
|
610
450
515
|
184
177
185
|
103
168
104
|
Требуется:
1. Определить индексы сезонности;
2. Изобразить
на графике сезонную волну изменения реализации картофеля. Сделать выводы.
3. Осуществить
прогноз реализации картофеля на следующий 4-й год по месяцам на основе
рассчитанных индексов сезонности при условии, что объем реализации картофеля составит в
прогнозируемом году 3300 т.
Решение:
Для исчисления
индексов сезонности применяют различные методы. Выбор метода определяется
наличием или отсутствием тенденции в ряде динамики. Чтобы выявить наличие тенденции в ряде динамики, воспользуемся
наиболее простым методом: сначала произведем сопоставление месячных уровней
одноименных месяцев, затем произведем
укрупнение месячных уровней в годовые и по годовым показателям исчислим
абсолютные приросты (цепные) и темпы роста.
|
Годы
|
Годовые уровни реализации картофеля, т
|
Темпы роста, %
|
Цепные абсолютные
приросты, Т
|
|
к предыдущему году
|
к первому году
|
|
I
II
III
|
3070
3144
3182
|
-
102,4
101,2
|
100
100,2
103,6
|
-
74
38
|
В среднем за
год интенсивность роста составила 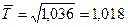 ; 101,8%, то есть 1,8 %.Это позволяет считать, что в анализируемом периоде динамики имеется незначительная
тенденция к росту и, значит, можно использовать метод постоянной средней для
расчета индекса сезонности. В этом случае
; 101,8%, то есть 1,8 %.Это позволяет считать, что в анализируемом периоде динамики имеется незначительная
тенденция к росту и, значит, можно использовать метод постоянной средней для
расчета индекса сезонности. В этом случае
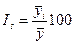 ,
,
где 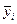 - средние месячные
уровни ряда (по одноименным месяцам);
- средние месячные
уровни ряда (по одноименным месяцам);
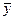 - общий средний
уровень ряда (постоянная средняя).
- общий средний
уровень ряда (постоянная средняя).
Применяя
формулу средней арифметической простой, определим средние месячные уровни за
три года:
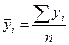 .
.
Тогда:
Январь: 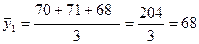 т.
т.
Февраль:  т. и т.д. (см. табл. 4 гр.5)
т. и т.д. (см. табл. 4 гр.5)
Исчислим общую
постоянную среднюю:
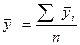 или
или 
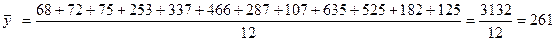 т.
т.
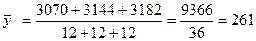 т.
т.
И, наконец,
исчислим за каждый месяц индексы сезонности:
Январь:
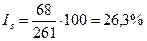 .
.
Февраль:
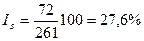 и т.д. (см. табл.5.5
гр.6.)
и т.д. (см. табл.5.5
гр.6.)
Таблица
5.5
|
Месяцы
|
Реализация
картофеля, т.
|
Индексы сезонности,
%
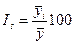
|
Планируемый объем
реализации картофеля
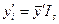
|
|
I
yi
|
II
yi
|
III
yi
|
Всего за три года,
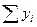
|
В среднем за три
года,
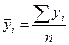
|
|
А
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Cсентябрь
Октябрь
Ноябрь
Декабрь
|
70
71
82
190
280
472
295
108
605
610
184
103
|
71
85
84
308
383
443
261
84
630
450
177
168
|
63
60
59
261
348
483
305
129
670
515
185
104
|
204
216
225
759
1011
1398
861
321
1905
1575
546
375
|
68
72
75
253
337
466
287
107
635
525
182
125
|
26,3
27,6
28,7
96,9
129,1
178,5
110,0
41,0
243,3
201,0
69,7
47,9
|
72.325
75,900
78,900
266,475
355,025
490,875
302,500
112,750
669,075
552,750
191,675
131,725
|
|
Итого
|
3070
|
3144
|
3182
|
9396
|
 =261 =261
|
100,0
|
3300
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 По
индексам сезонности можно наблюдать рост
или снижение продажи картофеля в различное время года. Для наглядности построим
график (рис.5.4):
По
индексам сезонности можно наблюдать рост
или снижение продажи картофеля в различное время года. Для наглядности построим
график (рис.5.4):
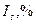

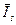
Рис. 5.4
Сезонная волна реализации картофеля на рынках города за три года по месяцам.
Индексы
сезонности показывают, что наименьший объем реализации картофеля приходится на I, IV кварталы, а наибольший – на II, III кварталы, т.е.
сезонная волна характеризует нарастание сезонности в летние месяцы ( с
максимумом в июне и сентябре, октябре), когда реализация превышает
среднегодовую реализацию на 78, 5%, 143, 3%, и 101 1 % (соответственно) и спад ее в зимние, весенне
– осенние месяцы (минимум в декабре,
январе, феврале, марте и августе, когда реализация на 52,1 % 73,7 %; 72, 4 % 71,3 % и 59 % соответственно меньше
среднегодовой). Эти индексы можно использовать во внутригодовом планировании.
3. Прогноз реализации
картофеля на рынках города по месяцам осуществляется на основе рассчитанных
индексов сезонности при условии, что объем реализации составит в прогнозируемом
году 3300 т по формуле:
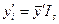 ,
,
где 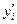 - прогнозируемые
уровни;
- прогнозируемые
уровни;
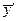 - среднемесячная
реализация в прогнозируемом году. В нашем примере
- среднемесячная
реализация в прогнозируемом году. В нашем примере 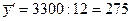 т.
т.
Прогноз
реализации картофеля в 4-ом году.
В январе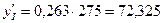 т.
т.
В феврале 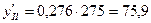 т.
т.
В марте 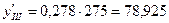 т. И т.д. См. гр. 7 табл.5.5.
т. И т.д. См. гр. 7 табл.5.5.
№13.
Имеются следующие данные о внутригодовой динамике заготовок
сельскохозяйственной продукции области по кварталам за три года (млн. руб.):
|
Кварталы
|
Первый год
|
Второй год
|
Третий год
|
|
I
II
III
IV
|
81,0
85,0
88,5
75,5
|
79,5
96,5
89,0
84,0
|
79,0
112,5
93,5
86,0
|
Для анализа
внутригодовой динамики заготовок
сельскохозяйственной продукции области требуется вычислить индексы
сезонности.
Решение:
По аналогии с
предыдущим примером для каждого года квартальные уровни укрупним до годовых и
по ним исчислим темпы роста:
|
Годы
|
Годовые уровни,
млн. руб.
|
Темпы роста , %
|
Цепные абсолютные
приросты, млн. руб.
|
|
к предыдущему году
|
к первому году
|
|
I
II
III
|
330
349
371
|
-
105,8
106,3
|
100
105,8
112,4
|
-
38
44
|
В среднем за
год интенсивность роста заготовок составила 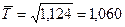 ; 6%. Это позволяет считать, что в анализируемом периоде
динамики имеется тенденция к росту и, значит, следует использовать метод
переменной средней для расчета индексов сезонности.
; 6%. Это позволяет считать, что в анализируемом периоде
динамики имеется тенденция к росту и, значит, следует использовать метод
переменной средней для расчета индексов сезонности.
Для расчета
индексов сезонности этим методом применяется формула:

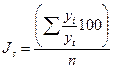 ,
,
где 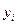 - фактические (эмпирические) уровни ряда;
- фактические (эмпирические) уровни ряда;
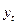 - выравненные
(теоретические ) уровни ряда;
- выравненные
(теоретические ) уровни ряда;
n -
число лет.
Определим
теоретические значения (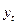 ) по уравнению:
) по уравнению:
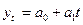 .
.
Для расчета
параметров а0 и а1 составим таблицу 5.6:
Таблица
5.6
Расчет
параметров а0 и а1
|
Кварталы
|
Эмпирические уровни
ряда, 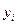
|
Обозначения
времени,
|
t2
|
yt
|
yt
|
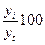
|
|
A
|
1
|
2
|
3
|
4
|
5
|
6
|
|
I год
|
|
I
II
II
IV
|
81,0
85,0
88,0
75,0
|
-11
-9
-7
-5
|
121
81
49
25
|
-891,0
-765,0
-619,5
-377,5
|
81,30
82,40
83,55
84,70
|
99,6
103,2
105,9
89,1
|
|
II год
|
|
I
II
II
IV
|
79,5
96,5
89,0
84,0
|
-3
-1
1
3
|
9
1
1
9
|
-238,5
-96,5
89,0
252,0
|
85,0
86,95
22,05
89,20
|
92,7
11,0
101,1
94,2
|
|
III год
|
|
|
I
II
III
IV
|
79,0
112,5
93,5
86,0
|
5
7
9
11
|
25
49
81
121
|
395,0
787,5
841,5
946,0
|
90,35
91,45
92,60
33,65
|
87,4
123,0
101,0
91,8
|
|
|
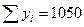
|
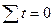 
|
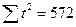
|
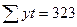
|
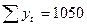
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исчислим
параметры:
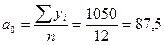 ,
,
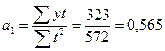
Следовательно,
уравнение прямой примет вид:
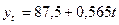 .
.
Подставив в
полученное уравнение значения t
(квартальные), получим выравненные значения ряда:
Для I года:
I квартал………………….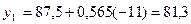 ;
;
II квартал………………….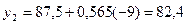 ;
;
III квартал…………………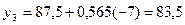 и т.д.(см. Табл.5.6
гр.5).
и т.д.(см. Табл.5.6
гр.5).
Сделаем
проверку:
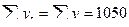 .
.
Далее
необходимо найти для каждого квартала процентные отношения эмпирических уровней
ряда (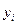 ) к теоретическим уровням
) к теоретическим уровням 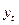 -
- 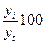 .
.
Тогда для I года:
I квартал………………….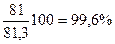 ;
;
II квартал………………….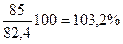 ;
;
III квартал…………………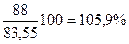 и т.д. см. табл. 5.6
гр.6.
и т.д. см. табл. 5.6
гр.6.
В выравненных
данных сезонность не проявляется. В них отражается лишь тенденция к росту. А в
фактических данных наряду с тенденцией к росту имеются и сезонные колебания.
Исчисляя процентные отношения фактических данных к выравненным, получаем
сезонные колебания внутри каждого года. Запишем эти процентные отношения в
табл. 5.7 гр.7,8,9.
После этого
нужно просуммировать полученные процентные отношения
(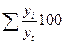 ) за три года по одноименным кварталам (табл.5.7 гр.10):
I квартал………………….
) за три года по одноименным кварталам (табл.5.7 гр.10):
I квартал………………….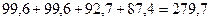 ;
;
II квартал………………….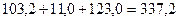 и т.д.
и т.д.
Случайные
колебания устраняем, исчисляя средние за три года с помощью индексов сезонности (см. табл. 5.7 гр. 11).
Таблица
5.7
Динамика
заготовок сельскохозяйственной продукции области по кварталам за три года.
|
кварталы
|
Фактические данные,
млн. руб. 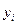
|
Выравненные данные
млн. руб., 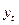
|
Фактические
данные в % к выравненым,
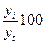
|
Сумма %-ных
отношений (гр.7+ гр.8.+ гр.9)
|
Индекс сезонности
%,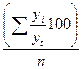
|
|
Годы
|
Годы
|
Годы
|
|
I
|
II
|
III
|
I
|
II
|
III
|
I
|
II
|
III
|
|
А
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
|
1234
|
81,0
85,0
88,5
75,5
|
79,5
96,5
89,0
84,0
|
79,0
112,5
93,5
86,0
|
81,30
82,40
83,55
84,70
|
85,80
86,95
88,05
89,20
|
90,35
91,45
92,60
93,65
|
99,6
103,2
105,9
89,1
|
92,7
111,0
101,1
94,2
|
87,4
123,0
101,0
91,8
|
279,7
337,2
308,0
275,1
|
93,2
112,4
102,7
91,7
|
|
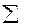
|
330,0
|
349
|
371,0
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
100
|
Индексы
сезонности характеризуют размеры
заготовки сельскохозяйственной продукции в зависимости от времени года.
Наибольший удельный вес заготовок сельскохозяйственной продукции приходится на
второй квартал. Максимум заготовок
приходится на апрель, май, июнь, когда объем заготовок на 12,4%
превышает среднегодовую, а минимум -
на ноябрь, декабрь, когда объем
заготовок на 8,3% меньше
среднегодовой. Эти данные можно использовать
во внутригодовом планировании.
 Чтобы
наглядно представить сезонную волну, индексы сезонности наносят на график:
Чтобы
наглядно представить сезонную волну, индексы сезонности наносят на график:


 I s
I s
Рис.
5.5 Сезонность заготовок сельскохозяйственной продукции
области
по кварталам за три года
Задачи
№5.1 Имеются следующие данные о
стоимости основных производственных
фондов предприятия (млн.руб.):
|
Год
|
1999
|
2000
|
2001
|
2002
|
2003
|
2004
|
|
Среднегодовая стоимость
Стоимость на конец
года
|
3,8
|
4,6
|
4,8
|
4,5
5,0
|
5,2
|
5,5
|
Вычислите
показатели анализа ряда динамики. Сделайте выводы.
№5.2 Получены следующие данные о
распределении родившихся детей по
кварталам 2004 г., чел.:
|
I
|
II
|
III
|
IV
|
|
1152
|
1097
|
1028
|
952
|
Установите
причину несопоставимости уровней ряда динамики для сравнительного анализа.
Приведите уровни ряда динамики к сопоставимому
виду. Определите вид полученного ряда динамики и нанесете его уровни на график.
№5.3 Имеются данные о товарных запасах
отдела «Галантерея» универмага города, тыс. руб.:
|
На I/I
|
На I/II
|
На I/III
|
На I/IV
|
|
310
|
330
|
320
|
315
|
Определите средний товарный запас
за I квартал.
№5.4 Имеются следующие
данные по сбербанкам города:
|
№ сбербанков
|
Остатки вклада в,
млн. руб.
|
|
На 1 января
|
На 1 марта
|
На 1 августа
|
На 1 января
|
|
№1
№2
|
600
800
|
450
650
|
500
700
|
800
1000
|
Вычислите среднемесячные остатки
вкладов за год по каждому сбербанку и в целом по двум сбербанкам.
№5.5 Динамика объема
промышленной продукции за 6 месяцев 2004 года характеризуется следующими
данными:
|
Месяцы
|
Январь
|
Февраль
|
Март
|
Апрель
|
Май
|
Июнь
|
|
В % к предыдущему месяцу
|
94
|
100,1
|
111,4
|
96,1
|
99,6
|
100,9
|
Исчислите
базисные темпы роста объема промышленной продукции. Определите, как в среднем
за месяц менялся объем промышленной
продукции за весь рассматриваемый
период.
№5.6 Численность безработных в РФ характеризуется следующими
данными:
|
Годы
|
1998
|
1999
|
2000
|
2001
|
2002
|
2003
|
|
Среднегодовая численность безработных, млн. чел.
|
8,6
|
9,3
|
7,5
|
6,4
|
5,7
|
6,0
|
По ряду динамики определите за
1998 – 2002 гг.:
1) среднегодовую
численность безработных;
2) базисные
темпы роста;
3) среднегодовой
темп роста.
Постройте график динамики
численности безработного населения. Сделайте выводы.
№ 5.7 Имеются следующие
данные, млрд. руб.
|
Кварталы
|
Объем промышленной
продукции в РФ
|
|
2000 г.
|
2001 г.
|
2002 г.
|
|
I
II
III
IV
|
1070,0
1104,0
1216,9
1370,8
|
1348,6
1412,8
1489,1
1630,5
|
1533,6
1633,7
1795,2
1905,3
|
1. Определите индексы сезонности
производства объема промышленной продукции:
2. Постройте график сезонной волны.
№5.8 Инвестиции в основной капитал за январь – июнь 2003 года в РФ
характеризуются следующими данными:
|
Месяцы
|
Январь
|
Февраль
|
Март
|
Апрель
|
Май
|
Июнь
|
|
Инвестиции в основной капитал, млрд. руб.
|
93,8
|
110,3
|
125,9
|
130,1
|
158,8
|
181,5
|
Определите:
1) среднемесячный
объем инвестиций в основной капитал;
2) базисные
и цепные темпы роста инвестиций;
3) среднемесячный темп роста инвестиций;
4) ожидаемый объем инвестиций в июле и августе при
условии, что среднемесячный темп сохранится и в эти месяцы.
№ 5.9 Имеются следующие данные об остатках задолженности по кредиту
на двух предприятиях, млн. руб.:
|
Предприятия
|
Остатки
задолженности по кредиту
|
|
1.01
|
1.02.
|
1.03.
|
1.04.
|
1.05.
|
1.06.
|
1.07.
|
|
1
2
|
13
26
|
11
22
|
14
21
|
14
23
|
13
25
|
10
27
|
12
29
|
Вычислите:
1) средние
остатки задолженности по кредиту в I и во II кварталах по двум предприятиям
вместе;
2) изменение
средних остатков во II
квартале по сравнению с I.
№5.10 Кредиторская
задолженность предприятий АО за II
квартал текущего года характеризуется следующими данными:
|
№ АО
|
Кредиторская
задолженность, тыс. руб.
|
|
1.04.
|
1.05.
|
1.06.
|
1.07.
|
|
1
2
|
555306
25600
|
565000
22300
|
540000
26000
|
580000
26500
|
Вычислите среднемесячную
кредиторскую задолженность за II
квартал года:
1) по
каждому предприятию;
2) по
двум вместе.
№ 5.11 Динамика
объема продукции предприятия характеризуется следующими показателями:
|
Месяцы
|
Январь
|
Февраль
|
Март
|
Апрель
|
Май
|
|
Темп прироста (+), снижения (-) к декабрю предыдущего года
|
+3,8
|
+5,3
|
+4,2
|
+4,1
|
+10,2
|
Вычислить:
1) помесячные
темпы прироста продукции;
2) среднемесячные
темпы прироста.
№5.12 Имеются следующие
данные по предприятию:
|
Год
|
Среднегодовая
стоимость основных производственных фондов (в сопоставимых ценах, тыс. руб.
|
По сравнению с
предыдущим годом
|
|
Абсолютный прирост,
тыс. руб.
|
Темп роста, %
|
Темп прироста, %
|
Абсолютное
содержание одного процента прироста тыс. руб.
|
|
1
|
|
|
|
|
|
|
2
|
|
|
102,4
|
|
|
|
3
|
|
|
|
3,1
|
20
|
|
4
|
|
38
|
|
|
|
|
5
|
|
|
101,7
|
|
|
Определите все недостающие
показатели ряда динамики и занесите их в таблицу. Постройте график. Сделайте
выводы.
№5.13 Кредиты Центрального банка предприятиям
России за II и III кварталы текущего года
характеризуются следующими данными:
|
|
Даты
|
|
1.04.
|
1.05.
|
1.06.
|
1.07.
|
1.08.
|
1.09.
|
1.10.
|
|
Кредиты, млрд. руб.
|
920
|
1020
|
1050
|
1390
|
1800
|
2100
|
2800
|
Вычислить:
1) среднемесячный
размер кредита за II и III кварталы и его прирост;
2) абсолютный
и относительный прирост кредита в сентябре по сравнению с апрелем.
№5.14 Имеются следующие
данные по РФ, млрд. руб.:
|
Показатели
|
Годы
|
|
1999
|
2000
|
2001
|
2002
|
|
Валовой внутренний
продукт (ВВП)
|
4823
|
7306
|
9039
|
10863
|
|
Денежная масса (М2)
|
576,5
|
924,5
|
1373,45
|
1801,1
|
Определите показатели динамики
ВВП и денежной массы М2: цепные темпы роста и прироста и среднегодовые темпы
роста и прироста.
№5.15 Имеются данные о динамике безналичного платежного оборота
банка:
|
Годы
|
2000
|
2001
|
2002
|
2003
|
2004
|
|
Темп прироста в % к 1999 году
|
+10
|
+12
|
+11
|
+8
|
+6
|
Определите цепные темпы и
среднегодовой темп роста безналичного платежного оборота за исследуемый период.
Постройте график.
№5.16 Темп прироста продукции по годам характеризуется следующими
данными:
|
Годы
|
2000
|
2001
|
2002
|
2003
|
2004
|
|
Прирост продукции к предыдущему году, в %
|
+1
|
+2
|
+3
|
+3
|
+2
|
Вычислите:
1) базисные
темпы роста и прироста продукции к 1999 г.;
2) среднегодовой
темп прироста с 2000 по 2004 гг.
Изобразите динамику производства
продукции на графике.
Сделайте краткие выводы.
№ 5.17 Имеются следующие данные о выплавке чугуна за отчетный
период на предприятии:
|
Месяцы
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII
|
IX
|
X
|
XI
|
XII
|
|
Выплавка чугуна,
тыс.т.
|
5,6
|
5,2
|
5,3
|
5,5
|
5,4
|
5,5
|
5,3
|
5,6
|
5,4
|
5,6
|
5,4
|
5,8
|
Определите основную тенденцию
ряда динамики методом укрупнения интервалов с помощью скользящей средней.
Вычислите показатели анализа ряда
динамики. Постройте график.
№ 5.18 Имеются следующие
данные о производстве часов:
|
Годы
|
2000
|
2001
|
2002
|
2003
|
2004
|
|
Производство часов, шт.
|
25
|
27
|
30
|
33
|
35
|
Определите основную тенденцию
развития рядов динамики методом аналитического выравнивания за 2000 – 2004
годы.
Сделайте выводы. Постройте
график.
№5.19 Имеются данные о производстве стали на одном из предприятии
по месяцам, в т:
|
Январь
Февраль
Март
Апрель
|
850
880
910
890
|
Май
Июнь
Июль
Август
|
920
950
990
980
|
Сентябрь
Октябрь
Ноябрь
Декабрь
|
960
1000
980
1010
|
Произвести сглаживание ряда способом скользящей средней по
3-м членам, по 4-м членам.
№5.20 Численность
безработных характеризуется данными:
|
Годы
|
1995
|
2000
|
2001
|
2002
|
2003
|
|
Общая численность безработных, млн. чел.
|
3,9
|
7,5
|
6,4
|
5,7
|
6,0
|
По ряду динамики определите за
2000 – 2003 гг.:
1) среднегодовую
численность безработного населения;
2) базисные
темпы динамики;
3) среднегодовые
темпы динамики за периоды: 1995 – 2000, 2000 – 2003.
4) постройте
график динамики безработного населения за 1995 – 2003 гг.
Сделайте выводы.
№5.21 По предприятию имеются данные задолженности по кредиту:
|
Остаток
задолженности по кредиту на начало месяца, тыс. руб.
|
|
1.07
|
1.08
|
1.09
|
1.10
|
1.11
|
1.12
|
1.01 след. года
|
|
200
|
220
|
230
|
232
|
340
|
350
|
258
|
Определить за II полугодие:
1) среднемесячные
уровни задолженности по кредиту;
2) базисные
темпы роста и прироста среднемесячной задолженности;
3) среднемесячный
темп задолженности по кредиту.
№5.22 На 1 апреля 2004 г. остаток
составлял по вкладу №1 – 1000 руб., по
вкладу № 2 – 1200 руб. В течение II квартала имели место следующие изменения величины остатков
вкладов (руб.):
|
№ вклада
|
Дата изменения
размера вклада , руб.
|
|
5.04
|
17.04
|
12.05
|
21.05
|
13.06
|
20.06
|
28.06
|
|
1
2
|
+200
Х
|
-250
Х
|
Х
+350
|
+550
+200
|
Х
-600
|
Х
-250
|
+150
+450
|
Определить, на сколько рублей и
процентов различаются средние остатки по вкладам за II квартал.
№5.23 Имеются следующие данные о
депозитах и вкладах на рублевых счетах населения в учреждениях Сберегательного
банка Российской Федерации (на начало года):
|
Годы
|
1998
|
1999
|
2000
|
2001
|
2002
|
2003
|
|
Вкладов и депозитов на рублевых счетах, млн.
|
115248,7
|
126829,2
|
184156,9
|
265996,1
|
375634,0
|
507409,4
|
Для анализа
динамики числа вкладов населения в учреждениях Сберегательного банка РФ исчислите за 1998 – 2002 годы:
1.
Среднегодовое число вкладов населения.
2.
Абсолютные и относительные изменения числа вкладов за
каждый год и к началу 1998 г., абсолютное содержание одного процента прироста.
Полученные показатели представьте в таблице.
3.
Среднегодовые темпы роста и прироста числа вкладов.
4.
Ожидаемое число вкладов на начало 2004 и 2005 гг. при
условии, что среднегодовой темп за 1998
– 2002 гг. сохранится на 2003 и 2004
годы.
№ 5.24 Динамика рыночных цен акции А за полугодие характеризуется
следующими данными:
|
Месяцы
|
Январь
|
Февраль
|
Март
|
Апрель
|
Май
|
Июнь
|
Июль
|
|
Темпы роста к
предыдущему месяцу, %
|
107
|
104
|
105
|
103
|
102
|
108
|
109
|
Исчислите
базисные темпы роста рыночной цены акции и среднемесячные темпы динамики за
полугодие.
№5.25 Имеются следующие данные, млн.
руб.:
|
Квартал
|
Остатки
задолженности по ссудам на конец квартала
|
|
2001
|
2002
|
2003
|
|
I
II
III
IV
|
36
24
33
42
|
39
21
31
45
|
42
22
34
48
|
Исчислите
индексы сезонности методом постоянной средней. Постройте график сезонности.
Сделайте выводы.
№5.26
|
Месяц
|
Объем кредита, тыс. руб.
|
По сравнению с июлем
|
|
Абсолютный прирост, тыс. руб.
|
Темп роста, %
|
Темп прироста, %
|
Абсолютное значение 1% прироста,
тыс. руб.
|
|
Июль
|
200
|
|
|
|
|
|
Август
|
|
|
|
|
|
|
Сентябрь
|
|
2,0
|
|
|
2,2
|
|
Октябрь
|
|
|
104
|
|
|
|
Ноябрь
|
|
|
|
10
|
|
Определите
недостающие показатели ряда динамики, занесите их в таблицу, сделайте выводы.
Постройте график.
№5.27
Реализация кондитерских изделий в магазинах города характеризуется
следующими данными, т:
|
Годы
|
Месяцы
|
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII
|
IX
|
X
|
XI
|
XII
|
|
2002
2003
2004
|
6,1
6,9
7,5
|
5,5
6,5
7,3
|
6,0
6,8
7,7
|
6,7
7,0
8,0
|
6,8
6,2
7,1
|
6,0
6,7
7,4
|
5,6
6,9
7,7
|
5,4
6,5
7,3
|
5,5
6,2
7,1
|
6,2
6,6
7,6
|
6,5
6,8
7,8
|
7,7
7,9
8,9
|
Для анализа
внутригодовой динамики определите сезонные колебания. Изобразите графически
сезонную волну. Сделайте выводы.
№5.28 Имеются данные о поставках сырья
предприятию, тыс. т:
|
Годы
|
Месяцы
|
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII
|
IX
|
X
|
XI
|
XII
|
|
2002
2003
2004
|
32
30
25
|
38
32
26
|
40
31
23
|
39
31
26
|
40
34
28
|
44
32
29
|
49
43
37
|
50
44
31
|
48
38
31
|
42
34
26
|
38
30
28
|
36
30
26
|
Для анализа
внутригодичной динамики поставок сырья определите индексы сезонности и
постройте график сезонной волны.
Тема 6. Индексы
Решение типовых задач
№1. Имеются
следующие данные:
|
Товары
|
Базисный период
|
Отчетный период
|
|
Количество товаров,
шт.
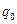
|
Цена единицы
товара, тыс. руб.,
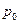
|
Количество товаров,
шт.
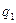
|
Цена единицы
товара, тыс. руб.,
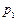
|
|
А
|
1
|
2
|
3
|
4
|
|
А
Б
|
46
500
|
16
15
|
50
600
|
20
30
|
Вычислить:
1)
индивидуальные индексы цен и количества проданного
товара;
2)
общий индекс товарооборота;
3)
общий индекс физического объема товарооборота;
4)
общий индекс цен и сумму экономии или перерасхода от изменения цен;
5)
прирост товарооборота за счет изменения цен и
количества продажи товаров.
Покажите
взаимосвязь между исчисленными индексами.
Решение:
1.
Индивидуальные индексы (однотоварные):
а) цен:
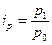 ;
;
б) количества
проданных товаров:
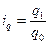 .
.
Так, для
товара «А» 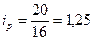 (125 %).
(125 %).
Следовательно,
цена на товар А выросла на 25 %.
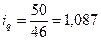 (108,7 %), т.е.
количество проданного товара «А» выросло на 8,7 % . Соответствующие индексы для
товара «Б» будут равны
(108,7 %), т.е.
количество проданного товара «А» выросло на 8,7 % . Соответствующие индексы для
товара «Б» будут равны 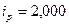 ;
; 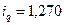 .
.
2.
Общий индекс товарооборота исчисляется по формуле:
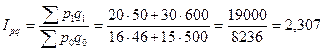 , или 230,7%,
, или 230,7%,
т.е.
товарооборот в отчетном году по сравнению с базисным вырос в 2,307 раза, или на
130,7 %.
3.
Общий индекс физического объема товарооборота (количества проданных товаров)
исчисляется по следующей агрегатной формуле индекса:
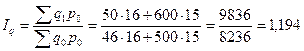 , или 119, 4%.
, или 119, 4%.
Это
значит, что количество проданного товара в отчетном периоде было в среднем на 19,4 % больше, чем в базисном периоде.
4.
Общий индекс цен подсчитаем по
агрегатной формуле Паше:
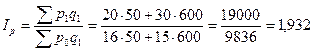 , или 193, 2%,
, или 193, 2%,
т.е.
цены на оба товара проданные в отчетном периоде в среднем выросли в 1,932 раза,
или на 93,2 %.
Между
исчисленными индексами существует взаимосвязь:
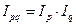 =
= 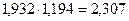 .
.
Потери,
которые несет население от роста цен в отчетном периоде, исчисляются по данным
общего индекса цен Пааше и равны разности между числителем и знаменателем этого
индекса:

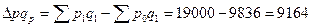 тыс. руб.
тыс. руб.
Следовательно,
в связи с ростом цен на 93,2 % население в отчетном периоде дополнительно израсходовало 9164 тыс. руб. на покупку товаров «А» и «Б».
5.
Абсолютный общий прирост товарооборота исчисляется как разность между
числителем и знаменателем общего индекса
товарооборота:

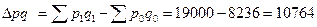 тыс. руб.
тыс. руб.
Этот
общий прирост обусловлен изменением цен
на товары и изменением количества проданных товаров. Прирост за счет изменения цен составил
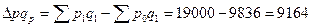 тыс. руб. и за счет изменения количества проданных товаров
тыс. руб. и за счет изменения количества проданных товаров
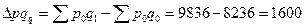 тыс. руб.
тыс. руб.
Следовательно,
увеличение товарооборота на 10764 тыс. руб. произошло за счет роста цен на 9164
тыс. руб. и роста количества проданного товара на 1600 тыс. руб.
Между
исчисленными абсолютными приростами существует взаимосвязь:
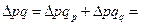 9164+1600=10764.
9164+1600=10764.
№2. Имеются данные о продаже товаров в текущем
году:
|
Товарные
группы
|
Продано
в январе, млн. руб., 
|
Снижение
объема продаж в декабре по сравнению с январем, %.
|
|
Ткани
шерстяные
Трикотажные
изделия
Обувь
|
840
1040
640
|
-45
-30
-20
|
Вычислить:
1)
общий индекс физического объема товарооборота
(количества проданных товаров) в декабре к январю;
2)
среднее изменение цен по товарным группам, если
известно, что товарооборот за этот период
вырос в 1,4 раза.
Решение:
1.
Индекс физического объема товарооборота определяется по
формуле средневзвешенного
арифметического индекса и равен :
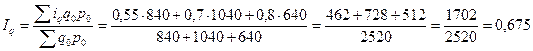 или 67,5%.
или 67,5%.
Количество
продажи товаров в среднем сократилось за год на 32,5%.
2.
Определим среднее изменение цен. Известно, что связь между индексами такая же,
как и между соответствующими показателями.
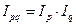 ,
, 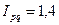 ,
, 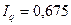 .
.
Следовательно,
индекс цен равен 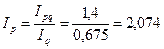 , или 207,4%. Цены в
среднем выросли к концу года в 2,074 раза.
, или 207,4%. Цены в
среднем выросли к концу года в 2,074 раза.
№3. Имеются
следующие данные:
|
Изделие
|
Стоимость
продукции базисного периода в базисных ценах, тыс. руб., 
|
Индивидуальные
индексы физического объема продукции, число раз
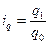
|
Доля
изделий в стоимости продукции базисного периода,
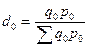
|
|
1
|
2
|
3
|
4
|
|
Б
В
|
1000
1600
|
1,06
1,12
|
0,385
0,615
|
|
Итого
|
2600
|
-
|
1,000
|
Определить общий
индекс физического объема.
Решение:
В
данном примере общий индекс физического объема рассчитаем по формуле среднего
арифметического индекса:
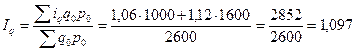 , или 109,7.
, или 109,7.
Это
означает, что в целом по всем изделиям выпуск продукции увеличился в среднем на
9,7 % (109,7 – 100).
Вместо
абсолютных данных о стоимости отдельных изделий в базисном периоде можно
принимать их доли (удельный вес) в общей
стоимости, т.е.
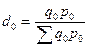 .
.
Тогда формула среднего арифметического индекса из индивидуальных будет иметь вид:
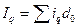 , поскольку
, поскольку 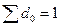 .
.
Расчет
по этой формуле дает тот же результат:
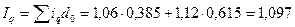 .
.
Если 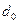 выражены в процентах,
формула среднего арифметического индекса будет:
выражены в процентах,
формула среднего арифметического индекса будет:
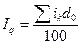 .
.
№ 4. Имеются следующие данные по предприятию:
|
Изделие
|
Удельный вес затрат
на производство изделий в июле, %
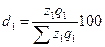
|
Изменение
себестоимости изделий в июле по сравнению с июнем , %
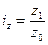
|
|
1
2
|
65
35
|
+2,8
без изменения
|
Определить:
1)
среднее изменение себестоимости по всем изделиям в июле
по сравнению с июнем.
2)
как изменился физический объем продукции, если денежные
затраты на производство выросли на 1,6 %.
Решение:
1.
Чтобы определить среднее изменение себестоимости по
всем изделиям, надо рассчитать индекс себестоимости. По данной информации его
можно определить лишь по формуле:
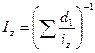 , где
, где 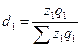 .
.
Подсчитаем его:
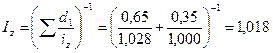 ; 101,8%
; 101,8%
Среднее
увеличение себестоимости всех изделий составило 1,8 %.
2.
Чтобы объяснить, как изменился физический объем
продукции, следует рассчитать индекс физического объема продукции. Его
определяем, используя взаимосвязь
индексов:
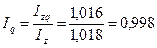 ; 99,8 % .
; 99,8 % .
Следовательно,
физический объем продукции снизился в среднем по изделиям на 0,2 %.
№5. Продажа сельхозпродуктов на рынках
города характеризуется следующими данными:
|
Товар
|
Продано в декабре,
тыс. руб.
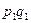
|
Изменение средней
цены покупки в декабре к январю, число раз
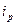
|
|
Картофель
Морковь
Яблоки
|
90000
20000
230000
|
1,20
1,28
1,15
|
Вычислить:
1)
среднее изменение цен на проданные товары;
2)
переплату денег от роста цен по каждому товару и по
совокупности товаров.
Решение:
1.
Общий индекс цен равен:
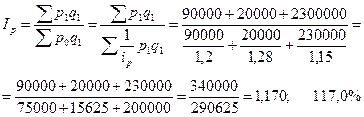
Цены в среднем выросли на 17 % на проданные
товары.
2.
Переплата денег населения в результате роста цен:
по картофелю 90000
– 75000 = 15000 тыс. руб.
по моркови 20000 – 15625 = 4375 тыс. руб.
по яблокам 230000
– 200000 = 30000 тыс. руб.
по
совокупности товаров 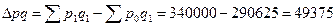 тыс. руб.
тыс. руб.
№6. Имеются следующие данные о
производстве продукции и ее себестоимости:
|
Продукция
|
Единица
измерения
|
Количество
продукции, ед., q
|
Себестоимость
единиц прод., тыс. руб. , z
|
|
Годы
|
Годы
|
|
|
|
1
|
2
|
3
|
1
|
2
|
3
|
|
А
Б
|
шт.
т.
|
3000
4000
|
2500
3000
|
2000
2000
|
5
10
|
8
15
|
10
18
|
Вычислить:
1) индивидуальные цепные и базисные индексы себестоимости на продукцию
«А»;
2) общие
цепные и базисные индексы себестоимости и
физического объема продукции.
Решение:
Цепные и
базисные индивидуальные индексы себестоимости:
а) цепные:
 ;
; 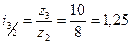 .
.
б) базисные:
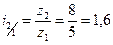 ;
; 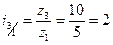 .
.
Между цепными
и базисными индивидуальными индексами существует связь – произведение цепных индексов
равно базисному:
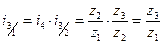 .
.
Зная базисные
индексы, можно вычислить цепные, разделив последующий базисный индекс на
предыдущий:
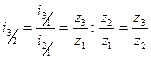 .
.
Аналогично
исчисляются индивидуальные индексы количества проданных товаров.
3.
Исчислим общие индексы себестоимости:
а) цепные:
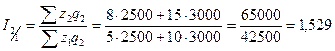 , или 152,9%;
, или 152,9%;
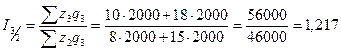 , или 121,7%;
, или 121,7%;
б) базисные:
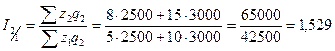 , или 152,9%;
, или 152,9%;
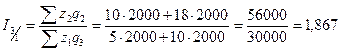 , или 186,7%.
, или 186,7%.
Как видно из
вычислений, цепные качественные общие индексы цен имеют переменные веса на
уровне отчетного периода. Для таких индексов нет взаимосвязи между цепными и
базисными индексами, что характерно для всех качественных индексов.
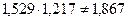
Исчислим общие
индексы физического объема товарооборота:
а) цепные:
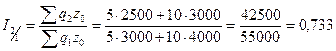 , или 77,3%;
, или 77,3%;
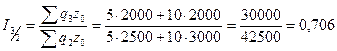 , или 70,6%;
, или 70,6%;
б) базисные:
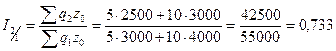 , или 77,3%;
, или 77,3%;
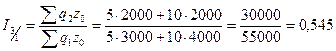 , или 54,5%.
, или 54,5%.
Данные примера
показывают, что общие цепные и базисные
индексы количественных показателей взвешиваются по постоянным весам, между ними
имеется связь: произведение цепных индексов равно базисному:
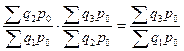 или
или 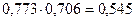
От базисных
индексов можно перейти к цепным, как это показано выше.
№7. Динамика себестоимости и объема продукции «А» на двух предприятиях
характеризуется следующими данными:
|
Продукция
|
Себестоимость
единиц. прод., тыс. руб.
|
Выработано
продукции, един.
|
Удельный вес
продукции
|
|
Базисный период,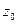
|
Отчетный период 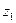
|
Базисный период,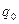
|
Отчетный период 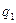
|
Базисный период,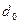
|
Отчетный период 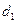
|
|
I
II
|
10
9
|
12
13
|
10000
10000
|
12000
18000
|
50
50
|
40
60
|
|
|
|
|
|
|
100
|
100
|
Вычислите:
1)
индекс себестоимости переменного состава;
2)
индекс себестоимости постоянного состава;
3)
индекс структурных сдвигов.
Покажите
взаимосвязь исчисленных индексов.
Решение:
1. Вычислим
индекс себестоимости переменного состава, который равен отношению средней
себестоимости единицы продукции вида «А» отчетного периода к средней
себестоимости единицы продукции базисного периода
 .
.
Средняя
себестоимость единицы продукции вида «А» по двум предприятиям в отчетном и базисном
периодах равна:
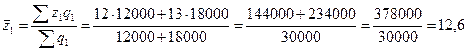 тыс. руб.
тыс. руб.
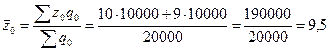 тыс. руб.
тыс. руб.
Следовательно,
индекс себестоимости переменного состава равен:
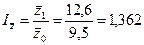 , или 132,6 %.
, или 132,6 %.
Он показывает,
что средняя себестоимость изделия по
двум предприятиям выросла на 32,6 %. Этот рост обусловлен изменением
себестоимости продукции по каждому
предприятию и изменением
структуры выпуска продукции (удельного веса продукции предприятий).
Выявим влияние каждого из этих факторов на динамику средней себестоимости,
исчислив индекс себестоимости постоянного состава и индекс структурных сдвигов.
2. Индекс
себестоимости постоянного состава (индекс фиксированного состава), показывающий, как изменилась средняя себестоимость за счет
изменения только себестоимости единицы продукции на предприятиях, равен:
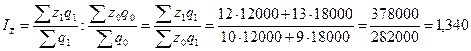 .
.
Себестоимость
продукции по двум предприятиям в среднем выросла на 34%.
3. Индекс
структурных сдвигов, характеризующий степень влияния структурных сдвигов на
изменение средней себестоимости единицы продукции, определяется:
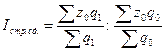 ,
,
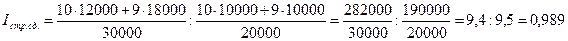 ,
,
или 98,9%.
Средняя
себестоимость изделия в отчетном периоде снизилась на 1,1% за счет изменения
структуры, т.е. за счет увеличения доли продукции второго предприятия с 50 до
60 %, на котором уровень себестоимости продукции был ниже по сравнению с
первым предприятием.
Исчисленные
выше индексы можно вычислять по удельным весам продукции предприятия, выраженным
в коэффициентах:
а) индекс
себестоимости переменного состава –
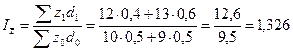 ;
;
б) индекс
себестоимости постоянного состава –
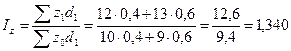 ;
;
в) индекс структурных сдвигов –
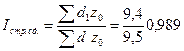 .
.
Индексы
переменного состава, постоянного состава и структурных сдвигов взаимосвязаны:
 .
.
Абсолютное
изменение средней себестоимости единицы продукции вида «А» составило:
- за счет
изменения двух факторов:
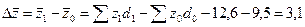 тыс. руб.;
тыс. руб.;
-за счет среднего роста собственно себестоимости:
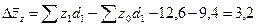 тыс. руб.;
тыс. руб.;
- за счет
изменения структуры выпуска продукции:
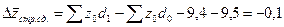 тыс. руб.
тыс. руб.
Взаимосвязь:
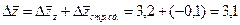 тыс. руб.
тыс. руб.
Задачи
№ 6.1 Имеются следующие данные о ценах
и продаже товаров на рынке:
|
Товары
|
Базисный период
|
Отчетный период
|
|
Цена за 1 кг. руб.
|
Количество тонн
|
Цена за 1 кг. руб.
|
Количество тонн
|
|
Картофель
Капуста
|
5
4
|
1000
300
|
8
6
|
1000
340
|
Определите
агрегатный индекс цен, агрегатный индекс физического объема товарооборота,
общий индекс товарооборота. Покажите взаимосвязь индексов.
№ 6.2 Имеются следующие данные о
производстве одноименной продукции и ее себестоимости по двум малым
предприятиям:
|
Предприятие
|
Уд. вес продукции к
итогу, %
|
Средняя
себестоимость 1 ед. руб.
|
|
В базисном периоде
|
В отчетном периоде
|
В базисном периоде
|
В отчетном периоде
|
|
№1
№2
|
52
48
|
40
60
|
600
450
|
800
600
|
Вычислите:
1)
индекс средней себестоимости продукции по двум
предприятиям (индекс себестоимости переменного состава);
2)
среднее изменение себестоимости продукции по двум
предприятиям (индекс постоянного состава);
3)
влияние на динамику средней себестоимости изменений в
структуре продукции (индекс структурных
сдвигов).
Поясните
полученные результаты и сделайте выводы.
№ 6.3 Себестоимость и объем продукции предприятий
характеризуются следующими показателями:
|
Номер предприятия
|
Изделия
|
Базисный период
|
Отчетный период
|
|
Произведено
продукции, тыс. шт.
|
Себестоимость
единицы продукции, тыс. руб.
|
Произведено
продукции, тыс. шт.
|
Себестоимость
единицы продукции, тыс. руб.
|
|
1
|
А – 3
К – 11
С - 12
|
80
60
10
|
10
8
20
|
90
100
20
|
9.8
7.5
19,0
|
|
2
|
А-3
|
100
|
9
|
200
|
8,5
|
I.
Для предприятия 1 (по трем видам изделий) вычислите:
1)
общий индекс себестоимости продукции;
2)
общий индекс физического объема продукции;
3)
общий индекс затрат на продукцию.
Покажите
взаимосвязь между исчисленными индексами.
II. Для двух предприятий вместе
( по изделию А-3) вычислите:
1) индекс себестоимости переменного
состава (индекс динамики средней себестоимости);
2) индекс себестоимости
постоянного состава;
3) индекс структурных сдвигов.
Поясните полученные результаты.
№ 6.4 Имеются следующие данные о
продаже товаров в розничной торговле города:
|
Товарные группы
|
Продано в январе,
млн. руб.
|
Изменение
количества продажи в декабре к январю, %
|
|
Ткани
хлопчатобумажные
Пальто женское
Куртки детские
|
42
360
30
|
-20
-40
-25
|
Вычислите:
1)
общий индекс физического объема товарооборота в декабре
к январю;
2)
среднее изменение цен на товары, если известно, что
товарооборот в фактических ценах за год вырос в 1,2 раза.
№ 6.5
По данным статистики продажа
товаров на рынках 2-х городов в феврале
характеризуется следующими данными:
|
Город
|
Товар
|
Базисный период
|
Отчетный период
|
|
Продано, т.
|
Средняя цена 1 кг.
руб.
|
Продано, т.
|
Средняя цена 1 кг.
руб.
|
|
А
|
Мясо
Картофель
Яблоки
|
350
120
36
|
85,0
6,0
28,0
|
60
180
12
|
106,0
8,0
34,0
|
|
Б
|
Мясо
|
400
|
94,0
|
120
|
5,0
|
I. Для города
«А» вычислите:
1)
общий индекс товарооборота;
2)
общий индекс цен на проданные товары (среднее изменение
цен);
3)
общий индекс физического объема товарооборота
(количества проданных товаров).
Покажите
взаимосвязь исчисленных индексов. Сделайте выводы.
II. Для двух городов вместе
(по мясу) вычислите:
1)
индекс цен переменного состава;
2)
индекс цен постоянного состава;
3)
индекс структурных сдвигов.
Покажите
взаимосвязь исчисленных индексов. Сделайте выводы.
№6.6 Имеются следующие данные о продаже
товаров в городе:
|
Товарная группа
|
Продано в базисном
году, тыс.ед.
|
Средняя цена
единицы товара в базисном году тыс. руб.
|
Изменение
количества проданных товаров в отчетному году к базисному, %
|
|
А
Б
В
|
241
120
10
|
1,4
20,0
10,0
|
-10
+5
+15
|
Вычислите:
1)
среднее изменение количества проданных товаров (индекс
физического объема товарооборота);
2)
среднее изменение цен на проданные товары, если
известно, что товарооборот в фактических ценах за прошедший период вырос на
12%.
№ 6.7
Имеются следующие данные:
|
Товары
|
Товарооборот, тыс.
руб.
|
|
III квартал
|
IV квартал
|
|
Мясные продукты
Молочные продукты
|
3000
1600
|
3600
1900
|
В IV квартале по сравнению с III кварталом цены на мясные продукты остались без изменения, на
молочные продукты повысились на 8 %.
Определите
средний гармонический индекс цен, индекс физического объема товарооборота,
индекс товарооборота. Сделайте выводы.
№6.8 Имеются следующие данные о продаже
товаров:
|
Товарные группы
|
Продано товаров в
базисном году, тыс. руб.
|
Изменение количество
товаров в отчетном году по сравнению с базисным
|
|
А
Б
В
|
3800
2400
2700
|
Без изменения
+10
-6
|
Вычислите: 1)
общий прирост физического объема товарооборота в отчетном году по сравнению с
базисным; 2) индекс цен, если известно, что товарооборот за этот период вырос
на 3%.
№ 6.9 Имеются следующие данные о ценах
и продаже товаров:
|
Товар
|
Единицы
измерения
|
I год
|
II год
|
III год
|
|
Цены за ед., тыс.
руб.
|
Кол-во, тыс.
|
Цены за ед., тыс.
руб.
|
Кол-во, тыс.
|
Цены за ед., тыс.
руб.
|
Кол-во, тыс.
|
|
А
Б
|
кг.
шт.
|
10
12
|
10
20
|
18
12
|
15
23
|
18
14
|
15
25
|
Определите
агрегатные индексы цен (базисные и цепные).
№ 6. 10
Как в среднем изменились цены, если известно, что товарооборот вырос на
80%, а физический объем товарооборота снизился на 2%?
№ 6.11 В отчетном году по сравнению с
базисным цены на товары в среднем выросли на 8% физический объем продажи
товаров вырос в среднем на 12%. Как изменился товарооборот?
№6.12
Затраты на производств чугуна на
заводе увеличились на 10% в отчетном периоде по сравнению с базисным. Количество
произведенного чугуна снизилось за этот
период на 5%. Как изменилась себестоимость чугуна?
№6.13 Индекс физического объема
произведенной продукции составил 96,5%, а индекс цен – 105%. Определите индекс
объема производства.
№ 6.14
В мае по сравнению с апрелем физический объем продаж вырос на 6%, в июне
по сравнению с маем на 5%. Определите изменение физического объема продаж в июне по сравнению с апрелем.
№ 6.15 Производственные затраты в
отчетном периоде по сравнению с
базисным увеличились на 15%. Себестоимость единицы продукции снизилась в
среднем на 21%. Определите индекс физического объема продукции.
№ 6.16 Определите индекс средней
выработки продукции в расчете на одного рабочего, если объем выпускаемой
продукции увеличился на 17%, а численность рабочих сократилась на 2,5%.
№ 6.17 Выясните как изменилась
численность рабочих, если средняя выработка продукции в расчете на одного
рабочего возросла на 11%, а объем выпуска продукции вырос с 55 тыс. шт. до 65
тыс. шт.
№ 6.18 Что произошло с ценами на
продукцию, если стоимость реализованной продукции за текущий период увеличилась на 16% и количество
реализованной продукции за этот период также
увеличилось на 16%.
№ 6.19 Определите индекс структурных
сдвигов, если известно, что индекс постоянного состава равен 103,1% а индекс
переменного состава 100,2%.
№ 6.20 Имеются данные по предприятию:
|
Продукция
|
Изменение объема производства в
марте по сравнению с февралем, %
|
Удельный вес трудозатрат на
производство в феврале, %
|
|
А
Б
В
|
- 2
- 10
+15
|
20
10
70
|
Определите
общий индекс физического объема и абсолютное изменение затрат труда вследствие
среднего изменения объема выпуска продукции, если на всю продукцию в феврале месяце было затрачено 500
человеко-часов времени.
Тема 7.
Статистические методы изучения взаимосвязей социально-экономических явлений
7.1. Виды и формы связей. Понятие о статистической
связи
Социально-экономические
явления формируются под действием многочисленных, разнообразных и
взаимосвязанных факторов (причин), т.е. находятся в причинно-следственных
отношениях.
Чтобы
правильно понять природу явления, надо исходить из того, что они связаны между
собой, зависят друг от друга, обуславливают друг друга и находятся в постоянном
движении и развитии. Только раскрывая взаимосвязи и можно познать их сущность и законы развития. Поэтому
изучение объективно существующих взаимосвязей между явлениями – важнейшая
задача всякого статистического анализа.
Выявление,
установление и измерение взаимосвязей имеет не только теоретическое,
познавательное значение, но и практическое значение, так как от объяснения
факторов позволяет перейти к активному воздействию на них. К управлению ими и
предсказанию их развития. В условиях развивающейся рыночной экономики это очень
важно.
Статистическое
изучение связей проходит три этапа. На первом этапе выясняется сущность явлений
и устанавливается возможность связи между ними с помощью теоретического анализа
методами экономической теории, социологии и конкретной экономики. На втором
этапе строится модель связи, базирующаяся на методах статистики. Третий этап –
интерпретация результатов, связанная с качественными особенностями явления.
Качественный
(теоретический) анализ позволяет выявить факторные и результативные признаки.
Признаки, характеризующие причины, обуславливающие изменения других, связанных
с ним признаков, называются факторными и
обозначаются х. Признаки,
характеризующие следствие, изменяющиеся под действием факторных признаков,
являются результативными и обозначаются у.
Существуют
различные виды и формы связи, различающиеся по существу, характеру, по
направлению, по тесноте, по аналитическому выражению и т.д..
По характеру
различают связи функциональные (жестко детерминированные) и стохастические (стохастически детерминированные).
Связь
результативного признака у с
факторным признаком х называется
функциональной, если каждому значению факторного признака х соответствует одно
или несколько строго определенных значений результативного признака у.
Характерной
особенностью функциональных связей является то, что в каждом отдельном случае
точно известен полный перечень факторов, определяющих значение результативного
признака у, а также точный механизм их влияния, выраженный определенным
уравнением.
В реальной
общественной жизни все явления связаны
между собой и нет конечного числа
факторов х, которые абсолютно полно
определяли бы собой результативный
признак у. Следовательно, и парная, и множественная функциональные зависимости
признаков являются лишь абстракциями, полезными и необходимыми при анализе
явлений, но упрощающими реальность. Чаще всего функциональные связи наблюдаются
в явлениях, описываемых математикой, физикой, механикой и другими точными
науками. Эти науки используют функциональные связи не только в аналитических
целях, но и в целях прогнозирования. Имеют
место функциональные связи и в социально-экономических процессах, но довольно
редко (они отражают взаимосвязь только
отдельных сторон сложных явлений общественной жизни). В экономике
примером функциональной связи может служить связь между оплатой труда у и количеством изготовленных деталей х при простой сдельной оплате труда.
Статистическая
связь не имеет ограничений и условий, присущих функциональным связям. Если с
изменением значений факторного признака х
результативный признак у в определенных пределах может принимать любые
значения с некоторой вероятностью, то
его среднее значение или иные статистические (массовые) характеристики
(показатели вариации, асимметрии, эксцесса и т.п.) изменяются по определенному
закону – связь является статистической (стохастически детерминированной). Иными
словами, при статистической связи разным
значениям факторного признаках соответствуют разные распределения значений
результативного признака у и с
изменением х ряды у закономерно
изменяются.
Корреляционной
связью называют важнейший частный случай статистической связи, состоящий в том,
что разным значениям факторного признака х
соответствуют различные средние значения результативного признака у. При
этом с изменением значения факторного
признака х закономерным образом
изменяется среднее значение результативного признака у; в то время как в каждом
отдельном случае значение признака у (с различными вероятностями) может
принимать множество различных значений.
Характерной
особенностью стохастических связей является то, что они проявляются не в каждом отдельном случае, а в общем, среднем,
при большом числе наблюдений. Причем не известен ни полный перечень факторов,
определяющих значение результативного признака, ни точный механизм их
функционирования и взаимодействия с результативным признаком. Всегда имеет
место влияние случайного. Появляющиеся различные значения результативного
признака у – реализация случайной величины.
По направлению
функциональные и статистические связи могут быть прямыми и
обратными. При прямой (положительной) связи направление изменения
результативного признака совпадает с направлением изменения факторного
признака, т.е. с увеличением факторного признака увеличивается и результативный
и, наоборот, с уменьшением факторного признака уменьшается и результативный
признак. В противном случае между рассматриваемыми величинами существуют
обратные (отрицательные) связи. Например, чем выше квалификации рабочего
(разряд), тем выше уровень производительности труда – прямая связь. Чем выше
производительность труда, тем ниже себестоимость единицы продукции – обратная
связь.
По степени
тесноты связи различают количественные критерии тесноты связи (табл. 7.1).
Таблица
7.1
Количественные
критерии оценки тесноты связи
|
Величина показателя
тесноты связи
|
Сила связи
|
|
До 0,3
0,3 – 0,5
0,5 – 0,7
0,7 – 1,0
|
Практически
отсутствует
Слабая
Умеренная
Сильная
|
По
аналитическому выражению выделяют связи прямолинейные и криволинейные. При
прямолинейной связи с возрастанием значений факторного признака происходит
непрерывное возрастание (или убывание) значений
результативного признака в среднем на определенную величину.
Математически такая связь представляется
уравнением прямой, а графически – прямой линией. Отсюда ее более короткое название – линейная
связь.
При криволинейной
связи с возрастанием значения факторного признака возрастание (или убывание) результативного признака происходит
неравномерно или же направление изменяется на обратное. Геометрически такие связи представляются
кривыми линиями (гиперболой, параболой, степенной, показательной,
экспоненциальной и т.д.)
По количеству
факторов, действующих на результативный признак, связи различаются
однофакторные (один фактор) и многофакторные (два и более факторов).
Однофакторные (простые) связи обычно называют парными (так как рассматривается
пара признаков). Например, корреляционная связь между суммой активов и
кредитными вложениями коммерческих банков или прибылью и производительностью
труда. В случае многофакторной (множественной) связи имеют в виду, что все
факторы действуют комплексно, т.е. одновременно и во взаимосвязи. Например, корреляционная связь между суммой активов и кредитными
вложениям, величиной собственного капитала коммерческих банков и другими
факторными признаками или между
производительностью труда и уровнем организации труда, автоматизации
производства и другими факторными признаками.
С помощью
множественной корреляции можно охватить весь комплекс факторных признаков и
объективно отразить существующие множественные связи. Существуют также связи
непосредственные и косвенные.
Фактор х может оказывать
влияние на у непосредственно или
косвенно, через другой фактор z.
7.2.
Основные статистические методы изучения взаимосвязей
После того как
с помощью теоретического анализа выяснена сущность явлений и возможность связи
между ними, установлены факторный и результативный признаки, необходимо определить направление и характер связи, выявить форму воздействия
одних факторов на другие и дать ей количественную оценку. Для выявления наличия
связи, характера и направления в статистике используются методы: сравнения
параллельных рядов, аналитической группировки, графический. Для выявления формы
воздействия одних факторов на другие используют регрессионный анализ, а
количественную оценку силы воздействия дают с помощью корреляционного анализа.
Метод
сравнения параллельных рядов основан на сопоставлении двух или нескольких рядов
показателей. Сущность этого метода состоит в том, что сначала показатели
характеризующие факторный признак, располагаются в порядке возрастания или
убывания (ранжируются), а затем параллельно им располагаются соответствующие
показатели результативного признака. Сравнение построенных таким образом рядов
дает возможность не только подтвердить само наличие связи, но и выявить ее
направление и характер.
Например,
возьмем данные по 15 коммерческим банкам региона о размере собственных
средств ((х), млн. руб.) и о размере привлеченных средств ((у), млн. руб.). Данные эти сведены в табл.
7.2, где банки расположены в порядке возрастания размера собственных средств:
Таблица
7.2
Размер
собственных (х) и привлеченных (у) средств по 15 банкам региона
|
№ п/п
|
х
|
у
|
№ п/п
|
х
|
у
|
№ п/п
|
х
|
у
|
|
1
2
3
4
5
|
15
20
28
38
41
|
52
86
102
106
124
|
6
7
8
9
10
|
42
43
49
52
57
|
150
140
192
190
240
|
11
12
13
14
15
|
58
60
65
72
75
|
230
220
267
270
315
|
Рассматривая
данные таблицы, видим, что с возрастанием признака х, размера собственных средств, растет (правда,
не всегда) признак у – размер привлеченных
средств. Следовательно,
между х и у имеется прямая статистическая (статистическая)
зависимость.
Возрастание
объема привлеченных средств с частыми отклонениями говорит о влиянии на этот
показатель других факторов помимо объема собственных средств.
Графический
метод рекомендуется применять для предварительного анализа и оценок. Так, выявленную с помощью сравнения параллельных
рядов связь между объемом собственных (х) и привлеченных средств (у) банков
можно наглядно увидеть, если построить график, отложив на оси абсцисс значение
признака х, а на оси ординат – значение признака у. Нанеся на график точки,
соответствующие значениям х и у, получим
корреляционное поле (рис. 7.1), где по характеру расположения точек можно
судить о направлении и силе связи.

Если
точки беспорядочно разбросаны по всему
полю, это говорит о том, что зависимости между двумя признаками нет, если они
будут концентрироваться вокруг оси, идущей от нижнего левого угла в верхний правый, то имеется прямая
зависимость между варьирующими признаками; если точки будут концентрироваться вокруг
оси, идущей от верхнего левого угла в нижний правый, то имеется обратная
зависимость.
В нашем
примере корреляционное поле ясно
показывает, что имеется тенденция к росту из левого нижнего угла в правый
верхний. Значит, имеется прямая корреляционная зависимость между объемом
собственных средств и привлеченными средствами коммерческих банков региона.
Стохастическая
связь будет проявляться отчетливее, если применить для выявления ее наличия и
направления метод аналитической группировки. Он состоит в том, что совокупность
единиц разбивается на группы по величине факторного признака и по каждой группе
исчисляется средняя величина результативного признака. Вариация средней
величины результативного признака от
группы к группе под влиянием изменения факторного признака будет указывать на
наличие, характер и направление связи.
В нашем примере произведем аналитическую группировку
коммерческих банков региона по объему собственных средств и по каждой группе
исчислим средний объем привлеченных
средств. Образуем четыре группы с равными интервалами. Размер интервала
определим по формуле:
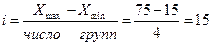 млн. руб.
млн. руб.
Все расчеты
проделаем в рабочей таблице 7.3:
Таблица
7.3
Распределение
банков по объему собственных средств
|
№ п/п
|
Группы банков по
объему собственных средств, млн. руб.
|
№ банка и число
банков
|
Объем собственных
средств, млн. руб.,
х
|
Объем привлеченных
средств, млн. руб.,
у
|
|
А
|
Б
|
1
|
2
|
3
|
|
I
|
15-30
|
1
2
3
|
15
20
28
|
52
86
102
|
|
|
Итого:
|
3
|
63
|
240
|
|
II
|
30-45
|
4
5
6
7
|
38
41
42
43
|
106
124
150
140
|
|
|
Итого
|
4
|
164
|
520
|
|
III
|
45-60
|
8
9
10
11
|
49
52
57
58
|
192
190
240
230
|
|
|
Итого
|
4
|
216
|
852
|
|
IV
|
60-75
|
12
13
14
15
|
60
65
72
75
|
220
267
270
315
|
|
|
Итого
|
4
|
272
|
1072
|
|
|
Всего
|
15
|
715
|
2684
|
Затем
групповые показатели рабочей таблицы и исчисленные на их основе средние
показатели заносим в построенную итоговую аналитическую таблицу (табл.7.4), и увидим,
изменяются эти средние в прямом соответствии с изменением объема собственных
средств или нет.
Таблица
7.4
Зависимость
объем привлеченных средств (у)
от
объема собственных средств (х)
|
Группы банков по
объему собственных средств (х), млн. руб.
|
Число банков
f
|
Объем собственных
средств, млн. руб.
|
Объем привлеченных
средств, млн. руб.
|
|
всего
|
В среднем на
банк 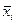
|
всего
|
В среднем на
банк 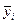
|
|
А
|
1
|
2
|
3
|
4
|
5
|
|
15-30
30-45
45-60
60-75
|
3
4
4
4
|
63
164
216
272
|
21
41
54
68
|
240
520
852
1072
|
80
130
213
268
|
|
Итого:
|
15
|
715
|
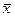 = 47,7 = 47,7
|
2684
|
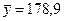
|
Данные табл. 7.4
показывают, что с ростом значений факторного признака (объем собственных
средств) растет (закономерным образом изменяется) среднее значение
результативного признака у (средний объем
привлеченных средств банк), следовательно, между х и у имеется прямая корреляционная
зависимость.
Прежде чем
применять корреляционно-регрессионный анализ для определения формы связи,
исчисления ее количественной характеристики и
измерения степени тесноты связи, нужно предварительно отобрать
факторы, оказывающие существенное
влияние на результативный признак. Помочь в этом может метод аналитической
группировки и расчет на его основе эмпирического корреляционного отношения.
Эмпирическое
корреляционное отношение (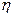 ) равно корню квадратному из эмпирического коэффициента
детерминации (
) равно корню квадратному из эмпирического коэффициента
детерминации (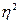 ):
):
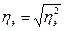 .
.
Коэффициент детерминации (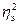 ) показывает, какая часть общей вариации (дисперсии)
результативного признака у объясняется вариацией группировочного
фактора х, определяется отношением
межгрупповой дисперсии к общей диспресии результативного признака:
) показывает, какая часть общей вариации (дисперсии)
результативного признака у объясняется вариацией группировочного
фактора х, определяется отношением
межгрупповой дисперсии к общей диспресии результативного признака:
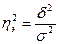 .
.
Межгрупповая
дисперсия результативного признака (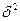 ), характеризующая его вариацию за счет группировочного
признака х, исчисляется по формуле:
), характеризующая его вариацию за счет группировочного
признака х, исчисляется по формуле:
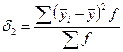 ,
,
где 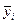 - групповые средние результативного признака у;
- групповые средние результативного признака у;
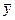 - общая средняя
результативного признака;
- общая средняя
результативного признака;
f – число единиц в группах.
Общая
дисперсия (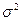 ), характеризующая его вариацию за счет всех факторов,
исчисляется по формулам:
), характеризующая его вариацию за счет всех факторов,
исчисляется по формулам:
1) 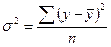 ; 2)
; 2)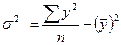 .
.
Таблица
7.5
Расчет
межгрупповой дисперсии результативного признака (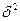 )
)
|
Объем привлеченных
средств, млн. руб. в среднем на банк, 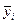
|
Число банков,
f
|
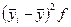
|
|
80
|
3
|
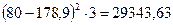
|
|
130
|
4
|
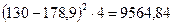
|
|
213
|
4
|
4651,24
|
|
268
|
4
|
31755,24
|
|
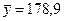
|
15
|
75314,95
|
 .
.
Таблица
7.6
Расчет
общей дисперсии объема привлеченных средств (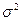 )
)
|
№ банка
|
у
|
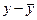
|
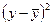
|
№ банка
|
у
|
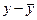
|
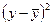
|
|
1
2
3
4
5
6
7
8
|
52
86
102
106
124
150
140
192
|
-126,9
-92,9
-76,9
-72,9
-54,9
-28,9
-38,9
13,1
|
16103,61
8630,41
5913,61
5314,41
3014,01
835,21
1513,21
171,61
|
9
10
11
12
13
14
15
|
190
240
230
220
267
270
315
|
11,1
61,1
51,1
41,1
88,1
91,1
136,1
|
123,21
3733,21
2611,21
1689,21
7761,61
8299,21
18523,21
|
|
|
|
|
|
|
|
Итого
|
84236,95
|
Подсчитаем
общую дисперсию результативного признака:
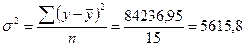 .
.
Следовательно,
коэффициент детерминации 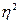 , показывающий роль группировочного признака в образовании
общей вариации, составит:
, показывающий роль группировочного признака в образовании
общей вариации, составит:
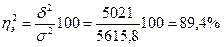 .
.
Это означает,
что вариация привлеченных средств у 15 банков на 89,4% обусловлена объемом
собственных средств банков и на 10,6 %- другими факторами.
Эмпирическое
корреляционное отношение (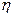 ) равно:
) равно:
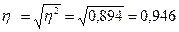 , что означает сильную степень тесноты связи.
, что означает сильную степень тесноты связи.
Убедившись в
этом, можно перейти к корреляционно-регрессионному анализу и прежде всего к
поискам функции теоретической линии связи, параметры которой при достаточно
высокой степени тесноты связи могут быть использованы в управлении.
7.3.
Корреляционно-регрессионный метод
анализа. Уравнение регрессии как форма аналитического выражения статистической
связи
Для более
глубокого исследования взаимосвязи явлений рассмотренные статистические методы
часто оказываются недостаточными, ибо они не позволяют выразить имеющуюся связь
в виде определенного математического
уравнения, характеризующего механизм взаимодействия факторных и результативного
признаков. Кроме того, методы параллельных рядов и аналитических группировок
эффективны лишь при малом числе факторных признаков, в то время как
социально-экономические явления оказываются обычно под воздействием множества
причин. Эти и другие ограничения
рассмотренных ранее статистических методов анализа взаимосвязей устраняет метод корреляций и регрессий
– корреляционно-регрессионный анализ, являющийся логически продолжением,
углублением более элементарных методов.
Корреляционно-регрессионный
анализ как общее понятие включает в себя измерение тесноты, направления связи и
установление аналитического выражения (формы) связи.
Корреляционный
анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между
результативным и множеством факторных признаков (при многофакторной связи).
Регрессионный
анализ заключается в определении аналитического выражения связи, в котором
изменение результативного признака у
обусловлено изменением факторных признаков, а множество всех прочих факторов,
также оказывающих влияние на результативный признак, принимается за постоянные
и средние значения.
Целью
регрессионного анализа является оценка функциональной зависимости условного
среднего значения результативного признака (у) от факторных (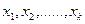 ).
).
Регрессия
может быть парной (однофакторной) и
множественной (многофакторной). По форме
зависимости – линейной и нелинейной, по направлению – прямой
(положительной) и обратной
(отрицательной).
Основной
предпосылкой применения корреляционного анализа является необходимость
подчинения совокупности значений всех факторных (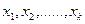 )и результативного (у) признаков к- мерному нормальному закону распределения
или близость к нему.
)и результативного (у) признаков к- мерному нормальному закону распределения
или близость к нему.
Это условие
связано с применением метода наименьших квадратов при расчете параметров
корреляционного уравнения: только при нормальном распределении метод наименьших
квадратов дает оценку параметров, отвечающую принципам максимального
правдоподобия. На практике эта предпосылка чаще всего выполняется
приблизительно, но и тогда метод наименьших квадратов дает неплохие результаты.
Основной
предпосылкой применения регрессионного анализа является то, что только результативный признак (у) подчиняется
нормальному закону распределения, а факторные признаки (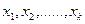 ) могут иметь произвольный закон распределения.
) могут иметь произвольный закон распределения.
Уравнение
регрессии или модель регрессии, выражаемая функцией
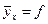 (
( ),
),
будет
достаточно адекватной реальному моделируемому явлению или процессу в случае
соблюдения следующих требований их построения:
1.
Совокупность исследуемых исходных данных должна быть
однородной и описываться непрерывными
функциями.
2.
Моделируемые явления должны оцениваться одним или
несколькими уравнениями причинно-следственных связей.
3.
Все признаки должны иметь количественное (цифровое) выражение.
4.
Наличие достаточно большого объема исследуемой
выборочной совокупности. Обычно считают, что число наблюдений должно быть не
менее чем в 5-6, а лучше – не менее чем в 10 раз больше числа факторов. Еще
лучше, если число наблюдений в несколько десятков или в сотни раз больше числа
факторов, тогда закон больших чисел, действует в полную силу, обеспечивает
эффективное взаимопогашение случайных
отклонений от закономерного характера связи признаков.
5.
Отсутствие количественных ограничений на параметры
модели связи.
Теоретическая
обоснованность моделей взаимосвязи, построенных на основе
корреляционно-регрессионного анализа, обеспечивается соблюдением следующих
основных условий:
1.
Все признаки и их совместные распределения должны
подчиняться нормальному закону распределения.
2.
Дисперсия моделируемого признака у должна
все время оставаться постоянной при изменении величины у и
значений факторных признаков.
3.
Отдельные наблюдения моделируемого признака у должны быть независимыми, т.е. результаты,
полученные в i-ом
наблюдении, не должны быть связаны с предыдущими и содержать информацию о
последующих наблюдениях, а также влиять на них.
Отступление от
выполнения этих условий и предпосылок приводит к тому, что модель регрессии
будет неадекватно отражать реально существующие связи между анализируемыми
признаками.
Одной из
проблем построения модели регрессии является ее размерность, т.е. определение
числа факторных признаков, включаемых в модель. Их число должно быть
оптимальным.
Сокращение
размерности за счет исключения второстепенных, несущественных факторов (эта
задача решается в основном на базе мер тесноты связи факторов с результативным
признаком) позволяет получить модель, реализуемую быстрее и качественнее. В то
же время построение модели малой
размерности может привести к тому, что она будет недостаточно полно
описывать исследуемое явление или процесс. Практика выработала определенный
критерий, позволяющий установить оптимальное соотношение между числом факторных признаков, включаемых в
модель, и объемом исследуемой совокупности. Согласно данному критерию число
факторных признаков х должно быть 5-6
раз меньше объема изучаемой совокупности.
Построение
корреляционно-регрессионных моделей, какими бы сложными они не были, само по себе не вскрывает полностью
всех причинно-следственных связей. Основой их адекватности является
предварительный качественный анализ,
основанный на учете специфики и особенностей сущности исследуемых социально-экономических явлений и процессов .
7.4. Однофакторные (парные) модели регрессии
Парная регрессия характеризует
связь между двумя признаками: результативным и факторным.
Процесс построения модели парной
регрессии включает следующие основные этапы:
1) выбор
формы связи;
2) определение
параметров уравнения связи и проверка адекватности регрессионной модели;
3) измерение
тесноты связи и проверка значимости (надежности) показателей тесноты связи.
Выбор формы
связи имеет решающее значение в корреляционно-регрессионном анализе. Все
дальнейшие самые тщательные расчеты могут быть обесценены, если форма связи избрана
неверно.
При выборе
формы уравнения регрессии качественный анализ играет важную роль для раскрытия
механизма формирования корреляционной связи. Пусть, например, измеряется связь
между сроком сева и урожайностью. Чрезмерно ранний и чрезмерно поздний сев
ведут к снижению урожайности, максимум которой достигается при севе в
оптимальные сроки. Таким образом, с ростом факторного признака (срок сева)
урожайность растет, а затем снижается. Зависимость такого рода может быть
выражена, например, уравнением параболы.
При всей
важности теоретического анализа следует, однако, учитывать, что
социально-экономические явления очень сложны. Как правило, мы не имеем о них
исчерпывающей информации, а внутренняя логика их связей мало изучена. Факторы,
влияющие на то или иное явление, взаимно
переплетаются и взаимодействуют друг с другом. Поэтому очень часто не удается
сделать теоретически обоснованный вывод уравнения регрессии, т.е. формы связи,
внутренне присущей изучаемому явлению. В ряде случаев на основе
теоретического анализа могут быть высказаны лишь более или менее обоснованные
предположения о том, что следует ожидать линейную или какую-либо нелинейную
(криволинейную) связь, имеет ли ожидаемая криволинейная функция экстремальные
значения и т.п. Так, в рассмотренном примере можно утверждать, что линия
регрессии – некоторая кривая, имеющая оптимум, но это отнюдь не обязательно
парабола. Более того, если явление мало изучено, иногда могут быть выдвинуты и
различные гипотезы о механизме и форме взаимосвязи.
Для проверки
этих предположений и гипотез может быть использован графический метод –
построение графика групповых средних, полученных в процессе аналитической
группировки. Ломаная линия, изображающая изменение групповых средних
результативного признака (
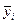 ) в зависимости от изменения
группировочного фактора, называется эмпирической линией регрессии
(эмпирической регрессией).
) в зависимости от изменения
группировочного фактора, называется эмпирической линией регрессии
(эмпирической регрессией).
Наглядное
представление о форме линии регрессии может дать график эмпирической линии
регрессии (рис. 7.2).
На график
корреляционное поле (рис. 7.1.) наносятся результаты аналитической группировки
(табл. 7.4) Абсциссами этих точек являются средние значения факторного признака
(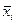 ), а ординатами – средние значения результативного признака (
), а ординатами – средние значения результативного признака (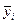 ).
).
Если
эмпирическая линия по своему виду приближается к прямой линии, это
свидетельствует о наличии прямолинейной корреляционной связи между признаками.
Если же эмпирическая линия связи будет приближаться к кривой (параболе, гиперболе,
показательной кривой), то это дает
основание считать, что в данном случае имеется

криволинейная
корреляционная связь, чем сильнее связь между признаками, тем теснее будут
группироваться точки вокруг эмпирической линии регрессии.
В нашем
примере можно предположить, что имеется прямая, прямолинейная сильная
корреляционная зависимость между объемом
собственных средств и привлеченными средствами.
Форма
эмпирической линии регрессии дает возможность проверить, соответствует ли фактическое соотношение
признаков тому или иному теоретически предполагаемому их соотношению. При этом
нужно, однако, иметь, в виду, что
при относительно небольшом числе единиц совокупности (числе наблюдения) форма
эмпирической линии регрессии может изменяться при изменении число групп и их
границ. Поэтому при небольшом числе наблюдений нельзя слишком полагаться на
форму эмпирической линии регрессии, графический метод в таких случаях может
оказаться недостаточно надежным.
Существуют
более общие указания, позволяющие
выявить уравнение связи, не прибегая к графическому изображению. Если
результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то это
свидетельствует о том, что связь между ними линейная, а при обратной связи –
гиперболическая.
Если факторный
признак увеличивается в арифметической прогрессии, а результативный –
значительно быстрее, то используется параболическая или степенная регрессия.
Если
относительно формы связи могут быть выдвинуты разные теоретические гипотезы, а
по виду эмпирической регрессии трудно судить о том, какой из этих гипотез
наиболее соответствуют фактические данные,
то в этих случаях строятся и
решаются уравнения регрессии с различными формами связи, а затем с помощью
специальных статистико-математических критериев оценивается их адекватность и
выбирается та форма связи, которая обеспечивает наилучшую аппроксимацию
(приближение) и достаточную статистическую достоверность и надежность.
Определение
параметров уравнения связи и их значимости.
Аналитическая
связь между факторным и результативным признаками описываются уравнениями:
прямой - 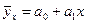 ;
;
гиперболы - 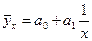 ;
;
параболы - 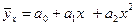 и т.д.
и т.д.
Выбрав тем или
иным путем форму связи и построив уравнение регрессии в общем виде, необходимо
далее найти числовые значения его параметров.
Оценка
параметров уравнения осуществляется методом наименьших квадратов, в основе которого лежит предположение о
независимости наблюдений исследуемой совокупности.
Сущность
метода наименьших квадратов заключается в нахождении параметров модели (а0 , ,а1), при
которых минимизируется сумма квадратов отклонений эмпирических (фактических)
значений результативного признака от теоретических, полученных по выбранному
уравнению регрессии:
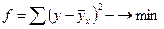 .
.
Для
прямолинейной зависимости:
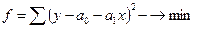 .
.
Рассматривая f в качестве функции а0 , и а1
и проводя математические преобразования (дифференцирование), получаем:
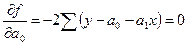 ;
;
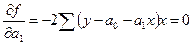 .
.
Откуда система
нормальных уравнений для нахождения параметров линейной полной регрессии имеет
следующий вид:
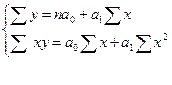 .
.
Решение этой
системы в общем виде дает следующие значения параметров:
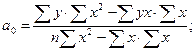
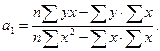
Иногда их
удобно исчислить по следующим формулам, дающим тот же результат:
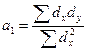 где
где 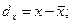

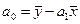
или
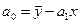 ;
; 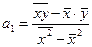 .
.
Определив
значения а0 , и а1 и подставив их в уравнение 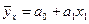 , находим значения
, находим значения 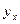 , зависящие только от заданного значения х.
, зависящие только от заданного значения х.
Корреляционное
уравнение по форме похоже на уравнение функциональной зависимости, но по
существу отличается тем, что оно справедливо лишь для совокупности, а не для отдельных явлений и зависит от
объема совокупности (чем она больше, тем параметры уравнения типичнее).
В уравнении
прямой параметр 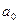 экономического смысла
не имеет. Параметр
экономического смысла
не имеет. Параметр 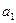 является коэффициентом
регрессии и показывает изменение
результативного признака при изменении факторного признака на единицу.
является коэффициентом
регрессии и показывает изменение
результативного признака при изменении факторного признака на единицу.
Широкое
применение линейных уравнений объясняется в значительной мере тем, что зачастую
значения признака х в изучаемой
совокупности варьируют в весьма узких пределах. Если кривизна линии
регрессии невелика, то в этих пределах отрезок кривой может быть достаточно
точно описан уравнением прямой.
Кроме того,
многие нелинейные функции (степенная, показательная, гипербола, парабола
второго порядка) путем логарифмирования или замены переменных преобразуют в
линейную форму.
Решения типовых задач
№1. Имеются выборочные данные по 15
коммерческим банкам региона:
|
№ п/п
|
х
|
у
|
№ п/п
|
х
|
у
|
№ п/п
|
х
|
у
|
|
1
2
3
4
5
|
15
20
28
38
41
|
52
86
102
106
124
|
6
7
8
9
10
|
42
43
49
52
57
|
150
140
192
190
240
|
11
12
13
14
15
|
58
60
65
72
75
|
230
220
267
270
315
|
Построить
однофакторную регрессионную линейную модель.
Решение: Предположим, что между объемом
собственных средств и привлеченных средств существует линейная корреляционная
связь, которую можно выразить уравнением прямой вида 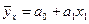 .
.
Для
определения параметров 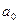 и
и 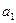 методом наименьших
квадратов воспользуемся формулами
методом наименьших
квадратов воспользуемся формулами 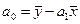 ,
, 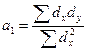 .
.
Таблица
7.7
Расчетные
значения, необходимые для исчисления 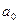 ,
, 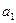 ,
,  ,
, 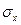 ,
, 
|
Исходные данные
|
Расчетные значения
|
|
№ банка
|
Объем собственных средств, млн. руб.
|
Объем привлеченных
средств, млн. руб.
|
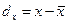
|
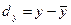
|
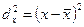
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
15
20
28
38
41
42
43
49
52
57
57
60
65
72
75
|
52
86
102
106
124
150
140
192
190
240
230
220
267
270
315
|
-32,6
-27,6
-19,6
-9,6
-6,6
-5,6
-4,6
1,4
4,4
9,4
9,4
12,4
17,4
24,4
27,4
|
-127
-93
-77
-73
-55
-29
39
13
12
61
51
41
88
91
136
|
1062,76
761,76
384,16
92,16
43,56
31,36
21,16
1,96
19,36
88,36
88,36
153,76
302,76
595,96
750,76
|
|
|
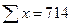
|
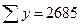
|
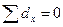
|
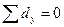
|
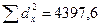
|
Продолжение
таблицы 7.7
|
Расчетные значения
|
|
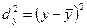
|
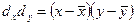
|
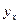
|
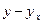
|
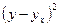
|
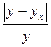
|
|
7
|
8
|
9
|
10
|
11
|
12
|
|
16129
8649
5929
5329
3025
841
1521
169
144
3721
2601
1681
7744
8281
18496
|
4140,2
2566,8
1509,2
700,8
363,0
162,4
179,4
18,2
52,8
573,4
479,4
508,4
1531,2
2220,4
3726,4
|
40
61
95
138
151
155
159
186
198
219
219
232
253
283
296
|
12
25
7
-32
-27
-5
-19
6
-7
21
11
-12
14
-13
19
|
144
625
49
1024
729
25
361
36
49
441
121
144
196
169
361
|
0,23
0,29
0,07
0,30
0,22
0,03
0,14
0,03
0,04
0,09
0,05
0,05
0,05
0,05
0,06
|
|
84260
|
18732,0
|
2685
|
0
|
4474
|
1,70
|
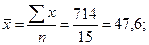
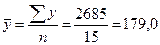 .
.
Пользуясь расчетными значениями (см. Табл. 7.7.),
подсчитаем параметры для данного уравнения регрессии:
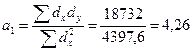 ,
,
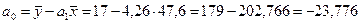 .
.
Следовательно,
регрессионная модель объема привлеченных средств по собственным средствам
банков для данного примера может быть записана в виде следующего уравнения
регрессии:
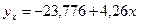 .
.
Это уравнение характеризует зависимость
среднего объема привлеченных средств банков от собственных средств. Расчетные
значения  , найденные по данному уравнению, приведены в таблице 7.7,
гр. 9.
, найденные по данному уравнению, приведены в таблице 7.7,
гр. 9.
Если параметры
регрессионного уравнения подсчитаны верно, то должно соблюдаться равенство сумм
теоретических и эмпирических значений объема привлеченных средств, 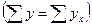 , а сумма разностей
между эмпирическими и теоретическими значениями объема привлеченных средств
должна быть равна 0
, а сумма разностей
между эмпирическими и теоретическими значениями объема привлеченных средств
должна быть равна 0 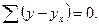 (гр.10. табл. 7.7).
(гр.10. табл. 7.7).
В нашем
уравнении регрессии параметр 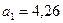 показывает, что с
увеличением объема собственных средств одного банка на 1 млн. руб. объем
привлеченных средств возрастает в среднем на 4,26 млн. руб.
показывает, что с
увеличением объема собственных средств одного банка на 1 млн. руб. объем
привлеченных средств возрастает в среднем на 4,26 млн. руб.
Если исследуемые
признаки имеют разные единицы измерения, для оценки влияния
факторного признака на результативный применяется коэффициент эластичности.
Коэффициент
эластичности рассчитывается для каждой точки по формуле:
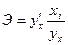 ,
,
где 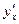 - первая производная
уравнения регрессии.
- первая производная
уравнения регрессии.
Он показывает,
на сколько процентов изменяется результативный признак при изменении факторного
признака на 1%.
Средний
коэффициент эластичности определяется для уравнения прямой по формуле:
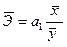 .
.
Если
зависимость величин результативного признака
у от значений факторного признака
х имеет форму гиперболической зависимости, то есть характеризуется корреляционным
уравнением 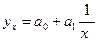 , то для определения параметров
, то для определения параметров 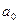 и
и 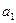 методом наименьших
квадратов находим две частные производные от функции
методом наименьших
квадратов находим две частные производные от функции 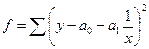 , по
, по 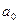 и
и 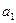 , приравниваем их к нулю, получаем систему нормальных
уравнений:
, приравниваем их к нулю, получаем систему нормальных
уравнений:
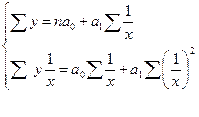 .
.
Производим
замену переменных 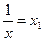 , получаем следующую систему нормальных уравнений:
, получаем следующую систему нормальных уравнений:
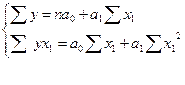 .
.
Параметры
уравнения гиперболы можно вычислить по формулам:
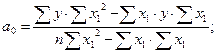
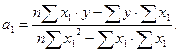
Гиперболическая
форма корреляционной связи используется при изучении зависимости уровня себестоимости единицы
продукции от объема выпуска продукции.
Если
зависимость величин результативного признака
у от значений факторного признака
х характеризуется корреляционным
уравнением параболы второй степени 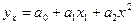 , то это параболическая зависимость.
, то это параболическая зависимость.
И парабола, и прямая
являются частным случаем полинома n-ой степени вида 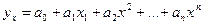 .
.
Систему
уравнений для определения параметров 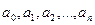 можно найти,
приравнивая нулю частные производные от
можно найти,
приравнивая нулю частные производные от 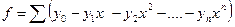 по
по 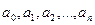 . Решив систему, определяем параметры корреляционного
уравнения.
. Решив систему, определяем параметры корреляционного
уравнения.
Проверка адекватности однофакторной регрессионной модели
Для
практического использования моделей регрессии
большое значение имеет их адекватность, т. е. соответствие фактическим
статистическим данным.
Адекватность
регрессионной модели при малой выборе можно оценить F критерием Фишера:
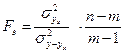 ,
,
где m – число параметров модели;
n - число единиц наблюдения;
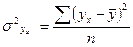 - факторная дисперсия,
которая характеризует вариацию результативного признака под влиянием признака
фактора, включенного в модель;
- факторная дисперсия,
которая характеризует вариацию результативного признака под влиянием признака
фактора, включенного в модель;
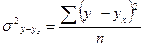 - остаточная дисперсия,
характеризующая вариацию результативного признака под влиянием прочих,
неучтенных факторов;
- остаточная дисперсия,
характеризующая вариацию результативного признака под влиянием прочих,
неучтенных факторов;
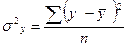 - общая дисперсия,
показывающая вариацию результативного признака под влиянием всех факторов,
вызывающих эту вариацию:
- общая дисперсия,
показывающая вариацию результативного признака под влиянием всех факторов,
вызывающих эту вариацию:
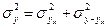 .
.
Эмпирическое
значение критерия 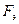 сравнивается с
критическим (табличным)
сравнивается с
критическим (табличным) 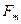 с уровнем значимости
0,01 или 0,05 и числом степеней свободы (m-1), (n-m).
с уровнем значимости
0,01 или 0,05 и числом степеней свободы (m-1), (n-m).
Если 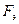 >
>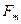 , то уравнение регрессии признается значимым.
, то уравнение регрессии признается значимым.
Проведем
оценку адекватности регрессионной
модели 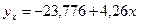 , выражающей зависимость среднего объема привлеченных средств
банков от собственных средств, с помощью F критерия Фишера:
, выражающей зависимость среднего объема привлеченных средств
банков от собственных средств, с помощью F критерия Фишера:
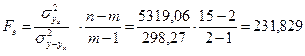 ;
;
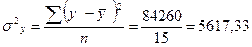 ;
;
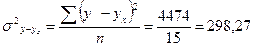 ;
;
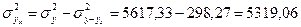 .
.
Табличное
значение Fт
с уровнем значимости 0,05 и числом степеней свободы (2-1), (15-2) равно 4,68. (См. Приложение 7).
Так как 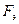 >
> , то уравнение
регрессии можно признать адекватным.
, то уравнение
регрессии можно признать адекватным.
При
численности объектов анализа до 30 единиц (при малой выборе) возникает
необходимость испытания параметров уравнения на их типичность (значимость). При
этом осуществляется проверка, насколько вычисленные параметры характерны для
отображаемого комплекса условий, не являются ли полученные значения параметров
результатами действия случайных причин.
Для проверки
значимости параметров уравнения регрессии используется t – критерий Стьюдента. Вычисляются фактические значения t критерия:
Для параметра 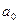 :
:
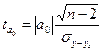 ;
;
для параметра 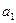 :
:
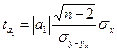 ,
,
где 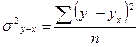 - среднее
квадратическое отклонение результативного признака от выравненных значений
- среднее
квадратическое отклонение результативного признака от выравненных значений 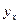 ;
;
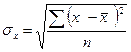 - среднее
квадратическое отклонение факторного признака
хот общей средней
- среднее
квадратическое отклонение факторного признака
хот общей средней 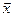 .
.
Полученные
фактические значения 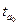 и
и 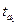 сравниваются с
критическим
сравниваются с
критическим 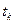 , который получают по таблице Стьюдента с учетом принятого
уровня значимости а (а=0,01 или а=0,05) и числа степеней свободы k=n-2.
, который получают по таблице Стьюдента с учетом принятого
уровня значимости а (а=0,01 или а=0,05) и числа степеней свободы k=n-2.
Параметр
признается значимым (типичным), если эмпирическое значение  больше критического
табличного
больше критического
табличного 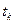 :
:
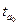 >
>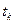 <
< 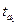 .
.
Оценим
значимость параметров уравнения регрессии 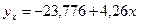 с помощью t – критерия Стьюдента:
с помощью t – критерия Стьюдента:
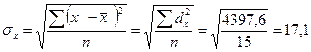 ;
;
 ;
;
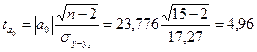 ;
;
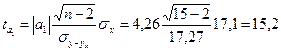 .
.
Табличное
значение t – критерия с
уровнем значимости 0,05 и числом степеней свободы k=n-2=15-2=13 равно 2,161 (Приложение 6).
Сравним фактические
значения 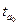 и
и 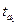 с критическим (
с критическим (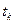 =2,161), получаем:
=2,161), получаем:
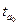 = 4,96 >
= 4,96 >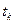 = 2,161<
= 2,161< 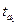 =15,2.
=15,2.
Следовательно,
вычисленные по уравнению регрессии параметры 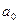 и
и 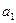 признаются значимыми.
признаются значимыми.
Измерение
тесноты корреляционной связи.
Проверка
адекватности регрессионной модели может быть дополнена корреляционным анализом.
Для этого необходимо определить тесноту корреляционной связи между переменными х и у.
Теснота связи
между двумя признаками может измеряться
линейным коэффициентов корреляции (r), корреляционным отношением (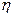 ) и индексом корреляции (R).
) и индексом корреляции (R).
Линейный
коэффициент корреляции определяется по формулам:
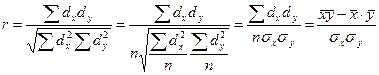
или
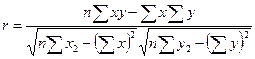 .
.
Линейный
коэффициент корреляции характеризует степень тесноты только при прямолинейной
корреляционной зависимости. С коэффициентом
регрессии 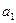 связан таким
соотношением:
связан таким
соотношением: 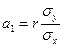 .
.
Величина 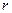 принимает значения в интервале:
принимает значения в интервале: 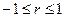 . Отрицательные значения указывают на обратную связь,
положительные – на прямую. При
. Отрицательные значения указывают на обратную связь,
положительные – на прямую. При 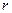 =0 линейная связь отсутствует. Чем ближе
=0 линейная связь отсутствует. Чем ближе  по абсолютной величине
к единице, тем теснее связь между признаками.
И, наконец, при
по абсолютной величине
к единице, тем теснее связь между признаками.
И, наконец, при  , связь функциональная.
, связь функциональная.
Квадрат
линейного коэффициента корреляции 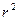 называется линейным
коэффициентом детерминации, показывает удельный вес влияния данного фактора в
общей сумме всех факторов, определяющих уровень результативного признака.
называется линейным
коэффициентом детерминации, показывает удельный вес влияния данного фактора в
общей сумме всех факторов, определяющих уровень результативного признака.
Линейный
коэффициент корреляции предложили в конце XIX века английские ученые Ф. Гальтон и К. Пирсон.
При наличии
криволинейной корреляционной связи  недооценивает тесноту
связи и в некоторых случаях может дать
неверное представление о степени тесноты связи.
недооценивает тесноту
связи и в некоторых случаях может дать
неверное представление о степени тесноты связи.
Теоретическое
корреляционное отношение (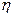 ) и индекс корреляции (
) и индекс корреляции ( ) служат для измерения тесноты связи как при прямолинейной,
так и при криволинейной корреляционной связи.
) служат для измерения тесноты связи как при прямолинейной,
так и при криволинейной корреляционной связи.
Теоретическое
корреляционное отношение определяется по
формулам:
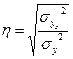 или
или 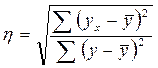 .
.
Корреляционное
отношение в квадрате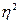 показывает, какую часть всей вариации результативного
признака составляет вариация, вызванная факторным признаком.
показывает, какую часть всей вариации результативного
признака составляет вариация, вызванная факторным признаком.
Для упрощения
расчетов степени тесноты связи часто применяется индекс корреляции. Индекс
корреляции определяется по следующим формулам:
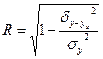 или
или 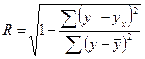 .
.
Абсолютные
размеры линейного коэффициента корреляции, корреляционного отношения, индекса
корреляции колеблются от 0 до 1. Направление
связи (знак перед 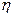 и
и  ) определяется непосредственно по исходным данным.
) определяется непосредственно по исходным данным.
Для
качественной оценки тесноты связи можно воспользоваться также шкалой Чеддока:
|
Величина показателя
тесноты связи
|
Характеристика
тесноты
|
|
0,1- 0,3
0,3 – 0,5
0,5 – 0,7
0,7 – 0,9
0,9 - 0,99
|
Слабая
Умеренная
Заметная
Высокая
Весьма высокая
|
Показатели 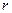 и
и 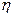 при прямолинейной
связи совпадают. Поэтому вычисленные по
одним и тем же данным величины
при прямолинейной
связи совпадают. Поэтому вычисленные по
одним и тем же данным величины 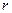 и
и 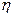 часто используют для
того, чтобы судить о том, насколько для данного случая правильно предположение
о наличии именно прямолинейной формы корреляционной связи. Английский статистик
Блекман предложил следующий критерий: если разность
часто используют для
того, чтобы судить о том, насколько для данного случая правильно предположение
о наличии именно прямолинейной формы корреляционной связи. Английский статистик
Блекман предложил следующий критерий: если разность 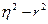 не превышает 0,1,
предположение о прямолинейной форме
корреляционной связи можно считать оправданным.
не превышает 0,1,
предположение о прямолинейной форме
корреляционной связи можно считать оправданным.
При выборе
вида уравнения можно воспользоваться еще критерием криволинейности 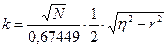 , если k>
2,5, то предположение о данном виде
криволинейной связи можно считать оправданным.
, если k>
2,5, то предположение о данном виде
криволинейной связи можно считать оправданным.
Используем
данные табл. 7.7 и рассчитаем линейный коэффициент корреляции, теоретическое
корреляционное отношение и индекс корреляции:
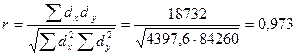 ;
;
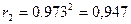 ;
;
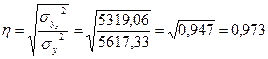 ;
;
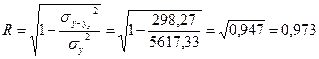 ;
;
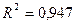 .
.
Все показатели
тесноты корреляционной связи показывают
весьма высокую связь между объемами привлеченных и собственных средств.
Коэффициент
детерминации 0,947 означает, что вариация привлеченных средств банков на 94,7%
объясняется вариацией собственных средств и на 5,7% - прочими факторами.
Так как 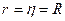 , то можно седлать заключение, что гипотеза о линейной форме
связи подтверждена.
, то можно седлать заключение, что гипотеза о линейной форме
связи подтверждена.
Проверка значимости показателей тесноты
корреляционной связи
Показатели
тесноты связи, исчисленные по данным небольшой статистической совокупности,
могут искажаться действием случайных причин. Это вызывает
необходимость проверки из значимости (надежности, существенности).
Для оценки
значимости коэффициента корреляции применяется t–критерий Стьюдента, который
определяется по формуле:
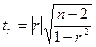 ,
,
где 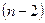 - число степеней
свободы при данном уровне значимости
- число степеней
свободы при данном уровне значимости 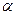 и объеме выборки n.
и объеме выборки n.
Вычисленное по
формуле значение 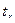 сравнивается с
критическим
сравнивается с
критическим 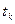 .
.
Если 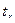 >
> 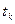 , то величина
коэффициента корреляции признается значимой.
, то величина
коэффициента корреляции признается значимой.
Для оценки
значимости индекса корреляции R применяется F -критерий Фишера.
Фактическое
значение критерия 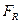 определяется по
формуле:
определяется по
формуле:
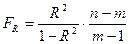 ,
,
где m– число параметров уравнения
регрессии.
Величина 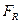 сравнивается с
критическим
сравнивается с
критическим 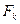 , которое определяется по таблице F –критерия с
учетом принятого уровня значимости а
и числа степеней свободы
, которое определяется по таблице F –критерия с
учетом принятого уровня значимости а
и числа степеней свободы  и
и 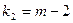 .
.
Если 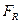 >
> 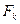 , то величина индекса корреляции признается значимой.
Проверим значимость показателей тесноты корреляционной связи в нашем примере.
Значимость линейного коэффициент корреляции оценим с помощью t–критерия:
, то величина индекса корреляции признается значимой.
Проверим значимость показателей тесноты корреляционной связи в нашем примере.
Значимость линейного коэффициент корреляции оценим с помощью t–критерия:
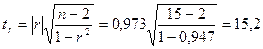 .
.
Табличное
значение t–критерия с
уровнем значимости 0,05 и числом степеней свободы 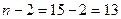 равно 2,161.
Фактическое значение
равно 2,161.
Фактическое значение 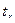 =15,2 больше табличного (критического)
=15,2 больше табличного (критического) 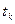 =2,161, следовательно, коэффициент корреляции можно признать
значимым.
=2,161, следовательно, коэффициент корреляции можно признать
значимым.
Оценка индекса
корреляции R=0,973
осуществляется по F–критерию.
Определяется фактическое значение:
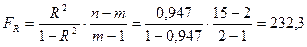 .
.
При уровне
значимости 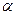 =0,05 и степенях свободы
=0,05 и степенях свободы 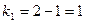 и
и 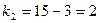 табличное значение
табличное значение 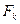 =4,675. Сравнение
=4,675. Сравнение 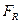 =232,3 с
=232,3 с 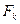 =4,675,
=4,675, 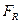 >
> 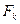 позволяет признать
индекс корреляции значимым.
позволяет признать
индекс корреляции значимым.
Вычислим ошибку
аппроксимации по формуле:
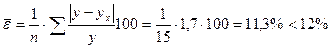 .
.
Так как параметры уравнения регрессии значимы,
уравнение значимо, показатели тесноты значимы, ошибка аппроксимации равна 11,3
%, коэффициент детерминации равен 0,947, то построенная регрессионная модель зависимости объема привлеченных
средств от объема собственных средств 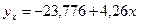 может быть использована для анализа и прогноза.
может быть использована для анализа и прогноза.
7.5. Показатели тесноты связи альтернативных
признаков
Для
определения тесноты связи двух качественных признаков, каждый из которых
состоит только из 2-х групп (т.е. имеет альтернативный характер), применяются
коэффициенты ассоциации и контингенции. При исследовании связи исходные данные
располагают в комбинационной четырех клеточной таблице (таблице четырех полей),
например, табл. 7.8:
Таблица
7.8
Таблица для
вычисления коэффициентов ассоциации и контингенции

|
Группы по признаку Б
Группы по признаку А
|
1
|
2
|
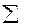
|
|
1
|
a
|
b
|
a + b
|
|
2
|
c
|
d
|
c + d
|
|
|
a + c
|
b + d
|
a + b + c + d
|
Если обозначим
данные в каждой из четырех клеток латинскими буквами a,b,c,d, то получим следующие
формулы расчета коэффициентов:
коэффициент
ассоциации (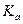 ):
):
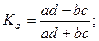
коэффициент
контингенции (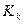 ):
):
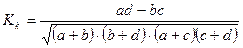 .
.
Коэффициент
контингенции всегда меньше коэффициента ассоциации, связь считается
подтвержденной, если 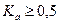 , а
, а 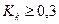 .
.
№2.
Исследовалась связь между выполнением норм выработки рабочими предприятия и их
технически обучением. Результаты обследования характеризуются следующими
данными:
Таблица 7.9
Зависимость
выполнения норм выработки рабочими от их технического обучения
|
 Группы рабочих по Группы рабочих по
выполнению норм
Группы
рабочих
по техническому обучению
|
Число рабочих
|
|
Выполнивших и
перевыполнивших норму
|
Не выполнивших
норму
|
Всего
|
|
Прошедшие техническое обучение
|
112
|
19
|
131
|
|
Не прошедшие техническое
обучение
|
15
|
52
|
67
|
|
Всего
|
127
|
71
|
198
|
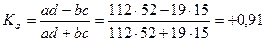
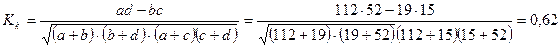
Так как 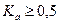 , а
, а 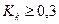 , можно говорить о
наличии существенной связи между выполнением норм рабочими и их техническим
обучением.
, можно говорить о
наличии существенной связи между выполнением норм рабочими и их техническим
обучением.
№3. Имеются
следующие данные:
Таблица
7.10
|
Номер предприятия
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Электровооруженность труда на 1
работающего, кВт. ч.
|
2
|
5
|
3
|
7
|
2
|
6
|
4
|
9
|
8
|
4
|
|
Выпуск готовой продукции на 1
работающего, тыс. руб.
|
3
|
6
|
4
|
6
|
4
|
8
|
6
|
9
|
9
|
5
|
Рассчитайте
параметры линейного уравнения зависимости выпуска готовой продукции на 1
работающего от энерговооруженности труда. Покажите эмпирические и теоретические
линии регрессии на графике. Определите степень тесноты связи между этими
признаками.
Решение:
Зависимость
между электровооруженностью труда и продукцией на одного работающего – линейная
и выражается уравнением прямой:
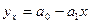 ,
,
где 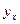 - выпуск готовой
продукции на одного работающего;
- выпуск готовой
продукции на одного работающего;
х –
электровооруженность труда на одного работающего;
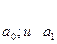 - параметры уравнения
регрессии.
- параметры уравнения
регрессии.
Параметры
уравнения прямой 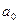 ,
, 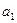 определяются путем
решения системы нормальных уравнений, полученных по методу наименьших квадратов:
определяются путем
решения системы нормальных уравнений, полученных по методу наименьших квадратов:
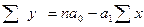 ,
,
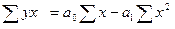 .
.
Для определения параметров уравнения регрессии
строим расчетную таблицу 7.11:
Таблица
7.11
|
№ предприятия
|
Электровооруженность труда на 1
работающего, кВт.ч., х
|
Выпуск готовой продукции на 1
работающего, тыс. руб., у
|
ху
|
х2
|
у2
|
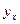
|
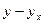
|
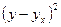
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
1
2
3
4
5
6
|
2
5
3
7
2
6
|
3
6
4
6
4
8
|
6
30
12
42
8
48
|
4
25
9
49
4
36
|
9
36
16
36
16
24
|
3,61
6,00
4,41
7,59
3,61
6,80
|
-0,61
0
-0,41
-1,59
0,39
1,20
|
0,372
0
0,618
2,528
0,152
1,440
|
Продолжение
таблицы 7.11
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
7
8
9
10
|
4
9
8
4
|
6
9
9
5
|
24
81
72
20
|
16
81
64
16
|
36
81
81
25
|
5,20
9,19
8,39
5,20
|
0,80
-0,19
0,6
-0,2
|
0,640
0,036
0,384
0,040
|
|
Итого
|
50
|
60
|
343
|
304
|
400
|
60
|
-
|
5,760
|
|
В
среднем
|
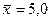
|
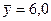
|
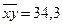
|
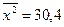
|
-
|
-
|
-
|
-
|
Подставим в
систему нормальных уравнений фактические данные из таблицы:
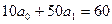
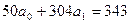
I способ.
Решаем систему
нормальных уравнений в следующей последовательности:
Домножим
каждый член первого уравнения на 5
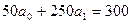
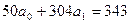 ,
,
вычтем из второго уравнения первое и получим
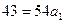 , откуда
, откуда 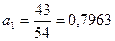 .
.
Подставим
значение 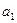 в первое уравнение
в первое уравнение
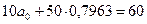 ,
,
получим 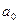 =2,02.
=2,02.
Уравнение
корреляционной связи примет вид
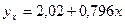 .
.
II способ.
Параметры
уравнения регрессии можно определять по формулам:
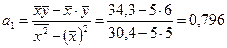 ,
,
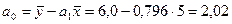 .
.
III способ.
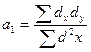 , где
, где 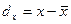 ;
; 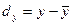 ;
; 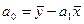 .
.
Для
определения параметров этим способом строим расчетную таблицу 7.12:
Таблица 7.12
|
№ предприятия
|
х
|
у
|
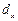
|
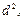
|
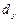
|
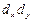
|
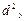
|
|
1
2
3
4
5
6
7
8
9
10
|
2
5
3
7
2
6
4
9
8
4
|
3
6
4
6
4
8
6
9
9
5
|
-3
0
-2
2
-3
1
-1
4
3
-1
|
9
0
4
4
9
1
1
16
9
1
|
-3
0
2
2
-2
2
0
3
3
-1
|
9
0
4
0
6
2
0
12
9
1
|
9
0
4
0
4
4
0
9
9
1
|
|
Итого
|
50
|
60
|
|
54
|
|
43
|
40
|
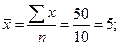
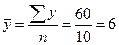 ;
;
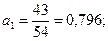
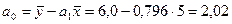 .
.
Корреляционное
уравнение 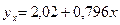 .
.
После
определения параметров уравнения регрессии рассчитываем теоретическую линию
регрессии 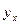 путем подстановки
значений х в уравнение корреляционной
связи:
путем подстановки
значений х в уравнение корреляционной
связи:
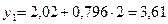 ;
;
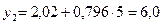 , и т.д.
, и т.д.
Если параметры
уравнения связи определены правильно, то 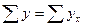 .
.
Окончательная
проверка правильности расчета параметров уравнения связи производится
подстановкой 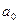 и
и 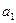 в систему нормальных
уравнений.
в систему нормальных
уравнений.
Используя
уравнение связи 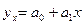 можно определить
теоретическое значение
можно определить
теоретическое значение 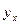 для любой
промежуточной точки (теоретическое значение выпуска готовой продукции на 1
работающего для любого промежуточного значения электровооруженности труда).
для любой
промежуточной точки (теоретическое значение выпуска готовой продукции на 1
работающего для любого промежуточного значения электровооруженности труда).
Коэффициент
регрессии 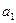 уточняет связь между х
и у. Он показывает, на сколько единиц увеличивается результативный признак при
увеличении факторного признака на единицу. В нашем примере
уточняет связь между х
и у. Он показывает, на сколько единиц увеличивается результативный признак при
увеличении факторного признака на единицу. В нашем примере 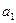 =0,796. Значит, при увеличении электровооруженности труда на
1 работающего на 1 кВт. ч. выпуск продукции увеличится на 0,796 тыс. руб.
=0,796. Значит, при увеличении электровооруженности труда на
1 работающего на 1 кВт. ч. выпуск продукции увеличится на 0,796 тыс. руб.
 Построим
эмпирическую и теоретическую линии регрессии на графике:
Построим
эмпирическую и теоретическую линии регрессии на графике:

Рис. 7.3
Зависимость выпуска готовой продукции на 1 работающего от электровооруженности
труда
 эмпирическая линия регрессии
эмпирическая линия регрессии
 теоретическая линия регрессии
теоретическая линия регрессии
При линейной
зависимости между признаками для определения тесноты корреляционной связи
применяются коэффициент корреляции (r) и индекс корреляции (R)
Наиболее
удобной формулой для расчета коэффициента корреляции является следующая:
1) 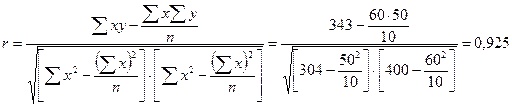 ,
,
r изменяется
от – 1 до +1 и показывает тесноту и направление корреляционной связи. В нашем
примере r=0,925, что
показывает весьма тесную прямую связь между электровооруженностью труда рабочих
и их производительностью труда.
Коэффициент
корреляции можно рассчитывать и по другим формулам:
2)
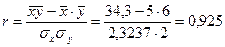 ,
,
где 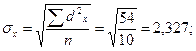
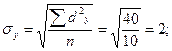
3) 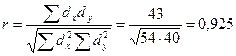 .
.
4) если
определена форма корреляционной связи и вычислен коэффициент регрессии 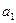 , линейный коэффициент можно определить, используя формулу:
, линейный коэффициент можно определить, используя формулу:
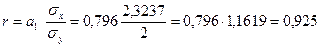 .
.
5) Индекс корреляции удобно рассчитать по
формуле:
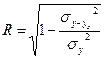 ,
,
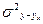 - остаточная дисперсия
характеризующая вариацию результативного признака от всех прочих, кроме х, факторов, определяется
- остаточная дисперсия
характеризующая вариацию результативного признака от всех прочих, кроме х, факторов, определяется
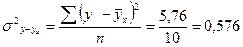 ;
;
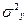 - общая дисперсия,
отображающая совокупное влияние всех факторов:
- общая дисперсия,
отображающая совокупное влияние всех факторов:
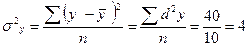 ;
;
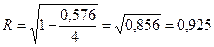 .
.
По абсолютной
величине линейный коэффициент корреляции r и индекс корреляции R при прямолинейной связи совпадают.
№ 4. По результатам решения типовой
задачи №3 дать оценку типичности параметров уравнения и значимости
показателей тесноты связи.
Решение:
1. Применительно
к совокупностям, у которых n<30, для проверки
типичности параметров уравнения регрессии используется t–критерий Стьюдента. При этом
вычисляются фактические значения t–критерия по формулам:
для параметра 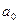 :
:
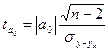 ;
;
для параметра 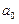 :
:
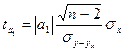 .
.
Полученные
фактические значения 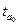 ,
, 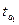 сравниваются с
критическим
сравниваются с
критическим 
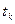 , которые получают по таблице Стьюдента с учетом принятого
уровня значимости
, которые получают по таблице Стьюдента с учетом принятого
уровня значимости 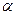 и числа степеней свободы (см. приложение 6).
и числа степеней свободы (см. приложение 6).
Полученные в
анализе корреляционной связи параметры уравнения регрессии признаются
типичными, если t фактическое больше t критического:
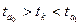 .
.
Подсчитаем
фактические значения t–критерия
Стьюдента. Для определения среднего квадратического отклонения результативного
признака у от выравненных значений 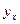 воспользуемся формулой:
воспользуемся формулой:
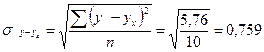 .
.
Среднее
квадратическое отклонение факторного признака х от общей средней 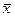 определим по формуле:
определим по формуле:
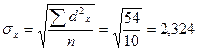
Фактические
значения t – критерия
равны:
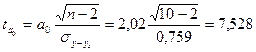 ,
,
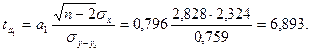
С учетом
принятого в экономико-статистических
исследованиях уровня значимости 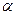 =0,05 и числа степеней свободы
=0,05 и числа степеней свободы 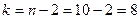 табличное критическое
значение
табличное критическое
значение 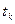 =2,307 (см. приложение
6).
=2,307 (см. приложение
6).
Сравним
фактические и табличное значения t – критерия:
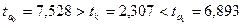 .
.
Это позволяет
признать вычисленные по уравнению параметры типичными.
2. Показатели
тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это
вызывает необходимость проверки их существенности.
Для оценки
значимости коэффициента корреляции r применяется t–критерий
Стьюдента. При этом определяется фактическое значение критерия 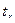 :
:
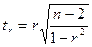 .
.
Фактическое
значение 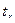 сравниваются с
критическими
сравниваются с
критическими 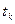 , которое берется из таблицы значений t–критерия Стьюдента с учетом заданного уровня
значимости
, которое берется из таблицы значений t–критерия Стьюдента с учетом заданного уровня
значимости 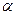 и числа степеней свободы к.
и числа степеней свободы к.
Если 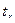 >
>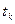 то величина
коэффициента корреляции признается существенной. В нашем примере r=0,925, фактическое значение критерия
то величина
коэффициента корреляции признается существенной. В нашем примере r=0,925, фактическое значение критерия
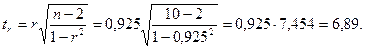
При
критическом значении 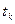 =2,307 получается.
=2,307 получается. 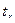 >
>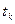 . Поэтому вычисленный коэффициент корреляции признается существенным.
. Поэтому вычисленный коэффициент корреляции признается существенным.
Из значения 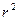 =0,856 следует, что 85,6 % общей вариации производительности
труда объясняется изменением электровооруженности труда. Поэтому корреляционное
уравнение
=0,856 следует, что 85,6 % общей вариации производительности
труда объясняется изменением электровооруженности труда. Поэтому корреляционное
уравнение 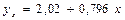 может быть
использовано для практических целей.
может быть
использовано для практических целей.
Для оценки
значимости индекса корреляции  применяется
применяется 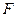 критерий Фишера.
критерий Фишера.
Фактическое
значение критерия 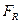 определяется по
формуле
определяется по
формуле
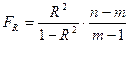
Величина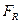 сравнивается с
критическим
сравнивается с
критическим 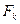 , которое определяется
по таблице
, которое определяется
по таблице 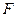 критерия с учетом
принятого уровня значимости
критерия с учетом
принятого уровня значимости 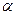 и числа степеней
свободы
и числа степеней
свободы 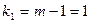 и
и 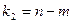 . Если
. Если 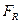 >
>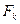 , то величина индекса корреляции признается существенной. Подсчитаем
, то величина индекса корреляции признается существенной. Подсчитаем
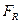 :
:
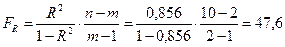
При уровне
значимости 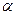 =0,05 и степенях свободы
=0,05 и степенях свободы 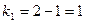 и
и 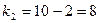 табличное значение
табличное значение 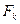 =5,32 (См. приложение 7). Следовательно,
=5,32 (См. приложение 7). Следовательно,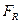 =47,6 >
=47,6 > 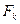 =5,32. Поэтому показатель тесноты связи
=5,32. Поэтому показатель тесноты связи  = 0,925 принимается существенным.
= 0,925 принимается существенным.
Задачи
№7.1 Исследуйте зависимость роста
производительность труда от роста фондовооруженности (прирост в %)
|
Производительность труда
|
2
|
4
|
7
|
8
|
6
|
|
Фондовооруженность
|
5
|
7
|
9
|
10
|
8
|
Представьте на
графике эмпирическую и теоретическую зависимости и сделайте выводы.
№7.2 Имеются следующие данные об уровне
энерговооруженности труда и себестоимости продукции:
|
Энерговооруженность труда, кВт
|
50
|
52
|
60
|
62
|
65
|
|
Себестоимость 1 ед. продукции
тыс. руб.
|
13
|
12
|
11
|
10
|
9
|
1.
Рассчитайте параметры линейного уравнения зависимости
себестоимости продукции от энерговооруженности труда.
2.
Покажите
эмпирические и теоретические линии регрессии на графике.
3.
Определите степень тесноты связи между признаками с
помощью индекса корреляции.
4.
Дайте оценку типичности параметров уравнения и
значимости индекса корреляции.
№7.3 Имеются следующие данные по предприятиям за
отчетный год:
|
Среднегодовая стоимость
основных промышленно-производственных фондов, млн. руб.
|
100
|
130
|
150
|
140
|
170
|
|
Фактический выпуск продукции,
млн. руб.
|
140
|
140
|
150
|
180
|
190
|
Рассчитайте
параметры линейного уравнения связи и дайте оценку их типичности. Сделайте
выводы.
№ 7.4 Имеются следующие данные о стаже и выработке
рабочих бригады:
|
Номер рабочего
|
Стаж, лет
|
Выработка (шт.)
|
ух
|
|
1
2
3
4
5
|
1
8
6
12
3
|
7
29
16
26
17
|
10
22
19
30
14
|
Для измерения
тесноты корреляционной связи между стажем и выработкой рабочих рассчитайте
индекс корреляции. Дайте оценку его значимости с помощью критерия Фишера.
Сделайте выводы.
№ 7.5 Имеются следующие данные по группе
предприятий:
|
№ предприятия п/п
|
Основные производственные
фонды, млн. руб.
|
Объем продукции,
млн. руб.
|
|
1
2
3
4
5
|
3
4
5
8
10
|
3
5
6
10
13
|
По исходным
данным определите линейное уравнение корреляционной связи между размером основных фондов и выпуском продукции. Дайте
оценку типичности параметров с помощью критерия Стьюдента.
Сделайте
выводы.
№7.6 Имеются следующие данные:
|
Стаж рабочего в годах
|
Выработка изделий за смену, шт
|
|
1
3
5
7
9
|
2
3
6
5
10
|
Для
установления характера связи между
стажем работы и производительностью труда вычислите линейное уравнение
связи. Поясните смысл коэффициента регрессии. Для характеристики тесноты связи
вычислите линейный коэффициент корреляции. Дайте оценку типичности параметров
уравнения и значимости линейного коэффициента корреляции.
Приложение 1

Приложение 2

Приложение 3
Формулы для расчета
предельной ошибки при различных видах выборки
|
Вид выборки
|
Повторный отбор
|
Бесповторный отбор
|
|
для средней
|
для доли
|
для средней
|
для доли
|
|
Собственно случайная
|
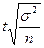
|
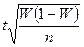
|

|
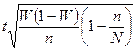
|
|
Механическая
|
Используются формулы собственно-
случайной выборки
|
|
Типическая
|
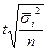
|
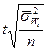
|
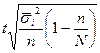
|
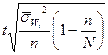
|
|
Серийная
|
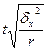
|
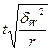
|
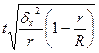
|
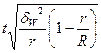
|
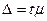 - предельная ошибка
выборки;
- предельная ошибка
выборки; 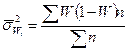 .
.
Приложение 4
Формулы для расчета численности
выборки при различных видах выборки
|
Вид выборки
|
Повторный отбор
|
Бесповторный отбор
|
|
для средней
|
для доли
|
для средней
|
для доли
|
|
Собственно случайная
|
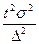
|
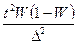
|
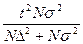
|
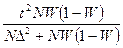
|
|
Механическая
|
Применяются формулы
собственно-
случайной выборки
|
|
Типическая
|
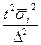
|
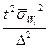
|
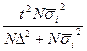
|
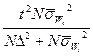
|
|
Серийная
|
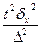
|
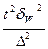
|
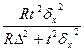
|
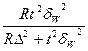
|
Приложение5
Таблица значений
интеграла вероятностей
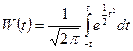
|
t
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
|
0000
0797
1585
2358
3108
3829
4515
5161
5763
6319
6827
7287
6799
8064
8385
8664
8904
9104
9281
9426
9545
9643
9722
9786
9836
9876
9907
9931
9949
9963
9973
|
0080
0876
1663
2434
3182
3899
4581
5223
5821
6372
6875
7339
7737
8098
8415
8690
8926
9127
9297
9439
9556
9651
9729
9791
9840
9879
9909
9933
9950
9964
9981
|
0160
0955
1741
2510
3255
3669
4647
5285
5878
6424
6923
7373
7775
8132
8444
8715
8948
9146
9312
9451
9566
9660
9735
9797
9845
9883
9912
9935
9952
9965
9986
|
0239
1034
1819
2586
3328
4039
4713
5346
5935
6476
6970
7415
7813
8165
8173
8740
8969
9164
9327
9464
9576
9668
9743
9802
9849
9886
9915
9937
9953
9956
9990
|
0319
1113
1897
2661
3401
4108
4778
5407
5991
6528
7017
7457
7850
8198
8501
8764
8990
9181
9342
9476
9586
9678
9749
9807
9853
9889
9917
9939
9955
9967
9993
|
0399
1192
1974
2737
3473
4177
4843
5467
6047
6579
7063
7499
7887
8230
8529
8789
9011
9199
9357
9488
9596
9684
9756
9812
9857
9892
9920
9940
9956
9968
9995
|
0478
1271
2051
2812
3545
4245
4907
5527
6102
6629
7109
7540
7923
8262
8557
8812
9031
9216
9371
9500
9606
9692
9762
9817
9861
9895
9922
9942
9958
9969
9997
|
0558
1350
2128
2886
3616
4313
4971
5587
6157
6680
7154
7580
7959
8293
8584
8836
9051
9233
9385
9512
9616
9700
9768
9822
9865
9898
9924
9944
9959
9970
9996
|
0638
1428
2205
2961
3688
4381
5035
5646
6211
6729
7199
7620
7925
8324
8611
8859
9070
9249
9399
9523
9625
9707
9774
9827
9869
9901
9926
9946
9960
9971
9999
|
0717
1507
2282
3035
3759
4448
5098
5705
6265
6778
7243
7650
8029
8355
8638
8882
9090
9265
9412
9534
9634
9715
9780
9832
9872
9904
9929
9947
9961
9971
9999
|
Все числа увеличены в 10 тысяч
раз.
Приложение 6
Таблица значения t Стьюдента для
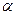 =0,05 и 0,01
=0,05 и 0,01
|
Число степеней свободы
|
 =0,05 =0,05
|
 =0,01 =0,01
|
Число степеней свободы
|
 =0,05 =0,05
|
 =0,01 =0,01
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
12,69
4,302
3,183
2,777
2,571
2,447
2,364
2,307
2,263
2,227
2,200
2,179
2,161
2,145
2,131
2,119
2,110
2,100
2,093
2,086
|
63,655
9,924
5,841
4,604
4,032
3,707
3,500
3,356
3,250
3,169
3,138
3,055
3,012
2,977
2,946
2,921
2,898
2,877
2,860
2,846
|
21
22
23
24
25
26
27
28
29
30
32
34
36
38
40
42
44
46
48
50
55
60
|
2,078
2,074
2,069
2,064
2,059
2,054
2,052
2,049
2,045
2,042
2,037
2,032
2,027
2,025
2,020
2,017
2,015
2,012
2,010
2,007
2,005
2,000
|
2,832
2,818
2,807
2,796
2,787
2,778
2,771
2,764
2,757
2,750
2,739
2,728
2,718
2,711
2,704
2,696
2,691
2,685
2,681
2,678
2,668
2,661
|
Приложение 7
Критические значения F- критерия
|
|
1
|
2
|
3
|
4
|
5
|
6
|
8
|
10
|
20
|
|
Уровень
значимости 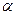 =0,05 =0,05
|
|
1
2
3
4
5
6
7
8
9
10
11
12
14
16
18
20
30
40
60
120
|
161,4
18,51
10,13
7,71
6,61
5,99
5,59
5,32
5,12
4,96
4,82
4,75
4,60
4,49
4,41
4,35
4,17
4,08
4,00
3,92
3,84
|
199,5
19,00
9,45
6,94
5,79
5,14
4,74
4,46
4,26
4,10
3,98
3,88
3,74
3,63
3,55
3,49
3,32
3,23
3,15
3,07
2,99
|
215,7
19,16
9,28
6,59
5,41
4,76
4,35
4,07
3,86
3,71
3,59
3,49
3,34
3,24
3,16
3,10
2,92
2,84
2,76
2,68
2,60
|
224,6
19,25
9,12
6,39
5,19
4,53
4,12
3,84
3,63
3,48
3,63
3,26
3,11
3,01
2,93
2,87
2,69
2,61
2,52
2,45
2,37
|
230,2
19,30
9,01
6,26
5,05
4,39
3,97
3,69
3,48
3,33
3,20
3,11
2,96
2,85
2,77
2,71
2,53
2,45
2,37
2,29
2,21
|
234,0
19,33
8,94
6,16
4,95
4,28
3,87
3,58
3,37
3,22
3,09
3,00
2,85
2,74
2,66
2,60
2,42
2,34
2,25
2,17
2,09
|
238,9
19,37
8,84
6,04
4,82
4,15
3,73
3,44
3,23
3,07
2,95
2,85
2,70
2,59
2,51
2,45
2,27
2,18
2,10
2,02
1,94
|
242,0
19,39
8,78
5,96
4,74
4,06
3,63
3,34
3,13
2,97
2,86
2,76
2,60
2,49
2,41
2,35
2,16
2,12
2,04
1,90
1,83
|
248,0
19,44
8,66
5,80
4,56
3,87
3,44
3,15
2,93
2,77
2,65
2,54
2,39
2,28
2,19
2,12
1,93
1,84
1,75
1,65
1,57
|
|
Уровень
значимости 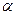 =0,01 =0,01
|
|
1
2
3
4
5
6
7
8
9
10
11
12
14
16
18
20
30
40
60
120
|
4052
98,49
34,12
21,20
16,26
13,74
12,25
11,26
10,56
10,04
9,65
9,33
8,86
8,58
8,28
8,10
7,56
7,31
7,08
6,85
6,64
|
4999
99,00
30,81
18,00
13,27
10,92
9,55
8,65
8,02
7,56
7,20
6,93
6,51
6,23
6,01
5,85
5,39
5,18
4,98
4,79
4,60
|
5403
99,17
29,46
16,69
12.06
9,78
8,45
7,59
6,99
6,55
6,22
5,95
5,56
5,29
5,09
4,94
4,51
4,31
4,13
3,95
3,78
|
5625
99,25
28,71
15,98
11,39
9,15
7,85
7,01
6,92
5,99
5,64
5,41
5,03
4,77
4,58
4,43
4,02
3,83
3,65
3,48
3,32
|
5764
99,30
28,24
15,52
10,97
8,75
7,46
6,63
6,02
5,64
5,32
5,06
4,69
4,44
4,25
4,10
3,70
3,51
3,34
3,17
3,02
|
5859
99,33
27,91
15,21
10,67
8,47
7,19
6,37
5,80
5,39
5,07
4,82
4,46
4,20
4,01
3,87
3,47
3,29
3,12
2,96
2,80
|
5981
99,36
27,49
14,80
10,27
8,10
6,84
6,03
5,47
5,06
4,74
4,50
4,14
3,89
3,71
3,56
3,17
2,99
2,82
2,66
2,51
|
6056
99,40
27,23
14,54
10,05
7,87
6,62
5,82
5,26
4,85
5,54
4,30
3,94
3,69
3,51
3,37
2,98
2,80
2,63
2,47
2,32
|
6208
99,45
26,69
14,02
10,55
7,39
6,15
5,36
4,80
4,41
4,10
3,86
3,51
3,25
3,07
2.94
2,55
2,37
2,20
2,03
1,87
|
Приложение 8
Статистические таблицы
Таблица – это форма наиболее
рационального изложения цифрового материала.
Таблица имеет подлежащее и
сказуемое.
Подлежащее таблицы - это объект изучения.
Сказуемое – это система
показателей, которыми характеризуется объект изучения.
