ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА
СТАТИСТИКИ
Курсовая
работа
Вариант №__24__
Выполнил: ст. III курса
ФК (город)
Проверил: Берлин Ю.И.
.
Архангельск, 2007 г.
Содержание
Введение
|
3
|
|
1.
Теоретическая часть
|
5
|
|
1.1. Финансовые показатели деятельности банка
|
5
|
|
1.2. Понятие и виды взаимосвязей
|
6
|
|
1.3. Этапы изучения взаимосвязей
|
9
|
|
1.4.
Методы выявления взаимосвязей финансовых показателей деятельности банка
|
10
|
|
1.4.1. Графический метод
|
10
|
|
1.4.2. Метод сопоставления двух параллельных рядов
|
12
|
|
1.4.3. Метод аналитических группировок
|
12
|
|
1.4.4. Метод корреляционно-регрессионного анализа
|
14
|
|
1.4.5. Непараметрические методы
|
19
|
|
2.
Расчетная часть
|
22
|
|
3.
Аналитическая часть
|
41
|
|
Заключение
|
51
|
|
Список
используемой литературы
|
52
|
|
Приложение
|
54
|
Введение
Изучение
статистических закономерностей – важнейшая познавательная задача статистики,
которую она решает с помощью особых методов, видоизменяющихся в зависимости от
характера исходной информации и целей познания. Знание характера и силы связей
позволяет управлять социально-экономическими процессами и предсказывать их
развитие. Особую актуальность это приобретает в условиях развивающейся рыночной
экономики. Изучение механизма рыночных связей, взаимодействия спроса и
предложения, влияния объема и структуры товарооборота на объем и состав
производства продукции, формирования товарных запасов, издержек производства,
прибыли и других качественных показателей имеет первостепенное значение для
прогнозирования конъюнктуры рынка, региональной организации производственных и
торговых процессов, успешного ведения бизнеса.
В работе рассмотрим
следующие основные вопросы:
- финансовые
показатели деятельности банка;
- понятие и виды
взаимосвязей;
- этапы изучения
взаимосвязей;
- следующие методы
выявления взаимосвязей финансовых показателей деятельности банка:
- графический метод;
- метод сопоставления двух параллельных
рядов;
- метод аналитических группировок;
- метод корреляционно-регрессионного
анализа.
В расчетной части решим
четыре задачи, в которых требуется:
Задание 1 – исследовать
структуру совокупности;
Задание 2 – выявить
наличие корреляционной связи между признаками, установить направление связи и
измерить ее тесноту;
Задание 3 – применить
выборочный метод;
Задание 4 – использовать
один из статистических методов (балансовый, индексный, анализа рядов динамики).
В аналитической
части работы проведем анализ данных о величине чистых активов и о
размере прибыли (убытка) 40 банков России (источник: www.banki.ru).
1. Теоретическая часть
1.1. Финансовые показатели деятельности банка
Ориентир
банковской деятельности в рыночном хозяйстве состоит в максимизации прибыли от
операций при сведении к минимуму потерь. Прибыль или убытки, полученные банком
- это показатели, концентрирующие в себе результаты различных пассивных и активных
операций банка и отражающие влияние всех факторов, воздействующих на
деятельность банка. Методика анализа результативности банковской деятельности
начинается с анализа доходов и расходов и завершается исследованием прибыли.
Цель анализа финансовых результатов – выявление резервов роста прибыльности
банковской деятельности и формирование на этой основе рекомендаций по дальнейшей
работе. При этом стратегия банка должна строится на следующих принципах:
-как
можно дешевле приобрести капитал;
-продавать
капитал и услуги по рентабельной ставке;
-снизить
банковские риски путем потерь отбора надежных клиентов и получения гарантий,
диверсификации операций и освоения рынков ссудного капитала.
Анализ
банковской деятельности с точки зрения ее доходности позволяет руководству сформировать
кредитную и процентную политику, выявить менее прибыльные операции и
разработать рекомендации возможного получения банком больших доходов. Решение
этих задач невозможно без грамотных финансового и экономического анализов, а
также финансового менеджмента, то есть системы рационального и эффективного
использования капитала, механизма управления движением финансовых ресурсов.
Конечная цель такого управления – получение прибыли. [1, с.430]
Структура
доходной базы банка:
1.
Проценты, полученные по ссудам.
2.
Доходы от операций с ценными бумагами.
3.
Доходы от операций с иностранной
валютой.
4.
Доходы от услуг и комиссий банка.
Расходы
коммерческого банка – это затраты денежных средств банка на выполнение операций
и обеспечение функционирования банка. Анализ расходов в целом осуществляется,
прежде всего, с выявления части процентных и непроцентных расходов.
Элементы
расходов коммерческого банка:
1.
Проценты, уплаченные за приобретенные
кредиты.
2.
Проценты, уплаченные юридическим лицам
за привлеченные средства.
3.
Проценты, уплаченные физическим лицам по
депозитам.
4.
Расходы на содержание аппарата банка.
5.
Штрафы, пени, неустойки.
6.
Другие расходы.
Прибыль коммерческого
банка – это финансовый результат деятельности
коммерческого банка в виде превышения доходов над расходами. Анализ прибыли
следует начинать с рассмотрения общей картины доходности банковских операций.
Анализ должен быть детализирован в динамике по изучению доходности статей по
отдельным видам деятельности.
При
оценке ежегодного прироста прибыли банка необходимо исходить из того, что он не
должен быть ниже темпов инфляции. В противном случае реальные доходы будут
сокращаться и произойдет обесценение банковского капитала. В связи с этим, при
анализе прибыли ее величину необходимо корректировать с учетом темпов инфляции.
1.2.
Понятие
и виды взаимосвязей
Среди многих форм связей финансовых показателей важнейшей является причинная, определяющая все другие
формы. Сущность причинности состоит в порождении одного явления другим. Вместе
с тем, причина сама по себе еще не определяет следствия, она зависит также от
условий, в которых протекает действие причины. Для возникновения следствия
нужны все определяющие его факторы - причина и условия. Необходимая
обусловленность явлений множеством факторов называется детерминизмом. [1,
с.181]
Объектами исследования при статистическом измерении связей служит, как
правило, детерминированность следствия факторами (причиной и условиями).
Признак, характеризующий следствие, называется результативным; признаки,
характеризующие причины, - факторными.
Прежде всего между различными явлениями и их признаками необходимо
выделить два типа связей: функциональную (жестко детерминированную) и статистическую
(стохастически детерминированную).
Связь признака у с признаком х называется функциональной, если каждому возможному значению независимого
признака х соответствует одно или несколько
строго определенных значений зависимого признака у. [1, с.182]
Характерной особенностью функциональных связей является то, что в каждом
определенном случае известен полный перечень факторов, определяющих значение
зависимого (результативного) признака, а также точный механизм их влияния,
выраженный определенным уравнением.
Функциональную связь можно представить уравнением:
уi = ƒ(xi) (1)
где уi – результативный признак;
хi - факторный признак.
В реальной общественной жизни, ввиду неполноты информации жестко детерминированной
системы, может возникнуть неопределенность, из-за которой эта система по своей
природе должна рассматриваться как вероятностная, при этом связь между
признаками становится стохастической.
Стохастическая
связь – это связь между
величинами, при которой одна из них, случайная величина у, реагирует на изменение другой величины х или других величин х1,
х2, …, хn, (случайных или неслучайных) изменением закона распределения.
Это обусловливается тем, что зависимая переменная (результативный признак),
кроме рассматриваемых независимых, подвержена влиянию ряда неучтенных или
неконтролируемых (случайных) факторов, а также некоторых неизбежных ошибок
измерения переменных. Поскольку значения зависимой переменной подвержены
случайному разбросу, они не могут быть предсказаны с достаточной точностью, а
только указаны с определенной вероятностью.[1, с.183]
Характерной особенностью стохастических связей является то, что они
проявляются во всей совокупности, а не в каждой ее единице (причем не известен
ни полный перечень факторов, определяющих значение результативного признака, ни
точный механизм их функционирования и взаимодействия с результативным
признаком).
Модель стохастической связи может быть представлена в общем виде уравнением:
уi = ƒ(xi) + εi (2)
где уi – расчетное значение результативного
признака;
ƒ(xi) - часть результативного
признака, сформировавшаяся под воздействием учтенных известных факторных
признаков (одного или множества), находящихся в стохастической связи с
признаком;
εi – часть результативного признака, возникшая
вследствие действия неконтролируемых или неучтенных факторов, а также измерения
признаков, неизбежно сопровождающегося некоторыми случайными ошибками.
Частный случай стохастической связи – корреляционная связь.
Корреляционная
связь существует
там, где взаимосвязанные явления характеризуются только случайными величинами.
При такой связи среднее значение (математическое ожидание) случайной величины
результативного признака у
закономерно изменяется в зависимости от изменения другой величины х или других случайных величин х1, х2, …, хn. Корреляционная связь
проявляется не в каждом отдельном случае, а во всей совокупности в целом.
Только при достаточно большом количестве случаев каждому значению случайного
признака х будет соответствовать
распределение средних значений случайного признака у. [1, с.184]
В зависимости от направления действия функциональные и стохастические
связи могут быть прямыми и обратными. При прямой связи направление изменения
результативного признака совпадает с направлением изменения признака-фактора,
т.е. с увеличением факторного признака увеличивается и результативный, и
наоборот, с уменьшением факторного признака уменьшается и результативный
признак. В противном случае между рассматриваемыми величинами существуют обратные
связи.
По аналитическому выражению (форме) связи могут быть прямолинейными и
криволинейными. При прямолинейной связи с возрастанием значения факторного
признака происходит непрерывное возрастание (или убывание) значений
результативного признака. Математически такая связь представляется уравнением
прямой, а графически – прямой линией. Отсюда ее более короткое название – линейная
связь.
При криволинейных связях с возрастанием значения факторного
признака возрастание (или убывание) результативного признака происходит
неравномерно или же направление его изменения меняется на обратное.
Геометрически такие связи представляются кривыми линиями (гиперболой, параболой
и т.д.).
По количеству факторов, действующих на результативный признак, связи
различаются однофакторные (один
фактор) и многофакторные (два
и более факторов). Однофакторные (простые) связи обычно называются парными (так
как рассматривается пара признаков).
1.3.
Этапы
изучения взаимосвязей
Выделяют следующие основные этапы анализа взаимосвязей:
1. Качественный анализ изучаемого явления. На этом этапе
устанавливаются статистические производственные показатели фирмы, их числовые
характеристики. Анализ проводится с помощью методов социологии, экономической
теории, конкретной области экономики.
2. Количественное подтверждение наличия или отсутствия взаимосвязей
между признаками. На этом этапе обобщаются результаты наблюдения по всей
совокупности в целом, т.к. в единичных явлениях проявляются не только закономерности,
Но и случайные отклонения.
3. Интерпретация результатов: объяснение причины взаимосвязи,
также основываясь на качественном анализе явлений.
Анализ взаимосвязи атрибутивных признаков на этом заканчивается; для
количественных признаков далее:
4. Построение модели взаимосвязи, т.е. аналитической зависимости между
признаками. В основе этого этапа лежат методы корреляционно-регрессионного
анализа.
Если о характере взаимосвязи заранее ничего не известно, то в процессе исследования
проверяются различные гипотезы, испытываются разные формулы и по формальным
признакам отбирается такая, которая наиболее правдоподобна и соответствует
имеющимся фактическим данным.
5. Оценка достоверности полученных результатов. На этом этапе
используются методы теории вероятности и математической статистики. Они позволяют
уточнить форму связи, отобрать наиболее существенные признаки.
1.4.
Методы
выявления взаимосвязей финансовых показателей деятельности банка
1.4.1.
Графический
метод
Так как финансовые показатели деятельности банка – это количественные
показатели, то для выявления их взаимосвязей можно использовать графический
метод.
Графический метод используют для предварительного определения формы связи
между изучаемыми признаками.
Для этого наносят на график точки, соответствующие значениям факторного
признака х и результативного признака
у, получают корреляционное поле,
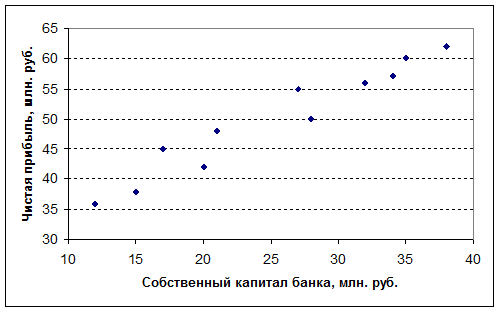
Рис.1.
Корреляционное поле
а соединив эти точки отрезками, - ломаную линию регрессии.
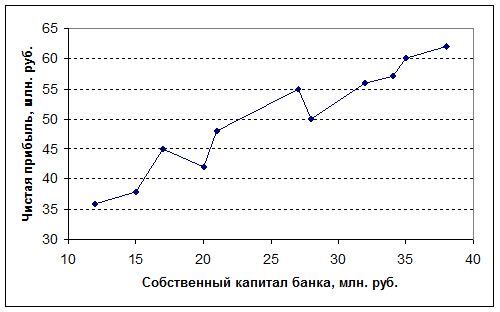
Рис.2. Ломаная
линия регрессии
Далее, анализируя ломаную линию, делают предположение о той или иной
форме связи.
Данный метод эффективен лишь при небольшом объеме совокупности и
достаточно тесной связи между признаками.
Графический метод позволяет наглядно определить форму связи между исследуемыми
признаками, а также выявить аномальные наблюдения.
1.4.2.
Метод
сопоставления двух параллельных рядов
Установить наличие стохастической связи, а также получить представление о
ее характере и направлении можно с помощью сопоставления двух параллельных
рядов финансовых показателей банка. Для этого факторы, характеризующие
результативный признак, располагают в возрастающем или убывающем порядке (в
зависимости от эволюции и целей исследования), а затем прослеживают изменение
величины результативного признака. Сопоставление и анализ расположенных таким
образом рядов значений изучаемых величин позволяют установить наличие связи и
ее направление. Зависимость между факторами и показателями может прослеживаться
во времени (параллельные динамические ряды).
Метод сопоставления двух параллельных рядов применяется также только для
количественных финансовых показателей деятельности банка.
Для приближенного определения направления связи и грубой оценки ее
тесноты может быть использован коэффициент Фехнера:
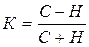 (3)
(3)
где С – число случаев
совпадения знаков отклонений,
Н – число случаев несовпадения этих знаков.
Этот коэффициент принимает значения в пределах от +1 (знаки всех отклонений
совпадают, связь прямая) до -1 (знаки всех отклонений не совпадают, связь
обратная). При К = 0 связь
отсутствует или очень слабая.
1.4.3.
Метод
аналитических группировок
Чтобы выявить зависимость с помощью этого метода, нужно произвести
группировку единиц совокупности по факторному признаку и для каждой группы
вычислить среднее или относительное значение факторного и результативного
признаков. Эта группировка строится с равными интервалами, либо рассчитываются
показатели изменения результата в расчете на единицу изменения фактора.
Для построения аналитической группировки обязательно количественным
должен быть результативный признак.
Группы не должен быть слишком малочисленными, в одну группу не должно
входить более половины всех единиц совокупности, в средних группах должно быть
единиц больше, чем в крайних группах.
Далее сравниваются изменения среднего значения результативного признака
от группы к группе по мере изменения среднего значения факторного признака. И если среднее значение результативного
признака систематически изменяется вслед за средним значением факторного
признака, то делают вывод, что связь есть. Также можно определить направление и
характер связи. Используя в аналитических группировках методы математической
статистики, можно определить показатель тесноты связи между изучаемыми
признаками (с помощью эмпирического корреляционного отношения):
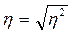 (4)
(4)
где 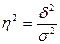 - коэффициент
детерминации;
- коэффициент
детерминации;
 - межгрупповая дисперсия;
- межгрупповая дисперсия;
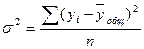 - общая дисперсия;
- общая дисперсия;
где yj – индивидуальные значения признака,
находящиеся в определенной группе;
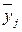 – среднее
значение результативного признака в j-группе;
– среднее
значение результативного признака в j-группе;
yобщ.сред – общее среднее значение результативного
признака в совокупности.
nj – число
единиц в j-группе;
Аналитическая группировка не позволяет определить
форму (аналитическое выражение) влияния факторных признаков на результативный,
но она может строиться непосредственно по эмпирическим данным, независимо от
закона распределения. Однако группировка дает возможность проанализировать не более
трех взаимосвязанных признаков, иначе таблица становится очень громоздкой и
невозможной для анализа.
1.4.4.
Метод
корреляционно-регрессионного анализа
В общем виде задача
статистики в области изучения взаимосвязей состоит не только в количественной
оценке их наличия, направления и силы связи, но и в определении формы
(аналитического выражения) влияния факторных признаков на результативный. Для
ее решения применяют методы корреляционного и регрессионного анализа.
Задачи корреляционного анализа
сводятся к измерению тесноты известной связи между варьирующими признаками,
определению неизвестных причинных связей (причинный характер которых должен
быть выяснен с помощью теоретического анализа) и оценке факторов, оказывающих
наибольшее влияние на результативный признак.
Задачи регрессионного анализа –
выбор типа модели (формы связи), установление степени влияния независимых
переменных на зависимую и определение расчетных значений зависимой переменной
(функции регрессии).
Исследование связей
в условиях массового наблюдения и действия случайных факторов осуществляется,
как правило, с помощью экономико-статистических моделей. [1, с.188]
Модель представляет
собой логическое или математическое описание компонентов и функций,
отображающих существенные свойства моделируемого объекта или процесса, дает
возможность установить основные закономерности изменения оригинала. В модели оперируют
показателями, исчисленными для качественно однородных массовых явлений
(совокупностей). Выражение модели в виде функциональных уравнений используют
для расчета средних значений моделируемого показателя по набору заданных
величин и для выявления степени влияния на него отдельных факторов.
По количеству
включаемых факторов модели могут быть однофакторными
и многофакторными (два
и более факторов).
Применение корреляционного и регрессионного анализа
требует, чтобы все признаки были количественно измеренными.
Основной
предпосылкой применения корреляционного анализа является необходимость
подчинения совокупности значений всех факторных и результативного признаков k-мерному нормальному закону распределения или
близость к нему.
Основной
предпосылкой регрессионного анализа является
то, что только результативный признак подчиняется нормальному закону
распределения, а факторные признаки могут иметь произвольный закон
распределения.
Наиболее
разработанной в теории статистики является методология так называемой парной
корреляции, рассматривающая влияние вариации факторного признака х на результативный признак у и представляющая собой однофакторный
корреляционный и регрессионный анализ.
Важнейшим этапом
построения регрессионной модели (уравнения регрессии) является установление в
анализе исходной информации математической функции. Сложность заключается в
том, что из множества функций нужно найти такую, которая лучше других выражает
реально существующие связи между анализируемыми признаками. Выбор типа функции
может опираться на теоретические знания об изучаемом явлении, опыт предыдущих
аналогичных исследований, или осуществляться эмпирически – перебором и оценкой
функций разных типов и т.п. [1, с.189]
При изучении связи финансовых
показателей банка используют различного вида уравнения прямолинейной и криволинейной
связи. Внимание к линейным связям объясняется ограниченной вариацией переменных
и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов
преобразуют (путем логарифмирования или замены переменных) в линейную форму. Уравнение однофакторной (парной) линейной
корреляционной связи имеет вид:
ŷ = а0 + а1х, (5)
где ŷ –
теоретические значения результативного признака, полученные по уравнению
регрессии;
а0, а1 – коэффициенты (параметры)
уравнения регрессии.
Коэффициент парной
линейной регрессии а1
имеет смысл показателя силы связи
между вариацией факторного признака х
и вариацией результативного признака у.
Уравнение (5)
показывает среднее значение изменения результативного признака у при изменении факторного признака х на одну единицу его изменения, т.е.
вариацию у, приходящуюся на единицу
вариации х. Знак а1 указывает направление этого изменения.
Параметры уравнения а0,
а1 находят методом наименьших квадратов (в основу
этого метода положено требование минимальности сумм квадратов отклонений
эмпирических данных уi от выровненных ŷ):
å(уi –ŷ)2 = å(уi - а0
- а1хi)2 → min.
(6)
Для нахождения минимума данной функции приравняем к нулю ее частные
производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:
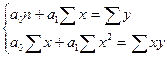 (7)
(7)
Корреляционный
и регрессионный анализ обычно (особенно в условиях так называемого малого и
среднего бизнеса) проводится для ограниченной по объему совокупности. Поэтому
показатели регрессии и корреляции могут быть искажены действием случайных
факторов. Чтобы проверить, насколько эти показатели характерны для всей генеральной
совокупности, не являются ли они результатом стечения случайных обстоятельств,
необходимо проверить адекватность построенных статистических моделей.
Модель
считается адекватной, если ряд
остатков обладает свойствами, которым подчиняется случайная компонента:
1)
колебания уровней остаточной компоненты должны быть случайными;
2)
уровни ряда остатков должны быть независимыми, т.е. в
ряду должна отсутствовать автокорреляция;
3)
остаточная компонента должна подчиняться нормальному
закону распределения;
4)
математическое ожидание остаточной компоненты должно
быть равно нулю.
Выполнение
этих требований проверяется на основании определенных критериев: критерия
поворотных точек, критерия Дарбина-Уотсона, R/S критерия и t-критерия
Стьюдента соответственно.
Проверка
адекватности регрессионной модели может быть дополнена корреляционным анализом.
Для этого необходимо определить тесноту
корреляционной связи между переменными х и у. Теснота корреляционной связи, как
и любой другой, может быть измерена эмпирическим
корреляционным отношением ηэ (4):
Говоря
о корреляционном отношении как о показателе измерения тесноты зависимости,
следует отличать от эмпирического корреляционного отношения – теоретическое.
Теоретическое корреляционное отношение η
представляет собой относительную величину, получающуюся в результате сравнения
среднего квадратического отклонения выровненных значений результативного
признака δ, т.е. рассчитанных по
уравнению регрессии, со средним квадратическим отклонением эмпирических
(фактических) значений результативного признака σ:
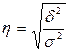 (8)
(8)
где
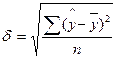 (9)
(9)
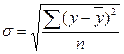 (10)
(10)
Тогда
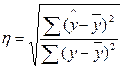 (11)
(11)
Формула теоретического корреляционного отношения может
иметь вид:
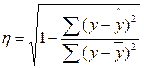 (12)
(12)
Подкоренное выражение
корреляционного отношения представляет собой коэффициент детерминации. Он показывает долю вариации
результативного признака под влиянием вариации факторного признака.
Теоретическое корреляционное
отношение применяется для измерения тесноты связи при линейной и криволинейной
зависимостях между результативным и факторным признаком. При криволинейных
связях теоретическое корреляционное отношение, исчисляемое по формуле (12),
часто называют индексом корреляции
R.
[1, с.196]
Корреляционное отношение может
находиться в пределах от 0 до 1. Чем ближе оно к 1, тем связь между признаками
теснее.
Кроме того, при линейной форме
уравнения применяется другой показатель тесноты связи – линейный коэффициент корреляции:
 (13)
(13)
где
n – число
наблюдений.
Значение
линейного коэффициента корреляции важно для исследования социально-экономических
явлений и процессов, распределение которых близко к нормальному. Он принимает
значения в интервале от –1 до +1. Отрицательные значения указывают на обратную
связь, положительные – на прямую. При r=0 линейная связь
отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к единице,
тем теснее связь между признаками. При r = ±1 связь –
функциональная.
Квадрат линейного коэффициента
корреляции r2 называется
линейным коэффициентом детерминации.
Его числовое значение заключено в пределах от 0 до 1. Степень тесноты связи
полностью соответствует теоретическому корреляционному отношению, которое
является более универсальным показателем тесноты связи по сравнению с линейным
коэффициентом корреляции.
Факт совпадений и несовпадений
значений теоретического корреляционного отношения η и линейного коэффициента корреляции r
используется для оценки формы связи. Значения η и r совпадают
только при наличии прямолинейной связи. Несовпадение этих значений
свидетельствует о том, что связь между изучаемыми признаками не прямолинейная,
а криволинейная. Установлено, что если разность квадратов η2 и r2
не превышает 0,1,
то гипотезу о прямолинейной форме связи можно считать подтвержденной. [1,
с.198]
Многофакторный
корреляционный и регрессионный анализ позволяет оценить меру
влияния на исследуемый результативный показатель каждого из включенных в модель
факторов при фиксированном положении (на среднем уровне) остальных факторов, а
также при любых возможных сочетаниях факторов с определенной степенью точности
найти теоретическое значение этого показателя (важным условием является
отсутствие между факторами функциональной связи).
1.4.5.
Непараметрические методы
Применение
корреляционного и регрессионного анализа требует, чтобы все признаки были
количественно измеренными. Построение аналитических группировок предполагает,
что количественным должен быть результативный признак. Параметрические методы
основаны на использовании основных количественных параметров распределения
(средних величин и дисперсий).
Вместе с тем в статистике
применяются также непараметрические методы,
с помощью которых устанавливается связь между качественными (атрибутивными)
признаками. Сфера их применения шире, чем параметрических, поскольку не
требуется соблюдения условия нормальности распределения зависимой переменной,
однако при этом снижается глубина исследования связей. При изучении зависимости
между качественными признаками не ставится задача представления ее уравнением.
Здесь речь идет только об установлении наличия связи и измерении ее тесноты.
В практике статистических
исследований приходится иногда анализировать связи между альтернативными
признаками, представленными только группами с противоположными (взаимоисключающими)
характеристиками. Тесноту связи в этом случае можно оценить, вычислив коэффициент ассоциации.
Для расчета коэффициента
ассоциации строится четырехклеточная корреляционная таблица, которая носит
название таблицы «четырех полей» и имеет следующий вид:
Таблица 1
|
a
|
b
|
a + b
|
|
c
|
d
|
c + d
|
|
a + c
|
b + d
|
a + b + c + d
|
Применительно к таблице
«четырех полей» с частотами a, b, c и d коэффициент ассоциации выражается формулой:
 (14)
(14)
Коэффициент ассоциации
изменяется от -1 до +1; чем ближе к +1 или -1, тем сильнее связаны между собой
изучаемые признаки.
Если ka не менее 0,3, то это свидетельствует
о наличии связи между качественными признаками.
Если по каждому из
взаимосвязанных признаков выделяется число групп более двух, то для подобного
рода таблиц теснота связи между качественными признаками может быть измерена с
помощью показателя взаимной сопряженности
А.А.Чупрова:
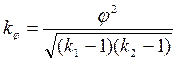 (15)
(15)
где k1 – число возможных значений первой
статистической величины (число групп по столбцам);
k2 - число возможных значений второй
статистической величины (число групп по строкам);
j2 - показатель взаимной сопряженности
(определяется как сумма отношений квадратов частот клетки таблицы распределения
к произведению итоговых частот соответствующего столбца и строки). Вычтя из
этой суммы единицу получим j2.
Коэффициент взаимной
сопряженности А.А.Чупрова изменяется от 0 до 1, но уже при значении 0,3 можно
говорить о тесной связи между вариацией изучаемых признаков.
2.
Расчетная часть
Имеются следующие выборочные
данные о деятельности российских банков (выборка 3%-ная механическая), млн.
руб.:
Механическая
выборка состоит в том, что отбор единиц в выборочную
совокупность из генеральной, разбитой по нейтральному признаку на равные
интервалы (группы), производится таким образом, что из каждой такой группы в
выборку отбирается лишь одна единица. Чтобы избежать систематической ошибки,
отбираться должна единица, которая находится в середине каждой группы.
При организации механического отбора единицы
совокупности предварительно располагают (обычно в списке) в определенном порядке
(например, по алфавиту, местоположению, в порядке возрастания или убывания
значений какого-либо показателя, не связанного с изучаемым свойством, и т.д.),
после чего отбирают заданное число единиц механически, через определенный
интервал. При этом размер интервала в генеральной совокупности равен обратному
значению доли выборки. Так, при 3%-ной выборке отбирается и проверяется каждая
33-я единица (1 : 0,03).
Таблица 1
|
№
банка п/п
|
Прибыль
|
Собственный
капитал
|
№
банка п/п
|
Прибыль
|
Собственный
капитал
|
|
1
|
62
|
1969
|
20
|
148
|
981
|
|
2
|
175
|
5207
|
21
|
165
|
3808
|
|
3
|
83
|
840
|
22
|
198
|
530
|
|
4
|
153
|
1828
|
23
|
163
|
895
|
|
5
|
118
|
589
|
24
|
240
|
2818
|
|
6
|
170
|
1369
|
25
|
224
|
3034
|
|
7
|
139
|
2080
|
26
|
165
|
1079
|
|
8
|
200
|
2400
|
27
|
213
|
2918
|
|
9
|
244
|
3681
|
28
|
64
|
985
|
|
10
|
268
|
5590
|
29
|
111
|
2020
|
|
11
|
342
|
6260
|
30
|
119
|
1576
|
|
12
|
329
|
2971
|
31
|
93
|
1152
|
|
13
|
289
|
6930
|
32
|
189
|
3810
|
|
14
|
66
|
1115
|
33
|
203
|
2400
|
|
15
|
121
|
1076
|
34
|
237
|
4077
|
|
16
|
129
|
1969
|
35
|
215
|
2338
|
|
17
|
166
|
4703
|
36
|
153
|
1517
|
|
18
|
67
|
440
|
37
|
306
|
2646
|
|
19
|
282
|
2960
|
Итого
|
6609
|
92561
|
Задание 1
По исходным данным таблицы
1:
1.
Постройте
статистический ряд распределения банков по признаку прибыль, образовав пять групп с равными интервалами.
2.
Постройте
графики полученного ряда распределения. Графически определите значения моды и
медианы.
3.
Рассчитайте
характеристики ряда распределения: среднюю арифметическую, среднее
квадратическое отклонение, коэффициент вариации.
4.
Вычислите
среднюю арифметическую по исходным данным, сравните ее с аналогичным
показателем, рассчитанным в п.3 для интервального ряда распределения. Объясните
причину их расхождения.
Сделайте выводы по
результатам выполнения задания.
Решение:
1. Построим
статистический ряд распределения банков по размеру прибыли, образовав пять
групп с равными интервалами.
Ширина интервала рассчитывается по формуле:
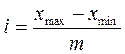
где xmax и xmin – наибольшее и наименьшее значения признака;
m – число
групп.
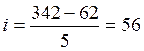 (млн. руб.)
(млн. руб.)
Отсюда путем прибавления величины интервала к
минимальному уровню признака в группе получим следующие группы банков по размеру
прибыли.
Таблица 2
Распределение
банков по размеру прибыли
|
№п/п
|
Группы
банков по размеру прибыли, млн. руб.
|
Число банков
|
|
единиц
|
%
|
|
|
|
f
|
d
|
|
1
|
62
- 118
|
8
|
21,6
|
|
2
|
118
- 174
|
12
|
32,4
|
|
3
|
174
- 230
|
8
|
21,6
|
|
4
|
230
- 286
|
5
|
13,5
|
|
5
|
286
- 342
|
4
|
10,8
|
|
|
ИТОГО
|
37
|
100,0
|
Таким образом, наиболее
типичными являются банки с размером прибыли от 118 до 174 млн. руб., доля таких
банков составляет 32,4%.
Доля банков с наименьшим
размером прибыли (от 62 до 118 млн. руб.) составляет 21,6%; а доля банков с
наибольшим размером прибыли (от 286 до 342 млн. руб.) составляет 10,8%.
2. Построим графики
полученного ряда распределения: гистограмму, полигон, кумуляту, и графически
определим значения моды и медианы.
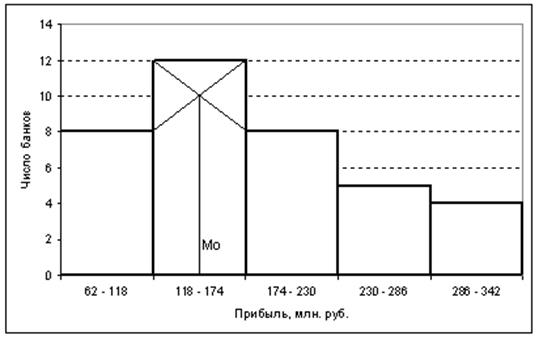
Рис.1. Гистограмма распределения банков по размеру прибыли
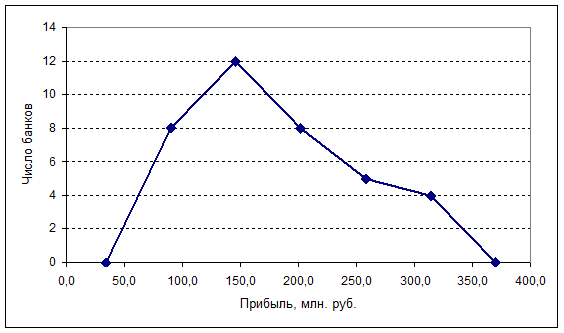
Рис.2. Полигон
распределения банков по размеру прибыли
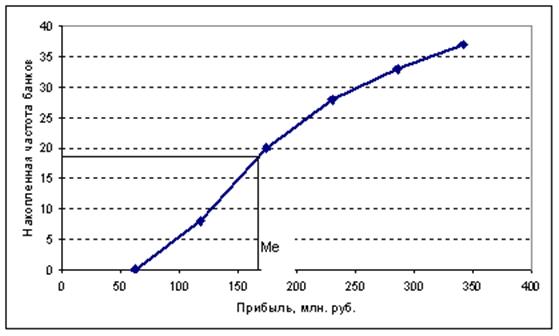
Рис.3. Кумулята распределения банков по размеру прибыли
3. Для расчета
характеристик ряда распределения составим расчетную таблицу:
Таблица 3
|
№п/п
|
Группы банков по размеру прибыли, млн. руб.
|
Число
банков
|
Расчетные графы
|
|
|
|
|
|
х (середина интервала)
|
f
|
Прибыль группы банков
xf
|
(x - 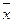 )2 f )2 f
|
|
1
|
62 - 118
|
90
|
8
|
720
|
63792
|
|
2
|
118 - 174
|
146
|
12
|
1752
|
13305
|
|
3
|
174 - 230
|
202
|
8
|
1616
|
4123
|
|
4
|
230 - 286
|
258
|
5
|
1290
|
30971
|
|
5
|
286 - 342
|
314
|
4
|
1256
|
72579
|
|
|
ИТОГО
|
-
|
37
|
6634
|
184770
|
Средний размер прибыли по всей совокупности банков
определим по формуле средней арифметической взвешенной (так как имеем интервальный
ряд распределения, то в качестве значений признака принимаем середины соответствующих
интервалов х).
Сумма прибыли всех банков
Средняя прибыль =
------------------------------------------
Количество банков
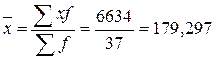 (млн. руб.)
(млн. руб.)
Дисперсия (или средний квадрат отклонений вариантов от
среднего значения):
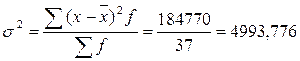
Среднее квадратическое отклонение:
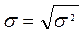
 (млн. руб.)
(млн. руб.)
Т.е. размер прибыли отдельных банков в среднем
отличается от среднего размера прибыли по совокупности банков на 70,667 млн.
руб.
Коэффициент вариации:
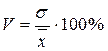
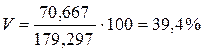
Так как V < 40%, то совокупность банков по данному признаку (размер
прибыли) однородная, вариация значений относительно их среднего значения не
сильная, следовательно, среднее значение надежно и его можно использовать для
оценки совокупности.
4. Вычислим средний
размер прибыли по исходным данным, т.е. по формуле средней арифметической
простой, т.к. имеем несгруппированные индивидуальные значения признака:
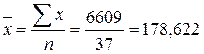 (млн. руб.)
(млн. руб.)
Данная средняя,
вычисленная по формуле средней арифметической простой, несколько отличается от
средней, вычисленной в п.3. по формуле средней арифметической взвешенной, т.к.
в п.3 заменяли интервальные значения их средними значениями, а при таком исчислении
средней допускается некоторая неточность, поскольку делается предположение о
равномерном распределении единиц признака внутри группы.
Мо ≈ 146 (млн.
руб.)
Т.е. наиболее часто
встречаются банки с прибылью в размере 146 млн. руб.
Ме ≈ 167 (млн.
руб.)
Т.е. половина всех банков
с прибылью менее 167 млн. руб., а другая половина – более 167 млн. руб.
хсред =
179,297 (млн. руб.)
Так как Мо < Ме
< хсред, то имеем правостороннюю асимметрию распределения банков
по размеру прибыли (т.е. вершина кривой распределения сдвинута от центра
влево).
Задание 2
По исходным данным:
Установите наличие и
характер связи между признаками прибыль и величина собственного
капитала, образовав пять групп с
равными интервалами по обоим признакам, методами:
а) аналитической группировки;
б) корреляционной таблицы.
Решение:
1. а) Чтобы установить
наличие и характер связи между прибылью и величиной собственного капитала
методом аналитической группировки, построим группировку по факторному признаку
(величина собственного капитала), образовав пять групп с равными интервалами.
Предварительно определим ширину интервала признака –
собственный капитал:
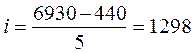 (млн. руб.)
(млн. руб.)
Сначала для того, чтобы
составить рабочую таблицу, в которой в каждой строчке будут данные отдельно по
каждому банку и итоговые данные по выделенным группам, а затем для составления
итоговой аналитической таблицы, в которой будут сведения только по группам в
целом, следует использовать макет.
Макет – это таблица,
состоящая из строк и граф, которые еще не заполнены цифрами.
Таблица 4
|
№ п/п
|
Группы
банков по размеру собственного капитала,
млн.
руб.
|
Число
банков
|
Собственный
капитал, млн. руб.
|
Прибыль,
млн. руб.
|
|
всего
|
в среднем на 1 банк
|
всего
|
в среднем на 1 банк
|
|
1
2
…
|
|
|
|
|
|
|
|
|
ИТОГО
|
|
|
|
|
|
Строим рабочую таблицу:
Таблица 5
|
№ п/п
|
Группы банков по размеру
собственного капитала, млн. руб.
|
№
банка
|
Собственный капитал, млн.
руб.
|
Прибыль, млн. руб.
|
Расчетная
графа
|
|
|
|
|
xi
|
yi
|
(yi
- 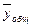 .)2 .)2
|
|
1
|
440 - 1738
|
3
|
840
|
83
|
6724,0
|
|
|
|
5
|
589
|
118
|
2209,0
|
|
|
|
6
|
1368
|
170
|
25,0
|
|
|
|
14
|
1115
|
66
|
9801,0
|
|
|
|
15
|
1076
|
121
|
1936,0
|
|
|
|
18
|
440
|
67
|
9604,0
|
|
|
|
20
|
981
|
148
|
289,0
|
|
|
|
22
|
530
|
198
|
1089,0
|
|
|
|
23
|
895
|
163
|
4,0
|
|
|
|
26
|
1079
|
165
|
0,0
|
|
|
|
28
|
985
|
64
|
10201,0
|
|
|
|
30
|
1576
|
119
|
2116,0
|
|
|
|
31
|
1152
|
93
|
5184,0
|
|
|
|
36
|
1517
|
153
|
144,0
|
|
|
ИТОГО
|
14
|
14143
|
1728
|
|
|
2
|
1738 - 3036
|
1
|
1969
|
62
|
13600,6
|
|
|
|
4
|
1828
|
153
|
656,5
|
|
|
|
7
|
2080
|
139
|
1569,9
|
|
|
|
8
|
2400
|
200
|
457,0
|
|
|
|
12
|
2971
|
329
|
22613,7
|
|
|
|
16
|
1969
|
129
|
2462,3
|
|
|
|
19
|
2960
|
282
|
10687,1
|
|
|
|
24
|
2818
|
240
|
3767,3
|
|
|
|
25
|
3034
|
224
|
2059,2
|
|
|
|
27
|
2918
|
213
|
1181,9
|
|
|
|
29
|
2020
|
111
|
4572,7
|
|
|
|
33
|
2400
|
203
|
594,3
|
|
|
|
35
|
2338
|
215
|
1323,4
|
|
|
|
37
|
2646
|
306
|
16225,3
|
|
|
ИТОГО
|
14
|
34351
|
2806
|
|
|
3
|
3036 - 4334
|
9
|
3681
|
244
|
4274,3
|
|
|
|
21
|
3808
|
165
|
185,5
|
|
|
|
32
|
3810
|
189
|
107,7
|
|
|
|
34
|
4077
|
237
|
3408,0
|
|
|
ИТОГО
|
4
|
15376
|
835
|
|
|
4
|
4334 - 5632
|
2
|
5207
|
175
|
13,1
|
|
|
|
10
|
5590
|
268
|
7988,5
|
|
|
|
17
|
4703
|
166
|
159,3
|
|
|
ИТОГО
|
3
|
15500
|
609
|
|
|
5
|
5632 - 6930
|
11
|
6260
|
342
|
26692,5
|
|
|
|
13
|
6930
|
289
|
12183,4
|
|
|
ИТОГО
|
2
|
13190
|
631
|
|
|
|
ВСЕГО
|
37
|
92560
|
6609
|
204562,7
|
Для установления наличия и характера связи между прибылью
и собственным капиталом по данным рабочей таблицы строим итоговую аналитическую
таблицу:
Таблица 6
|
№ п/п
|
Группы
банков по размеру собственного капитала,
млн.
руб.
|
Число
банков
|
Собственный
капитал, млн. руб.
|
Прибыль,
млн. руб.
|
|
всего
|
в среднем на 1 банк
|
всего
|
в среднем на 1 банк
|
|
|
|
nj
|
xj
|
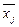
|
yj
|
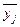
|
|
1
|
440
- 1738
|
14
|
14143
|
1010,2
|
1728
|
123,4
|
|
2
|
1738
- 3036
|
14
|
34351
|
2453,6
|
2806
|
200,4
|
|
3
|
3036
- 4334
|
4
|
15376
|
3844,0
|
835
|
208,8
|
|
4
|
4334
- 5632
|
3
|
15500
|
5166,7
|
609
|
203,0
|
|
5
|
5632
- 6930
|
2
|
13190
|
6595,0
|
631
|
315,5
|
|
|
ИТОГО
|
37
|
92560
|
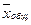 = 2501,6 = 2501,6
|
6609
|
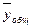 = 178,6 = 178,6
|
Вычисляем в каждой группе среднее значение факторного
признака 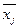 и среднее значение результативного
признака
и среднее значение результативного
признака 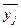 по формулам:
по формулам:
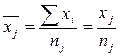
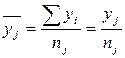
где nj – число единиц в j-той
группе.
Sxi = xj и Sуi = yj - это соответственно
прибыль и собственный капитал в j-той группе.
Вычислим общее среднее значение каждого признака в
совокупности:
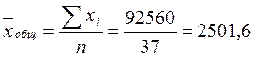 (млн. руб.)
(млн. руб.)
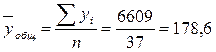 (млн. руб.)
(млн. руб.)
Общее среднее значение
каждого признака в совокупности можно вычислить и другим способом, как среднее
арифметическое взвешенное из средних групповых 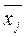 и
и  (весом является численность единиц в каждой
группе nj):
(весом является численность единиц в каждой
группе nj):
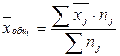
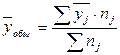
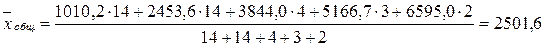 (млн.руб.)
(млн.руб.)
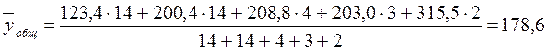 (млн.руб.)
(млн.руб.)
Сравниваем изменения 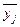 от группы к группе с изменениями
от группы к группе с изменениями 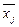 от группы к группе. Среднее значение
результативного признака систематически изменяется вслед за средним значением
факторного признака, следовательно, делаем вывод о том, что связь между ними
существует. Причем с ростом размера собственного капитала средний размер
прибыли также увеличиваются. Следовательно, между исследуемыми признаками
существует прямая корреляционная зависимость.
от группы к группе. Среднее значение
результативного признака систематически изменяется вслед за средним значением
факторного признака, следовательно, делаем вывод о том, что связь между ними
существует. Причем с ростом размера собственного капитала средний размер
прибыли также увеличиваются. Следовательно, между исследуемыми признаками
существует прямая корреляционная зависимость.
Измерим тесноту связи между исследуемыми признаками с
использованием эмпирического корреляционного отношения:

где 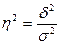 –
коэффициент детерминации;
–
коэффициент детерминации;
δ2
– межгрупповая дисперсия;
σ2 –
общая дисперсия.
Межгрупповая
дисперсия характеризует вариацию между группами. Ее рассчитываем по формуле:
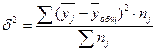
где 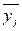 – среднее значение
результативного признака в j-группе;
– среднее значение
результативного признака в j-группе;
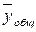 – общее среднее
значение результативного признака в совокупности;
– общее среднее
значение результативного признака в совокупности;
nj – число единиц в j-группе;
j –
счетчик групп.
Составим расчетную таблицу:
Таблица 7
|
№ п/п
|
Группы банков по размеру собственного капитала,
млн. руб.
|
Число
банков
|
Прибыль в среднем на 1 банк, млн. руб.
|
Расчетная графа
|
|
|
|
nj
|
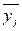
|
(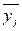 - - 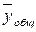 )2 nj )2 nj
|
|
1
|
440 - 1738
|
14
|
123,4
|
42647,819
|
|
2
|
1738 - 3036
|
14
|
200,4
|
6657,603
|
|
3
|
3036 - 4334
|
4
|
208,8
|
3630,877
|
|
4
|
4334 - 5632
|
3
|
203,0
|
1782,916
|
|
5
|
5632 - 6930
|
2
|
315,5
|
37471,381
|
|
|
ИТОГО
|
37
|
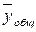 = 178,6 = 178,6
|
92190,596
|
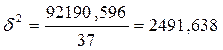 .
.
Нашли дисперсию, характеризующую вариацию прибыли,
возникающую под влиянием размера собственного капитала.
Общая дисперсия характеризует вариацию отдельных
значений признака относительно общей средней. Ее определяем по формуле:
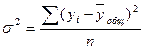
Расчет 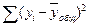 представлен в последней графе таблицы №5.
представлен в последней графе таблицы №5.
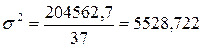
Нашли дисперсию, характеризующую вариацию прибыли,
возникающую под влиянием всех причин, действующих на совокупность.
Коэффициент детерминации равен:

Т.е. 45,1% вариации прибыли вызывает вариация размера
собственного капитала.
Эмпирическое корреляционное отношение составляет:
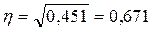
Т.к. 0,5 < η < 0,7, то связь между размером
собственного капитала и прибылью умеренно тесная т.е. размер собственного
капитала не сильно влияет на размер прибыли.
Значимость коэффициента
детерминации можно проверить по критерию Фишера:
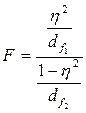
где df1 = k – 1 – степень свободы 1;
k - число групп;
df2 = n – k - степень свободы 2;
n – число
единиц совокупности.
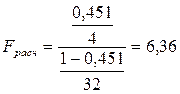
Fтабл. (0,05; 4; 32) = 2,69
Fрасч. > Fтабл. Þ связь между исследуемыми признаками
статистически значимая и коэффициент детерминации достоверен.
б) Установим наличие и характер связи между размером собственного
капитала и прибылью методом корреляционной таблицы.
Составим корреляционную таблицу, образовав пять групп
с равными интервалами по обоим признакам.
Таблица 8
|
Прибыль,
млн. руб.
Собственный капитал, млн. руб.
|
62 - 118
|
118 - 174
|
174 - 230
|
230 - 286
|
286 - 342
|
Итого
|
|
440
- 1738
|
6
|
7
|
1
|
|
|
14
|
|
1738
- 3036
|
2
|
3
|
5
|
2
|
2
|
14
|
|
3036
- 4334
|
|
1
|
1
|
2
|
|
4
|
|
4334
- 5632
|
|
1
|
1
|
1
|
|
3
|
|
5632
- 6930
|
|
|
|
|
2
|
2
|
|
Итого
|
8
|
12
|
8
|
5
|
4
|
37
|
Анализ корреляционной
таблицы также свидетельствует о том, что между собственным капиталом и прибылью
существует прямая, не очень тесная корреляционная зависимость.
Задание 3
По результатам выполнения
задания 1 с вероятностью 0,683 определите:
1.
Ошибку
выборки средней прибыли и границы, в которых будет находиться средний размер прибыли
в генеральной совокупности.
2.
Ошибку
выборки доли банков с прибылью 153 млн. руб. и более и границы, в которых будет
находиться генеральная доля.
Решение:
1. Так как дана 3%-ная,
механическая выборка, то ошибку выборки средней прибыли m
определим по формуле:
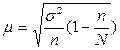
n = 37
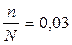
σ2
= 4993,776
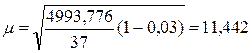 (млн. руб.)
(млн. руб.)
Границы, в которых будет
находиться средний размер прибыли в генеральной совокупности, определяются
следующим образом:
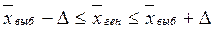
где 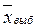 – средний размер прибыли в выборке;
– средний размер прибыли в выборке;
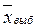 = 179,297 (млн. руб.)
= 179,297 (млн. руб.)
D - предельная ошибка выборки.
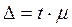
где t – коэффициент
доверия. Для доверительной вероятности 0,683 он равен: t = 1.
D = 1 * 11,442 = 11,442 (млн. руб.)
179,297 – 11,442 £ 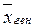 £ 179,297
+ 11,442
£ 179,297
+ 11,442
167,855 £ 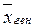 £ 190,739
£ 190,739
Т.е. с вероятностью 0,683
можно ожидать, средний размер прибыли в генеральной совокупности находится в
пределах от 167,855 до 190,739 млн. руб.
2. Доля банков с прибылью
153 млн. руб. и более составляет:
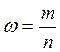
где m – количество банков с прибылью 153 млн. руб. и более.
m = 24
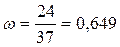 или 64,9%
или 64,9%
Т.е. доля банков с
прибыль. 153 млн. руб. и более составляет 64,9% от общего числа банков выборки.
Ошибку выборки доли
банков с прибылью 153 млн. руб. и более определим по той же формуле:
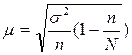
где дисперсия σ2 равна:
σ2
= w * (1 - w) = 0,649 * (1 – 0,649) = 0,228
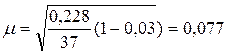
Предельная ошибка выборки
составляет:
D = t * m = 1 * 0,077 = 0,077
Границы, в которых будет
находиться генеральная доля р, равны:
w - D £ р £ w + D
0,649
– 0,077 £ р £ 0,649 + 0,077
0,572
£ р £ 0,726
Т.е. с вероятностью 0,683
можно ожидать, что доля банков с прибылью 153 млн. руб. и более в генеральной
совокупности будет составлять от 57,2% до 72,6%.
Задание 4
Имеются данные по
коммерческому банку, млрд. руб.:
Таблица 9
|
Показатели
|
Период
|
|
базисный
|
отчетный
|
|
Капитал банка
|
610
|
720
|
|
Активы банка – всего
|
4270
|
5148
|
|
в том числе
работающие активы
|
3030
|
3700
|
|
Доходы – всего
|
595
|
698
|
|
в том числе
процентные доходы
|
476
|
572
|
|
Расходы – всего
|
482
|
550
|
|
в том числе
процентные расходы
|
380
|
455
|
|
Платежи в бюджет из
прибыли
|
35
|
44
|
Определите:
1.
Показатели
прибыли и рентабельности коммерческого банка за каждый период;
2.
Изменение
балансовой прибыли в результате изменения капитала, эффективности использования
активов, мультипликатора капитала и доли маржи прибыли.
Решение:
1. Определим показатели
прибыли и рентабельности.
Балансовая прибыль определяется как разница между
доходами (Д) (без налога на
добавленную стоимость) и расходами банка (Р):
ПБ 0 = Д
– Р = 595 – 482 = 113 (млн. руб.)
ПБ 1 = 698 – 550 = 148 (млн. руб.)
Процентная маржа (прибыль) – разница между процентными доходами (ДП) и процентными расходами (РП):
М0 = ДП – РП = 476 – 380 = 96 (млн. руб.)
М1 = 572 –
455 = 117 (млн. руб.)
Чистая прибыль определяется как разница балансовой прибыли и платежей в
бюджет из прибыли (ПБ):
ЧП0 = ПБ – ПБ = 113 – 35 = 78 (млн. руб.)
ЧП1 = 148 – 44
= 104 (млн. руб.)
Рентабельность капитала:

где К – капитал.
RК 0 = 113 / 610 * 100 = 18,5%
RК 1 = 148 / 720 * 100 = 20,6%
Рентабельность активов:
а) по балансовой прибыли:
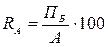
где А – активы банка.
RА 0 = 113 / 4270 * 100 = 2,65%
RА 1 = 148 / 5148 * 100 = 2,87%
б) по чистой прибыли:
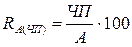
RА(ЧП) 0 = 78 / 4270 * 100 = 1,83%
RА(ЧП) 1 = 104 / 5148 * 100 = 2,02%
в) по процентной марже:
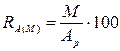
где АР – работающие активы.
RА(М) 0 = 96 / 3030 * 100 = 3,17%
RА(М) 1 = 117 / 3700 * 100 = 3,16%
Результаты расчетов
представим в таблице:
Таблица 10
Показатели прибыли
и рентабельности коммерческого банка
|
Показатели
|
Базисный период
|
Отчетный период
|
Абсолютное изменение
|
Темп роста, %
|
|
1. Балансовая прибыль, млн. руб.
|
113
|
148
|
35
|
131,0
|
|
2. Чистая прибыль, млн. руб.
|
78
|
104
|
26
|
133,3
|
|
3. Процентная прибыль (маржа), млн. руб.
|
96
|
117
|
21
|
121,9
|
|
4. Рентабельность капитала
|
18,5
|
20,6
|
2,1
|
111,4
|
|
5. Рентабельность активов, %:
|
|
|
|
|
|
А) по балансовой прибыли
|
2,65
|
2,87
|
0,22
|
108,3
|
|
Б) по чистой прибыли
|
1,83
|
2,02
|
0,19
|
110,4
|
|
В) по процентной прибыли
|
3,17
|
3,16
|
-0,01
|
99,7
|
Данные таблицы
свидетельствуют о том, что балансовая прибыль по банку в отчетном периоде
составила 148 млн. руб. и выросла по сравнению с предыдущим периодом на 35 млн.
руб. или на 31,0%.
Следует отметить более
высокие темпы роста чистой прибыли (133,3%) по сравнению с балансовой и
процентной прибылью. Рост прибыли позволил улучшить все показатели
рентабельности. Рентабельность капитала составила 20,6% и возросла на 2,1
процентных пункта.
Наблюдается также и рост
рентабельности активов. Наибольший рост составила рентабельность по балансовой
прибыли (0,22%).
2. Факторный анализ
балансовой прибыли можно произвести на основании следующей формулы:
П = К * КМК * КDА * dП,
где К – капитал;
КDА - коэффициент доходности активов 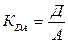 ;
;
КМК
- мультипликатор
капитала 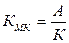 ;
;
dП – доля балансовой прибыли в доходах банка 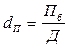 .
.
Определим доходность
активов:
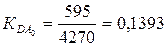 или 13,93%
или 13,93%
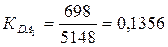 или 13,56%
или 13,56%
Рассчитаем мультипликатор
капитала:
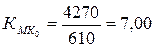
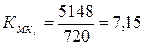
И рассчитаем долю
балансовой прибыли в доходах банка:
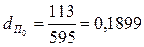 или 18,99%
или 18,99%
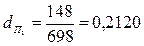 или 21,20%
или 21,20%
Определим влияние
отдельных факторов на прирост суммы балансовой прибыли:
а) влияние изменения
собственного капитала:
ΔП(К)
= (К1 – К0) * КМК 1 * КDА 1 * dП 1
ΔП(К)
= (720 – 610) * 7,15 * 0,1356 * 0,2120 = 22,609 (млн. руб.)
б) влияние изменения
мультипликатора капитала:
ΔП(КМК)
= (КМК 1 – КМК
0)
* К0 * КDА 1 * dП 1
ΔП(КМК)
= (7,15 – 7,00) * 610 * 0,1356 * 0,2120 = 2,630 (млн. руб.)
в) влияние изменения
эффективности использования активов:
ΔП(КDА) = (КDА 1 – КDА 0)
* К0 * КМК 0 * dП 1
ΔП(КDА) = (0,1356 – 0,1393) * 610 * 7,00 * 0,2120 = -3,349 (млн. руб.)
г) влияние изменения доли
маржи на прибыль:
ΔП(dП) = (dП 1 – dП 0) * К0
* КМК 0* КDА 0
ΔП(dП) = (0,2120 – 0,1899) * 610 * 7,00 *
0,1393 = 13,145 (млн. руб.)
ΔП = 22,609 + 2,630 – 3,349 + 13,145 = 35,035
(млн. руб.)
Прирост балансовой
прибыли на 35,035 млн. руб. в наибольшей мере был обеспечен увеличением
капитала банка и снижением расходов, что повысило долю балансовой прибыли в
доходах. Это позволило увеличить прибыль соответственно на 22,609 и 13,145 млн.
руб. Рост мультипликатора капитала дал прирост прибыли на 2,630 млн. руб.
Отрицательно на динамику балансовой прибыли повлияло снижение эффективности
использования активов, что привело к ее уменьшению на 3,349 млн. руб.
3.
Аналитическая часть
1. Постановка задачи
Одним из направлений в
изучении взаимосвязей финансовых показателей деятельности банков является
выявления зависимости прибыли банков от размера чистых активов.
Имеются данные о величине
чистых активов и о размере прибыли 40 банков России (источник: www.banki.ru).
Таблица 1
|
Банк
|
Чистые активы, тыс. руб.
|
Прибыль / убыток,
тыс. руб.
|
|
Внешторгбанк РФ
|
59541726
|
177525
|
|
Газпромбанк
|
48871735
|
376641
|
|
Альфабанк
|
33846875
|
150975
|
|
Банк Москвы
|
24780922
|
160925
|
|
Российский кредит
|
24088888
|
549728
|
|
Росбанк
|
14607308
|
257913
|
|
Промышленно-строительный
|
13407157
|
186284
|
|
Сургутнефтегазбанк
|
12828991
|
55281
|
|
Автобанк
|
10652330
|
227757
|
|
Гута-банк
|
9279083
|
63232
|
|
Конверсбанк
|
8731714
|
32220
|
|
Возрождение
|
7590406
|
21957
|
|
Менатеп Санкт-Петербург
|
5876419
|
310773
|
|
Московский
индустриальный
|
4078533
|
27295
|
|
Банк «Зенит»
|
3779614
|
68293
|
|
Бин
|
2543430
|
60278
|
|
Нефтехимик
|
2337640
|
227456
|
|
Банк «Санкт-Петербург»
|
2198039
|
6143
|
|
Пробизнесбанк
|
2192018
|
24312
|
|
Промрадтехбанк
|
2166721
|
70082
|
|
Солидарность
|
1901500
|
25600
|
|
Глобэкс
|
1826613
|
13894
|
|
Авангард
|
1609061
|
7638
|
|
Югбанк
|
1477522
|
26456
|
|
Тольяттихимбанк
|
1381563
|
148244
|
|
Инфобанк
|
1357308
|
44217
|
|
Московский кредитный
|
1345012
|
9964
|
|
Газбанк
|
1327380
|
45502
|
|
Комнейвабанк
|
1320645
|
25202
|
|
Росэксимбанк
|
1266026
|
5045
|
|
Русский банк
имущественной опеки
|
1249646
|
20729
|
|
Евротраст
|
1242604
|
18493
|
|
Далькомбанк
|
1221682
|
44798
|
|
Кредитимпекс
|
1199046
|
9446
|
|
Желдорбанк
|
1169676
|
56357
|
|
Флора-Москва
|
1135085
|
9156
|
|
Олимпийский
|
1097024
|
2570
|
|
Интерпромбанк
|
1076024
|
51145
|
|
Дальневосточный
|
1061285
|
13521
|
|
Инкасбанк
|
972306
|
12245
|
Проанализируем наличие,
направление и характер взаимосвязи между величиной чистых активов банков и размером
прибыли (убытка) методом корреляционно-регрессионного анализа. Для чего сделаем
следующее:
- установим наличие статистической
связи между величиной чистых активов банков (х) и размером прибыли (у)
графическим методом;
- установим наличие корреляционной
связи между признаками методом аналитической группировки;
- оценим тесноту связи
признаков на основе:
а)
эмпирического корреляционного отношения η;
б)
линейного коэффициента корреляции r.
- построим однофакторную
линейную регрессионную модель связи признаков Х и Y;
- оценим адекватность и
практическую пригодность построенной линейной регрессионной модели;
- дадим экономическую
интерпретацию.
2. Методика решения задачи
Факторным является
признак – чистые активы, результативным – прибыль (убыток) банка, потому что
именно размер чистых активов влияет на величину прибыли банков, а не наоборот.
Аналитическую группировку строим с равнонаполненными
группами, используя пять интервалов группировки.
Расчет показателей осуществим по формулам:
Общее
среднее значение размера прибыли (на один банк):
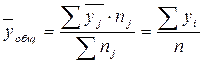
где 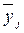 – среднее значение прибыли в j-группе;
– среднее значение прибыли в j-группе;
nj – число банков
в j-группе.
Внутригрупповые
дисперсии:
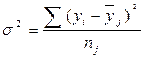
где yj – индивидуальные значения признака,
находящиеся в определенной группе;
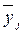 – среднее
значение результативного признака в j-группе;
– среднее
значение результативного признака в j-группе;
nj – число
единиц в j-группе;
Средняя из внутригрупповых дисперсий:
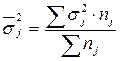
где σj2 – внутригрупповые дисперсии.
Общая дисперсия:
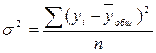
где yобщ.сред – общее среднее значение
результативного признака в совокупности.
Межгрупповая
дисперсия:
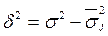
Коэффициент детерминации:
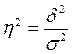
Эмпирическое корреляционное
отношение:
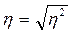
Линейный коэффициент корреляции:
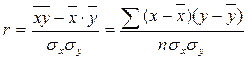
3. Технология выполнения
компьютерных расчетов
Все расчеты проводим с помощью пакета прикладных
программ Microsoft Excel
(приложения 2, 3).
Графики получаем с помощью функции Мастер диаграмм; величину
линейного коэффициента корреляции – используя инструмент Корреляция надстройки Пакет анализа; однофакторную линейную
регрессионную модель - используя инструмент Регрессия надстройки Пакет
анализа в меню Сервис.
Результаты расчетов приведены в таблицах 2-7.
На рис.1 представлено графическое изображение
зависимости прибыли банков от величины чистых активов и модель линейной
регрессии.
Таблица 2
Расположение
банков по возрастанию величины чистых активов
|
Банк
|
Чистые активы, тыс.
руб.
|
Прибыль, тыс. руб.
|
Предсказанное Y
|
|
Инкасбанк
|
972306
|
12245
|
53109,472
|
|
Дальневосточный
|
1061285
|
13521
|
53591,509
|
|
Интерпромбанк
|
1076024
|
51145
|
53671,357
|
|
Олимпийский
|
1097024
|
2570
|
53785,123
|
|
Флора-Москва
|
1135085
|
9156
|
53991,316
|
|
Желдорбанк
|
1169676
|
56357
|
54178,710
|
|
Кредитимпекс
|
1199046
|
9446
|
54337,820
|
|
Далькомбанк
|
1221682
|
44798
|
54460,449
|
|
Евротраст
|
1242604
|
18493
|
54573,793
|
|
Русский банк имущественной опеки
|
1249646
|
20729
|
54611,942
|
|
Росэксимбанк
|
1266026
|
5045
|
54700,680
|
|
Комнейвабанк
|
1320645
|
25202
|
54996,575
|
|
Газбанк
|
1327380
|
45502
|
55033,061
|
|
Московский кредитный
|
1345012
|
9964
|
55128,581
|
|
Инфобанк
|
1357308
|
44217
|
55195,194
|
|
Тольяттихимбанк
|
1381563
|
148244
|
55326,594
|
|
Югбанк
|
1477522
|
26456
|
55846,445
|
|
Авангард
|
1609061
|
7638
|
56559,048
|
|
Глобэкс
|
1826613
|
13894
|
57737,622
|
|
Солидарность
|
1901500
|
25600
|
58143,317
|
|
Промрадтехбанк
|
2166721
|
70082
|
59580,133
|
|
Пробизнесбанк
|
2192018
|
24312
|
59717,178
|
|
Банк «Санкт-Петербург»
|
2198039
|
6143
|
59749,796
|
|
Нефтехимик
|
2337640
|
227456
|
60506,075
|
|
Бин
|
2543430
|
60278
|
61620,929
|
|
Банк «Зенит»
|
3779614
|
68293
|
68317,871
|
|
Московский индустриальный
|
4078533
|
27295
|
69937,244
|
|
Менатеп Санкт-Петербург
|
5876419
|
310773
|
79677,168
|
|
Возрождение
|
7590406
|
21957
|
88962,576
|
|
Конверсбанк
|
8731714
|
32220
|
95145,534
|
|
Гута-банк
|
9279083
|
63232
|
98110,868
|
|
Автобанк
|
10652330
|
227757
|
105550,339
|
|
Сургутнефтегазбанк
|
12828991
|
55281
|
117342,251
|
|
Промышленно-строительный
|
13407157
|
186284
|
120474,426
|
|
Росбанк
|
14607308
|
257913
|
126976,162
|
|
Российский кредит
|
24088888
|
549728
|
178341,973
|
|
Банк Москвы
|
24780922
|
160925
|
182091,020
|
|
Альфабанк
|
33846875
|
150975
|
231205,200
|
|
Газпромбанк
|
48871735
|
376641
|
312601,351
|
|
Внешторгбанк РФ
|
59541726
|
177525
|
370405,297
|
Таблица 3
Зависимость
прибыли банков от размера чистых активов (аналитическая группировка)
|
Номер
группы
|
Группы банков по размеру чистых активов, тыс. руб.
|
Число
банков, ед.
|
Прибыль, тыс. руб.
|
|
Всего
|
В среднем на один банк
|
|
1
|
970000 - 1230000
|
8
|
199238,00
|
24904,750
|
|
2
|
1230000 - 1400000
|
8
|
317396,00
|
39674,500
|
|
3
|
1400000 - 2500000
|
8
|
401581,00
|
50197,625
|
|
4
|
2500000 - 11000000
|
8
|
811805,00
|
101475,625
|
|
5
|
11000000 - 60000000
|
8
|
1915272,00
|
239409,000
|
|
ИТОГО
|
|
40
|
3645292
|
91132,300
|
Таблица 4
Расчет
внутригрупповых дисперсий
|
Номер группы
|
Группы банков по размеру чистых активов, тыс. руб.
|
Число предприятий, ед.
|
Внутригрупповая дисперсия прибыли
|
|
|
|
1
|
970000 - 1230000
|
8
|
343966512,688
|
|
|
2
|
1230000 - 1400000
|
8
|
375082010,800
|
|
|
3
|
1400000 - 2500000
|
8
|
1471317400,331
|
|
|
4
|
2500000 - 11000000
|
8
|
23762478434,204
|
|
|
5
|
11000000 - 60000000
|
8
|
10141914168,000
|
|
|
ИТОГО
|
|
40
|
288758068208,177
|
|
Таблица 5
Дисперсии
и эмпирические показатели тесноты взаимосвязи
|
Общая
дисперсия
|
Средняя из
внутригрупповых
дисперсий
|
Межгрупповая
дисперсия
|
Эмпирический
коэффициент
детерминации
|
Эмпирическое
корреляционное
отношение
|
|
|
|
13851989235,310
|
7218951705,204
|
6633037530,106
|
0,479
|
0,692
|
|
Таблица 6
Линейный
коэффициент корреляции признаков
|
|
Столбец 1
|
Столбец 2
|
|
Столбец 1
|
1
|
|
|
Столбец 2
|
0,597
|
1
|
Таблица 7
Регрессионный
анализ
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
|
|
Множественный
R
|
0,597
|
|
|
|
|
|
|
|
|
R-квадрат
|
0,357
|
|
|
|
|
|
|
|
|
Нормированный
R-квадрат
|
0,340
|
|
|
|
|
|
|
|
|
Стандартная
ошибка
|
96835,991
|
|
|
|
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
|
|
|
Регрессия
|
1
|
197745624295,886
|
197745624295,886
|
21,088
|
0,000
|
|
|
|
|
Остаток
|
38
|
356333945116,514
|
9377209082,014
|
|
|
|
|
|
|
Итого
|
39
|
554079569412,400
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 68,3%
|
Верхние 68,3%
|
|
Y-пересечение
|
47842,071
|
17980,502
|
2,661
|
0,011
|
11442,446
|
84241,695
|
29610,002
|
66074,139
|
|
Переменная
X 1
|
0,005
|
0,001
|
4,592
|
0,000
|
0,003
|
0,008
|
0,004
|
0,007
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД
ОСТАТКА
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
|
|
|
|
|
|
1
|
53109,472
|
-40864,472
|
|
|
|
|
|
|
|
2
|
53591,509
|
-40070,509
|
|
|
|
|
|
|
|
3
|
53671,357
|
-2526,357
|
|
|
|
|
|
|
|
4
|
53785,123
|
-51215,123
|
|
|
|
|
|
|
|
5
|
53991,316
|
-44835,316
|
|
|
|
|
|
|
|
6
|
54178,710
|
2178,290
|
|
|
|
|
|
|
|
7
|
54337,820
|
-44891,820
|
|
|
|
|
|
|
|
8
|
54460,449
|
-9662,449
|
|
|
|
|
|
|
|
9
|
54573,793
|
-36080,793
|
|
|
|
|
|
|
|
10
|
54611,942
|
-33882,942
|
|
|
|
|
|
|
|
11
|
54700,680
|
-49655,680
|
|
|
|
|
|
|
|
12
|
54996,575
|
-29794,575
|
|
|
|
|
|
|
|
13
|
55033,061
|
-9531,061
|
|
|
|
|
|
|
|
14
|
55128,581
|
-45164,581
|
|
|
|
|
|
|
|
15
|
55195,194
|
-10978,194
|
|
|
|
|
|
|
|
16
|
55326,594
|
92917,406
|
|
|
|
|
|
|
|
17
|
55846,445
|
-29390,445
|
|
|
|
|
|
|
|
18
|
56559,048
|
-48921,048
|
|
|
|
|
|
|
|
19
|
57737,622
|
-43843,622
|
|
|
|
|
|
|
|
20
|
58143,317
|
-32543,317
|
|
|
|
|
|
|
|
21
|
59580,133
|
10501,867
|
|
|
|
|
|
|
|
22
|
59717,178
|
-35405,178
|
|
|
|
|
|
|
|
23
|
59749,796
|
-53606,796
|
|
|
|
|
|
|
|
24
|
60506,075
|
166949,925
|
|
|
|
|
|
|
|
25
|
61620,929
|
-1342,929
|
|
|
|
|
|
|
|
26
|
68317,871
|
-24,871
|
|
|
|
|
|
|
|
27
|
69937,244
|
-42642,244
|
|
|
|
|
|
|
|
28
|
79677,168
|
231095,832
|
|
|
|
|
|
|
|
29
|
88962,576
|
-67005,576
|
|
|
|
|
|
|
|
30
|
95145,534
|
-62925,534
|
|
|
|
|
|
|
|
31
|
98110,868
|
-34878,868
|
|
|
|
|
|
|
|
32
|
105550,339
|
122206,661
|
|
|
|
|
|
|
|
33
|
117342,251
|
-62061,251
|
|
|
|
|
|
|
|
34
|
120474,426
|
65809,574
|
|
|
|
|
|
|
|
35
|
126976,162
|
130936,838
|
|
|
|
|
|
|
|
36
|
178341,973
|
371386,027
|
|
|
|
|
|
|
|
37
|
182091,020
|
-21166,020
|
|
|
|
|
|
|
|
38
|
231205,200
|
-80230,200
|
|
|
|
|
|
|
|
39
|
312601,351
|
64039,649
|
|
|
|
|
|
|
|
40
|
370405,297
|
-192880,297
|
|
|
|
|
|
|
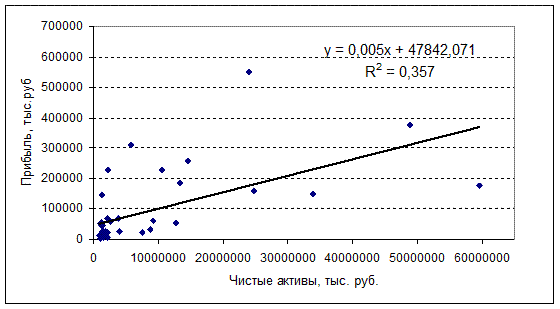
Рис.1. Зависимость
прибыли банков о величины чистых активов
4. Анализ результатов статистических
компьютерных расчетов
На основе графического
изображения фактических данных (рис.1) данных очень трудно судить о возможной
форме и направлении связи между признаками. Можно только предположить, что
связь между чистыми активами и прибылью банков слабая.
Анализируя аналитическую
группировку (таблица 3), можно заметить, что при переходе от одной группы к
другой, вслед за увеличением размера чистых активов среднее значение прибыли
банков возрастает. Следовательно, между данными признаками существует прямая
корреляционная связь.
Эмпирическое
корреляционное отношение составляет η = 0,692, что свидетельствует о
наличии умеренной связи между размером чистых активов и прибылью банков, в
которой 47,9% вариации прибыли зависит от вариации размера чистых активов
банков.
Линейный коэффициент
корреляции равен 0,597, что также свидетельствует о наличии умеренной связи
между размером чистых активов и прибылью банков. Линейный коэффициент
корреляции и эмпирическое корреляционное отношение не равны, следовательно,
зависимость прибыли от размера чистых активов не является линейной.
Уравнение однофакторной линейной
регрессионной модели связи признаков Х и Y имеет вид:
у = 47842,071 + 0,005*х
Коэффициент регрессии a1 = 0,005 показывает, что при увеличении чистых активов
на 1 тыс. руб. прибыль банков в среднем увеличится на 0,005 тыс. руб.
Коэффициент парной корреляции
(множественный R) равен
0,597, что свидетельствует о том, что связь между размером чистых активов и прибылью
банков умеренная.
Коэффициент детерминации
(R-квадрат) равен 0,357,
следовательно, 35,7% вариации прибыли объясняются вариацией размера чистых
активов.
Расчетное значение F-критерия Фишера составляет 21,088.
Значимость F составляет 0,000, следовательно, уравнение зависимости прибыли банков от
размера чистых активов является статистически значимым.
Заключение
Таким образом, из
вышеизложенной работы можно сделать следующие основные выводы:
- существуют
различные методы выявления взаимосвязей финансовых показателей деятельности
банка:
- графический метод;
- метод параллельных рядов;
- метод аналитических группировок;
- метод корреляционно-регрессионного
анализа.
- графический метод
позволяет установить наличие, направление и характер связи;
- метод
параллельных рядов – наличие и направление связи (характер связи установить
очень трудно);
- метод
аналитических группировок также позволяет установить наличие и направление
связи, а также измерить тесноту связи с помощью методов математической
статистики;
- и только метод
корреляционно-регрессионного анализа позволяет получить аналитическое выражение
(уравнение регрессии).
Список используемой литературы
1. Боярский
А.Я., Громыко Г.Л. Общая теория статистики. - М.: изд. Московские университеты,
1985 г. – 372 с.
2. Горин А.М. Статистика: Учебник. – 2-е изд., прераб.
– М.: Издательство – торговая корпорация «Долинов и Ко», 2003.
-472с.
3. Гусаров В.М. Статистика: Учебное пособие для вузов.
– М.: ЮНИТИ-ДАНА, 2002. – 463с.
4.
Глинский В.В., Ионин В.Г. Статистический
анализ: Учебное пособие. – М.: Филинъ, 1998. – 264 с.
5.
Елисеева И.И., Юзбашев М.М. Общая теория статистики:
Учебник для вузов. – М.: Финансы и статистика, 1995. –398с.
6.
Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория
статистики: Учебник. – М.: ИНФРА – М, 2000. – 416 с.
7.
Под редакцией Громыко Г.Л. Теория статистики: Учебник.
– М.: ИНФРА – М, 2000. – 414 с.
8.
Практикум по статистике: Учебное пособие для вузов /
Под ред. В.М.Симчеры / ВЗФЭИ. – М.: Финстатинформ, 1999. – 259с.
9.
Ряузов Н.Н. Общая теория статистики: Учебник для
вузов. – М.: Финансы и статистика, 1984. – 426с.
10.
Сироткина Т.С., Каманина А.М. Основы
теории статистики: Учебное пособие для вузов / ВЗФЭИ. Под ред. проф.
В.М.Симчеры. – М.: АО «Финстатинформ», 1995. – 347с.
11.
Сулицкий В.Н. Методы статистического анализа в управлении:
Учебное пособие. – М.: Дело, 2002. – 520с.
12.
Суслов И.П. Общая теория статистики. Учебное пособие.
– М.: Статистика, 1978. – 392 с.
13. Теория статистики: Учебник. Под
редакцией Громыко Г.Л. – М.: ИНФРА – М, 2000. – 414 с.
14.
Экономическая статистика: Учебник / Под ред.
Ю.Н.Иванова. – М.: ИНФРА-М, 1998. – 274с.
15.
Экономика и статистика фирм: Учебник / Под ред.
С.Д.Ильенковой. – М.: Финансы и статистика, 1996. – 322с.
ПРИЛОЖЕНИЕ 1
Исходные данные
ПРИЛОЖЕНИЕ 2
Расчетные таблицы в режиме формул
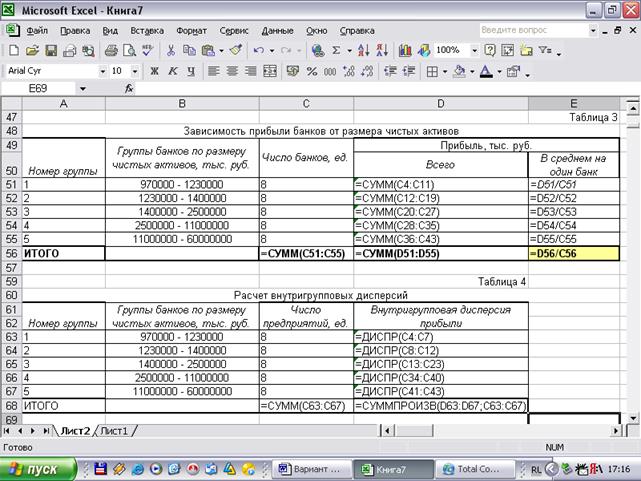
ПРИЛОЖЕНИЕ 3
Расчеты в режиме формул и результаты
применения встроенных функций в Excel