Содержание
Задание № 1____________________________________________________ 3
Задание № 2____________________________________________________ 4
Задание № 3____________________________________________________ 5
Задание № 4____________________________________________________ 6
Задание № 5____________________________________________________ 7
Задание № 6____________________________________________________ 8
Задание № 7___________________________________________________ 12
Задание № 8___________________________________________________ 13
Задание № 9___________________________________________________ 14
Задание № 10__________________________________________________ 15
Задание № 11__________________________________________________ 16
Задание № 12__________________________________________________ 17
Литература___________________________________________________ 20
Задание № 1
Укажите, какие пары понятий находятся в отношении подчинения, какое понятие для таких пар является видовым
А – подчинения (первое понятие родовое);
В – подчинения (первое понятие видовое);
С – пересечения;
D – соподчинения;
E – противоречия.
Ответ:
1) Находятся в отношении В – подчинения (первое понятие видовое), т.к. живое существо в любом случае теплокровное живое существо
2) Находятся в отношении D – соподчинения
3) В отношении подчинения видовым понятием является «а»
4) Находятся в отношении E – противоречия
5) Находятся в отношении E – противоречия
6) Находятся в отношении С – пересечения
7) Находятся в отношении С – пересечения
8) В отношении подчинения вид «ректор УрГЮА»
Задание № 2
Ответ:
Перечню данных понятий соответствуют круги Эйлера «4».
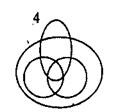
Задание № 3
Установите, какие перечни понятий соответствуют кругам Эйлера
Ответ:
Данным кругам Эйлера соответствует перечень понятий 4).
Задание № 4
Ответ:
Отношение подчинения (является видовым понятием), т.е. понятие более меньшее, чем родовое, либо очень приближенно равны между собой. Если в отношении подчинения находятся два общих понятия, то подчиняющее понятие называется родовым, подчиненное видовым.
А – 2
В – 1,4,6,5,8
С – 3,7
D – 1,3
В отношении соподчинения находятся два или более неперекрещивающихся понятий, подчиненных общему для них понятию.
Задание № 5
Перечислите, какие деления понятий нарушают правила:
А – соразмерности;
В – проведения деления по одному основанию;
С – взаимоисключения членов деления.
Ответ:
Деления понятий, нарушающие правила А – соразмерности:
5) Деления понятий, нарушающие правила В – проведения деления по одному основанию, т.к. есть другие формы обучения
1) совместимые понятия делятся по многим основаниям
4) Деления понятий, нарушающие правила В – проведения деления по одному основанию
Задание № 6
Пусть А – Арнольд проголосовал за законопроект; В – Билл проголосовал за законопроект; C – Саймон проголосовал за законопроект. Формализуйте приведенные ниже суждения. Для получившихся формул постройте таблицы истинности и укажите:
А – какие из них соответствуют приведенной ниже таблице;
В – какие являются тавтологиями (логическими законами).
|
A |
B |
C |
Результат |
|
И |
И |
И |
Л |
|
И |
И |
Л |
Л |
|
И |
Л |
И |
И |
|
И |
Л |
Л |
И |
|
Л |
И |
И |
И |
|
Л |
И |
Л |
И |
|
Л |
Л |
И |
И |
|
Л |
Л |
Л |
И |
1. По крайней мере, Саймон или Билл проголосовали за законопроект. Если Арнольд не голосовал «за», то без сомнения также не голосовал «за» и Саймон. Следовательно, если Билл проголосовал «за», то точно не голосовал «за» Арнольд.
2. Если Арнольд проголосовал «за», то Саймон точно не голосовал «за». А если Арнольд не проголосовал «за», то Билл тоже не голосовал «за». Следовательно, если Билл проголосовал «за», то точно не голосовал «за» Арнольд.
3. Если Саймон и Арнольд проголосовали «за», то Билл уж точно не голосовал «за». А если «за» голосует Арнольд, то обязательно «за» голосует и Саймон. Следовательно, если Билл проголосовал «за», то точно не голосовал «за» Арнольд.
4. Саймон голосует «за» тогда и только тогда, когда «за» голосует Арнольд. Однако Арнольд не голосует «за», если и только если «за» голосует Билл. Следовательно, если Билл проголосовал «за», то точно не голосовал «за» Арнольд.
Решение:
Формализуем приведенные суждения:
1. ![]() .
.
Построим таблицы истинности для первого суждения:
|
A |
B |
C |
|
|
|
|
|
|
f1 |
|
И |
И |
И |
Л |
Л |
И |
И |
Л |
И |
Л |
|
И |
И |
Л |
Л |
И |
И |
И |
Л |
И |
Л |
|
И |
Л |
И |
Л |
Л |
И |
И |
И |
И |
И |
|
И |
Л |
Л |
Л |
И |
Л |
И |
И |
Л |
И |
|
Л |
И |
И |
И |
Л |
И |
Л |
И |
Л |
И |
|
Л |
И |
Л |
И |
И |
И |
И |
И |
И |
И |
|
Л |
Л |
И |
И |
Л |
И |
Л |
И |
Л |
И |
|
Л |
Л |
Л |
И |
И |
Л |
И |
И |
Л |
И |
2.
![]() .
.
Построим таблицы истинности для второго суждения:
|
A |
B |
C |
|
|
|
|
|
|
|
f2 |
|
И |
И |
И |
Л |
Л |
Л |
Л |
И |
Л |
Л |
И |
|
И |
И |
Л |
Л |
Л |
И |
И |
И |
И |
Л |
Л |
|
И |
Л |
И |
Л |
И |
Л |
Л |
И |
Л |
И |
И |
|
И |
Л |
Л |
Л |
И |
И |
И |
И |
И |
И |
И |
|
Л |
И |
И |
И |
Л |
Л |
И |
Л |
Л |
И |
И |
|
Л |
И |
Л |
И |
Л |
И |
И |
Л |
Л |
И |
И |
|
Л |
Л |
И |
И |
И |
Л |
И |
И |
И |
И |
И |
|
Л |
Л |
Л |
И |
И |
И |
И |
И |
И |
И |
И |
3. ![]() .
.
Построим таблицы истинности для третьего суждения:
|
A |
B |
C |
|
|
|
|
|
|
f3 |
|
И |
И |
И |
Л |
И |
Л |
И |
Л |
Л |
И |
|
И |
И |
Л |
Л |
Л |
И |
Л |
Л |
Л |
И |
|
И |
Л |
И |
И |
И |
И |
И |
И |
И |
И |
|
И |
Л |
Л |
И |
Л |
И |
Л |
Л |
И |
И |
|
Л |
И |
И |
Л |
Л |
И |
И |
И |
И |
И |
|
Л |
И |
Л |
Л |
Л |
И |
И |
И |
И |
И |
|
Л |
Л |
И |
И |
Л |
И |
И |
И |
И |
И |
|
Л |
Л |
Л |
И |
Л |
И |
И |
И |
И |
И |
4.
![]() .
.
Построим таблицы истинности для четвертого суждения:
|
A |
B |
C |
|
|
|
|
|
f4 |
|
И |
И |
И |
Л |
И |
Л |
Л |
Л |
И |
|
И |
И |
Л |
Л |
Л |
Л |
Л |
Л |
И |
|
И |
Л |
И |
Л |
И |
И |
И |
И |
И |
|
И |
Л |
Л |
Л |
Л |
И |
Л |
И |
И |
|
Л |
И |
И |
И |
Л |
И |
Л |
И |
И |
|
Л |
И |
Л |
И |
Л |
И |
Л |
И |
И |
|
Л |
Л |
И |
И |
Л |
Л |
Л |
И |
И |
|
Л |
Л |
Л |
И |
Л |
И |
Л |
И |
И |
Из таблицы истинности для получившихся формул следует, что:
- суждение 1 соответствуют приведенной таблице;
- суждения 3 и 4 являются тавтологиями (логическими законами).
Задание № 7
Ответ:
Для противоречия характерна строгая несовместимость: при истинности любого из суждений другое всегда будет ложным. Следовательно, пара суждений, находящаяся в отношении А – противоречия: 3, 5.
Для подчинения характерно то, что если одно суждение истинно, то и другое будет истинным, но не наоборот. Следовательно, пары суждений, находящиеся в отношении В – подчинения: 1, 2.
Задание № 8
Ответ:
Из приведенных непосредственных умозаключений, являются А – правильным превращением: 1, 4.
Из приведенных непосредственных умозаключений, являются В – правильным обращением: 2, 5.
Из приведенных непосредственных умозаключений, являются C – правильным противопоставлением предикату: 3.
Задание № 9
Установите, в каких силлогизмах термин «политик» является: А – средним термином; В – большим термином.
1. Все адвокаты – юристы, значит, М. не юрист, так как он не адвокат.
2. М. не адвокат, так как он не юрист, а все адвокаты – юристы.
3. Некоторые адвокаты – юристы, так как М. – адвокат и юрист.
4. Некоторые люди – юристы, все юристы – адвокаты, значит, некоторые люди – адвокаты.
Решение:
Меньшим термином силлогизма называется понятие, которое в заключении является субъектом.
Большим термином силлогизма называется понятие, которое в заключении является предикатом.
Средним термином силлогизма называется понятие, входящее в обе посылки и отсутствующее в заключении.
Термин «адвокат» является средним термином в силлогизмах: 1, 3.
Термин «адвокат» является большим термином в силлогизмах: 2, 4.
Задание № 10
Укажите, в каких силлогизмах нарушены правила:
А – средний термин должен быть распределен хотя бы в одной из посылок;
В – хотя бы одна из посылок должна быть общим суждением (для разных вариантов разные правила);
C – все правила соблюдаются.
1. Все юристы – люди, некоторые люди неподкупны, следовательно, некоторые юристы неподкупны.
2. Все преступления наказуемы, значит, действия К. не наказуемы, так его действия не являются преступлением.
3. Некоторые ораторы неразумны, так как некоторые политики разумны, а многие ораторы не политики.
4. У всех снайперов хорошее зрение, значит, Иванов – снайпер, так как у него хорошее зрение.
5. Многие юристы внимательны, но часть внимательных людей совершают оплошности, значит, некоторые юристы совершают оплошности.
Решение
Термин считается распределенным, если он взят в полном объеме. Нарушено правило А – средний термин должен быть распределен хотя бы в одной из посылок в силлогизмах: 3.
Нарушено правило В – хотя бы одна из посылок должна быть общим суждением в силлогизмах: 3.
C – все правила соблюдаются в силлогизмах: 1, 2.
Задание № 11
Установите, какие умозаключения являются:
А – правильными условно-категорическими;
В – правильными разделительно-категорическими.
1. Я не успею оформить документы, если задержусь на работе. Меня задержали на работе, следовательно, документы я оформить не успел.
2. Нормы права (по методу правового регулирования) бывают императивными или диспозитивными. Эта норма не диспозитивная, следовательно, она является императивной.
3. Если свидетель дал ложные показания, то обвиняемый не виновен. Свидетель П. не давал ложных показаний, следовательно, обвиняемый виновен.
4. Сложные суждения бывают соединительными или разделительными. Это суждение не разделительное, следовательно, оно соединительное.
5. Юристы бывают прокурорами и нотариусами. Сидоров не прокурор, следовательно он нотариус.
6. Если Н. понял теоретический материал, то он решит все задания; а если Н. решит все задания, то он получит положительную оценку. Значит, если Н. понял теоретический материал, он получит положительную оценку.
Решение
Умозаключения являются:
А – правильными условно-категорическими 1, 6, 3.
В – правильными разделительно-категорическими 2, 4, 5.
Задание № 12
Законспектируйте тему «Умозаключение по аналогии»
Умозаключение по аналогии (или просто аналогия) – индуктивное умозаключение, когда на основе сходства двух объектов по каким-то одним параметрам делается вывод об их сходстве также по другом параметрам.
Например, планеты Марс и Земля во многом сходны: они расположены рядом в Солнечной системе, на обеих есть вода и атмосфера и т.д.; на Земле есть жизнь; поскольку Марс похож на Землю с точки зрения условий, необходимых для существования живого, можно сделать вывод, что на Марсе также имеется жизнь. Это заключение является, конечно, только правдоподобным.
Общая схема умозаключения по аналогии:
Объект А имеет признаки а, b, с.
Объект B сходен с A в том, что имеет признаки а и b.
Значит, объект В имеет, вероятно, и признак с.
Сопоставление двух объектов, как бы далеко оно не шло, способно дать только предположительное знание, гипотезу, нуждающуюся в дальнейшей проверке.
Не всегда аналогия выступает в такой прозрачной форме, как в приведенных примерах.
У книгопечатника Д.Дантона был счастливый, но очень, короткий брак: молодая жена его рано скончалась. Спустя всего полгода он, однако, вновь женился. В истории своей жизни Дантон оправдывал столь скорое утешение тем, что вторая жена была всего лишь повторением первой: "Я поменял только лицо, женские же добродетели в моем домашнем круге остались те же. Моя вторая жена – не что иное, как первая, но лишь в новом издании, исправленном и расширенном, и я бы сказал: заново переплетенном".
Здесь отношение новой жены к предыдущей уподобляется отношению второго издания книги к первому ее изданию. Какое значение имеет то, что второе издание вышло сразу же вслед за первым? Любопытно заметить, что, как истинный любитель книги, Дантон ценит именно первое издание, даже несмотря на то, что оно утрачено.
Аналогия может выступать в форме, напоминающей популярную индукцию.
К примеру, человек прочел "Записки Пиквикского клуба" Ч.Диккенса – понравилось, прочел "Оливера Твиста" – тоже понравилось. На этом основании он заключает, что и роман Диккенса "Домби и сын", к чтению которого он только приступил, окажется интересным.
В начале этого и подобных ему рассуждений констатируется, что каждый из встречавшихся ранее предметов некоторого рода имел определенное свойство. В заключении выражается предположение, что и следующий встреченный предмет этого рода также будет обладать данным свойством. Если бы, прочитав два-три произведения Диккенса и найдя их интересными, кто-то пришел к мысли, что все произведения этого классика интересны, – это была бы популярная индукция. В примере же с романом "Домби и сын" от знания об отдельных объектах совершается переход к знанию еще об одном, опять-таки индивидуальном объекте.
Другой пример – уже из астрономии – позволит яснее понять различие между аналогией и популярной индукцией. И.Кеплер нашел, что Марс описывает вокруг Солнца траекторию в форме эллипса. Зная также, что имеется много общего между Марсом и Меркурием, Венерой, Землей, Юпитером и Сатурном, Кеплер заключил, что все планеты Солнечной системы движутся по эллиптическим орбитам. В этом рассуждении комбинируются аналогия и популярная индукция. Форма траектории Марса известна, значит, и похожий на него Меркурий описывает такую же траекторию. Это верно также для Венеры, Земли, Юпитера и Сатурна. Получив посредством аналогии знание об орбитах отдельных планет, можно выдвинуть индуктивное обобщение: не только рассмотренные, но и вообще все планеты Солнечной системы движутся по эллипсам.
Итак, в обычном мышлении умозаключение по аналогии редко встречается в ясной, не требующей размышления и реконструкции форме. Чаще всего аналогия оказывается свернутой, какие-то части умозаключения опускаются. Иногда она протекает так, что ее можно спутать с популярной индукцией.
Умозаключение по аналогии — это умозаключение от частного к частному. Сущность умозаключения по аналогии состоит в том, что на основании сходства двух предметов в некоторых отношениях делается вывод о сходстве этих предметов и в других отношениях. Умозаключение по аналогии лежит в основе создания многих гипотез, догадок.
Литература
1. Афанасьева О.В. Логика. М.: Академия, 2001.
2. Бочаров В.А. , Маркин В.И. Основы логики. М., 1999.
3. Войшвилло Е.К. Понятие как форма мышления. М.,1996.
4. Ивлеев Ю.В. Логика. М., 1993.
5. Кириллов В.И., Старченков А.А. Логика. М., 2000.