Содержание
Вопросы......................................................................................... 3
1. Ответ на вопрос..................................................................... 3
2. Ответ на вопрос..................................................................... 8
Задачи.......................................................................................... 11
3. Решение задачи.................................................................... 11
4. Решение задачи.................................................................... 12
Тесты........................................................................................... 13
5. Ответ на тест:....................................................................... 13
6. Ответ на тест:....................................................................... 13
7. Ответ на тест:....................................................................... 14
8. Ответ на тест:....................................................................... 14
9. Ответ на тест:....................................................................... 14
10. Ответ на тест:..................................................................... 15
Список используемой литературы:......................................... 16
Вопросы
1. Ответ на вопрос.
Деятельность предприятия
принято рассматривать в краткосрочном и долгосрочном периоде. Краткосрочным
периодом называется такой период, в течение которого производственные мощности
каждого предприятия фиксированы, но выпуск может быть увеличен или снижен за
счет изменения объема использования переменных факторов. Общее число
предприятий в отрасли остается неизменным[1].
Определим выпуск,
обеспечивающий максимум прибыли совершенно конкурентного предприятия в
краткосрочном периоде при заданных условиях рынка и технологии. Заметим, что
максимумом прибыли называется как максимум положительной разницы между выручкой
и затратами производства продукции, так и минимум отрицательной разности между
теми же величинами. Поэтому минимум убытков может рассматриваться как максимум
прибыли, если получить положительную прибыль невозможно.
Пусть условия товарного
рынка таковы, как показано на рис. 1а, где DS и SS – рыночные кривые спроса и предложения; Р* и Q* –
соответственно рыночная цена равновесия и равновесный объем выпуска
(продаж) отрасли в единицу времени. Пусть, далее, кривые SMC, SATC и STC на рис. 1б, в представляют кривые
предельных, средних общих и общих затрат типичного предприятия в коротком
периоде. Поскольку предприятие является ценополучателем, линия AR = MR на рис. 1б является линией спроса на
продукцию предприятия, тогда как луч TR на рис. 1в – линия его общей выручки. Наклон линии TR неизменен на всем ее протяжении,
поскольку цена не зависит от объема выпуска данного предприятия, и потому TR = P*q.
Прибыль предприятия
представляет разность между общей выручкой и общими затратами короткого
периода:
π(q) = TR(q) - STC(q).
|
|
|
Рис. 1.
Равновесие совершенно
конкурентного предприятия. Прибыль положительна.
|
|

Условием максимизации
прибыли первого порядка (необходимым) будет, очевидно,
∂π(q)/ ∂q = ∂TR(q)/ ∂q - ∂STS(q)/ ∂q = 0 → ∂TR(q)/ ∂q = ∂STS(q)/ ∂q[2].
Поскольку ∂TR(q)/ ∂q = MR(q) и ∂STC(q)/ ∂q = MC(q), условием первого порядка является
равенство предельной выручки предельным затратам:
MR(q*) = MC(q*). (1)
Но для совершенно
конкурентного предприятия Р = AR = MR, и, следовательно, условие первого порядка может быть
представлено и как равенство предельных затрат цене:
MC(q*) = P. (2)
В ситуации,
представленной на рис. 1б, условие первого порядка выполняется дважды, в точках
А и С, которым соответствуют объемы выпуска q*1 и q*2. Однако, как видно на рис. 1г, в
первом случае максимальны убытки, во втором – прибыль. Для различения этих
случаев используется условие второго порядка (достаточное):
∂2p/∂q2 = (∂2TR/∂q2) - (∂2STC/∂q2) < 0, (3)
откуда
∂2TR/∂q2 < ∂2STC/∂q2.
Левая часть (3)
характеризует наклон кривой MR, правая – наклон кривой SMC. Следовательно, условие второго
порядка (3) требует, чтобы наклон кривой предельных затрат был больше наклона
кривой предельной выручки, или, иначе, чтобы кривая SMC пересекала кривую MR снизу (как в точке С, но не в А на
рис. 1б).
Поскольку же для
совершенно конкурентного предприятия цена не зависит от объема выпуска, наклон
кривой предельной выручки
∂2TR/∂q2 = 0,
условие второго порядка можно
представить неравенством
0 <∂2STC/∂q2
Последнее означает, что
прибыль будет максимальна, если в точке пересечения с MR кривая SMC имеет положительный наклон. Таким
образом, если
∂2p/∂q2 < 0
объем выпуска q*2 максимизирует (положительную)
прибыль, если же
∂2p/∂q2 > 0
объем выпуска q*1 максимизирует (отрицательную)
прибыль, т. е. убытки.
Другими словами, прибыль
(положительная) будет максимальна, если MR = SMC и кривая SMC восходящая. Напротив, отрицательная
прибыль (убытки) будет максимальна, если MR = SMC и кривая SMC нисходящая. На рис. 1б максимальная
положительная прибыль при выпуске q2* соответствует площади заштрихованного
прямоугольника. Она равна разности между общей выручкой и затратами короткого
периода:
π
= P*q2*
- [SATC(q2*)]* q2*
Кривая предложения
совершенно конкурентного предприятия в коротком периоде тождественна части его
кривой предельных затрат. На рис. 2а представлены кривые SMC, SATC и SAVC. При цене P1 максимум положительной прибыли достигается при
выпуске q1 значит,
точка А на кривой SMC принадлежит кривой предложения данного
прибылемаксимизирующего предприятия. При более низкой цене, P2, прибыль будет максимальна при выпуске q2, значит, и точка В на кривой SMC принадлежит кривой предложения.
Заметим, что в этом случае максимум прибыли равен нулю, поскольку цена P2 равна минимуму средних общих затрат (P2 = AR = MR = min SATC).
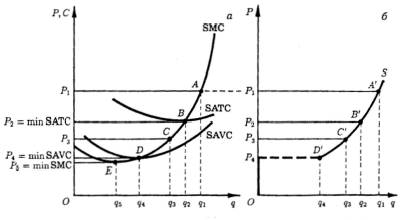
Рис. 2.
Если цена снизится до P3 < SATC, прибылемаксимизирующий объем производства упадет до q3. Прибыль в этом случае будет отрицательна, поскольку
точка С на кривой SMC лежит ниже кривой SATC и, значит, выручка от продажи
выпуска q3 не
возместит общих затрат его производства:
P3q3 < SATC(q3)q3.
Но, с другой стороны, P3 > SAVC(q3). А это значит, что выручка от продажи выпуска q3 возместит все переменные и, кроме того, часть
постоянных затрат предприятия. Таким образом, убытки от выпуска q3 будут меньше, чем сумма общих постоянных затрат (TFC) в коротком периоде. Поэтому по сравнению
с нулевым выпуском выпуск q3 будет прибылемаксимизирующим. Следовательно, и точка С
принадлежит кривой предложения предприятия.
При еще более низкой цене
P4 = minSAVC выпуск q4 удовлетворяет обоим условиям максимизации прибыли.
Это значит, что TR(q4)
= q4*(SAVC(q4)) = TVC(q4) и, следовательно, убытки предприятия равны сумме постоянных
затрат. В этих условиях предприятию безразлично, производить ли q4 единиц продукции или закрыться. Поэтому точку D на кривой SMC часто называют точкой закрытия. Эта
точка может принадлежать кривой предложения предприятия, а может и не
принадлежать.
Наконец, при цене P5 = minSMC выпуск q5 также удовлетворяет условиям максимизации, но цена не
возмещает средних переменных затрат (P5 < SAVC(q5)), и при любом отличном от нуля выпуске убытки окажутся выше
постоянных затрат. Следовательно, в этом случае нулевой выпуск окажется оптимальным.
Иначе говоря, при Р < minSAVC прибылемаксимизирующее предприятие предпочтет
закрыться. Поэтому точка Е на кривой SMC определенно не принадлежит кривой
предложения совершенно конкурентного предприятия[3].
Кривая предложения
совершенно конкурентного предприятия представлена на рис. 2б. Здесь точки А' ,
В' , С' , D' соответствуют точкам А, В, С, D кривой SMC на рис. 2а. Множество подобных точек
формирует участок кривой предложения, лежащий выше точки D', соответствующей минимуму SAVC на рис. 2a. Заметим, что участок кривой SMC, лежащий ниже SAVC, не входит в кривую предложения,
поскольку прибылемаксимизирующее поведение диктует закрытие предприятия, если
цена продукции окажется ниже средних переменных затрат.
Таким образом, кривая
предложения совершенно конкурентного предприятия в коротком периоде
представляет собой возрастающую ветвь кривой предельных затрат, которая лежит
выше минимума средних переменных затрат. При более низком, чем minSAVC, уровне рыночной цены кривая предложения
сливается с осью цен (участок OP4 на рис. 2б).
2. Ответ на вопрос.
Минимальные резервы - это
наиболее ликвидные активы, которые обязаны иметь все кредитные учреждения, как
правило, либо в форме наличных денег в кассе банков, либо в виде депозитов в
центральном банке или в иных высоколиквидных формах, определяемых центральным
банком[4].
Возможно всего три модели
резервирования вкладов:
1. Частичное резервирование вкладов.
2. 100% резервирование.
3. Отсутствие нормы резервирования (фактически,
норма резервирования равна 0)
Рассмотрим случай 100%
резервирования вкладов и сравним эту ситуацию с ситуацией частичного
резервирования.
Представим ситуацию,
когда в экономике нет ни одного кредитного института. В этом случае наличность
– единственная форма денег. Предположим, что общее количество денег составляет
М денежных единиц. Тогда предложение денег также будет равно М денежных единиц.
Теперь представим, что
где-то открылся банк, который мы назовем первым национальным банком. Допустим,
что на первых порах он выполняет только
депозитарные функции, то есть принимает вклады, но не выдает ссуды, следовательно, ставка
резервирования равна 100%. Деньги лежат на депозитах и не оказывают влияние на
экономику. Предложение денег так и осталось М денежных единиц.
Теперь рассмотрим
ситуацию, когда норма резервирования равна r. Тогда банк оставит на депозитах rМ денежных единиц, а (1-r)М денежных единиц выдаст в кредит.
Денег в экономике так и осталось М денежных единиц, а предложение денег выросло
и стало М + (1- r)М = М(2- r) единиц, т.е. денежная масса возросла. При усложнении модели и введения
большего количества банков, исполняющих кредитные функции, денежная масса и
предложение денег будут возрастать.
Данная модель выявила
некоторые преимущества частичного резервирования вкладов над 100%
резервированием[5]:
1. Частичная норма
резервирования, в отличие от 100%, позволяет пустить депозитные деньги в
оборот. Следовательно, повышается предложение денег.
2.
У банков появляется возможность выдавать больше кредитов, за счет прибавления к
уставному капиталу банка части депозитных денег, вследствие чего повышается
покупательная способность населения. Повышается совокупный спрос и, как
следствие, рост валового выпуска в стране в краткосрочном периоде.
3.
Использование политики частичного резервирования также позволяет кредитным учреждениям
получать прибыль, что опять же приводит к росту благосостояния экономики.
Рассмотрим,
почему банки могут функционировать в режиме частичного резервирования. Банки
оставляют соответствующую ставке резервирования часть денег на
корреспондентских счетах в центральном банке страны. Замороженные резервы
являются некоторой гарантией сохранности вкладов населения и предотвращения
банка от банкротства.
Так
как постоянно в банки на депозитные счета вкладываются деньги, то у банка на
определенном этапе развития должна находиться достаточно большая сумма денег.
Следовательно, при превышении текущего уровня снятия денег с депозитных счетов
над ожидаемым, банку может не хватить текущих наличных средств, находящихся в
кассах для оплаты всех требований, тогда банк может задействовать резервы – и
удовлетворить потребность населения в наличных деньгах. Если же банку не хватит
резервов для удовлетворения потребностей населения, банк может обратиться за
помощью к центральному банку и взять у последнего кредит под ставку
рефинансирования[6].
Из
вышесказанного следует, что введение нормы обязательного резервирования вкладов
коммерческими банками является достаточно рентабельной политикой центрального
банка по отношению к коммерческим банкам, причем из такой политики извлекается
прибыль не только коммерческими банками, но и всей экономической системой в
целом[7].
Рассмотрим модель
отсутствия ставки обязательного резервирования денежных депозитов. Коммерческие
банки могут свободно распоряжаться вверенными им деньгами, следовательно,
существует побуждение пустить все деньги в оборот. Но, с другой стороны,
отсутствие резервов может подвести коммерческие банки либо к банкротству, либо
к взятию кредита у центрального банка или у коммерческого, что не рентабельно,
т.к. банку пришлось бы выплачивать проценты по кредиту, вследствие чего,
прибыль бы уменьшилась. Но если учесть, что почти всегда на практике ставка
рефинансирования ниже, чем ставка по кредитам у коммерческих банков, то банку
было бы целесообразно пустить все депозитные деньги в оборот, а при
необходимости взять у центрального банка кредит под ставку рефинансирования,
которая ниже чем процент под которым коммерческий банк выдает кредит,
следовательно, банк опять же получит прибыль. Но тут нужно учесть фактор
ожидания[8]. Если
население будет видеть, что банк, в который они вложили деньги, пускает их полностью
в оборот и постоянно берет кредиты у центрального банка, они решат, что банк
ненадежный и будет массовое снятие депозитов со счетов такого коммерческого
банка, что грозит последнему банкротством. Следовательно, если банк не
собирается заниматься спекуляциями, он не будет стремиться установить нулевой
уровень резервов и установит индивидуальный процент резервирования в
зависимости от экономической ситуации.
Задачи
3. Решение задачи.
Пусть производители производят Qs единиц продукции, а потребители
потребляют Qd единиц продукции, тогда по условию задачи: Qs – Qd = 60 или
Qd = Qs – 60. Найдем цену при которой выполняется
данное условие:
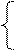 Qs
– 60 = 200 – 2P,
Qs
– 60 = 200 – 2P,
Qs = -10 + P,
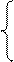 Qs
= -10 + P,
Qs
= -10 + P,
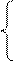 -10
+ P – 60 = 200 – 2P,
-10
+ P – 60 = 200 – 2P,
P = 90,
Qs = 80.
Таким образом, при цене 90 у.е. за
единицу продукции производители будут предлагать 80 единиц продукции, а
потребители приобретать 20 единиц продукции (200 – 2*90 = 20).
Графически ситуация выглядит
следующим образом:
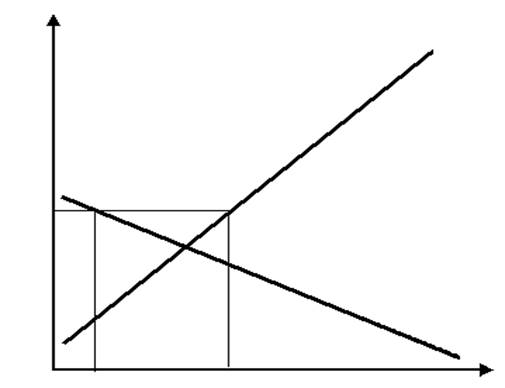

Ответ: 90 у.е.
4. Решение задачи.
Пусть rd – средняя норма резервирования,
cd – норма предпочтения наличных денег
безналичным.
Тогда, rd = 10%, cd = 20%.
Центральный банк предоставляет кредит
правительству в размере 40 млрд. руб. Одну часть 40*cd/(1+cd) = 66.(6) правительство оставит в
виде наличных, а другую часть разместит на банковском депозите, причем пропорция,
в которой 40 млрд. будут поделены между наличными и депозитом равна cd. В результате на депозите окажется 40/(1+cd) = 33,(3) млрд. руб.
Банки 10%, т.е. депозитов поместят в
резервы (rd*[40/(1+cd)] = 3,(3)), а остальную часть величиной (1-rd)*[40/(1+cd)] = 30 млрд. руб. пойдут на выдачу
кредитов.
Кредиты идут на оплату товаров и
услуг и, в результате, эти деньги окажутся на руках у домохозяйств, которые
вновь поделят их на наличные и депозиты в отношении cd. В результате весь процесс,
описанный выше, повторится по отношению к сумме в (1-rd)*[40/(1+cd)] млрд. руб. и так далее.
Совокупное изменение предложения
денег, полученное как сумма прямого эффекта и всех косвенных эффектов (после
бесконечного числа шагов), будет равно:
∆M = ∆H + ∆H
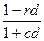 + ∆H
+ ∆H 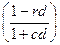 ^ 2 + … = ∆H
^ 2 + … = ∆H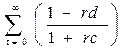 ^ t =
^ t =
= ∆H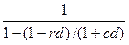 = mm*∆H
= mm*∆H
Где mm – денежный мультипликатор (money
multiplicator). mm = 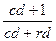
Mm = 1,2/(0,2+0,1) = 4.
Следовательно, ∆М = 4*40 = 160
млрд. руб.
Ответ: 160 млрд. руб.
Тесты
5. Ответ на тест:
в) Если цена на товар X вырастет, спрос на него спадет,
следовательно, покупатели захотят приобретать больше товара-субститута Y по неизменившейся цене,
следовательно, при прочих равных условиях, спрос на товар Y повысится и кривая спроса сдвинется
вправо.
Т.к. эластичность спроса по цене
является показателем отражающем относительное изменение объема спроса на товар
при относительном изменении его цены, то эластичность спроса по цене на товар Y не изменится при изменении цены на
товар X.
6. Ответ на тест:
б) При цене на товар, ниже чем AVC предприятию будет невыгодно оставаться
на рынке, т.к. оно будет получать отрицательную прибыль и даже не сможет
покрыть переменные затраты. Следовательно предприятию будет азумней уйти с
рынка и нести только постоянные издержки.
Остальные утверждения не верны по следующим
причинам:
а) предприятие может оставаться на
рынке даже не получая положительной экономической прибыли, потому что оно
всегда несет постоянные затраты, которые оно не будет покрывать при выходе с
рынка, однако при производстве продукции оно могло бы покрывать хотя бы часть
из них.
В)
если цена на товар ниже, чем AFC, предприятие может иметь положительную
прибыль при цене выше, чем AVC. Тогда при определенном выпуске оно сможет покрыть и AVC, и AFC, получая при этом положительную прибыль.
Г) т.к. MR имеет вид прямой, параллельной оси
выпуска, а MC пересекает AVC в точке минимума, причем один раз, то AVC может лежать только по одну сторону
от MR, при условии,
что MC не
пересекается с MR. Т.к. на рынке совершенной конкуренции MR ≡ Р, то AVC может лежать на всей оси выпуска ниже
прямой P=MR (кривая AVC и МС – восходящие, но не достигают
прямой Р=MR, которая является их асимптотой), тогда предприятие будет наращивать
производство до бесконечности, увеличивая прибыль. Либо AVC и МС будут лежать выше прямой Р=MR, следовательно предприятие уйдет с
рынка, т.к. цена будет ниже AVC – точки закрытия. Нам недостаточно данных, для того чтобы
сказать, будет ли предприятие действовать на рынке при таких условиях.
Д) при P<AC = AVC + AFC может быть выполнено, что P>AVC, следовательно, предприятие
останется на рынке, т.к. сможет покрывать хотя бы часть постоянных затрат,
уменьшая отрицательную прибыль. Нам не хватает данных, чтобы точно ответить,
уйдет предприятие с рынка или нет.
7. Ответ на тест:
б) рост цен на товары сдвинет кривую
безразличия влево, т.к. при том же доходе потребитель сможет купить меньшее
количество товаров.
Сдвиг кривой безразличия –
некорректный ответ, т.к. через каждую точку плоскости проходит кривая
безразличия и их количество бесконечно. Если имеется ввиду сдвиг кривой
безразличия, на которой до изменения цен находился потребитель, то этого не
произойдет – потребитель только перейдет на другую кривую безразличия. Кривые
безразличия могут менять свой внешний вид только при изменении предпочтений
потребителей.
8. Ответ на тест:
д) Данный человек не относится к
безработному, т.к. по определению безработным считается человек, который может
работать и ищет работу, в данном случае этот человек не ищет работу, следовательно,
не может быть отнесен к какому-нибудь виду безработицы.
9. Ответ на тест:
б), г) Это следует из определения
денежных агрегатов:
М0 – наличные деньги в обращении,
банкноты и монеты;
М1 = М0 + средства на расчетных и
текущих счетах в банках, дорожные чеки;
М2 = М1 + срочные вклады в банках;
М3 = М2 + ценные государственные
бумаги.
Ответ а) и в) неверны, т.к.
сберегательные счета населения в банках и текущие депозиты могут включать в
себя срочные вклады в банках, следовательно, они не полностью входят в агрегат
М1.
10. Ответ на тест:
д) Уровень безработицы есть отношение
числа безработных к численности экономически активного населения (рабочей
силы). Экономическая активное население по определению – это занятые и
безработные. В состав же взрослого населения входят лица, которые не относятся
к рабочей силе (например, лице, ведущие домашнее хозяйство, пенсионеры…).
Поэтому определить уровень безработицы по исходным данным нельзя.
Список
используемой литературы:
1.
Н.
Грегори Мэнькью, Макроэкономика, изд-во Московского университета, 1996, 613 с.
2.
Синявская Э. Г. Микроэкономика: теория и практика решения задач. Новосибирск 2004, 256 с.
3.
Гальперин
В.М. Микроэкономика. Часть 2. Москва 2003, 315 с.
4.
Гребенников
П. И. Микроэкономика. СПбГУЭФ 2001, 308 с.
5.
Экономическая
теория под ред. Камаева. 6-е изд. – М.: 2000 г., 322 с.
6.
Р.
Дорнбуш, С. Фишер, Макроэкономика, изд-во Московского университета, 1997, 647
с.
7.
Антонов
Н. Г., Пессель М. А., Денежное обращение, кредит и банки. – М. : Финстатинформ,
1995 г.,
133 с.
[1] Гальперин В.М.
Микроэкономика. Часть 2. Москва 2003, с. 29.
[2] Синявская
Э. Г. Микроэкономика: теория и практика решения задач. Новосибирск 2004, с. 103
[3] Гребенников П. И.
Микроэкономика. СПбГУЭФ 2001, с. 154.
[4] Н. Грегори Мэнькью, Макроэкономика,
изд-во Московского университета, 1996, с. 324.
[5] Экономическая теория под
ред. Камаева. 6-е изд. – М.: 2000
г., с. 115.
Антонов Н. Г.,
Пессель М. А., Денежное обращение, кредит и банки. – М. : Финстатинформ, 1995 г, с 45.
[6] Н. Грегори Мэнькью,
Макроэкономика, изд-во Московского университета, 1996. – с. 89.
[7] Антонов Н. Г., Пессель М.
А., Денежное обращение, кредит и банки. – М. : Финстатинформ, 1995 г, с.47
[8] Р. Дорнбуш, С. Фишер,
Макроэкономика, изд-во Московского университета, 1997, с. 326.