Сравнить значения η и r и сделать вывод о возможности линейной связи между признаками Х и Y.

4.     Построить однофакторную линейную регрессионную модель связи признаков Х и Y, используя инструмент Регрессия надстройки Пакет анализа, и рассчитать доверительные интервалы коэффициентов уравнения линейной регрессии.

Построить теоретическую линию регрессии.

Дать экономическую интерпретацию коэффициента регрессии.

Рассчитать коэффициент эластичности и дать его экономическую интерпретацию.

5.     Найти наиболее адекватное нелинейное уравнение регрессии с помощью средств инструмента Мастер диаграмм. Построить для этого уравнения теоретическую кривую регрессии.

6.     Сделать заключение о возможности практического использования в качестве адекватной модели взаимосвязи признаков линейной модели 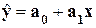, полученной с использованием инструмента Регрессия.

II. Рабочий файл с результативными таблицами и графиками.

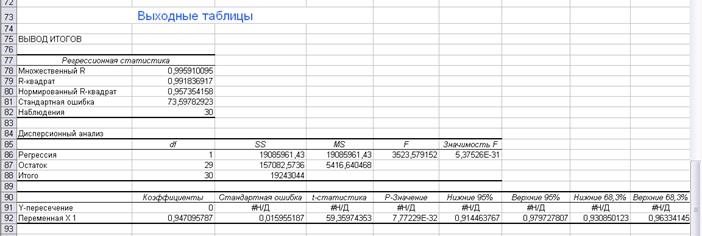
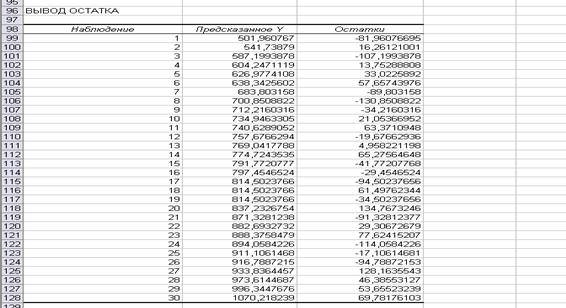
Рис.2.1

Графики для 4-х видов нелинейной зависимости между признаками

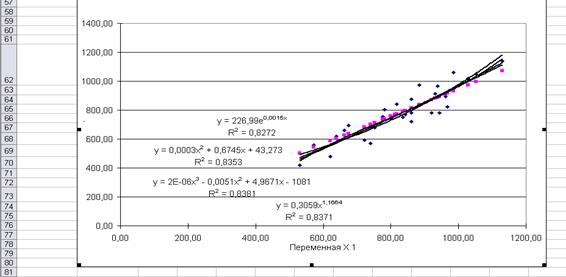
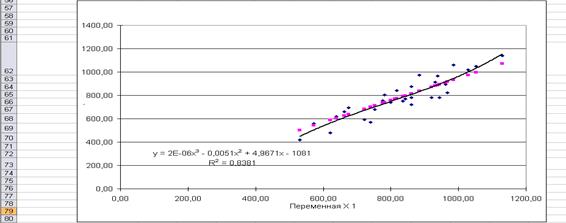
Рис.2.2

Вид искомого уравнения регрессии и его график

III. Выводы по результатам выполнения лабораторной работы.

Задача 1. Установление наличия стохастической связи между факторным признаком Х и результативным признаком Y:

а) графическим методом.

Вывод: На основе анализа диаграммы рассеяния из Лабораторной  работы №1, полученной после удаления аномальных значений, можно сделать вывод, что имеет место стохастическая связь. Предположительный вид связи: линейная прямая.

б) методом сопоставления параллельных рядов.

Вывод: Табл.2.1, полученная путем ранжирования предприятий по возрастанию значения факторного признака Х, показывает, что с увеличением значений факторного признака увеличиваются значения результативного признака, за исключением некоторых отклонений от общей тенденции, что позволяет сделать вывод о том, что связь есть  и она прямая.

Задача 2. Установление наличия корреляционной связи между признаками Х и Y методом аналитической группировки.

Вывод:  Результаты выполнения аналитической группировки предприятий по факторному признаку Среднегодовая стоимость основных производственных фондов даны в табл. 2.2 Рабочего файла, которая показывает, что, что связь есть.

Задача 3.Оценка тесноты связи признаков Х и Y:

а) на основе эмпирического корреляционного отношения.

Для анализа тесноты связи между факторным и результативным признаками, рассчитывается показатель η - эмпирическое корреляционное отношение, задаваемое формулой

           .

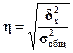Для вычисления η необходимо знать общую диспе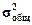рсию  и межгрупповую дисперсию 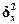 результативного признака Y - Выпуск продукции.

Результаты выполненных расчетов представляются табл. 2.4 Рабочего файла.

Вывод:  Величина η=0,90 является близкой к единице, что свидетельствует о том, что связь тесная.

б) на основе линейного коэффициента корреляции признаков.

В предположении, что связь между факторным и результативным признаками прямолинейная, для определения тесноты связи на основе линейного коэффициента корреляции r был использован инструмент Корреляция надстройки Пакет анализа.

Результатом работы инструмента Корреляции является табл. 2.5 Рабочего файла.

Вывод: Значение коэффициента корреляции r=0,91 лежит в интервале от 0,9 до 0,95, что в соответствии со шкалой Чэддока, говорит о тесной связи между факторным и результативным признаками.

Так как значение коэффициента корреляции r положительное, то связь между признаками прямая.

Посредством показателя η измеряется теснота связи любой формы, а с помощью коэффициента корреляции r – только прямолинейная, следовательно, значения η и r совпадают только при наличии прямолинейной связи. В теории статистики установлено, что если 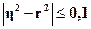, то гипотезу о прямолинейной связи можно считать подтвержденной.

Вывод: 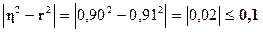,это значит, что гипотезу о прямолинейной связи можно считать подтвержденной.

Задача 4. Построение однофакторной линейной регрессионной модели связи изучаемых признаков с помощью инструмента Регрессия надстройки Пакет анализа.

Построение регрессионной модели заключается в определении аналитического выражения связи между факторным признаком X и результативным признаком Y.

Инструмент Регрессия производит расчет параметров а₀ и а₁ уравнения однофакторной линейной регрессии 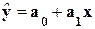 и проверку его адекватности исследуемым фактическим данным.

В результате работы инструмента Регрессия были получены результативные таблицы 2.6 – 2.9 Рабочего файла.

Вывод: Однофакторная линейная регрессионная модель связи факторного и результативного признаков имеет вид у =0,9471х-3Е-12

Доверительные интервалы коэффициентов уравнения регрессии представлены в нижеследующей таблице:

С увеличением надежности границы доверительных интервалов нижняя граница увеличивается, а верхняя, наоборот, - уменьшается.

Экономическая интерпретация коэффициента регрессии а₁: параметр а₁ > 0, значит, с возрастанием среднегодовой стоимости основных производственных фондов увеличивается выпуск продукции. Из уравнения следует, что возрастание на 1 млн. руб. среднегодовой стоимости основных производственных фондов приводит к увеличению выпуска продукции в среднем на 0,9471 млн. руб.

Коэффициент эластичности 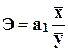=0,9471⁸³⁰/_782,6=1,00.

Экономическая интерпретация коэффициента эластичности Э: с возрастанием среднегодовой стоимости основных производственных фондов на 1 % выпуск продукции в среднем увеличивается на 1,00%

Задача 5. Нахождение наиболее адекватного уравнения регрессии с помощью средств инструмента Мастер диаграмм. Построение для этого уравнения теоретической линии регрессии.

Уравнения регрессии и их графики построены для 4-х видов нелинейной зависимости между признаками и представлены на диаграмме 2.1 Рабочего файла.

Уравнения регрессии и соответствующие им коэффициенты детерминации R2 приведены в следующей таблице:

Регрессионные модели связи[1]

Выбор наиболее адекватного уравнения регрессии определяется максимальным значением коэффициента детерминации R2: чем ближе значение R2 к единице, тем более точно регрессионная модель соответствует фактическим данным

Вывод: Максимальное значение коэффициента детерминации R2 =0,8381.

Вид искомого уравнения регрессии – У=2Е-0,6х³-0,0051х²+4,9671х-1081. Это уравнение регрессии и его график приведены на отдельной диаграмме рассеяния 2.2 Рабочего файла.

Задача 6. Значения коэффициентов детерминации кубического (R2) и линейного уравнения (η2), найденного с помощью инструмента Регрессия надстройки Пакет анализа, расходятся очень незначительно (на величину -0,18). В теории статистики установлено, что если для показателей тесноты связи имеет место неравенство 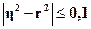, то в качестве адекватного исходным данным уравнения регрессии может быть принято линейное уравнение.

Вывод: 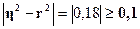, значит, гипотеза о прямолинейной связи отклоняется. Соответственно связь криволинейная.

[1] Коэффициенты уравнений необходимо указывать не в компьютерном формате, а в общепринятой десятичной форме чисел.