Министерство
образования и науки РФ
Федеральное агентство
по образованию
Государственное
образовательное учреждение
Высшего
профессионального образования
Всероссийский заочный
финансово-экономический институт
Филиал в г. Туле
ЛАБОРАТОРНАЯ РАБОТА № 2
По дисциплине «Статистика»
На тему: «Автоматизированный
корреляционно-регрессионный анализ взаимосвязи
статистических данных в среде MS Excel»
Вариант № 39
Выполнил:
студент 3 курса
Факультета: УС
Специальности: БУ А и А
вечерняя группа
Выполнила: Прокопьева А.Ю.
№ л/д 05 убд
12286
Проверил: ст. пр. Шелобаева Ирина
Сергеевна
Тула 2007
Содержание
ПОСТАНОВКА
ЗАДАЧИ………...……………………………………………3
РЕЗУЛЬТАТИВНЫЕ
ТАБЛИЦЫ И ГРАФИКИ……………………...……....6
ВЫВОДЫ…………...………………………………………………….…….…11
ПОСТАНОВКА ЗАДАЧИ
При проведении статистического наблюдения
за деятельностью предприятий корпорации получены выборочные данные по 32-м
предприятиям, выпускающим однородную продукцию (выборка 10%-ная, механическая),
о среднегодовой стоимости основных производственных фондов и о выпуске
продукции за год.
В проводимом статистическом исследовании
обследованные предприятия выступают как единицы выборочной совокупности, а
показатели Среднегодовая стоимость производственных фондов и Выпуск продукции -
как изучаемые признаки единиц.
Корреляционно-регрессионный анализ (КР-анализ)
взаимосвязи признаков является составной частью проводимого статистического
исследования двух экономических показателей статистической совокупности 32
предприятий и частично использует результаты Лабораторной работы №1.
В Лабораторной работе №2 изучается взаимосвязь между
факторным признаком Среднегодовая
стоимость основных производственных фондов (признак X) и результативным признаком Выпуск продукции (признак Y), значениями которых
являются исходные данные Лабораторной работы №1 после исключения из них
аномальных значений.
В процессе статистического исследования необходимо решить ряд
задач.
1. Установить наличие статистической связи между факторным
признаком X и
результативным признаком Y:
а) графическим методом;
б) методом сопоставления параллельных рядов.
2. Установить наличие корреляционной
связи между признаками X
и Y методом
аналитической группировки.
3. Оценить тесноту
связи признаков X и Y на основе:
а) эмпирического корреляционного отношения h;
б) линейного коэффициента корреляции r.
4. Построить
однофакторную линейную регрессионную модель связи признаков X и Y, используя инструмент Регрессия
надстройки Пакет анализа.
5. Оценить адекватность и практическую пригодность
построенной линейной регрессионной модели, указав:
а) доверительные интервалы коэффициентов 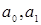 ;
;
б) степень тесноты связи признаков X и Y;
в) погрешность регрессионной модели.
6. Дать экономическую
интерпретацию:
а) коэффициента регрессии 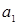 ;
;
б) коэффициента эластичности К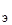 ;
;
в) остаточной величины 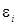 .
.
7. Найти наиболее адекватное нелинейное уравнение регрессии с
помощью средств инструмента Мастер
диаграмм. Построить для этого уравнения теоретическую кривую регрессии.
Таблица
2.1
Исходные данные
|
Номер предприятия
|
Среднегодовая стоимость основных производственных фондов,
млн.руб.
|
Выпуск продукции, млн. руб.
|
|
1
|
2204,00
|
2111,50
|
|
2
|
2593,50
|
2316,50
|
|
3
|
2675,50
|
2583,00
|
|
4
|
2819,00
|
2870,00
|
|
5
|
1835,00
|
1435,00
|
|
6
|
2962,50
|
2460,00
|
|
7
|
3044,50
|
3321,00
|
|
8
|
2286,00
|
2255,00
|
|
9
|
2798,50
|
2644,50
|
|
10
|
3229,00
|
3300,50
|
|
11
|
3536,50
|
3485,00
|
|
13
|
2696,00
|
2747,00
|
|
14
|
2962,50
|
2993,00
|
|
15
|
3393,00
|
3628,50
|
|
16
|
3885,00
|
3895,00
|
|
17
|
2901,00
|
2624,00
|
|
18
|
3208,50
|
3116,00
|
|
19
|
2552,50
|
1947,50
|
|
20
|
3249,50
|
2665,00
|
|
21
|
3618,50
|
3587,50
|
|
22
|
2491,00
|
2029,50
|
|
23
|
1978,50
|
1906,50
|
|
24
|
3311,00
|
3054,50
|
|
25
|
2962,50
|
2665,00
|
|
26
|
2757,50
|
2521,50
|
|
27
|
2142,50
|
1640,00
|
|
28
|
2880,50
|
2562,50
|
|
29
|
3331,50
|
2808,50
|
|
30
|
3167,50
|
2665,00
|
|
32
|
2327,00
|
2378,00
|
РЕЗУЛЬТАТИВНЫЕ ТАБЛИЦЫ И
ГРАФИКИ
Таблица 2.2
Исходные данные
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
5
|
1835,00
|
1435,00
|
|
23
|
1978,50
|
1906,50
|
|
27
|
2142,50
|
1640,00
|
|
1
|
2204,00
|
2111,50
|
|
8
|
2286,00
|
2255,00
|
|
32
|
2327,00
|
2378,00
|
|
22
|
2491,00
|
2029,50
|
|
19
|
2552,50
|
1947,50
|
|
2
|
2593,50
|
2316,50
|
|
3
|
2675,50
|
2583,00
|
|
13
|
2696,00
|
2747,00
|
|
26
|
2757,50
|
2521,50
|
|
9
|
2798,50
|
2644,50
|
|
4
|
2819,00
|
2870,00
|
|
28
|
2880,50
|
2562,50
|
|
17
|
2901,00
|
2624,00
|
|
6
|
2962,50
|
2460,00
|
|
14
|
2962,50
|
2993,00
|
|
25
|
2962,50
|
2665,00
|
|
7
|
3044,50
|
3321,00
|
|
30
|
3167,50
|
2665,00
|
|
18
|
3208,50
|
3116,00
|
|
10
|
3229,00
|
3300,50
|
|
20
|
3249,50
|
2665,00
|
|
24
|
3311,00
|
3054,50
|
|
29
|
3331,50
|
2808,50
|
|
15
|
3393,00
|
3628,50
|
|
11
|
3536,50
|
3485,00
|
|
21
|
3618,50
|
3587,50
|
|
16
|
3885,00
|
3895,00
|
Таблица 2.3
Зависимость выпуска
продукции от среднегодовой стоимости
основных фондов
|
Номер группы
|
Группы предприятий по стоимости
основных фондов
|
число предприятий в группе
|
Выпуск продукции
|
|
Всего
|
В среднем на одно предприятие
|
|
1
|
1835;2245
|
4
|
7093,00
|
1773,25
|
|
2
|
2245;2655
|
5
|
10926,50
|
2185,3
|
|
3
|
2655;3065
|
11
|
29991,50
|
2726,5
|
|
4
|
3065;3475
|
7
|
21238,00
|
3034
|
|
5
|
3475;3885
|
3
|
10967,50
|
3655,833333
|
|
Итого
|
|
30
|
80216,50
|
2673,883333
|
Таблица 2.4
Показатели внутригрупповой
вариации
|
Номер группы
|
Группы предприятий по стоимости
основных фондов
|
Число предприятий
|
Внутригрупповая дисперсия
|
|
1
|
1835;2245
|
4
|
66084,3125
|
|
2
|
2245;2655
|
5
|
28005,46
|
|
3
|
2655;3065
|
11
|
57001,18182
|
|
4
|
3065;3475
|
7
|
107824,1429
|
|
5
|
3475;3885
|
3
|
30351,38889
|
|
Итого
|
|
30
|
289266,4861
|
Таблица 2.5
Показатели дисперсии и
эмпирического
корреляционного отношения
|
Общая дисперсия
|
Средняя из внутригрупповых дисперсий
|
Межгрупповая дисперсия
|
Эмпирическое корреляционное отношение
|
|
338208,3281
|
62573,35722
|
275634,9708
|
0,902765617
|
Таблица 2.6
Линейный коэффициент корреляции признаков
|
|
Столбец
1
|
Столбец
2
|
|
Столбец
1
|
1
|
|
|
Столбец
2
|
0,91318826
|
1
|
Выходные таблицы
Таблица 2.7
Регрессионная статистика
|
Множественный
R
|
0,91318826
|
|
R-квадрат
|
0,833912798
|
|
Нормированный
R-квадрат
|
0,827981112
|
|
Стандартная
ошибка
|
245,3250209
|
|
Наблюдения
|
30
|
Таблица
2.8
Дисперсионный
анализ
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
Регрессия
|
1
|
8461087,596
|
8461087,596
|
140,5861384
|
1,97601E-12
|
|
Остаток
|
28
|
1685162,245
|
60184,3659
|
|
|
|
Итого
|
29
|
10146249,84
|
|
|
|
Таблица 2.9
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
Верхние
95%
|
Нижние
68,3%
|
Верхние
68,3%
|
|
Y-пересечение
|
-441,6724842
|
266,553115
|
-1,656977387
|
0,10868894
|
-987,681781
|
104,3368131
|
-713,2486017
|
-170,0963667
|
|
Переменная X 1
|
1,089355181
|
0,09187519
|
11,85690257
|
1,976E-12
|
0,90115739
|
1,277552975
|
0,995748668
|
1,182961694
|
Таблица 2.10
Вывод
остатка
|
Наблюдение
|
Предсказанное
Y
|
Остатки
|
|
1
|
1557,294273
|
-122,2942729
|
|
2
|
1713,616741
|
192,8832587
|
|
3
|
1892,270991
|
-252,270991
|
|
4
|
1959,266335
|
152,2336654
|
|
5
|
2048,593459
|
206,4065405
|
|
6
|
2093,257022
|
284,7429781
|
|
7
|
2271,911272
|
-242,4112716
|
|
8
|
2338,906615
|
-391,4066152
|
|
9
|
2383,570178
|
-67,07017761
|
|
10
|
2472,897302
|
110,1026976
|
|
11
|
2495,229084
|
251,7709163
|
|
12
|
2562,224427
|
-40,72442729
|
|
13
|
2606,88799
|
37,6120103
|
|
14
|
2629,219771
|
240,7802291
|
|
15
|
2696,215115
|
-133,7151145
|
|
16
|
2718,546896
|
-94,54689575
|
|
17
|
2785,542239
|
-325,5422394
|
|
18
|
2785,542239
|
207,4577606
|
|
19
|
2785,542239
|
-120,5422394
|
|
20
|
2874,869364
|
446,1306358
|
|
21
|
3008,860051
|
-343,8600515
|
|
22
|
3053,523614
|
62,47638611
|
|
23
|
3075,855395
|
224,6446049
|
|
24
|
3098,187176
|
-433,1871763
|
|
25
|
3165,18252
|
-110,6825199
|
|
26
|
3187,514301
|
-379,0143012
|
|
27
|
3254,509645
|
373,9903552
|
|
28
|
3410,832113
|
74,16788675
|
|
29
|
3500,159238
|
87,34076192
|
|
30
|
3790,472394
|
104,5276062
|
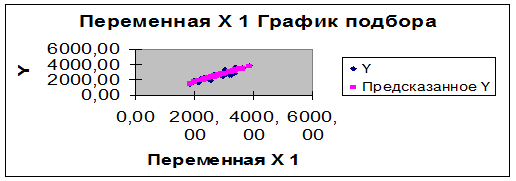
Рис. 1 График подбора
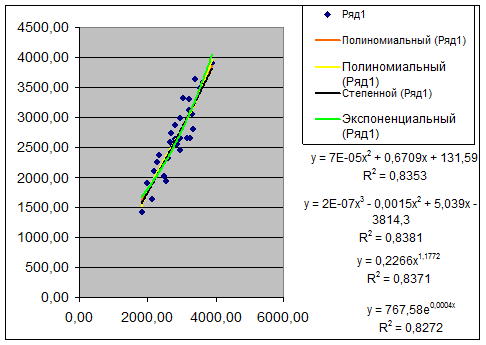
Рис. 2 Уравнения регрессии и их
графики
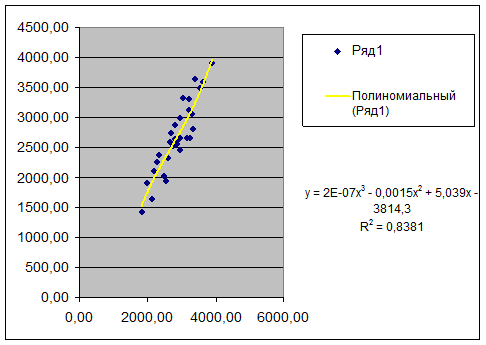
Рис. 3 Наиболее адекватное уравнение регрессии и
его график
ВЫВОДЫ ПО РЕЗУЛЬТАТАМ ВЫПОЛНЕНИЯ
ЛАБОРАТОРНОЙ
РАБОТЫ