СОДЕРЖАНИЕ
Задача
3. 2
Задача
11. 3
Задача
20. 6
Задача
26. 9
Задача
40. 12
Задача
41. 14
СПИСОК
ЛИТЕРАТУРЫ.. 17
Задача 3.
Имеются данные о себестоимости транспортной работы по автотранспортным
предприятиям объединения:
|
№ предприятия,
входящего в объединение
|
Август
|
Сентябрь
|
|
Транспортная
работа, тыс. руб.
|
Себестоимость, 10
ткм, руб.
|
Общая сумма затрат
на транспортную работу, тыс. руб.
|
Себестоимость, 10
ткм, руб.
|
|
1
2
3
|
20 800
8 500
30 000
|
0,512
0,540
0,497
|
10 784,7
4 609,6
14 526,2
|
0,521
0,536
0,481
|
Определите среднюю себестоимость 10 тонно-километров по объединению в
августе и сентябре.
Решение
Вид и форма средней выбирается исходя из экономического содержания
исчисленного показателя.
Себестоимость 10 тонно-километров определяется отношением общей сумма затрат на транспортную работу к
транспортной работе. В условии задачи имеются данные за август о себестоимости 10 тонно-километров и объеме
транспортной работы. Исходя из экономического содержания показателя для
определения средней себестоимости 10 тонно-километров, применяется средняя
арифметическая взвешенная:
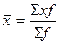 ,
(1)
,
(1)
где х – себестоимость,
f – транспортная работа.
Тогда средняя себестоимость 10 тонно-километров по объединению в августе
составит:
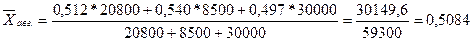 руб.
руб.
В условии задачи за сентябрь даны показатели себестоимости 10 тонно-километров и общей
суммы затрат на транспортную работу. Исходя из экономического содержания
показателя для определения средней себестоимости 10 тонно-километров, применяем
формулу средней гармонической взвешенной:
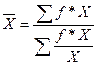 (2)
(2)
Тогда средняя себестоимость 10 тонно-километров по объединению в сентябре
составит:
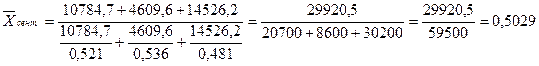 руб.
руб.
Таким образом, средняя себестоимость 10 тонно-километров по объединению в
сентябре по сравнению с августом снизилась на 0,0055 руб.
Задача 11.
Распределение основных фондов по малым предприятиям отрасли
характеризуется следующими данными:
|
Группы предприятий
по стоимости основных фондов, млн. руб.
|
Число предприятий
|
Прибыль в среднем
на предприятие, млн. руб.
|
Групповые дисперсии
|
|
12 – 27
27 – 42
42 – 57
57 – 72
|
18
40
26
12
|
1,8
3,2
4,8
6,9
|
1,14
1,09
1,69
1,84
|
Рассчитайте коэффициент детерминации и эмпирическое корреляционное
отношение. Сделайте выводы.
Решение
Строим расчетную таблицу 1.
Таблица 1
|
Группы предприятий по стоимости основных фондов,
млн. руб.
|
Число предприятий
(f)
|
Прибыль, млн. руб.
|
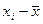
|
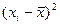
|
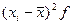
|
|
Всего
|
В среднем на предприятие
|
|
12 – 27
|
18
|
32,4
|
1,8
|
-2,03
|
4,1209
|
74,1762
|
|
27 – 42
|
40
|
128,0
|
3,2
|
-0,63
|
0,3969
|
15,876
|
|
42 – 57
|
26
|
124,8
|
4,8
|
0,97
|
0,9409
|
24,4634
|
|
57 – 72
|
12
|
82,8
|
6,9
|
3,07
|
9,4249
|
113,0988
|
|
Итого:
|
96
|
368
|
−
|
−
|
−
|
227,6144
|
Найдем общую среднюю арифметическую для всей изучаемой совокупности по
формуле:
 (3)
(3)
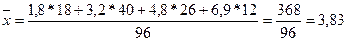 млн. руб.
млн. руб.
Найдем среднюю из групповых дисперсий по формуле:
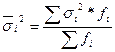 , (4)
, (4)
где fi – число
единиц в определенной группе;
σi2 – средняя по отдельной
группе.
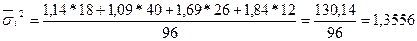 млн. руб.
млн. руб.
Найдем межгрупповую дисперсию по формуле:
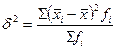 , (5)
, (5)
где 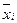 ─ средние значения результативного признака в
соответствующих группах;
─ средние значения результативного признака в
соответствующих группах;
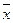 ─ общая средняя для всей совокупности;
─ общая средняя для всей совокупности;
fi ─ число наблюдений в
соответствующей группе.
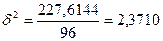 млн. руб.
млн. руб.
Зная любые две
дисперсии, можно определить третью:
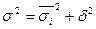 (6)
(6)
Тогда, общая
дисперсия составит:
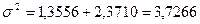 млн. руб.
млн. руб.
Коэффициент детерминации определяется по формуле
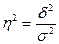 ,
(7)
,
(7)
где 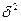 ─ межгрупповая дисперсия;
─ межгрупповая дисперсия;
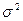 ─ общая дисперсия.
─ общая дисперсия.
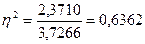 , или 63,62%
, или 63,62%
Коэффициент детерминации показывает, что прибыль на 63,62% зависит от
стоимости основных фондов и на 36,38% от других факторов.
Оценить тесноту
связи можно по величине эмпирического корреляционного отношения, используя
формулу
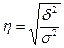 (8)
(8)
Эмпирическое
корреляционное отношение изменяется 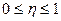 ,
,  – при отсутствии
связи,
– при отсутствии
связи, 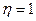 – при функциональной
зависимости.
– при функциональной
зависимости.
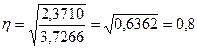
Это говорит о
том, что связь между прибылью и стоимостью основных фондов тесная.
Задача 20.
В порядке случайной 20%-й выборки обследован дневной надой молока 50
коров. Результаты обследования приведены в таблице:
|
Дневная удойность,
кг
|
10 – 14
|
14 – 18
|
18 – 22
|
Свыше 22
|
Итого
|
|
Количество коров
|
5
|
15
|
20
|
10
|
50
|
Определите: 1) средний дневной удой; 2) дисперсию, среднее квадратическое
отклонение, коэффициент вариации; 3) с вероятностью 0,997 определите пределы, в
которых находится средний дневной удой от одной коровы во всем стаде; 4) долю
коров, у которых дневной удой свыше 22 кг, гарантируя результат с вероятностью 0,954.
Решение
1) средний дневной удой определяется по формуле средней арифметической
взвешенной:
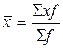 (9)
(9)
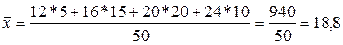 кг
кг
Строим расчетную таблицу 2.
Таблица 2
|
Дневная удойность,
кг
|
Количество коров (f)
|
Сере-дина
интерва-ла (х)
|
Накоп-ленная
частота (S)
|
xf
|
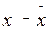
|
(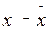 )2 )2
|
(х-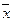 )2*f )2*f
|
|
10 – 14
|
5
|
12
|
5
|
60
|
-6,8
|
46,24
|
231,2
|
|
14 – 18
|
15
|
16
|
20
|
240
|
-2,8
|
7,84
|
117,6
|
|
18 – 22
|
20
|
20
|
40
|
400
|
1,2
|
1,44
|
28,8
|
|
Свыше 22 (26)
|
10
|
24
|
50
|
240
|
5,2
|
27,04
|
270,4
|
|
ИТОГО:
|
50
|
─
|
─
|
940
|
─
|
─
|
648
|
2) Дисперсия признака х определяется
по формуле:
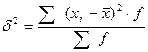 (10)
(10)
Среднее квадратическое отклонение определяется по формуле:
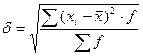 (11)
(11)
Коэффициент
вариации определяется по формуле:
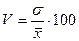 , (12)
, (12)
Коэффициент
вариации показывает степень однородности совокупности. Если V <
33% − совокупность однородна.
Определим
дисперсию признака х:
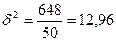 кг
кг
Определим
среднее квадратическое отклонение:
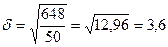 кг
кг
Определим
коэффициент вариации:
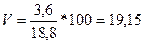
Коэффициент вариации V < 30 %, значит, совокупность
однородная и средняя – надежная.
3) Определим пределы
с вероятностью 0,997, в которых находится средний дневной удой от одной коровы
во всем стаде:
Границы
генеральной средней определяются по формуле:
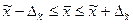 , (13)
, (13)
где 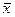 − генеральная
средняя,
− генеральная
средняя,
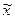 − выборочная средняя,
− выборочная средняя,
Δ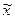 − предельная ошибка выборочной средней:
− предельная ошибка выборочной средней:
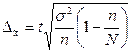 , (14)
, (14)
где 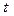 − коэффициент
доверия, зависящий от того, с какой вероятностью
− коэффициент
доверия, зависящий от того, с какой вероятностью
определяется предельная ошибка, при
вероятности 0,997
он равен 3.
n –
объем выборочной совокупности,
N – объем генеральной
совокупности.
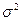 − дисперсия
признака выборочной совокупности.
− дисперсия
признака выборочной совокупности.
Предельная ошибка
выборочной средней составит:
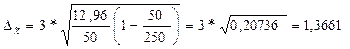
Пределы:
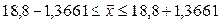
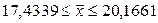
Средний дневной удой от одной коровы во всем стаде находится в пределах
17,4339≤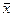 ≤20,1661 с вероятностью 0,997.
≤20,1661 с вероятностью 0,997.
4) Определим долю коров, у которых дневной удой свыше 22 кг, гарантируя
результат с вероятностью 0,954:
Границы
генеральной доли находятся по формуле:
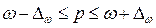 , (15)
, (15)
где р – генеральная доля,
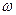 − выборочная
доля:
− выборочная
доля:
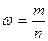 ,
(16)
,
(16)
где 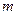 − число единиц,
обладающих данным признаком,
− число единиц,
обладающих данным признаком,
n − объем выборочной
совокупности.
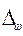 − предельная
ошибка доли:
− предельная
ошибка доли:
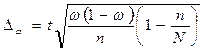 , (17)
, (17)
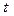 − коэффициент
доверия, зависящий от того, с какой вероятностью
− коэффициент
доверия, зависящий от того, с какой вероятностью
определяется предельная
ошибка, при вероятности 0,997
он равен 2.
Определим
выборочную долю:
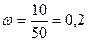
Тогда предельная ошибка доли составит:
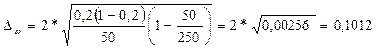
Определим границы генеральной доли:
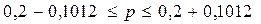
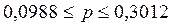
Доля коров, у которых дневной удой свыше 22 кг, находится в пределах 0,0988≤р≤0,3012 с вероятностью 0,954.
Задача 26.
Имеются следующие данные о себестоимости и объемах производства продукции
промышленного предприятия:
|
Изделие
|
Период
|
|
базисный
|
отчетный
|
|
Себестоимость
единицы продукции, тыс. руб.
|
Произведено, тыс.
шт.
|
Себестоимость
единицы продукции, тыс. руб.
|
Произведено, тыс.
шт.
|
|
А
Б
В
|
220
183
67
|
63,4
41,0
89,2
|
247
215
70
|
52,7
38,8
91,0
|
Определите: 1) индивидуальный и сводный индексы себестоимости;
2) сводный индекс физического объема продукции;
3) сводный индекс затрат на производство;
4) абсолютное изменение затрат: а) общее; б) за счет изменения цен; в) за
счет изменения физического объема
продукции.
Сделайте выводы.
Решение
Индивидуальные индексы используются для оценки динамики экономических
показателей по каждой отдельно взятой единице совокупности.
1) Индивидуальный индекс себестоимости определяется по следующей формуле:
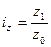 (18)
(18)
где z1 – себестоимость в отчетном периоде;
z0 – себестоимость в базисном
периоде.
Определим индивидуальный индекс себестоимости:
− изделия А: 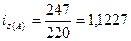 , или
112,27%
, или
112,27%
− изделия Б: 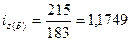 , или
117,49%
, или
117,49%
− изделия В: 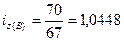 , или
104,48%
, или
104,48%
Таким образом, в отчетном периоде по сравнению с базисным себестоимость
изделия А увеличилась на 12,27%, изделия Б – на 17,49% и изделия В – на 4,48%.
Общий (сводный) индекс характеризует изменение по всей совокупности
элементов сложного явления.
Сводный индекс себестоимости определяется по следующей формуле:
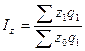 (19)
(19)
где z1, z0 – себестоимость в отчетном и базисном периоде
соответственно;
q1 – физический объем
производства в отчетном периоде.
Определим сводный индекс себестоимости:
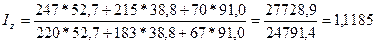 , или 111,85%
, или 111,85%
Сводный индекс себестоимости показывает, что в отчетном периоде по
сравнению с базисным по трем изделиям себестоимость увеличилась на 11,85%.
2) Сводный индекс физического объема продукции определяется по формуле:
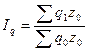 (20)
(20)
Определим сводный индекс физического объема продукции:
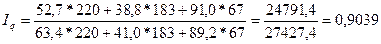 , или
90,39%
, или
90,39%
Сводный индекс физического объема продукции показывает, что в отчетном
периоде по трем изделиям было выпущено продукции на 9,6% меньше, чем в базисном.
3) Сводный индекс затрат на производство определяется по формуле:
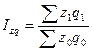 (21)
(21)
Определим сводный индекс затрат на производство:
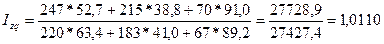 , или
101,1%
, или
101,1%
В отчетном периоде по сравнению с базисным общая сумма затрат по трем
изделиям выросла на 1,1%.
4) а) общее изменение затрат составит:
∆zq = Σz1q1 − Σz0q0
∆zq = 27728,9 – 27427,4 = 301,5 тыс. руб.
б) абсолютное изменение
затрат за счет изменения цен составит:
∆zq(z) = Σz1q1 − Σz0q1
∆zq(z) = 27728,9 – 24791,4 = 2937,5 тыс. руб.
в) абсолютное изменение
затрат за счет изменения физического объема продукции составит:
∆zq(q) = Σq1z0 − Σq0z0
∆zq(q) = 24791,4 – 27427,4 = -2636 тыс. руб.
Таким образом,
можно сделать следующий вывод: в отчетном периоде по сравнению с
базисным общая сумма затрат по трем изделиям выросла на 1,1%, или на 301,5 тыс.
руб. Под влиянием изменения цен затраты увеличились на 2937,5 тыс. руб. Однако за счет
снижения физического объема продукции затраты снизились на 2636 тыс. руб.
Задача 40.
По одному из банков имеются данные:
|
Группы владельцев
счетов
|
Сумма привлеченных
депозитов (вкладов), млн. руб.
|
Средняя депозитная
ставка, % годовых
|
|
Год
|
|
базисный
|
отчетный
|
базисный
|
отчетный
|
|
Юридические лица
|
50
|
70
|
22,0
|
20,0
|
|
Физические лица
|
40
|
80
|
18,0
|
16,0
|
Определите: 1) индивидуальные индексы суммы привлеченных депозитов,
средней депозитной ставки;
2) индексы средней депозитной ставки переменного, постоянного составов и
структурных сдвигов.
Решение
Схема расчета индивидуального индекса:
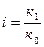 ,
(22)
,
(22)
где к1 – индексируемый показатель
в отчетном периоде;
к0 – индексируемый показатель
в базисном периоде.
1) По этой схеме
определяем индивидуальные индексы суммы привлеченных депозитов, средней
депозитной ставки:
а) индекс суммы привлеченных депозитов:
• юридических лиц: 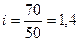 , или 140% (↑ 40%)
, или 140% (↑ 40%)
• физических лиц:
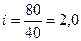 , или 200% (↑
100%)
, или 200% (↑
100%)
б) индекс средней депозитной ставки:
• юридических лиц: 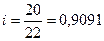 , или 90,91% (↓ 9,09%)
, или 90,91% (↓ 9,09%)
• физических лиц:
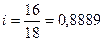 , или 88,89% (↓
11,11%)
, или 88,89% (↓
11,11%)
2) Индекс средней депозитной ставки переменного состава определяется по
формуле:
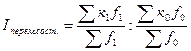 , (23)
, (23)
где к1, к0 – изучаемый показатель в отчетном и
базисном периоде соответственно.
Определим индекс средней депозитной ставки переменного состава:
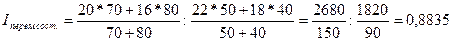 , или 88,35%
, или 88,35%
Индекс средней депозитной ставки постоянного состава определяется по
формуле:
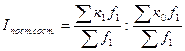 (24)
(24)
Определим индекс средней депозитной ставки постоянного состава:
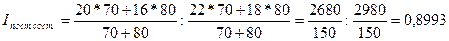 , или 89,93%
, или 89,93%
Индекс средней депозитной ставки структурных сдвигов определяется по
формуле:
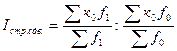 , (25)
, (25)
или
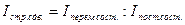 (26)
(26)
Определим индекс средней депозитной ставки структурных сдвигов:
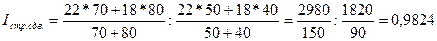 , или 98,24%
, или 98,24%
или 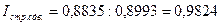 , или 98,24%
, или 98,24%
Задача 41.
По имеющимся данным о производстве хлопка-волокна рассчитать недостающие
показатели:
|
Годы
|
Млн. т
|
Цепные показатели
динамики
|
Абсолютное значение
1% прироста
|
|
Абсолютный прирост,
млн. т
|
Темп роста, %
|
Темп прироста, %
|
|
1995
|
2,8
|
─
|
─
|
─
|
─
|
|
1996
|
|
-0,2
|
|
|
|
|
1997
|
|
|
96,2
|
|
|
|
1998
|
|
|
|
4,0
|
|
|
1999
|
|
|
|
0,0
|
|
|
2000
|
|
|
|
|
|
|
2001
|
2,8
|
|
|
|
0,027
|
|
2002
|
|
|
107,1
|
|
|
Решение
Цепной абсолютный прирост определяется по формуле:
∆ц = уi – уi-1 ,
(27)
где уi
– уровень ряда динамики за изучаемый период;
уi-1 – уровень ряда динамики
за период предшествующий изучаемому.
Цепной темп роста рассчитывается по формуле:
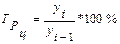 (28)
(28)
Цепной темп прироста рассчитывается по формуле:
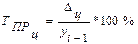 (29)
(29)
или
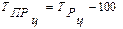 (30)
(30)
Абсолютное значение 1 % прироста рассчитывается делением
величины абсолютного прироста за период на величину темпа прироста в том же
периоде:
А% = 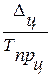 (31)
(31)
или
А% = 0,01 уi-1 (32)
Из исходных формул аналитических показателей ряда
динамики могут быть найдены отдельные составляющие (показатели).
Используя формулу цепного абсолютного прироста (27)
определим уровень 1996 года: у1996 = у1995 + ∆ц
= 2,8 + (-0,2) = 2,6 млн. т.
Используя формулу цепного темпа роста (28) определим
уровень 1997 года: у1997 = 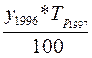 =
=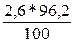 = 2,5 млн. т.
= 2,5 млн. т.
Используя формулу цепного темпа прироста (30)
определим темп роста 1998 года: Трц 1998 = Тпрц
+ 100% = 4,0+100 = 104%
Используя формулу цепного темпа роста (28) определим
уровень 1998 года: у1998 = 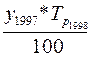 =
=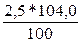 = 2,6 млн. т.
= 2,6 млн. т.
Используя формулу цепного темпа прироста (30)
определим темп роста 1999 года: Трц 1999 = Тпрц
+ 100% = 0,0+100 = 100%
Используя формулу цепного темпа роста (28) определим
уровень 1999 года: у1999 = 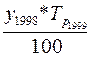 =
=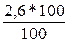 = 2,6 млн. т.
= 2,6 млн. т.
Используя формулу абсолютного значения 1 % прироста
(32) определим уровень 2000 года: у2000 =  = 2,7 млн.
т.
= 2,7 млн.
т.
Используя формулу цепного темпа роста (28) определим
уровень 2002 года: у2002 = 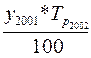 =
=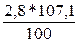 = 3,0 млн. т.
= 3,0 млн. т.
Далее по формуле (27) находим абсолютные приросты. По
формуле (28) находим недостающие значения цепных темпов роста. По формуле (30)
определяем недостающие значения цепных темпов прироста. По формуле (31)
определяем абсолютные значения 1% прироста. Результаты занесем в таблицу 3.
Таблица 3
Показатели
динамики производства хлопка-волокна
|
Годы
|
Млн. т
|
Цепные показатели
динамики
|
Абсолютное значение
1% прироста
|
|
Абсолютный прирост,
млн. т
|
Темп роста, %
|
Темп прироста, %
|
|
1995
|
2,8
|
─
|
─
|
─
|
─
|
|
1996
|
2,6
|
-0,2
|
92,9
|
-7,1
|
0,028
|
|
1997
|
2,5
|
-0,1
|
96,2
|
-3,8
|
0,026
|
|
1998
|
2,6
|
+0,1
|
104,0
|
4,0
|
0,025
|
|
1999
|
2,6
|
0
|
100,0
|
0,0
|
0
|
|
2000
|
2,7
|
+0,1
|
103,9
|
3,9
|
0,026
|
|
2001
|
2,8
|
+0,1
|
103,7
|
3,7
|
0,027
|
|
2002
|
3,0
|
+0,2
|
107,1
|
7,1
|
0,028
|
СПИСОК ЛИТЕРАТУРЫ
1. Гусаров В.М. Теория статистики. – М.: ЮНИТИ, 1998. – 448 с.
2. Елисеева И.И., Юзбашев М.М. Общая теория статистики. – М.: Финансы и
статистика, 1998. – 368 с.
3. Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. –
М.: ИНФРА-М. 2002. – 416 с.
4. Савицкая Г. В. Анализ хозяйственной деятельности предприятия. 2-е
изд., испр. и доп. – М.: ИНФРА-М. 2003. − 400 с.
5. Теория статистики / Под редакцией Шмойловой Р. А. – М.: Финансы и
статистика, 2002. – 576 с.