1. Методом Гаусса решить
систему уравнений:
2х1 – х2 + х3 + 2х4 = 14
5х1 + 3х2 – х3 + х4 = 2
4х1 – х2 + 2х3 – х4 = 0
3х1 – х2 + 3х3 + 3х4 = 12
2 –1
1 2 14 2 –1
1 2 14
А
= 5 3 –1
1 2 ~ 0 -5,5
3,5 4 33
~
4 –1 2
–1 0 0 -1
0 5 28
3 –1
3 3 12 0
-0,5 –1,5 0 9
2 –1
1 2 14 2 –1
1 2 14
~ 0 –11 7
8 66 ~ 0 –1 
6 ~
0 –1
0 5 28 0 0 -
-22
0 –1 –3
0 18 0 0 
-12
2 –1
1 2 14 2 –1
1 2 14
~ 0 –11
7 8 66
~ 0
–11 7 8
66
0 0
7 –47 242 0
0 7 –47 -242
0 0
40 8 -132 0 0
0 
-
х4 = -
х4 = -
7х3 - 47 * ( -) = -242
7х3 = -242 - 
7х3 = -
х3 = -
-11х2 + 7 * (-) + 8 * (-) = 66
-11х2 - 
- 
= 66
-11х2 = 66 + +
-11х2 = 
х2 = -
2х1 – (-) + (-) + 2 * (-) = 14
2х1 + - - 
= 14
2х1 = 14 - + +
2х1 = 
х1 = 
х1
х2 =
-
х3 -
х4 -
Проверка:
2 * + - - 2 * = 14
= 14
= 14
14=14
2. Найти предел:
= 
= 
=
= 
= 
= 
=
= 
= 
= 
=
= 
= 
= 
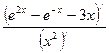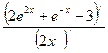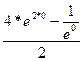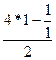3. Найти производную функцию:
y = 
= 
= 
=
= 
=
= 
=
= 
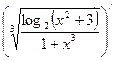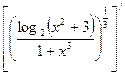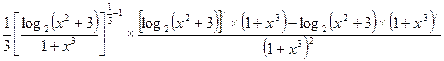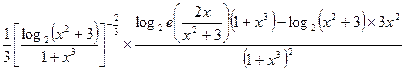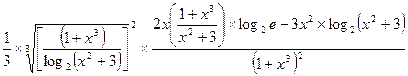
4.
Сумма двух чисел равна 28. Каковы должны быть эти
числа, чтобы произведение квадрата одного из них было наибольшим?
Пусть первое число х, тогда
второе число 28 – х. Искомое произведение обозначим у. Получаем
уравнение:
.
будет при:
= 
= 
= 
т. к. 
, а 
, получаем уравнение:
, значит
- первое число.
Второе
число:
.
5. Написать уравнение прямой,
проходящей через начало координат и точку пересечения касательных к параболе 
в точках с ординатой 
. Сделать чертеж.
1.
Найдем уравнения касательных:
1.1.
Найти 
от 
:
= 2, тогда
1.2.
Найти 
:
= 
= 
1.3.
Найти 
:
= 2
2 – 1 = 3
1.4.
Найти 
:
= 2(-1) – 1 = -3
1.5.
Подставить значения в формулу касательной 
:
1.5.1.
Для :
у – 2 = 3(х -
2)
у = 3х – 6 + 2
у = 3х – 4 –
уравнение первой касательной.
1.5.2. Для :
у – 2 = -3(х
+ 1)
у = -3х – 3 +
2
у = -3х – 1 –
уравнение второй касательной.
2. Найти
уравнение искомой прямой:
2.1. Найдем
точку пересечения двух касательных:
2.2. По
уравнению построения прямой по двум точкам найдем уравнение искомой прямой:
(0;0)
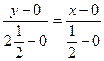
- искомая прямая
2.
Построить график:
6.
Исследовать функцию 
и схематично построить
ее график.
1.
D(f): x
2,5.
2.
При 
При 
.
3.
Функция общего вида.
4.
Асимптоты.
4.1.
Вертикальная асимптота:
х = 2,5 (т. к. функция в этой точке имеет бесконечный
разрыв).
4.2. Невертикальная асимптота:
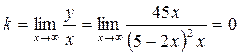
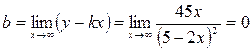
у = 0 –
невертикальная асимптота.
5. Найти :
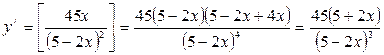
= 0 не существует при 
, т. е. при 
(точка разрыва);
при 
< -2,5 <0;
при > -2,5 >0.
В точке 
имеем минимум функции.
при 
< х < -2,5 –
функция убывает;
при
-2,5< х < 2,5 – функция
возрастает;
при 2,5
< х < 
– функция убывает.
7.
Найти 
:
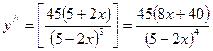
В точке 
перегиб, т. к. при 
.
при
х < -5 < 0 - выпуклость вверх;
при
х > -5 > 0 - выпуклость вниз.
8.
Построить график:
у -5 -2,5
х -1 -1,125
