Валерий Галасюк –
академик АЭН Украины, генеральный директор аудиторской фирмы “КАУПЕРВУД” (г.
Днепропетровск), член Президиума Совета Союза аудиторов Украины, член
Аудиторской Палаты Украины, председатель ревизионной комиссии Украинского
общества оценщиков, заместитель председателя Правления Ассоциации
налогоплательщиков Украины, заместитель председателя комиссии по оценке
эффективности инвестиционной деятельности Украинского общества финансовых
аналитиков, ведущий оценщик Украинского общества оценщиков
®

О
"конфликте" критериев IRR и NPV
Специалистам, занимающимся сравнением вариантов инвестиционных
затрат, хорошо известна проблема “конфликта” критериев IRR и NPV, заключающаяся
в том, что при определенных обстоятельствах критерии IRR и NPV отдают
предпочтение разным вариантам из сравниваемой пары. В этой ситуации
предлагается отказаться от критерия IRR и использовать только критерий NPV.
Автору такой подход представляется нецелесообразным.
Е.Ф.Бригхем представил наиболее детальный сравнительный анализ
методов NPV и IRR [1, с. 410 - 411]. Поэтому целесообразно более
тщательно рассмотреть изложенные им положения.
Для сравнения методов NPV и IRR Е.Ф.Бригхем использует, в частности,
понятие контура чистой текущей стоимости. Контур чистой текущей
стоимости он определяет как кривую, показывающую связь между NPV проекта и
стоимостью капитала фирмы [1, с.
402].
Далее Е.Ф.Бригхем рассматривает контуры NPV для двух проектов S и L
при различных значениях стоимости капитала (См. Рис. 1).
На рисунке 1 видно, что точки пересечения контуром NPV соответствующего
проекта горизонтальной оси 0-r, показывают внутреннюю норму доходности (IRR)
этого проекта.
На рисунке есть еще особые точки. В частности - точка пересечения
контуров чистой приведенной стоимости (rф). Эту точку пересечения
называют точкой пересечения или точкой Фишера. Она показывает
дисконтную ставку (rф), при которой контуры NPV двух проектов
пересекаются и, следовательно, при которой NPV обоих проектов одинаковы.
MNPVL
> MNPVS;
rф < IRRL
< IRRS.
NPV, $


 MNPVL Контур
NPV проекта L
MNPVL Контур
NPV проекта L
Точка
пересечения NPVrфL=NPVrфS


 MNPVS
MNPVS

 Контур NPV проекта S
Контур NPV проекта S


0 rф IRRL IRRS r,
%
Рис. 1. Контуры NPV проектов L и S
Кроме того, автор считает необходимым зафиксировать еще одну особую
группу точек. Речь идет о точках пересечения контуров NPV проектов с
вертикальной осью 0-NPV. Эти точки показывают, по мнению автора, значение NPV
проекта при нулевой стоимости капитала. По сути, они отражают максимально
возможное (предельное) значение NPV для рассматриваемого проекта при понижении
стоимости капитала до нуля. В дальнейшем автор будет называть эти точки
предельными (marginal) NPV и обозначать, соответственно, MNPV.
Е.Ф.Бригхем утверждает, что
конфликт между критериями NPV и IRR возникает лишь в случае сравнения проектов
(вариантов), исключающих один другого. В случае, “если два проекта
независимы, то критерии NPV и IRR приводят к одинаковым решениям” [1, с.
404].
Р.Брейли и С.Майерс также
фиксируют возникновение конфликта между критериями NPV и IRR в случае выбора
одного из взаимоисключающих проектов [2, с. 87].
Вместе с тем на эту проблему можно посмотреть с иной точки зрения.
Она заключается в том, что когда необходимо ранжировать множество проектов
(вариантов) инвестиционных затрат, для того, чтобы отобрать из него
подмножество вариантов, которое в дальнейшем будет принято к реализации, то,
во-первых, варианты, вошедшие в подмножество вариантов, отобранных для
реализации, не являются взаимоисключающими один по отношению к другому, а,
во-вторых, даже те варианты, которые будут отобраны в подмножество, подлежащее
реализации, могут быть ранжированы в различном порядке на основе критериев NPV
и IRR. То есть, иными словами, решение проблемы ранжирования множества
вариантов вовсе не требует того, чтобы варианты взаимно исключали один другого.
Тем не менее, ранжирование множества вариантов, осуществленное на основе
критериев NPV и IRR может приводить к противоречивым результатам.
Е.Ф.Бригхем рассматривает один вариант возможного соотношения контуров
NPV двух проектов (См. Рис.1). Рассмотрим остальные пять возможных вариантов
соотношения контуров NPV (См. Рис. 2 - 6).
Если проанализировать все шесть вариантов возможных соотношений
контуров NPV двух сравниваемых проектов L и S, учитывая то, что рассматриваться
должны варианты только с положительными значениями NPV (NPV > 0) и
значениями стоимости капитала r ³ 0, то
можно зафиксировать следующее.
Подмножества вариантов, представленные на рисунках 2, 4, 5, 6, при
выполнении указанных условий, не содержат конфликта при ранжировании вариантов
на основе критериев NPV и IRR. То есть, выводы относительно предпочтительности
одного из сравниваемых вариантов, сделанные на основе критериев NPV и IRR,
совпадают.
Подмножество вариантов, представленное на рисунке 3, содержит
конфликт критериев NPV и IRR лишь при значении rф = 0. В этом случае
с точки зрения критерия NPV варианты L и S равноценны, а с точки зрения
критерия IRR – вариант L предпочтительнее варианта S, так как IRRL
> IRRS.
MNPV
L > MNPV
S;

 = ;
= ;
 NPV, $
rф – отсутствует.
NPV, $
rф – отсутствует.
 MNPVL
MNPVL
 MNPVS
MNPVS
 0
r, %
0
r, %
IRRS IRRL
Рис.
2. Контуры NPV проектов L и S
MNPVL = MNPVS;
 IRRL > IRRS;
IRRL > IRRS;
NPV, $
rф = 0.

 MNPVL=MNPVS
MNPVL=MNPVS
 0
r, %
0
r, %
IRRS IRRL
Рис.
3. Контуры NPV проектов L и S
MNPVL > MNPVS;
IRRL = IRRS = rф.
 NPV, $
NPV, $
 MNPVL
MNPVL
 MNPVS
MNPVS
r, %

 0
0
rф =
IRRS = IRRL
Рис.
4. Контуры NPV проектов L и S
MNPVL > MNPVS;
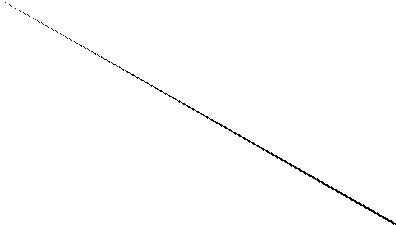
 rф > IRRL > IRRS.
rф > IRRL > IRRS.
 NPV, $
NPV, $
MNPVL
 MNPVS
MNPVS
 0
0
IRRS IRRL
r, %
NPVL =
NPVS
Рис.
5. Контуры NPV проектов L и S
MNPVL > MNPVS;
 IRRL > IRRS;
IRRL > IRRS;
NPV, $ rф – отсутствует.
 MNPVL
MNPVL
 MNPVS
MNPVS
 0
0
IRRS IRRL r, %
Рис.
6. Контуры NPV проектов L и S
Рассмотрим более внимательно подмножество вариантов, представленное
на рисунке 1.
Очевидно, что с точки зрения критерия IRR вариант S предпочтительнее
варианта L. Но с точки зрения критерия
NPV:
а) в точке Фишера (rф) – варианты равноценны;
б) в интервале 0 £ r < rф – вариант L
предпочтительнее варианта S, то есть, возникает конфликт критериев;
в) в интервале r > rф
– вариант S предпочтительнее варианта L, то есть, конфликт критериев
отсутствует.
На первый взгляд рассуждения по поводу конфликта критериев NPV и
IRR, предпринятые автором вслед за Е.Ф.Бригхемом и целым рядом других
исследователей представляются относительно обоснованными. Но это лишь на первый
взгляд.
Рассмотрим вначале один “недостаток” метода IRR. Е.Ф.Бригхем пишет:
“Важный вопрос возникает при разрешении конфликтов между взаимоисключающими
проектами: чему равна стоимость ранее и позже возникших денежных потоков?
Стоимость денежных потоков зависит от возможной ставки, под которую мы сможем
реинвестировать различные денежные потоки, получаемые в ближайшие годы. Применение метода NPV допускает, что ставка
реинвестирования денежных потоков равняется стоимости капитала, в то время как
применение метода IRR допускает, что фирма имеет возможность реинвестирования
по ставке, которая равна IRR. Эти допущения свойственны математической
стороне дисконтирования. Таким образом, метод NPV дисконтирует денежные потоки
на стоимость капитала, а метод IRR - на IRR проекта.
Какое наилучшее решение для инвестирования денежных потоков проекта
при ставке, которая равна стоимости капитала или IRR? Мы приходим к выводу, что
наилучшее допущение в отношении ставки
реинвестирования – стоимость капитала, которая свойственна методу NPV. Это,
в свою очередь, приводит нас к отдаче предпочтения методу NPV, по крайней мере,
для фирм, которые хотят и могут получить капитал, стоимость которого
приблизительно равна текущей стоимости капитала.
Нам следует напомнить, что пока проекты независимые, методы NPV и
IRR приводят к одинаковым решениям. Однако, когда
мы оцениваем взаимоисключающие проекты, особенно те, которые различаются
размером и (или) во времени, следует использовать метод NPV” [1, с. 405].
До сих пор автор вслед за Е.Ф.Бригхемом и другими авторами
анализировал “конфликт” между критериями NPV и IRR. Однако, по
мнению автора, “конфликт” между показателями NPV и IRR является формой
проявления конфликта “доходность-риски”.
Для того, чтобы обосновать этот тезис необходимо еще раз внимательно
посмотреть на формулу, из которой определяется величина IRR, а также вспомнить
определение IRR [2, с. 83]. Анализ указанного, а также
содержание формулы для определения величины NPV [2, с.
30] позволяют сделать
вывод о том, что IRR является максимально возможной ставкой реинвестирования по
рассматриваемому проекту, обеспечивающей неотрицательное значение его NPV.
Очевидно, что при нулевой ставке реинвестирования величина NPV проекта будет
иметь наибольшее значение, а при ставке реинвестирования, равной IRR, NPV
проекта будет иметь значение, равное нулю. Это хорошо видно на рисунке 1.
Таким образом, величина IRR конкретного проекта является
пределом, который показывает, что данный проект может осуществляться по
множеству ставок реинвестирования, однако для того, чтобы проект имел
положительное значение NPV, наибольшая из них должна быть меньше величины IRR. То есть, величина rt в
формуле для определения величины NPV [2, с.
30] сверху ограничена неравенством:
rt
< IRR. (1)
Поскольку это так, то становится очевидной некорректность
ранжирования вариантов проектов по предельной максимально допустимой величине
ставки реинвестирования (IRR). Ведь реально применяемые ставки реинвестирования
не должны быть равны IRR, они должны быть меньше величины IRR, для того, чтобы
обеспечить выполнение условия NPV > 0.
Причем, чем меньше величина ставки реинвестирования rt, тем больше
значение NPV.
Поскольку величина IRR не применима для процедуры
ранжирования вариантов инвестиционных затрат, с точки зрения их инвестиционной
привлекательности, то и о конфликте критериев IRR и NPV в контексте, зафиксированном
Е.Ф.Бригхемом, Р.Брейли и С.Майерсом, говорить не приходится.
На первый взгляд может показаться, что последние положения автора
входят в противоречие с положениями, изложенными им же ранее, в которых
указывалось, что между двумя исходными типами критериев экономической
эффективности затрат существуют объективные противоречия [4, 5, 6]. На самом деле эти
противоречия действительно будут существовать, если воспринимать величину IRR,
как конкретную ставку реинвестирования, а не как предельное значение множества
возможных ставок реинвестирования (rt) рассматриваемого проекта,
обеспечивающих неотрицательное значение его NPV.
Следует отметить, что рекомендации в отношении применения критерия
IRR для ранжирования вариантов инвестиций не являются редкостью. Так, И.А.Бланк
отмечает: “Характеризуя показатель “внутренняя норма доходности”, следует
отметить, что он наиболее применим для сравнительной оценки” [7, с. 173]. Эксперт и консультант с
мировым именем в области финансового менеджмента Эрик А. Хелферт пишет:
“Внутренняя норма окупаемости намного более пригодна для ранжирования
инвестиций, чем простые методы, которые рассматривались нами ранее”1 [8, с.
324].
“Отметим, что внутренней нормой окупаемости, как и всеми другими
критериями, следует пользоваться осторожно. Ввиду того, что данный критерий
дает аналитику единственную ("истинную") норму окупаемости по каждому
проекту, доход от инвестиций позволяет их ранжировать по одному параметру. Из нашей предыдущей дискуссии о чистой
текущей стоимости помним, что там использовалась принятая в компании ставка
доходности, отражающая ее ожидания от инвестиций.
Напротив,
подход через внутреннюю норму
окупаемости предполагает уникальный уровень доходности для каждого проекта. При
сравнении внутренних норм окупаемости различных проектов предполагают, что
денежные потоки, получаемые в течение жизненного цикла проекта, могут быть
реинвестированы по своим уникальным нормам.
Мы
знаем, тем не менее, что ставки доходности компании являются выражением
долгосрочной способности данной компании получать прибыль, хотя бы
приблизительно. Таким образом, менеджеры, применяя 15 или 20 % как
инвестиционный стандарт, должны понимать, что денежные потоки от проекта с
внутренней нормой окупаемости 30 % не удастся реинвестировать по этой высокой
ставке. Если только общие ставки доходности компании не являются совершенно
нереальными, то можно ожидать реинвестирования полученных от инвестиции фондов
по более низким средним для компании ставкам.
Но эта
частная дилемма не делает непригодным критерий внутренней нормы окупаемости,
поскольку любой проект определенно достигнет своей вычисленной доходности при
учете всех условий в течение своего жизненного цикла. Поэтому будет правильно
ранжировать проекты по их относительному доходу” [8, с.
325].
Дж. Фридман и Ник. Ордуэй отмечают: “Во многих случаях IRR служит
полезным средством ранжирования альтернативных инвестиций” [9, с.
325].
Название показателя IRR – внутренняя норма доходности, вводит в
заблуждение тех, кто использует его, подталкивая к тому, чтобы воспринимать
величину IRR как конкретную ставку реинвестирования. Даже такие известные
ученые с мировым именем, как Е.Ф.Бригхем, Дж. Фридман и Ник. Ордуэй,
воспринимая величину IRR как конкретную ставку реинвестирования, предприняли
попытку избежать этого “недостатка”, предложив модифицированные методы IRR.
Дж. Фридман и Ник. Ордуэй, раскрывая экономическое содержание
критерия IRR, пишут: “IRR показывает ставку дохода на капитал, которую приносят
инвестиции. Это сложная ставка дохода на доллар инвестиций за период времени” [9, с. 332 - 333].
Вместе с тем существуют и
другие точки зрения. Так, В.В.Ковалев пишет: “Смысл расчета этого коэффициента
при анализе эффективности планируемых инвестиций заключается в следующем: IRR
показывает максимально допустимый относительный уровень расходов, которые могут
быть ассоциированы с данным проектом. Например, если проект полностью
финансируется за счет ссуды коммерческого банка, то значение IRR показывает
верхнюю границу допустимого уровня банковской процентной ставки, превышение
которого делает проект убыточным” [10, с.
202]. Далее В.В.Ковалев,
вводя понятие “цены” авансированного капитала (СС) и характеризуя его как
минимум возврата на вложенный в деятельность предприятия капитал, делает следующие
выводы:
“Если:
IRR > СС, то проект следует
принять;
IRR < СС, то проект следует
отвергнуть;
IRR = СС, то проект ни прибыльный, ни убыточный” [10, с. 202].
Авторы первого Российского учебника по оценке бизнеса, в частности,
отмечают: “Оценка инвестиционных проектов с помощью ВСДП1
основана на определении максимальной величины ставки дисконтирования, при
которой проекты останутся безубыточными” [11, с.
272].
“ВСПД можно интерпретировать как некий “запас прочности” проекта,
отражающий его устойчивость в условиях возможного повышения риска.
Неблагоприятные изменения, затрагивающие как экономику в целом, так и конкретный
вид бизнеса, требуют адекватного уровня ставки дисконтирования. Проекты с
максимальной величиной ВСДП более привлекательны, так как потенциально способны
выдерживать большие нагрузки на инвестиционный капитал, связанные с возможным
повышением его стоимости” [11, с.
275].
Профессор П.Орлов (г. Харьков) отмечает, что величина внутренней
нормы доходности (или “внутренней рентабельности проекта”) “… соответствует
максимальной годовой банковской ставке, под которую можно взять кредит на
реализацию инвестиционного проекта и рассчитаться с ним, не получив ни прибыли,
ни убытка. Чем большим окажется превышение iв над действительной
величиной годового банковского процента, тем выше эффективность проекта” [12, с. 32].
Подводя итоги изложенному можно заключить, что субъект экономических
отношений, стремясь к максимизации разницы между положительными и отрицательными условными денежными потоками
выбирает, в первую очередь, варианты с наибольшим значением NPV. Величина NPV,
кроме прочего, зависит и от конкретной ставки реинвестирования rt.
Значения этой ставки ограничены значением IRR (См. формулу 1). Кроме того,
ставка реинвестирования ограничена снизу значением “цены авансированного
капитала” (ra):
ra £ rt
(2)
Очевидно, что для случаев, когда контуры NPV проектов являются
постепенно убывающими функциями ставки реинвестирования и пересекаются в
области положительных значений NPV и rt, и если
IRR £ ra, (3)
то это
будет означать невозможность осуществления данного варианта инвестиционных
затрат с положительными значениями NPV.
В случае, если ra < IRR, то чем больше будет
интервал между значениями ra и
IRR, тем меньше будет риск неполучения положительных значений NPV при
реализации конкретного проекта. При прочих равных условиях больший интервал
между значениями ra и IRR
будет обеспечиваться при больших значениях IRR. Таким образом, для случаев, когда контуры NPV проектов являются
постепенно убывающими функциями ставки реинвестирования и пересекаются в
области положительных значений NPV и rt, варианты, у которых IRR
больше, в случае выполнения условия IRR > ra, являются менее рискованными с точки зрения возможности неполучения
положительных значений NPV. То
есть, они имеют большую “устойчивость” или “больший запас прочности” при
реализации конкретного проекта с положительным NPV. Вместе с тем, поскольку
значение ra в
значительной степени определяется внешними условиями на рынке
капиталов и поэтому для двух сравниваемых вариантов величину ra можно
условно считать приблизительно одинаковой, то вариант с большим значением IRR
будет менее рискованным, но при этом он будет обеспечивать меньшие значения NPV
в случае, если конкретная ставка реинвестирования будет находиться в
диапазоне: (См. Рис. 7).
ra £ rt < rф. (4)
Анализируя рисунок 7 нетрудно заметить, что
проект S, названный автором “осторожный”, обеспечивает положительное значение
NPV в большем интервале возможных значений ставок реинвестирования. В этом,
собственно говоря, и состоит его “осторожность”. Проект L, названный автором
“авантюрный”, обеспечивает положительное значение NPV в меньшем интервале
возможных значений ставок реинвестирования, однако он имеет возможность
обеспечения большего значения NPV при условии ra £ rt < rф. В случае, если
окажется, что rф < ra £ rt, то
“осторожный” вариант будет обеспечивать и большие значения NPV.
NPV, $ Проект L – “авантюрный”;
Проект L – “авантюрный”;
Проект S – “осторожный”.
MNPVL




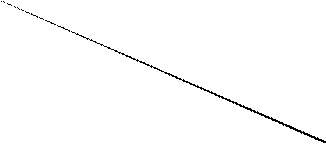 MNPVS
Контур NPV проекта L
MNPVS
Контур NPV проекта L
Контур NPV проекта S
 0 ra rф IRRL IRRS r, %
0 ra rф IRRL IRRS r, %
Рис.
7. “Осторожный” и “авантюрный” проекты
Поэтому, если NPV проектов является постепенно
убывающей функцией то, в случае, если сравниваемые варианты будут
характеризоваться условиями:
MNPVL > MNPVS;
rф < IRRL
< IRRS,
и при условии, rф < ra, необходимо выбирать
вариант с большим значением IRR, то есть вариант S. Если окажется, что rф > ra, то необходимо более
тщательно производить анализ устойчивости условий финансового рынка на прогнозируемый
период. В случае прогнозируемого повышения стоимости авансированного капитала
на рынке необходимо выяснить насколько велика вероятность того, что стоимость
авансированного капитала (ra) превысит значение rф.
Если вероятность этого велика, то необходимо выбирать “осторожный” вариант с
большим значением IRR. Если же вероятность того, что стоимость авансированного
капитала (ra) превысит значение rф
невелика, то необходимо исследовать вероятность попадания возможного значения
ставки реинвестирования в один из интервалов, либо в интервал
ra £ rt < rф,
либо в интервал
rф
£ rt < IRRL,
либо в интервал
IRRL
£ rt < IRRS,
и с учетом результатов
исследования принимать соответствующее решение.
Таким
образом, как представляется, автору удалось показать, что конфликт между
показателями NPV и IRR в контексте, зафиксированном Е.Ф.Бригхемом, Р.Брейли и
С.Майерсом, является формой проявления конфликта “доходность-риски”. И поэтому
предложения использовать при сравнении вариантов инвестиционных затрат лишь
критерий NPV не являются следствием объективной необходимости.
Литература:
1.
Брігхем Євхен Основи фінансового
менеджменту: Пер. з англ. - Київ:
Молодь, 1997, - 1000 с.
2.
Ричард Брейли, Стюарт Майерс. Принципы
корпоративных финансов: Пер. с англ. - М.: ЗАО "Олимп-Бизнес", 1997,
- 1120 с.
3. Галасюк В.В. Сферы применения расчетов общей и
сравнительной экономической эффективности//Тезисы доклада Всесоюзной отраслевой
научно-практической конференции: “Проблемы совершенствования управления трудом
на промышленном предприятии”. – Гомель: Б.И., 1988.
4. Галасюк
В.В. Вопрос о единстве принципов оценки экономической эффективности затрат и
перспективы его разрешения. – Днепропетровск, 1986, – Деп. в ИНИОН АН СССР
15.10.86, - № 27119.
5. Галасюк
В.В. Вопрос о сферах применения расчетов общей и сравнительной экономической
эффективности. – Днепропетровск, 1987, - 17 с. – Деп. в ИНИОН АН СССР 31.03.87,
- № 28929.
6. Галасюк
В.В. К вопросу о сферах применения принципов абсолютной эффективности и
интегрального эффекта при оценке экономической эффективности хозяйственных
мероприятий. - Днепропетровск, 1986, - 14 с. – Деп. в ИНИОН АН СССР 15.10.86, №
27120.
7.
Бланк И.А. Инвестиционный менеджмент, - Киев, ММ
"ИТЕМ" ЛТД, "Юнайтед
Лондон Трейд Лимитед", 1995, - 448 с.
8.
Хелферт Э. Техника финансового анализа/Пер. с
англ. Под ред. Белых Л.П. - М. "Аудит", ЮНИТИ, 1996, - 663 с.
9.
Фридман Дж., Ордуэй Ник. Анализ и оценка
приносящей доход недвижимости/Пер. с англ.- М.: "Дело ЛТД", 1995, -
480 с.
10.
Ковалев В.В. Финансовый анализ: Управление
капиталом. Выбор инвестиций. Анализ отчетности - М.: "Финансы и
статистика", 1995, - 432 с.
11.
Оценка бизнеса: Учебник/Под ред. А.Г. Грязновой,
М.А. Федотовой, - М.- "Финансы и статистика", 1998, - 512 с.
12.
Орлов П. Оценка эффективности инвестиций/
“Экономика Украины”, № 1, - 1997, С. 30-36.
Координаты авторов:
Консалтинговая группа «КАУПЕРВУД»,
Украина, г. Днепропетровск, ул. Гоголя 15-а,
тел./факсы: (38 0562) 47-16-36, 47-83-98, (38 056) 370-19-76
www: www.galasyuk.com,
www.cowperwood.dnepr.net,
www.ccf.com.ua,
e-mail: vit@galasyuk.com, vit@inkon.dnepr.net, av@galasyuk.com, maria@inkon.dnepr.net
1 В данном
случае речь идет о внутренней норме доходности. Использование понятия
“окупаемости” вместо понятия “доходности” явилось, очевидно, результатом
перевода.
1 ВСДП –
внутренняя норма доходности проекта (IRR).